Modular Architectures for Interpretable Credit Scoring for Heterogeneous Borrower Data
Abstract
1. Introduction
Related Work
2. Methodology
2.1. Data Preprocessing
2.1.1. Dataset Description
- Delinquency (D_*): Indicators of late or missed payments, e.g., number of overdue installments or historical delinquency counts.
- spending (S_*): Measures of transaction volume and frequency, capturing overall consumption behavior and trends.
- payments (P_*): Features related to payment amounts, payment-to-balance ratios, and payment regularity.
- balances (B_*): Measures of credit utilization, outstanding balances, and revolving amounts.
- risks (R_*): Aggregated risk-related indicators, e.g., derived scores or ratios reflecting risk exposure.
2.1.2. Handling Missing Values
2.1.3. Data Splitting
2.2. Optimal Binning Using Weight of Evidence (WoE)
- Proportion of Non-Defaults in Bin i
- Proportion of Defaults in Bin i
2.3. Single-Factor Analysis
- Weight of Evidence (WoE) and Information Value (IV): To quantify the strength and predictive power of the relationship between the attribute and the target variable.
- Gini value: Calculated on the training set and test set to measure the model’s discriminatory power and stability across different subsets.
- p-value: To assess the statistical significance of the feature in predicting the target.
- Gini Train minus Gini Test: To evaluate the model’s overfitting by comparing performance across datasets.
- Population Stability Index (PSI): To measure the stability of the attribute’s distribution over time in different subsets.
- Event Rate, Event Count, and Non-Event Count: To obtain the descriptive statistics ratios of the target variable class within each bin.
Feature Selection Criteria
- Duplicate Features: Features that are identical or highly redundant are deleted to avoid multicollinearity and reduce dimensionality.
- Single-Bin or Binning Errors: Features that result in only one bin or encounter errors during the optimal binning process are removed as they lack sufficient variability to contribute meaningfully to the model.
- Predictive capabilities: Features with Gini value < 0.1 are excluded as they do not have a strong connection to the target.
- Statistical Significance: Features with a p-value greater than 0.05 are excluded as they are not statistically significant in predicting the target variable.
- Population Stability Index (PSI): Features with a PSI greater than 0.2 between the training set and the full dataset are removed as this indicates instability in the feature’s distribution.
- PSI: Similarly, features with a PSI greater than 0.2 between the training set and the subsets of the full dataset (default = 1 and default = 0) are excluded to ensure consistency across different target classes.
- Predictive Power: Features with a Gini coefficient on the training set (Gini_train) less than 0.1 are discarded as they demonstrate insufficient discriminatory power.
- Overfitting Check: Features where the difference between the Gini coefficient on the training set and the test set (Gini_train minus Gini_test) exceeds 0.1 are removed to mitigate overfitting and ensure generalization.
- Correlation Level (Optional): Features with a correlation level greater than 0.7 with other features may be excluded to reduce multicollinearity. However, this criterion is optional and can be waived if the customer deems the feature to be of high importance.
- Duplicate Features: Ensure that redundant information does not skew the model.
- Single-Bin or Binning Errors: Ensure that features have meaningful variability for analysis.
- Statistical Significance (p-value): Ensures that only features with a significant relationship with the target are taken.
- Population Stability Index (PSI): Ensures that the feature’s distribution remains stable across datasets and target classes, which is critical for model reliability.
- Predictive Power (Gini_train): Ensures that features contribute meaningfully to the model’s predictive performance.
- Overfitting Check (Gini_train minus Gini_test): Ensures that the model generalizes well to unseen data.
- Correlation Level: Reduces multicollinearity, which can destabilize the model, but remains flexible based on customer requirements.
2.4. Multi-Factor Analysis
- Model Features: The set of features included in the model.
- Coefficients: The estimated coefficients of the logistic regression model, indicating the strength and direction of the relationship between each feature and the target variable.
- p-value: The statistical significance of each feature’s coefficient. A low p-value indicates that the model results are significantly related to the target.
- Max p-value: The highest p-value among all features in the model, ensuring that no insignificant features are included.
- Max Correlation Max Corr: The highest pairwise correlation between features in the model. A high correlation can indicate multicollinearity, which may destabilize the model.
- Max Variance Inflation Factor (Max VIF): Measures the severity of multicollinearity. A VIF is considered acceptable as higher values indicate redundancy among features.
- Gini Train and Gini Test: The Gini coefficient measures the model’s discriminatory power on the training and test datasets. A higher Gini indicates better predictive performance.
- Converged or Not: Indicates whether the logistic regression model successfully converged during training.
- Gini Train minus Gini Test: The difference in Gini coefficients between the training and test sets. A small difference indicates good generalization and minimal overfitting.
- Abs (Gini Train minus Gini Test) : Ensures that the model generalizes well to unseen data and is not overfitted.
- Max VIF : Ensures that multicollinearity is within acceptable limits, maintaining model stability.
- Max Corr : Prevents high correlation between features, which can distort coefficient estimates.
- Max p-value : Ensures that all features in the model are statistically significant.
2.5. Architecture Design
- Modular Logistic Regression (MLR, Stacking)Separate logistic regression models are trained for each module (set of attributes), and their predictions are combined using a meta-model.Steps:
- (a)
- Train an LR model for each module using its shortlisted features.
- (b)
- Combine predictions using techniques like weighted averaging or stacking.
- Advantages: Interpretable, handles heterogeneous attribute sets naturally.
- Disadvantages:
- (a)
- May lose global interactions between modules.
- (b)
- Combining predictions can introduce complexity.
- Hierarchical Logistic RegressionA cascading approach where predictions from one module are used as inputs to another module’s model.Steps:
- (a)
- Train an LR model for the first module.
- (b)
- Use its predictions as an additional feature for the next module’s model.
- (c)
- Repeat for all modules.
- Advantages: Captures dependencies between modules while maintaining interpretability.
- Disadvantages:
- (a)
- The order of modules can affect performance.
- (b)
- May introduce bias if earlier modules are noisy.
- Ensemble of Logistic Regression ModelsMultiple LR models are trained on different subsets of features or modules, and their predictions are aggregated using techniques like majority voting or averaging.Steps:
- (a)
- Train multiple LR models on different combinations of modules.
- (b)
- Aggregate predictions using voting or averaging.
- Advantages: Reduces variance, improves robustness, and handles missing attributes effectively.
- Disadvantages:
- (a)
- Increases computational complexity.
- (b)
- May reduce interpretability due to the ensemble nature.
- Dynamic Model SelectionA dynamic architecture where the model used for prediction depends on the available attributes for a given input.Steps:
- (a)
- Train separate LR models for each possible combination of modules.
- (b)
- For a given input, select the model trained on the available attributes.
- Advantages: Highly flexible and adaptable to heterogeneous attribute sets.
- Disadvantages:
- (a)
- Requires training and maintaining multiple models.
- (b)
- Model selection logic can become complex.
- Feature Union with Logistic Regression (Single LR)Combine features from all modules into a single feature set and train a single LR model.Missing attributes are handled using imputation or masking.Steps:
- (a)
- Create a unified feature set by combining attributes from all modules.
- (b)
- Handle missing attributes using imputation or by treating them as a separate category.
- (c)
- Train a single LR model on the unified feature set.
- Advantages: Simple and captures interactions between modules.
- Disadvantages:
- (a)
- Imputation can introduce noise or bias.
- (b)
- Interpretability may be lost if the feature set becomes too large.
2.6. Evaluation and Comparison
- Gini Coefficient Dynamics:
- Training and Test Set:
- -
- Lower Gini Test (confidence interval lower bound).
- -
- Gini Test (mean value).
- -
- Upper Gini Test (confidence interval upper bound).
- -
- Gini Test Dynamics:
- *
- Test Max Gini: Maximum Gini value across time intervals.
- *
- Test Min Gini: Minimum Gini value across time intervals.
- *
- Test Interquartile Range (IQR): The range between the 25th and 75th percentiles of Gini values.
- *
- Test Max Gini Step: The maximum change in Gini between consecutive time intervals.
- Generalization Metric:
- Relation (Gini Test - Gini Train)/Gini Train: Measures the relative difference between test and training performance, indicating overfitting or generalization ability.
- Module Frequency:
- The frequency of each module’s models within the architecture provides insights into the contribution of individual modules to the overall performance.
Ranking and Scoring
- Rank Calculation:
- For each metric (e.g., Gini Train, Gini Test, Precision, and Recall), models were ranked, where a lower value indicates a higher rank (better performance).
- Ranks were assigned for all metrics, including Gini dynamics, generalization metrics, and module frequency.
- Weighted Scoring:
- Each rank was multiplied by a predefined weight, reflecting the importance of the metric in the final decision.
- The total score for each model was calculated as the weighted sum of its ranks across all metrics.
- Final Selection:
- The model with the highest total score was selected as the best-performing architecture.
- The ranking and scoring process ensures a balanced evaluation of predictive performance, interpretability, and robustness.
3. Experimental Results
3.1. Stacking Model Architecture, MLR
3.2. Hierarchical Multi-Model Logistic Regression Approach
3.3. Ensemble Architectures with Mean and Median Aggregation
3.4. Multi-Model Logistic Regression Approach
3.5. Feature Union LR Model
4. Discussion
4.1. Comparative Analysis of Model Architectures
4.1.1. Single Logistic Regression
4.1.2. Multi-Model Logistic Regression with Feature Subsets
4.1.3. Hierarchical Logistic Regression
4.1.4. Ensemble with Median Aggregation
4.1.5. Ensemble with Mean Aggregation
4.1.6. Stacking
4.2. Comparative Summary Table
- Predictive Power: Stacking and hierarchical models generally achieve the highest predictive performance as they can learn complex interactions and optimal combinations of base models. Ensemble methods (mean and median) are robust but may underperform if base models are not equally informative. Single logistic regression provides a reliable baseline but may lack the flexibility to capture complex patterns.
- Robustness: Ensemble with median is the most robust to outliers and noise. Ensemble with mean is less robust but smoother. Stacking and hierarchical models are less robust if base models are highly correlated or if the meta-model overfits.
- Computational Efficiency: Single logistic regression and ensemble methods are computationally efficient. Stacking and hierarchical models are more demanding due to additional training steps.
- Interpretability: Single logistic regression and ensemble methods are highly interpretable. Stacking and hierarchical models are less interpretable due to their complexity.
- Flexibility: Stacking and hierarchical models are the most flexible, capable of capturing complex patterns and interactions. Ensemble methods are less flexible but more robust and easier to implement.
| Architecture | Predictive Power | Robustness | Computational Cost | Interpretability | Flexibility | Key Limitation(s) |
|---|---|---|---|---|---|---|
| Single Logistic Regression | Moderate | Low | Low | High | Low | Overfitting, linearity assumption |
| Multi-Model Logistic Regression | Moderate | Moderate | Moderate | High | Moderate | No inter-module interaction |
| Hierarchical/ Multi-Stage Logistic | High | Moderate | High | Moderate | High | Error propagation, complexity |
| Ensemble with Median | Moderate | High | Low | High | Low | Loss of probabilistic info |
| Ensemble with Mean | Moderate | Moderate | Low | High | Low | Sensitive to outliers |
| Stacking (Meta-Learning) | High | High | High | High | High | Overfitting, complexity |
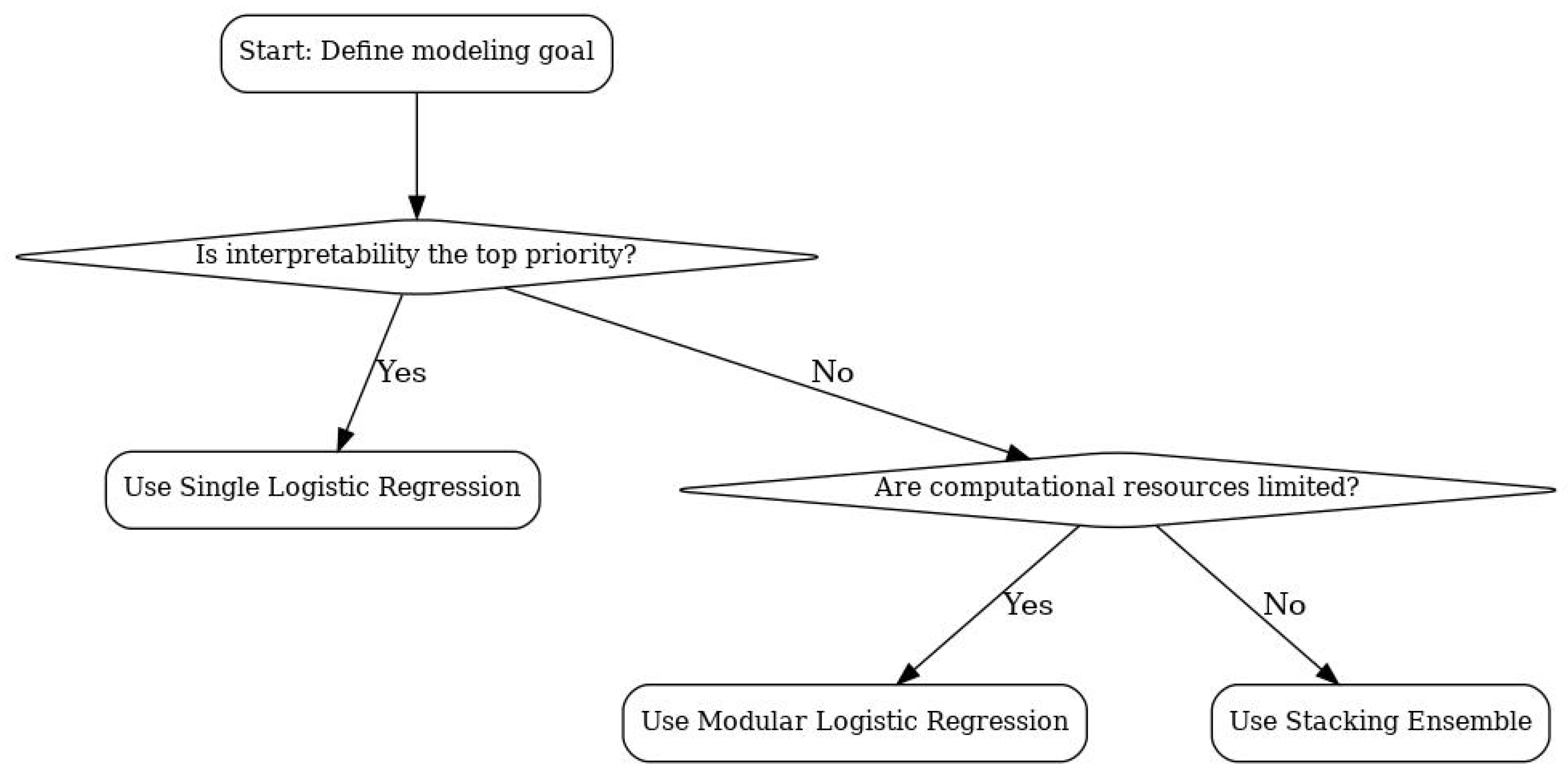
5. Practical Recommendations
- Single logistic regression is appropriate when interpretability is the primary requirement, computational resources are limited, or when models must be deployed in highly constrained environments.
- Modular logistic regression offers a middle ground, allowing interpretability at the module level (delinquency, balances, etc.) while delivering stronger performance and stability than a single model.
- Stacking ensembles should be chosen when the marginal gain in accuracy and robustness is critical, such as in large-scale credit portfolios where even small improvements in prediction translate to substantial financial impact. However, they come with higher computational and maintenance costs.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Computational Considerations and Meta-Model Interpretability
Appendix A.1. Computational Cost and Scalability
Appendix A.2. Meta-Model Interpretability
| Domain Module | Meta-Model Coefficient | Interpretation |
|---|---|---|
| Risk Indicators | +1.22 | Strong positive contribution to default risk |
| Payment History | +0.87 | Moderate positive impact |
| Balance Utilization | –0.34 | Slightly lowers predicted default probability |
| Delinquency Profile | +0.65 | Positive association with risk |
| Spending Behavior | –0.15 | Weak stabilizing effect |
References
- Appiahene, P., Missah, Y. M., & Najim, U. (2020). Predicting bank operational efficiency using machine learning algorithm: Comparative study of decision tree, random forest, and neural networks. Advances in Fuzzy Systems, 2020(1), 8581202. [Google Scholar] [CrossRef]
- Ben-Gal, I. (2008). Bayesian networks. In Encyclopedia of statistics in quality and reliability. Wiley. [Google Scholar] [CrossRef]
- Cutler, A., Cutler, D. R., & Stevens, J. R. (2012). Random forests. In Ensemble machine learning: Methods and applications (pp. 157–175). Springer. [Google Scholar] [CrossRef]
- Fidrmuc, J., & Lind, R. (2020). Macroeconomic impact of Basel III: Evidence from a meta-analysis. Journal of Banking & Finance, 112, 105359. [Google Scholar] [CrossRef]
- Hastie, T. J. (2017). Generalized additive models. In Statistical Models in S (pp. 249–307). Routledge. [Google Scholar] [CrossRef]
- Kaggle. (2022). American express-default prediction. Available online: https://www.kaggle.com/competitions/amex-default-prediction/data (accessed on 3 June 2025).
- Lee, G. H. (2008). Rule-based and case-based reasoning approach for internal audit of bank. Knowledge-Based Systems, 21(2), 140–147. [Google Scholar] [CrossRef]
- Mahadevan, A., & Mathioudakis, M. (2023). Cost-effective retraining of machine learning models. arXiv, arXiv:2310.04216. [Google Scholar] [CrossRef]
- Martens, D., Baesens, B., Van Gestel, T., & Vanthienen, J. (2007). Comprehensible credit scoring models using rule extraction from support vector machines. European Journal of Operational Research, 183(3), 1466–1476. [Google Scholar] [CrossRef]
- Olaniran, O. R., Sikiru, A. O., Allohibi, J., Alharbi, A. A., & Alharbi, N. M. (2025). Hybrid random feature selection and recurrent neural network for diabetes prediction. Mathematics, 13(4), 628. [Google Scholar] [CrossRef]
- Scheres, S. H. (2010). Classification of structural heterogeneity by maximum-likelihood methods. In Methods in enzymology (Vol. 482, pp. 295–320). Elsevier. [Google Scholar]
- Tarka, P. (2018). An overview of structural equation modeling: Its beginnings, historical development, usefulness and controversies in the social sciences. Quality & Quantity, 52, 313–354. [Google Scholar]
- U.S. Department of Housing and Urban Development. (2009). Fair lending: A guide for housing counselors. Available online: https://www.hud.gov/sites/documents/fair_lending_guide.pdf (accessed on 3 June 2025).
- Van Ginkel, J. R., Linting, M., Rippe, R. C., & Van Der Voort, A. (2020). Rebutting existing misconceptions about multiple imputation as a method for handling missing data. Journal of Personality Assessment, 102(3), 297–308. [Google Scholar] [CrossRef] [PubMed]
- West, D. (2000). Neural network credit scoring models. Computers & Operations Research, 27(11–12), 1131–1152. [Google Scholar] [CrossRef]

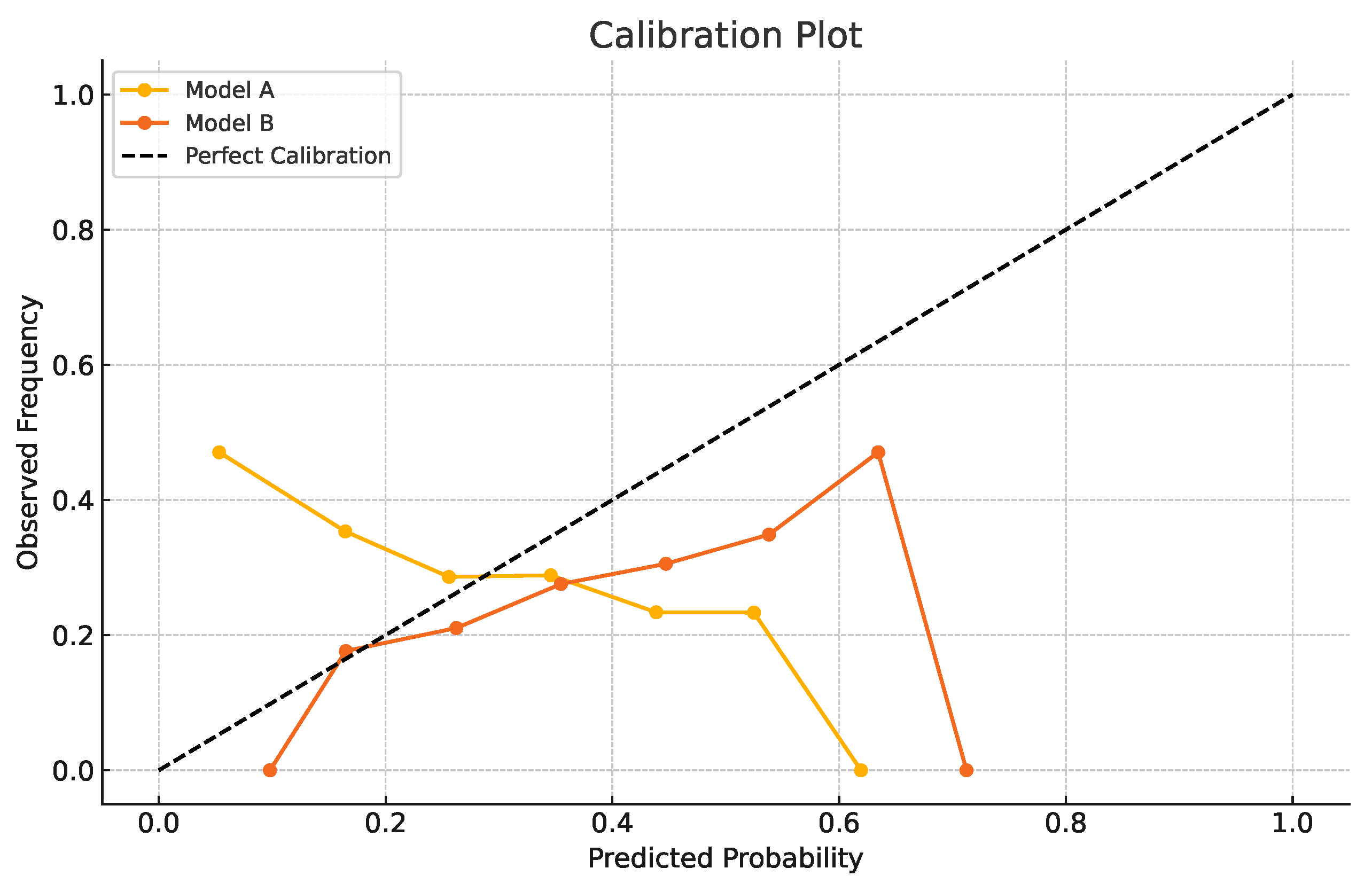
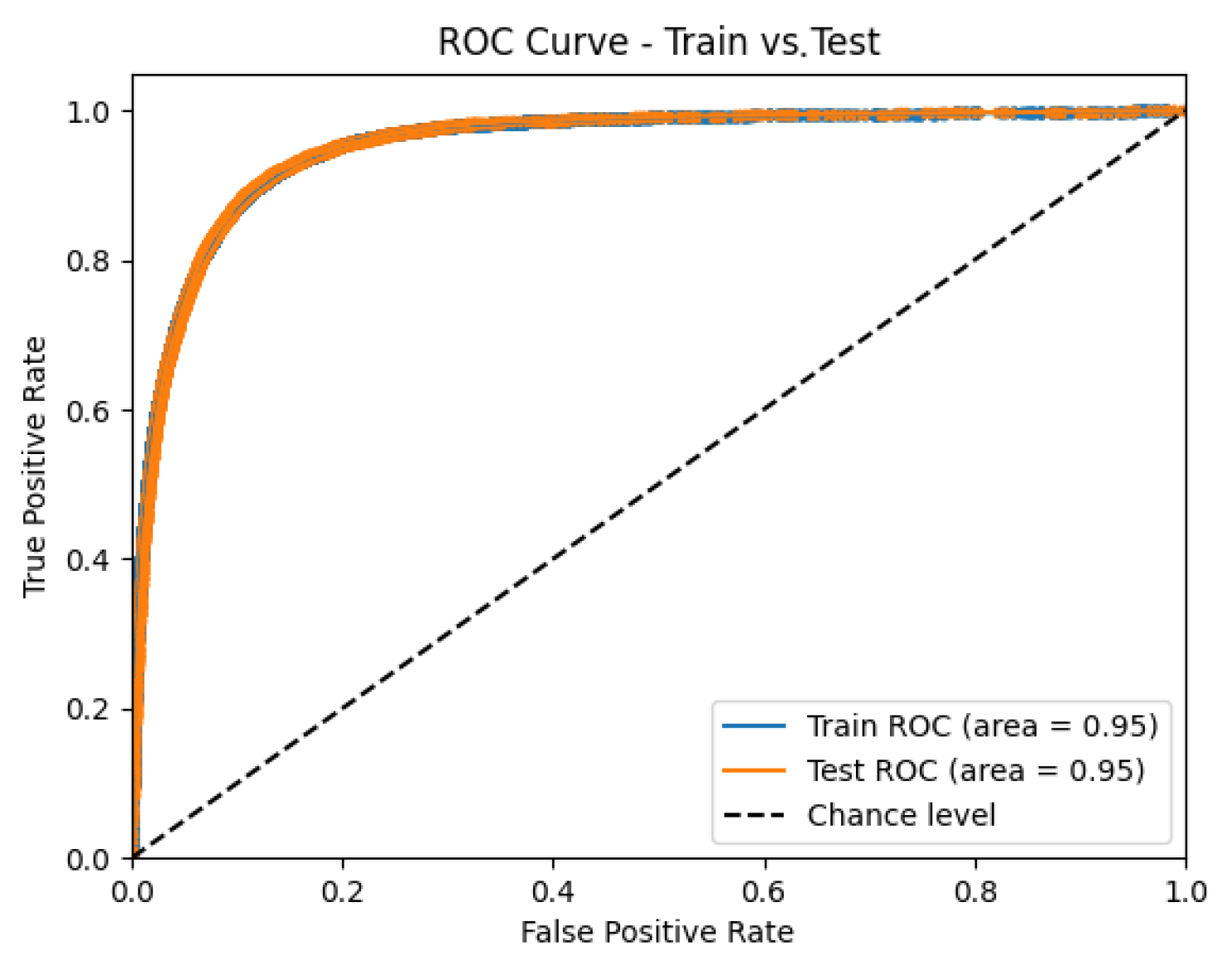



| Metric | [’risks_6’, ’delinq_7’, ’pays_3’, ’spends_8’, ’balances_7’] | [’risks_7’, ’delinq_5’, ’pays_3’, ’spends_2’, ’balances_6’] | [’risks_2’, ’delinq_4’, ’pays_3’, ’spends_3’, ’balances_1’] |
|---|---|---|---|
| Gini (Train) | 0.9054 | 0.9068 | 0.9058 |
| Gini (Test) | 0.9054 | 0.9068 | 0.9058 |
| ROC AUC (Test) | 0.9527 | 0.9534 | 0.9529 |
| Log Loss (Test) | 0.2414 | 0.2394 | 0.2406 |
| Brier Score (Test) | 0.0721 | 0.0715 | 0.0718 |
| KS Statistic (Test) | 0.7814 | 0.7835 | 0.7806 |
| Relative Gini Gap (%) | 0.0003 | 0.0024 | 0.0028 |
| Metric | [’delinquency’, ’spends’, ’risks’] | [’spends’, ’delinquency’, ’balances’] | [’delinquency’, ’spends’, ’balances’] |
|---|---|---|---|
| Gini (Train) | 0.812 | 0.810 | 0.809 |
| Gini (Test) | 0.807 | 0.805 | 0.804 |
| Log Loss (Test) | 0.292 | 0.293 | 0.294 |
| Brier Score (Test) | 0.094 | 0.095 | 0.095 |
| KS Statistic (Test) | 0.714 | 0.712 | 0.711 |
| (Test–Train)/Train (%) | 0.62 | 0.62 | 0.62 |
| Metric | Median | Mean |
|---|---|---|
| Gini (Test) | 0.81 | 0.80 |
| Log Loss (Test) | 0.29 | 0.30 |
| Brier Score (Test) | 0.09 | 0.10 |
| KS Statistic (Test) | 0.72 | 0.70 |
| Relative Gini Gap (%) | 0.62 | 0.75 |
| Category | Item | Description |
|---|---|---|
| Strength | Robustness | Median aggregation resists outliers, while mean aggregation smooths predictions by reflecting the overall consensus. |
| Simplicity | Both approaches are easy to implement and computationally efficient, especially when compared to stacking architectures. | |
| Generalization | Demonstrate strong generalization with small train–test performance gaps (less than 1%), even when diverse features are involved. | |
| Limitation | Loss of Probabilistic Information | Thresholding discards nuanced probability estimates, which can limit sensitivity to subtle predictive signals. |
| Equal Weighting Assumption | All base models are treated equally, potentially ignoring performance differences among them. | |
| Threshold Sensitivity | Model performance is highly dependent on the chosen threshold, requiring additional tuning effort. | |
| Interpretability Trade-Off | Aggregating predictions hides individual model contributions, making it difficult to interpret feature-level importance. |
| Metric | Model 1 | Model 2 | Model 3 | Model 4 | Model 5 |
|---|---|---|---|---|---|
| Gini (Train) | 0.8190 | 0.8191 | 0.8189 | 0.8189 | 0.8189 |
| Gini (Test) | 0.8167 | 0.8167 | 0.8165 | 0.8165 | 0.8165 |
| Converged | True | True | True | True | True |
| 0.29 | 0.29 | 0.29 | 0.29 | 0.29 |
| Metric | Training Set | Test Set |
|---|---|---|
| Gini | 0.857 | 0.856 |
| ROC AUC | 0.928 | 0.928 |
| PR AUC | 0.796 | 0.796 |
| Log Loss | 0.291 | 0.292 |
| Brier Score | 0.092 | 0.092 |
| KS Statistic | 0.723 | 0.724 |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Interpretability | Coefficients directly indicate feature importance, aiding in model transparency. |
| Simplicity | The method is easy to implement and computationally efficient. | |
| Baseline | Serves as a benchmark for evaluating more complex models. | |
| Vulnerability to Multicollinearity | Correlated features can distort coefficient estimates and reduce model reliability. | |
| Cons | Overfitting Risk | Including many features, especially with limited data, increases the chance of overfitting. |
| Linearity Assumption | Assumes a linear relationship between log-odds and features, which may not reflect real-world complexities. |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Feature Selection | Identifies which subsets of features or modules are most predictive of the target. |
| Reduced Overfitting | Smaller, more relevant feature sets help prevent overfitting, especially with limited data. | |
| Insightful | Offers interpretability by highlighting the contribution of each module or feature group to model performance. | |
| Cons | Combinatorial Explosion | The number of possible feature combinations increases exponentially, making exhaustive evaluation impractical. |
| No Inter-Module Interaction | Treats feature modules independently, ignoring potential interactions or dependencies between them. | |
| Computational Overhead | Requires training and validating many models, which is computationally expensive and time-consuming. |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Hierarchical Learning | Captures layered relationships and dependencies between feature modules or learning stages. |
| Improved Performance | Can increase predictive accuracy by refining outputs across multiple levels of modeling. | |
| Flexibility | Capable of adapting to complex and structured data representations, offering modeling versatility. | |
| Cons | Computational Complexity | Requires sequential training, which increases runtime and resource consumption. |
| Sensitivity to Order | Model performance can vary depending on the order in which modules are processed. | |
| Error Propagation | Mistakes in earlier stages of learning can propagate through the system and degrade final outcomes. | |
| Interpretability Challenges | The layered nature of the model complicates interpretation and reduces transparency. |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Robustness | Median aggregation is resistant to outliers and noisy model predictions. |
| Simplicity | The method is straightforward to implement and computationally efficient. | |
| Stability | Produces reliable ensemble results even when some individual models perform poorly. | |
| Cons | Loss of Probabilistic Information | Discards detailed prediction probabilities in favor of a thresholded decision. |
| Equal Weighting | Treats all contributing models equally, potentially ignoring differences in model quality. | |
| Limited Flexibility | Cannot dynamically adjust to changing model relevance or performance. |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Smooth Aggregation | The mean combines outputs to reflect the overall consensus among models. |
| Simplicity | The method is easy to implement and understand. | |
| Flexibility | Can reveal subtle patterns in predictions, provided that outliers are not dominant. | |
| Cons | Sensitivity to Outliers | Extreme model predictions can skew the mean and distort the ensemble outcome. |
| Equal Weighting | Assumes all models contribute equally, which may not reflect their true predictive value. | |
| Loss of Probabilistic Information | Aggregated outputs are often thresholded, losing richer probability estimates. |
| Pros/Cons | Item | Description |
|---|---|---|
| Pros | Optimal Combination | Learns the best linear combination of base model predictions to maximize performance. |
| Flexibility | Able to capture complex dependencies and relationships between base models. | |
| High Performance | Often delivers superior predictive accuracy compared to individual or simpler ensemble methods. | |
| Cons | Computational Complexity | Involves training multiple base models and an additional meta-model, increasing processing time and resources. |
| Risk of Overfitting | Without careful cross-validation, stacking can overfit or leak information across folds. | |
| Interpretability | While the meta-model may be interpretable, the overall system becomes more opaque than individual models. | |
| Data Requirements | Requires ample data to effectively train and validate both base and meta-level models. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sunagatullin, A.A.; Bahrami, M.R. Modular Architectures for Interpretable Credit Scoring for Heterogeneous Borrower Data. J. Risk Financial Manag. 2025, 18, 615. https://doi.org/10.3390/jrfm18110615
Sunagatullin AA, Bahrami MR. Modular Architectures for Interpretable Credit Scoring for Heterogeneous Borrower Data. Journal of Risk and Financial Management. 2025; 18(11):615. https://doi.org/10.3390/jrfm18110615
Chicago/Turabian StyleSunagatullin, Ayaz A., and Mohammad Reza Bahrami. 2025. "Modular Architectures for Interpretable Credit Scoring for Heterogeneous Borrower Data" Journal of Risk and Financial Management 18, no. 11: 615. https://doi.org/10.3390/jrfm18110615
APA StyleSunagatullin, A. A., & Bahrami, M. R. (2025). Modular Architectures for Interpretable Credit Scoring for Heterogeneous Borrower Data. Journal of Risk and Financial Management, 18(11), 615. https://doi.org/10.3390/jrfm18110615






