Abstract
We develop a binary tree pricing model with underlying asset price dynamics following Itô–McKean skew Brownian motion. Our work was motivated by the Corns–Satchell, continuous-time, option pricing model. However, the Corns–Satchell market model is incomplete, while our discrete-time market model is defined in the natural world, extended to the risk-neutral world under the no-arbitrage condition where derivatives are priced under uniquely determined risk-neutral probabilities, and is complete. The skewness introduced in the natural world is preserved in the risk-neutral world. Furthermore, we show that the model preserves skewness under the continuous-time limit. We provide empirical applications of our model to the valuation of European put and call options on exchange-traded funds tracking the S&P Global 1200 index.
JEL Classification:
G12; G13; C32; C61
1. Introduction
In the academic literature on dynamic asset pricing theory, discrete-time option pricing models traditionally play a subordinate role to their continuous-time counterparts. This is due to the highly developed theory of semimartingales, Lévy processes, and the fundamental theorem of asset pricing. (Table 1 provides a comprehensive list of literature citations for these topics). However, as discussed in Section 2 the standard option pricing approach, based upon passing to the continuous-time limit, results in the loss of the significant information provided by the stylized-fact capturing parameters that can be embedded in discrete-time market models. This loss in the continuum limit produces a dislocation between the information on spot prices that is available to spot traders versus option traders1 (see, e.g., Ross 2015; Audrino et al. 2014). We further note that pure continuum models that attempt to incorporate stylized facts such as the heavy tails and skewness properties of realistic price processes through the use of semimartingale (e.g., Lévy) processes, generally lead to incomplete market models. The choice of the equivalent risk-neutral martingale becomes ad hoc, and any unique relationship between the probability measures driving price processes in the natural and risk-neutral worlds is lost.

Table 1.
Cited literature for selected topics addressed in the text.
This motivates us to propose a primary role for discrete-time option pricing models and proposes that any continuous-time option pricing model should only be considered as a benchmark model for a more precise discrete pricing model that preserves valuable market characteristics2 (see, e.g., Marroni and Perdomo 2014, p. 123; Joshi 2008, p. 197; Rebonato 2004, p. 169). Based on this proposal, we identify the following three fundamental research issues:
- The first is to develop pricing trees that capture valuable market characteristics (stylized facts) in the natural world and retain these in the risk-neutral world.
- The second is to ensure that the model is market-complete.
- In recognition of the role that continuous-time benchmark models play, the third would be to determine whether the pricing tree retains these characteristics in the limit that the transaction time interval .3 (While this step is of interest, it is no longer of fundamental importance if the primacy of discrete-time pricing models is recognized.)
These research issues have been the focus of a series of papers (Hu et al. 2020a, 2020b, 2022). In Hu et al. (2022), the authors developed a market-complete option valuation based on a generalization of the Jarrow–Rudd (JR) pricing model (Jarrow and Rudd 1983). In contrast to other similar works, all of which placed the binomial tree model directly in the risk-neutral world (and were, therefore, unable to state what the determining tree is in the natural world), Hu et al. begin in the natural world and, from that, derived the unique (and hence market-complete) risk-neutral tree. Their generalization involved the use of skew Brownian motion (SBM) (Itô and McKean 1996) with the incorporation of a parameter (in addition to the mean and standard deviation ) to capture skewness and kurtosis effects in the real-world pricing tree. These three parameters, and , carry over into the risk-neutral world. Using the Cherny et al. (2003) invariance principle, Hu et al. (2022) showed that for a fixed, but relatively small, time increment, , the pricing tree behavior was geometric SBM (GSBM). However, in the limit , the model converged to geometric BM (GBM), losing the skewness and kurtosis properties of the discrete model.
Corns and Satchell (2007) developed a continuous-time pricing model combining a standard BM and an SBM to capture skewness in option pricing models. Unfortunately, their model, as well as the model by Zhu and He (2017), which provides corrections to the Corns–Satchell (CS) model, is market incomplete since the equivalent martingale obtained in their work only provides hedging against the risks associated with the standard BM. These two papers serve as motivation for the present article on discrete-option pricing.
In this paper, beginning in the natural world with a skewed, heavy-tailed, binomial process, we derive the unique, market-complete, risk-neutral pricing tree that preserves these features. We then show that the continuum-time model preserves these properties. The “cost” to achieve this is the addition of a second Brownian motion to the discrete pricing process. As a result, we show that the risk-free rate in the risk-neutral process cannot be arbitrary but is a rate determined by an appropriate combination of the means and variances governing the returns of the underlying risky assets.
More specifically, we introduce a binary pricing tree, which we refer to as the Itô–McKean skew pricing tree (IMSPT), that can model either standard BM or Itô–McKean SBM. As we ensure hedging against the risks associated with standard BM or SBM in the model, the IMSPT will lead to a complete market model for option pricing. In the IMSPT, the mean return of the underlying stock is preserved in the resulting option pricing model.4 The role of the uptick probability governing the drift of a standard binomial price process is replaced by a skewness parameter in the IMSPT. The skewness parameter remains present in both the natural and the risk-neutral world. In contrast to the model of Hu et al. (2022), we show continuous time convergence of the IMSPT model to skew GBM, preserving the skew properties of the pricing tree.
The paper is organized as follows: We begin by reviewing (Section 2) the standard four-step approach used in binomial option pricing, which results in the loss of critical natural world information. In Section 3, we introduce the Itô–McKean SBM, first as represented by Itô and McKean (1996) and then in a representation developed by Corns and Satchell (2007). The conditional probability density governing the Corns–Satchell SBM is a skewed normal distribution. The properties of this distribution are presented in Appendix A.
Section 3.1 and Section 3.2 are devoted to developing preparatory material for option pricing on the IMSPT. Specifically, in Section 3.1, we develop the continuous-time stochastic dynamics of Itô–McKean SBM. In Section 3.2, we develop the risk-free rate for a Black–Scholes–Merton market model where the uncertainty in the price of the risky asset is driven by the Itô–McKean GSBM. The risk-free rate contains a delta-function jump term, which must be eliminated through the addition of a second risky asset in the market model.
In Section 4, we develop the discrete option pricing model on the IMSPT for this market model. In order to remove the aforementioned delta-function term from option (derivative) prices, it is necessary to add a third risky asset to the market model. In Section 4.1, we show that the resultant model is still market-complete. Section 4.2 then develops option pricing for a European call option. Appendix B supplies the formulas for the determinants that appear in the option pricing.
The IMSPT option pricing formulas developed in Section 4.2 require knowledge of the values of the drift, diffusion, and skewness parameters of an asset’s return process. In practice, these parameter values are obtained by fitting a SBM model to a historical return series. However, fitting a return series by either the Corns–Satchell or the original Itô–McKean versions of SBM is impractical. In Section 5, we consider a practical method for generating an Itô–McKean SBM as the limiting process of a skew random walk. Relevant properties of the skew random walk are discussed in Appendix C, and a procedure for fitting this skew random walk to the historical return series is developed in Appendix D. This procedure is demonstrated in Section 5.1 by fitting the parameters of the return process of an exchange-traded fund (ETF) (the SPDR S&P 500 ETF Trust). In Section 5.2, using the IMPST option pricing formulas of Section 4.2, we compute European call and put option prices having, as underlying, three ETFs that track component indices of the S&P Global 1200 Index. Concluding remarks follow in Section 6.
2. The Standard Approach−Loss of Information in Passing to the Continuous Time Limit
Consider the standard four-step approach to binomial option pricing (see, e.g., Cox and Rubinstein 1985, chp. 5; Korn and Korn 2000, sct. 4.3; Bingham and Kiesel 2004, chp. 4; Hull 2012, chps. 12, 20; or Marroni and Perdomo 2014, chp. 4).
Step 1. A binomial pricing tree is introduced in the natural world . The price dynamics of the underlying risky asset (stock) follow a binomial tree conditionally on as follows:
The no-arbitrage condition requires that where is the instantaneous riskless rate. The log-return is assumed to have a mean and a variance to guarantee that the binomial pricing tree has a weak Gaussian limit (needed in Step 2). With the pair () is then uniquely determined as and (Rendleman and Bartter 1979).
Step 2. From Step 1 and the Donsker–Prokhorov invariance principle (DPIP), the price process generated by the tree in Step 1 converges weakly in the Skorokhod -space to a GBM, where is a BM on . (For references on DPIP, see Table 1). With this step, the information about the probability for stock-price uptick that was available in the discrete-time process has been lost.
Step 3. Using the no-arbitrage condition on the continuum model from Step 2, the dynamics of the underlying asset in the risk-neutral world is where is a BM on . Now a hedger, who takes the short position in an option contract and who, in any real trading situation, will trade only in discrete-time instances, has lost information about both the instantaneous mean return and .
In the Black–Scholes–Merton formulation, the loss of in the risk-neutral world means that the instantaneous drift can be arbitrarily large while the option price remains unchanged, a condition known as the option pricing discontinuity puzzle. This puzzle has been addressed by Hu et al. (2020a). The loss of is due to the absurd assumption that the trader can trade continuously in time. We note that including trading costs in continuous-time option pricing cannot retrieve the information lost about and (Leland 1985; Hodges and Neuberger 1989; Boyle and Vorst 1992; Davis et al. 1993; Edirisinghe et al. 1993; Broadie et al. 1998; Kabanov and Stricker 2001; Zakamouline 2009; Lai and Lim 2009; Guasoni et al. 2012). No real trader can trade in continuous time, with or without transaction costs.
Step 4. Step 3 and the DPIP imply that the risk-neutral, continuous asset price dynamics can be approximated by a risk-neutral binomial tree with price dynamics given by the following:
where
for any arbitrarily chosen value of Setting
results in the CRR (Cox et al. 1979) pricing tree.5 Setting results in the JR pricing tree6 (Jarrow and Rudd 1983, chps. V, VI; and Hull 2012, p. 442). By the DPIP, the value of controls the rate of convergence of the binomial option price to its continuous-time limit (Kim et al. 2016)7 and is otherwise irrelevant in that limit. Thus, returning to the realistic case when the hedger trades in discrete-time instances, the pricing tree (which the hedger is supposed to use to hedge his short position in the option contract) is now without the parameters and . This, in turn, leads to a dislocation in the information available to spot traders and to option traders with regard to spot prices.
Remark 1.
There is no need to pass to continuous-time price dynamics when using binomial option pricing.(For various generalizations of the binomial pricing market model in Step 1, see Hu et al. 2020a, 2020b, 2022. See also Jarrow et al. 20098). Proceeding immediately from Step 1 to the discrete risk-neutral pricing tree, the no-arbitrage argument implies that the risk-neutral probability, ), over the interval is uniquely determined by , where is the market price of risk (Kim et al. 2016, 2019). The risk-neutral asset pricing tree is as follows:
The four parameters , and are preserved in the risk-neutral price process. (The trader’s information about and could be gathered from stock market data or be based on the trader’s active trading alpha-strategy; see, e.g., Grinold and Kahn (2000, chp. 4)). The resultant binomial market model is an arbitrage-free, complete market model. Therefore, if the option trader had bypassed Steps 2, 3, and 4 and passed directly from Step 1 to the discrete risk-neutral pricing tree, information about and would be preserved when valuing the option price with the uniquely determined risk-neutral probabilities given by and
Remark 2.
Trinomial and multinomial pricing trees appearing in the literature are placed directly in the risk-neutral world, bypassing Steps 1, 2, and 3 altogether. (For references on tri- and multinomial trees, see Table 1). These option pricing trees in complete market models do not address the critical question as to which uniquely determined pricing tree in the natural world leads to the selected trinomial or multinomial pricing tree in the risk-neutral world.
3. Itô–McKean Skew Brownian Motion
A SBM is defined as follows (See Table 1 for references on SBM). Let be a standard BM generating a stochastic basis . Let and set
where . The process is called a SBM with parameter (Cherny et al. 2003). The SBM is a semimartingale satisfying the strong Markov property and (Cherny et al. 2003, sct. 4; Corns and Satchell 2007). For every the density of is given by:
As noted by Cherny et al. (2003), there are other ways of defining a SBM, all of which are equal in distribution. Trajectories of can be simulated using the Itô–McKean representation, , where
with being a standard BM. This representation first appears in Itô and McKean (1996, §4.2, Problem 1, p. 115). Corns and Satchell (2007) (CS) developed a representation which they called Itô–McKean SBM. The Itô–McKean SBM with parameter is defined as follows:
where and are two independent BMs. CS showed that has the conditional probability density:
where , and and are, respectively, the standard normal density and cumulative distribution functions. CS showed that:
The density governing a continuous random variable is referred to as a skewed normal distribution (SND). Relevant properties of an SND are presented in Appendix A. Using the moment properties of an SND, the moments are given by . In particular, the mean, variance, skewness, and excess kurtosis of are given by the following:
The terms , and are introduced in (12) to isolate the time dependence of each moment.
We develop asset and option pricing based upon Itô–McKean SBM using the Corn–Satchel version (9) rather than the original version (8). However, neither of these two versions of SBM is useful for estimating the parameter values (which need to be obtained by fitting an SBM model to a real asset return process) required in the option price formulas. Estimation using (8) requires knowledge of trajectories of in the limit , while estimation using (9) requires working with two independent Brownian motions as well as a Dirac -function (see Section 3.1). In Section 5, we describe a third representation of an Itô–McKean SBM as a limiting process of a single skew random walk. This representation is used in our empirical examples to provide fits to historical return time series to estimate the appropriate parameter values.
3.1. Stochastic Dynamics of Itô–McKean SBM
The goal in this subsection and the next is to motivate the market-complete tree model needed for derivative pricing.9 The stochastic differential equation for is derived directly from Tanaka’s formula (Chung and Williams 1991, sct. 7.3; Björk 2019, chp. 4). If is a Brownian motion, then
In (13), is the Brownian motion local time at defined by
where is the Lebesgue measure. Informally (Björk 2019, Proposition 2.4), where is the Dirac delta function at and
For with probability 1 (Revuz and Yor 1999, Corollary 2.4, chp. VI). If and , then . (See Revuz and Yor 1999, Theorem 2.3, chp. VI for a more general result10). From (13)–(15),
where is a standard BM. Equation (16) succinctly encapsulates the challenges faced in developing asset and derivative pricing in a model whose risky asset prices are driven by . There are two independent Brownian motions and as well as the Dirac -function to be considered in developing an appropriate riskless rate as well as a feasible strategy for a hedging portfolio. We first consider the issue of an appropriate risk-free rate.
3.2. The Risk-Free Rate in a Market with Uncertainties Determined by Itô–McKean SBM
We start from the basic Black–Scholes–Merton market model , (Black and Scholes 1973; Merton 1973; Duffie 2001, chps. 5 and 6), with and defined as follows.
- (i)
- is a risky asset (stock) with price dynamics given by Itô–McKean GSBM,In (17), is an Itô–McKean SBM as defined in (9), with dynamics determined by (16), where and are two independent Brownian motions generating a stochastic basis
- (ii)
- is a riskless asset (bond) with price dynamics.
- (iii)
- is a European Contingent Claim (ECC)11 with underlying asset and maturity time . The price dynamics of is given by the following:where and satisfy the usual regularity conditions (Duffie 2001, chp. 5).
With the underlying risky asset having price dynamics (17), the riskless rate in (18) cannot be chosen arbitrarily. This is due to the delta-function jump in the instantaneous mean return of the stock; that is, from (15)–(17) and the extended Itô formula (Björk 2019, Theorem 4.3),
The -function remains in the model if only a single risky asset is considered. To illustrate how to eliminate the -function term in the rate of the riskless asset , it is necessary to consider a market model with at least two risky assets, 12, each having price dynamics as follows:
where
Then
To evaluate the rate in the corresponding riskless asset , we follow the approach in Section 6D of Duffie (2001) (based upon Black 197213). The portfolio is free of arbitrage and complete if there exists a unique state price deflator on . We search for having the dynamics
such that are martingales on . The martingale condition implies that
and
The riskless rate in the market is now determined by via (Duffie 2001, sct. 6D)
Thus, as long as
then14
eliminating the -function term from the riskless rate. We shall assume that (26) holds in our development of derivative pricing.
4. Derivative Pricing with an Itô–McKean Skew Pricing Tree
While the market model is arbitrage-free and complete, and the riskless rate is free of the uncertainties under (26), as the price uncertainty is determined by , any derivative price remains affected by the three market uncertainties To enable a feasible hedging strategy (via a unique replicating portfolio), the -function term must be removed from the deterministic drift in the asset prices. To remove this term while retaining market completeness, we add a third risky asset and assume a derivative price dependence:
where each of the underlying assets has price dynamics determined by:
To guarantee the appropriate riskless rate, consistent with (26) we ensure the same skewness parameter for the three price processes.
4.1. Completeness of the IMSPT
We show that the market model determined by (30), (18) and (29) is complete. First, we will derive the price dynamics of , as a limit of two dependent binomial trees. Let , with , be a sequence of pairs of independent random signs, 15. Let and Consider the processes
Then, as , converges weakly in to by DPIP. Let
Then, converges weakly in to Define the filtration . For conditionally on ,
Consider the triplet of dependent binomial pricing trees , where
Conditionally on
where
for .
We call (35) the Itô–McKean skew pricing tree. It generates a -valued process , where
By the DPIP, weakly converges to as As stated in the Introduction, the parameter capturing the skewed behavior of the discrete prices processes in the natural world is therefore retained in the continuum limit.
Remark 3.
In the special case when the second random sign sequence , the SRW tree (35) becomes a single binomial tree with up and down prices given, respectively, by and . The upward risk-neutral probability then becomes , where .
4.2. Option Pricing with the IMSPT
Having confirmed in Section 4.1 that the continuum limit of the discrete SBM model retains dependence on the skewness parameter , for notational brevity, we drop the superscript on all -dependent terms in the remainder of the paper.
Suppose the ECC , with the triplet of underlying assets and maturity time , has a price process , where is a sufficiently smooth, real-valued function on The payoff of at maturity is for some real-valued function . and satisfy the usual regularity conditions (Duffie 2001, chps. 5 and 6). Consider the finite price dynamics of on the lattice Conditionally on
where , with analogous definitions for , , and . For , consider the replicating risk-neutral portfolio where are the hedging deltas to be determined later on. Then, conditionally on , From the risk-neutrality condition, it follows that
where
Then (39) and (40) imply that the hedging deltas are given by
where the 3 × 3 determinants , , are defined in Appendix B. Given , portfolio is riskless. This leads to the following:
Thus, given the derivative price at is given by
Now, (41) and (43) imply that
In (44) the conditional-on- risk-neutral probabilities , have the form,
where the terms in (45) are defined in Appendix B.
Remark 4.
Consider the special case Then the underlying price process follows the Jarrow-Rudd binomial tree (Jarrow and Rudd 1983, chps. V, VI; Hull 2012, p. 442; Kim et al. 2016, 2019),
having risk-neutral probabilities
With , where is the market price of risk (Kim et al. 2016, 2019).
Remark 5.
Consider the special case Then the underlying price process follows the path-dependent binomial tree; conditionally on
for In this case, the risk-neutral probabilities are
given
5. Empirical Examples
In Section 5.1, we show how to generate an SBM based upon a skew random walk, which is equal in distribution to Itô–McKean SBM. In Section 5.2, we describe how to fit an empirical return series to this skew random walk model to obtain the required parameter values for the discrete option pricing model of Section 4.2. An empirical example of the generation of option prices is given in Section 5.3.
5.1. Generating an SBM via a Skew Random Walk
Using the Harrison–Shepp functional limit theorem (HSFLT: Harrison and Shepp 1981; see also Cherny et al. 2003 for a more general principle), we elucidate a discrete-time process defined on a finite time interval that converges weakly in (Skorokhod 1956; Billingsley 1999, chp. 3) to Itô–McKean SBM16. Let be a Markov chain, with , having the transition probabilities:
for . is called a skew random walk (SRW) with parameter (Harrison and Shepp 1981; Cherny et al. 2003). If , is a random walk. Relevant properties of the SRW are discussed in Appendix C. With let . Consider the following processes in ,
Then HSFLT states that, as , converges weakly in to the SBM .
Consider the pricing tree given by (Hu et al. 2022):
adapted to the filtration . Define the -process:
Then, by HSFLT, converges weakly in to a GSBM.
With and , then by (11) the price process (54) is equal in distribution to the price process (30) driven by Itô–McKean SBM.
Note that the coefficient appearing in (54) and in its discrete version (52) (and hence in (30) and its discrete version (35)) is not the usual volatility, which appears when the driving random motion is Brownian. When the driving motion is Brownian (), and have the same distribution. However, when the driving motion is skew Brownian (), then and will not have the same distribution. Thus, when the driving motion is Brownian, the restriction can be imposed, since any negative sign can be inverted by the change , with no change in the resulting random distribution. For SBM, this is not possible and the sign of is important. Therefore, is not volatility in the usual sense but rather a “diffusion” parameter, .
5.2. Fitting Itô–McKean SBM to ETF Return Values
Let denote an empirical price series and and denote, respectively, its cumulative and daily log-returns. Fitting the price series to (52) involves solving both of the following:
for the parameters , and . Fitting (55) to data requires identifying best fit values for the parameters , , over an ensemble of BM trajectories, . Appendix D presents a procedure for fitting daily closing prices. That appendix also presents the results of testing the procedure on synthetic data sets produced from (50) and (52) with known values of , and . The test results show that can be computed very accurately for any single price trajectory. Since the standard deviation of daily returns is larger than the mean value , estimation of from a single price trajectory is much less accurate. Estimation of from a single price trace is slightly better than for estimation of ; critically, it is possible to infer whether differs from 0.5, and in what direction.
To apply the fitting procedure to an empirical data set, we consider data (source: Bloomberg Professional Services, accessed 24 August 2021, 10:00 PM EDT) for the SPDR S&P 500 ETF Trust (SPY) covering the period 3 January 2000 to 17 February 2022. The results of the fits, using a 252-day moving window, to the parameters , and for SPY are given in Figure 1. The parameters and were computed using the minimization (A4) of Appendix D, with set to the realized average value of over each respective window.17 The time series of mean square errors (MSE) for this minimization are also plotted. To smooth the results for and , we computed the median value time series, and using a 1-month moving window. The smoothed series are also shown in Figure 1. The effects of the financial crises of 2008 and the COVID-19 pandemic are discernible in each time series, although they are almost “washed out” of the smoothed time series and . Mean and standard deviation values for each of these parameter time series are given in Table 2. To reasonably high precision, is consistent with a value of 0.549, indicating that SPY acted as an SBM with positive skewness over this long time period.
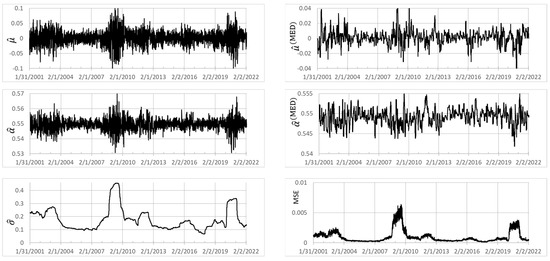
Figure 1.
Time series of optimal parameter values and mean square error of minimization fit.

Table 2.
Mean values and standard deviations for the fitted parameters.
We desire to construct the pricing tree
for , with that approximates an empirical price series . To do so, we need the “best fit” Markov trajectory . Consider the daily log-returns defined by (56):
This implies that
Equating with the observed daily returns, , enables computation of a sequence, from (58). However, the values will (undoubtedly) not be in . Consequently, we estimate the chain using the revised formula, as follows:
where is defined in (13). Use of (59) enables computation of a data-fitting Markov chain for where is the size of the window.
To illustrate, we used the parameter estimates18 and obtained for 24 August 2021 to generate the pricing tree via (56) and (59) over the period 25 August 2020 to 24 August 202119. The resulting price series is shown in Figure 2, where it is compared to that of the empirical SPY price, . The R-squared value of the fit is 0.94, the RMSE is 10.2.
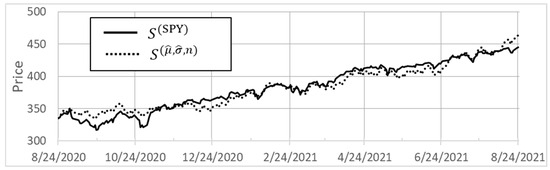
Figure 2.
Fit of model price to SPY market price over indicated time period.
5.3. Option Pricing
We consider an empirical example of option pricing under the IMSPT model. As noted, we assume the same skewness parameter for all three risky assets. To ensure the accuracy of this assumption, we choose three ETFs that track sub-indices of the same composite index. Specifically, we consider the S&P Global 1200 index (SPG1200) and the ETFs: SPY, iShares Europe ETF (IEV), and iShares JPX-NIKKEI 400 ETF (JPXN), which track the three major components20 of this index.
There are strong numerical considerations behind our choice of three ETFs tracking sub-indices of a composite index. Consider an alternate choice consisting of the S&P 500 index and the three ETFs: SPY, IVV (iShares Core S&P 500 ETF), and VOO (Vanguard S&P 500 ETF) each of which tracks the full index. The similarity of the price processes governing these three ETFs leads to numerical instability (division by very small denominators) in the computations of the risk neutral probabilities (45). This can be seen more immediately in the case of two-risky assets. Computation of the riskless rate (45) diverges whenever , which happens frequently when the ETFs closely track the same index. By choosing ETFs that track separate components of a composite index, we ensure that the volatilities of each ETF have both a systemic and an idiosyncratic component. In practice, the (differing) systemic components will ensure that the values of the required denominators remain sufficiently large compared to the values of their numerator terms.
We compute assuming that the dynamics of the SPG1200 index follows the GSBM
where is given by (9). As noted in Section 3, for . As the processes on a time interval defined by either (60) or (54) generate the same probability law (Corns and Satchell 2007), we use the procedure outlined in the previous empirical example on the SPG1200 index values over the period 13 September 2016 through 14 September 2021 using 1-year moving windows to generate a time series , where, as above, “Med” refers to a moving 1-month median value. As in the previous empirical example, we restrict values of to the range [0.45, 0.55]. The resultant time series, , is shown in Figure 3.
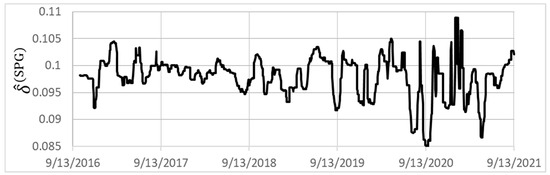
Figure 3.
Time series of estimated for the indicated period.
We model the price dynamics of each ETF over the one-year (252 trading day) period 15 September 2020–14 September 2021 by the following:
where is the value obtained for 14 September 2021. To compute the values and , we perform least-squares minimization on the relation:
Table 3 presents the fitted estimates and and the and root mean square error (RMSE) values for each minimization. Note that, for SPY and IEV, the fitted value is negative; their cumulative returns have a negative dependence on . Plots of these fits are shown (and briefly discussed) in Appendix E.

Table 3.
The constrained minimization results from (62).
Consider a European put option with payoff . Using (dividend adjusted) starting prices for SPY ($432.51), IEV ($52.25) and JPXN ($76.09) for 14 September 2021, we compute the risk neutral probabilities (45) and form the risk-neutral tree (44) over a time period , where is the time to maturity in days. In Figure 4, we plot the put option price as a function of and moneyness over the range , . Repeating this for a European call with payoff , Figure 4 also plots as a function of and moneyness , over the same range of maturity and moneyness values. The difference in price range for the put and call options represents the disparity in the computed prices of the ETFs at maturity, which in turn is based upon differences in their starting prices, drift, , and diffusion parameter, , values. For the specific values in Table 3, the ETFs IEV and JPXN dominate the computation of , while SPY dominates the computation of .
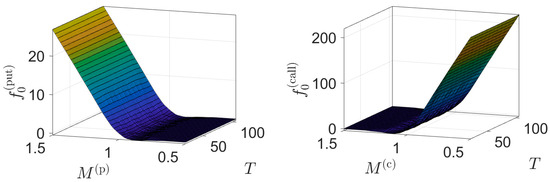
Figure 4.
Computed values of European put and call options.
6. Conclusions
Continuous-time formulations of derivative pricing, while attractive in terms of their theoretical bases (semimartingales, Lévy processes, and the fundamental theorem of asset pricing) and the convenience of smoothly varying, closed-form solutions, are generally limited in their ability to capture many of the stylized facts of real asset dynamics and/or their ability to achieve arbitrage-free, market-complete models. It is our view that any continuous time model should only be considered as a benchmark model for a more precise discrete pricing model that is: defined in the natural world; capable of capturing valuable market characteristics; extended to the risk-neutral world under the no-arbitrage condition where derivatives are priced under uniquely determined risk-neutral probabilities with no loss of natural world parameters; and market-complete. Previous work (Hu et al. 2020a, 2020b, 2022; Kim et al. 2016, 2019) has variously demonstrated the capabilities of discrete models to achieve these goals.
We have presented here a binomial tree model based upon a single Itô–McKean skew random walk (IMSRW) driving process. Although an arbitrage-free, market-complete model is achieved by requiring a Black–Scholes–Merton market containing two risky assets, to achieve a practical hedging strategy, it is necessary to include three risky assets in the replicating portfolio. The requirement of a single IMSRW driving process ensures that the riskless asset return rate is independent of the IMSRW. The model contains seven parameters: the drift and diffusion values , , for the risky asset price processes (30) and the parameter (equivalently ) controlling the deviation of the IMSRW from a standard random walk. The parameter therefore controls the central moments of the IMSRW driving process, providing the ability to match central moments (mean through kurtosis) of realistic price processes. As a result, in our arbitrage-free, market-complete model, the underlying price processes exhibit the stylized facts of skewness and distributional heavy tails of asset returns, without passing to an incomplete market model.
Using an empirical example, we demonstrate the computation of option prices from the theoretical model. It is natural to wonder how such prices compare to existing approaches. Such a comparison is not straightforward, as most existing models (e.g., the standard Black–Scholes–Merton model, or binomial models of the Cox–Ross–Rubenstein or Jarrow–Rudd style) are designed for a market containing only a single risky asset. Most existing approaches, such as the three mentioned above, are based on the assumption that log returns are normally distributed. It is well known that this is not the case and that the return distributions are generally skewed and have heavier tails than the normal distribution. As our model is developed specifically to capture skewness and kurtosis behavior, it offers greater flexibility and, consequently, accuracy. Exact details depend on the asset considered. It would require a carefully designed study with appropriately considered assets to quantify the improvement that our proposed method provides against others, which we leave for a future investigation.
Our development was initially motivated by the continuous-time pricing model of Corns and Satchell (2007), which combined standard Brownian motion with skew Brownian motion. As the equivalent martingale obtained in their work only provides hedging against the risks associated with the standard Brownian motion, their model is market-incomplete. The approach to achieving market completeness in our discrete formulation indicates how one might achieve the same in the Corns–Satchell formulation, should one wish to do so.
Author Contributions
Conceptualization, S.T.R.; methodology, all authors.; software, Y.H.; validation, all authors; investigation, Y.H., W.B.L., S.T.R.; data curation, Y.H.; writing—original draft preparation, S.T.R., Y.H., W.B.L.; writing—review and editing, W.B.L.; visualization, Y.H., W.B.L.; supervision, S.T.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Asset data was obtained under license from Bloomberg Professional Services. Services. Parties interested in the asset data should contact Bloomberg Professional Services directly.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Skew Normal Distribution
Definition A1.
A continuous random variable has a skew normal distribution (SND) with parameter if its probability density function has the form where is the standard normal density, and is the standard normal cumulative distribution function (Azzalini 1985, 1986; Azzalini and Capitanio 2003, 2014; Dalla Valle 2005).
Relevant properties of the SND are the following (Dalla Valle 2005). (Here and in what follows stands for “equal in distribution” or “equal in probability law”).
SND 1. (a1) ; (b1) (c1) The density of is unimodal; and (d1) The moment-generating function of is given by
SND 2. Let be a pair of independent standard normal random variables, (a2) If for some then with . In particular, if is an Itô–McKean SBM with parameter then for every with . (b2) If , then
SND 3. Let be a bivariate normal random variable with , having correlation coefficient Then (a3) the conditional distribution of given that is SND with parameter and (b3) with .
SND 4. (a4) and with ; (b4) For all and (Henze 1986, Proposition 1.2.3)
Appendix B. The Determinants
The determinants appearing in Equation (41) are
The terms appearing in Equation (45) are the following:
where
for .
Appendix C. Properties of the Skew Random Walk (α)
From (12) and the fact that in (51) converges weakly in to the SBM as , we conclude that
where . As for , then
As we expect markets to be efficient, we are interested in the range To verify (A1) for any fixed value of , we generated a sample of SRWs, each of length 6000 time-steps, and performed the expectations required in (A1) over the sample. The results for the random walk and the SRW are shown in Figure A1. Table A1 quantifies the root mean square error
with analogous definitions for , and , between the ensemble averaged and the theoretical values for select values of . and grow with over this range, while and are relatively constant.
Since the skew parameter only “comes into play” at times for which , the question of how frequently this occurs is important for assessing the ability to determine using a fitting procedure on any single trajectory. Since the trajectory of a SRW between successive values of is governed solely by a standard random walk (i.e. with up/down probabilities of ½), the distribution of the frequency of occurrence of is determined solely by a standard random walk, independent of . Figure A2 confirms this by displaying the relative frequency distribution of the occurrence rate (in percent) of during a random walk for five choices of . Each distribution was determined based upon randomly generated trajectories, each of length 6000 steps. The occurrence distribution is highly skewed, with occurrences ranging from once in 6000 steps (0.017%) to greater than 250 times (4.17%). The quartile values are .
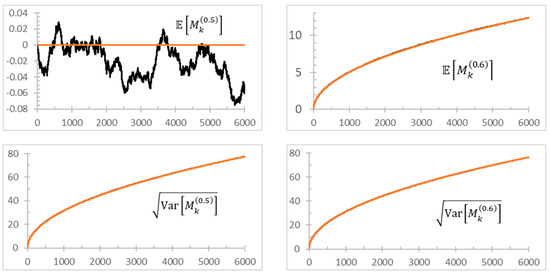
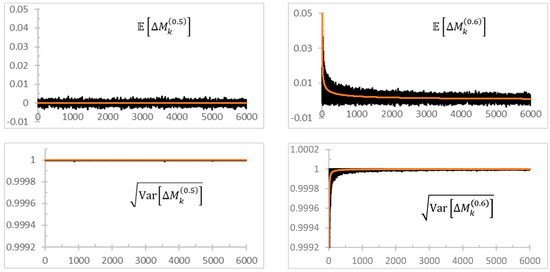
Figure A1.
(black) Estimates of the indicated quantity from an ensemble of SRWs. (red) The theoretical value (A1).

Table A1.
Root mean square error between ensemble averaged and theoretical measures.
Table A1.
Root mean square error between ensemble averaged and theoretical measures.
| 0.50 | ||||
| 0.52 | ||||
| 0.54 | ||||
| 0.56 | ||||
| 0.58 | ||||
| 0.60 |
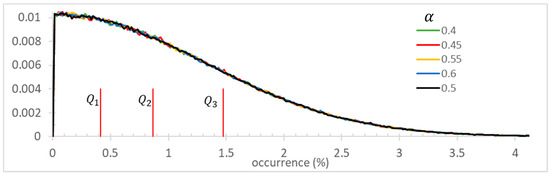
Figure A2.
Relative frequency distribution of the occurrence rate (in percent) of during a SRW governed by the listed value of . The vertical red lines indicate the quartile values for the distribution. The distribution is truncated at 4.17%.
Appendix D. Parameter Fitting Procedure
Let denote an empirical price series and and denote, respectively, its cumulative and daily log-returns. From (55) and (A1) note that
Based upon Figure A1 we see that the right-hand side of (A2) can be accurately approximated by
where the right-hand side of (A3) is independent of . Thus, computing the variance of over all values from a single price series provides an accurate estimation of . Estimating from (A3) is the first step in our fitting procedure. We have found no method that allows useful determination of and independently of each other, thus the second step in the parameter fitting procedure involves simultaneous estimation of and (using the value obtained in the first step). As numerical realizations of the SRW can be computed extremely rapidly, the second step consists of generating a large ensemble of return series , each series based upon an independent sample pair , and determining the parameter pair that satisfies
Setting (or, if necessary, adjusting) the limits is relatively straightforward. For the numerical examples, we have used , . If the minimization produces values of that approach either limit, the limits can be adjusted and the minimization rerun. To determine the limits , one can consider the approximation
to obtain a rough value , and then set the limits , . However, the approximation in (A5) is poor, as can be comparable in value to . Consequently, we set the wide limits, , , which proved to be satisfactory in our minimizations.
The fitting procedure was tested on synthetic price series, each consisting of a price trajectory generated from (50) and (52), with known values of , and . Using these values, an SRW , k = 1, …, 6000 was generated, from which a price trajectory was computed from (52) consisting of a sequence of 6000 daily prices (5999 returns or 23.8 years of data). The synthetic return series and were generated from to represent the empirical data set (55) used in the fitting procedure. Table A2 presents the results of empirical fits to synthetic data sets generated with , and . For each choice of , 10 synthetic price trajectories were computed to assess accuracy by computing the average and sample standard deviation of the parameter fits over the sample of 10. We see that can be computed very accurately for any individual price series. Since the standard deviation of daily returns is larger than the value , the term in (55) is comparable in magnitude (in our synthetic data sets, roughly 37% of the magnitude) of the drift term , making an estimation of from a single price trajectory much less accurate. However, averaging over as small a sample as 10 price traces leads to an average value that is within one standard deviation of the true value . Estimation of from a single price trace is slightly better than single-trace estimation of ; consequently, estimation of from the small set of 10 traces yields better results than that for . Critically, from a single price trace, it is possible to infer whether differs from 0.5, allowing for the possible refinement of a value for by narrowing the search limits in the optimization procedure.

Table A2.
Results of the application of the fitting procedure to synthetic data sets.
Table A2.
Results of the application of the fitting procedure to synthetic data sets.
| Synthetic Data Set | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.099993 | 0.015 | 0.53 | 0.099997 | 0.000 | 0.52 | 0.099995 | 0.066 | 0.34 |
| 2 | 0.100002 | 0.061 | 0.66 | 0.099996 | 0.048 | 0.57 | 0.099994 | 0.019 | 0.34 |
| 3 | 0.100008 | 0.027 | 0.63 | 0.099990 | 0.016 | 0.50 | 0.099984 | 0.015 | 0.47 |
| 4 | 0.100008 | 0.052 | 0.65 | 0.100008 | 0.035 | 0.59 | 0.099985 | 0.083 | 0.48 |
| 5 | 0.100001 | 0.057 | 0.64 | 0.099991 | 0.010 | 0.44 | 0.100006 | 0.059 | 0.48 |
| 6 | 0.100008 | 0.043 | 0.51 | 0.099994 | 0.064 | 0.54 | 0.100000 | 0.069 | 0.36 |
| 7 | 0.100002 | 0.029 | 0.66 | 0.099998 | 0.039 | 0.56 | 0.0999471 | −0.016 | 0.47 |
| 8 | 0.099971 | 0.087 | 0.63 | 0.100003 | 0.057 | 0.54 | 0.100008 | 0.025 | 0.45 |
| 9 | 0.100007 | 0.055 | 0.52 | 0.100008 | 0.039 | 0.58 | 0.099994 | 0.008 | 0.49 |
| 10 | 0.100007 | 0.054 | 0.58 | 0.100008 | 0.019 | 0.47 | 0.099995 | 0.016 | 0.38 |
| Average | 0.100001 | 0.048 | 0.60 | 0.099999 | 0.033 | 0.53 | 0.099991 | 0.035 | 0.43 |
| St. Dev. | 0.000011 | 0.021 | 0.06 | 0.000007 | 0.021 | 0.05 | 0.000017 | 0.032 | 0.06 |
Appendix E
Figure A3 plots the fits to (62) for the ETFs SPY, IEV, and JPXN. As noted in Table 3, the theoretical model only accounts for 64% of the variability of over this 252-day period. In contrast, the respective values for IEV and SPY are 89% and 96%. The augmented Dickey–Fuller test performed on the difference series rejects the null hypothesis of a unit root at the 5% significance level, but not at the 1% level, for both JPXN and IEV difference series; while rejecting the null hypothesis for SPY even at the 0.1% level. We have therefore investigated fitting these series to ARFIMA(1,d,1)-GARCH(1,1)-Student models, with . Analysis of these results suggests that a standard , ARMA(1,1)-GARCH(1,1)-Student model with 6 degrees of freedom works well for both SPY and IEV. For JPXN, the model produced the best results.
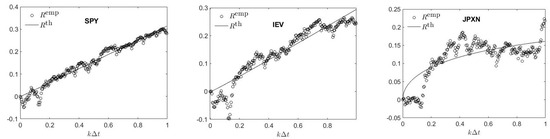
Figure A3.
Plots of the fits to (62) for the ETFs SPY, IEV and JPXN. denotes the empirical data, is the fitted theoretical model.
Notes
| 1 | In our discrete option pricing model, there is a unique one-to-one mapping between the risk-neutral and natural probability measures. Thus, option traders can calibrate the risk-neutral measure from option data and pass to the unique natural measure to see whether the “implied spot prices” significantly differ from the market spot prices. In particular, option traders can calibrate the “implied” mean instantaneous return and compare it with the instantaneous return derived from the spot price data. These techniques for determining market dislocation, i.e., the discrepancies in the views of option traders on spot prices and the market values of spot prices, were used during the market crash of 2008. However, in incomplete markets where there is no unique one-to-one mapping of the risk-neutral and natural measures, determining such market dislocation is not possible. |
| 2 | The implied volatility, a parameter used to fit continuous-time option pricing models to existing market data, is a case in point. It fully deserves the aphorism: “The implied volatility is the wrong number that, used in the wrong formula, gives the right price for the option”. |
| 3 | The notation indicates “converges to zero from positive values”. |
| 4 | In the CS option pricing model, as in any continuous time option pricing model, the mean stock return parameter is not present. |
| 5 | If , then since (and under the condition ), the probability for stock price upturn in the natural world is uniquely determined as . The value of that is historically observed is generally different from . |
| 6 | If , then since (and under the condition ), the probability for stock price upturn in the natural world is uniquely determined as . The value of that is historically observed is generally different from . |
| 7 | When approaches or , the rate of convergence becomes slower and vanishes when or . The rate of convergence (in a suitably chosen metric) is fastest when . |
| 8 | The idea of Jarrow, Protter and Savit is to disallow continuous trading and, moreover, to require a minimal fixed time between successive trades. This fixed time can be as small as one likes, but once chosen, it cannot be changed. This disallows a clustering of trades around a fleeting arbitrage opportunity, such as might occur from a drift process that the random generating process cannot “see”. |
| 9 | These two subsections are of illustrative (informal) character. The rigorous results are presented in the cited references. |
| 10 | The more general result, known as the Lévy Theorem, is
|
| 11 | We use terms ECC, options, and derivative interchangeably. |
| 12 | Heuristically, one can view and as two portfolios on the “capital market line”. |
| 13 | The general framework of a market without a risk-free asset was first outlined by Black in his development of the zero-beta capital asset pricing model. |
| 14 | We adopt the notation in (27) to acknowledge that it follows ideas from Black for riskless rate computation. See footnote 13. |
| 15 | The sequences and are assumed independent. |
| 16 | See Equation (54). As noted in Section 3, all SBMs are equal in distribution. An Itô–McKean SBM is just one representation of an SBM. |
| 17 | As seen from Figure 1, varied by factors of 2 to 5 over this long time period. Using an average value of over each moving window for the computation of and produced slightly better results than using a single value of , representing an average over the entire time period. |
| 18 | With in (58) replaced by in (59) and with , the pricing tree no longer has explicit dependence on (only implicitly through the empirical return). |
| 19 | We use the price of SPY on 24 August 2020 as . |
| 20 | S&P Global 1200 is a composite index comprised of seven regional and country indices. The major three are the S&P 500, S&P Europe 350, and S&P/TOPIX 150 (Japan). |
References
- Amin, Kaushik. 1991. On the computation of continuous time option prices using discrete approximation. Journal of Financial and Quantitative Analysis 26: 477–95. [Google Scholar] [CrossRef]
- Applebaum, David. 2004. Lévy Processes and Stochastic Calculus. Cambridge: Cambridge University Press. [Google Scholar]
- Atar, Rami, and Amarjit Budhiraja. 2015. On the multi-dimensional skew Brownian motion. Stochastic Processes and Their Applications 125: 1911–25. [Google Scholar] [CrossRef]
- Audrino, Francesco, Robert Huitema, and Markus Ludwig. 2014. An Empirical Analysis of the Ross Recovery Theorem. Economics Working Paper Series, No. 1411; St. Gallen: University of St. Gallen. [Google Scholar]
- Azzalini, Adelchi. 1985. A class of distributions which includes the normal ones. Scandinavian Journal of Statistics 12: 171–78. [Google Scholar]
- Azzalini, Adelchi. 1986. Further results on a class of distributions which includes the normal ones. Scandinavian Journal of Statistics 46: 199–208. [Google Scholar]
- Azzalini, Adelchi, and Antonella Capitanio. 2003. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. Journal of the Royal Statistical Society, Series B 65: 367–89. [Google Scholar] [CrossRef]
- Azzalini, Adelchi, and Antonella Capitanio. 2014. The Skew-Normal and Related Families. Cambridge: Cambridge University Press. [Google Scholar]
- Barndorff-Nielsen, Ole E., and Robert Stelzer. 2013. The multivariate supOU stochastic volatility model. Mathematical Finance 23: 275–96. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., Thomas Mikosch, and Sidney I. Resnick. 2001. Lévy Processes: Theory and Applications. Boston: Birkhäuser. [Google Scholar]
- Bensoussan, Alain. 1984. On the theory of option pricing. Acta Applicandae Mathematicae 2: 139–58. [Google Scholar] [CrossRef]
- Bertoin, Jean. 1996. Lévy Processes. Cambridge: Cambridge University Press. [Google Scholar]
- Billingsley, Patrick. 1999. Convergence of Probability Measures, 2nd ed. New York: Wiley-Interscience. [Google Scholar]
- Bingham, Nicholas H., and Rüdiger Kiesel. 2004. Risk-Neutral Valuation: Pricing and Hedging of Financial Derivatives, 2nd ed. London: Springer. [Google Scholar]
- Björk, Tomas. 2004. Arbitrage Theory in Continuous Time. Oxford: Oxford University Press. [Google Scholar]
- Björk, Tomas. 2019. The pedestrian’s guide to local time. In Risk and Stochastics. Edited by Pauline Barrieu. Singapore: World Scientific, Chapter 3. pp. 43–67. [Google Scholar]
- Black, Fischer. 1972. Capital market equilibrium with restricted borrowing. Journal of Business 45: 444–53. [Google Scholar] [CrossRef]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bock, Alona, and Ralf Korn. 2016. Improving convergence of binomial schemes and the Edgeworth expansion. Risks 4: 1–22. [Google Scholar] [CrossRef]
- Boyle, Phelim P. 1986. Option valuation using a three-jump process. International Options Journal 3: 7–12. [Google Scholar]
- Boyle, Phelim P. 1988. A lattice framework for option pricing with two state variables. Journal of Financial and Quantitative Analysis 23: 1–12. [Google Scholar] [CrossRef]
- Boyle, Phelim P., and Sok Hoon Lau. 1994. Bumping up against the barrier with the binomial method. Journal of Derivatives 1: 6–14. [Google Scholar] [CrossRef]
- Boyle, Phelim P., and Ton Vorst. 1992. Optimal replication in discrete time with transaction costs. Journal of Finance 47: 271–93. [Google Scholar] [CrossRef]
- Boyle, Phelim P., Jeremy Evnine, and Stephen Gibbs. 1989. Numerical evaluation of multivariate contingent claims. Review of Financial Studies 2: 241–51. [Google Scholar] [CrossRef]
- Brennan, Michael J., and Eduardo S. Schwartz. 1978. Finite difference methods and jump processes arising in the pricing of contingent claims: A synthesis. Journal of Financial and Quantitative Analysis 13: 461–74. [Google Scholar] [CrossRef]
- Broadie, Mark, Jakša Cvitanić, and H. Mete Soner. 1998. Optimal replication of contingent claims under portfolio constraints. Review of Financial Studies 11: 59–79. [Google Scholar] [CrossRef]
- Campbell, John Y., Andrew W. Lo, A. Craig MacKinlay, and Robert F. Whitelaw. 1996. The Econometrics of Financial Markets. Princeton: Princeton University Press. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2004. Time-changed Lévy processes and option pricing. Journal of Financial Economics 71: 113–41. [Google Scholar] [CrossRef]
- Chan, Terence. 1999. Pricing contingent claims on stocks driven by Lévy processes. Annals of Applied Probability 9: 504–28. [Google Scholar] [CrossRef]
- Chang, Lo-Bin, and Ken Palmer. 2007. Smooth convergence in the binomial model. Finance and Stochastics 11: 91–105. [Google Scholar] [CrossRef]
- Cherny, Aleksander S., Albert N. Shiryaev, and Marc Yor. 2003. Limit behavior pf the ‘horizontal-vertical” random walk and some extensions of the Donsker-Prokhorov invariance principle. Theory of Probability and its Applications 47: 377–94. [Google Scholar] [CrossRef]
- Chung, Kai Lai, and Ruth J. Williams. 1991. Introduction to Stochastic Integration, 2nd ed. Boston: Birkhäuser. [Google Scholar]
- Corns, T. Richard A., and Stephen E. Satchell. 2007. Skew Brownian motion and pricing European options. European Journal of Finance 13: 523–44. [Google Scholar] [CrossRef]
- Cox, John C., and Mark Rubinstein. 1985. Options Markets. Englewood Cliffs: Prentice-Hall. [Google Scholar]
- Cox, John C., and Stephen A. Ross. 1976. The valuation of options for alternative stochastic processes. Journal of Financial Economics 3: 145–66. [Google Scholar] [CrossRef]
- Cox, John C., Stephen A. Ross, and Mark Rubinstein. 1979. Options pricing: A simplified approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Dalla Valle, Alessandra. 2005. The skew-normal distribution. In Skew-Elliptical Distributions and Their Applications: A Journey Beyond Normality. Edited by Marc G. Genton. Boca Raton: Chapman and Hall/CRC, Chapter 1. pp. 3–25. [Google Scholar]
- Davis, Mark HA, Vassilios G. Panas, and Thaleia Zariphopoulou. 1993. European option pricing with transaction costs. SIAM Journal of Control and Optimization 31: 470–93. [Google Scholar] [CrossRef]
- Davydov, Youri, and Vladimir Rotar. 2008. On a non-classical invariance principle. Statistics and Probability Letters 78: 2031–38. [Google Scholar] [CrossRef]
- Delbaen, Freddy, and Walter Schachermayer. 1994. A general version of the fundamental theorem of asset pricing. Mathematische Annalen 300: 463–520. [Google Scholar] [CrossRef]
- Delbaen, Freddy, and Walter Schachermayer. 1998. The fundamental theorem of asset pricing for unbounded stochastic processes. Mathematische Annalen 312: 215–50. [Google Scholar] [CrossRef]
- Deutsch, Hans-Peter. 2009. Derivatives and Internal Models, 4th ed. New York: Palgrave Macmillan. [Google Scholar]
- Donsker, Monroe D. 1951. An invariant principle for certain probability limit theorems. Memoirs of the American Mathematical Society 6: 1–10. [Google Scholar]
- Duffie, Darrell. 2001. Dynamic Asset Pricing Theory, 3rd ed. Princeton: Princeton University Press. [Google Scholar]
- Eberlein, Ernst, Antonis Papapantoleon, and Albert N. Shiryaev. 2008. On the duality principle in option pricing: Semimartingale setting. Finance and Stochastics 12: 265–92. [Google Scholar] [CrossRef]
- Edirisinghe, Chanaka, Vasanttilak Naik, and Raman Uppal. 1993. Optimal replication of options with transactions costs and trading restrictions. Journal of Financial and Quantitative Analysis 28: 117–38. [Google Scholar] [CrossRef]
- Elliott, Robert J., and P. Ekkehard Kopp. 2005. Mathematics of Financial Markets. New York: Springer. [Google Scholar]
- Emery, Michel, and Marc Yor. 2002. Séminaire de Probabilités, 1967–1980, A Selection in Martingale Theory. Berlin: Springer. [Google Scholar]
- Florescu, Ionuţ, and Frederi G. Viens. 2008. Stochastic volatility: Option pricing using a multinomial recombining tree. Applied Mathematical Finance 15: 151–81. [Google Scholar] [CrossRef]
- Fouque, Jean-Pierre, George Papanicolaou, and K. Ronnie Sircar. 2000. Derivatives in Financial Markets with Stochastic Volatility. Cambridge: Cambridge University Press. [Google Scholar]
- Gikhman, Iosif I., and Anatoly V. Skorokhod. 1969. Introduction to the Theory of Random Processes. Philadelphia: W.B. Saunders Company. [Google Scholar]
- Grinold, Richard, and Ronald Kahn. 2000. Active Portfolio Management: A Quantitative Approach for Providing Superior Returns and Controlling Risk. New York: McGraw-Hill. [Google Scholar]
- Guasoni, Paolo, Emmanuel Lépinette, and Miklós Rásonyi. 2012. The fundamental theorem of asset pricing under transaction costs. Finance and Stochastics 16: 741–77. [Google Scholar] [CrossRef]
- Harrison, J. Michael, and David M. Kreps. 1979. Martingales and arbitrage in multiperiod securities markets. Journal of Economic Theory 20: 381–408. [Google Scholar] [CrossRef]
- Harrison, J. Michael, and Lawrence A. Shepp. 1981. On skew Brownian motion. The Annals of Probability 9: 309–13. [Google Scholar] [CrossRef]
- Harrison, J. Michael, and Stanley R. Pliska. 1981. Martingales and stochastic integrals in the theory of continuous trading. Stochastic Processes and Their Applications 11: 215–60. [Google Scholar] [CrossRef]
- Harrison, J. Michael, and Stanley R. Pliska. 1983. A stochastic calculus model of continuous trading: Complete markets. Stochastic Processes and Their Application 15: 313–16. [Google Scholar] [CrossRef]
- He, Hua. 1990. Convergence from discrete- to continuous-time contingent claims prices. Review of Financial Studies 3: 523–46. [Google Scholar] [CrossRef]
- Henze, Norbert. 1986. A probabilistic representation of the “skew normal” distribution. Scandinavian Journal of Statistics 13: 271–75. [Google Scholar]
- Heston, Steven L. 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Hodges, Stewart D., and Anthony Neuberger. 1989. Optimal replication of contingent claims under transactions costs. Review of Futures Markets 8: 222–39. [Google Scholar]
- Hu, Yuan, Abootaleb Shirvani, Stoyan Stoyanov, Young Shin Kim, Frank J. Fabozzi, and Svetlozar T. Rachev. 2020a. Option pricing in markets with informed traders. International Journal of Theoretical and Applied Finance 23: 2050037. [Google Scholar] [CrossRef]
- Hu, Yuan, Abootaleb Shirvani, W. Brent Lindquist, Frank J. Fabozzi, and Svetlozar T. Rachev. 2020b. Option pricing incorporating factor dynamics in complete markets. Journal of Risk and Financial Management 13: 321. [Google Scholar] [CrossRef]
- Hu, Yuan, W. Brent Lindquist, Svetlozar T. Rachev, Abootaleb Shirvani, and Frank J. Fabozzi. 2022. Market complete option valuation using a Jarrow-Rudd pricing tree with skewness and kurtosis. Journal of Economic Dynamics and Control 137: 104345. [Google Scholar] [CrossRef]
- Huang, Jing-zhi, and Liuren Wu. 2004. Specification analysis of option pricing models based on time-changed Lévy Processes. Journal of Finance 59: 1405–39. [Google Scholar] [CrossRef]
- Hull, John. 2012. Options, Futures, and Other Derivatives, 8th ed. Hoboken: Pearson. [Google Scholar]
- Hull, John, and Alan White. 1987. The pricing of options on assets with stochastic volatilities. Journal of Finance 42: 281–300. [Google Scholar] [CrossRef]
- Hunt, Philip, and Joanne Kennedy. 2004. Financial Derivatives in Theory and Practice. Chichester: John Wiley and Sons. [Google Scholar]
- Itô, Kiyosi, and Henry P. McKean. 1996. Diffusion Processes and Their Sample Paths. Berlin: Springer. [Google Scholar]
- Jacod, Jean, and Albert Shiryaev. 2003. Limit Theorems for Stochastic Processes, 2nd ed. Berlin: Springer. [Google Scholar]
- Jarrow, Robert A. 2012. The third fundamental theorem of asset pricing. Annals of Financial Economics 7: 1250007. [Google Scholar] [CrossRef]
- Jarrow, Robert A., and Andrew Rudd. 1983. Option Pricing. Homewood: Irwin. [Google Scholar]
- Jarrow, Robert A., Philip Protter, and Hasanjan Sayit. 2009. No arbitrage without semimartingales. The Annals of Applied Probability 19: 596–616. [Google Scholar] [CrossRef]
- Joshi, Mark S. 2008. The Concepts and Practice of Mathematical Finance, 2nd ed. Cambridge: Cambridge University Press. [Google Scholar]
- Kabanov, Yu M., and Ch Stricker. 2001. The Harrison-Pliska arbitrage pricing theorem under transaction costs. Journal of Mathematical Economics 35: 185–96. [Google Scholar] [CrossRef]
- Kamrad, Bardia, and Peter Ritchken. 1991. Multinomial approximating models for options with K-state variables. Management Science 37: 1640–52. [Google Scholar] [CrossRef]
- Karatzas, Ioannis. 1988. On the pricing American options. Applied Mathematics and Optimization 17: 37–60. [Google Scholar] [CrossRef]
- Karatzas, Ioannis, and Steven E. Shreve. 1991. Brownian Motion and Stochastic Calculus, 2nd ed. New York: Springer. [Google Scholar]
- Karatzas, Ioannis, and Steve G. Kou. 1996. In the pricing of contingent claims under constraints. Annals of Applied Probability 6: 321–69. [Google Scholar] [CrossRef]
- Kim, Young Shin, Stoyan Stoyanov, Stelozar Rachev, and Frank Fabozzi. 2016. Multi-purpose binomial model: Fitting all moments to the underlying Brownian motion. Economics Letters 145: 225–29. [Google Scholar] [CrossRef]
- Kim, Young Shin, Stoyan Stoyanov, Svetlozar Rachev, and Frank J. Fabozzi. 2019. Enhancing binomial and trinomial option pricing models. Finance Research Letters 28: 185–90. [Google Scholar] [CrossRef]
- Korn, Ralf, and Elke Korn. 2000. Option Pricing and Portfolio Optimization: Modern Methods and Financial Mathematics. Graduate Studies in Mathematics. Providence: American Mathematical Society, vol. 31. [Google Scholar]
- Korn, Ralf, and Stefanie Müller. 2010. Binomial trees in option pricing—History, practical applications and recent developments. In Recent Developments in Applied Probability and Statistics. Edited by Luc Devroye, Blent Karasözen, Michael Kohler and Ralf Korn. Heidelberg: Physica-Verlag HD. [Google Scholar] [CrossRef]
- Kou, Steven G. 2002. A jump-diffusion model for option pricing. Management Science 48: 1086–101. [Google Scholar] [CrossRef]
- Lai, Tze Leung, and Tiong Wee Lim. 2009. Option hedging theory under transaction costs. Journal of Economic Dynamics and Control 33: 1945–61. [Google Scholar] [CrossRef]
- Lang, Reinhard. 1995. Effective conductivity and skew Brownian motion. Journal of Statistical Physics 80: 125–148. [Google Scholar] [CrossRef]
- Leccadito, Arturo, Pietro Toscano, and Radu S. Tunaru. 2012. Hermite binomial trees: A novel technique for derivatives pricing. International Journal of Theoretical and Applied Finance 15: 1–36. [Google Scholar] [CrossRef]
- Lejay, Antoine. 2006. On the constructions of the skew Brownian motion. Probability Surveys 3: 413–66. [Google Scholar] [CrossRef]
- Leland, Hayne E. 1985. Option pricing and replication with transactions costs. Journal of Finance 40: 1283–301. [Google Scholar] [CrossRef]
- Li, Liping. 2019. On general skew Brownian motions. arXiv arXiv:1812.08415v2. [Google Scholar]
- Ma, Jingtang, and Tengfei Zhu. 2015. Convergence rates of trinomial tree methods for option pricing under regime-switching models. Applied Mathematics Letters 39: 13–18. [Google Scholar] [CrossRef]
- Madan, Dilip B., and Frank Milne. 1991. Option pricing with VG martingale components. Mathematical Finance 1: 39–56. [Google Scholar] [CrossRef]
- Madan, Dilip B., Peter P. Carr, and Eric C. Chang. 1998. The variance gamma process and option pricing. European Finance Review 2: 79–105. [Google Scholar] [CrossRef]
- Markus, Leippold, and Liuren Wu. 2002. Asset pricing under the quadratic class. Journal of Financial and Quantitative Analysis 37: 271–29. [Google Scholar]
- Marroni, Leonardo, and Irene Perdomo. 2014. Pricing and Hedging Financial Derivatives: A Guide for Practitioners. Chichester: Wiley. [Google Scholar]
- Merton, Robert C. 1973. Theory of rational option pricing. Bell Journal of Economics and Management Science 4: 141–83. [Google Scholar] [CrossRef]
- Merton, Robert C. 1976. Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics 3: 125–44. [Google Scholar] [CrossRef]
- Miyahara, Yoshio. 2012. Option Pricing in Incomplete Markets: Modeling Based on Geometric Lévy Processes and Minimal Entropy Martingale Measures. London: Imperial College Press. [Google Scholar]
- Milne, Frank, Dilip Madan, and Hersh Shefrin. 1989. The multinomial option pricing model and its Brownian and Poisson limits. Review of Financial Studies 2: 251–65. [Google Scholar]
- Nelson, Daniel B., and Krishna Ramaswamy. 1990. Simple binomial processes as diffusion approximations in financial models. Review of Financial Studies 3: 393–430. [Google Scholar] [CrossRef]
- Omberg, Edward. 1987. The convergence of binomial pricing and compound option models. Journal of Finance 42: 463–69. [Google Scholar]
- Omberg, Edward. 1988. Efficient discrete time jump process models in option pricing. Journal of Financial and Quantitative Analysis 23: 161–74. [Google Scholar] [CrossRef]
- Ouknine, Youssef, Francesco Russo, and Gerald Trutnau. 2015. On countably skewed Brownian motion with accumulation point. arXiv arXiv:1308.0441v2 [math.PR]. [Google Scholar]
- Pan, Jun. 2002. The jump-risk premia implicit in options: Evidence from an integrated time-series study. Journal of Financial Economics 63: 3–50. [Google Scholar] [CrossRef]
- Pedersen, Hal W., and Elias S. W. Shiu. 1993. Pricing of Options on Bonds by Binomial Lattices and by Diffusion Processes. Working paper. Winnipeg, CA: Investment Policy Department, Great West Life Assurance Company. [Google Scholar]
- Prokhorov, Yu V. 1956. Convergence of random processes and limit theorems in probability theory. Theory of Probability and Its Applications 1: 157–214. [Google Scholar] [CrossRef]
- Protter, Philip E. 2004. Stochastic Integration and Differential Equations, 2nd ed. Berlin: Springer. [Google Scholar]
- Rachev, Svetlozar T., Young Shin Kim, Michele L. Bianchi, and Frank J. Fabozzi. 2011. Financial Models with Lévy Processes and Volatility Clustering. Hoboken: Wiley. [Google Scholar]
- Ramirez, Jorge. 2011. Multi-skewed Brownian motion and diffusion in layered media. Proceedings of the American Mathematical Society 139: 3739–52. [Google Scholar] [CrossRef]
- Rebonato, Riccardo. 2004. Volatility and Correlation: The Perfect Hedger and the Fox. Chichester: Wiley and Sons. [Google Scholar]
- Rendleman, Richard J., and Brit J. Bartter. 1979. Two-state option pricing. Journal of Finance 34: 1093–110. [Google Scholar]
- Revuz, Daniel, and Marc Yor. 1999. Continuous Martingales and Brownian Motion. Berlin: Springer. [Google Scholar]
- Rogers, L. Chris G., and E. J. Stapleton. 1997. Fast accurate binomial pricing. Finance and Stochastics 2: 3–17. [Google Scholar] [CrossRef]
- Ross, Steve. 2015. The recovery theorem. The Journal of Finance 70: 615–48. [Google Scholar] [CrossRef]
- Rubinstein, Mark. 1998. Edgeworth binomial trees. Journal of Derivatives 5: 20–27. [Google Scholar] [CrossRef]
- Sato, Ken-Iti. 1999. Lévy Processes and Infinitely Divisible Distributions. Cambridge: Cambridge University Press. [Google Scholar]
- Schoutens, Wim. 2003. Lévy Processes in Finance: Pricing Financial Derivatives. Chichester: Wiley. [Google Scholar]
- Scott, Louis O. 1997. Pricing stock options in a jump-diffusion model with stochastic volatility and interest rates: Applications of Fourier inversion methods. Mathematical Finance 7: 413–26. [Google Scholar] [CrossRef]
- Shirvani, Abootaleb, Yuan Hu, Svetlozar T. Rachev, and Frank J. Fabozzi. 2020. Option pricing with mixed Lévy subordinated price process and implied probability weighting function. Journal of Derivatives 28: jod.2020.1.102. [Google Scholar] [CrossRef]
- Shreve, Steven E. 2004. Stochastic Calculus for Finance II: Continuous-Time Models. New York: Springer. [Google Scholar]
- Simonato, Jean-Guy. 2011. Johnson binomial trees. Quantitative Finance 11: 1165–76. [Google Scholar] [CrossRef][Green Version]
- Skorokhod, Anatoly V. 1956. Limit theorems for stochastic processes. Theory of Probability and Its Applications 1: 261–90. [Google Scholar] [CrossRef]
- Skorokhod, Anatoly V. 2005. Basic Principles and Applications of Probability Theory. Berlin: Springer. [Google Scholar]
- Tian, Yisong. 1999. A flexible binomial option pricing model. Journal of Futures Markets 19: 817–43. [Google Scholar] [CrossRef]
- Walsh, John B. 2003. The rate of convergence of the binomial tree scheme. Finance and Stochastics 7: 337–61. [Google Scholar] [CrossRef]
- Yeap, Claudia, Simon S. Kwok, and S. T. Boris Choy. 2018. A flexible generalized hyperbolic option pricing model and its special cases. Journal of Financial Econometrics 16: 425–60. [Google Scholar] [CrossRef]
- Yuen, Fei Lung, Tak Kuen Siu, and Hailiang Yang. 2013. Option valuation by a self-exciting threshold binomial model. Mathematical and Computer Modelling 58: 28–37. [Google Scholar] [CrossRef]
- Zakamouline, Valeri. 2009. The best hedging strategy in the presence of transaction costs. International Journal of Theoretical and Applied Finance 12: 833–60. [Google Scholar] [CrossRef]
- Zhu, Song-Ping, and Xin-Jiang He. 2017. A new closed-form formula for pricing European options under skew Brownian motion. The European Journal of Finance 24: 1063–74. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).