Knowledge Sharing and Cumulative Innovation in Business Networks
Abstract
1. Introduction
2. The Model
2.1. The Intratemporal Profit Function
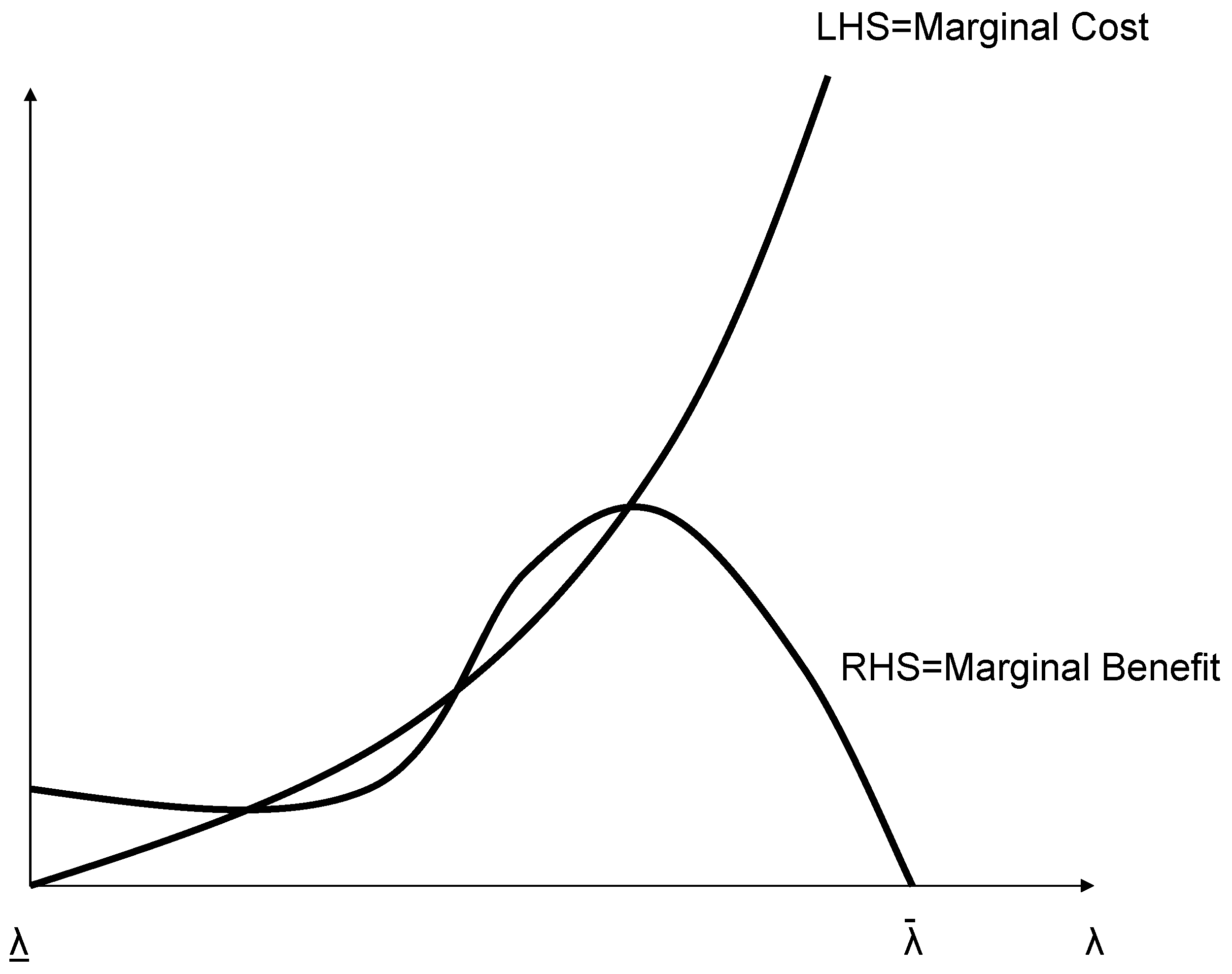
2.2. The Dynamics of Innovation
- Do not share its innovation with other firms, in which case they all remain at level .
- Share the innovation, in which case all firms such that can upgrade to level .
2.3. The Nash Solution
3. Cooperative Equilibria
4. Endogenous R&D Effort: The Role of Strategic Complementarities
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| 1 | See also Curley and Salmelin (2017) for a survey of the innovative culture of the software industry. |
| 2 | See Nonaka and Nishiguchi (2001); Nonaka et al. (2001), and, in that same volume, the case studies of Nishiguchi (2001); Nishiguchi and Caspary (2001); Lincoln and Ahmadjian (2000), and de Michelis (2001). |
| 3 | See, for example, Carvalho Vieira et al. (2021); Hitchen et al. (2017); Rexhepi et al. (2019), and Seyfettinoglu et al. (2020). |
| 4 | On the other hand, obviously, many firms avoid making their innovations open and rely instead on patents or even trade secrets. A famous example is the Coca-Cola beverage formula (see Crittenden et al. 2015). Clearly, revealing such a secret would be of little interest to the firm, as it is likely to lead to imitation instead of cumulative process innovation (see Morikawa 2014 for a discussion of the effect of trade secrets on product vs. process innovation). Another famous example is the Google search algorithm. Here, the explanation is likely to be different. While revealing that algorithm is likely to lead to a wave of improvements that Google could benefit from, provided they were made public, the firm’s market share is so big that it loses too much in the short term by making its algorithm public. In terms of the model, this is similar to a case where the number of firms is too small for the cooperative equilibrium to exist. |
| 5 | |
| 6 | This is the option in Aloysius (1999). See also Brod and Shivakumar (1997). Petit and Tolwinski (1999) assume away any problem in enforcing cooperation. |
| 7 | An interesting paper by Dutta and Seabrigh (2002) looks at the impact of the extent to which knowledge is explicit on growth and at its cross-impact with competition. However, the degree of explicitness of knowledge is exogenous, whereas it can be viewed as endogenous in the current paper. Katz and Ordover (1990) discuss informally how improvements in intellectual property rights may enhance incentives to share information by licensing. Licensing is not considered in the present paper. |
| 8 | We can simply assume that firms do observe whether one competitor is struck by an innovation even though they need not benefit from the innovation. Thus, there is no asymmetry of information as far as the structure of the game is concerned. The asymmetry of information with respect to the contents of the innovation are summarized by the payoffs and play no further role in the determination of the equilibrium strategies. |
| 9 | One has to check that exists, i.e., is finite. That is actually an implication of the derivations that follow. |
| 10 | In the model’s setting, a deviation would be detected as other firms would observe a fall in profits without an innovation being released, but that would change if profits were subject to shocks. |
| 11 | This restriction implies that goes up with k, so that . |
| 12 | It is slightly weaker than (4). |
| 13 | Note that we rule out any cooperation on , which may be unobservable, and continue to focus on the incentive to make one’s innovation public. |
| 14 | Furthermore, this restriction prevents degenerate solutions where the growth rate is greater than the interest rate. |
| 15 | The model is clearly silent about consumer surplus. One may conceive of innovations that reduce the elasticity of demand and may thus harm consumers. |
| 16 | Lerner and Tirole (2002), though, deal with the role of career concerns in the development of open source software. |
References
- Aghion, Philippe, and Peter Howitt. 1992. A Model of Growth Through Creative Destruction. Econometrica 60: 323–51. [Google Scholar] [CrossRef]
- Aloysius, John A. 1999. Membership in a Research Consortium: The project selection game. Journal of Economic Behavior and Organization 40: 325–36. [Google Scholar] [CrossRef]
- Baumol, William. 1992. Horizontal collusion and innovation. Economic Journal 102: 129–37. [Google Scholar] [CrossRef]
- Bessen, James, and Eric Maskin. 2008. Sequential Innovation, Patents, and Imitation. The Rand Journal of Economics 40: 611–35. [Google Scholar] [CrossRef]
- Brod, Andrew, and Ram Shivakumar. 1997. R&D cooperation and the joint exploitation of R&D. Canadian Journal of Economics 30: 673–84. [Google Scholar]
- Cabigiosu, Anna. 2023. Open and collaborative innovation in the automotive industry. In The Green Transition of the Automotive Industry. Edited by A. Cabigiosu and P. Lancini. Cham: Springer, pp. 131–59. [Google Scholar]
- Carvalho Vieira, Filipe, Leandro R. C. Bonfim, and Aline Cristina da Cruz. 2021. The process of opening innovation networks: Open innovation at Embrapa Florestas. Innovation & Management Review 19: 123–39. [Google Scholar]
- Chesbrough, Henry W. 2003. Open Innovation. The New Imperative for Creating and Profiting from Technology. Harvard: Harvard Business School Press. [Google Scholar]
- Chesbrough, Henry W., Wim Vanhaverbeke, and Joel West, eds. 2014. New Frontiers in Open Innovation. Oxford: Oxford University Press. [Google Scholar]
- Cooper, Russell, and Andrew John. 1988. Multiple equilibria and strategic complementarities. Quarterly Journal of Economics 103: 441–63. [Google Scholar] [CrossRef]
- Cozzi, Guido. 1999. R and D cooperation and growth. Journal of Economic Theory 86: 17–49. [Google Scholar] [CrossRef]
- Crittenden, William F., Victoria L. Crittenden, and Allison Pierpont. 2015. Trade secrets: Managerial guidance for competitive advantage. Business Horizons 58: 607–13. [Google Scholar] [CrossRef]
- Curley, Martin, and Bror Salmelin. 2017. Open Innovation 2.0. The New Mode of Digital Innovation for Prosperity and Sustainability. Berlin/Heidelberg: Springer. Available online: https://link.springer.com/book/10.1007/978-3-319-62878-3 (accessed on 23 January 2024).
- d’Aspremont, Claude, and Alexis Jacquemin. 1988. Cooperative and Noncooperative R&D in Duopoly with spillovers. American Economic Review 78: 1133–37. [Google Scholar]
- de Michelis, Giorgio. 2001. Cooperation and Knowledge Creation. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 124–46. [Google Scholar]
- Dutta, Jayasri, and Paul Seabrigh. 2002. Competition and Economic Growth. Available online: https://www.researchgate.net/publication/255653065_Competition_and_Economic_Growth (accessed on 23 January 2024).
- Fudenberg, Drew, and Jean Tirole. 1991. Game Theory. Cambridge: MIT Press. [Google Scholar]
- Grossman, Gene M., and Elhanan Helpman. 1993. Innovation and Growth in the Global Economy. Cambridge: MIT Press. [Google Scholar]
- Hitchen, Emma L., Petra A. Nylund, and Eric Viardot. 2017. The Effectiveness of Open Innovation: Do Size and Performance of Open Innovation Groups Matter? International Journal of Innovation Management 21: 1–24. [Google Scholar] [CrossRef]
- Hyde, Alan. 1998. The Wealth of Shared Information: Silicon Valley’s High-Velocity Labor Market, Endogenous Economic Growth, and the Law of Trade Secrets. mimeo, Rutgers U. Available online: http://andromeda.rutgers.edu/~hyde/ (accessed on 23 January 2024).
- Katz, Michael, and Janusz Ordover. 1990. R&D cooperation and competition. In Brookings Papers on Economic Activity. Washington, DC: Brookings Papers on Economic Activity. [Google Scholar]
- Leahy, Dermot, and Peter Neary. 1997. Public policy toward R&D in oligopolistic industries. American Economic Review 8: 642–62. [Google Scholar]
- Lerner, Josh, and Jean Tirole. 2002. Some Economics of Open Source Mimeo. Cambridge: Harvard and Toulouse University. [Google Scholar]
- Lincoln, James, and Christina Ahmadjian. 2000. Shukko (Employee Transfers) and Tacit Knowledge Exchange in Japanese Supply Networks: The Electronics Industry Case. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 247–69. [Google Scholar]
- Morikawa, Masayuki. 2014. Innovation in the Service Sector and the Role of Patents and Trade Secrets. AJRC Working Papers 1403. Canberra: Australia-Japan Research Centre, Crawford School of Public Policy, The Australian National University. [Google Scholar]
- Nishiguchi, Toshihiro. 2001. Coevolution of Interorganizational Relations. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 197–222. [Google Scholar]
- Nishiguchi, Toshihiro, and Sigrun Caspary. 2001. “Co-opetition” in the Japanese Aircraft Industry. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 223–46. [Google Scholar]
- Nonaka, Ikujiro, and Toshihiro Nishiguchi. 2001. Introduction: Knowledge Emergence. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 3–12. [Google Scholar]
- Nonaka, Ikujiro, Noboru Konno, and Ryoko Toyama. 2001. Emergence of “Ba”: A Conceptual Framework for the Continuous and Self-transcending Process of Knowledge Creation. In Knowledge Emergence: Social, Technical, and Evolutionary Dimensions of Knowledge Creation. Edited by Ikujiro Nonaka and Toshihiro Nishiguchi. Oxford: Oxford University Press, pp. 13–29. [Google Scholar]
- Petit, Maria Luisa, and Boleslaw Tolwinski. 1999. R&D cooperation or competition? European Economic Review 43: 185–208. [Google Scholar]
- Piore, Michael, and Charles Sabel. 1986. The Second Industrial Divide: Possibilities for Prosperity. New York: Basic Books. [Google Scholar]
- Polanyi, Michael. 1962. Personal Knowledge: Towards a Post-Critical Philosophy. Chicago: University of Chicago Press. [Google Scholar]
- Purificato, Marco. 2014. The Open Innovation Paradigm in Electric Vehicle Industry: A Case Study of Tesla Motors. Bachelor’s thesis, LUISS Guido Carli, Rome, Italy. [Google Scholar]
- Raymond, Eric S. 1999. The Cathedral and the Baazar. Available online: https://monoskop.org/images/e/e0/Raymond_Eric_S_The_Cathedral_and_the_Bazaar_rev_ed.pdf (accessed on 23 January 2024).
- Rexhepi, Gadaf, Robert D. Hisrich, and Veland Ramadani, eds. 2019. Open Innovation and Entrepreneurship. Springer Books. Berlin/Heidelberg: Springer. [Google Scholar]
- Romer, Paul M. 1990. Endogenous Technological Change. Journal of Political Economy 98: S71–S102. [Google Scholar] [CrossRef]
- Saint-Paul, Gilles. 2003. Growth effects of non proprietary innovation. Journal of the European Economic Association 1: 429–39. [Google Scholar] [CrossRef]
- Schumpeter, Joseph A. 1942. Capitalism, Socialism, and Democracy. London: Routledge. [Google Scholar]
- Scotchmer, Suzanne. 1991. Standing on the Shoulders of Giants: Cumulative Research and the Patent Law. Journal of Economic Perspectives 5: 29–41. [Google Scholar] [CrossRef]
- Scotchmer, Suzanne. 1996. Protecting Early Innovators: Should Second-Generation Products be Patentable? RAND Journal of Economics 27: 322–31. [Google Scholar] [CrossRef]
- Scotchmer, Suzanne. 2004. Innovation and Incentives. Cambridge: MIT Press. [Google Scholar]
- Seyfettinoglu, Ümit K., Şebnem Arik, and Selim Çagatay. 2020. Determinants of Industry and Region Based Open Innovation in Turkey. Istanbul Business Research 49: 1–35. [Google Scholar] [CrossRef]
- Tirole, Jean. 1990. The Theory of Industrial Organization. Cambridge: MIT Press. [Google Scholar]
| r | Maximum Value of N | Range over Which (13) Holds |
|---|---|---|
| 0.04 | 3 | 2–3 |
| 0.05 | 4 | 2–4 |
| 0.06 | 5 | 2–5 |
| 0.07 | 5 | 2–5 |
| 0.08 | 6 | 4–6 |
| 0.1 | 8 | 6–8 |
| 0.13 | 10 | 9–10 |
| 0.16 | 13 | 13–13 |
| 0.18 | 15 | – |
| r | Maximum Value of N | Range over Which (14) Is Violated |
|---|---|---|
| 0.04 | 3 | — |
| 0.05 | 4 | 2–2 |
| 0.06 | 5 | 2–2 |
| 0.07 | 5 | 2–3 |
| 0.09 | 7 | 2–4 |
| 0.1 | 8 | 2–5 |
| 0.12 | 10 | 2–6 |
| 0.14 | 11 | 2–8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saint-Paul, G. Knowledge Sharing and Cumulative Innovation in Business Networks. J. Risk Financial Manag. 2024, 17, 137. https://doi.org/10.3390/jrfm17040137
Saint-Paul G. Knowledge Sharing and Cumulative Innovation in Business Networks. Journal of Risk and Financial Management. 2024; 17(4):137. https://doi.org/10.3390/jrfm17040137
Chicago/Turabian StyleSaint-Paul, Gilles. 2024. "Knowledge Sharing and Cumulative Innovation in Business Networks" Journal of Risk and Financial Management 17, no. 4: 137. https://doi.org/10.3390/jrfm17040137
APA StyleSaint-Paul, G. (2024). Knowledge Sharing and Cumulative Innovation in Business Networks. Journal of Risk and Financial Management, 17(4), 137. https://doi.org/10.3390/jrfm17040137





