Option Pricing with the Logistic Return Distribution
Abstract
1. Introduction
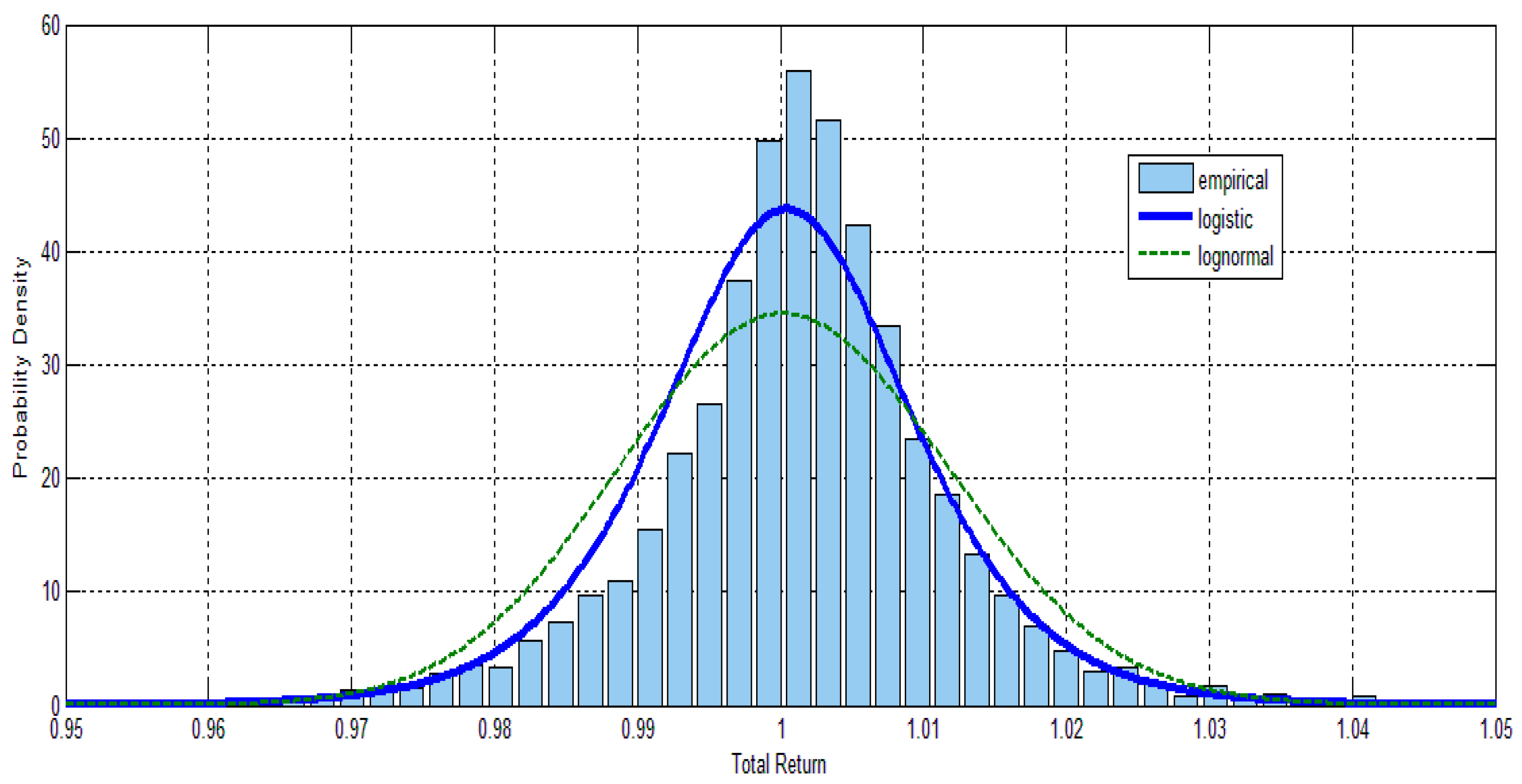
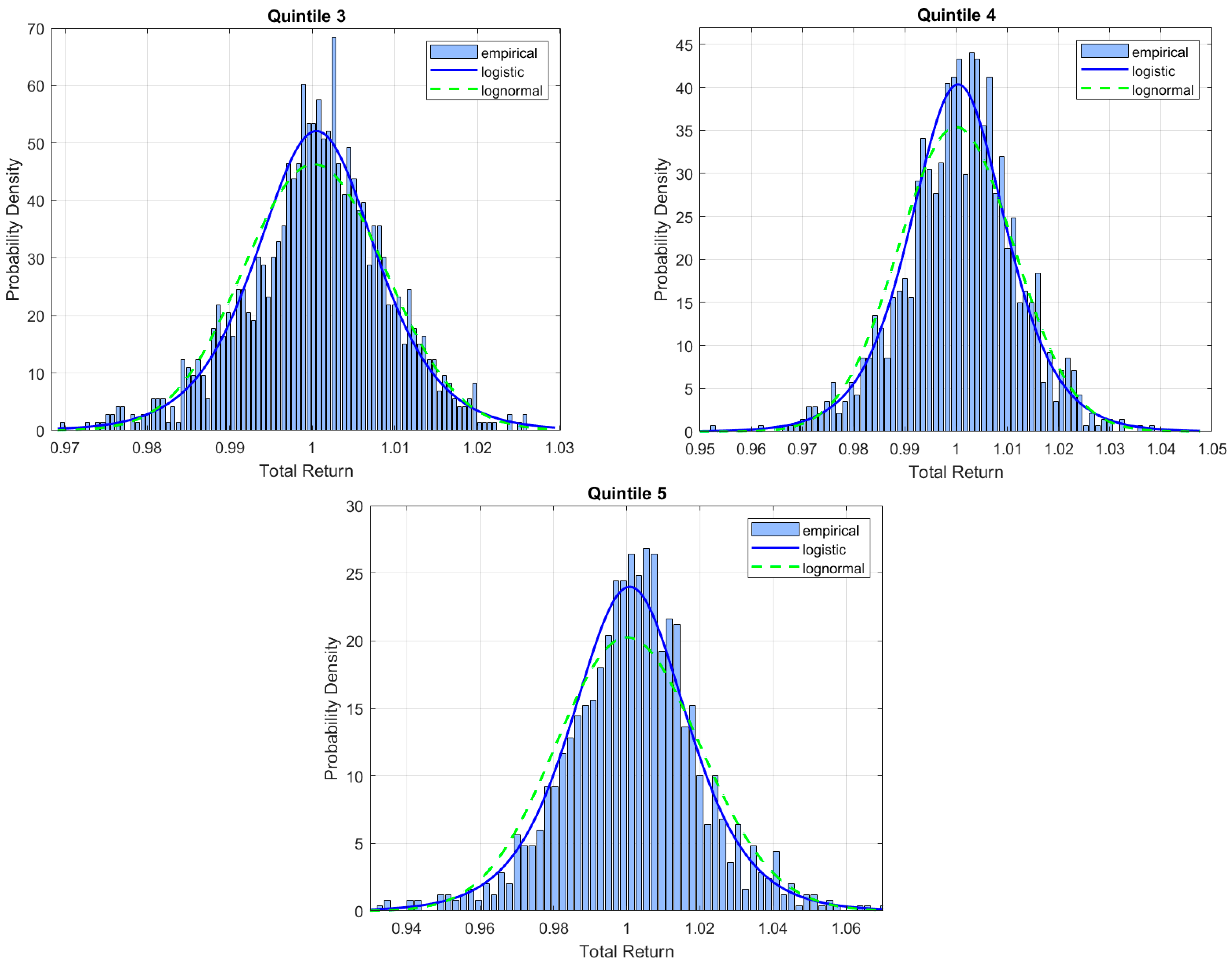
2. The Empirical Return Distribution
They find this result for stock indices, individual stocks, and even bonds.2“For investment horizons shorter than one year the logistic distribution best describes the empirical data”.(p. 61)
3. Logistic Option Pricing
4. Empirical Performance of the Logistic Option Pricing Formula
4.1. Data
- The bid-ask spread is less than 2.5% of (bid + ask)/2.
- Bid > USD 10
- Open interest > 500
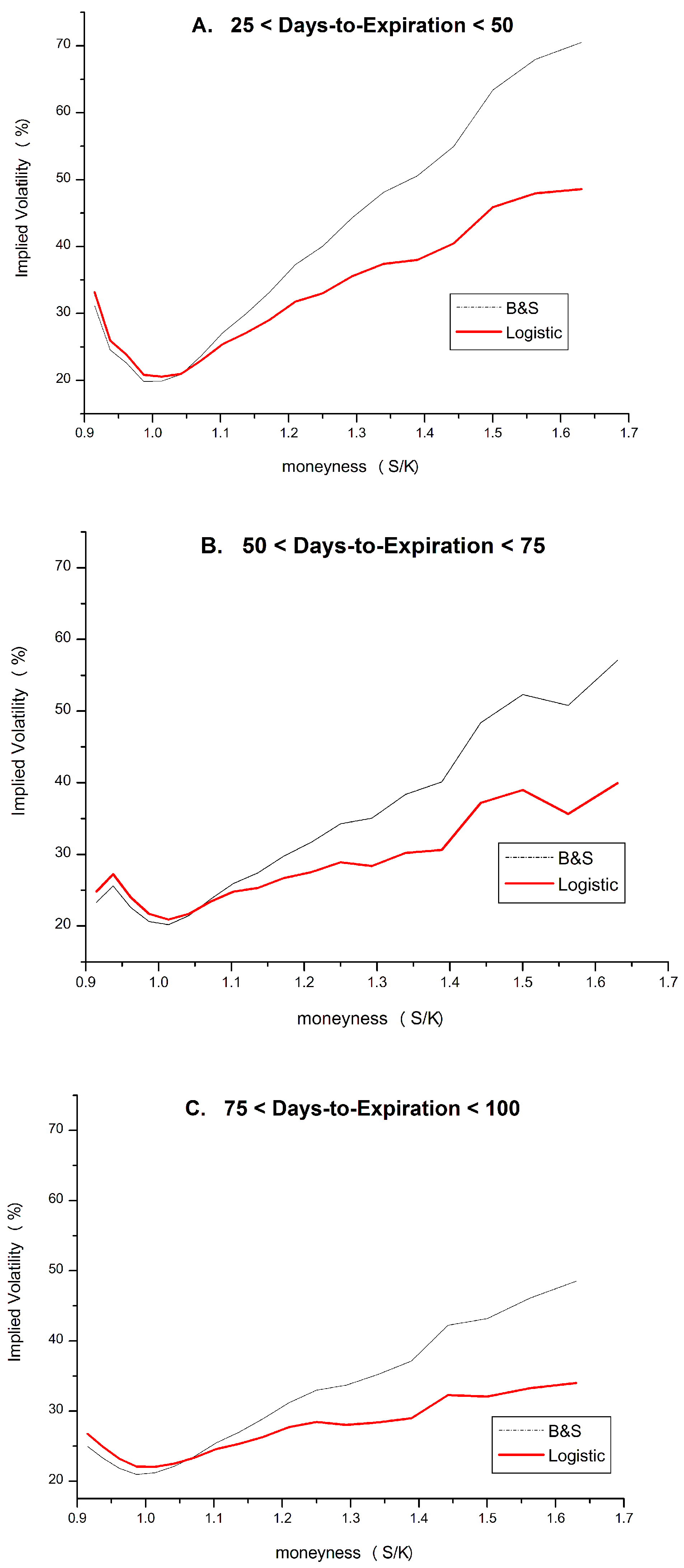
4.2. Volatility Smile
4.3. Hedging Errors
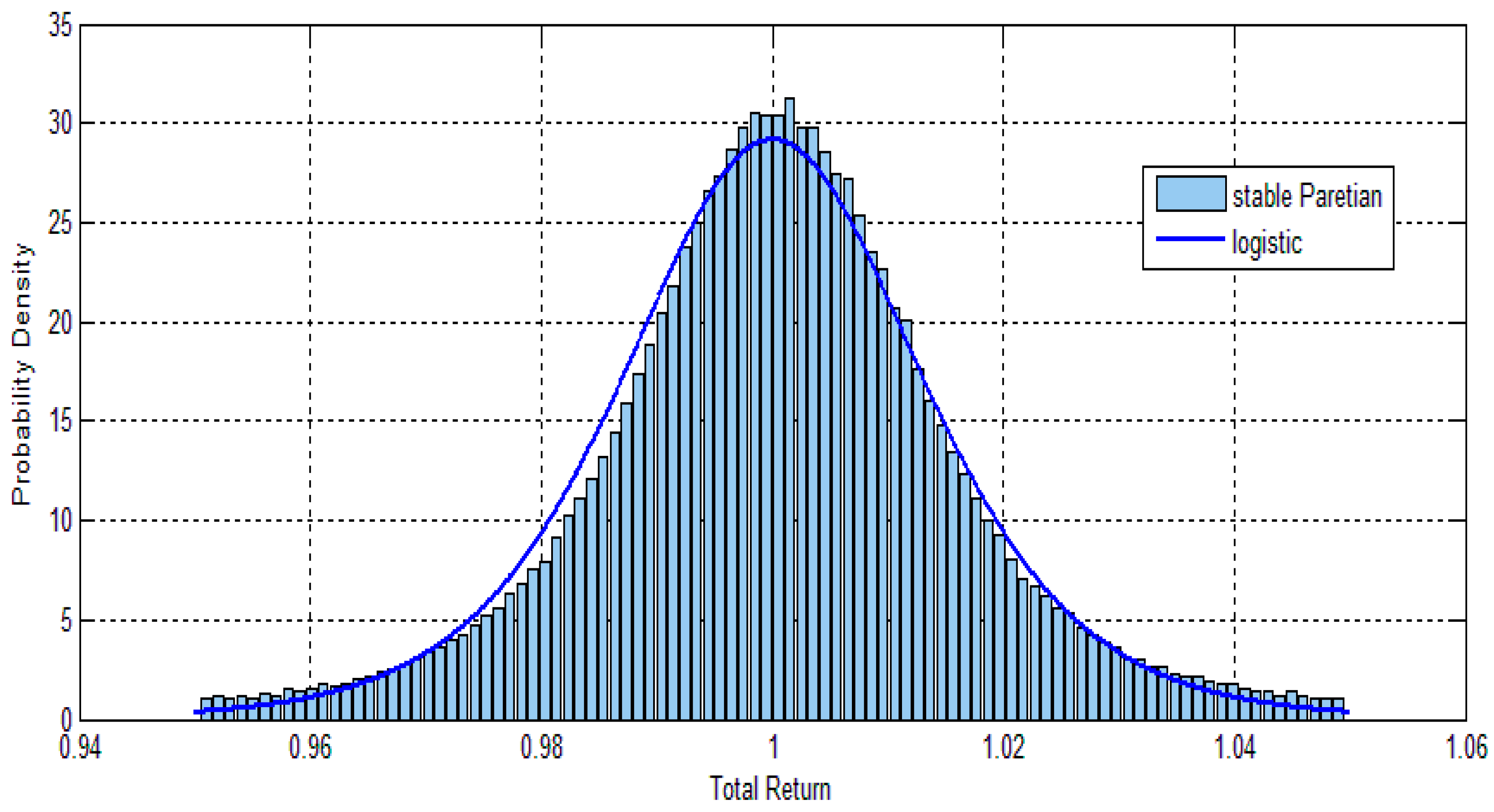
5. Possible Origin of the Logistic Return Distribution
- The empirical return distribution over very short periods (15 s to a minute) is very close to a truncated Lévy (stable Paretian) distribution with an exponent α of approximately 1.4 (Mantegna and Stanley 1995).
- This distribution is very similar to the logistic distribution. Figure 4 demonstrates this point by comparing these two distributions.
- It is well-known that the Lévy distribution is stable. When the Lévy distribution is truncated, it is pseudo-stable. This means that it eventually converges to the normal distribution because it has finite variance and the conditions of the central limit theorem hold; however, this convergence can take a very long time (Mantegna and Stanley 1994). For holding periods shorter than this convergence time, the distribution remains an approximately truncated Lévy distribution, and hence approximately logistic.
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| 1 | An important exception that does not imply a log-normal return distribution is the model of Carr and Wu (2003), who employ the stable Pareto return distribution to explain the observation that the volatility smirk does not flatten out as maturity increases. The logistic distribution employed in the present study is very similar to a truncated stable Paretian distribution (see Section 5 and Figure 4). The advantage of using the logistic distribution is that it yields a very simple analytic option pricing formula. |
| 2 | |
| 3 | For the longer holding periods the conditional distribution analysis is both less relevant and less feasible. The typical length of volatility regimes is probably not very long. Practically, partitioning the 88 year sample into quintiles leads to less than 18 annual observations per quintile, which makes estimating the shape of the conditional distribution impractical. Finney (1978) shows that for a special choice of parameters, the logistic distribution is close to the normal distribution. This is employed by Hofstetter and Selby (2001) to obtain an analytic approximation for the B&S implied volatility. The results reported in this section show that the empirical return distribution is significantly different than the log-normal and normal distributions and is much closer to the logistic distribution. In other words, for the empirical distribution, the special parametrization under which the logistic and the normal are similar does not hold, and the two distributions are quite different. |
| 4 | If the asset’s end-of-period value at maturity is distributed log-normally, the return distribution is also log-normal. This is true both for the physical return distribution and the risk-neutral return distribution, although these two distributions have different means. Similarly, a logistic end-of-period asset value implies a logistic risk-neutral return distribution. |
| 5 | The logistic distribution is a part of the family of elliptical distributions, of which the normal distribution is also a member. The CAPM holds for all distributions in this family (with the other standard assumptions; see Chamberlain (1983), Owen and Rabinovitch (1983), and Berk (1997)). |
| 6 | For practical purposes, it is convenient to have a simple way to translate annual volatility to the volatility for different horizons. While the scaling of the standard deviation with time by is mathematically precise only for log-returns and under the assumption of no serial correlation, Figure A1 in the Appendix A shows that this scaling is a very good approximation for empirical returns (rather than log-returns) as well. |
| 7 | Similar results, although more noisy, are obtained when the option’s implied volatility is used instead of the VIX. |
| 8 | For example, suppose that new information/liquidity shocks arrive every second, and this determines some 1 s return distribution. One could technically define a 1 ms return distribution for this process, but this would be meaningless—it would not change the 1 s return distribution dictated by Nature, nor induce it to be log-normal. For the advantages of the discrete-time approach see Brennan (1979). |
| 9 | The idea is based on the fact that the sum of i.i.d. random variables drawn from any distribution with a power law tail and exponent α < 2 converges to the Lévy distribution with an exponent α. Thus, if an individual’s influence on the stock price is proportional to her wealth, and the wealth distribution has a power law tail, then the return, which is the sum of the actions of many individuals, will be distributed according to the Lévy distribution with the same exponent as that of the wealth distribution. The truncation is due to the finiteness of the economy. |
References
- Ackerer, Damien, and Damir Filipović. 2020. Option pricing with orthogonal polynomial expansions. Mathematical Finance 30: 47–84. [Google Scholar] [CrossRef]
- Amin, Kaushik I., and Robert. A. Jarrow. 1992. Pricing options on risky assets in a stochastic interest rate economy. Mathematical Finance 2: 217–37. [Google Scholar] [CrossRef]
- Amin, Kaushik I., and Victor. K. Ng. 1993. Option valuation with systematic stochastic volatility. The Journal of Finance 48: 881–910. [Google Scholar] [CrossRef]
- Bailey, Warren, and Rene. M. Stulz. 1989. The pricing of stock index options in a general equilibrium model. Journal of Financial and Quantitative Analysis 24: 1–12. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 1997. Empirical performance of alternative option pricing models. The Journal of Finance 52: 2003–49. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Robert F. Engle, and Loriano Mancini. 2008. A GARCH option pricing model with filtered historical simulation. Review of Financial Studies 21: 1223–58. [Google Scholar] [CrossRef]
- Bartl, Daniel, Samuel Drapeau, and Ludovic Tangpi. 2020. Computational aspects of robust optimized certainty equivalents and option pricing. Mathematical Finance 30: 287–309. [Google Scholar] [CrossRef]
- Bates, David S. 1991. The crash of ’87: Was it expected? The evidence from options markets. The Journal of Finance 46: 1009–44. [Google Scholar] [CrossRef]
- Becker, Garry F. 1931. Hyperbolic Functions. Redditch: Read Books. [Google Scholar]
- Berk, Jonathan B. 1997. Necessary conditions for the CAPM. Journal of Economic Theory 73: 245–57. [Google Scholar] [CrossRef][Green Version]
- Billingsley, Patrick. 2008. Probability and Measure. Hoboken: John Wiley & Sons. [Google Scholar]
- Black, Fischer, and Myron Scholes. 1973. The pricing of options and corporate liabilities. The Journal of Political Economy 81: 637–54. [Google Scholar] [CrossRef]
- Bradley, Richard C. 2005. Basic properties of strong mixing conditions. A survey and some open questions. Probability Surveys 2: 107–44. [Google Scholar] [CrossRef]
- Brennan, Michael. 1979. The pricing of contingent claims in discrete time models. The Journal of Finance 24: 53–68. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2003. The finite moment log stable process and option pricing. The Journal of Finance 58: 753–78. [Google Scholar] [CrossRef]
- Chamberlain, Gary. 1983. A characterization of the distributions that imply mean—Variance utility functions. Journal of Economic Theory 29: 185–201. [Google Scholar] [CrossRef]
- Cox, John C., Stephen A. Ross, and Mark Rubinstein. 1979. Option pricing: A simplified approach. Journal of Financial Economics 7: 229–63. [Google Scholar] [CrossRef]
- Cremers, K. Marijn, Joost Driessen, and Pascal Maenhout. 2008. Explaining the level of credit spreads: Option-implied jump risk premia in a firm value model. Review of Financial Studies 21: 2209–42. [Google Scholar] [CrossRef]
- Duffie, Darrell, Jun Pan, and Kenneth Singleton. 2000. Transform analysis and asset pricing for affine jump-diffusions. Econometrica 68: 1343–76. [Google Scholar] [CrossRef]
- Durrett, Rick. 2010. Probability: Theory and Examples. Cambridge: Cambridge University Press. [Google Scholar]
- Eraker, Bjorn. 2004. Do stock prices and volatility jump? Reconciling evidence from spot and option prices. The Journal of Finance 59: 1367–404. [Google Scholar] [CrossRef]
- Fama, Eugene. F. 1965. The behavior of stock-market prices. Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Finney, David J. 1978. Statistical Methods in Biological Assay, 3rd ed. London: Griffin. [Google Scholar]
- Geske, Robert. 1979. The valuation of compound options. Journal of Financial Economics 7: 63–81. [Google Scholar] [CrossRef]
- Heston, Steven L. 1993. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Hofstetter, Etienne, and Michael J. Selby. 2001. The Logistic Function and Implied Volatility: Quadratic Approximation and Beyond. Working Paper. Coventry: Warwick Business School. [Google Scholar]
- Hull, John. 2009. Options, Futures and Other Derivatives. London: Pearson Education. [Google Scholar]
- Hull, John, and Alan White. 1987. The pricing of options on assets with stochastic volatilities. The Journal of Finance 42: 281–300. [Google Scholar] [CrossRef]
- Kirkby, J. Lars, and Duy Nguyen. 2020. Efficient Asian option pricing under regime switching jump diffusions and stochastic volatility models. Annals of Finance 16: 307–51. [Google Scholar] [CrossRef]
- Kou, Steven G. 2002. A jump-diffusion model for option pricing. Management Science 48: 1086–101. [Google Scholar] [CrossRef]
- Levy, Haim, and Ran Duchin. 2004. Asset return distributions and the investment horizon. The Journal of Portfolio Management 30: 47–62. [Google Scholar] [CrossRef]
- Levy, Moshe. 2005. Market Efficiency, the Pareto Wealth Distribution, and the Lévy Distribution of Stock Returns. In The Economy as an Evolving Complex System, III: Current Perspectives and Future Directions. Oxford: Oxford Academic, p. 101. [Google Scholar]
- Madan, Dilip B., Peter P. Carr, and Eric C. Chang. 1998. The variance gamma process and option pricing. European Finance Review 2: 79–105. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 1963. The Variation of Certain Speculative Prices. Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Mantegna, Rosario N., and Eugene H. Stanley. 1994. Stochastic process with ultraslow convergence to a Gaussian: The truncated Lévy flight. Physical Review Letters 73: 2946. [Google Scholar] [CrossRef] [PubMed]
- Mantegna, Rosario N., and Eugene H. Stanley. 1995. Scaling behaviour in the dynamics of an economic index. Nature 376: 46–49. [Google Scholar] [CrossRef]
- Melino, Angelo, and Stuart M. Turnbull. 1990. Pricing foreign currency options with stochastic volatility. Journal of Econometrics 45: 239–65. [Google Scholar] [CrossRef]
- Merton, Robert C. 1973. Theory of rational option pricing. The Bell Journal of Economics and Management Science 4: 141–83. [Google Scholar] [CrossRef]
- Merton, Robert C. 1976. Option pricing when underlying stock returns are discontinuous. Journal of Financial Economics 3: 125–44. [Google Scholar] [CrossRef]
- Naik, Vasanttilak. 1993. Option valuation and hedging strategies with jumps in the volatility of asset returns. The Journal of Finance 48: 1969–84. [Google Scholar] [CrossRef]
- Officer, Robert R. 1972. The distribution of stock returns. Journal of the American Statistical Association 67: 807–12. [Google Scholar] [CrossRef]
- Owen, Joel, and Ramon Rabinovitch. 1983. On the class of elliptical distributions and their applications to the theory of portfolio choice. The Journal of Finance 38: 745–52. [Google Scholar] [CrossRef]
- Pan, Jun. 2002. The jump-risk premia implicit in options: Evidence from an integrated time-series study. Journal of Financial Economics 63: 3–50. [Google Scholar] [CrossRef]
- Raftery, Adrian E. 1995. Bayesian model selection in social research. Sociological Methodology 25: 111–63. [Google Scholar] [CrossRef]
- Raja, Ammar. 2009. Future of Option Pricing: Use of Log Logistic Distribution Instead of Log Normal Distribution in Black Scholes Model. MPRA Working Paper. Munich: University Library of Munich. [Google Scholar]
- Scott, Louis O. 1987. Option pricing when the variance changes randomly: Theory, estimation, and an application. Journal of Financial and Quantitative Analysis 22: 419–38. [Google Scholar] [CrossRef]
- Stein, Elias M., and Jeremy C. Stein. 1991. Stock price distributions with stochastic volatility: An analytic approach. Review of Financial Studies 4: 727–52. [Google Scholar] [CrossRef]
- Wiggins, James B. 1987. Option values under stochastic volatility: Theory and empirical estimates. Journal of Financial Economics 19: 351–72. [Google Scholar] [CrossRef]
- Willems, Sander. 2019. Asian option pricing with orthogonal polynomials. Quantitative Finance 19: 605–18. [Google Scholar] [CrossRef]

| Unconditional | Quintile 1 (Lowest VIX) | Quintile 2 | Quintile 3 | Quintile 4 | Quintile 5 (Highest VIX) | |
|---|---|---|---|---|---|---|
| Logistic | −18,958 | −4566 | −4274 | −4010 | −3701 | −3063 |
| Log-logistic | −18,955 | −4565 | −4273 | −4009 | −3700 | −3062 |
| Rice | −18,399 | −4534 | −4253 | −4005 | −3683 | −3012 |
| Normal | −18,399 | −4534 | −4253 | −4005 | −3683 | −3011 |
| Gamma | −18,396 | −4533 | −4252 | −4004 | −3681 | −3011 |
| Log-normal | −18,394 | −4532 | −4251 | −4004 | −3680 | −3010 |
| Quintile | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| VIX range (%) | 9.3–13.6 | 13.6–16.9 | 16.9–20.5 | 20.5–25.1 | 25.1–80.9 |
| Mean of next-day return: (%) | 0.04 | 0.01 | 0.01 | 0.02 | 0.07 |
| Standard deviation of next-day return: (%) | 0.56 | 0.70 | 0.86 | 1.14 | 1.97 |
| Goodness-of-Fit Criterion | 1 Month | 3 Months | 6 Month | 9 Months | 12 Months |
|---|---|---|---|---|---|
| Negative log-likelihood | logistic—1667 log-logistic—1660 normal—1568 Rice—1568 Gamma—1566 log-normal—1562 | logistic—324 log-logistic-322 log-normal—286 inverse Guassian—285 gamma—285 Rice—274 | logistic—101 log-logistic-97 normal—94 Rice—94 gamma—90 log-normal—86 | logistic—42 Weibull—41 normal—40 Rice—40 general extreme value—39 log-logistic—37 | general extreme value—22 Weibull—21 normal—19 Rice—19 logistic—19 gamma—16 |
| Bayesian information criterion | logistic—3319 log-logistic—3306 normal—3122 Rice—3122 gamma—3118 log-normal—3110 | logistic—635 log-logistic—632 log-normal—561 inverse Guassian—559 gamma—558 Rice—537 | logistic—192 log-logistic—185 normal—177 Rice—177 gamma—170 log-normal—162 | logistic—73 Weibull—72 normal—70 Rice—70 general extreme value—64 log-logistic—64 | Weibull—34 normal—30 Rice—30 general extreme value—30 logistic—28 gamma—23 |
| 25–50 Days to Expiration | 50–75 Days to Expiration | 75–100 Days to Expiration | ||||
|---|---|---|---|---|---|---|
| B&S | Logistic | B&S | Logistic | B&S | Logistic | |
| Mean absolute normalized hedging error | 2.79 | 2.64 | 2.94 | 2.76 | 2.47 | 2.41 |
| Mean square normalized hedging error | 2.65 | 2.24 | 3.57 | 2.86 | 1.92 | 1.71 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Levy, H.; Levy, M. Option Pricing with the Logistic Return Distribution. J. Risk Financial Manag. 2024, 17, 67. https://doi.org/10.3390/jrfm17020067
Levy H, Levy M. Option Pricing with the Logistic Return Distribution. Journal of Risk and Financial Management. 2024; 17(2):67. https://doi.org/10.3390/jrfm17020067
Chicago/Turabian StyleLevy, Haim, and Moshe Levy. 2024. "Option Pricing with the Logistic Return Distribution" Journal of Risk and Financial Management 17, no. 2: 67. https://doi.org/10.3390/jrfm17020067
APA StyleLevy, H., & Levy, M. (2024). Option Pricing with the Logistic Return Distribution. Journal of Risk and Financial Management, 17(2), 67. https://doi.org/10.3390/jrfm17020067







