Markov-Regime Switches in Oil Markets: The Fear Factor Dynamics
Abstract
1. Introduction
2. Literature Review
3. Markov-Regime Switching Modeling of Return Dynamics in Oil Futures Markets
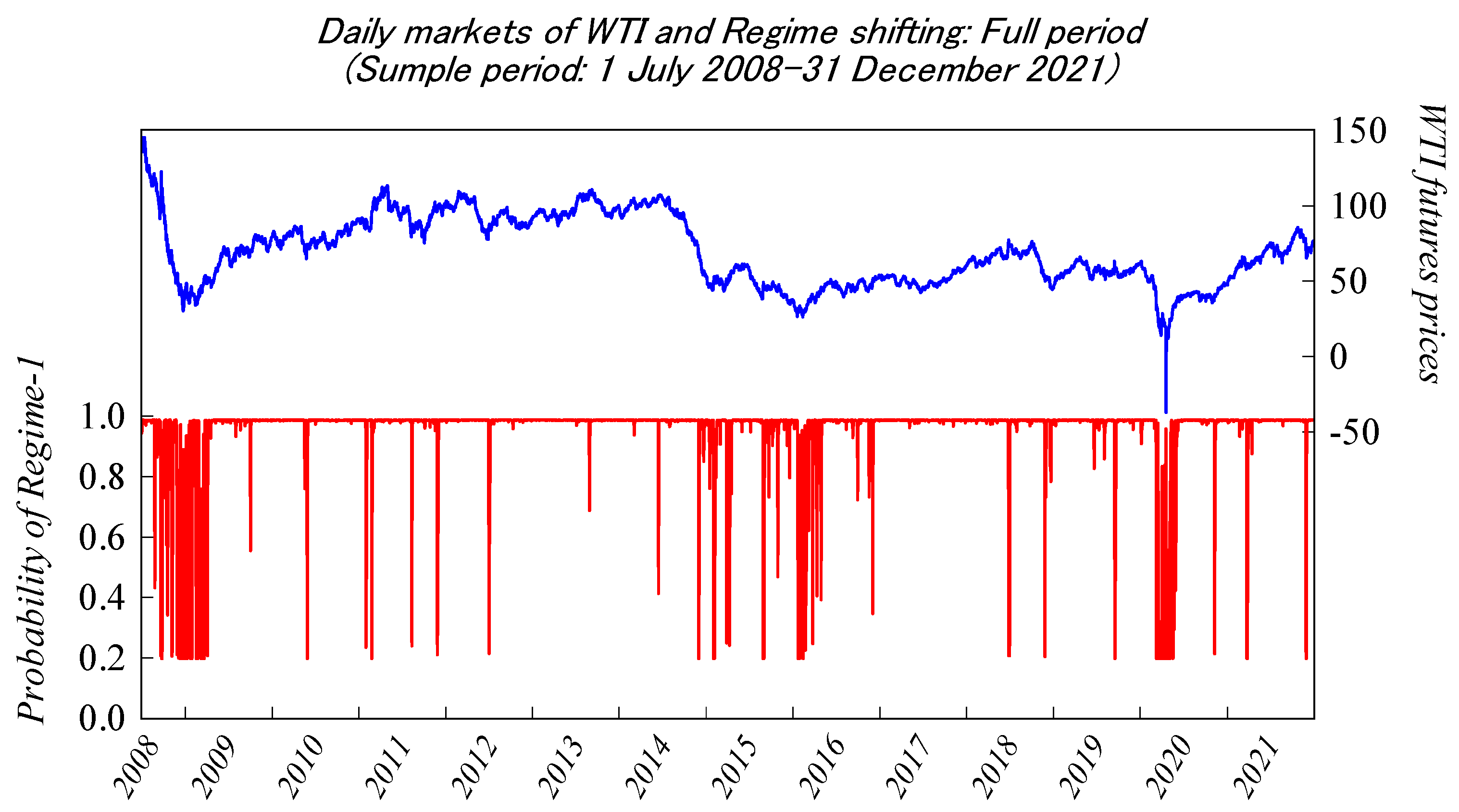
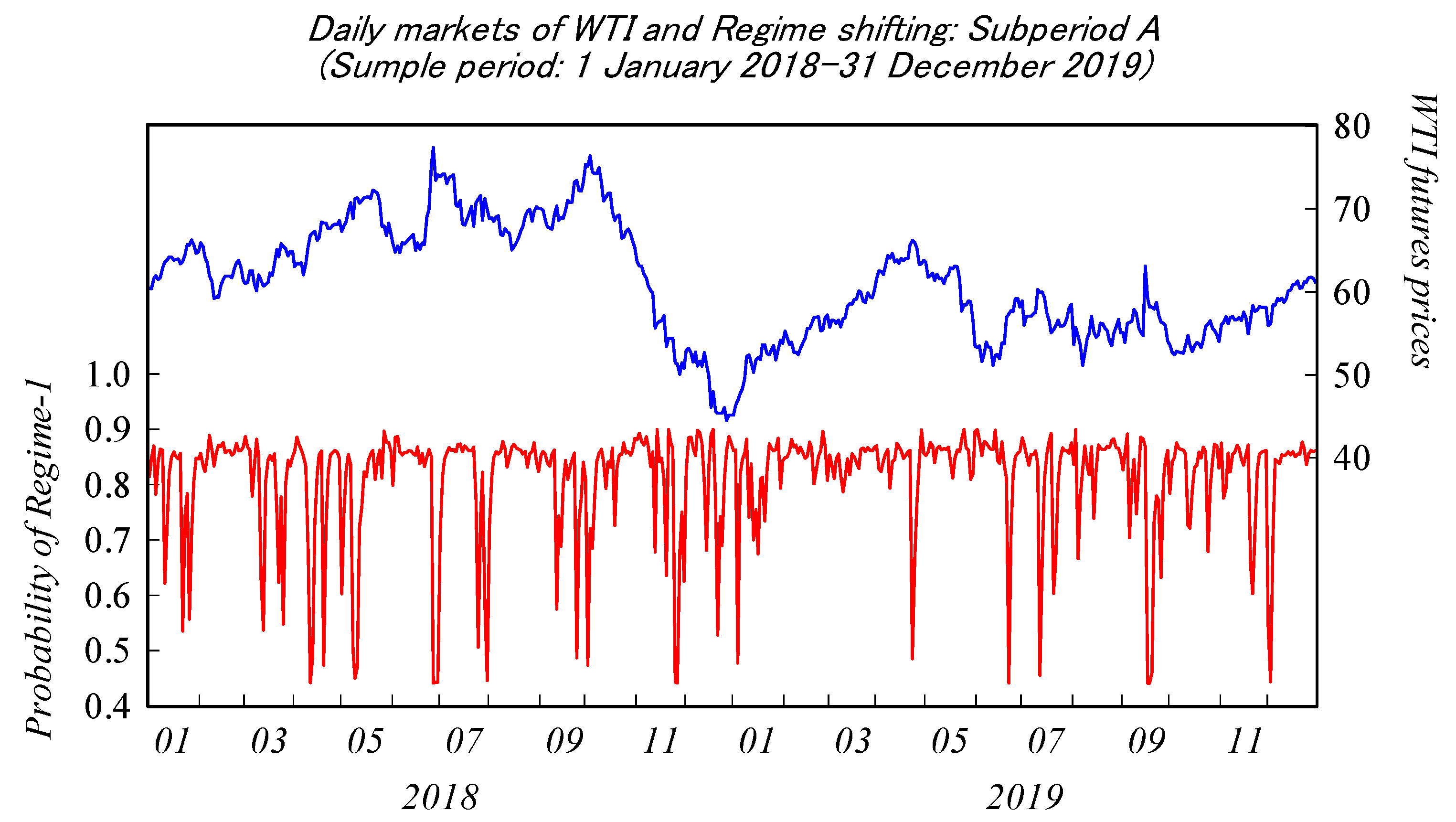
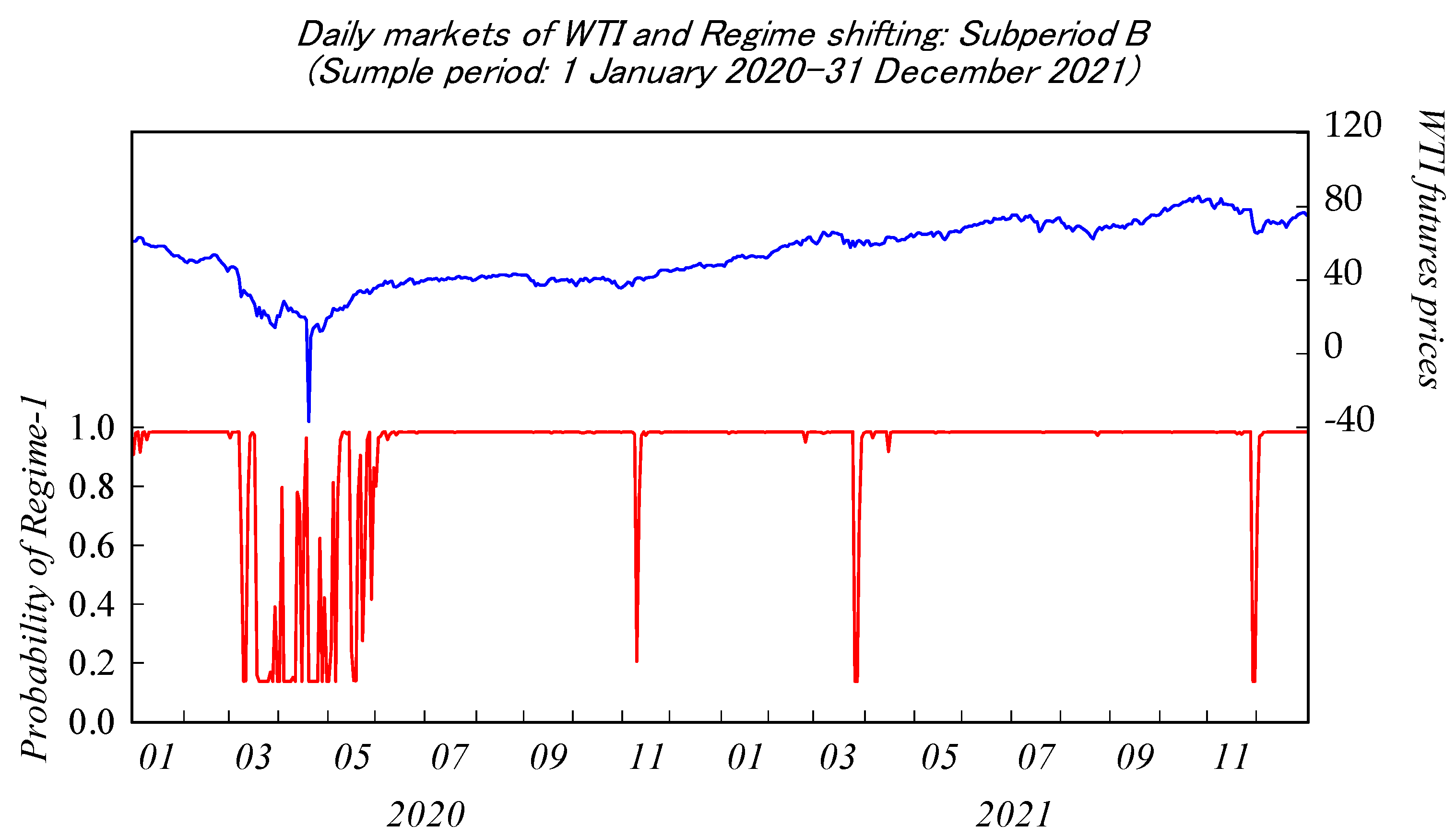
4. Empirical Evidence
4.1. Data Description and Distributional Properties
4.2. Model Estimation Results
4.3. Robustness Checks
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | It is noted that the study by Fleming et al. (1995) was performed with a volatility index based on the S&P 100 stock market index, formerly known as VIX index. |
| 2 | The focus is also placed, as in Mencia and Sentana (2013), on the valuation of VIX derivatives, where the volatility index serves as the underlying asset for derivatives contracts. |
| 3 | See for instance, S. Kim et al. (2019), Wang and Xie (2012), Choi and Hammoudeh (2010), Mensi et al. (2013), Raza et al. (2016) and Creti et al. (2013), inter alia. |
References
- Aboura, Sofiane, and Julien Chevallier. 2013. Leverage vs. feedback: Which Effect drives the oil market? Finance Research Letters 10: 131–41. [Google Scholar] [CrossRef]
- Baiardi, Lorenzo Cerboni, Massimo Costabile, Domenico De Giovanni, Fabio Lamantia, Arturo Leccadito, Ivar Massabó, Massimiliano Menzietti, Marco Pirra, Emilio Russo, and Alessandro Staino. 2020. The Dynamics of the S&P 500 under a crisis context: Insights from a Three-Regime Switching Model. Risks 8: 71. [Google Scholar]
- Baumeister, Christian, and Lutz Kilian. 2012. Real-Time Forecasts of the Real Price of Oil. Journal of Business & Economic Statistics 30: 326–36. [Google Scholar]
- Baumeister, Christian, and Lutz Kilian. 2015. Forecasting the Real Price of Oil in a Changing World: A Forecast Combination Approach. Journal of Business & Economic Statistics 33: 338–51. [Google Scholar]
- Beckmann, Joscha, Robert L. Czudaj, and Vipin Arora. 2020. The relationship between oil prices and exchange rates: Revisiting theory and evidence. Energy Economics 88: 104772. [Google Scholar] [CrossRef]
- Bodie, Zvi, and Victor I. Rosansky. 1980. Risk and Return in Commodity Futures. Financial Analysts Journal 36: 27–39. [Google Scholar] [CrossRef]
- Chen, Yanhui, Kaijian He, and Lean Yu. 2015. The Information Content of OVX for Crude Oil Returns Analysis and Risk Measurement: Evidence from the Kalman Filter Model. Annals of Data Science 2: 471–87. [Google Scholar] [CrossRef]
- Cheng, Ing-Haw, and Wei Xiong. 2014. Financialization of Commodity Market. Annual Review of Financial Economics 6: 419–41. [Google Scholar] [CrossRef]
- Cheung, C. Sherman, and Peter Miu. 2010. Diversification benefits of commodity futures. Journal of International Financial Markets, Institutions and Money 20: 451–74. [Google Scholar] [CrossRef]
- Choi, K., and S. Hammoudeh. 2010. Volatility behavior of oil, industrial commodity and stock markets in a regime-switching environment. Energy Policy 38: 4388–99. [Google Scholar] [CrossRef]
- Connolly, Robert A., Chris Stivers, and Licheng Sun. 2005. Stock Market Uncertainty and the Stock-Bond Return Relation. Journal of Financial and Quantitative Analysis 40: 161–94. [Google Scholar] [CrossRef]
- Creti, Anna, Marc Joëts, and Valérie Mignon. 2013. On the links between stock and commodity markets’ volatility. Energy Economics 37: 16–28. [Google Scholar] [CrossRef]
- Diebold, Francis X., Joon-Haeng Lee, and Gretchen C. Weinbach. 1994. Regime switching with time-varying transition probabilities. In Advanced Texts in Econometrics. Edited by Clive William John Granger and Grayham Mizon. Oxford: Oxford University Press, pp. 283–302. [Google Scholar]
- Dupoyet, Brice V., and Corey A. Shank. 2018. Oil prices implied volatility or direction: Which matters more to financial markets? Financial Markets and Portfolio Management 32: 275–95. [Google Scholar] [CrossRef]
- Dutta, Anupam. 2017. Oil price uncertainty and clean energy stock returns: New evidence from crude oil volatility index. Journal of Cleaner Production 164: 1157–66. [Google Scholar] [CrossRef]
- Federal Reserve Board. 2022. Financial Stability Report; Washington, DC: The United States of America Board of Governors of The Federal Reserve System, May 9.
- Ferraro, Domenico, Kenneth Rogoff, and Barbara Rossi. 2015. Can oil prices forecast exchange rates? An empirical analysis of the relationship between commodity prices and exchange rates. Journal of International Money and Finance 54: 116–41. [Google Scholar] [CrossRef]
- Filardo, Andrew J. 1994. Business cycle phases and their transitions. Journal of Business and Economic Statistics 12: 299–308. [Google Scholar]
- Fleming, Jeff, Barbara Ostdiek, and Robert E. Whaley. 1995. Predicting stock market volatility: A new measure. The Journal of Futures Markets 15: 265–302. [Google Scholar] [CrossRef]
- Fukasawa, Masaaki, Isao Ishida, Nabil Maghrebi, Kosuke Oya, Masato Ubukata, and Kazutoshi Yamazaki. 2011. Model-free implied volatility: From surface to index. International Journal of Theoretical and Applied Finance 14: 433–63. [Google Scholar] [CrossRef]
- Giot, Pierre. 2003. The Asian Financial Crisis: The Start of a Regime Switch in Volatility. CORE Discussion Paper, No.2003/78. Rochester: SSRN. [Google Scholar]
- Goldstein, Itay, and Liyan Yang. 2022. Commodity Financialization and Information Transmission. The Journal of Finance 77: 2613–67. [Google Scholar] [CrossRef]
- Gong, Xu, and Jun Xu. 2022. Geopolitical risk and dynamic connectedness between commodity markets. Energy Economics 110: 106028. [Google Scholar] [CrossRef]
- Gorton, Gary, and K. Geert Rouwenhorst. 2006. Facts and Fantasies about Commodity Futures. Financial Analysts Journal 62: 47–68. [Google Scholar] [CrossRef]
- Grima, Simon, Letife Özdemir, Ercan Özen, and Inna Romānova. 2021. The Interactions between COVID-19 Cases in the USA, the VIX Index and Major Stock Markets. International Journal of Financial Studies 9: 26. [Google Scholar] [CrossRef]
- Hamilton, James D. 1989. A New approach to the economic analysis of nonstationary time series and the business cycle. Econometrica 57: 357–84. [Google Scholar] [CrossRef]
- Hamilton, James D. 1994. Time Series Analysis. Princeton: Princeton University Press. [Google Scholar]
- Hamilton, James D. 2008. Understanding Crude Oil Prices. National Bureau of Economic Research Working Paper, No. 14492. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Harris, Glen R. 1999. Markov chain Monte Carlo estimation of regime switching vector autoregressions. Austin Bulletin 29: 47–79. [Google Scholar] [CrossRef]
- Jensen, Gerald R., Robert R. Jhonson, and Jeffrey M. Mercer. 2000. Efficient use of commodity futures in diversified portfolios. The Journal of Futures Markets 20: 489–506. [Google Scholar] [CrossRef]
- Just, Małgorzata, and Krzysztof Echaust. 2020. Stock market returns, volatility, correlation and liquidity during the COVID-19 crisis: Evidence from the Markov Switching approach. Finance Research Letters 37: 101775. [Google Scholar] [CrossRef]
- Kim, Chang-Jin, Jeremy M. Piger, and Richard Startz. 2008. Estimation of Markov regime-switching regression models with endogenous switching. Journal of Econometrics 143: 263–73. [Google Scholar] [CrossRef]
- Kim, Suyi, So-Yeun Kim, and Kyungmee Choi. 2019. Analyzing oil price shocks and exchange rates movements in Korea using Markov Regime-Switching models. Energies 12: 4581. [Google Scholar] [CrossRef]
- Liu, Bing-Yue, Qiang Ji, and Ying Fan. 2017. Dynamic return-volatility dependence and risk measure of CoVaR in the oil market: A time-varying mixed copula model. Energy Economics 68: 53–65. [Google Scholar] [CrossRef]
- Lombardi, Marco, and Francesco Ravazzolo. 2013. On the Correlation between Commodity and Equity Returns: Implications for Portfolio Allocation. BIS Working Papers No, 420. Basel: Bank for International Settlements. [Google Scholar]
- MacKinnon, James G. 1996. Numerical Distribution Function for Unit root and Cointegration tests. Journal of Applied Econometrics 11: 601–18. [Google Scholar] [CrossRef]
- Maghrebi, Nabil, Moo-Sung Kim, and Kazuhiko Nishina. 2007. The Kospi 200 Implied Volatility Index: Evidence of Regime Switches in Volatility Expectations. Asia-Pacific Journal of Financial Studies 36: 163–87. [Google Scholar]
- Maghrebi, Nabil, Mark J. Holmes, and Kosuke Oya. 2014. Financial instability and the short-term dynamics of volatility expectations. Applied Financial Economics 24: 377–95. [Google Scholar] [CrossRef]
- Mencia, Javier, and Enrique Sentana. 2013. Valuation of VIX derivatives. Journal of Financial Economics 108: 367–91. [Google Scholar] [CrossRef]
- Mensi, Walid, Makram Beljid, Adel Boubaker, and Shunsuke Managi. 2013. Correlations and volatility spillovers across commodity and stock markets: Linking energies, food, and gold. Economic Modelling 32: 15–22. [Google Scholar] [CrossRef]
- Nishina, Kazuhiko, Nabil Maghrebi, and Moo-Sung Kim. 2006. Stock Market Volatility and the Forecasting Accuracy of Implied Volatility Indices. Discussion Papers in Economics and Business No. 06-09. Toyonaka: Graduate School of Economics and Osaka School of International Public Policy. [Google Scholar]
- Nishina, Kazuhiko, Nabil Maghrebi, and Mark J. Holmes. 2012. Nonlinear Adjustments of Volatility Expectations to Forecast Errors: Evidence from Markov-Regime Switches in Implied Volatility. Review of Pacific Basin Financial Markets and Policies 15: 1250007. [Google Scholar] [CrossRef]
- Pesaran, M. Hashiem, Yongcheol Shin, and Richard J. Smith. 2001. Bounds Testing Approaches to the Analysis of Level Relationships. Journal of Applied Econometrics 16: 289–326. [Google Scholar] [CrossRef]
- Pindyck, Robert S. 2001. The dynamics of commodity spot and futures markets: A Primer. The Energy Journal 22: 1–29. [Google Scholar] [CrossRef]
- Pouzo, Demian, Zacharias Psaradakis, and Martin Sola. 2022. Maximum likelihood estimation in Markov regime-switching models with covariate-dependent transition probabilities. Econometrica 90: 1681–710. [Google Scholar] [CrossRef]
- Raza, Naveed, Syed Jawad Hussain Shahzad, Aviral Kumer Tiwari, and Muhammad Shahbaz. 2016. Asymmetric impact of gold, oil prices and their volatilities on stock prices of emerging markets. Resources Policy 49: 290–301. [Google Scholar] [CrossRef]
- Sarwar, Ghulam. 2012. Is VIX an investor fear gauge in BRIC equity markets? Journal of Multinational Financial Management 22: 55–65. [Google Scholar] [CrossRef]
- Silvennoinen, Annastiina, and Susan Thorp. 2013. Financialization, crisis and commodity correlation dynamics. Journal of International Financial Markets, Institutions and Money 24: 42–65. [Google Scholar] [CrossRef]
- Smales, Lee A. 2022. Spreading the fear: The central role of CBOE VIX in global stock market uncertainty. Global Finance Journal 51: 100679. [Google Scholar] [CrossRef]
- Szado, Edward. 2009. VIX Futures and options: A Case Study of Portfolio Diversification During the 2008 Financial Crisis. The Journal of Alternative Investments 12: 68–85. [Google Scholar] [CrossRef]
- Tang, Ke, and Wei Xiong. 2012. Index Investment and the Financialization of Commodities. Financial Analysts Journal 68: 54–74. [Google Scholar] [CrossRef]
- Wang, Gang-Jin, and Chi Xie. 2012. Cross-correlations between WTI crude oil market and U.S. stock market: A perspective from econophysics. Acta Physica Polonica B 43: 10. [Google Scholar] [CrossRef]
- Whaley, Robert E. 2000. The investor fear gauge. Journal of Portfolio Management 26: 12–17. [Google Scholar] [CrossRef]
- Whaley, Robert E. 2009. Understanding the VIX. The Journal of Portfolio Management 35: 98–105. [Google Scholar] [CrossRef]

| Distributional Moments | Mean | Std. Dev. | Skewness | Kurtosis | Jarque Bera | ADF Test |
|---|---|---|---|---|---|---|
| WTI returns | −0.0007 | 0.062728 | −33.5240 | 1569.688 | 3.61 × 108 | −43.544 ***b |
| OVX daily changes | 0.00174 | 0.063033 | 4.9582 | 87.09921 | 1,052,944.0 | −61.760 ***a |
| Dollar index daily changes | 0.00009 | 0.004761 | −0.0492 | 5.870737 | 1211.493 | −58.464 ***b |
| S&P 500 returns | 0.00045 | 0.012766 | −0.2904 | 17.14844 | 29,442.39 | −68.718 ***a |
| Model Parameters | Full Period (July 2008–December 2021) | |
|---|---|---|
| Markov-Regime 1 | Markov-Regime 2 | |
| −0.0001 (0.6697) | 0.0174 (0.2269) | |
| −0.0196 (0.1708) | 0.1592 *** (0.0045) | |
| −0.1452 *** (0.0000) | −0.9643 *** (0.0000) | |
| −0.8659 *** (0.0000) | −1.4004 (0.4340) | |
| 0.3820 *** (0.0000) | −0.6599 (0.2359) | |
| −4.1048 *** (0.0000) | −1.6497 *** (0.0000) | |
| Log likelihood | 9124.611 | |
| AIC | −4.9880 | |
| Hypothesis Tests | ||
| 1.4408 (0.2300) | ||
| 9.5865 *** (0.0020) | ||
| 76.7273 *** (0.0000) | ||
| 0.0259 (0.8723) | ||
| 3.2807 * (0.0701) | ||
| Model Parameters | Subperiod A (January 2018–December 2019) | Subperiod B (January 2020–December 2021) | ||
|---|---|---|---|---|
| Regime 1 | Regime 2 | Regime 1 | Regime 2 | |
| −0.0009 (0.2648) | 0.0056 * (0.0811) | 0.0014 * (0.0835) | 0.0135 (0.7792) | |
| 0.0145 (0.7738) | −2.4246 ** (0.0153) | 0.0014 (0.9667) | 0.1383 (0.1553) | |
| −0.2205 *** (0.0000) | 0.2100 *** (0.0000) | −0.1802 *** (0.0000) | −1.2691 *** (0.0000) | |
| −0.4526 * (0.0671) | −0.1772 (0.8440) | −0.5188 ** (0.0379) | −2.3555 (0.7371) | |
| 0.0913 (0.3084) | 0.8216 ** (0.0488) | 0.2888 *** (0.0003) | −1.9662 (0.1892) | |
| −4.3179 *** (0.0000) | −3.7329 *** (0.0000) | −4.1164 ** (0.0000) | −1.1437 *** (0.0000) | |
| Log Likelihood | 1403.674 | 1219.407 | ||
| AIC | −5.324421 | −4.609587 | ||
| Hypothesis tests | ||||
| 3.4875 * (0.0618) | 0.0636 (0.8009) | |||
| 4.3483 ** (0.0370) | 1.7564 (0.1851) | |||
| 84.6471 *** (0.0000) | 38.8884 *** (0.0000) | |||
| 0.0783 (0.7796) | 0.0684 (0.7936) | |||
| 2.6231 (0.1053) | 2.2305 (0.1353) | |||
| Model Parameters | Subperiod C (July 2008–June 2010) | |
|---|---|---|
| Markov-Regime 1 | Markov-Regime 2 | |
| 0.0006 (0.4797) | −0.0008 (0.8519) | |
| 0.0621 (0.1126) | −0.0018 (0.8062) | |
| −0.1402 *** (0.0000) | −0.0958 (0.1062) | |
| −1.7029 *** (0.0000) | −1.1439 ** (0.0169) | |
| 0.3553 *** (0.0000) | 0.4894 *** (0.0006) | |
| −4.1663 *** (0.0000) | −2.9762 *** (0.0000) | |
| Log likelihood | 1220.131 | |
| AIC | −4.6212 | |
| Hypothesis Tests | ||
| 0.1054 (0.7454) | ||
| 0.8807 (0.3480) | ||
| 0.3969 (0.5287) | ||
| 1.0965 (0.2950) | ||
| 0.5650 (0.4523) | ||
| Model Parameters [ARDL (5,3,2,0)] | Subperiod A (January 2018–December 2019) | |
|---|---|---|
| Coefficient | t-Statistic | |
| 0.0007 | 0.8380 | |
| −0.1567 *** | −3.5950 | |
| −0.0658 | −1.4974 | |
| −0.0814 * | −1.8818 | |
| 0.0582 | 1.4148 | |
| 0.0733 * | 1.7949 | |
| −0.1010 *** | −6.2670 | |
| −0.0648 *** | −4.0226 | |
| −0.0360 ** | −2.2070 | |
| −0.0317 * | −1.9481 | |
| −0.2385 | −0.9302 | |
| −0.5504 ** | −2.1447 | |
| −0.4391 * | −1.7066 | |
| 0.2806 *** | 2.9526 | |
| Log Likelihood | 1340.482 | |
| AIC | −5.0823 | |
| F-Bounds Test (At the 1% significance level) | ||
| F-Statistic | I(0) | I(1) |
| 29.9258 | 3.65 | 4.66 |
| Model Parameters [ARDL (4,0,4,1)] | Subperiod B (January 2020–December 2021) | |
|---|---|---|
| Coefficient | t-Statistic | |
| 0.0037 | 0.7861 | |
| 0.2494 *** | 7.2207 | |
| −0.1279 *** | −3.6187 | |
| 0.0400 | 1.1396 | |
| 0.0577 * | 1.7318 | |
| −0.8823 *** | −18.6752 | |
| −1.2195 | −0.9081 | |
| 0.5592 | 0.4318 | |
| −1.5832 | −1.2145 | |
| −3.7311 *** | −2.8466 | |
| 3.2288 ** | 2.4446 | |
| −1.4937 *** | −4.2291 | |
| −1.5759 *** | −4.5938 | |
| Log Likelihood | 426.7656 | |
| AIC | −1.5823 | |
| F-Bounds Test (At the 1% significance level) | ||
| F-Statistic | I(0) | I(1) |
| 109.6350 | 3.65 | 4.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Okawa, H. Markov-Regime Switches in Oil Markets: The Fear Factor Dynamics. J. Risk Financial Manag. 2023, 16, 67. https://doi.org/10.3390/jrfm16020067
Okawa H. Markov-Regime Switches in Oil Markets: The Fear Factor Dynamics. Journal of Risk and Financial Management. 2023; 16(2):67. https://doi.org/10.3390/jrfm16020067
Chicago/Turabian StyleOkawa, Hiroyuki. 2023. "Markov-Regime Switches in Oil Markets: The Fear Factor Dynamics" Journal of Risk and Financial Management 16, no. 2: 67. https://doi.org/10.3390/jrfm16020067
APA StyleOkawa, H. (2023). Markov-Regime Switches in Oil Markets: The Fear Factor Dynamics. Journal of Risk and Financial Management, 16(2), 67. https://doi.org/10.3390/jrfm16020067






