Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum?
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
- ri is the return on security i
- rM is the return on the market
- βi is the calculated beta coefficient
- αi is the intercept term, and
- ei is the residual term
- interval length in days (D, W, M);
- for each security i = 1, ….. N;
- and over time .
- N = The total number of periods examined (our current sample has 186 periods);
- λ = The number of return periods per year (when forecasting daily returns, λ = 252; for weekly returns, λ = 52; and for monthly returns, λ = 12);
- βP = The equal-weighted portfolio beta based on a given interval and estimation window;
- rp,t+1 = The actual portfolio return for the period immediately following the beta calculations and portfolio formation;
- rm,t+1 = The actual return of the Market, as proxied by the total return of the Russell 1000, for the period immediately following the beta calculations and portfolio formation.
4. Results
5. Further Research
- Some preliminary work indicates that, in down markets, it appears that weekly betas accomplish lower TE’s than daily betas. It would be interesting to explore this further, though we do think that the increased volatility witnessed during down-markets may have an association with this observation and that the use of daily betas during bear markets may be too unstable for next day forecasting (Alexeev et al. 2016). With and as the excess returns to security i and down market excess returns, respectively, where is the full market excess return, then the downside dual beta (Chong 2022) is:The upside dual beta would be of a similar construct but with the inequalities reversed.
- Given the extensive amount of computational time it took to analyze the time series of returns in their various permutations and combinations, additional work could be undertaken to design an appropriate and efficient scanning mechanism to identify the optimal combinations of interval, window-lengths and the beta-size dimension.
- The impact of varying intervals and window-lengths on the one-period ahead predictability of systematic risk can alternatively (to the tracking error, TE) be assessed by the Information Coefficient (IC); stable and robust betas will likely result in higher IC’s, but the formal assessment could be a future research item (Appendix B).
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

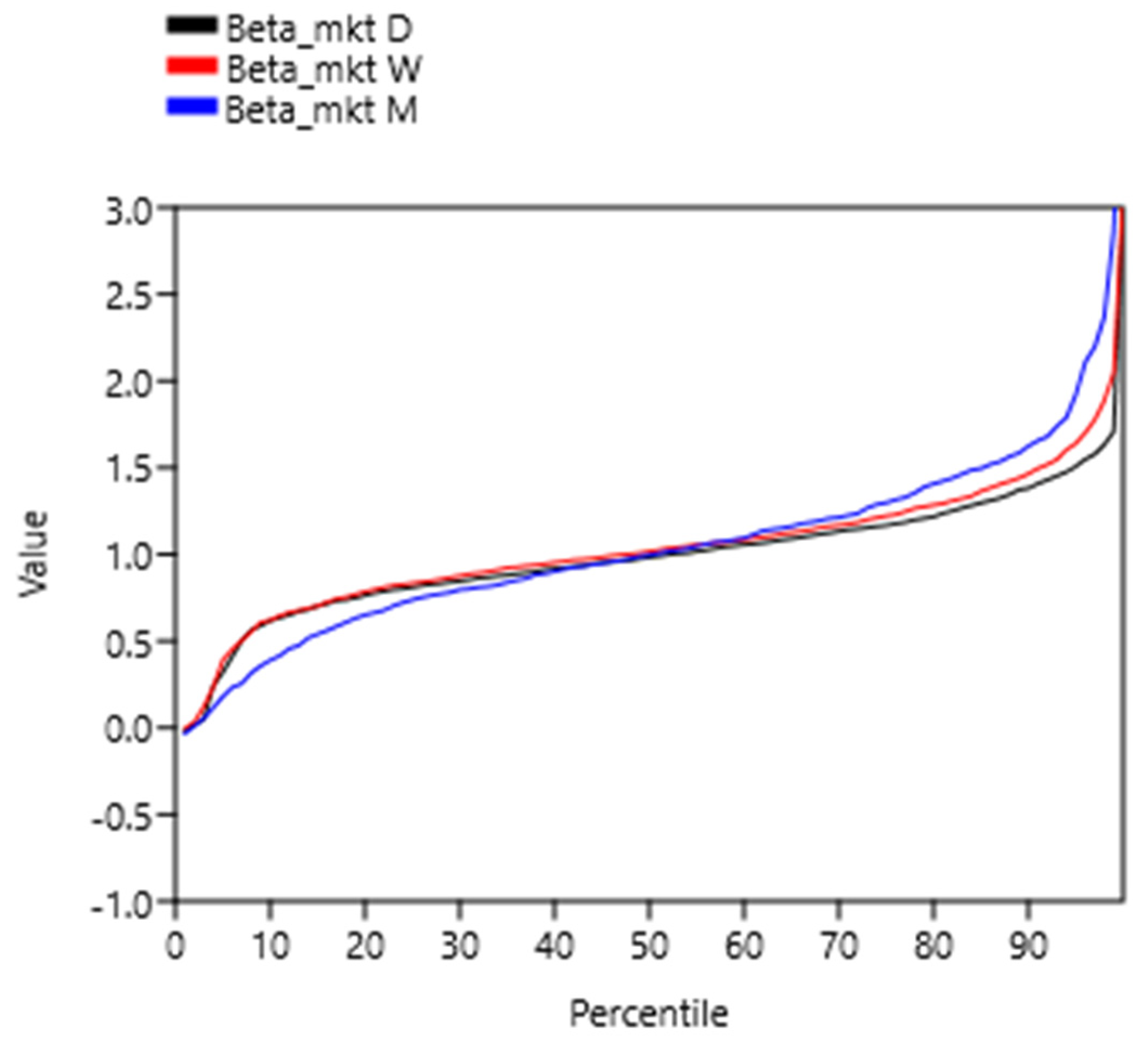
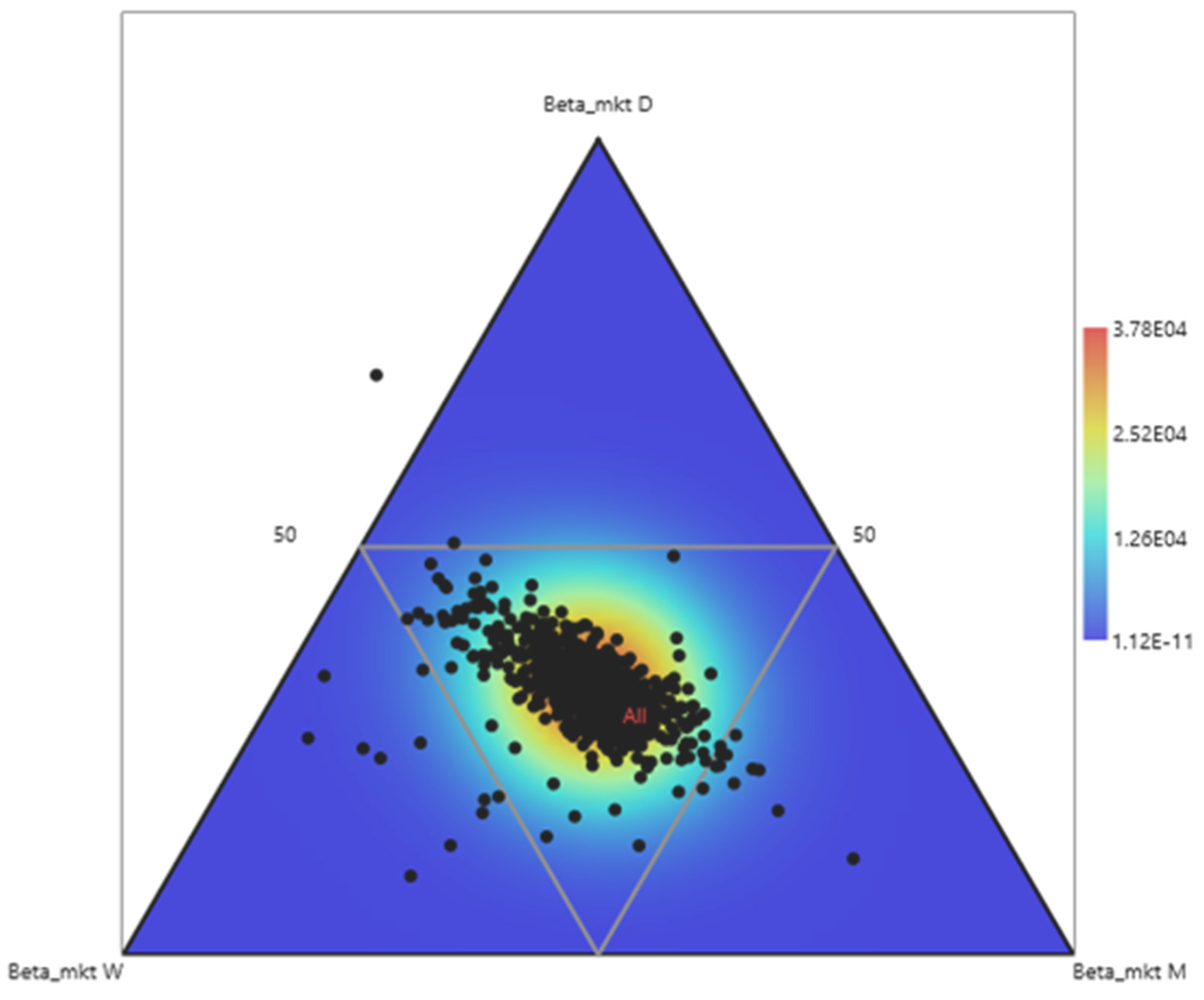
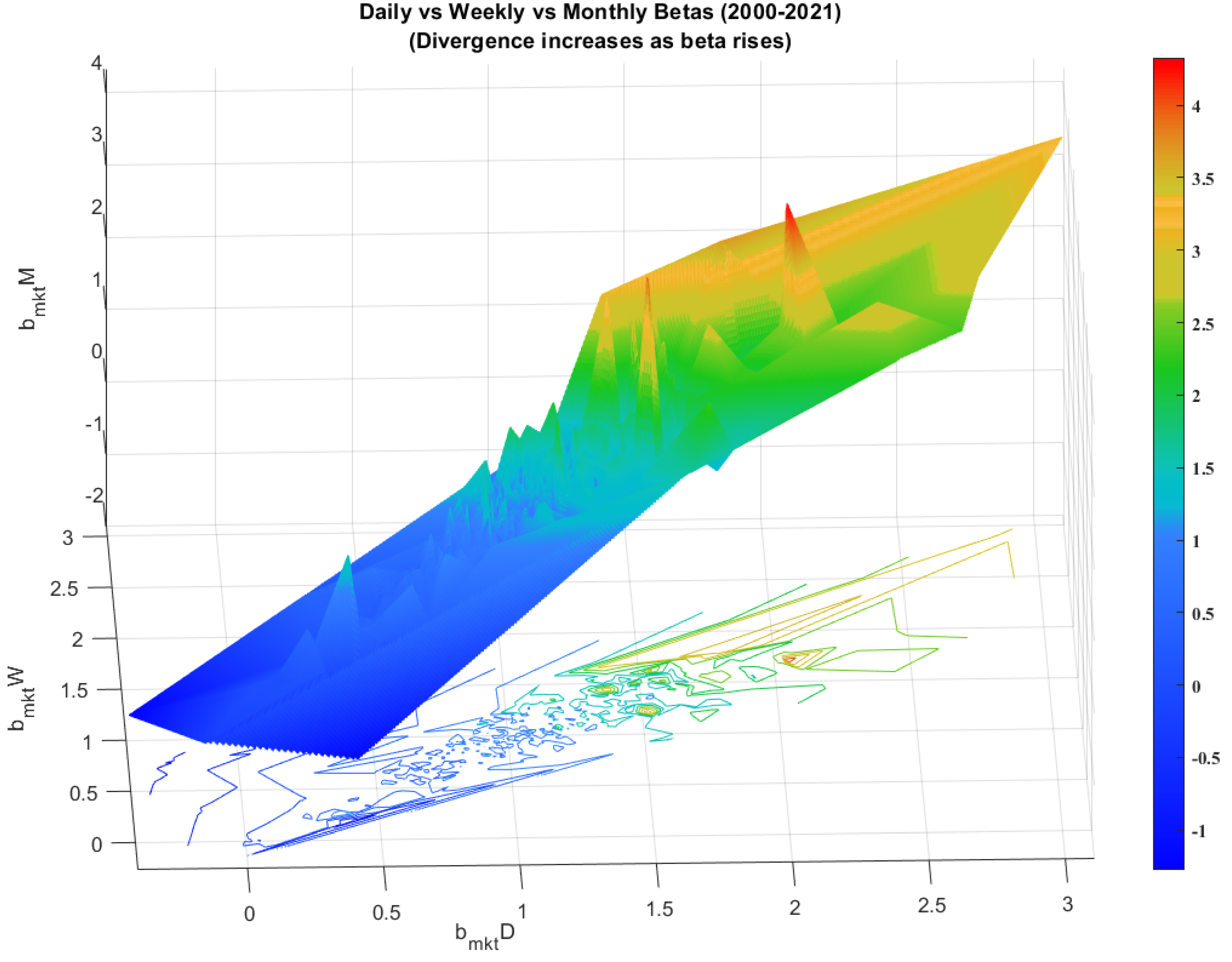
Appendix B
- for each T and where ,
- t is a discrete period 1…N within each interval length of size T,
- rit is the return on each security at time t within each interval T, and
- IC is the information coefficient.
| 1 | Advent of firms such as BARRA, Berkeley, 1975 and Vestek Systems, San Francisco, 1983. |
| 2 | Does not equate with lower total risk (volatility). |
| 3 | The inverse relationship between interval length and average beta values, especially for smaller sized firms is intriguing. Perhaps there is an implicit tradeoff between a downward bias in the estimated beta and its ability to correctly provide an estimate for next period systematic risk. The idiosyncratic component of risk for small capitalization stocks is generally higher than for large capitalization stocks, thus it is not surprising that a longer estimation interval would smooth out the variability (influential residuals canceling each other out) resulting in a reduction in the downward bias reported by Corhay (1992). It may be possible that there is information decay and loss with the increase in the estimation interval. |
| 4 | To keep the computational implications reasonable (each pass data file would be about 10 MB, with 1000 × 252 rows for just a 1 year run, with a moving window depending on the interval length), our interval length iterations have 1, 5 and 21 trading days corresponding to D, W and M return frequencies. Our window lengths vary from 1 through 5 years. While most of current literature uses a 60 monthly period window, the only other length we observe is the use of the full period for which data is available. This also meets the minimum lower bound of 30 based on the Central Limit Theorem. |
| 5 | TE is the standard deviation of the difference between the realized and CAPM based forecast return vector. |
| 6 | We are operating within the Russell 1000 universe in a long time series dimension, hence three fractiles for Large, Mid and Small capitalization groups are formed. |
| 7 | p-value < 0.10 for all cells in Table 1 (A, B, C) |
| 8 | Across Row 1, in the 3 × 3 Classification matrix. |
References
- Abate, Guido, Tommaso Bonafini, and Pierpaolo Ferrari. 2022. Portfolio Constraints: An Empirical Analysis. International Journal of Financial Studies 10: 9. [Google Scholar] [CrossRef]
- Agrrawal, Pankaj. 2009. An automation algorithm for harvesting capital market information from the web. Managerial Finance 35: 427–38. [Google Scholar] [CrossRef][Green Version]
- Agrrawal, Pankaj. 2013. Using Index ETFs for Multi-Asset-Class Investing: Shifting the Efficient Frontier Up. The Journal of Index Investing 4: 83–94. [Google Scholar] [CrossRef]
- Agrrawal, Pankaj, John M. Clark, Rajat Agarwal, and Jivendra K. Kale. 2014. An Intertemporal Study of ETF Liquidity and Underlying Factor Transition, 2009–14. The Journal of Trading 9: 69–78. [Google Scholar] [CrossRef]
- Akono, Henri, Khondkar Karim, and Emeka Nwaeze. 2019. Analyst rounding of EPS forecasts and stock recommendations. Advances in Accounting 44: 68–80. [Google Scholar] [CrossRef]
- Alexeev, Vitali, Mardi Dungey, and Wenying Yao. 2016. Continuous and jump betas: Implications for portfolio diversification. Econometrics 4: 27. [Google Scholar] [CrossRef]
- Armitage, Seth, and Janusz Brzeszczynski. 2011. Heteroscedasticity and interval effects in estimating beta: UK evidence. Applied Financial Economics 21: 1525–38. [Google Scholar] [CrossRef]
- Black, Fischer. 1972. Capital market equilibrium with restricted borrowing. Journal of Business 45: 444–55. [Google Scholar] [CrossRef]
- Buckle, David. 2022. The Impact of Options on Investment Portfolios in the Short-Run and the Long-Run, with a Focus on Downside Protection and Call Overwriting. Mathematics 10: 1563. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Carroll, Carolyn, and KC John Wei. 1988. Risk, Return, and Equilibrium: An Extension. The Journal of Business 61: 485. [Google Scholar] [CrossRef]
- Chen, Nai-Fu, Richard Roll, and Stephen A. Ross. 1986. Economic Forces and the Stock Market. Journal of Business 59: 383. [Google Scholar] [CrossRef]
- Chu, Patrick, and Dan Xu. 2021. Tracking Errors and Their Determinants. Journal of Prediction Markets 1: 1851–65. [Google Scholar] [CrossRef]
- Chong, James. 2022. A trading strategy with dual-beta estimates. Managerial Finance 48: 720–32. [Google Scholar] [CrossRef]
- Cohen, Kalman J., Gabriel A. Hawawini, Steven F. Maier, Robert A. Schwartz, and David K. Whitcomb. 1983a. Estimating and Adjusting for the Intervalling-Effect in Beta. Management Science 29: 135. [Google Scholar] [CrossRef]
- Cohen, Kalman J., Gabriel A. Hawawini, Steven F. Maier, Robert A. Schwartz, and David K. Whitcomb. 1983b. Friction in the Trading Process and the Estimation of Systematic Risk. Journal of Financial Economics 12: 263. [Google Scholar] [CrossRef]
- Cooper, Ian. 2009. On Tests of the Conditional Relationship between Beta and Returns. Applied Financial Economics 19: 155–78. [Google Scholar] [CrossRef]
- Corhay, Albert. 1992. The Intervalling Effect Bias in Beta: A Note. Journal of Banking & Finance 16: 61. [Google Scholar]
- Corhay, Albert, and Alireza Tourani Rad. 1993. Return Interval, Firm Size and Systematic Risk on the Dutch Stock Market. Review of Financial Economics 2: 19. [Google Scholar] [CrossRef]
- Cremers, KJ Martijn, and Antti Petajisto. 2009. How Active is Your Fund Manager? A New Measure that Predicts Performance. The Review of Financial Studies 22: 3329–65. [Google Scholar] [CrossRef]
- CRSP via WRDS. 2022. Calculated (or Derived) Based on Data from Database Name ©2022 Center for Research in Security Prices (CRSP), The University of Chicago Booth School of Business and the Wharton Research Database Services. Available online: https://wrds-www.wharton.upenn.edu/ (accessed on 1 March 2022).
- Eichengreen, Barry. 2021. Bretton Woods After 50. Review of Political Economy 33: 552–69. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-Section of Expected Stock Returns. Journal of Finance 47: 427. [Google Scholar] [CrossRef]
- Fang, Yan, Florian Ielpo, and Benoît Sévi. 2012. Empirical Bias in Intraday Volatility Measures. Finance Research Letters 9: 231–37. [Google Scholar] [CrossRef]
- Fung, William KH, Robert A. Schwartz, and David K. Whitcomb. 1985. Adjusting for the Intervalling Effect Bias in Beta: A Test Using Paris Bourse Data. Journal of Banking & Finance 9: 443. [Google Scholar]
- Girard, Eric, and Amit K. Sinha. 2006. Does Total Risk Matter? The Case of Emerging Markets. Multinational Finance Journal 10: 117–51. [Google Scholar] [CrossRef]
- Goldsticker, Ralph, and Pankaj Agrrawal. 1999. The Effects of Blending Primary and Diluted EPS Data. Financial Analysts Journal 55: 51–60. [Google Scholar] [CrossRef]
- Graham, John R., and Campbell R. Harvey. 2001. The Theory and Practice of Corporate Finance: Evidence from the Field. Journal of Financial Economics 60: 187. [Google Scholar] [CrossRef]
- Groenewold, Nicolaas, and Patricia Fraser. 2000. Forecasting Beta: How well does the ‘Five-Year Rule of Thumb’ do? Journal of Business Finance & Accounting 27: 953. [Google Scholar]
- Hawawini, Gabriel A. 1980. An Analytical Examination of the Intervalling Effect on Skewness and Other Moments. Journal of Financial and Quantitative Analysis 15: 1121. [Google Scholar] [CrossRef]
- Hawawini, Gabriel A., and Ashok Vora. 1980. Evidence of Intertemporal Systematic Risks in the Daily Price Movements of NYSE and AMEX Common Stocks. Journal of Financial and Quantitative Analysis 15: 331. [Google Scholar] [CrossRef]
- Ho, Li-Chin Jennifer, and Jeffrey J. Tsay. 2001. Option Trading and the Intervalling Effect Bias in Beta. Review of Quantitative Finance and Accounting 17: 267. [Google Scholar] [CrossRef]
- Hollstein, Fabian, Marcel Prokopczuk, and Chardin Wese Simen. 2020. The Conditional Capital Asset Pricing Model Revisited: Evidence from High-Frequency Betas. Management Science 66: 2474–94. [Google Scholar] [CrossRef]
- Jarque, Carlos M., and Anil K. Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Jurdi, Doureige J., and Sam M. AlGhnaimat. 2021. The effects of ERM adoption on European insurance firms performance and risks. Journal of Risk and Financial Management 14: 554. [Google Scholar] [CrossRef]
- Lakonishok, Josef, and Alan C. Shapiro. 1986. Systematic Risk, Total Risk and Size as Determinants of Stock Market Returns. Journal of Banking & Finance 10: 115. [Google Scholar]
- Lei, Nuoa, Eric Masanet, and Jonathan Koomey. 2021. Best practices for analyzing the direct energy use of blockchain technology systems: Review and policy recommendations. Energy Policy 156: 112422. [Google Scholar] [CrossRef]
- Levene, Howard. 1960. Robust tests for equality of variances. In Ingram Olkin and Harold Hotelling: Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling. Palo Alto: Stanford Press. [Google Scholar]
- Lin, Qi. 2021. The q5 model and its consistency with the intertemporal CAPM. Journal of Banking and Finance 127: 106096. [Google Scholar] [CrossRef]
- Lintner, John. 1965. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Levy, Haim, Ilan Guttman, and Isabel Tkatch. 2001. Regression, Correlation, and the Time Interval: Additive-Multiplicative Framework. Management Science 47: 1150. [Google Scholar] [CrossRef]
- Mantsios, Georgios, and Stylianos Xanthopoulos. 2016. The Beta intervalling effect during a deep economic crisis: Evidence from Greece. International Journal of Business and Economic Sciences Applied Research 9: 19–26. [Google Scholar]
- Milonas, Nikolaos T., and Gerasimos G. Rompotis. 2013. Does intervalling effect affect ETFs? Managerial Finance 39: 863–82. [Google Scholar] [CrossRef]
- Pettengill, Glenn, Sridhar Sundaram, and Ike Mathur. 1995. The Conditional Relation between Beta and Returns. Journal of Financial and Quantitative Analysis 30: 101–16. [Google Scholar] [CrossRef]
- Reilly, Frank K., and David J. Wright. 1988. A Comparison of Published Betas. Journal of Portfolio Management 14: 64. [Google Scholar] [CrossRef]
- Roman, Mestre, and Michel Terraza. 2018. Time-Frequency varying beta estimation—A continuous wavelets approach. Economics Bulletin 38: 1796–810. [Google Scholar]
- Sharpe, William F. 1964. Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Smith, Keith V. 1978. The Effect of Intervalling on Estimating Parameters of the Capital Asset Pricing Model. Journal of Financial and Quantitative Analysis 13: 313. [Google Scholar] [CrossRef]
- Terraza, Michel, and Mestre Roman. 2021. Adjusted beta based on an empirical comparison of OLS-CAPM and the CAPM with EGARCH errors. International Journal of Finance and Economics 26: 3588–98. [Google Scholar] [CrossRef]
- Verhoeven, Peter, Florian Sinn, and Tino T. Herden. 2018. Examples from Blockchain Implementations in Logistics and Supply Chain Management: Exploring the Mindful Use of a New Technology. Logistics 2: 20. [Google Scholar] [CrossRef]
- WRDS. 2022. Pricing Data on Stocks. Wharton Research Data Services. Available online: https://wrds-www.wharton.upenn.edu/ (accessed on 1 March 2022).

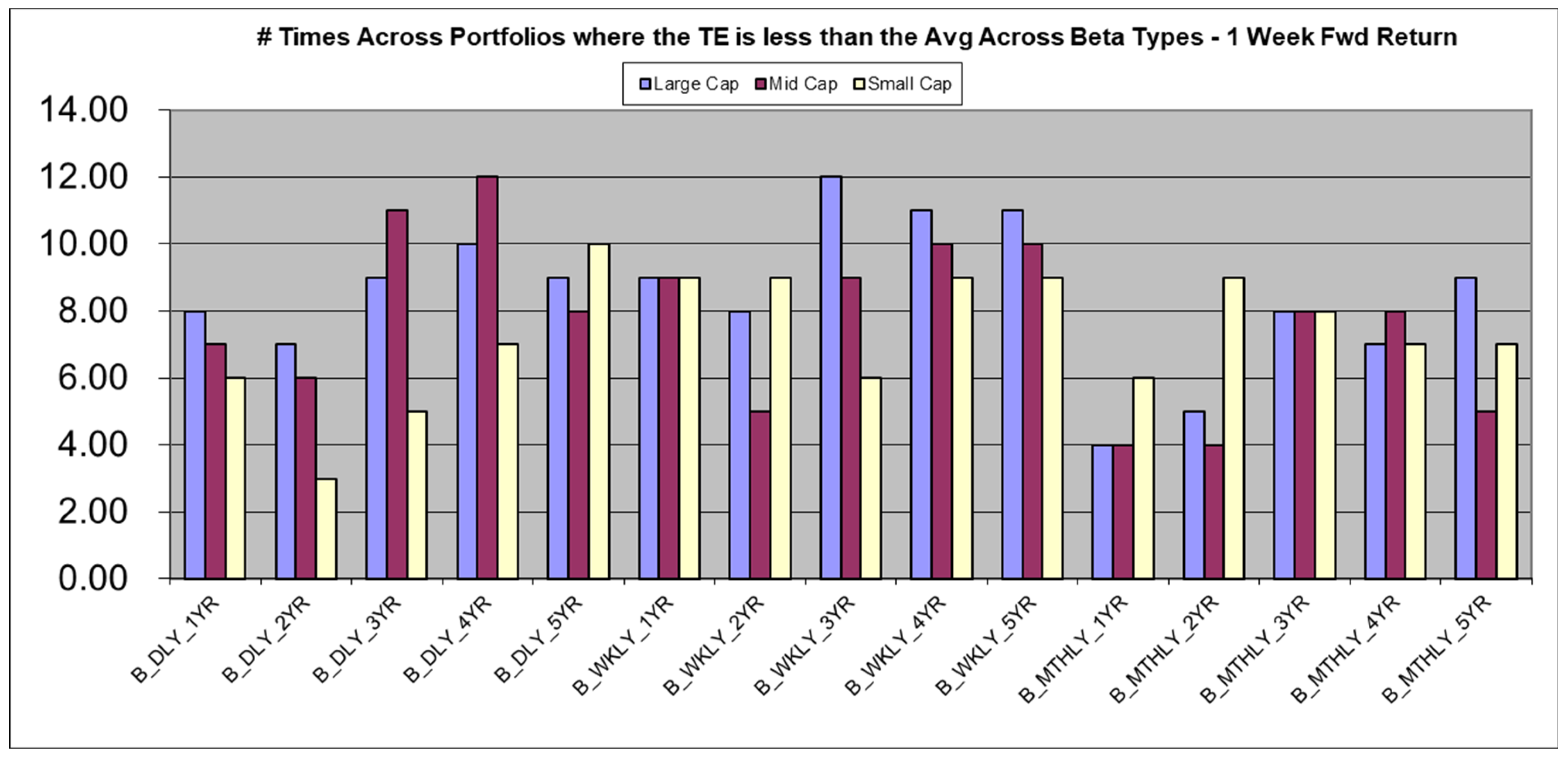
| A. Prediction of 1 Day Forward Return | |||||||||||||
| Interval Period | Estimation Window | Large Cap | Mid Cap | Small Cap | Large Cap/High Beta | Large Cap/Mid Beta | Large Cap/Low Beta | Mid Cap/High Beta | Mid Cap/Mid Beta | Mid Cap/Low Beta | Small Cap/High Beta | Small Cap/Mid Beta | Small Cap/Low Beta |
| Daily | 1 Year | 2.68 | 6.64 | 9.50 | 11.34 | 4.80 | 6.47 | 13.87 | 6.93 | 6.43 | 17.67 | 9.74 | 6.93 |
| 2 Years | 2.58 | 6.25 | 8.97 | 10.05 | 5.33 | 7.06 | 12.90 | 6.80 | 6.85 | 16.67 | 8.89 | 7.24 | |
| 3 Years | 2.61 | 6.03 | 8.54 | 8.87 | 5.51 | 6.91 | 11.87 | 6.93 | 6.72 | 15.63 | 8.88 | 6.94 | |
| 4 Years | 2.64 | 5.89 | 8.43 | 8.36 | 5.60 | 6.86 | 11.25 | 7.07 | 6.76 | 15.14 | 8.78 | 7.27 | |
| 5 Years | 2.62 | 5.82 | 8.19 | 7.88 | 5.79 | 6.83 | 10.48 | 7.10 | 6.77 | 14.49 | 8.78 | 7.34 | |
| Weekly | 1 Year | 2.74 | 6.88 | 9.74 | 9.75 | 3.86 | 6.72 | 13.80 | 7.00 | 6.91 | 17.61 | 9.97 | 7.58 |
| 2 Years | 2.61 | 6.32 | 9.09 | 9.42 | 4.97 | 6.76 | 12.69 | 6.95 | 6.46 | 16.98 | 9.20 | 7.16 | |
| 3 Years | 2.68 | 6.07 | 8.67 | 8.35 | 5.25 | 6.96 | 12.08 | 6.84 | 6.76 | 15.80 | 8.99 | 7.34 | |
| 4 Years | 2.72 | 5.93 | 8.61 | 7.95 | 5.29 | 6.93 | 11.48 | 7.16 | 6.60 | 15.16 | 8.94 | 7.48 | |
| 5 Years | 2.71 | 5.89 | 8.37 | 7.44 | 5.28 | 6.80 | 11.13 | 7.10 | 6.56 | 14.27 | 8.98 | 7.43 | |
| Monthly | 1 Year | 3.26 | 7.78 | 12.58 | 12.75 | 3.84 | 10.76 | 19.20 | 7.46 | 11.54 | 27.26 | 11.55 | 10.65 |
| 2 Years | 3.07 | 6.77 | 10.56 | 11.12 | 5.25 | 9.78 | 15.99 | 7.25 | 9.04 | 22.51 | 10.25 | 9.06 | |
| 3 Years | 3.15 | 6.40 | 9.59 | 9.66 | 5.51 | 9.31 | 14.11 | 7.38 | 8.68 | 19.52 | 9.54 | 8.36 | |
| 4 Years | 3.02 | 6.19 | 9.36 | 9.13 | 5.72 | 8.68 | 12.67 | 7.35 | 8.11 | 17.59 | 9.66 | 8.33 | |
| 5 Years | 2.89 | 6.10 | 8.84 | 8.62 | 5.72 | 8.12 | 11.66 | 7.32 | 7.82 | 16.22 | 9.12 | 8.21 | |
| Average | 2.80 | 6.33 | 9.27 | 9.38 | 5.18 | 7.66 | 13.01 | 7.11 | 7.47 | 17.50 | 9.42 | 7.82 | |
| B. Prediction of 1 Week Forward Return | |||||||||||||
| Interval Period | Estimation Window | Large Cap | Mid Cap | Small Cap | Large Cap/High Beta | Large Cap/Mid Beta | Large Cap/Low Beta | Mid Cap/High Beta | Mid Cap/Mid Beta | Mid Cap/Low Beta | Small Cap/High Beta | Small Cap/Mid Beta | Small Cap/Low Beta |
| Daily | 1 Year | 2.77 | 6.18 | 9.95 | 9.16 | 5.03 | 7.57 | 12.52 | 6.93 | 7.34 | 17.79 | 10.44 | 7.65 |
| 2 Years | 2.76 | 6.23 | 9.79 | 8.42 | 5.18 | 7.63 | 11.89 | 7.02 | 7.98 | 17.30 | 9.92 | 7.75 | |
| 3 Years | 2.87 | 6.11 | 9.62 | 8.15 | 5.50 | 7.71 | 11.27 | 6.71 | 7.63 | 16.98 | 9.82 | 7.87 | |
| 4 Years | 2.90 | 6.04 | 9.42 | 8.00 | 5.62 | 7.56 | 10.67 | 7.00 | 7.80 | 16.36 | 9.95 | 7.89 | |
| 5 Years | 2.96 | 6.12 | 9.20 | 7.64 | 5.75 | 7.63 | 10.45 | 7.01 | 8.10 | 15.97 | 9.90 | 7.79 | |
| Weekly | 1 Year | 2.75 | 5.94 | 9.46 | 8.68 | 4.47 | 7.56 | 12.15 | 6.54 | 7.07 | 16.73 | 9.73 | 7.98 |
| 2 Years | 2.83 | 5.92 | 9.38 | 8.75 | 5.28 | 7.57 | 11.57 | 7.22 | 7.41 | 16.67 | 9.55 | 7.39 | |
| 3 Years | 2.98 | 5.80 | 9.19 | 8.22 | 5.60 | 7.75 | 11.09 | 7.01 | 7.48 | 16.34 | 9.26 | 7.55 | |
| 4 Years | 3.01 | 5.75 | 8.96 | 7.97 | 5.61 | 7.83 | 10.59 | 7.10 | 7.42 | 15.78 | 9.43 | 7.60 | |
| 5 Years | 3.07 | 5.85 | 8.75 | 7.85 | 5.70 | 7.98 | 10.33 | 7.61 | 7.47 | 15.14 | 9.37 | 7.59 | |
| Monthly | 1 Year | 3.09 | 6.11 | 9.61 | 10.06 | 4.62 | 10.23 | 14.60 | 6.53 | 10.75 | 20.64 | 8.95 | 11.73 |
| 2 Years | 3.19 | 6.15 | 9.17 | 8.67 | 4.67 | 9.09 | 12.41 | 6.89 | 9.36 | 17.34 | 9.20 | 9.17 | |
| 3 Years | 3.27 | 5.95 | 8.97 | 7.82 | 4.97 | 8.54 | 11.16 | 7.09 | 8.31 | 15.92 | 9.31 | 8.70 | |
| 4 Years | 3.24 | 5.93 | 8.80 | 7.59 | 5.38 | 8.17 | 10.56 | 7.10 | 8.20 | 15.59 | 9.09 | 8.41 | |
| 5 Years | 3.25 | 6.01 | 8.62 | 7.49 | 5.69 | 7.96 | 10.30 | 7.29 | 8.02 | 15.07 | 9.37 | 8.09 | |
| Average | 3.00 | 6.01 | 9.26 | 8.30 | 5.27 | 8.05 | 11.44 | 7.00 | 8.02 | 16.64 | 9.55 | 8.21 | |
| C. Prediction of 1 Month Forward Return | |||||||||||||
| Interval Period | Estimation Window | Large Cap | Mid Cap | Small Cap | Large Cap/High Beta | Large Cap/Mid Beta | Large Cap/Low Beta | Mid Cap/High Beta | Mid Cap/Mid Beta | Mid Cap/Low Beta | Small Cap/High Beta | Small Cap/Mid Beta | Small Cap/Low Beta |
| Daily | 1 Year | 2.93 | 6.40 | 10.58 | 10.19 | 5.15 | 7.23 | 11.41 | 7.97 | 8.43 | 18.41 | 11.34 | 9.35 |
| 2 Years | 3.01 | 6.62 | 10.27 | 8.76 | 5.40 | 7.82 | 11.29 | 8.26 | 8.85 | 17.73 | 10.97 | 9.36 | |
| 3 Years | 3.03 | 6.67 | 10.28 | 8.25 | 5.57 | 7.89 | 11.00 | 8.15 | 8.68 | 17.08 | 11.14 | 9.30 | |
| 4 Years | 3.05 | 6.70 | 10.13 | 7.89 | 5.72 | 7.96 | 10.76 | 8.35 | 8.61 | 16.68 | 10.96 | 9.30 | |
| 5 Years | 3.15 | 6.70 | 10.04 | 7.27 | 5.91 | 8.11 | 10.46 | 8.45 | 8.61 | 16.37 | 11.09 | 9.30 | |
| Weekly | 1 Year | 3.00 | 6.06 | 10.03 | 9.20 | 4.37 | 7.11 | 10.52 | 7.63 | 7.85 | 17.21 | 10.45 | 9.19 |
| 2 Years | 3.07 | 6.32 | 9.78 | 9.36 | 4.95 | 7.52 | 10.86 | 7.97 | 8.10 | 16.71 | 10.24 | 8.69 | |
| 3 Years | 3.13 | 6.41 | 9.77 | 8.48 | 5.45 | 7.55 | 10.52 | 7.98 | 8.24 | 16.13 | 10.64 | 8.77 | |
| 4 Years | 3.16 | 6.45 | 9.63 | 8.32 | 5.47 | 7.65 | 10.45 | 8.13 | 8.19 | 15.85 | 10.57 | 8.79 | |
| 5 Years | 3.27 | 6.49 | 9.58 | 7.73 | 5.74 | 7.76 | 10.25 | 8.38 | 8.29 | 15.61 | 10.70 | 8.86 | |
| Monthly | 1 Year | 3.13 | 6.39 | 10.36 | 10.75 | 4.55 | 8.95 | 14.00 | 7.16 | 11.06 | 20.22 | 10.60 | 12.42 |
| 2 Years | 3.36 | 6.46 | 9.71 | 8.74 | 5.04 | 8.11 | 11.86 | 7.80 | 8.92 | 17.36 | 10.66 | 9.57 | |
| 3 Years | 3.41 | 6.55 | 9.66 | 7.91 | 5.39 | 7.98 | 10.78 | 8.16 | 8.65 | 15.51 | 10.89 | 9.04 | |
| 4 Years | 3.38 | 6.59 | 9.53 | 7.71 | 5.44 | 7.57 | 10.40 | 7.90 | 8.31 | 15.33 | 10.33 | 8.95 | |
| 5 Years | 3.44 | 6.63 | 9.51 | 7.36 | 5.73 | 7.54 | 10.17 | 8.20 | 8.15 | 15.02 | 10.39 | 8.99 | |
| Average | 3.17 | 6.50 | 9.92 | 8.53 | 5.33 | 7.78 | 10.98 | 8.03 | 8.60 | 16.75 | 10.73 | 9.33 | |
| Interval Length Forecast Length | Daily Betas | Weekly Betas | Monthly Betas | Total TE’s | %Best |
|---|---|---|---|---|---|
| 1 Day | 9, a1 | 2 | 1 | 12 | 75.0%, a1 |
| 1 Week | 0 | 6, b2 | 6 | 12 | 50.0%, b2 |
| 1 Month | 2 | 6 | 4, c3 | 12 | 33.3%, c3 |
| Test for equal means | |||||
| Sum of Squares | df | Mean square | F | p (same) | |
| Between Beta groups: | 1.7319 | 2 | 0.8660 | 4.5720 | 0.010420 |
| Within Beta groups: | 543.8350 | 2871 | 0.1894 | Permutation p (n = 99,999) | |
| Total: | 545.5670 | 2873 | 0.0105 | ||
| Kruskal-Wallis test for equal medians | H (chi2): | 6.327 | |||
| (non-parametric test) | p (same): | 0.04227 | |||
| There is a significant difference betweenthe sample means and also the medians | |||||
| Levene’s test for homogeneity of variance | p (same): | 4.94 × 10−27 | |||
| Welch F test for unequal variances: F = 5.734, df = 1857, p = 0.003293 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agrrawal, P.; Gilbert, F.W.; Harkins, J. Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum? J. Risk Financial Manag. 2022, 15, 520. https://doi.org/10.3390/jrfm15110520
Agrrawal P, Gilbert FW, Harkins J. Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum? Journal of Risk and Financial Management. 2022; 15(11):520. https://doi.org/10.3390/jrfm15110520
Chicago/Turabian StyleAgrrawal, Pankaj, Faye W. Gilbert, and Jason Harkins. 2022. "Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum?" Journal of Risk and Financial Management 15, no. 11: 520. https://doi.org/10.3390/jrfm15110520
APA StyleAgrrawal, P., Gilbert, F. W., & Harkins, J. (2022). Time Dependence of CAPM Betas on the Choice of Interval Frequency and Return Timeframes: Is There an Optimum? Journal of Risk and Financial Management, 15(11), 520. https://doi.org/10.3390/jrfm15110520








