On Financial Distributions Modelling Methods: Application on Regression Models for Time Series
Abstract
1. Introduction
2. Financial Distributions
Financial Time Series Volatility, Leverage and Drift
3. Financial Time Series Models
3.1. Box–Jenkins Time Series Model Notation
3.2. GARCH Type Models
3.3. Geometric Brownian Motion Type Models
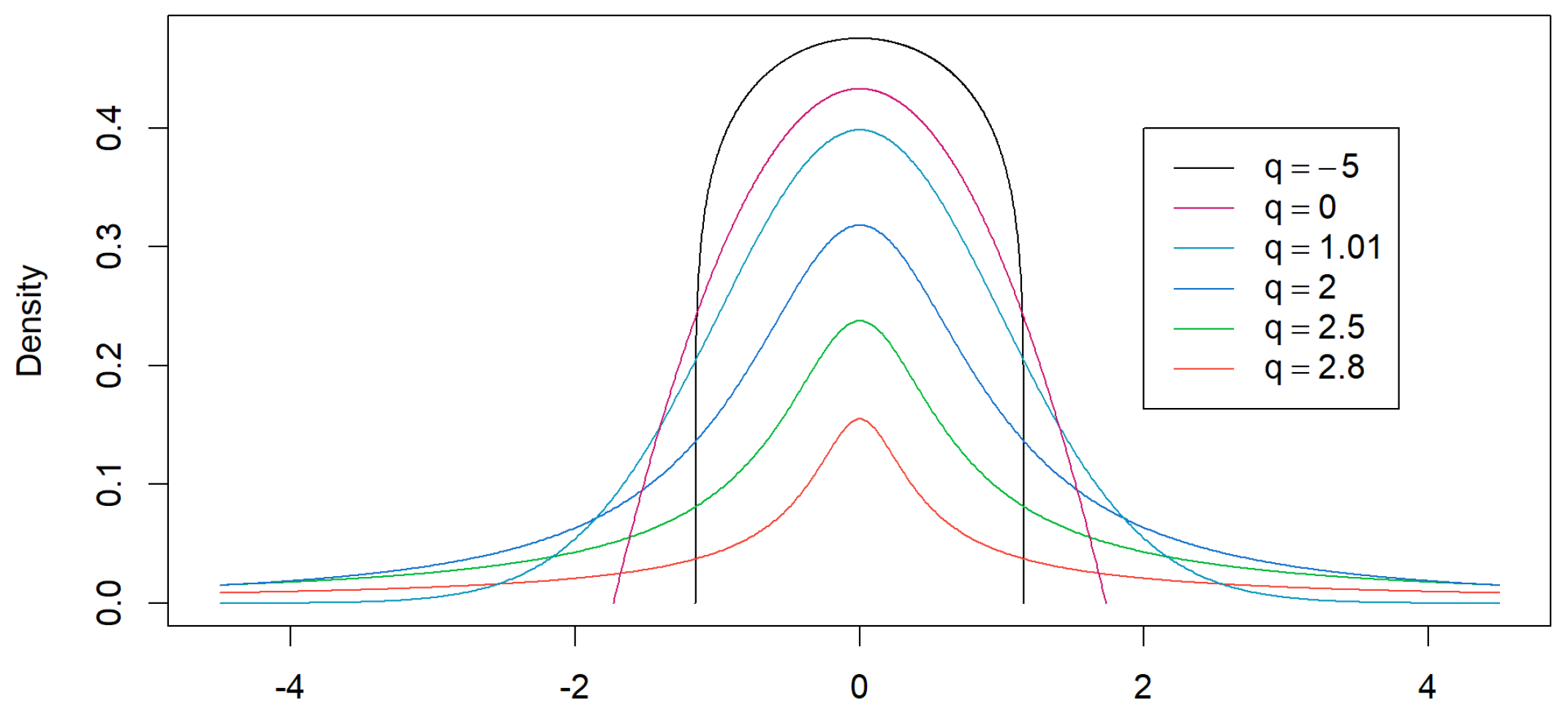
3.4. Tsallis Entropy Type Models
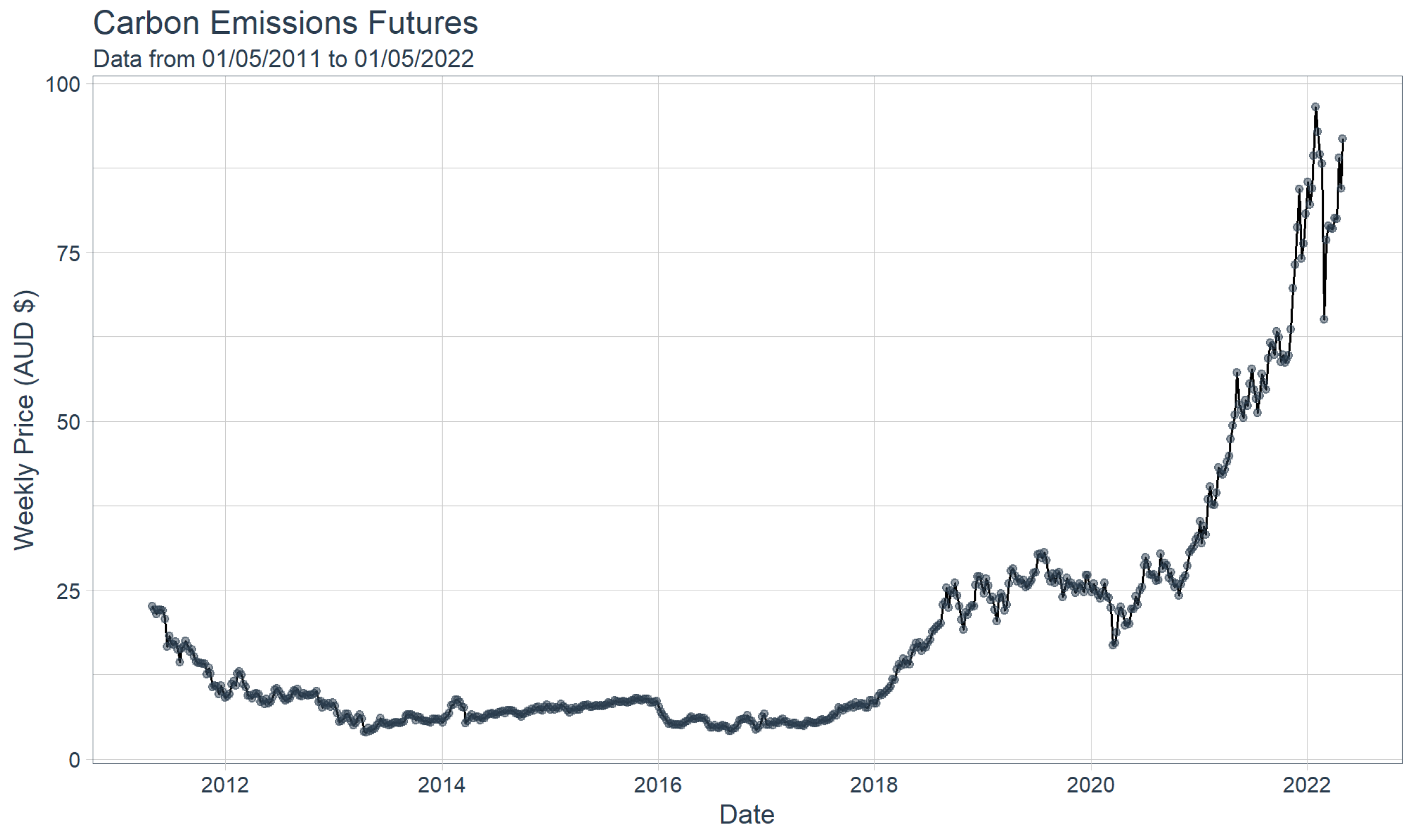
4. A Financial Time Series Modelling Application
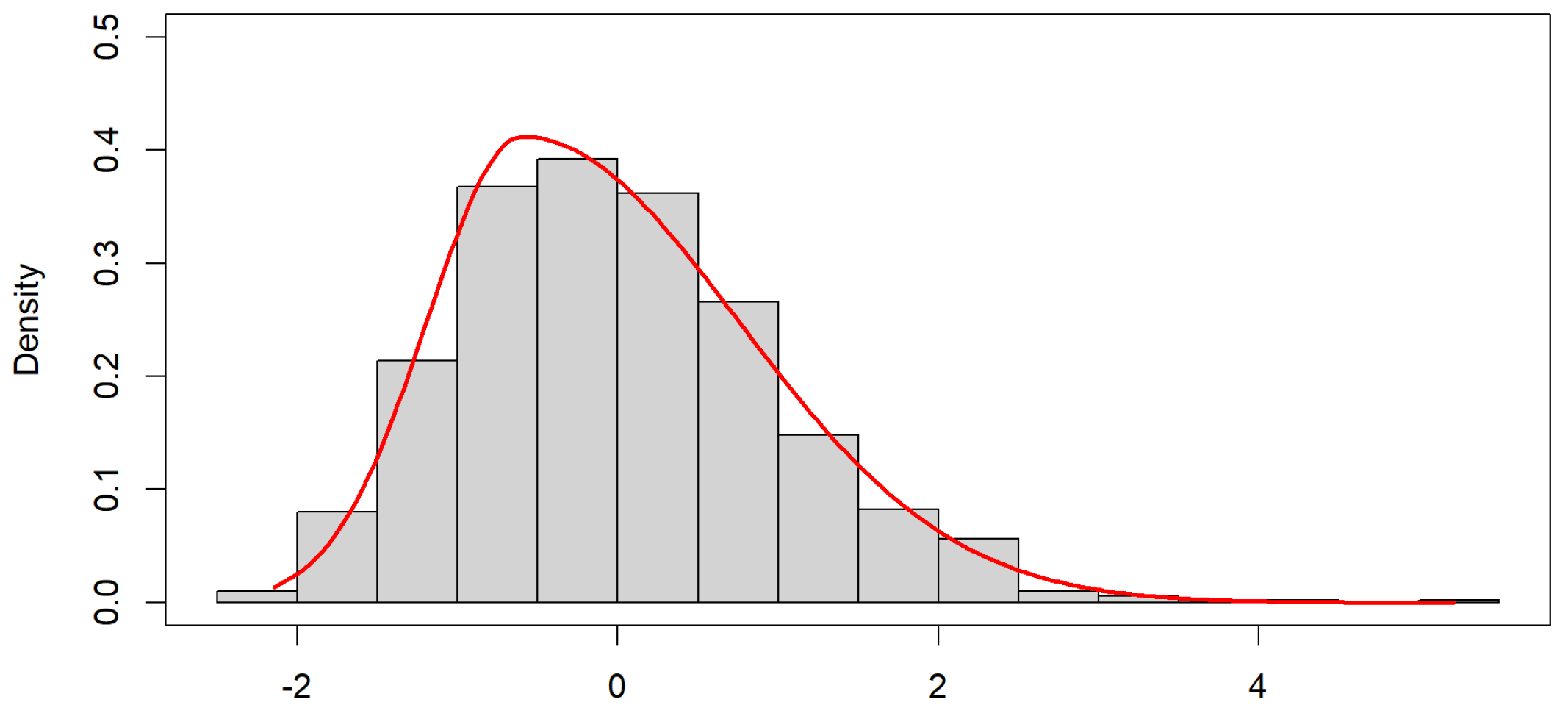
4.1. Determining the Initial Distribution
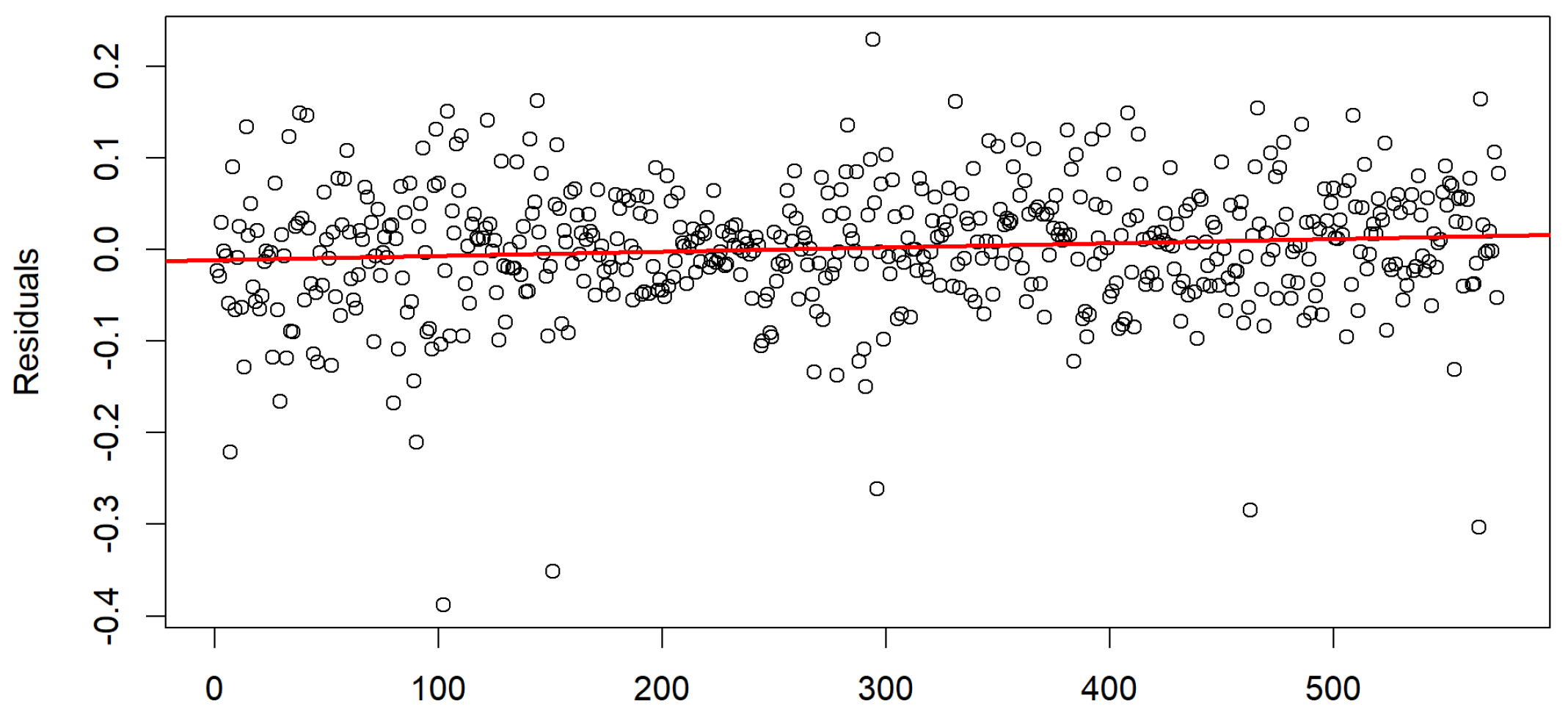
4.2. Box–Jenkins Time Series Modelling Methodology
4.3. Time Series Brownian Motion Results
4.4. Tsallis Entropy Results
5. Modelling Results Summary
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abdulla, Suhail Najm, and Heba Dhaher Alwan. 2022. Using apgarch/avgarch models Gaussian and non-Gaussian for modeling volatility exchange rate. International Journal of Nonlinear Analysis and Applications 13: 3029–38. [Google Scholar]
- Afuecheta, Emmanuel, Artur Semeyutin, Stephen Chan, Saralees Nadarajah, and Diego Andrés Pérez Ruiz. 2020. Compound distributions for financial returns. PLoS ONE 15: e0239652. [Google Scholar] [CrossRef] [PubMed]
- Agustini, W. Farida, Ika Restu Affianti, and Endah R. M. Putri. 2018. Stock price prediction using geometric Brownian motion. Journal of Physics: Conference Series 974: 012047. [Google Scholar]
- Bentes, Sónia R., Rui Menezes, and Diana A. Mendes. 2008. Stock market volatility: An approach based on Tsallis entropy. arXiv arXiv:0809.4570. [Google Scholar]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Caporin, Massimiliano, and Michele Costola. 2019. Asymmetry and leverage in GARCH models: A news impact curve perspective. Applied Economics 51: 3345–64. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2019. The accuracy of asymmetric GARCH model estimation. International Economics 157: 179–202. [Google Scholar] [CrossRef]
- Charpentire, Arthur. 2014. Computational Actuarial Science with R. New York: CRC Press. [Google Scholar]
- de Santa Helena, Emerson Luis, C. M. Nascimento, and G. Gerhardt. 2015. Alternative way to characterize a q-Gaussian distribution by a robust heavy tail measurement. Physica A: Statistical Mechanics and Its Applications 435: 44–50. [Google Scholar] [CrossRef][Green Version]
- de Santa Helena, Emerson Luis, and Wagner Santos de Lima. 2018. Package ‘qGaussian’. R Package Version 0.1.8. Available online: https://CRAN.R-project.org/package=qGaussian (accessed on 24 April 2022).
- Devi, Sandhya. 2021. Asymmetric Tsallis distributions for modeling financial market dynamics. Physica A: Statistical Mechanics and Its Applications 578: 126109. [Google Scholar] [CrossRef]
- Dewick, Paul R., and Liu Shuangzhe. 2022. Copula modelling to analyse financial data. Journal of Risk and Financial Management 15: 104. [Google Scholar] [CrossRef]
- Ermogenous, Angeliki. 2006. Brownian Motion and Its Applications in the Stock Market. Available online: https://ecommons.udayton.edu/cgi/viewcontent.cgi?article=1010&context=mth_epumd (accessed on 12 May 2022).
- Fukuda, Kosei. 2021. Selecting from among 12 alternative distributions of financial data. Communications in Statistics-Simulation and Computation 51: 3943–3954. [Google Scholar] [CrossRef]
- Ghani, I. M. Md, and H. A. Rahim. 2019. Modeling and forecasting of volatility using arma-garch: Case study on malaysia natural rubber prices. IOP Conference Series: Materials Science and Engineering 548: 012023. [Google Scholar] [CrossRef]
- Hambuckers, Julien, and Cedric Heuchenne. 2017. A robust statistical approach to select adequate error distributions for financial returns. Journal of Applied Statistics 44: 137–61. [Google Scholar] [CrossRef]
- Heyde, C. Heyde, and Shuangzhe Liu. 2001. Empirical Realities for Minimal Description Risky Asset Model. The Need for Fractal Features. Journal of the Korean Mathematical Society 38: 1047–59. [Google Scholar]
- Heyde, C. Heyde, Roger Gay, and Shuangzhe Liu. 2001. Fractal scaling and Black-Scholes [A new view of long-range dependence in stock prices]. JASSA 1: 29–32. [Google Scholar]
- Hongwiengjan, Warunya, and Dawud Thongtha. 2021. An analytical approximation of option prices via TGARCH model. Economic Research-Ekonomska Istraživanja 34: 948–69. [Google Scholar] [CrossRef]
- Islam, Mohammad Rafiqul, and Nguyet Nguyen. 2021. Comparison of Financial Models for Stock Price Prediction. Joint Mathematics Meetings (JMM) 13: 181. [Google Scholar] [CrossRef]
- Kapusta, Joseph I. 2021. Perspective on Tsallis statistics for nuclear and particle physics. International Journal of Modern Physics E 30: 2130006. [Google Scholar] [CrossRef]
- Khamis, Azme, M. A. A. Sukor, M. E. Nor, S. N. A. M. Razali, and R. M. Salleh. 2017. Modeling and Forecasting Volatility of Financial Data using Geometric Brownian Motion. International Journal of Advanced Research in Science, Engineering and Technology 4: 4599–605. [Google Scholar]
- Lim, Ching Mun, and Siok Kun Sek. 2013. Comparing the performances of GARCH-type models in capturing the stock market volatility in Malaysia. Procedia Economics and Finance 5: 478–87. [Google Scholar] [CrossRef]
- Liu, Shuangzhe, and Chris C. Heyde. 2008. On estimation in conditional heteroskedastic time series models under non-normal distributions. Statistical Papers 49: 455–69. [Google Scholar] [CrossRef]
- Liu, Timina, Shuangzhe Liu, and Lei Shi. 2020. Time Series Analysis Using SAS Enterprise Guide. Singapore: Springer Nature. [Google Scholar]
- Oliveira, Gustavo H. F. M., Rodolfo C. Cavalcante, George G. Cabral, Leandro L. Minku, and Adriano L. I. Oliveira. 2017. Time series forecasting in the presence of concept drift: A pso-based approach. Paper presented at the 2017 IEEE 29th International Conference on Tools with Artificial Intelligence ICTAI), Boston, MA, USA, November 6–8; pp. 239–46. [Google Scholar]
- Pavlos, G. P., L. P. Karakatsanis, M. N. Xenakis, E. G. Pavlos, A. C. Iliopoulos, and D. V. Sarafopoulos. 2014. Universality of non-extensive Tsallis statistics and time series analysis: Theory and applications. Physica A: Statistical Mechanics and Its Applications 395: 58–95. [Google Scholar] [CrossRef]
- Sato, Aki-Hiro. 2010. q-Gaussian distributions and multiplicative stochastic processes for analysis of multiple financial time series. Journal of Physics: Conference Series 201: 012008. [Google Scholar] [CrossRef]
- Shalizi, Cosma, and Christophe Dutang. 2021. tsallisqexp: Tsallis Distribution. R Package Version 0.9-4. Available online: https://CRAN.R-project.org/package=tsallisqexp (accessed on 15 May 2020).
- Sheraz, Muhammad, and Imran Nasir. 2021. Information-Theoretic Measures and Modeling Stock Market Volatility: A Comparative Approach. Risks 9: 89. [Google Scholar] [CrossRef]
- Stoyanov, Stoyan V., Svetlozar T. Rachev, Boryana Racheva-Yotova, and Frank J. Fabozzi. 2011. Fat-tailed models for risk estimation. The Journal of Portfolio Management 37: 107–17. [Google Scholar] [CrossRef]
- Teräsvirta, Timo. 2009. An introduction to univariate GARCH models. In Handbook of Financial Time Series. Berlin and Heidelberg: Springer, pp. 17–42. [Google Scholar]
- Tsallis, Constantino. 2017. Economics and Finance: q-Statistical stylized features galore. Entropy 19: 457. [Google Scholar] [CrossRef]
- Wheelwright, Steven, Spyros Makridakis, and Rob J. Hyndman. 1998. Forecasting: Methods and Applications. Hoboken: John Wiley & Sons. [Google Scholar]











| Model | Intercept | Slope | Std Error | p-Value | AIC | BIC | |||
|---|---|---|---|---|---|---|---|---|---|
| Log-diff. | 0.002 | 0.068 | −0.011 | 0.000 | 0.068 | 0.011 | 0.007 | −1457.4 | −1444.4 |
| ARIMA | 0.000 | 0.084 | 0.000 | 0.000 | 0.084 | −0.002 | 0.986 | −1206.6 | −1193.6 |
| SGARCH | 0.061 | 0.999 | −0.156 | 0.001 | 0.993 | 0.014 | 0.003 | 1627.4 | 1640.4 |
| TGARCH | 0.026 | 1.000 | −0.237 | 0.001 | 0.990 | 0.021 | 0.000 | 1624.3 | 1637.4 |
| GJR-GARCH | 0.057 | 1.036 | −0.323 | 0.001 | 1.013 | 0.043 | 0.000 | 1651.1 | 1664.1 |
| GBM | 0.002 | 0.068 | −0.006 | 0.000 | 0.063 | 0.011 | 0.011 | −1532.1 | −1519.0 |
| Tsallis | 0.033 | 0.806 | −0.452 | 0.000 | 0.890 | 0.001 | 0.644 | 725.8 | 736.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dewick, P.R. On Financial Distributions Modelling Methods: Application on Regression Models for Time Series. J. Risk Financial Manag. 2022, 15, 461. https://doi.org/10.3390/jrfm15100461
Dewick PR. On Financial Distributions Modelling Methods: Application on Regression Models for Time Series. Journal of Risk and Financial Management. 2022; 15(10):461. https://doi.org/10.3390/jrfm15100461
Chicago/Turabian StyleDewick, Paul R. 2022. "On Financial Distributions Modelling Methods: Application on Regression Models for Time Series" Journal of Risk and Financial Management 15, no. 10: 461. https://doi.org/10.3390/jrfm15100461
APA StyleDewick, P. R. (2022). On Financial Distributions Modelling Methods: Application on Regression Models for Time Series. Journal of Risk and Financial Management, 15(10), 461. https://doi.org/10.3390/jrfm15100461






