Utility Indifference Option Pricing Model with a Non-Constant Risk-Aversion under Transaction Costs and Its Numerical Approximation
Abstract
:1. Introduction
2. Utility Indifference Option Pricing Model
2.1. Risk Aversion and the Concept of a Certainty Equivalent
2.2. Utility Indifference Option Pricing Model under Transaction Costs
2.3. Hamilton-Jacobi-Bellman Equations for Value Functions
2.4. Penalty Method for Solving HJB Equations
3. Transformation of the HJB Equation Involving Risk Aversion Function
4. Construction of a Numerical Discretization Upwind Finite Difference Scheme
4.1. Finite Difference Approximation of a Solution to the Penalized Problem
| Algorithm 1: The algorithm for computing the value function V for . |
 |
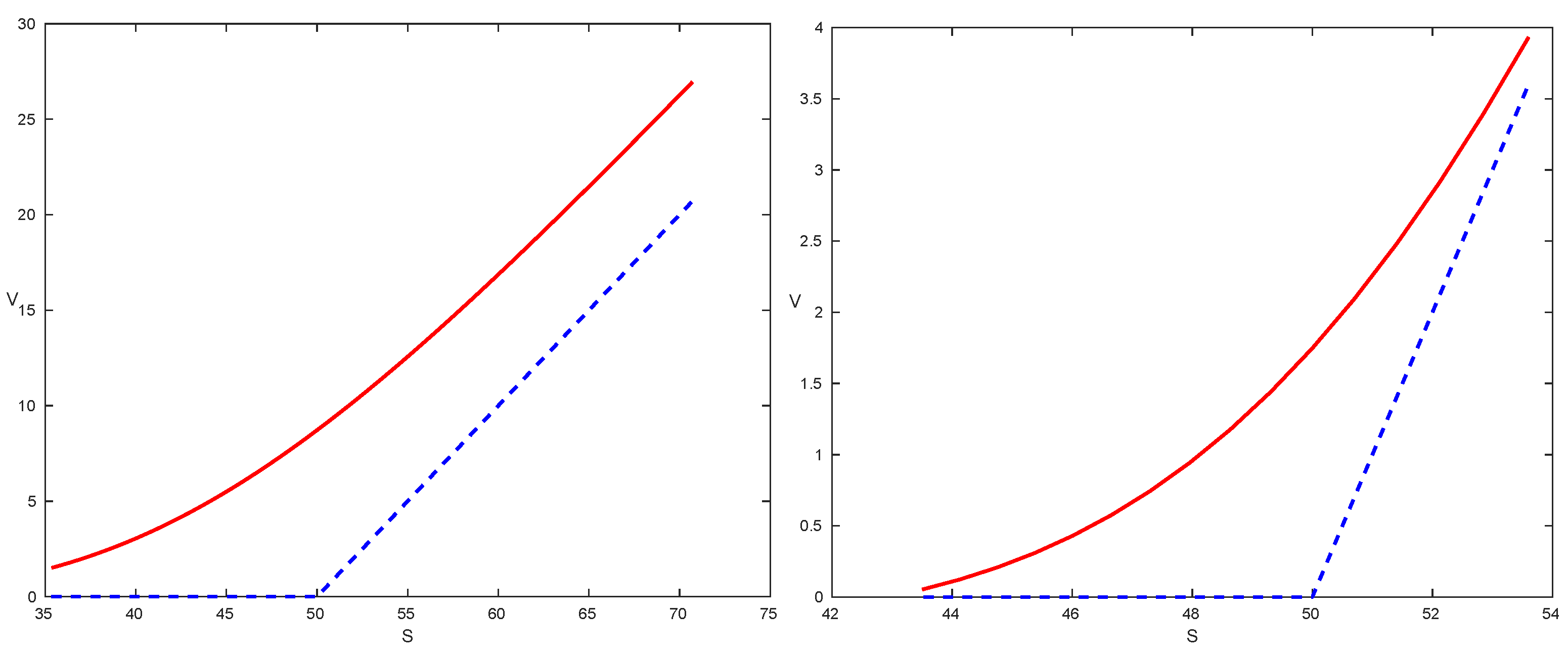
4.2. Results of Numerical Approximation of Option Prices
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barles, Guy, and Halil Mete Soner. 1998. Option pricing with transaction costs and a nonlinear Black-Scholes equation. Finance and Stochastics 2: 369–97. [Google Scholar] [CrossRef]
- Bučková, Zuzana, Matthias Ehrhardt, Michael Günther, and Pedro Pólvora. 2017. Alternating direction explicit methods for linear, nonlinear and multi-dimensional Black-Scholes models. In Novel Methods in Computational Finance. Cham: Springer, pp. 333–71. [Google Scholar]
- Cantarutti, Nicola, Joao Guerra, Manuel Guerra, and Maria do Rosário Grossinho. 2017. Indifference pricing in a market with transaction costs and jumps. In Novel Methods in Computational Finance. Cham: Springer, pp. 31–46. [Google Scholar] [CrossRef]
- Carmona, René, and Erhan Çinlar. 2009. Indifference Pricing: Theory and Applications. Princeton: Princeton University Press. [Google Scholar]
- Chernogorova, Tatiana P., Miglena N. Koleva, and Radoslav L. Valkov. 2018. A two-grid penalty method for American options. Journal of Computational and Applied Mathematics 37: 2381–98. [Google Scholar] [CrossRef]
- Clevenhaus, Anna, Matthias Ehrhardt, Michael Günther, and Daniel Ševčovič. 2020. Pricing American Options with a Non-Constant Penalty Parameter. Journal of Risk and Financial Management 13: 124. [Google Scholar] [CrossRef]
- Davis, Mark H. A., Vassilios G. Panas, and Thaleia Zariphopoulou. 1993. European option pricing with transaction costs. SIAM Journal on Control and Optimization 31: 470–93. [Google Scholar] [CrossRef]
- Dempster, Michael A. H., and Stanley R. Pliska, eds. 1997. Mathematics of Derivative Securities. Volume 15 of Publications of the Newton Institute. Cambridge: Cambridge University Press. [Google Scholar]
- Dong, Yan, and Xiaoping Lu. 2021. Utility-indifference pricing of European options with proportional transaction costs. Journal of Computational and Applied Mathematics 397: 12. [Google Scholar] [CrossRef]
- Hodges, Stewart D., and Anthony Neuberger. 1989. Optimal replication of contingent claims under transaction costs. Review of Futures Markets 8: 222–39. [Google Scholar]
- Kallsen, Jan, and Johannes Muhle-Karbe. 2015. Option pricing and hedging with small transaction costs. Mathematical Finance 25: 702–23. [Google Scholar] [CrossRef] [Green Version]
- Kilianová, Soňa, and Daniel Ševčovič. 2018. Expected utility maximization and conditional value-at-risk deviation-based Sharpe ratio in dynamic stochastic portfolio optimization. Kybernetika (Prague) 54: 1167–83. [Google Scholar]
- Leland, Hayne E. 1985. Option pricing and replication with transactions costs. The Journal of Finance 40: 1283–301. [Google Scholar] [CrossRef]
- Lesmana, Donny Citra, and Song Wang. 2015. Penalty approach to a nonlinear obstacle problem governing American put option valuation under transaction costs. Applied Mathematics and Computation 251: 318–30. [Google Scholar] [CrossRef]
- Li, Wen, and Song Wang. 2009. Penalty approach to the hjb equation arising in european stock option pricing with proportional transaction costs. Journal of Optimization Theory and Applications 143: 279–93. [Google Scholar] [CrossRef]
- Li, Wen, and Song Wang. 2014. A numerical method for pricing european options with proportional transaction costs. Journal of Global Optimization 60: 59–78. [Google Scholar] [CrossRef]
- Meyer, John, and David Needham. 2014. Extended weak maximum principles for parabolic partial differential inequalities on unbounded domains. Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences 478: 20140079. [Google Scholar] [CrossRef]
- Monoyios, Michael. 2004. Option pricing with transaction costs using a Markov chain approximation. Journal of Economic Dynamics and Control 28: 889–913. [Google Scholar] [CrossRef] [Green Version]
- Perrakis, Stylianos, and Jean Lefoll. 2000. Option pricing and replication with transaction costs and dividends. Journal of Economic Dynamics and Control 24: 1527–61. [Google Scholar] [CrossRef] [Green Version]
- Post, Thierry, Yi Fang, and Martin Kopa. 2015. Linear tests for DARA stochastic dominance. Management Science 61: 1615–29. [Google Scholar] [CrossRef]
- Ševčovič, Daniel. 2017. Nonlinear parabolic equations arising in mathematical finance. In Novel Methods in Computational Finance. Cham: Springer, pp. 3–15. [Google Scholar]
- Ševčovič, Daniel, and Magdaléna Žitňanská. 2016. Analysis of the nonlinear option pricing model under variable transaction costs. Asia-Pacific Financial Markets 23: 153–74. [Google Scholar] [CrossRef] [Green Version]
| Type | Utility Function | Parameter | Inverse Utility Function | Risk Aversion |
|---|---|---|---|---|
| Linear | — | |||
| Exp. | ||||
| Power | ||||
| Log. |
| Model Parameters | Value | Num Params | Value | Num Params | Value |
|---|---|---|---|---|---|
| Strike price K | 50 | 6 | 100 | ||
| Transaction costs | 0.01 | 0.2 | 100 | ||
| Volatility | 0.3 | 0.6 | 10 | ||
| Risk-free rate r | 0.05 | 6 | N | 10 | |
| Drift | 0.1 | −100 | T | 1 | |
| Risk-aversion | 0.1 | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pólvora, P.; Ševčovič, D. Utility Indifference Option Pricing Model with a Non-Constant Risk-Aversion under Transaction Costs and Its Numerical Approximation. J. Risk Financial Manag. 2021, 14, 399. https://doi.org/10.3390/jrfm14090399
Pólvora P, Ševčovič D. Utility Indifference Option Pricing Model with a Non-Constant Risk-Aversion under Transaction Costs and Its Numerical Approximation. Journal of Risk and Financial Management. 2021; 14(9):399. https://doi.org/10.3390/jrfm14090399
Chicago/Turabian StylePólvora, Pedro, and Daniel Ševčovič. 2021. "Utility Indifference Option Pricing Model with a Non-Constant Risk-Aversion under Transaction Costs and Its Numerical Approximation" Journal of Risk and Financial Management 14, no. 9: 399. https://doi.org/10.3390/jrfm14090399
APA StylePólvora, P., & Ševčovič, D. (2021). Utility Indifference Option Pricing Model with a Non-Constant Risk-Aversion under Transaction Costs and Its Numerical Approximation. Journal of Risk and Financial Management, 14(9), 399. https://doi.org/10.3390/jrfm14090399







