Volatility-Adjusted 60/40 versus 100—New Risk Investing Paradigm
Abstract
1. Introduction
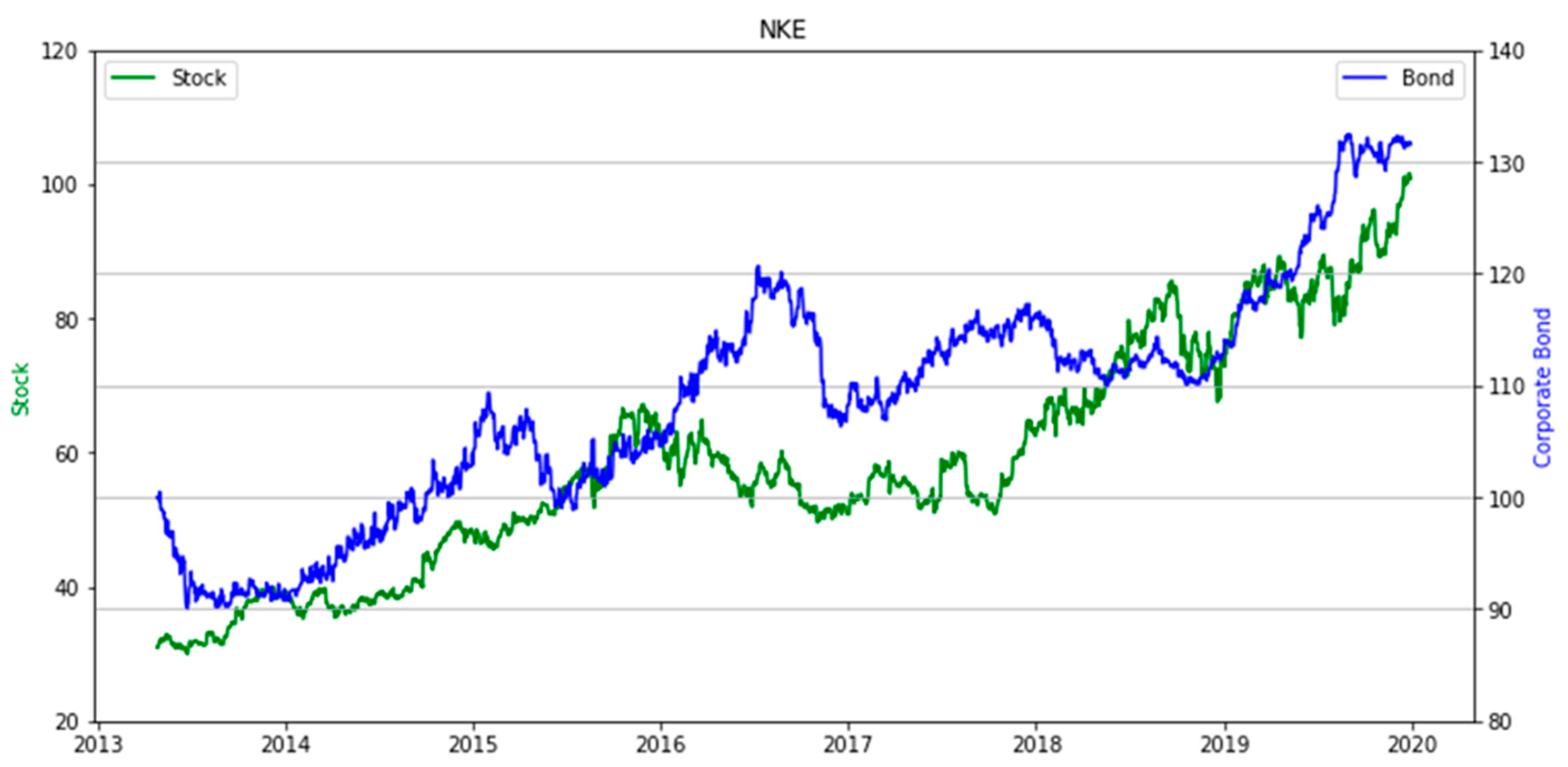
2. Materials and Methods
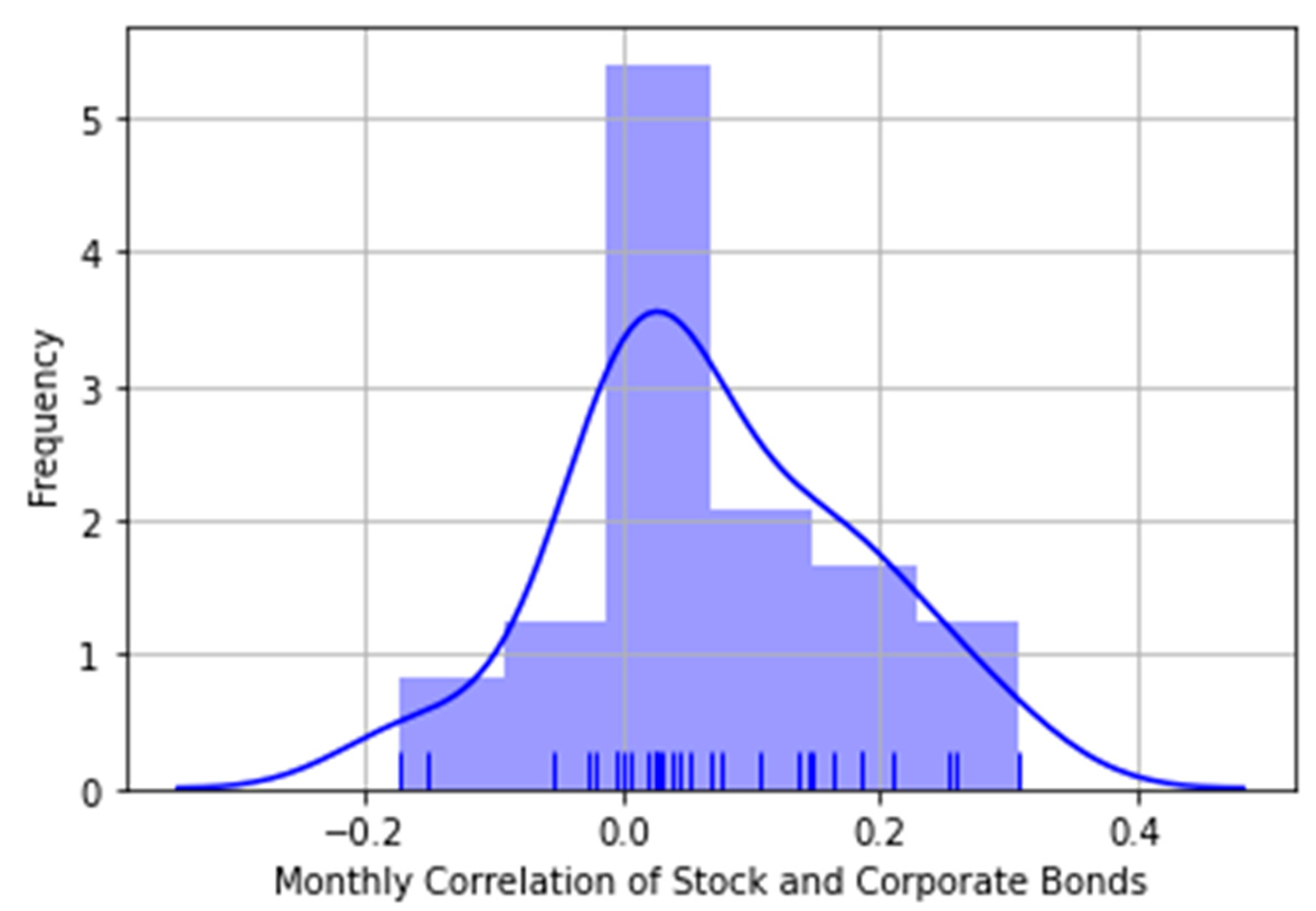
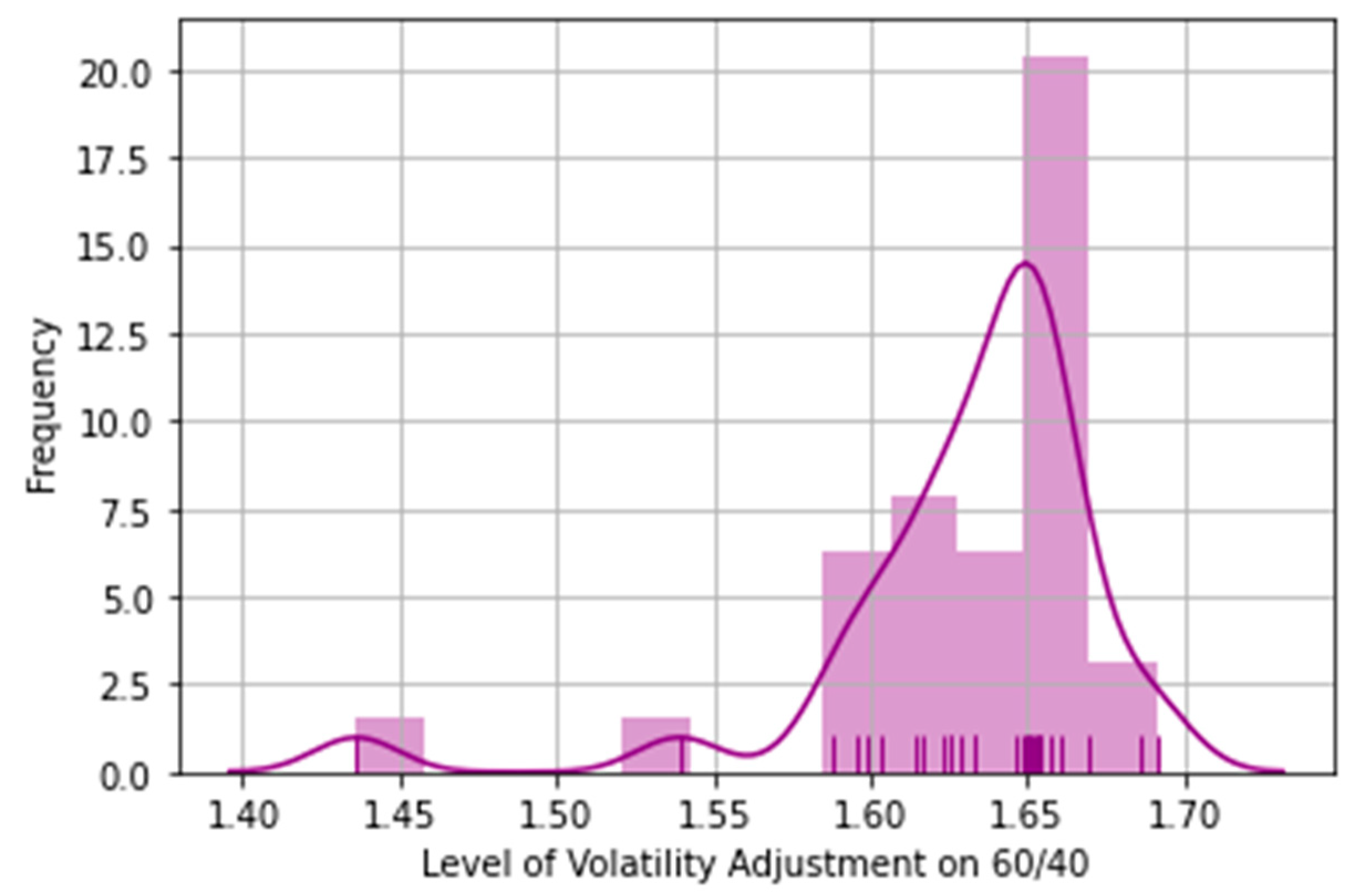
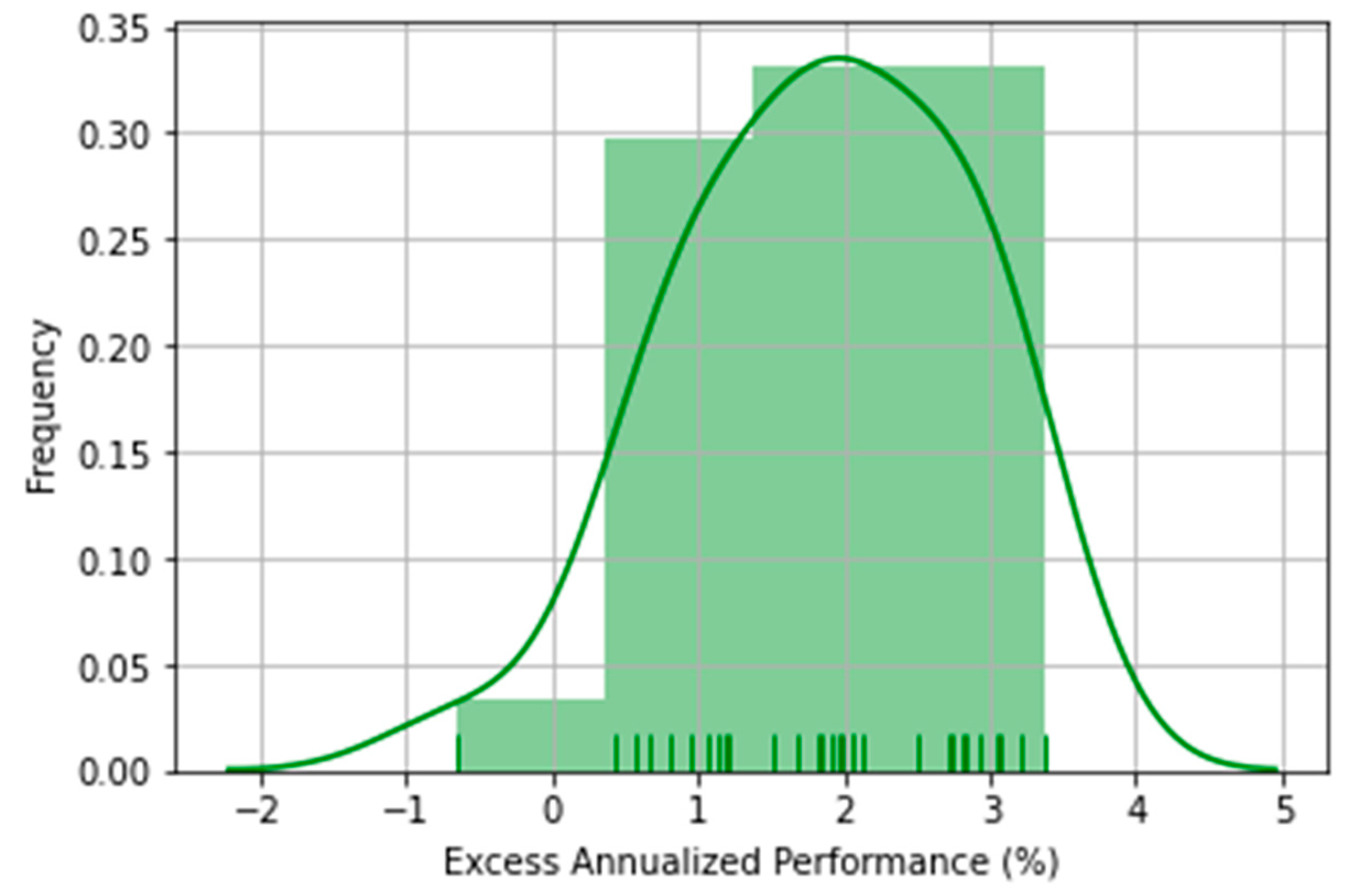
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Anginer, Deniz, and Çelim Yıldızhan. 2017. Is there a distress risk anomaly? Pricing of systematic default risk in the cross section of equity returns. Review of Finance 22: 633–60. [Google Scholar] [CrossRef]
- Asness, Clifford S., Andrea Frazzini, and Lasse H. Pedersen. 2012. Leverage Aversion and Risk Parity. Financial Analysts Journal 68: 47–59. [Google Scholar] [CrossRef]
- Campello, Murillo, Long Chen, and Lu Zhang. 2008. Expected returns, yield spreads, and asset pricing tests. Review of Financial Studies 21: 1297–338. [Google Scholar] [CrossRef]
- Collin-Dufresne, Pierre, Robert S. Goldstein, and J. Spencer Martin. 2001. The determinants of credit spread Changes. The Journal of Finance 56: 2177–207. [Google Scholar] [CrossRef]
- Demirovic, Amer, Cherif Guermat, and Jon Tucker. 2017. The relationship between equity and bond returns: An empirical investigation. Journal of Financial Markets 35: 47–64. [Google Scholar] [CrossRef]
- Fabozzi, Frank. 1992. Investing: The Collected Works of Martin L. Leibowitz. Carolina: Probus Professional Pub, p. 521. [Google Scholar]
- Fama, Eugene. 1972. Components of Investment Performance. The Journal of Finance 27: 551–67. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 2012. Size, value, and momentum in international stock returns. Journal of Financial Economics 105: 457–72. [Google Scholar] [CrossRef]
- Friewald, Nils, Christian Wagner, and Josef Zechner. 2014. The Cross-section of credit risk premia and equity returns. The Journal of Finance 69: 2419–69. [Google Scholar] [CrossRef]
- Hicks, Sir John. 1939. Value and Creation. Oxford: Clarendon Press. [Google Scholar]
- Jegadeesh, Narasimhan, and Sheridan Titman. 1993. Returns to buying winners and selling losers: Implications for stock market efficiency. The Journal of Finance 48: 65–91. [Google Scholar] [CrossRef]
- Kapadia, Nikunj, and Xiaoling Pu. 2012. Limited arbitrage between equity and credit markets. Journal of Financial Economics 105: 542–64. [Google Scholar] [CrossRef]
- Koopmans, T. C. 1942. The Risk of Interest Fluctuations in Life Insurance Companies. Horsham Township: Penn Mutual Life Insurance Company. [Google Scholar]
- Liew, Jim Kyung-Soo, and Maria Vassalou. 2000. Can book-to-market, size, and momentum be risk factors that predict economic growth? Journal of Financial Economics 57: 221–45. [Google Scholar] [CrossRef]
- Macaulay, Frederick. 1938. Some Theoretical Problems Suggested by the Movements of Interest Rates, Bond Yields, and Stock Price in the United States Since 1856. Cambridge: National Bureau of Economic Research, pp. 44–53. [Google Scholar]
- Markowitz, Harry. 1952. Portfolio Selection. The Journal of Finance 7: 77–91. [Google Scholar]
- Redington, F. M. 1952. Review of the Principles of Life-Office Valuations. Journal of the Institute of Actuaries 78: 286–340. [Google Scholar] [CrossRef]
- Simaan, Yusif. 1997. Estimation risk in portfolio selection: The mean variance model versus the mean absolute deviation model. Management Science 43: 1437–46. [Google Scholar] [CrossRef]
- Yin, George, and Xun Yu Zhou. 2004. Markowitz’s mean-variance portfolio selection with regime switching: From discrete-time models to the continuous-time limits. IEEE Transactions on Automatic Control 49: 349–60. [Google Scholar] [CrossRef]
- Zhu, Yingzi, and Guofo Zhou. 2009. Technical Analysis: An asset allocation perspective on the use of moving averages. Journal of Financial Economics 92: 519–44. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liew, J.K.-S.; Ajakh, A. Volatility-Adjusted 60/40 versus 100—New Risk Investing Paradigm. J. Risk Financial Manag. 2020, 13, 190. https://doi.org/10.3390/jrfm13090190
Liew JK-S, Ajakh A. Volatility-Adjusted 60/40 versus 100—New Risk Investing Paradigm. Journal of Risk and Financial Management. 2020; 13(9):190. https://doi.org/10.3390/jrfm13090190
Chicago/Turabian StyleLiew, Jim Kyung-Soo, and Ahmad Ajakh. 2020. "Volatility-Adjusted 60/40 versus 100—New Risk Investing Paradigm" Journal of Risk and Financial Management 13, no. 9: 190. https://doi.org/10.3390/jrfm13090190
APA StyleLiew, J. K.-S., & Ajakh, A. (2020). Volatility-Adjusted 60/40 versus 100—New Risk Investing Paradigm. Journal of Risk and Financial Management, 13(9), 190. https://doi.org/10.3390/jrfm13090190



