Bitcoin Network Mechanics: Forecasting the BTC Closing Price Using Vector Auto-Regression Models Based on Endogenous and Exogenous Feature Variables
Abstract
1. Introduction
2. Background on Bitcoin
2.1. Bitcoin Ledger
2.2. Bitcoin Development Process
- The network effect;
- Cryptocurrency volatility;
- Cryptocurrency-pegging technology.
2.2.1. The Network Effect
2.2.2. Cryptocurrency Volatility
2.2.3. Cryptocurrency-Pegging Technology
2.3. Market Participants
- Miners—The market participants who are proactively adding transaction records to Bitcoin’s public ledger of past transactions or blockchain and fueling the supply of BTC.
- Individual investors—Investors for the digital assets to purchase goods or services with the digital currency.
- Payment mechanism—Conduct business internationally as international payments are now available via BTC.
- Retail investors—Funds that are likely to pick up the currency as a portion of their portfolio to hedge, like gaining exposure to traditional currency markets.
2.4. Stakeholders
3. Related Work
3.1. Machine Learning Prediction Methods
3.2. Time-Series Prediction Methods
4. BTC Closing Price Prediction Models
4.1. Endogenous and Exogenous Variables
4.2. Vector Autoregression (VAR) Model
4.2.1. Model Assumptions
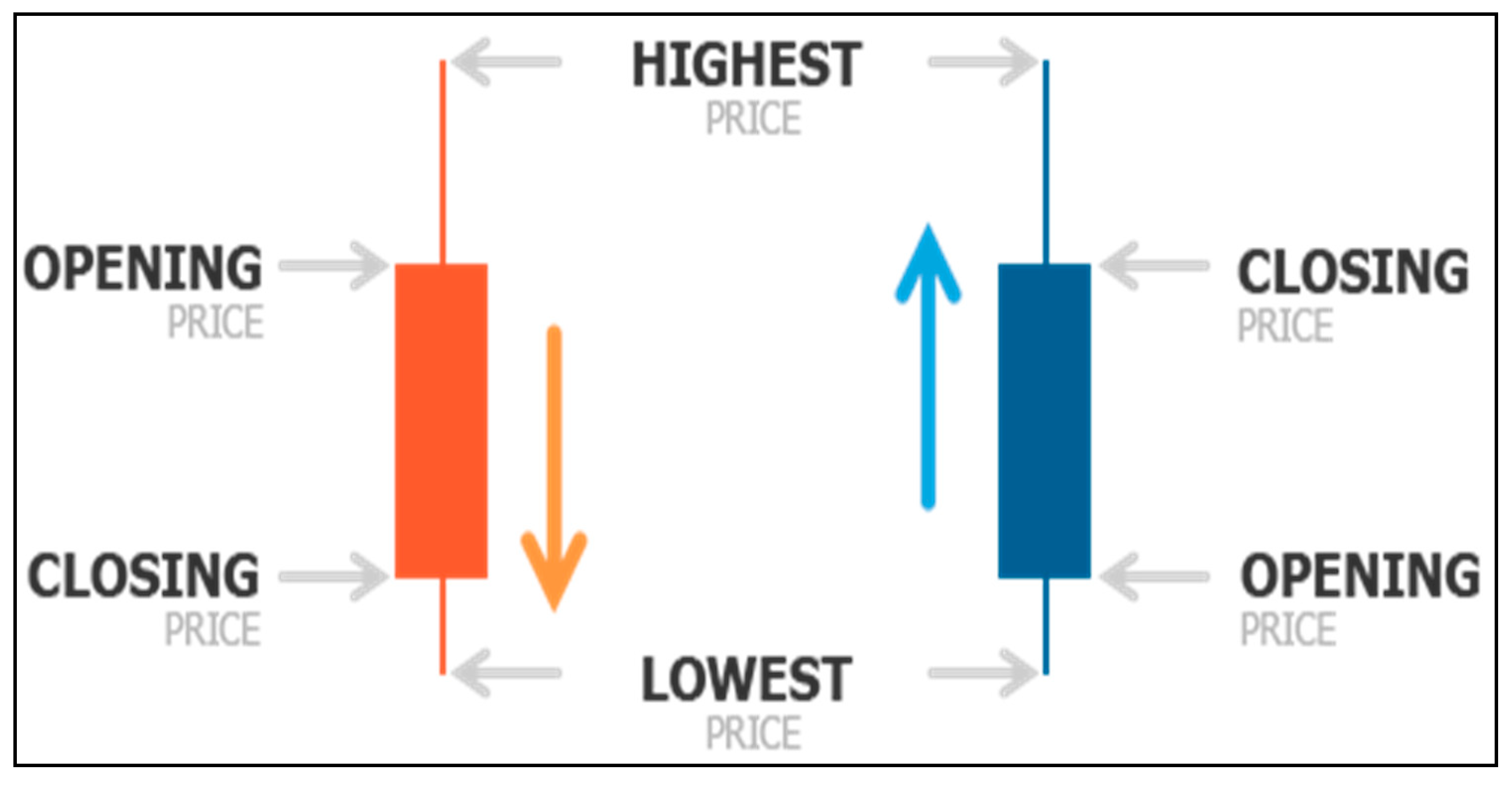
4.2.2. Model Validation and Verifications
- lag.max = 366—to accommodate a full year of seasonal behavior and trends;
- type = ‘both’—to evaluate the deterministic regressors.
4.3. Bayesian Vector Autoregression (BVAR) Model
Prior Specification
- Parameter λ with max = 5 and min = 0.0001, to control the tightness of the prior;
- Parameter α with max = 3 and min = 1, to manage variance decay with increasing lag order;
- var = 10,000,000, to set the prior variance on the model’s constant.
5. Experimental Analysis
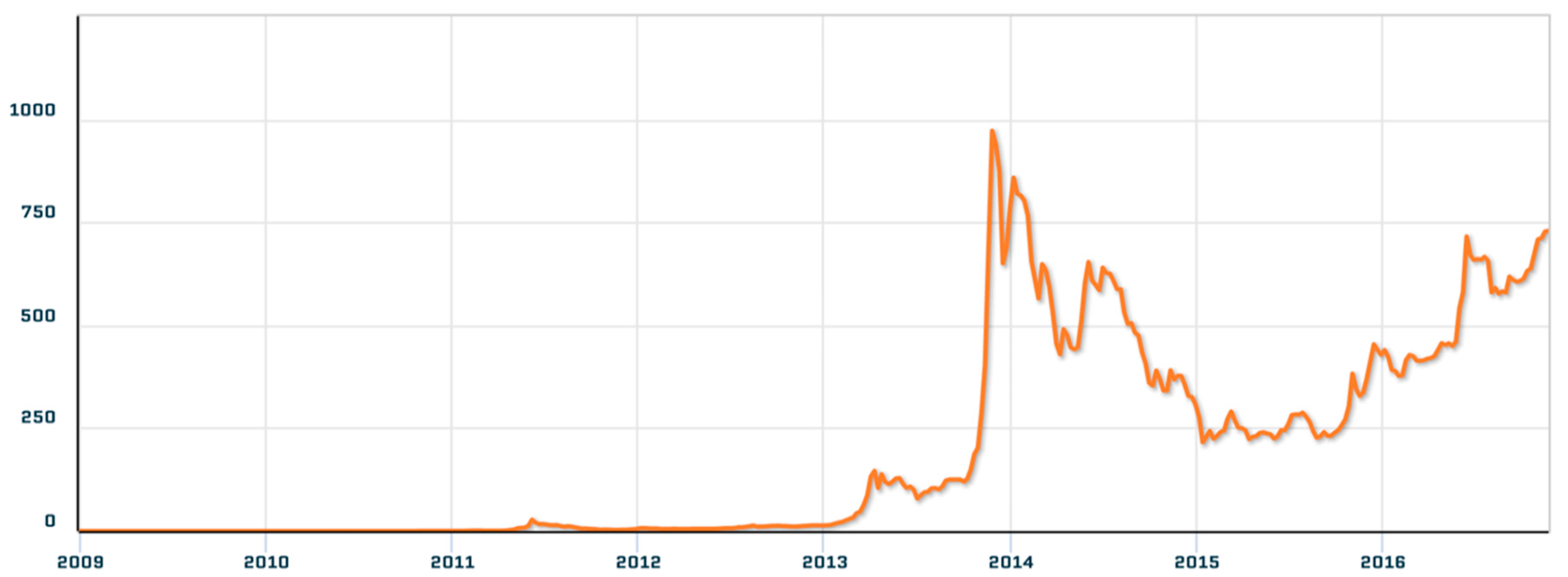
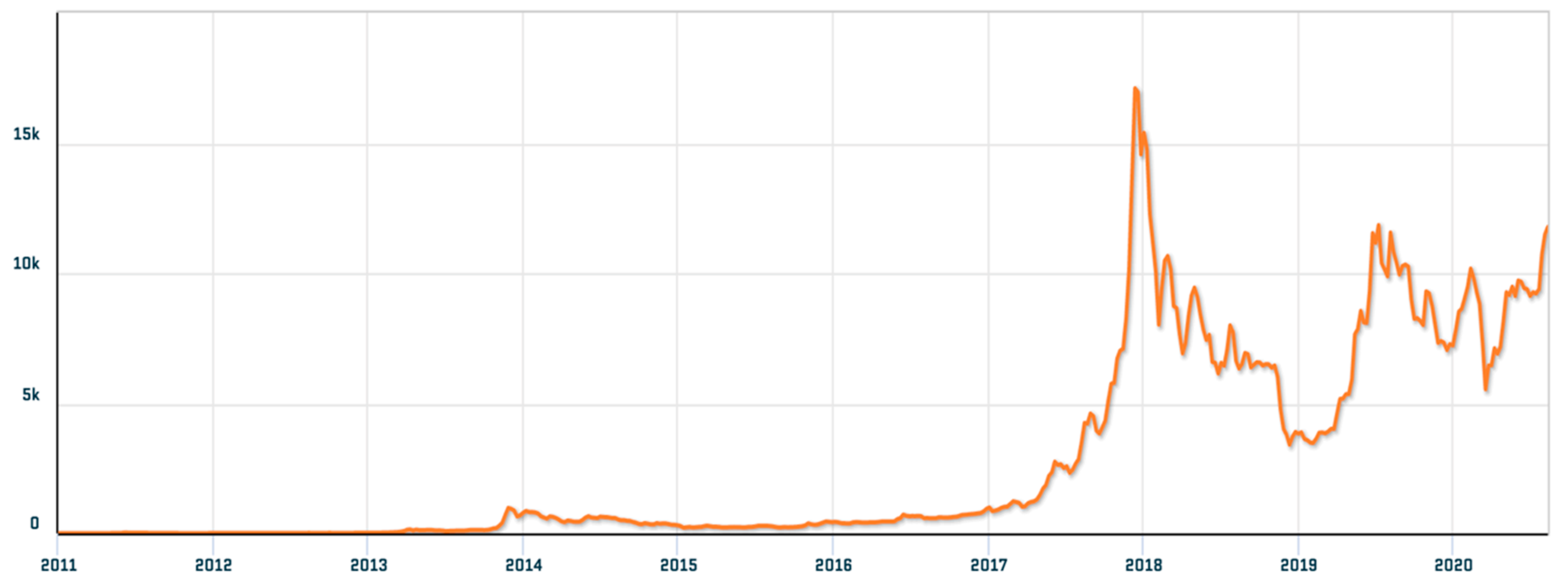
5.1. Experimental Dataset
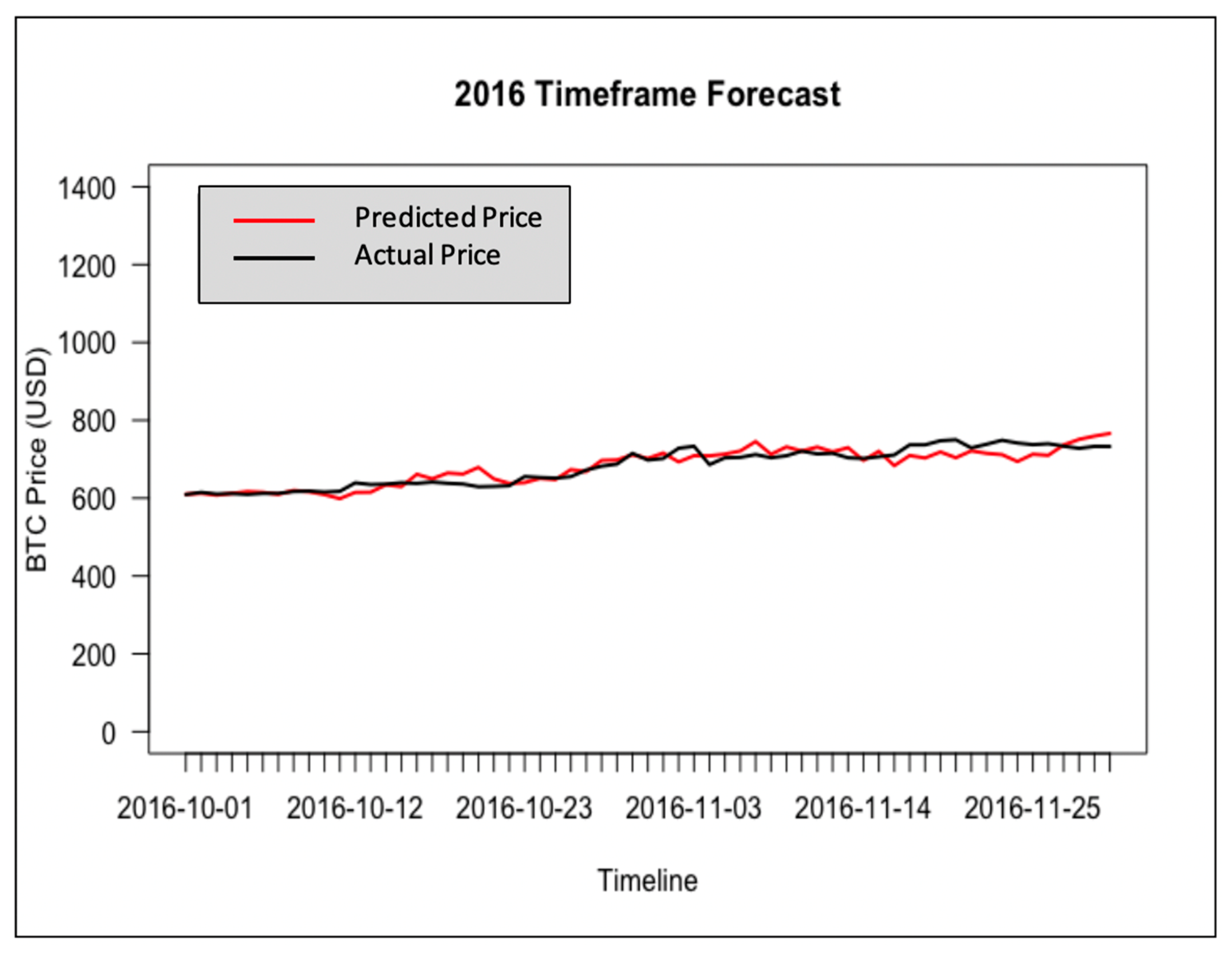
5.2. Forecasting Results
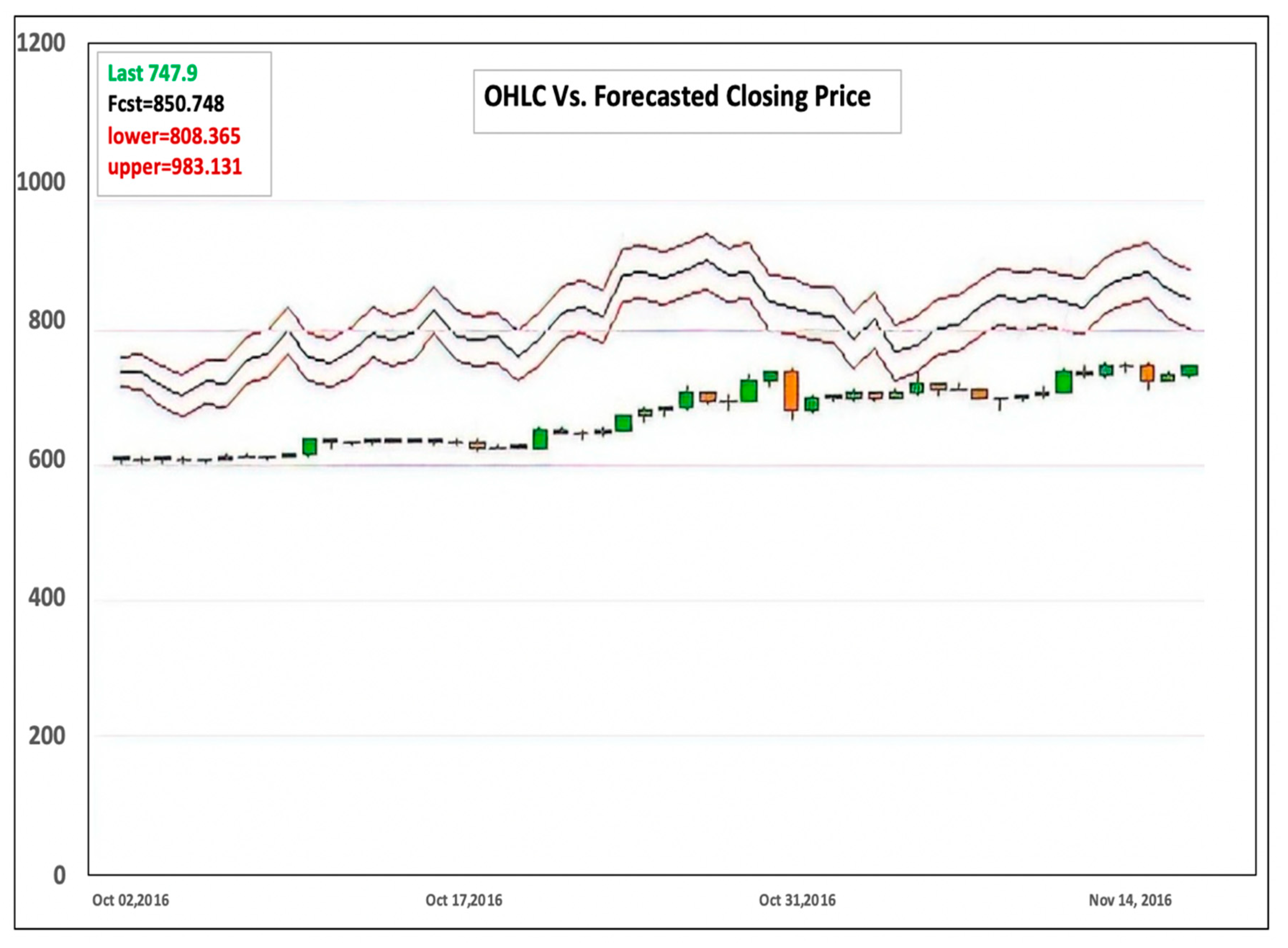
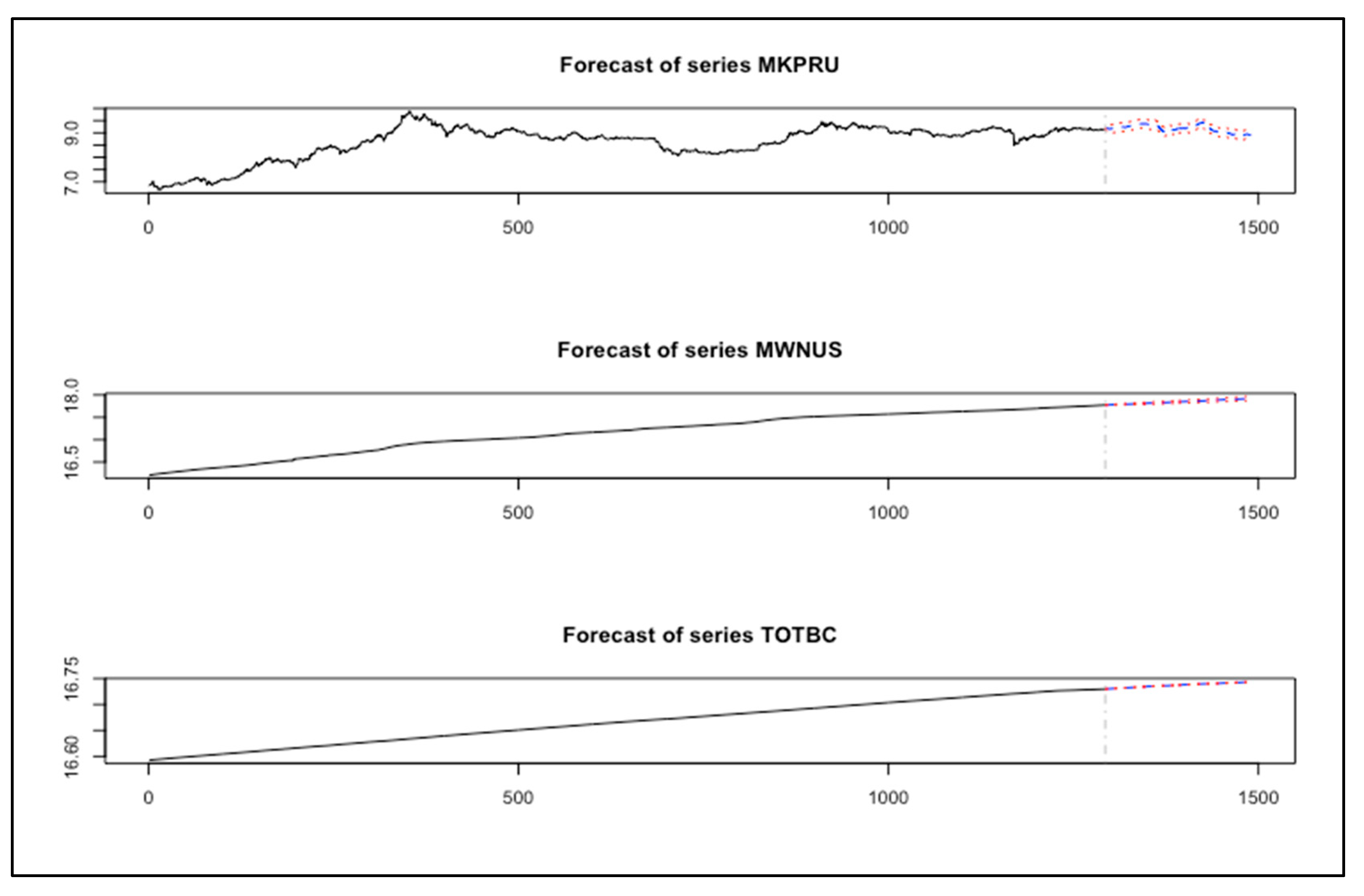
5.2.1. Results of the VAR Model: Experiment A
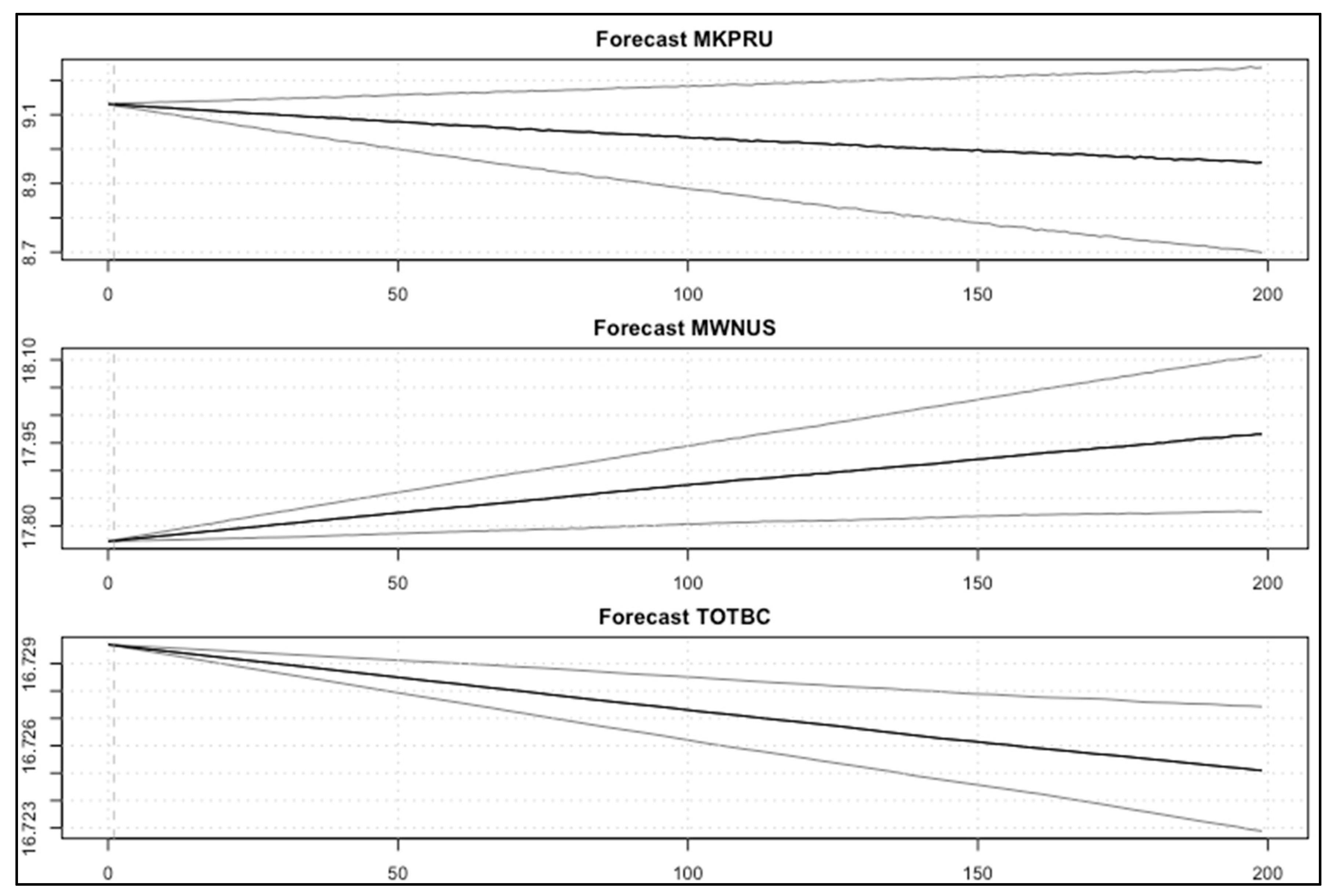
5.2.2. Results of the VAR Model: Experiment B
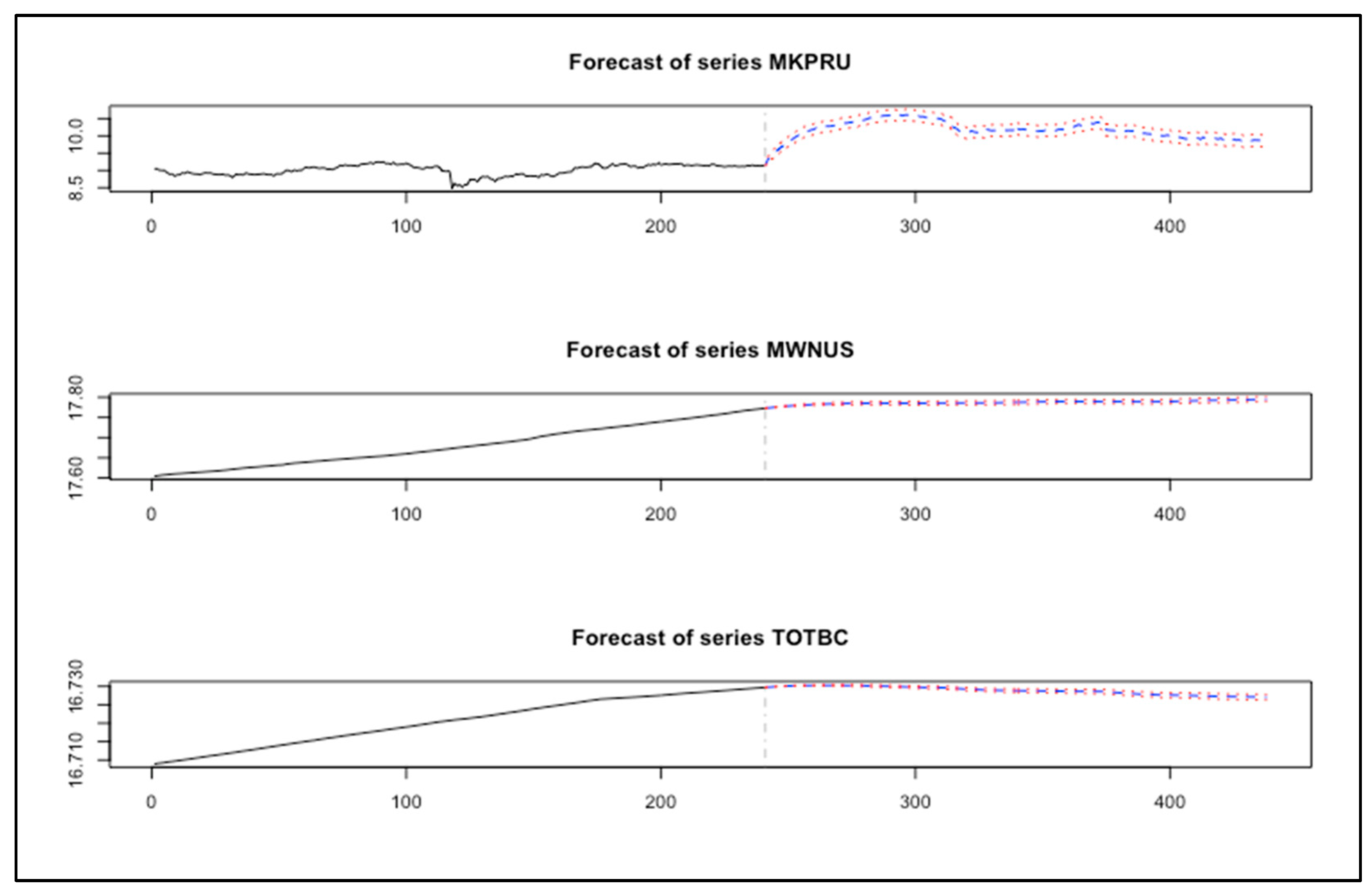
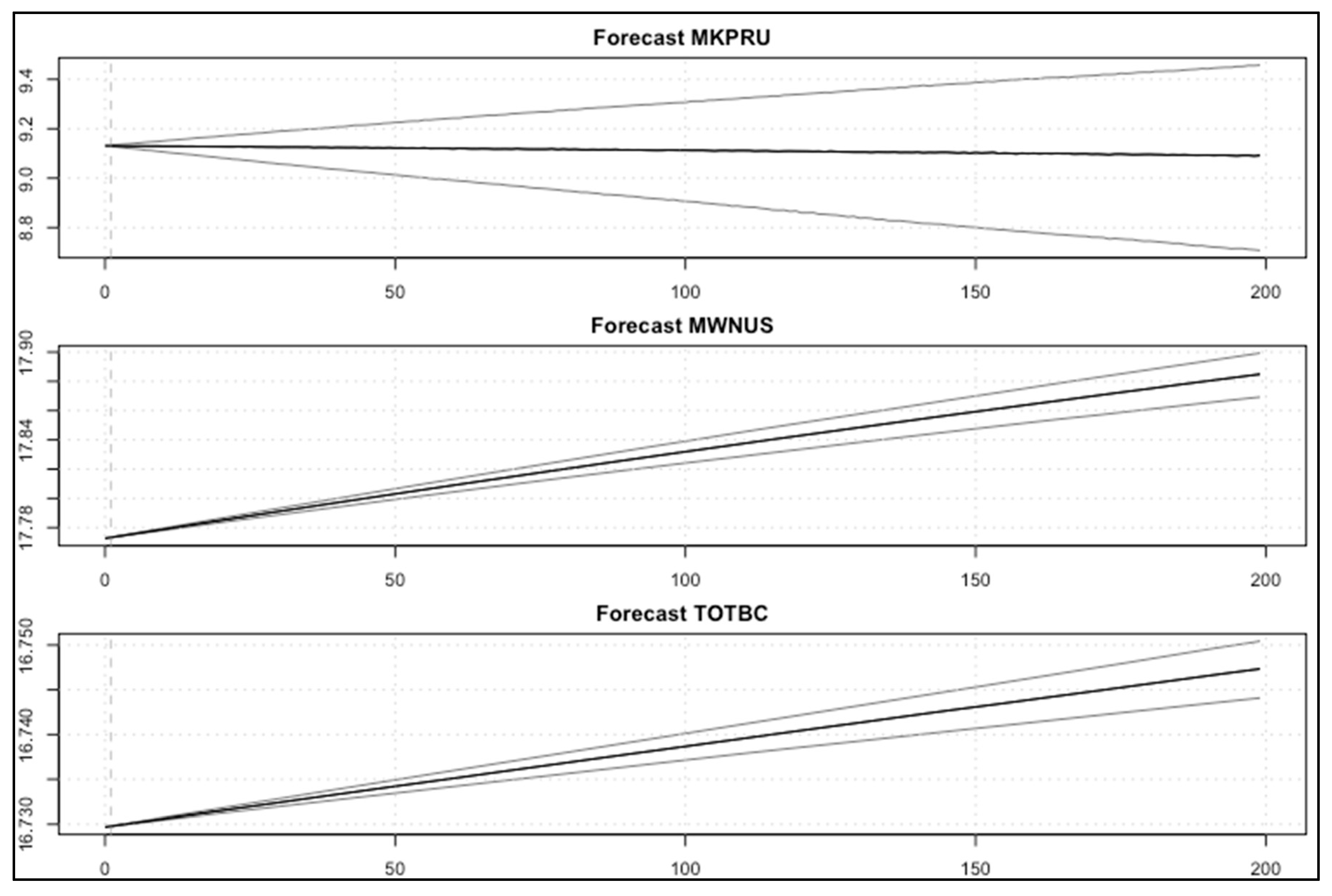
5.2.3. Results of the BVAR Model: Experiment A
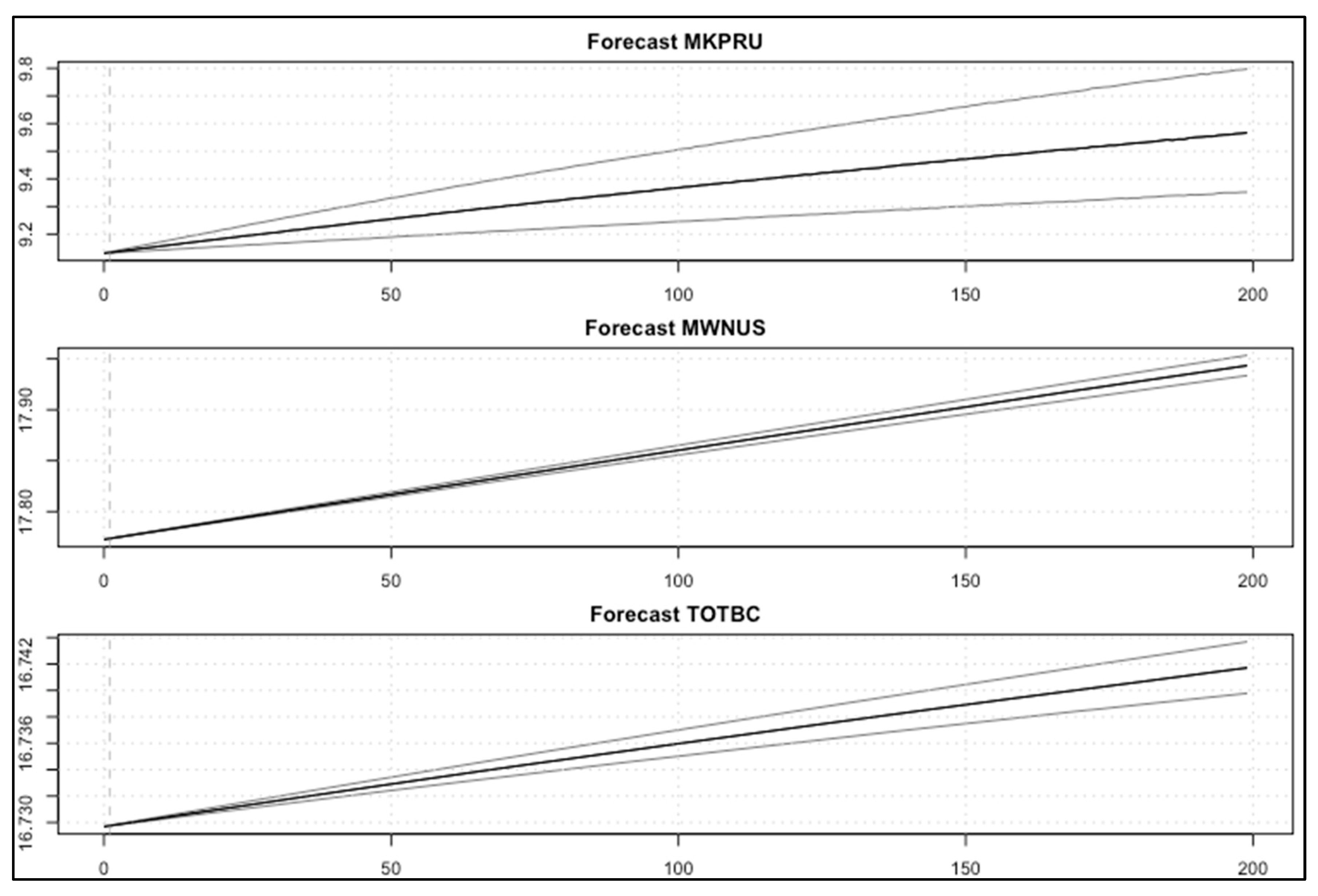
5.2.4. Results of the BVAR Model: Experiment B
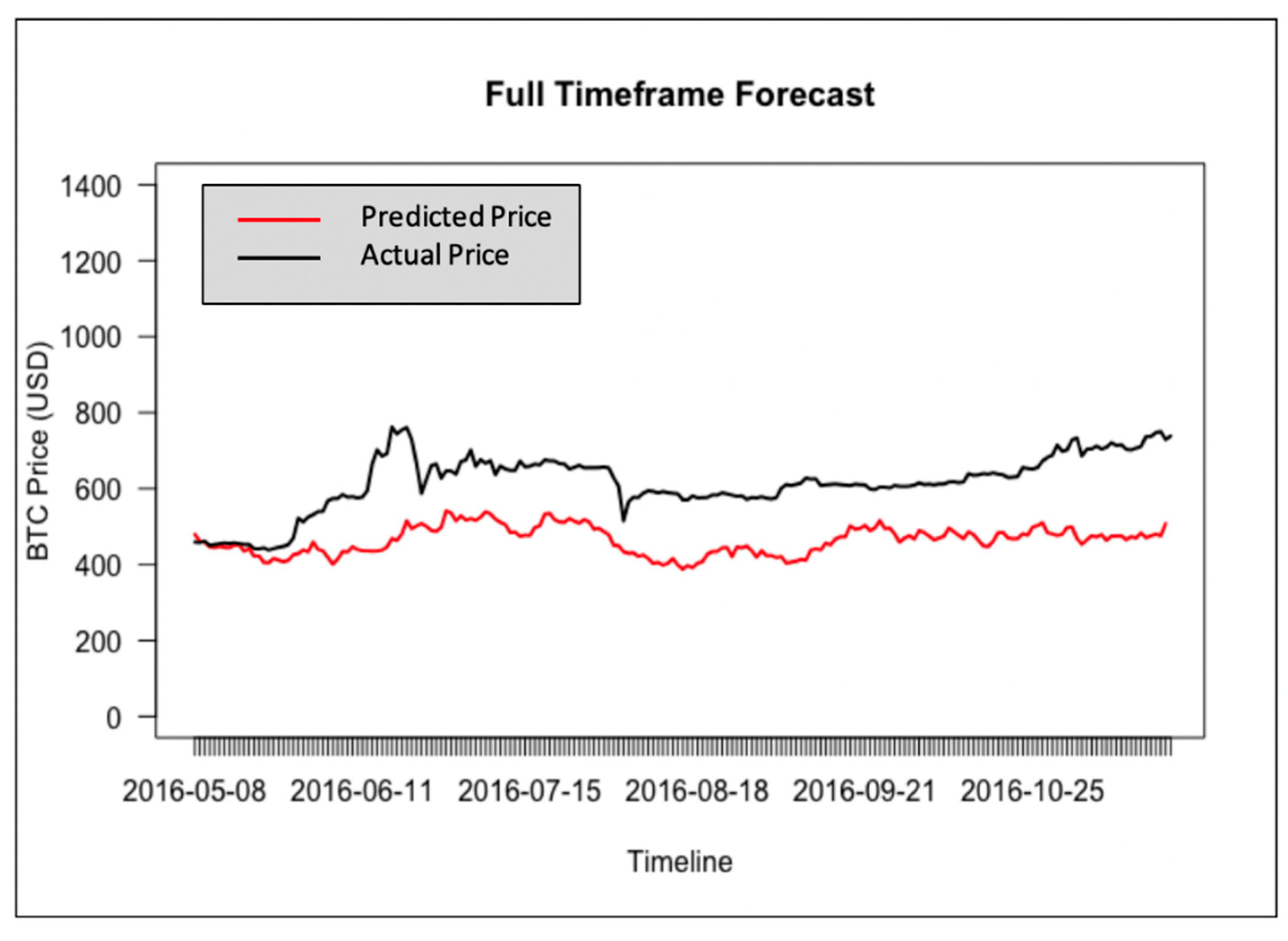
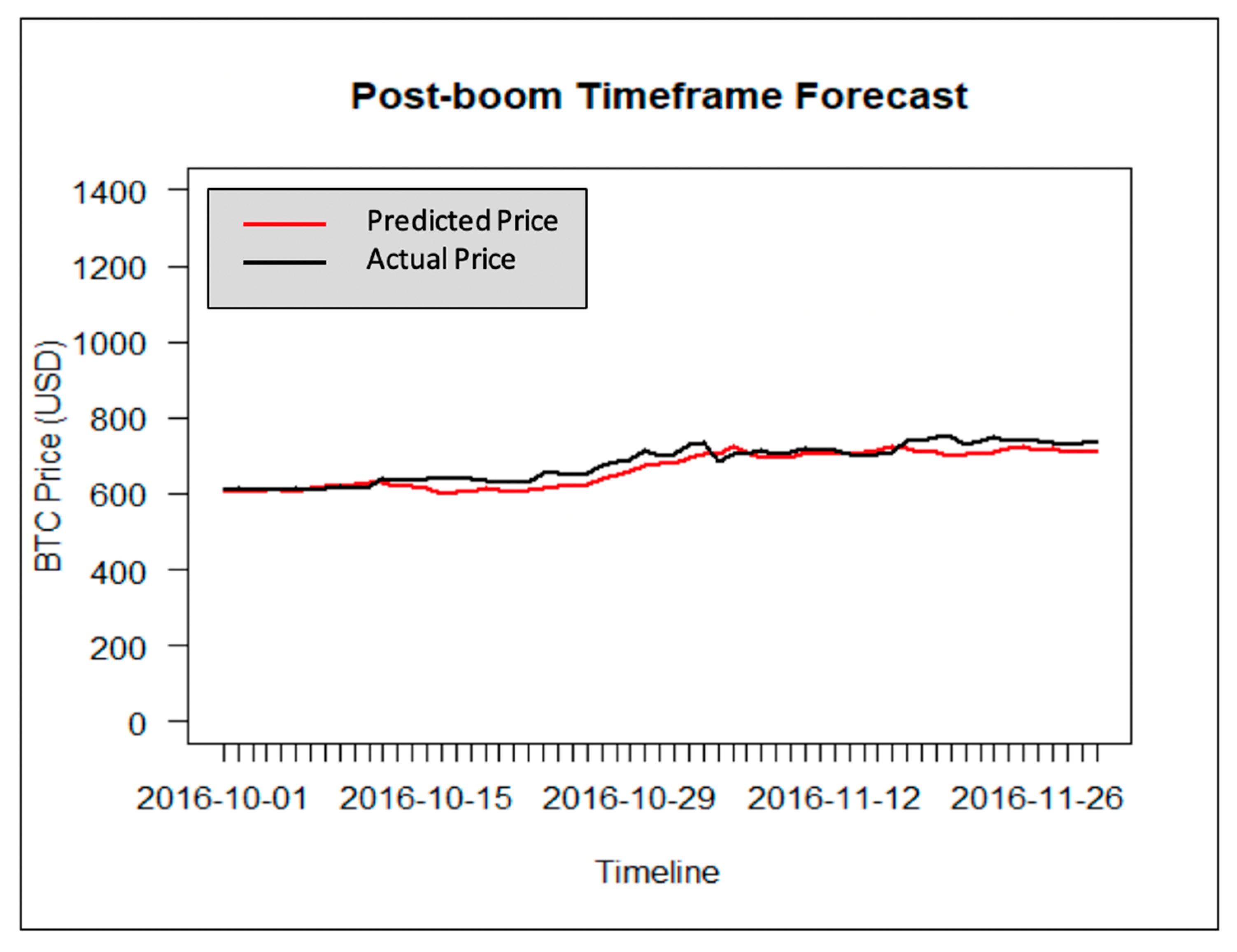
5.2.5. Analysis and Discussion of Results
5.3. Comparative Analysis
6. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Alquist, R., L. Kilian, and R. J. Vigfusson. 2013. Forecasting the Price of Oil. Handbook of Economic Forecasting 2: 427–507. [Google Scholar]
- Antonopoulos, Andreas M. 2014. Mastering Bitcoin. Unlocking Digital Crypto-Currencies. Newton: O’Reilly Media. [Google Scholar]
- Anupriya, and Shruti Garg. 2018. Autoregressive Integrated Moving Average Model based Prediction of Bitcoin Close Price. Paper presented at the 2018 International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, December 13–14. [Google Scholar]
- Ariyo, Ayodele Adebiyi, Aderemi Adewumi, and Charles Ayo. 2014. Stock Price Prediction Using the ARIMA Model. Paper presented at the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, March 26–28; pp. 106–12. [Google Scholar]
- Bakar, Nashirah Abu, and Sofian Rosbi. 2017. Autoregressive integrated moving average (arima) model for forecasting cryptocurrency exchange rate in high volatility environment: A new insight of bitcoin transaction. International Journal of Advanced Engineering Research and Science 4: 130–37. [Google Scholar] [CrossRef]
- Barski, Conrad, and Chris Wilmer. 2015. Bitcoin for the Befuddled. San Francisco: No Starch Press. [Google Scholar]
- Bianchi, Daniele, Matteo Iacopini, and Luca Rossini. 2020. Stablecoins and Cryptocurrency Returns: Evidence from Large Bayesian Vars. SSRN Working Paper. Available online: https://ssrn.com/abstract=3605451 (accessed on 15 June 2020).
- Bianchi, Daniele. Forthcoming. Cryptocurrencies as an asset class? An empirical assessment. Journal of Alternative Investment. [CrossRef]
- Bitcoin Charts. 2020. Bitcoincharts. Available online: https://bitcoincharts.com/charts/ (accessed on 18 August 2020).
- Bohte, Rick, and Luca Rossini. 2019. Comparing the forecasting of cryptocurrencies by bayesian time- varying volatility models. Journal of Risk and Financial Management 12: 150. [Google Scholar] [CrossRef]
- Brito, Jerry. 2014. “Bitcoin: Examining the Benefits and Risks for Small Business,” Statement from Jerry Brito. Available online: https://www.govinfo.gov/content/pkg/CHRG-113hhrg87403/pdf/CHRG-113hhrg87403.pdf (accessed on 2 April 2014).
- Campbell, John Young, Andrew Wen-Chuan Lo, and Craig MacKinlay. 1996. The Econometrics of Financial Markets. Princeton: Princeton University Press. [Google Scholar]
- Carriero, Andrea, George Kapetanios, and Massimiliano Marcellino. 2009. Forecasting exchange rates with a large Bayesian VAR. International Journal of Forecasting 25: 400–17. [Google Scholar] [CrossRef]
- Catania, Leopoldo, Stefano Grassi, and Francesco Ravazzolo. 2019. Forecasting cryptocurrencies under model and parameter instability. International Journal of Forecasting 35: 485–501. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Stephen Chan, Saralees Nadarajah, and Joerg Osterrieder. 2017. GARCH modelling of cryptocurrencies. Journal of Risk and Financial Management 10: 17. [Google Scholar] [CrossRef]
- Cocco, Luisanna, and Michele Marchesi. 2016. Modeling and Simulation of the Economics of Mining in the Bitcoin Market. PLoS ONE 11: 10. [Google Scholar] [CrossRef] [PubMed]
- Felizardo, Leonardo, Roberth Oliveira, Emilio Del-Moral-Hernandez, and Fabio Cozman. 2019. Comparative study of Bitcoin price prediction using WaveNets, Recurrent Neural Networks and other Machine Learning Methods. Paper presented at 2019 6th International Conference on Behavioral, Economic and Socio-Cultural Computing (BESC), Beijing, China, October 28–30. [Google Scholar]
- Hashish, Iman Abu, Fabio Forni, Gianluca Andreotti, Tullio Facchinetti, and Shiva Darjani. 2019. A Hybrid Model for Bitcoin Prices Prediction using Hidden Markov Models and Optimized LSTM Networks. Paper presented at the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, September 10–13. [Google Scholar]
- Hencic, Andrew, and Christian Gouriéroux. 2017. “Noncausal Autoregressive Model in Application to bitcoin/USD Exchange Rates.” Econometrics of Risk. Cham: Springer, pp. 17–40. [Google Scholar]
- Ito, Takatoshi, and Kiyotaka Sato. 2006. Exchange Rate Changes and Inflation in Post-Crisis Asian Economies: VAR Analysis of the Exchange Rate Pass-Through. National Bureau of Economic Research 40: 1407–38. [Google Scholar]
- Koop, Gary, and Dimitris Korobilis. 2009. Bayesian Multivariate Time Series Methods for Empirical Macroeconomics. Foundations and Trends® in Econometrics 3: 267–358. [Google Scholar] [CrossRef]
- Koray, Faik, and William Lastrapes. 1989. Real Exchange Rate Volatility and U.S. Bilateral Trade: A Var Approach. The Review of Economics and Statistics 71: 708. [Google Scholar] [CrossRef]
- Kuschnig, Nikolas, and Lukas Vashold. 2019. BVAR: Bayesian Vector Autoregressions with Hierarchical Prior Selection in R. Department of Economics Working Paper No. 296. Available online: https://epub.wu.ac.at/7216/1/WP296.pdf (accessed on 22 October 2019).
- Kuschnig, Nikolas, Lukas Vashold, Michael McCracken, and Serena Ng. 2020. “Package ‘BVAR,’” CRAN-Project. Available online: https://cran.r-project.org/web/packages/BVAR/BVAR.pdf (accessed on 6 May 2020).
- Litterman, Robert. 1980. A Bayesian Procedure for Forecasting with Vector Autoregressions. MIT Working Paper. Cambridge: MIT. [Google Scholar]
- Miranda-Agrippino, Silvia, and Giovanni Ricco. 2018. Bayesian vector autoregressions. Staff Working Paper No. 756. Available online: https://www.bankofengland.co.uk/-/media/boe/files/working-paper/2018/bayesian-vector-autoregressions.pdf?la=en&hash=1C0BC1906BDCB85150FFF8D2D4321C8CB6D43F91 (accessed on 1 September 2018).
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System (PDF). Archived (PDF) from the original on 20 March 2014. Available online: bitcoin.org (accessed on 28 April 2014).
- Pagnottoni, P., and T. Dimpfl. 2019. Price discovery on Bitcoin markets. Digital Finance 1: 139–61. [Google Scholar] [CrossRef]
- Quandl. 2020. quandl.com. Available online: https://www.quandl.com/data/BCHAIN (accessed on 18 August 2020).
- Rane, Prachi Vivek, and Sudhir Dhage. 2019. Systematic Erudition of Bitcoin Price Prediction using Machine Learning Techniques. Paper presented at the 2019 5th International Conference on Advanced Computing & Communication Systems (ICACCS), Coimbatore, India, March 15–16. [Google Scholar]
- Roy, Shaily, Samiha Nanjiba, and Amitabha Chakrabarty. 2018. Bitcoin Price Forecasting Using Time Series Analysis. Paper presented at the 2018 21st International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, December 21–23. [Google Scholar]
- Shah, Devavrat, and Kang Zhang. 2014. Bayesian regression and Bitcoin. Paper presented at the 2014 52nd Annual Allerton Conference on Communication, Control, and Computing, Allerton, IL, USA, October 1–3. [Google Scholar]
- Sims, Christopher. 1980. Macroeconomics and Reality. Econometrica: Journal of the Econometric Society 48: 1–48. [Google Scholar] [CrossRef]
- Sims, Christopher. 1993. A Nine-Variable Probabilistic Macroeconomic Forecasting Model. In Business Cycles, Indicators and Forecasting. Chicago: University of Chicago Press, pp. 179–212. [Google Scholar]
- Tan, Xue, and Rasha Kashef. 2019. Predicting the closing price of cryptocurrencies: A comparative study. Paper presented at the Second International Conference on Data Science, E-Learning and Information Systems (DATA ’19), Dubai, Arab Emirates, December 2–5; New York: Association for Computing Machinery, pp. 1–5. [Google Scholar] [CrossRef]
- Tandon, Sakshi, Shreya Tripathi, Pragya Saraswat, and Chetna Dabas. 2019. Bitcoin Price Forecasting using LSTM and 10-Fold Cross validation. Paper presented at the 2019 International Conference on Signal Processing and Communication (ICSC), Noida, India, March 7–9. [Google Scholar]
- Tobin, Turner, and Rasha Kashef. 2020. Efficient Prediction of Gold Prices Using Hybrid Deep Learning. In Image Analysis and Recognition. ICIAR 2020. Lecture Notes in Computer Science. Edited by A. Campilho, Fakhri Karray and Z. Wang. Cham: Springer, vol. 12132. [Google Scholar] [CrossRef]
- United States Securities and Exchange Commission. 2017. Annual Report Archive. Available online: http://www.annualreports.com/HostedData/AnnualReportArchive/m/AMEX_MGT_2017.pdf (accessed on 31 December 2017).
- Wang, Shujuan, Shujun Ye, and Xinyang Li. 2017. The impact of real effective exchange rate volatility on economic growth in the process of renminbi internationalization an empirical study based on VAR model. Paper presented at the 2017 4th International Conference on Industrial Economics System and Industrial Security Engineering (IEIS), Kyoto, Japan, July 24–27. [Google Scholar]
- Wu, Chih-Hung, Chih-Chiang Lu, Yu-Feng Ma, and Ruei-Shan Lu. 2018. A New Forecasting Framework for Bitcoin Price with LSTM. Paper presented at the 2018 IEEE International Conference on Data Mining Workshops (ICDMW), Singapore, November 17–20. [Google Scholar]

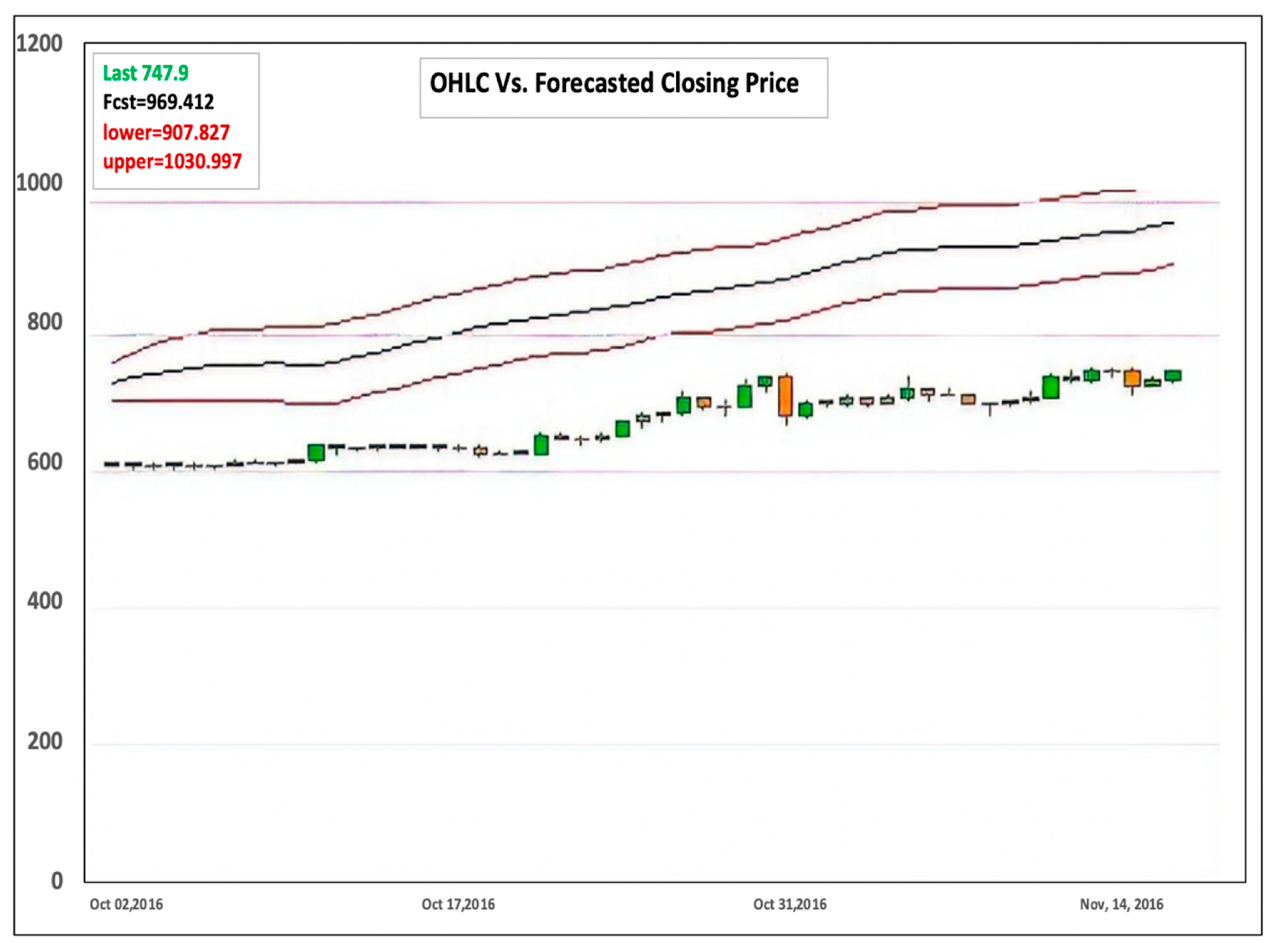
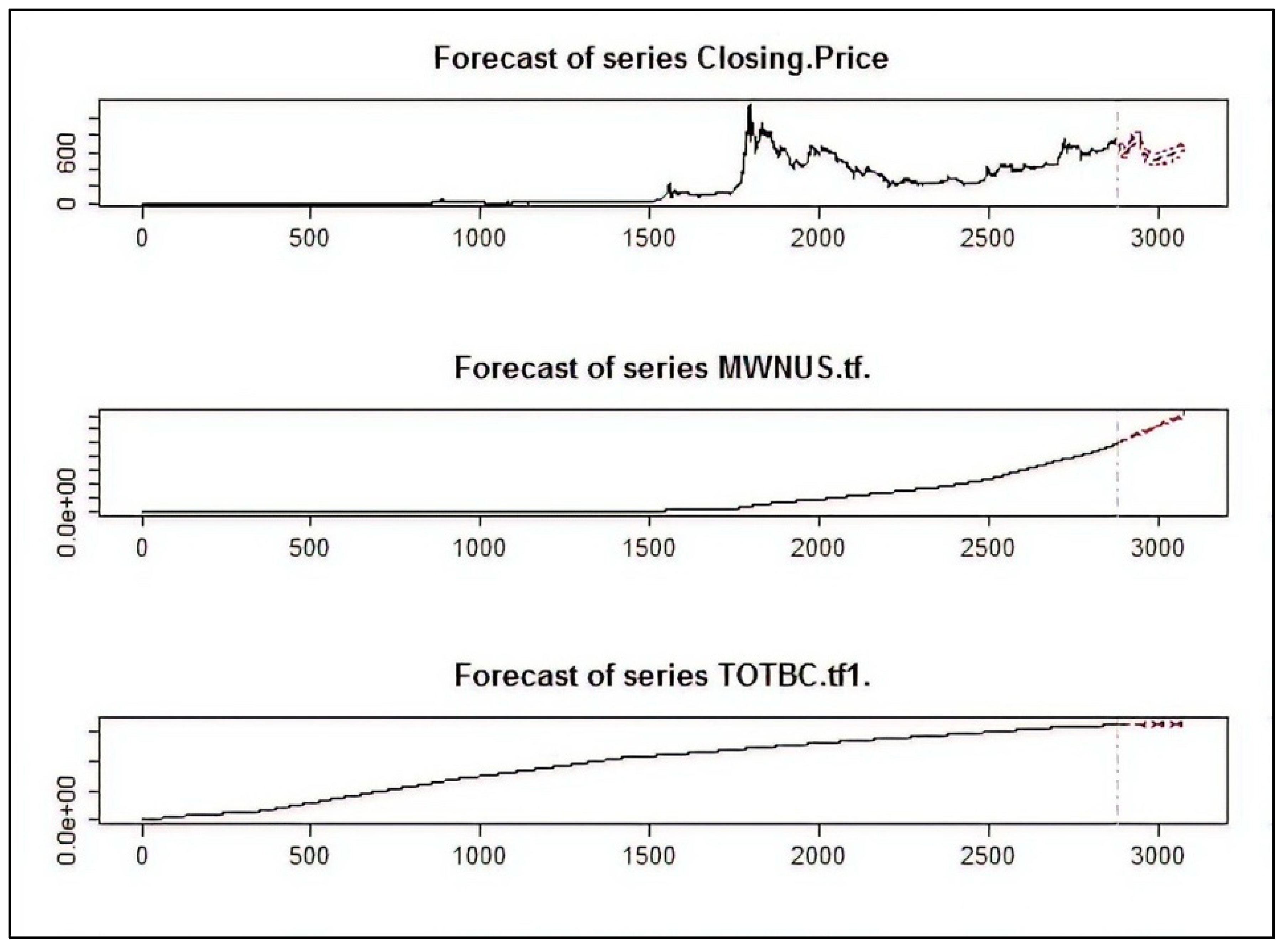
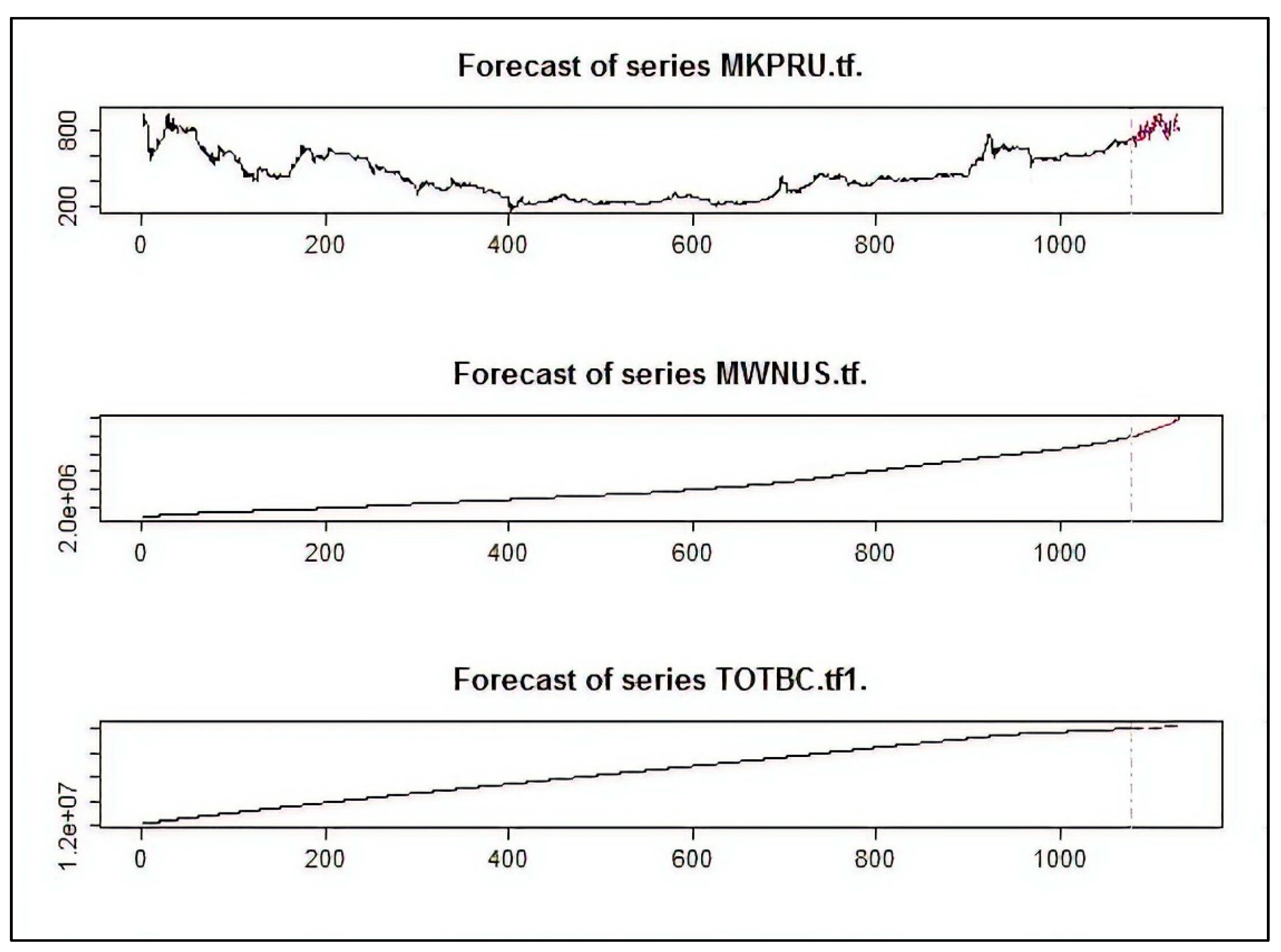
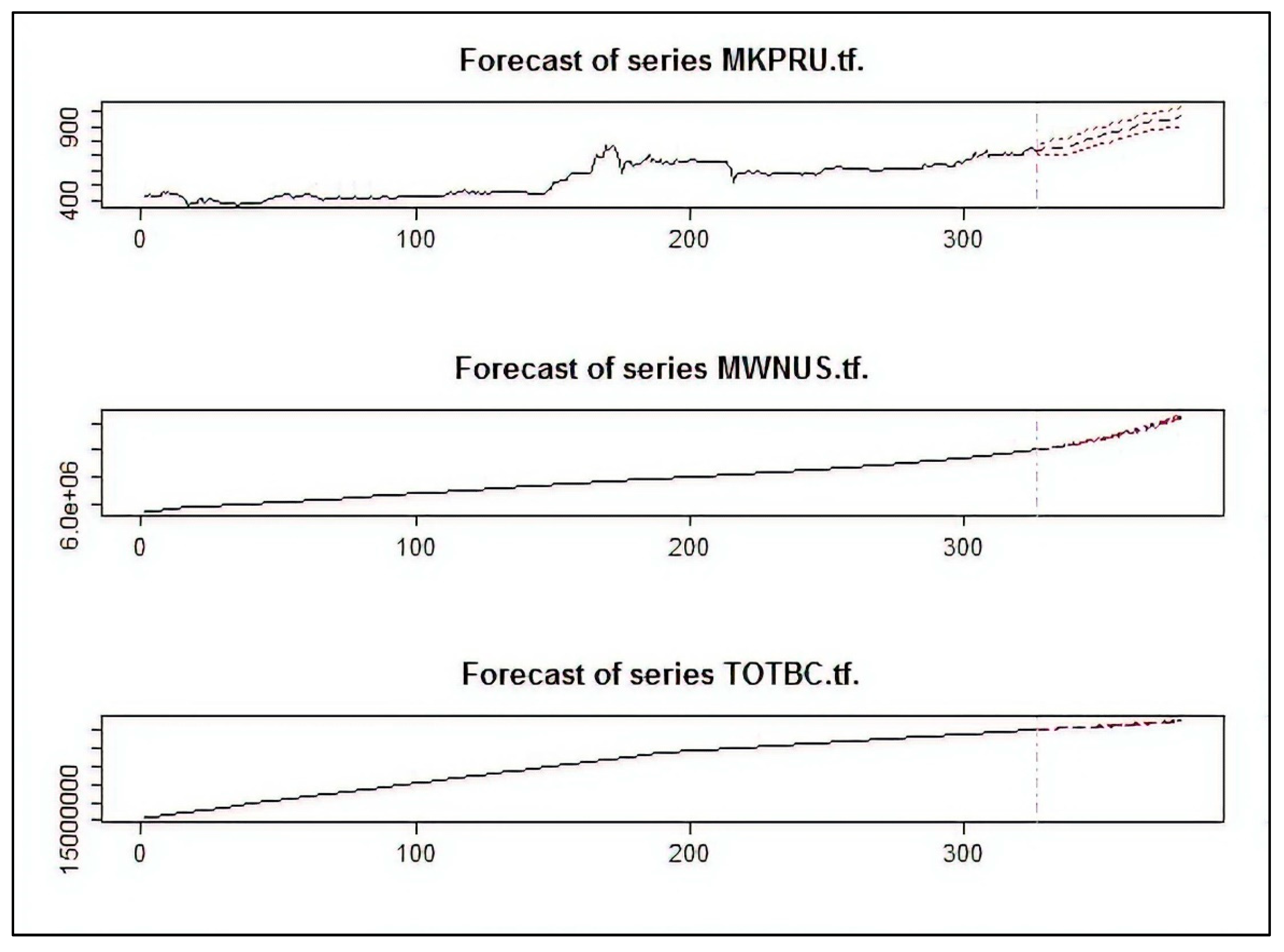

| Variables of Significance | Effect |
|---|---|
| 1, 2, 4, 5, 9, 11, 17, 20 day lag of BTC | + |
| 7, 8, 10, 12, 16, 18, day lag of BTC | − |
| 1, 4, 6, 10 day lag of MyWallet users | + |
| 2, 5, 12 day lag of MyWallet users | − |
| Miner’s Revenue, BTC Difficulty, Change in the Number of unique addresses | + |
| Number of Transactions per Block, Hash Rate | − |
| Variable | R2 | F-Statistics |
|---|---|---|
| BTC Price | 99+% | 99+% |
| MyWallet User | 99+% | 99+% |
| Total BTC | 99+% | 99+% |
| MAPE | RMSE | MAE | |
|---|---|---|---|
| VAR | 0.0249 | 0.3102 | 0.2260 |
| ARIMA (2,2,1) | 0.0421 | 0.3900 | 0.3258 |
| BR | 0.0362 | 0.3554 | 0.3826 |
| BVAR | 0.0286 | 0.3375 | 0.2501 |
| MAPE | RMSE | MAE | |
|---|---|---|---|
| VAR | 0.0248 | 0.2708 | 0.2212 |
| ARIMA (2,2,1) | 0.0421 | 0.3900 | 0.3258 |
| BR | 0.0351 | 0.3693 | 0.2776 |
| BVAR | 0.0264 | 0.2806 | 0.2286 |
| RMSE | MAE | MAPE | |
|---|---|---|---|
| VAR | 0.0123 | 0.1235 | 0.1023 |
| ARIMA (2,2,1) | 0.0143 | 0.1908 | 0.1262 |
| BR | 0.0129 | 0.1418 | 0.1158 |
| BVAR | 0.0130 | 0.1273 | 0.1247 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, A.; Kashef, R.; Li, M.; Valencia, E.; Huang, E. Bitcoin Network Mechanics: Forecasting the BTC Closing Price Using Vector Auto-Regression Models Based on Endogenous and Exogenous Feature Variables. J. Risk Financial Manag. 2020, 13, 189. https://doi.org/10.3390/jrfm13090189
Ibrahim A, Kashef R, Li M, Valencia E, Huang E. Bitcoin Network Mechanics: Forecasting the BTC Closing Price Using Vector Auto-Regression Models Based on Endogenous and Exogenous Feature Variables. Journal of Risk and Financial Management. 2020; 13(9):189. https://doi.org/10.3390/jrfm13090189
Chicago/Turabian StyleIbrahim, Ahmed, Rasha Kashef, Menglu Li, Esteban Valencia, and Eric Huang. 2020. "Bitcoin Network Mechanics: Forecasting the BTC Closing Price Using Vector Auto-Regression Models Based on Endogenous and Exogenous Feature Variables" Journal of Risk and Financial Management 13, no. 9: 189. https://doi.org/10.3390/jrfm13090189
APA StyleIbrahim, A., Kashef, R., Li, M., Valencia, E., & Huang, E. (2020). Bitcoin Network Mechanics: Forecasting the BTC Closing Price Using Vector Auto-Regression Models Based on Endogenous and Exogenous Feature Variables. Journal of Risk and Financial Management, 13(9), 189. https://doi.org/10.3390/jrfm13090189







