Abstract
We present a modelling approach for sector asset pricing studies that incorporates sector-level risk factors, subgroup portfolios, and structural breakpoint tests that are better at isolating the time-varying nature and the firm-specific component of returns. Our results show considerable subsector heterogeneity, while the asset pricing model using local risk factors and inductive structural breaks results in a superior model ( of 80.42% relative to of 68.79% of “conventional” models). Finally, we show that some of the variances of residuals, normally assumed to be the firm-specific component of returns, can be attributed to the changing relationship between sector returns and risk factors.
1. Introduction
This paper outlines a modelling approach for implementing asset pricing studies at the sector level that builds on the Fama and French (1993) time-series approach. We show how enhanced understanding of sector returns and risk factors can be achieved through four analytical foci: (1) by calculating stock market risk factors at the sector level, (2) by creating subgroup portfolios to explore within-sector heterogeneity, (3) by applying inductive structural breakpoint tests to identify time-varying risk loadings, and (4) by better isolating the firm-specific component of returns by comparing unconditional models and second pass regressions on residuals to Bai and Perron (2003) sequential breakpoint models. We do so in the context of the European energy utility sector, which has undergone dramatic changes over the last two decades, making it an ideal context to explore local and time-varying risk factors as well as within-sector heterogeneity.
Fama and French (1997) documented that sector-level peculiarities with regard to stock market risk factors can be a major influence in capturing variation in stock returns. Fama and French (1997) explored the sector-level performance of the capital asset pricing model (CAPM) and the three-factor model, employing both models on 48 US industries between 1963 and 1994. They found that the choice between the two models can result in large differences in the valuation of investments; the cost of equity calculation differed by more than 2% for 17 industries and more than 3% for eight industries. Fama and French (1997) argued that discrepancies in the cost of equity estimates at the sector level are partly caused by estimation error in two risk factors: size and value. The cause for the large estimation error arises from the return profiles of a sector differing to that of the market as a whole.
Further motivation for examining returns using sector-level data comes from Boni and Womack (2006). Their results showed that a sector-based momentum strategy substantially improves the returns relative to risks borne. The overall conclusion is that sector-specific analysts are good stock pickers within their sector of expertise, and investors acknowledge that the analysts’ information is valuable with respect to identifying within-sector mispricing. These results imply that within-sector characteristics need to be accounted for in sector analyses (Boni and Womack 2006).
The typical approach to building an asset pricing model is to use broad market-level (global) stock market risk factors. Global risk factors capture a wide range of variation in returns across a variety of different stocks and sectors in the same market. For example, a researcher may be interested in explaining the average returns of European energy utilities against a broad portfolio of European stocks. However, for a more nuanced understanding of the average returns within a sector, it is preferable to use sector-level (local) risk factors, i.e., risk factors calculated against the sector rather than relative to the market. A potential criticism of using local risk factors is that risk factors are meant to represent undiversifiable risk and should capture the source of undiversifiable risk for investors. Thus, for global investors, it could be argued that global factors are needed. Although many institutional investors are global in terms of their operations, the majority of their investment mandates are defined by geography or sector. Indeed, there are many investment funds that are sector-specific. In the case where there are sector mandates or sector funds, sector risk is undiversifiable. In this context, local risk factors ensure that only the variations in return which are relevant to the sector of interest are retained in the asset pricing model, for example, to explain the average returns of small energy utility stocks relative to the average returns of energy utility stocks. Stocks from other sectors contribute little to explaining the variation in returns within the sector.
Recently, Fama and French (2012) adopted this approach from a regional perspective. Specifically, Fama and French (2012) compared the performance of global and local four-factor model specifications across four regions between 1989 and 2011, including North America, Europe, Japan, and Asia-Pacific. They concluded that asset pricing regressions on a regional basis typically had greater explanatory power as regression fits were tight, resulting in much higher values. However, the asset pricing model may lose generalisability to other sectors as calculating the stock market risk factors at the sector level reduces dispersion in the unconditional mean for the risk factors. However, the benefit is that local risk factors provide more accurate measurements of the impact of size, value, and momentum on average returns. Nevertheless, as noted above, what level (global, regional, or local) the risk factors are implemented at, should be determined by the scope of the investment mandate or fund in question.
We extend the Fama and French (2012) regional approach to the sector level. Accordingly, this paper implements a local “augmented” four-factor time series model (AFFM) on the European energy utility sector. Our model is augmented in that it includes additional commodity and macroeconomic risk factors used in the energy economics literature (Tulloch et al. 2017a; Batten et al. 2017). Commodities are a major input into the production of electricity, and a driver of profitability in the output of natural gas industries. Therefore, fluctuations in commodity prices can affect the profitability of business operations, and therefore their stock returns (Silvapulle et al. 2017).
In the second part of our analysis, we take the analysis one step further by examining within-sector heterogeneity. A review of recent energy economics literature found that many studies explicitly fail to control for heterogeneity when examining the effects of risk factors on aggregate stock returns (Smyth and Narayan 2018). In principle, there is little reason to assume that risk factors such as commodities have a uniform effect across a sector because individual firms may experience heterogeneous profits or losses in response to commodity price fluctuations (Mollick and Assefa 2013). We expect this principle to apply to energy companies, which have unique exposure to market and commodity risk factors affecting their underlying profitability. We control for heterogeneity by implementing the local AFFM in the context of 12 energy portfolios: the energy sector as a whole, two portfolios based on size, three portfolios based on book-to-market (BE/ME) ratios, three portfolios based on momentum, and three portfolios based on industry (subsector).
The third and fourth parts of the analysis explore time-varying risk factor sensitivities and the firm-specific component of return. The energy sector has undergone a significant market transformation between 1996 and 2009 as a result of EU policy objectives to create an internal market for energy. Structural breaks in a time series can cause pure and partial changes in model parameters, affecting the firm-specific component returns after filtering out systematic components, especially over such long horizons (Fama and French 1993; Hansen 2001). Past literature has found that the relationships between stock returns and commodity risk factors are not stable and can be affected by changing commodity prices or significant market events (Tulloch et al. 2017a; Batten et al. 2017; Silvapulle et al. 2017). Accordingly, we implement Bai and Perron (1998, 2003) parameter stability diagnostic tests, then control for structural breaks using a Bai and Perron (1998, 2003) inductive structural breakpoint modelling approach. We adopt the inductive approach because the deductive approach to testing breakpoints can lead to biased significance tests unless the breaks are known with certainty. Surplus observations, which are unaffected by structural breaks, skew the mean residuals towards zero, reducing the power of statistical tests and biasing significance tests (Quandt 1960). The objective of the regression is to better isolate the firm-specific component of returns. We compare the results of the inductive breakpoint test to conditional annual regressions.
As noted previously, the analysis is conducted in the context of the European energy utility sector. The EU’s drive to create a single European energy market and the “greening” of the energy supply has been described as the most extensive cross-border reform of energy networks and operating structures in the world (Tulloch et al. 2017a, 2017b; Jamasb and Pollitt 2005). As such, the EU energy sector is an ideal context to explore local and time-varying risk factors, as well as within-sector heterogeneity. We do so over the period 1996 to 2013, utilising a comprehensive sample of European energy utilities that controls for survivorship bias1.
Our results show that local stock market risk factors explain a greater proportion of sector returns compared with global stock market risk factors, and can capture average returns missed by global risk factors. For the energy sector, the adjusted increases from 68.79% using the global AFFM to 72.77% using the local AFFM.
Second, this paper identifies within-sector heterogeneity, examining the risk exposure of various energy utilities grouped on the similarity of characteristics. Heterogeneous sensitivity to size, value, and momentum risk factors were the largest determinants for the differences in expected returns across various energy portfolios. The overall results indicate that electricity utilities are riskier than the natural gas and multi-utility industries. Interestingly, the multi-utilities showed one of the lowest cumulative abnormal returns across all portfolios—possibly indicating a lower risk–return relationship. The multi-utilities have less commodity risk exposure than both the natural gas and electricity industries. This is consistent with the economy of scope—diversified operations allow multi-utilities to switch operations when faced with regulatory changes or fluctuations in commodity prices.
Third, the inductive method of controlling for structural breaks improves the local AFFM’s adjusted to 80.42%. This is a large improvement in fit relative to using the conventional approach to asset pricing; full period (unconditional) regression produces adjusted of 68.79% for the global AFFM and 72.77% for the local AFFM. This highlights the importance of controlling for time-varying risk factor sensitivities, especially in the context of long time periods and sectors that have undergone large structural changes. Specifically, it shows that temporal instability in the correlation structure between returns and risk factors require constant portfolio rebalancing (Batten et al. 2017).
Finally, we introduce a better method to isolate the firm-specific component of returns and filter out systematic risk by using a Bai and Perron (1998, 2003) breakpoint regression on the residuals of the original asset pricing regression. Our results show that, when using a conventional asset pricing model, almost 28% of the variance of residuals that are normally assumed to be the firm-specific component of returns can be attributed to the changing relationship between sector returns and risk factors.
Overall, this paper provides a template for conducting sector-level asset pricing studies that can be adapted to other sectors since it suggests an approach that more accurately controls for time-varying risk factor sensitivities and better isolates the firm-specific component of returns for any sector. This is important not just to investors but also regulators in regulated sectors who want to understand the impact of policies on sector risk–return dynamics and the cost of capital.
2. Methodology
2.1. Models and Econometric Approach
As noted earlier, we build on the portfolio time series approach for testing risk factor sensitivities evident in the literature (notably, Fama and French 1993, 2012). A list of variables and their definitions are provided in Appendix A. Energy utility portfolio returns are denoted in the generalised form , where denotes the excess return2 over a one-month UK treasury bill for the th portfolio on day . The econometric modelling begins with, respectively, the unconditional global AFFM and the local AFFM specifications, estimated using ordinary least squares regressions:
where denotes the intercept, denotes the market coefficient, denotes the excess return on the market factor over the one-month UK treasury bill at time , denotes the coefficient, () denotes the global (local) size factor at time , denotes the coefficient, denotes the global (local) value factor at time , denotes the coefficient, ( denotes the global (local) momentum factor at time , denotes the term premium coefficient, denotes the term premium3 at time , denotes the oil price risk coefficient, denotes the return on oil price at time , denotes the coal price risk coefficient, denotes the return on coal price at time , denotes the natural gas price risk coefficient and denotes the return on natural gas price at time . We include term premium and commodity risk factors based on empirical evidence of their significance in explaining oil industry and energy utility returns (El-Sharif et al. 2005; Koch and Bassen 2013; Oberndorfer 2009; Sadorsky 2001) or stock returns generally (Fama and French 1993; Batten et al. 2017; Smyth and Narayan 2018).
Despite superficially similar model specifications, there are major differences between the global and local AFFMs. The global AFFM in Equation (1) uses global stock market risk factors calculated across a diversified sample of 600 European stocks as independent variables, with the objective of creating an integrated global AFFM which can be applied across sectors; i.e., , and calculations. In contrast, the local AFFM in Equation (2) uses local stock market risk factors calculated across a sample of 88 European energy utilities as the independent variables, with the objective of more accurately explaining within-sector returns; i.e., , and . For the third analytical focus, the analysis of time-varying risk factors, the local AFFM specification is applied in the following conditional regressions:
where the variables are the same as in Equation (2) (see Section 2.1) save for the addition of , which denotes the carbon price risk coefficient, and , which denotes the return on carbon4.
The regressions are estimated using Newey and West (1987) heteroskedastic and autocorrelated consistent (HAC) standard errors, and subject to standard regression diagnostic tests.
2.2. Sample and Data5
Data were extracted from Thomson Reuters Datastream, S&P Capital IQ and publicly available sources. Data were measured in euros (€) to represent value and cost to European market participants. The daily stock prices and market capitalisations of the energy utilities cover the period 30 June 1995 to 28 June 20136. Stock prices are measured at day close and adjusted for corporate actions. Returns for all stocks and risk factors are calculated using the first-log difference. Excess returns for equities are calculated as the difference between daily returns and the daily yield on the one-month UK Treasury bill. Regarding the accounting data, all data are extracted for fiscal year-end, covering the period 1995 to 2013. To be eligible for analysis and to allow portfolio rebalancing, all companies must have data on stock price, market capitalisation and book value of equity for both year and year . This condition ensures companies have traded for at least two years (Fama and French 1993). The STOXX® 600 Europe index ( is used as a proxy for market returns, representing 600 large-, mid-, and small-capitalisation stocks across 18 countries of the EU. The inclusion of mid- and small-cap stocks prevents bias towards larger companies. The three global stock market risk factors of size (), value ( and momentum ( are calculated using all 600 stocks and the extensive portfolio method outlined by Fama and French (1993) and Carhart (1997), with annual portfolio rebalancing. The stock market risk factors are calculated using the same 600 stocks as the STOXX® 600 Europe index.7 The momentum factor calculation consumes the first year of daily data, so the analysis covers 01 July 1996 and 28 June 2013.
We construct a sample of 88 European energy utilities. The STOXX® 600 Europe Utilities index is used to provide an initial list of 28 utilities currently operating and trading on equity markets. We remove all utilities whose primary revenue is derived from waste or water operations to prevent biased estimated coefficients. We extend the sample by including all companies explicitly mentioned in energy sector restructuring legislation or are elected members of various electricity and gas groups8. Using Standard Industrial Classification (SIC) codes, we control for survivorship bias by including all active and non-active energy utilities registered under the same product segments and SICs. The median number of stocks in the energy portfolio is 45.5 across all years.
2.3. The Local Stock Market Risk Factors: Size, Value and Momentum
While a diversified portfolio of 600 European stocks is used to create the global stock market risk factors, the local AFFM uses the 88 European energy utilities to create the local stock market risk factors. The sector-level-mimicking portfolios are used as independent variables in Equations (2) and (3).
The local (small minus big) risk factor () mimics the risk factor in returns, which is related to energy utility size, representing a local size factor. The represents a zero-sum investment that is long on small energy utilities and short on big energy utilities. Small energy utilities are expected to generate higher returns than big energy utilities. The local (high minus low) risk factor () mimics the risk factor in returns, which is related to the energy utility book-to-market ratio. The represents a zero-sum investment that is long on high-BE/ME (value) energy utilities and short on low-BE/ME (growth) energy utilities, representing local value factor. High-BE/ME utilities are expected to generate higher returns than low-BE/ME utilities. The local (up minus down) risk factor () mimics the risk factor in returns, which is related to the energy utility persistence of earnings (momentum). The represents a zero-sum investment that is long on up-momentum energy utilities and short on down-momentum energy utilities and represents the momentum factor. Up-momentum energy utilities are expected to generate higher returns than down-momentum energy utilities.
2.4. The 12 Energy Utility Portfolios
Beyond examining average returns for the energy sector as a whole, the 88 European energy utilities are also sorted into various portfolios based on the similarity of characteristics. The groupings, outlined in the following paragraphs, produce 12 portfolios to be examined: the energy sector as a whole, two portfolios based on size, three portfolios based on BE/ME ratios, three portfolios based on momentum and three portfolios based on industry.
The value-weighted returns of the 12 portfolios become dependent variables in the local AFFM in Equation (2) and the three ancillary asset pricing models: CAPM, augmented-CAPM and a local four-factor model. The purpose of the portfolio approach is to examine the within-sector heterogeneity of energy utility returns based on company characteristics. The benefit of this approach is the ability to examine the risk exposure of particular groups of utilities in isolation, for example, the risk exposure of small utilities.
First, we construct two stock portfolios based on company size. At the end of June of each year , from 1996 to 2013, all energy utility stocks are ranked on market capitalisation to proxy for size. Annually, the median market capitalisation is used as the breakpoint to put stocks into two portfolios: small or big energy utilities. Value-weighted returns are calculated for both the small and big portfolios from July of year to end of June for , denoted as and . The portfolios are rebalanced annually at the end of June for . Visual inspection showed that the two portfolios were well balanced each year, containing approximately equal numbers of stocks. The median number of stocks in the and portfolios, across all years, is 22.5. Although balanced, big energy utilities naturally dominate sector valuation—the combined value of small energy utilities account for 6.4% of total sector valuation; this is consistent with the global AFFM and Fama and French (1995). For the global AFFM, small stocks account for 5.84% of the total market value, across all stocks and years, while for Fama and French (1995), small stocks accounted for about 7.3% of total market value in 1991. The and portfolios will be used as dependent variables in Equation (2) to examine heterogeneous risk exposure based on utility size.
To form the three BE/ME portfolios, all energy utilities are ranked on their BE/ME ratios annually. The BE/ME ratio is calculated as the book value of common equity for the fiscal year ending in calendar year t − 1, scaled by market capitalisation at the end of December in year t − 1. The energy utilities are allocated to groups based on Fama and French’s (1993, 1995, 1997, 1998, 2006, 2012) three breakpoints: the top 30% (high-BE/ME), the middle 40% (mid-BE/ME) and the bottom 30% (low-BE/ME). The three groups represent value, neutral and growth stocks, respectively (Fama and French 2006, 2012; French 2015). There were only two negative BE/ME calculations, which were excluded from the portfolio. The high-, mid- and low-BE/ME portfolios contain a median of 13, 18 and 13.5 companies, respectively, across all years. Value-weighted returns are calculated for the high-BE/ME, mid-BE/ME and low-BE/ME portfolios, denoted as , and , respectively. The portfolios are rebalanced at the end of June for . The three portfolios will be used as dependent variables in Equation (2) to examine heterogeneous risk exposure based on the book-to-market ratio.9
To form the three momentum portfolios, the average excess return for all 88 European energy utilities is calculated daily over the formation period from day to day and excludes the sort month. To be considered as an up-momentum utility, the energy stock’s returns during the formation period and on must be positive; similarly, the stock returns during the formation period and return on must be negative for down-momentum utilities. The condition ensures that the up and down momentums continue until the end of the formation period, and reversal has not already begun. The daily breakpoints are defined as the top 30% (up-momentum), the middle 40% (neutral-momentum) and the bottom 30% (down-momentum). The median number of stocks in the three momentum portfolios, across all years, is 13, 18, and 13, respectively. The value-weighted daily returns on the up, neutral and down momentum portfolios are calculated, rebalanced daily and denoted as , and , respectively. The , and portfolios will be used as dependent variables in Equation (2) to identify whether the risk factors for energy utilities differ based on momentum. Based on Moskowitz and Grinblatt (1999), Boni and Womack (2006) and Fama and French (2012), the three momentum portfolios are expected, by definition, to have extreme momentum tilt, and thus the local AFFM may have difficulty capturing average returns.
To form the three industry portfolios (electricity, natural gas or multi-utility), we obtain up to 10 SICs for each energy utility annually between 1996 and 201310. We group the companies into portfolios based on their SICs. The SIC system is designed to categorise industries using a four-digit code. Grouping companies by SICs is similar to the approach employed by Moskowitz and Grinblatt (1999).
Based on the SICs, companies that exclusively contained only electricity and “other” operations are defined as electric utilities, companies which contained only natural gas and “other” operations are defined as natural gas utilities, and companies which contained operations from both electricity and natural gas, or were otherwise defined as multi-utilities, are defined as multi-utilities. Auxiliary operations outside the electricity sector are minor and are not expected to significantly impact returns.
As SIC codes define the business operations which generate the highest revenue for the companies in the past year (, SIC codes for year are matched11 to returns for July of year to June of . The value-weighted daily returns on the electricity, natural gas and multi-utility portfolios are calculated, denoted as , and , respectively. The number of stocks in the three industry portfolios, across all years, is 24, 7, and 14, respectively. The portfolios are rebalanced annually in June of year to control for utilities that change operations or industries. We do so to control for company mergers, where the acquiring company shifts operations from, say, electricity to multi-utility operations. Although rare, some of the SICs of utilities have changed across the years but were mostly confined to ancillary operations rather than primary operations.
The 12 portfolios defined above are used as dependent variables for analysis in Equation (2), where , , , , , ,, , , or . Each portfolio is regressed independently. The following section explains the construction of the local stock market risk factors used as independent variables in Equation (2).
2.5. Time-Varying Risk Factor Sensitivities
To address the third analytical focus, relating to time-varying risk factor sensitivities (stage one of the analysis) involves implementing conditional annual regressions in Equation (3) to account for slope shifts over time, as has been the norm in the literature (Tulloch et al. 2017a; Batten et al. 2017; El-Sharif et al. 2005). We compare the results to those obtained from the Bai and Perron (2003) sequential multiple breakpoint models.
In the second part of the analysis, we employ the Bai and Perron (1998, 2003) inductive structural breakpoint algorithm to examine the presence of multiple structural changes in model parameters. The inductive approach can overcome many of the misspecification criticisms of the deductive approach (our annual regressions in stage one), such as assumptions regarding the break date, and allows the examination of structural change where the breakpoint is entirely unknown. The Bai and Perron (1998, 2003) algorithm utilises previously forgotten dynamic programming of pure structural change models for a more general partial structural change model, specifically, partitioned regressions and cluster analysis, curve fitting by use of segmented straight lines (polygonal curves) and grouping for maximum homogeneity by minimising variance within groups (see, respectively, Guthery 1974; Bellman and Roth 1969; Fisher 1958). The Bai and Perron (1998, 2003) algorithm is implemented in two steps: (1) a posthoc multiple breakpoint test, and (2) the breakpoint regression, as explained below.
The first step implements posthoc parameter stability diagnostic tests on the results of the local AFFM in Equation (2). The multiple breakpoint test identifies whether there are potential breakpoints in the unconditional local AFFM’s parameters. The break specification is sequential, testing the null of versus the alternative of breaks. The information criterion is set to allow up to 18 structural breaks, the maximum available, and employs a trimming percentage of 5%. As the dataset consists of 4435 observations, the trimming value implies that regimes must have at least 222 observations to be considered a structural break; this was the minimum period permissible by the model. The significance level is , and error distributions are allowed to differ across breaks to control for heterogeneity across time periods. The results of the test report an estimate for the number of potential breaks in the sample and the estimated break dates.
The second step implements a breakpoint regression, specifying the local AFFM (Equation (2)) as the mean equation. The breakpoint regression estimates a linear regression where the parameters are subject to structural change. The algorithm obtains global minimisers of the sum of squared residuals (SSR) based on dynamic programming. Based on the evidence of heteroskedasticity and autocorrelation, Newey-West HAC standard errors for the coefficient covariance matrix are used, and error distribution is allowed to differ across breaks to account for the heterogeneity of time periods. The results of Bai and Perron (2003) show that this allowed for the detection of smaller breaks, which were otherwise obscured in the data. The HAC coefficient covariance matrix automatically determines optimised lag structuring using the Akaike Information Criterion12 (AIC). The kernel bandwidth is automatically determined using Andrew’s autoregressive method with 1 lag (AR(1)) and uses quadratic-spectral kernels. To remain congruent with the first stage, the break specification is also sequential, testing the null of versus the alternative of breaks. Again, the information criterion is also set to allow a maximum of 18 structural breaks, employing the same trimming percentage of 5% and test significance at . The test will estimate the date of structural breaks in the relationship between returns in the energy sector and the risk factors of the local AFFM. The results also report the estimated coefficients across each of the break dates, allowing examination of the changing relationship with risk factors through time.
2.6. Better Isolate Firm-Specific Returns
To address the fourth analytics focus, we use the Bai and Perron (1998, 2003) algorithm to introduce a better method to isolate the firm-specific component of returns and filter out systematic risk. We posit that the assumption of constant risk factors in the asset pricing model forces any changes in the relationship between risk factors and returns into the residuals of an unconditional linear regression. We examine this proposition by extracting the residuals of three different modelling approaches and performing a “second pass” test on the residual using the inductive Bai and Perron (1998, 2003) algorithm.
The three modelling approaches include constant parameters using the unconditional local AFFM regression (Equation (2)), time-varying parameters using conditional annual local AFFM regressions (Equation (3)) and time-varying parameters of the local AFFM sequential breakpoint regression. The “second pass” examines whether the residuals are capturing any change in the relationship between the stock returns and the risk factors. If the modelling approaches adequately filter out systematic risk, leaving only the firm-specific component of returns, the residuals of the regression should have no relationship with the model parameters. We show this is not the case with the assumption of constant parameters. We compare the performance of the models and make a recommendation as to which approach better isolates firm-specific returns.
3. Results
3.1. Descriptive Statistics
Figure 1 (Plot A) compares the cumulative returns for the entire European energy utility sector and the two size portfolios of small and big energy utilities. As expected, the small energy utilities have higher cumulative returns than the big energy utilities, illustrating a clear size effect. Plot B of Figure 1 shows the cumulative return profiles for the three BE/ME portfolios. The high-BE/ME (value) energy utilities have higher cumulative returns than mid-BE/ME (neutral) energy utilities. The cumulative returns are consistent with the literature; high-BE/ME utilities are expected to outperform low-BE/ME utilities (Rosenberg et al. 1985; Chan et al. 1991; Fama and French 1992, 1993, 1995, 1998). Plot C of Figure 1 illustrates the cumulative returns for the three momentum portfolios. Naturally, up-momentum stocks outperform down-momentum stocks. Finally, Plot D of Figure 1 presents the cumulative returns for the three industry portfolios. The results show that the electricity utility portfolio generated the greatest cumulative returns across time, indicating a higher risk–return relationship. In contrast, the natural gas and multi-utility portfolios show similar returns through time. The multi-utilities show one of the lowest cumulative abnormal returns across all portfolios. This is consistent with the economy of scope. A diversified portfolio of operations is less likely to be exposed to the regulatory and operational risks of single utilities.
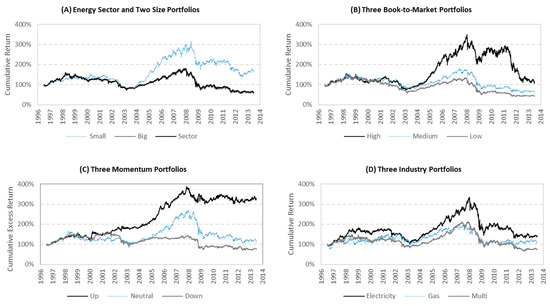
Figure 1.
Cumulative return for the 12 energy portfolios. This figure presents the cumulative return profile of the 12 energy utility portfolios constructed. Plot (A) contains the whole energy sector, small utilities and big utilities. Plot (B) contains the three portfolios formed on book-to-market: high-, mid- and low-BE/ME. The portfolios represent value, neutral and growth stocks, respectively. Plot (C) contains the three momentum portfolios: up, neutral and down momentum. Plot (D) contains the three industry portfolios: electricity-, natural gas- and multi-utility.
Figure 2 (Plot A) shows the global and local SMB factors are relatively consistent. The positive cumulative returns show a consistent size effect between small and big stocks. Small stocks consistently outperform big stocks for all European stocks and within the energy utility sector. Plot B of Figure 2 shows that the value effect, the spread between high- and low-BE/ME stocks, is greater in the energy sector compared with all European stocks. Finally, Plot C of Figure 2 shows a consistent momentum effect. Up-momentum stocks outperform down-momentum stocks for both all European stocks and within the energy utility sector. The important implications for the results above are that there are some differences between global and local stock market risk factors, especially with respect to the value factor. While the size and momentum factors are similar between the global and local risk factors, the cumulative return profiles are not identical.
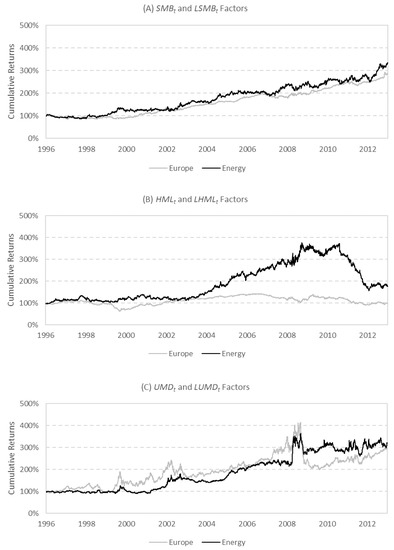
Figure 2.
Comparison of cumulative returns for global and local stock market risk factors. This figure presents the cumulative returns of the three stock market risk factors: the size, value and momentum. The black line represents local stock market risk factors specific to energy utilities, including , and . The grey line represents global stock market risk factors for European stocks generally, including , and .
The summary statistics for all 12 portfolios and 12 risk factors are presented in Table 1. Most of the returns across all portfolios and risk factors are not statistically different from zero, with the exception of the up-momentum portfolio (), the risk factor, risk factor, term premium and carbon risk. The summary statistics indicate that the mean daily return for the energy utility sector is −0.0051%, losing value over time. Small utilities achieve a greater mean return (0.0155%) compared with big utilities (−0.0062%), reflecting the greater risk-return relationship of small utilities. For momentum portfolios, the up-momentum portfolio achieves a mean return of 0.0291%, significant at and greater than the neutral and down momentum portfolios (0.0095% and −0.0022%, respectively). For the industry portfolios, the electricity and natural gas industries achieve mean returns of 0.0136% and 0.0127%, respectively. Multi-utilities only achieved a mean return of 0.0006%, consistent with the lower perceived risk and economy of scope argument presented above.

Table 1.
Summary statistics for the portfolios and risk factors.
3.2. Local Stock Market Risk Factors Better Explain Sector-Level Returns
Table 2 reports the results of estimating Equation (1) (global AFFM) and Equation (2) (local AFFM). Augmented Dickey and Fuller (1979) (ADF) unit root tests were implemented (not reported) to confirm the stationarity of the time series, ensuring the dependent and independent variables were integrated to the same order and that a linear relationship can exist between the variables. The results of the ADF test, confirm that the time series is integrated to order zero, I(0), and stationary. To address the assumptions of the linear regression, regression diagnostic tests identified heteroskedasticity and autocorrelation of residuals, which are reported in Table 2 and corrected for. All coefficients are estimated using the Newey and West (1987) HAC covariance matrices. The variance inflation factor statistics found no evidence of multicollinearity among variables.

Table 2.
Capital asset pricing model (CAPM), four-factor and local augmented asset pricing models.
Addressing the first analytical focus, the use of local stock market risk factors captures a greater proportion of returns. The adjusted for the energy sector as a whole is 72.77% using the local AFFM (Table 2, Model 4), compared with 68.79% using the global AFFM (Table 3, Model 5). These results are congruent with Moskowitz and Grinblatt (1999) and Fama and French (2012). The local AFFM also produces the highest adjusted in comparison with existing asset pricing models: the CAPM (66.96%), the augmented-CAPM used in the energy economics literature (67.17%) and the (local) four-factor model (72.56%).

Table 3.
Inter-temporal analysis of sector portfolio using the local “augmented” four-factor time series model (AFFM).
Interpreting the results of the local AFFM (Model 4), our results are consistent with existing literature: the sector is relatively defensive over the whole time period, with a market beta of 0.6306 (). Further, the energy utility sector’s returns covary with the returns on big energy utilities (they have a large negative slope on the factor), are marginally tilted towards behaving like low-BE/ME (growth) stocks (they have a small negative slope on the factor) and are tilted towards behaving like down-momentum utilities (they have a marginally negative slope on the factor). Consistent with Silvapulle et al. (2017), stock market fundamentals play a significant role in determining long-run commodity-stock price relationships. Silvapulle et al. (2017) also found that the effect of other substitutable energy sources, like coal, is more dominant than increases in oil price. Our results agree, finding coal to be the only statistically significant commodity that affects returns at the sector level, with a marginally negative slope.
It is informative to explore the differences between the estimated coefficients of the local AFFM and the global AFFM. The largest difference occurs in the slopes; the global AFFM shows that the energy utility sector behaved like high-BE/ME European stocks based on the global risk factors, typically associated with distressed companies. In contrast, the local AFFM shows that there is a slightly negative coefficient with the factor, suggesting a marginal tilt towards the low-BE/ME (growth) utilities.
Concluding the implications for the first analytical focus is that the use of local stock market risk factors explains a greater proportion of returns at the sector level, a distinct improvement over the global stock market risk factors.
3.3. Portfolios within the Energy Sector Have Heterogeneous Risk Exposure
The second analytical focus of this paper is concerned with identifying within-sector heterogeneity. We do so by applying the local AFFM (Equation (2)) on the 12 portfolios identified in Section 2.3. The results are also reported in Table 2 for ease of comparison.
The first observation regarding the energy portfolios is that it is rare for portfolios to experience extreme size, value or momentum tilt. Addressing the two size portfolios, the interpretation for big utilities is similar to the sector as a whole. Big utilities have a market beta of 0.640 and have a negative coefficient, which is expected. Big utilities are tilted towards behaving like low-BE/ME utilities (a negative coefficient) and towards down-momentum (negative coefficient). Coal is the only significant commodity risk factor for big utilities, with a negative impact. The local AFFM typically performs poorly at explaining the returns on small energy utilities, with an adjusted of 44.68%, consistent with the argument that smaller companies are typically harder to value and often informationally sparse (Kumar 2009). Overall, small energy utilities are still defensive investments, with a market beta of 0.494, but are more exposed to stock market and commodity risk factors in comparison with big utilities. Naturally, the small utilities are expected to have a positive slope, but they also behave like high-BE/ME (value) utilities (positive coefficient) and are marginally tilted towards down-momentum (negative coefficient). The positive size and value factor sensitivities are consistent with utilities being distressed and/or marginal companies, requiring a greater return on investment. Small utilities have positive oil risks and negative coal risks. The increased commodity risk exposure suggests that small utilities do not effectively hedge against commodity risk.
Regarding the three book-to-market portfolios, the mid-BE/ME (neutral) energy utilities have the greatest systematic risk, in comparison with high-BE/ME (value) and low-BE/ME (growth) utilities. The size sensitivity suggests that the three portfolios behave like big energy utilities, while the momentum sensitivity shows that the portfolios show some tilt towards down-momentum. Interestingly, the high-BE/ME utilities, which are typically associated with company distress and fallen angels, show sensitivities to all commodities: oil, coal and natural gas risk. In contrast, the mid- and low-BE/ME portfolios show less commodity risk exposure. The significant commodity risk of the high-BE/ME and small utilities is consistent with Oberndorfer’s (2009) and Kumar’s (2009) propositions: commodities serve as informational signals for price developments in the energy sector when less information is available.
We do not draw inferences regarding the three momentum portfolios. Fama and French (2012) argue that local models have difficulty when capturing average returns for portfolios with extreme momentum tilt. We find similar results. Also, the momentum strategy does not represent a realistically viable investment opportunity, as an active portfolio strategy such as momentum requires extremely high turnover (Moskowitz and Grinblatt 1999). The trading costs of rebalancing the portfolio daily would have a negative impact on the strategy’s performance (Rosenberg et al. 1985). Note, none of the criticisms above affect the use of the risk factor when used to explain returns on other energy portfolios. In summary, the risk factor is useful as an independent variable but encounters known econometric issues as a dependent variable.
Turning to the three industry portfolios in Table 2, the electricity industry portfolio has the lowest market beta, is tilted towards big stock (negative coefficient), is marginally tilted towards low-BE/ME (negative coefficient) and marginally tilted towards down-momentum (negative coefficient). The electricity industry has the greatest commodity risk exposure of all three industries; all commodities are statistically significant. Second, the natural gas industry has the highest market beta of the three industries, showing an increased systematic risk. Natural gas utilities behave like big utilities (negative coefficient), are tilted towards low-BE/ME (growth) utilities (negative coefficient) and tilted towards up-momentum (positive coefficient). The natural gas industry is the only industry with positive momentum, possibly indicating profiteering. Unsurprisingly, the natural gas sector has positive relationships with oil and natural gas prices. The implications for the sector are that they generally perform well relative to other utilities and have a larger market capitalisation. Finally, the multi-utility sector, unsurprisingly, shares risk exposure with both electricity and natural gas utilities.
Table 2 shows that the multi-utility portfolio shares similar market beta, momentum and coal price coefficients with the electricity industry and similar size and value coefficients with the natural gas industry. This result is expected, as the multi-utilities contain a combination of electricity and natural gas operations. Interestingly, the multi-utility industry has little commodity risk exposure, suggesting either effective hedging strategies or economy of scope; diversified operations allow multi-utilities to reprioritise operations when faced with regulatory changes or commodity price fluctuations.
The following two sections outline tests concerning evolving risk factor sensitivity through time. Deductive conditional annual regressions are presented in Section 3.4, while the inductive structural breakpoint tests are presented in Section 3.5. Although the conditional regressions do not directly address the analytical foci of this paper, they are included for various reasons. First, the annual regressions allow the inclusion of carbon prices from 2006 onwards. Second, the conditional regressions represent a model utilised in current literature (see Tulloch et al. 2017a; Batten et al. 2017; El-Sharif et al. 2005) and, as such, provide a benchmark for comparison with the more sophisticated approach presented in Section 3.5.
3.4. Time-Varying Risk Factor Sensitivities: Annual Regressions
The established literature has reported substantial intertemporal and intersectoral variability in the relationships between average returns and risk factors (Batten et al. 2017; El-Sharif et al. 2005; Faff and Brailsford 1999; Fama and French 1997, 1998, 2012; Oberndorfer 2009; Sadorsky 2001). To address time-varying risk loadings, the time series is separated into annual periods, and the local AFFM, Equation (3), is applied annually. This provides results comparable with Tulloch et al. (2017a), Batten et al. (2017), and El-Sharif et al. (2005). Table 3 reports the annual regression results for the energy sector portfolio, estimated using Newey-West HAC standard errors. Regression coefficients through time and 95% confidence intervals are shown in Figure 3.
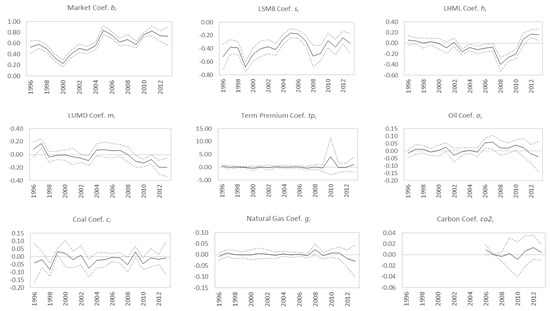
Figure 3.
Local AFFM estimated coefficients and 95% confidence intervals over time. This figure illustrates the estimated coefficients for the nine risk factors through time, using the annual local AFFM results from Table 3. The solid line represents the estimated coefficient, while the dotted line represents the 95% confidence interval. When the 95% confidence interval overlaps zero, the test of significance fails at the 5% level.
Overall, the results indicate evolving sensitivity to risk factors over the entire time series. Further, the intertemporal AFFM improves the goodness of fit, from an adjusted of 72.77% in the unconditional regression of Table 2 to a mean-adjusted of 74.52% in Table 3.
The coefficients for the size effect are negative and significant for all 18 years tested. The results show that the average returns in the energy sector behave like big energy utilities through time. The relationship is not stable through time; there are years where the coefficient becomes more negative, suggesting that the returns of big utilities have a greater influence on overall sector returns. In Table 3, the magnitude of negative coefficients is large around 1999 and 2008–2009; the biggest utilities have a large influence on energy sector returns in these years.
The coefficients for the value effect are nominally negative for 10 of the 18 years tested, eight of which were significant. This indicates that average returns in the energy sector covary with those of the low-BE/ME (growth) utilities through time. However, the years 2011 to 2013 show a shift in the coefficient, with 2012 and 2013 being positive and significant. This shows that average returns in the energy utility sector behave like high-BE/ME (value) stocks between 2011 and 2013, typically associated with company distress. This is broadly consistent with observations in the financial press, which highlighted the negative impact of regulatory and technological change on the sector (The Economist 2013).
The coefficients for the effects of momentum indicate that the average returns of the utility sector are rarely affected by momentum. The energy sector as a whole only behaved like up-momentum utilities in 1997. Of the 18 years tested, only seven years produced results consistent with the energy sector behaving like down-momentum utilities. In particular, down-momentum utilities explain average sector returns in 2002 and 2003, and from 2009 onwards. The timing of these latter two shocks coincides with large regulatory changes described as the second and third packages of liberalisation in 2003 and 2009, respectively (Tulloch et al. 2017a, 2017b).
For the most part, commodities explain very little in energy sector returns. Natural gas produced one marginally significant coefficient in 2008, remaining insignificant otherwise, indicating effective hedging strategies over time. Carbon becomes significant in 2006 and 2007, and insignificant thereafter. Results are consistent with El-Sharif et al. (2005); there is varying commodity risk exposure across time. The number of significant commodity coefficients increases in later years, possibly reflecting the uncertainty of rapidly changing commodity prices over the period.
3.5. Time-Varying Risk Factor Sensitivities: Inductive Structural Breakpoint Tests
This section implements the Bai and Perron (1998, 2003) parameter stability diagnostic test and breakpoint regression. Daily returns in the energy sector, between 1 July 1996 and 28 June 2013, were used for all structural breakpoint tests. The breakpoint test was implemented using the local AFFM (Equation (2)), rather than the global AFFM, as the local stock market risk factors have tighter regression fits. The results in Table 4 present the stability diagnostic tests, while the results in Table 5 present the results of the breakpoint regression. The break conditions of the two tests are also outlined in Table 4 and Table 5.

Table 4.
Local AFFM stability diagnostic tests.

Table 5.
Results of the local AFFM breakpoint regression.
First, we address the posthoc stability diagnostic test. The significant results of the -tests indicate a minimum of one and a maximum of eight structural breaks in the time series, diminishing as the ninth break appears. The repartition dates serve as likely candidates for the structural breaks, where one or more of the parameters have significantly shifted.
Based on the evidence of the existence of structural breaks in the local AFFM, we implement the second stage of the Bai and Perron (1998, 2003) test: the breakpoint regression. The second stage specifies the local AFFM (Equation (2)) as the mean equation. The result of the breakpoint regression is shown in Table 5. The result shows that the estimated breakpoints are identical to those in Table 4, identifying eight structural breaks in the time series.
The Bai and Perron (1998, 2003) breakpoint regression provides marked improvements to regression fits for the energy sector. The initial full-period global AFFM produced an adjusted R2 of 68.79% (Table 2, Model 5). The adjusted of the intertemporal global AFFM varied between 28.24% and 85.63%, with a mean of 69.64% (Table 3). When controlling for inductive structural breaks, the Bai and Perron (1998, 2003) breakpoint regression increases the adjusted of the AFFM to 80.42%, greater than the mean adjusted values of 74.52% from annual regressions in Table 3. With regard to the third analytical focus, inductive structural breakpoint tests are better at identifying time-varying risk factor sensitivities.
Similar to the annual regressions, the results of the partial break point tests show that the market beta is increasing towards unity through time with some fluctuation, indicating increasing systematic risk. Between 1998 and 2007, the market beta increases from 0.33 to 0.75. The upward shift in market beta, occurring late-2004, is consistent with that observed in Table 3. The size factor coefficient () is consistently negative, indicating that the average returns in the energy utility sector behave like big energy utilities, with a greater impact in Partition 2 (September 1998 to March 2000) and Partition 7 (June 2008 to April 2009). The greater impact in 2008 onwards is of concern, as liberalisation objectives were introduced to counteract market dominance from big utilities. The value factor coefficient () shows that average returns in the energy sector mostly behave like low-BE/ME (growth stocks), although there are two partitions where average returns behave like high-BE/ME (value) stocks: Partition 2 (September 1998 to March 2000) and Partition 9 (February 2011 to June 2013). The partial breakpoint test shows that average returns in the energy sector are explained by both up and down momentum over time. Energy utilities behave like down-momentum stocks in Partition 4 (September 2001 to August 2004) and Partitions 8 and 9 (April 2009 onwards). There is a clear shift in the risk profile of energy utilities from 2009 onwards (beyond macroeconomic risk factors). Similar to the intertemporal analysis in Table 3, after 2009, the sector is characterised by big, high-BE/ME and down-momentum utilities, which are taking on increased systematic risk.
Regarding the term premium and commodity risk factors, the results also show changing significance through time. Term premium becomes temporarily significant in Partition 4 (September 2001 to August 2004), which encompasses the second packages of liberalisation and the lead-up to the global financial crisis (GFC), indicating a significant relationship between borrowing costs and returns. Oil price risk shows increased significance immediately before the GFC, showing that returns in the energy sector were highly sensitive to oil price risk. Coal price risk has sporadic significance across time, which continues to be negative (when significant). Natural gas price risk continues to be insignificant through time, again, indicating effective hedging strategies. The differences between these results and the deductive method of Table 3 are manifestations of Quandt’s (1960) criticisms: Unless the breakpoints are known with certainty, the significance tests and estimated coefficients are likely to be biased.
3.6. Better Isolate Firm-Specific Returns: Inductive Structural Breakpoint Tests
The fourth analytical focus of this paper addresses better isolating of the firm-specific returns of sector-level returns. This approach can be useful in applications that require more precise estimates of expected stock return, including (1) portfolio selection, (2) evaluating portfolios performance, (3) estimates of the cost of capital and (4) measuring abnormal return in event studies (Fama and French 1993). Specifically, Tulloch et al. (2017a) utilise the local AFFM to perform an event study analysis on the impact of liberalization and environmental policy on the financial returns of European energy utilities.
The standard approach includes extracting the residuals from a regression, for example, the unconditional CAPM, where the residuals are assumed to be the unsystematic or firm-specific component of returns (Chan et al. 1985; Fama and French 1993). However, any omitted variables from the model specification will bias the estimates of regression coefficients, while intercorrelated disturbances will bias standard errors; both result in a false-positive.
Typically, the three- and four-factor models capture common returns across a variety of stocks and are better at isolating the firm-specific components of returns (Fama and French 1993). The assumption that these parameters are stable can result in spurious significant correlations between residuals and exogenous risk factors. Fama and French (1993) have also drawn inferences based on this fallacy, performing residual diagnostic tests with constant slopes; the authors acknowledge that the assumption on constant slopes may be a misconception but do not investigate the claim further. The following paragraph demonstrates the consequences of this erroneous assumption.
The residuals of the local AFFM model are extracted using three different methods, including (1) the assumption of constant parameters in the unconditional local AFFM regression of Table 2—similar to Fama and French (1993), (2) the time-varying parameters of the conditional annual local AFFM regressions in Table 3—similar to the Batten et al. (2017) and El-Sharif et al. (2005), who did not perform additional residual diagnostic tests, and (3) time-varying parameters of the local AFFM sequential breakpoint test in Table 5—based on the minimisation of the SSR from Bai and Perron (2003).
The cumulative and daily residuals through time are shown in Figure 4. The first observation is that the residuals of Method (1), the unconditional constant parameter assumption, are generally larger than the other two, time-varying assumptions, Methods (2) and (3). For Method (1), the assumption of constant parameters results in the cumulative residuals for energy utilities, reaching 200% by mid-2008. The first invalid inference would be that this represents a firm-specific component to returns, increasing from 2003 to the GFC, and decreasing thereafter. It could also be hastily concluded that this shift represents a structural break after the second packages of liberalisation (in 2003), expected to be a major regulatory event. Further, empirical tests will also identify significant breaks in returns which coincide with such an interpretation, in 2003 and 2008, as shown in Table 6.
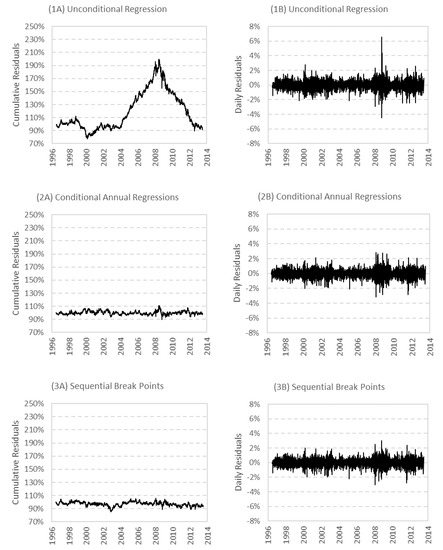
Figure 4.
Cumulative and daily residuals of regression specifications. This figure illustrates the daily and cumulative residuals of three different local AFFM specifications: (1) the unconditional local AFFM (Plots 1A,1B), the conditional annual local AFFMs (Plots 2A,2B) and the sequential structural breakpoint tests (Plots 3A,3B).

Table 6.
Bai and Perron (2003) breakpoint tests.
Although the structural breaks are significant, the adjusted shows that these breaks explain a small proportion of the variation in the residuals, the fraction of variance unexplained. In contrast to the significant structural breaks in the unconditional Method (1), the time-varying Methods (2) and (3) find no structural breaks. How can this result be reconciled? An explanation may be that the residuals of the unconditional approach in Method (1), in fact, contain systematic risk factors beyond the firm-specific components of returns. The residuals reflect the changing relationship between the stock returns and the risk factors. This can be demonstrated in two ways. First, the time-varying methods, Methods (2) and (3), both allow the risk factors to vary across time, capturing parameter shifts. Table 6 and Figure 4 show that the residuals in these two methods fall close to zero, suggesting few impacts from factors beyond those specified in the mean equation. Second, the expectation is that the residuals of the unconditional regression should have filtered out the impact of all risk factors, leaving an orthogonalised return series that represents only the firm-specific element of returns.
A second pass of the unconditional residuals in Method (1), using either linear regressions or sequential breakpoints model specifications, is expected to have no relationship with the risk factors, as they should have been filtered out in the first pass. However, this is not the case. To demonstrate, a second sequential breakpoint test is employed on the unconditional residuals of Method (1) against the market factor, local stock market risk factors, term premium and commodity risk factors; the results are shown in Table 7. The first observation is the presence of significant relationships between the unconditional residuals and the risk factors. The adjusted shows that the unconditional full-period regression is insufficient at removing the risk factor sensitivities, explaining 27.95% of the residual variation. The economic rationale is simple: A linear relationship is insufficient to capture time-varying common risk over long horizons; the polygonal curve–fitting approach of Bai and Perron (2003) is able to control for the nonlinearity and partial breaks across time.

Table 7.
Second-pass sequential breakpoint test on residuals.
The dates of the sequential breakpoints in Table 7 are identical to those in Table 4 and Table 5, giving confidence that the residuals are capturing a shift in the relationship with risk factors. The estimated coefficients in Table 7 represent the difference between the estimated coefficients of the unconditional local AFFM (Table 2) and the estimated coefficients of the local AFFM breakpoint regression (Table 5). Put simply, the estimated coefficients in Table 7 represent the increasing or decreasing relationship between average returns and the risk factors during the partition. For example, the long-term market beta in Table 2 (also shown in Table 7) is 0.6306, while Partition 2 of Table 7 estimates that the market beta experienced a statistically significant downwards shift of −0.3297, providing an overall market beta of 0.3009. Allowing for rounding, this value matches the estimated market beta of Partition 2 in Table 5. In fact, the difference between each coefficient in Table 7 and the unconditional estimate equals the coefficient in Table 5.
This implies that the residuals of the unconditional regression still contain risk factor effects, failing to accurately represent the firm-specific component of returns over long horizons. These results show that asset pricing models must control for this changing relationship with risk factors over time to better isolate the firm-specific component of returns, necessary to calculate abnormal performance as a result of regulatory changes.
The overall results indicate that structural breakpoints in parameters, previously ignored in the unconditional model assuming constant slopes, account for around 28% of the residuals, which were previously assumed to be the firm-specific element of excess returns. These results demonstrate that the sequential partial breakpoint approach has a much greater ability to filter out systematic elements of returns.
3.7. Robustness
In this section, we check the robustness of our inference that local stock market risk factors provide an enhanced understanding of sector-level returns compared to global stock market risk factors. We do so to address concerns that the local stock market risk factors are no better than global stock market risk factors in explaining average returns at the sector level and that too much weight is placed on the importance of adjusted as a measure of model fit. If the local stock market risk factors are no better at explaining average sector-level returns than global stock market risk factors, then regressing the local risk factors against the residuals of the unconditional global AFFM we implemented in Equation (1) should provide results with no explanatory power and insignificant coefficients.
To test this hypothesis, we approach the analysis by reimplementing the unconditional global AFFM specification in Equation (1) and extracting the regression residuals, denoted as . This approach ensures that all systematic risk factors are filtered out from the regression. The residuals should now contain only sector-specific energy utility returns, having already controlled for the market factor, global stock market risk factors, term premium, and commodity risk factors in the prior step.
We regress against the local stock market risk factors in the following model specification:
The is a time series of residuals from the global AFFM, denotes the intercept, denotes the coefficient, denotes the local size factor at time , denotes the coefficient, denotes the local value factor at time , denotes the coefficient, denotes the local momentum factor at time , and denotes the error term at time .
Prior to interpreting the results, we performed a multicollinearity diagnostics test to confirm the local and global stock market risk factors were not highly correlated. Pairwise correlations among local and global risk factors were all below 0.3235, and variance inflation factors were below 1.21.
The estimates of Equation (4) show that the local stock market risk factors are indeed important in explaining the residuals of the global AFFM model. That is, they are significant in explaining some of the sector-specific returns after controlling for systematic, global risk factors. Our results show an coefficient of −0.3891 , a coefficient of −0.0229 ), and an coefficient of −0.1526 . All coefficients are in the same direction and similar magnitude to the results were found when implementing the unconditional local AFFM regression (Equation (2)). The intercept was not significantly different from zero, and the model’s adjusted was 17.81%.
The largest difference between the global risk factors (Equation (1)) and local risk factors (Equation (2)) results occur in the HML slopes; thus, the following paragraphs concentrate on explaining this difference. For context, the global risk factors explore how the energy sector behaves relative to other European stocks and sectors, whereas the local risk factors explore how the energy portfolio behaves relative to other European energy utilities. The positive slope in the global AFFM shows that the energy utility sector behaves like high-BE/ME European stocks when measured against the global risk factors. In contrast, small but the negative slope in the local AFFM suggests a marginal tilt towards the low-BE/ME (growth) utilities.
The results suggest that when looking at the energy sector in isolation, energy stocks with low-BE/ME ratios (high market capitalisation relative to book value) have a slightly greater influence on average sector returns, and average returns within the sector is being driven by growth opportunities. This is consistent with the ongoing growth and expansion of industry participants in the energy sector. However, when considering the energy sector in the context of the wider 600 European stocks across various sectors, the energy sector as a portfolio tends to have relatively higher BE/ME ratios than the average European stock. The implication is that when an investor is faced with a choice among a broad selection of European stocks, energy utilities do not provide comparable capital growth opportunities available from other European stocks, but will appeal to value investors—that is, investors or funds which typically foregoes capital growth for more steady dividend streams.
The fact that the local stock market risk factors explain average sector returns, after controlling for global and systematic risk factors, supports our inference that the local stock market risk factors provide an enhanced understanding of sector-level returns compared to global risk factors, and can explain returns not captured by global stock market risk factors.
4. Conclusions
This paper outlines a modelling approach for implementing sector asset pricing studies. This is achieved through the four analytical foci of the paper, namely: (1) by calculating stock market risk factors at the sector level, (2) by creating subgroup portfolios to explore within-sector heterogeneity, (3) by applying inductive structural breakpoint tests to identify time-varying risk factor sensitivities, and (4) by better isolating the firm-specific component of returns though a “second pass” structural break regression on residuals. We do so by creating a comprehensive asset pricing model, the AFFM, which includes commodity and macroeconomic risk factors previously found to affect sector returns. We improve on the asset pricing model by calculating local risk factors—risk factors that are more relevant to the sector of interest and better account for within-sector characteristics.
For the first analytical focus, the use of local stock market risk factors, specific to the energy utility sector, improves the performance of asset pricing models and can explain a greater proportion of average returns at the sector level. Our results show the asset pricing models which use local risk factors had greater explanatory power as regression fits were tight, resulting in higher values, increasing adjusted from 68.79% using the standard risk factors to 72.77% using the local risk factors.
Addressing the second analytical focus, we grouped the energy stocks into 12 subsector portfolios based on company characteristics. Our results show substantial heterogeneity across the 12 portfolios. The spread in estimated coefficients shows that the heterogeneous sensitivity to size, value and momentum factors are the largest determinants for the differences in expected returns across various energy portfolios. Interestingly, the multi-utility portfolios show one of the lowest cumulative abnormal returns across all portfolios—possibly indicating a lower risk–return relationship. This is consistent with the economy of scope—diversified operations allow multi-utilities to switch operations when faced with regulatory changes or fluctuations in commodity prices.
The third analytical focus examines how to account for time-varying risk factor sensitivities using deductive conditional annual regressions and the inductive Bai and Perron (1998, 2003) structural breakpoint tests. The annual regressions, using the local AFFM, result in a mean-adjusted of 74.52%. The inductive method improves the local AFFM’s goodness of fit further, producing an adjusted of 80.42%. The interpretations of the results from both time-varying methods are qualitatively the same. The energy sector’s market beta has been increasing towards unity through time, suggesting the sector is taking on increasing systematic risk. The size effect coefficient indicates that market returns of big utilities dominate sector returns. The sector was characterised by growth opportunities, with the exception of a few distressing years. The sector also experienced downward momentum in the years following major regulatory changes, which were expected to negatively impact incumbent utilities. Commodity factors and term premia show sporadic significance through time, with coal and oil being the most important two commodities in explaining sector returns. The results highlight the importance of measuring time-varying risk factors, especially in the context of long time periods and sectors that have undergone large structural changes. Similar to Batten et al. (2017), our results demonstrate a need for active management of portfolios given the instability in the relationship between returns and risk factors.
Finally, the fourth analytical focus explores methods of isolating the firm-specific component of returns using the residuals of the unconditional regressions, conditional annual regressions and inductive structural breakpoint test. This paper demonstrates that the common method of isolating the residuals of the unconditional regressions, such as the method implemented by Fama and French (1993), performs poorly at capturing the firm-specific components of returns. This is because the assumption of constant parameters forces the changing relationship between the sample returns and the risk factors into the residuals of a linear regression. We examine this proposition using the residuals of an unconditional local AFFM and applying a “second pass” test on these residuals using the Bai and Perron (1998, 2003) structural breakpoint regression. Our results, specific to this paper’s energy sample and time period, show that 28% of the residuals’ variance is related to the changing relationship between sector returns and risk factors. We detect structural breaks in the residuals of an unconditional regression, which correlate with structural breaks in the relationship between sector returns and risk factors. We show that a better method of isolating the firm-specific component of returns is to account for multiple structural changes in model parameters using polygonal curves and minimising variance within groups.
Overall, our approach to modelling sector-level returns better captures the complexity of the evolving relationship between energy sector returns and underlying risk factors over long periods of time. Our work contributes to the asset pricing literature as a template for conducting sector asset pricing studies in other sectors since it suggests an approach of more accurately examining time-varying risk factors and isolating the firm-specific component of returns. A possible extension to our analysis would be to compare global versus local Fama and French (2015) five-factor models, given the increased popularity of this model (e.g., Sarwar et al. 2018).
This is important not just to investors who have sector-defined mandates and funds but also regulators in regulated sectors who want to understand the impact of policies on sector risk–return dynamics and the cost of capital. Our approach to explaining average returns over time can also be used by policymakers to understand or estimate the impact of existing or future policy changes. For example, if a policymaker can see that a series of prior legislative changes has dramatically increased the historical risk–return profile of a sector, they can used this to inform their cost–benefit analyses, estimates of net efficiency gains, and sector strategy for future policy changes. Moreover, they can use this approach to measure whether the intended policy objective has been achieved or whether their policy has induced undue risk and hardship into the sector. Finally, if a policymaker suspects that hallmarks of market failure have occurred or are occurring, without any associated policy intervention, they can measure whether average returns in the sector have changed, or whether there is a significant structural break in the average returns or relationships with market/commodity risk factors. This can act as the starting point of any policy investigation. As such, this approach could be applied to sectors such as banking, automotive, oil and gas and telecommunications, which are undergoing dramatic technologically and policy/regulatorily driven changes.
Author Contributions
Conceptualization, D.J.T. and I.D.-R.; methodology, D.J.T.; software, D.J.T.; validation, D.J.T. and I.M.P.; formal analysis, D.J.T.; investigation, D.J.T. and I.D.-R.; resources, D.J.T. and I.D.-R.; data curation, D.J.T.; writing—original draft preparation, D.J.T.; writing—review and editing, D.J.T. and I.D.-R.; visualization, D.J.T.; supervision, I.D.-R. and Prechachandra; project administration, D.J.T. and I.D.-R.; funding acquisition, D.J.T. and I.D.-R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Otago Business School Dean’s PhD Scholarship.
Acknowledgments
We thank participants at the 2018 New Zealand Finance Meeting in Queenstown. We are particularly grateful to the paper discussant Yihui Lan and session chair Annette Vissing-Jorgensen. We also thank participants at the New Zealand Finance Colloquium (Hamilton, 2015), the University of Otago Department of Accountancy and Finance Seminar Series (2014), the 34th Annual International Conference of the IAEE (2012, Perth, Australia) and the 9th International Conference on the European Energy Market (2012, Florence Italy). The usual disclaimer applies.
Conflicts of Interest
The authors declare that they have no conflict of interest.
Appendix A. Data Variables and Description
| Symbol | Data Variable | Description |
| The 12 value-weighted portfolios include the energy sector | Twelve portfolios of energy stocks grouped based on characteristics: portfolios of energy utilities grouped on firm characteristics, including the energy sector as a whole; small and big utilities; high-BE/ME (value), mid-BE/ME (neutral) and low-BE/ME (growth) utilities; upper, medium and down momentum utilities; and electricity, natural gas and multi-utilities. | |
| A portfolio of high-BE/ME utilities | High BE/ME stocks are value stocks. The market capitalisation of value stocks is equal to or below the book value of equity. The top 30% of BE/ME values in our sample is used as the breakpoint. | |
| A portfolio of mid-BE/ME utilities | Mid BE/ME are neither value nor growth stocks. The market capitalisation of value stocks is almost equal to the book value of equity. This group represents the middle 40% BE/ME values in our sample. | |
| A portfolio of low-BE/ME utilities | Low BE/ME stocks are growth stocks. Growth stocks’ market capitalisation is well above their book value of equity. The bottom 30% of BE/ME values in our sample is used as the breakpoint. | |
| A portfolio of up momentum utilities | Upper-momentum stocks are stocks with the top 30% of average excess returns calculated over the formation period from day t − 251 to day t − 21 and exclude the sort month. This is commonly known as a portfolio of winners. | |
| A portfolio of neutral momentum utilities | Neutral-momentum stocks are stocks with the middle 40% average excess returns calculated over the formation period from day t − 251 to day t − 21 and exclude the sort month. | |
| A portfolio of down momentum utilities | Down-momentum stocks are stocks with the bottom 30% of average excess returns calculated over the formation period from day t − 251 to day t − 21 and exclude the sort month. This is commonly known as a portfolio of losers. | |
| A portfolio of electricity utilities | A portfolio of stocks where electric utilities operations are defined as the primary revenue source. | |
| A portfolio of natural gas utilities | A portfolio of stocks where natural gas operations are defined as the primary revenue source. | |
| A portfolio of multi utilities | A portfolio of stocks where multi-utility, or combined utility services, are defined as the primary revenue source. | |
| A portfolio of small utilities | A portfolio of stocks where market capitalisation was below the median sample market capitalisation | |
| A portfolio of big utilities | A portfolio of stocks where market capitalisation was above the median sample market capitalisation. | |
| A market factor | The STOXX® 600 Europe Index is used as a proxy for broad market returns. | |
| A global size factor | The global SMB factor is calculated as the daily difference between the arithmetic average return of the three small portfolios (S/L, S/M and S/H) minus the arithmetic average return of the three big portfolios (B/L, B/M and B/H). The global risk factors are calculated with a universe of 600 European companies across various sectors. | |
| A global value factor | The global HML factor is calculated as the daily difference between the arithmetic average of the two high-BE/ME portfolios (S/H and B/H) minus the arithmetic average of the two low-BE/ME portfolios (S/L and B/L). The global risk factors are calculated using 600 European companies across various sectors. | |
| A global momentum factor | The global UMD factor is calculated as the daily difference between the returns of the upper momentum and down momentum portfolios. The global risk factors are calculated using 600 European companies across various sectors. | |
| A local size factor | The local SMB factor is calculated as the daily difference between the arithmetic average return of the three small portfolios (S/L, S/M and S/H) minus the arithmetic average return of the three big portfolios (B/L, B/M and B/H). The global risk factors are calculated using 600 European companies across various sectors. | |
| A local value factor | The local HML factor is calculated as the daily difference between the arithmetic average of the two high-BE/ME portfolios (S/H and B/H) minus the arithmetic average of the two low-BE/ME portfolios (S/L and B/L). The global risk factors are calculated using our sample of 91 European energy utilities. | |
| A local momentum factor | The local UMD factor is calculated as the daily difference between the returns of the up-momentum and down-momentum portfolios. The global risk factors are calculated using our sample of 91 European energy utilities. | |
| Term premium | Term premium is calculated as the difference between the daily yields on the three- and one-month UK Treasury bills. | |
| Return on oil prices | London Brent Crude Oil Index proxies for oil price, sourced from the Intercontinental Exchange (ICE). | |
| Return on coal prices | Coal price is measured using a European-specific steam (thermal) coal index for power and heat generation, sourced from the Hamburg Institute of International Economics (HWWI). | |
| Return on gas prices | Natural gas price is measured using the one-month forward index, also sourced from the ICE. | |
| Return on carbon prices | Carbon allowance prices, measured as the price (in euros) per EUA, are sourced from the ICE European Climate Exchange (ECX). |
References
- Alford, Andrew W., Jennifer J. Jones, and Mark E. Zmijewski. 1994. Extensions and violations of the statutory SEC form 10-K filing requirements. Journal of Accounting and Economics 17: 229–54. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 1998. Estimating and Testing Linear Models with Multiple Structural Changes. Econometrica 66: 47–78. [Google Scholar] [CrossRef]
- Bai, Jushan, and Pierre Perron. 2003. Computation and Analysis of Multiple Structural Change Models. Journal of Applied Econometrics 18: 1–22. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Harald Kinateder, Peter G. Szilagyi, and Niklas F. Wagner. 2017. Can stock market investors hedge energy risk? Evidence from Asia. Energy Economics 66: 559–70. [Google Scholar] [CrossRef]
- Bellman, Richard, and Robert Roth. 1969. Curve Fitting by Segmented Straight Lines. Journal of the American Statistical Association 64: 1079–84. [Google Scholar] [CrossRef]
- Boni, Leslie, and Kent L. Womack. 2006. Analysts, Industries, and Price Momentum. Journal of Financial and Quantitative Analysis 41: 85–109. [Google Scholar] [CrossRef]
- Carhart, Mark M. 1997. On Persistence in Mutual Fund Performance. The Journal of Finance 52: 57–82. [Google Scholar] [CrossRef]
- Chan, Kevin C., Nai-fu Chen, and David A. Hsieh. 1985. An Exploratory Investigation of the Firm Size Effect. Journal of Financial Economics 14: 451–71. [Google Scholar] [CrossRef]
- Chan, Louis K. C., Yasushi Hamao, and Josef Lakonishok. 1991. Fundamentals and Stock Returns in Japan. The Journal of Finance 46: 1739–64. [Google Scholar] [CrossRef]
- Conover, C. Mitchell, Robert E. Miller, and Andrew Szakmary. 2008. The timeliness of accounting disclosures in international security markets. International Review of Financial Analysis 17: 849–69. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the Estimators for Autoregressive Time Series with a Unit Root. Journal of the American Statistical Association 74: 427–31. [Google Scholar] [CrossRef]
- El-Sharif, Idris, Dick Brown, Bruce Burton, Bill Nixon, and Alex Russell. 2005. Evidence on the Nature and Extent of the Relationship between Oil Prices and Equity Values in the UK. Energy Economics 27: 819–30. [Google Scholar] [CrossRef]
- Faff, Robert W., and Timothy J. Brailsford. 1999. Oil Price Risk and the Australian Stock Market. Journal of Energy Finance & Development 4: 69–87. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1992. The Cross-section of Expected Stock Returns. The Journal of Finance 47: 427–65. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1993. Common Risk Factors in the Returns on Stocks and Bonds. Journal of Financial Economics 33: 3–56. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1995. Size and Book-to-market Factors in Earnings and Returns. The Journal of Finance 50: 131–55. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1997. Industry Costs of Equity. Journal of Financial Economics 43: 153–93. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1998. Value versus Growth: The International Evidence. The Journal of Finance 53: 1975–99. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2006. The Value Premium and the CAPM. The Journal of Finance 61: 2163–85. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2012. Size, Value, and Momentum in International Stock Returns. Journal of Financial Economics 105: 457–72. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2015. A five-factor asset pricing model. Journal of Financial Economics 116: 1–22. [Google Scholar] [CrossRef]
- Fisher, Walter D. 1958. On Grouping for Maximum Homogeneity. Journal of the American Statistical Association 53: 789–98. [Google Scholar] [CrossRef]
- French, Kenneth R. 2015. Data Library. Available online: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html (accessed on 20 December 2015).
- Guthery, Scott B. 1974. Partition Regression. Journal of the American Statistical Association 69: 945–47. [Google Scholar] [CrossRef]
- Hansen, Bruce E. 2001. The New Econometrics of Structural Change: Dating Breaks in U.S. Labor Productivity. The Journal of Economic Perspectives 15: 117–28. [Google Scholar] [CrossRef]
- Jamasb, Tooraj, and Michael Pollitt. 2005. Electricity Market Reform in the European Union: Review of Progress toward Liberalization & Integration. The Energy Journal 26: 11–41. [Google Scholar] [CrossRef]
- Koch, Nicolas, and Alexander Bassen. 2013. Valuing the Carbon Exposure of European Utilities. The Role of Fuel Mix, Permit Allocation and Replacement Investments. Energy Economics 36: 431–43. [Google Scholar] [CrossRef]
- Kumar, Alok. 2009. Hard-to-Value Stocks, Behavioral Biases, and Informed Trading. Journal of Financial and Quantitative Analysis 44: 1375–401. [Google Scholar] [CrossRef]
- Mollick, André Varella, and Tibebe Abebe Assefa. 2013. US stock returns and oil prices: The tale from daily data and the 2008–2009 financial crisis. Energy Economics 36: 1–18. [Google Scholar] [CrossRef]
- Moskowitz, Tobias J., and Mark Grinblatt. 1999. Do Industries Explain Momentum? The Journal of Finance 54: 1249–90. [Google Scholar] [CrossRef]
- Newey, Whitney K., and Kenneth D. West. 1987. A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelation Consistent Covariance Matrix. Econometrica 55: 703–8. [Google Scholar] [CrossRef]
- Oberndorfer, Ulrich. 2009. Energy Prices, Volatility, and the Stock Market: Evidence from the Eurozone. Energy Policy 37: 5787–95. [Google Scholar] [CrossRef]
- Quandt, Richard E. 1960. Tests of the Hypothesis That a Linear Regression System Obeys Two Separate Regimes. Journal of the American Statistical Association 55: 324–30. [Google Scholar] [CrossRef]
- Rosenberg, Barr, Kenneth Reid, and Ronald Lanstein. 1985. Persuasive Evidence of Market Inefficiency. The Journal of Portfolio Management 11: 9–16. [Google Scholar] [CrossRef]
- Sadorsky, Perry. 2001. Risk Factors in Stock Returns of Canadian Oil and Gas Companies. Energy Economics 23: 17–28. [Google Scholar] [CrossRef]
- Sarwar, Golam, Cesario Mateus, and Natasa Todorovic. 2018. US sector rotation with five-factor Fama–French alphas. Journal of Asset Management 19: 116–32. [Google Scholar] [CrossRef]
- Silvapulle, Param, Russell Smyth, Xibin Zhang, and Jean-Pierre Fenech. 2017. Nonparametric panel data model for crude oil and stock market prices in net oil importing countries. Energy Economics 67: 255–67. [Google Scholar] [CrossRef]
- Smyth, Russell, and Paresh Kumar Narayan. 2018. What do we know about oil prices and stock returns? International Review of Financial Analysis 57: 148–56. [Google Scholar] [CrossRef]
- The Economist. 2013. How to Lose Half a Trillion Euros. The Economist, October 15. [Google Scholar]
- Tulloch, Daniel J., Ivan Diaz-Rainey, and Inguruwatt M. Premachandra. 2017a. The Impact of Liberalization and Environmental Policy on the Financial Returns of European Energy Utilities. The Energy Journal 38: 77–106. [Google Scholar] [CrossRef]
- Tulloch, Daniel J., Ivan Diaz-Rainey, and Inguruwatt M. Premachandra. 2017b. The Impact of Regulatory Change on EU Energy Utility Returns: The Three Liberalization Packages. Applied Economics 50: 957–72. [Google Scholar] [CrossRef]
| 1 | This paper is part of a wider research project which includes Tulloch et al. (2017a) and Tulloch et al. (2017b). Tulloch et al. (2017a) is a direct precursor to this paper, as it implements the global AFFM to make comparisons across sectors and relies on deductive structural breaks. Tulloch et al. (2017b) use an event-study approach to explore the effect of various policy reforms on the returns of the energy sector as a whole. The focus in this paper is a more nuanced understanding of sector-level returns, using subcategories of energy utilities, local risk factors, and time-varying risk factor sensitivities, and isolating the firm-specific component of return. This paper is distinct yet complementary to Tulloch et al. (2017a) and Tulloch et al. (2017b). |
| 2 | For brevity, we denote all excess returns over the one-month UK treasury bill in bold; simple returns are nonbold. |
| 3 | Term premium represents borrowing costs and is calculated as the spread between the yields of a three- and one-month treasury bill. Term premium represents the risk-free short-term discount rate and an indicator of the present state of the economy, which tends to be lower during economic downturn and higher in times of growth (Sadorsky 2001). |
| 4 | The European Union Emissions Trading Scheme was established in 2005, meaning the annual conditional regressions can only examine the impact of carbon prices in the latter years. |
| 5 | The underlying dataset used in this paper is similar to that used in [author identifying citation] with some additions: namely, the use of multiple sector-level portfolios. |
| 6 | Note, Tulloch et al. (2017b) use weekly stock market data. The results are substantively the same. |
| 7 | This is a key requirement of Fama and French (1993), where the premia of size and value are argued to be buried within the market factor. Thus, we must isolate our size and value factors from the sample of companies, which proxy for the market factor. |
| 8 | Groups include the European Distribution System Operators’ Association (EDSO), ENTSO-E, Gas Infrastructure Europe (GIE), Gas Transmission Europe (GTE), Gas Storage Europe (GSE), Gas LNG Europe (GLE), ENTSO-G, and Eurogas. |
| 9 | To ensure the accounting variables predate the returns they are used to explain, the accounting data for fiscal year t − 1 are matched with the returns for July of year t to June of t + 1 (Fama and French 1992). This six-month lag is based on research by Alford et al. (1994) and Conover et al. (2008) regarding the lag between the fiscal year-end and the publication of annual reports. |
| 10 | Due to the significant data omissions for 2014, 2013 was the most comprehensive end date possible, and, therefore, also determined the end date of the analysis. |
| 11 | Matching SICs of year to returns of year t only made minor differences to the cumulative returns of the natural gas and multi-utility portfolios. The overall trend of the three portfolios did not change. |
| 12 | Note, three alternative lag structures were also tested but made no difference to estimates: (1) no lag specification, (2) Schwarz information criterion and (3) Hannan-Quinn Information Criterion. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).