Cryptocurrency Returns before and after the Introduction of Bitcoin Futures
Abstract
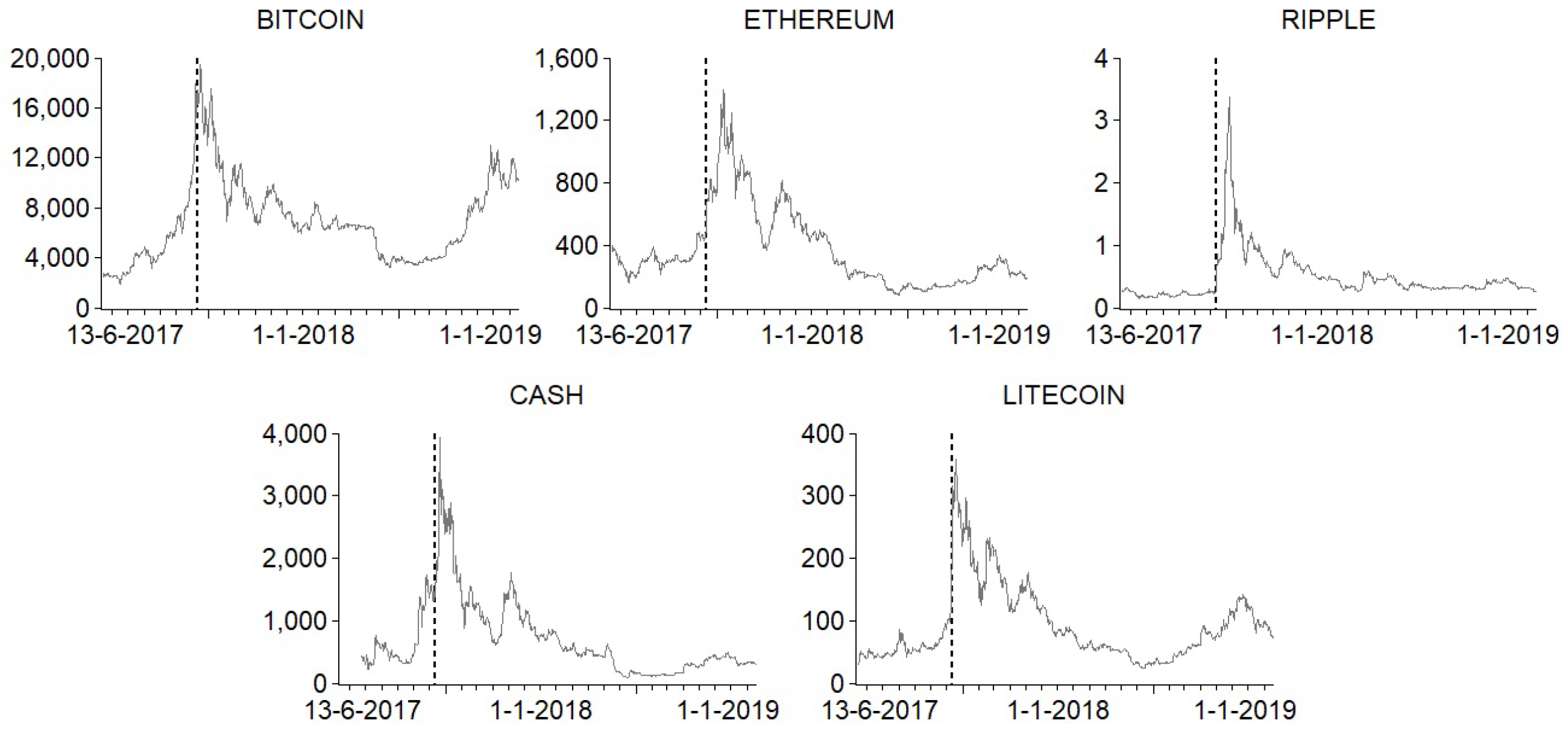
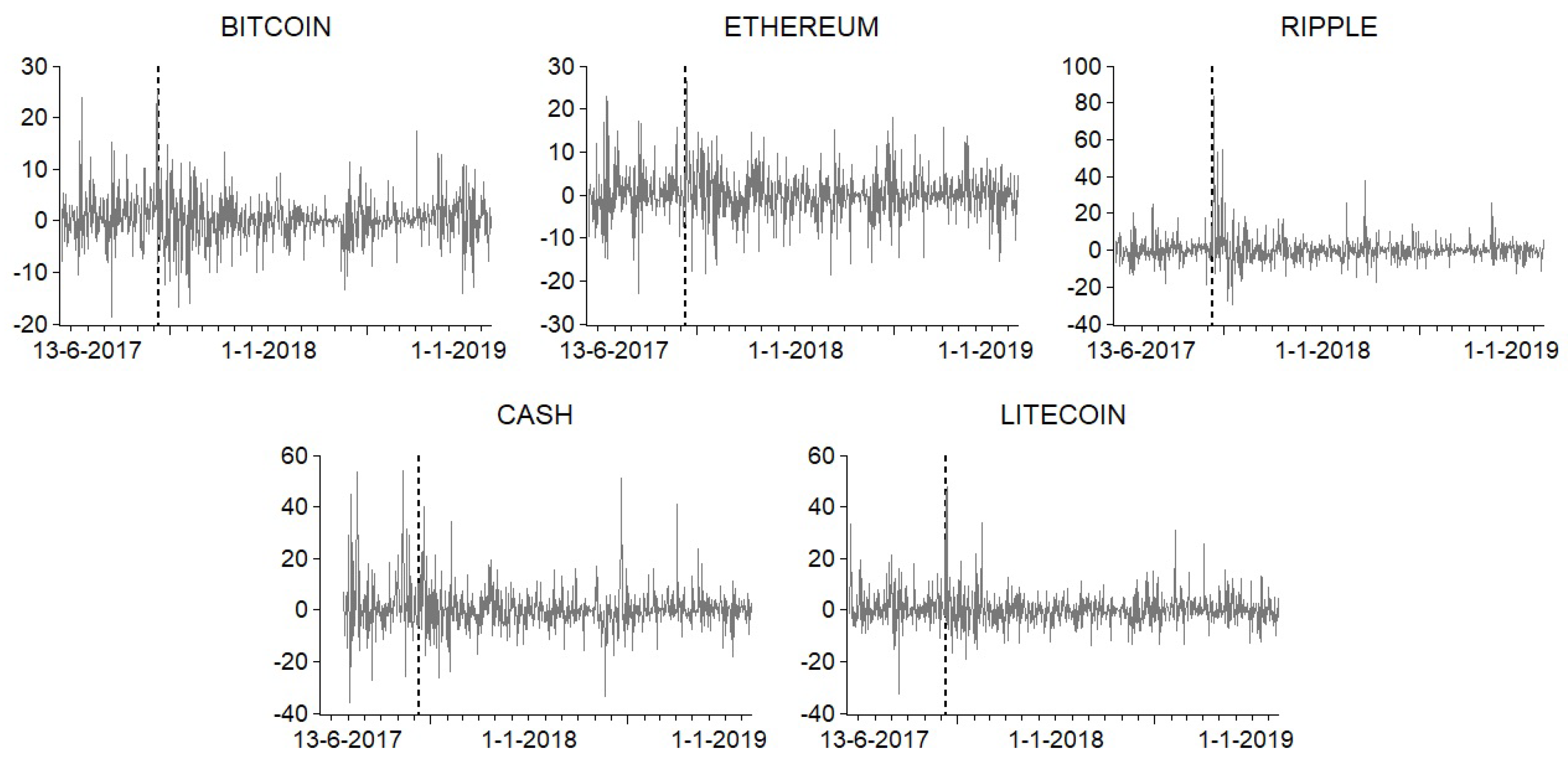
1. Introduction
2. Data and Methodology
2.1. Data
2.2. Methodology
2.2.1. PC-LASSO
2.2.2. GARCH-M Model
3. Empirical Findings
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Pre and Post Period Analyses
| Variable | Pre-30 | Post-30 | Pre-60 | Post-60 | Pre-90 | Post-90 |
|---|---|---|---|---|---|---|
| €/$ | 0.05797 | −0.06112 | 0.04370 | 0.00000 | 0.08528 | 0.00000 |
| Gold | 0.01325 | 0.00000 | 0.03587 | 0.00000 | 0.00127 | 0.00000 |
| NYSE | 0.00000 | 0.00686 | 0.00000 | 0.03944 | 0.00000 | 0.00000 |
| Oil price | 0.00000 | −0.02636 | 0.02719 | 0.00000 | −0.01326 | 0.00000 |
| GTrends | −0.08592 | −0.07312 | −0.09030 | −0.14124 | −0.03892 | −0.14067 |
| China | 0.00000 | −0.00051 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| VIX | 0.00000 | 0.00000 | −0.03018 | −0.04220 | −0.01026 | −0.03466 |
| FFR | 0.00000 | −0.08267 | 0.00000 | −0.04378 | 0.00000 | −0.05206 |
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Variable | Pre-120 | Post-120 | Pre-150 | Post-150 | Pre-180 | Post-180 |
| €/$ | 0.07214 | 0.00000 | 0.07686 | 0.00000 | 0.05873 | 0.00000 |
| Gold | 0.02406 | 0.00000 | 0.00000 | 0.00000 | 0.01647 | 0.00000 |
| NYSE | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Oil price | 0.00000 | 0.00000 | −0.01884 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | −0.04826 | −0.11394 | 0.00000 | −0.09425 | 0.00000 | −0.09571 |
| China | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.03256 | 0.00000 |
| VIX | −0.01647 | −0.02691 | 0.00000 | −0.03041 | 0.00000 | −0.02155 |
| FFR | 0.00000 | −0.01705 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Variable | Pre-30 | Post-30 | Pre-60 | Post-60 | Pre-90 | Post-90 |
|---|---|---|---|---|---|---|
| €/$ | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Gold | 0.00000 | 0.00000 | 0.06074 | 0.00565 | 0.05274 | 0.00000 |
| NYSE | 0.02333 | 0.00000 | 0.00000 | 0.00000 | 0.01320 | 0.00000 |
| Oil price | 0.00292 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | −0.07065 | −0.05535 | −0.06001 | −0.09956 | −0.06491 | −0.10650 |
| China | 0.00000 | 0.02429 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| VIX | 0.00000 | 0.09031 | −0.01531 | 0.00000 | −0.04728 | −0.08191 |
| FFR | 0.00000 | −0.01027 | 0.00000 | −0.07337 | 0.00000 | 0.00000 |
| EPU | 0.08298 | 0.00000 | 0.11181 | 0.00000 | 0.08644 | 0.00000 |
| Variable | Pre-120 | Post-120 | Pre-150 | Post-150 | Pre-180 | Post-180 |
| €/$ | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Gold | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| NYSE | 0.05410 | 0.00000 | 0.02893 | 0.00000 | 0.04384 | 0.00000 |
| Oil price | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | −0.00497 | −0.08598 | −0.01832 | −0.07421 | −0.02516 | −0.07788 |
| China | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.01425 | 0.00000 |
| VIX | −0.09069 | 0.00000 | −0.05761 | 0.00000 | −0.04949 | 0.00000 |
| FFR | 0.00000 | −0.03492 | −0.00740 | −0.00225 | −0.01483 | −0.00834 |
| EPU | 0.02202 | 0.00000 | 0.02258 | 0.00000 | 0.02380 | 0.00000 |
| Variable | Pre-30 | Post-30 | Pre-60 | Post-60 | Pre-90 | Post-90 |
|---|---|---|---|---|---|---|
| €/$ | 0.00000 | 0.02043 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Gold | 0.06636 | 0.00000 | 0.00762 | 0.00782 | 0.01986 | 0.00000 |
| NYSE | −0.02661 | −0.06739 | −0.05978 | 0.00000 | −0.05335 | 0.00000 |
| Oil price | 0.00000 | −0.00465 | 0.00529 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | 0.00000 | 0.00000 | 0.00000 | −0.09794 | 0.00000 | −0.10878 |
| China | 0.00000 | 0.00128 | −0.01140 | 0.00000 | −0.03693 | 0.00000 |
| VIX | 0.02349 | 0.02554 | 0.00924 | −0.05607 | 0.00989 | −0.00845 |
| FFR | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 | −0.02171 | 0.00000 |
| Variable | Pre-120 | Post-120 | Pre-150 | Post-150 | Pre-180 | Post-180 |
| €/$ | 0.00000 | 0.00000 | 0.00000 | 0.00000 | ||
| Gold | 0.01163 | 0.00000 | 0.00000 | 0.00000 | ||
| NYSE | −0.09299 | 0.00000 | 0.00000 | 0.00000 | ||
| Oil price | 0.00000 | 0.00000 | 0.00000 | 0.00000 | ||
| GTrends | 0.00000 | −0.08825 | −0.07688 | −0.08235 | ||
| China | 0.00000 | 0.00000 | 0.00000 | 0.00000 | ||
| VIX | 0.02653 | −0.00629 | −0.01039 | −0.00046 | ||
| FFR | 0.00000 | 0.00000 | 0.00000 | 0.00000 | ||
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Variable | Pre-30 | Post-30 | Pre-60 | Post-60 | Pre-90 | Post-90 |
|---|---|---|---|---|---|---|
| €/$ | 0.00000 | −0.11001 | 0.00000 | −0.01104 | 0.00428 | 0.00000 |
| Gold | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00674 | 0.00000 |
| NYSE | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Oil price | 0.02470 | −0.00478 | 0.02981 | 0.00000 | −0.01220 | 0.00000 |
| GTrends | −0.09051 | 0.00000 | −0.07668 | −0.08981 | −0.05857 | −0.08395 |
| China | 0.02133 | 0.00000 | 0.08864 | 0.00000 | 0.00000 | 0.00000 |
| VIX | 0.00000 | 0.00000 | 0.00000 | −0.00148 | −0.02796 | −0.04056 |
| FFR | 0.00000 | −0.11581 | 0.00000 | −0.13053 | 0.00000 | −0.12258 |
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Variable | Pre-120 | Post-120 | Pre-150 | Post-150 | Pre-180 | Post-180 |
| €/$ | 0.00000 | 0.00000 | 0.00877 | 0.00000 | 0.00000 | 0.00000 |
| Gold | 0.04201 | 0.00000 | 0.01465 | 0.00000 | 0.00328 | 0.00000 |
| NYSE | 0.00000 | 0.01919 | 0.00000 | 0.01539 | 0.00000 | 0.00803 |
| Oil price | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | −0.05496 | −0.08195 | −0.04049 | −0.07049 | −0.04516 | −0.07398 |
| China | 0.00000 | 0.00000 | 0.00441 | 0.00000 | 0.00000 | 0.00000 |
| VIX | −0.03459 | −0.04667 | −0.03398 | −0.04767 | −0.03155 | −0.04121 |
| FFR | 0.00000 | −0.05128 | −0.00172 | −0.00206 | 0.00000 | −0.00627 |
| EPU | 0.00000 | 0.00000 | 0.00747 | 0.00000 | 0.00000 | 0.00000 |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.4675 *** | −0.1141 | −0.7912 * | −0.4358 *** | −0.2475 * | −0.7289 *** | |
| (0.1506) | (0.2416) | (0.4619) | (0.1685) | (0.1450) | (0.2204) | |
| −0.0350 | −0.0010 | −0.1585 *** | 0.0251 | −0.0992 ** | −0.1089 ** | |
| (0.0499) | (0.0572) | (0.0601) | (0.0489) | (0.0491) | (0.0525) | |
| 0.5264 *** | 0.1282 | 0.7816 | 0.4585 ** | 0.2081 | 0.7805 *** | |
| (0.1727) | (0.2738) | (0.5049) | (0.2032) | (0.1660) | (0.2510) | |
| 0.0555 | 0.0856 | 0.0417 | 0.0980 ** | 0.0488 | 0.0396 | |
| (0.0891) | (0.0825) | (0.0796) | (0.0415) | (0.0575) | (0.0669) | |
| −0.3571 *** | −0.2048 *** | −0.3597 *** | −0.2482 *** | −0.2984 *** | −0.4509 *** | |
| (0.0719) | (0.0761) | (0.1195) | (0.0719) | (0.0689) | (0.0735) | |
| Variance Equation | ||||||
| 0.7580 *** | 0.1202 ** | −0.4421 ** | 0.1502 *** | 1.0254 *** | 0.9304 *** | |
| (0.0680) | (0.0472) | (0.1838) | (0.0039) | (0.2319) | (0.1406) | |
| ARCH () | 0.3373 *** | 0.0819 ** | 0.3985 ** | 0.1696 *** | 0.2683 *** | 0.0889 |
| (0.0772) | (0.0327) | (0.1862) | (0.0324) | (0.0939) | (0.0679) | |
| GARCH () | −0.1310 *** | 0.7165 *** | −0.0340 | 0.7091 *** | −0.2371 | 0.1826 |
| (0.0461) | (0.0795) | (0.1689) | (0.0240) | (0.1661) | (0.1130) | |
| 0.0566 | −0.0515 | 0.1132 | −0.0196 | 0.0629 | 0.0142 | |
| (0.1007) | (0.0609) | (0.1550) | (0.0182) | (0.0635) | (0.0512) | |
| 0.2796 *** | 0.2581 *** | 0.3316 * | 0.0888 *** | 0.3164 *** | 0.0753 | |
| (0.0511) | (0.0645) | (0.1930) | (0.0302) | (0.1004) | (0.1232) | |
| TGARCH () | 0.1501 * | |||||
| (0.0873) | ||||||
| EGARCH () | 0.0393 | |||||
| (0.0979) | ||||||
| Variance Equation | ||||||
| APARCH () | 0.1035 | |||||
| (0.1412) | ||||||
| (A)CGARCH () | 0.9480 *** | 0.9361 *** | ||||
| (0.0323) | (0.0239) | |||||
| (A)CGARCH () | 0.0368 | 0.0057 | ||||
| (0.0332) | (0.0235) | |||||
| ACGARCH () | 0.3570 *** | |||||
| (0.1112) | ||||||
| AIC | 2.6756 | 2.6935 | 2.6392 | 2.6934 | 2.5995 | 2.6234 |
| SIC | 2.7838 | 2.8125 | 2.7690 | 2.8124 | 2.7401 | 2.7748 |
| LL | −470.27 | −472.49 | −461.73 | −472.46 | −453.60 | −456.90 |
| JB stat | 33.30 | 33.54 | 38.92 | 26.12 | 43.18 | 64.73 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 1.9968 | 0.3147 | 0.0286 | 0.3058 | 1.2229 | 0.7757 |
| [0.0785] | [0.9040] | [0.8660] | [0.9093] | [0.2978] | [0.5678] | |
| 1.3503 | 0.4346 | 1.9568 | 0.0000 | 0.8557 | 0.3332 | |
| [0.2450] | [0.5100] | [0.0845] | [0.9950] | [0.3550] | [0.5640] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.2030 | −0.3726 ** | −0.2401 *** | −0.3679 *** | −0.2793 *** | −0.3668 *** | |
| (0.1602) | (0.1896) | (0.0798) | (0.0911) | (0.0770) | (0.0968) | |
| −0.0284 | −0.0520 | −0.0999 ** | −0.2151 *** | −0.1066 ** | −0.1031 ** | |
| (0.0641) | (0.0639) | (0.0413) | (0.0400) | (0.0434) | (0.0440) | |
| 0.1545 | 0.3915 * | 0.1310 | 0.4189 *** | 0.1809 * | 0.3061 ** | |
| (0.2028) | (0.2380) | (0.1067) | (0.1167) | (0.1089) | (0.1267) | |
| −0.0228 | 0.0050 | −0.0185 | −0.0092 | −0.0207 | −0.0276 | |
| (0.0238) | (0.0496) | (0.0257) | (0.0330) | (0.0233) | (0.0306) | |
| −0.1985 ** | −0.2365 *** | −0.1177 *** | −0.3163 *** | −0.1161 ** | −0.1662 ** | |
| (0.0900) | (0.0862) | (0.0457) | (0.0584) | (0.0453) | (0.0536) | |
| Variance Equation | ||||||
| 0.0587 *** | 0.0840 *** | −0.2302 *** | 0.2145 *** | 0.5443 *** | 0.5788 *** | |
| (0.0082) | (0.0118) | (0.0583) | (0.0303) | (0.1832) | (0.2172) | |
| ARCH () | 0.1516 *** | 0.2374 *** | 0.2668 *** | −0.0512 *** | 0.2191 *** | 0.1181 * |
| (0.0226) | (0.0376) | (0.0816) | (0.0080) | (0.0143) | (0.0661) | |
| GARCH () | 0.7970 *** | 0.7493 *** | 0.9089 *** | 0.8111 *** | −0.1932 | −0.0921 |
| (0.0195) | (0.0245) | (0.0298) | (0.0328) | (0.1199) | (0.1309) | |
| −0.0881 *** | −0.0980 *** | −0.2875 * | −0.1153 *** | −0.0532 *** | −0.0402 | |
| (0.0230) | (0.0107) | (0.1482) | (0.0144) | (0.0204) | (0.0327) | |
| 0.2080 *** | 0.1444 ** | 0.2364 | −0.0082 | 0.1896 *** | 0.2470 *** | |
| (0.0557) | (0.0663) | (0.1602) | (0.0154) | (0.0537) | (0.0764) | |
| TGARCH () | −0.1718 *** | |||||
| (0.0431) | ||||||
| EGARCH () | 0.0857 | |||||
| (0.0550) | ||||||
| APARCH () | 0.9995 *** | |||||
| (0.0125) | ||||||
| Variance Equation | ||||||
| (A)CGARCH () | 0.9788 *** | 0.9864 *** | ||||
| (0.0120) | (0.0082) | |||||
| (A)CGARCH () | 0.0425 *** | 0.0204 *** | ||||
| (0.0017) | (0.0078) | |||||
| ACGARCH () | 0.2784 *** | |||||
| (0.0693) | ||||||
| AIC | 2.5585 | 2.5409 | 2.3566 | 2.7027 | 2.3191 | 2.3491 |
| SIC | 2.6666 | 2.6599 | 2.4864 | 2.8217 | 2.4597 | 2.5006 |
| LL | −449.24 | −445.10 | −411.01 | −474.13 | −403.27 | −407.67 |
| JB stat | 432.02 | 314.41 | 511.96 | 514.13 | 703.90 | 822.11 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.9767 | 0.5925 | 0.6531 | 5.9086 | 1.2792 | 2.6045 |
| [0.4319] | [0.7057] | [0.6594] | [0.0000] | [0.2723] | [0.0249] | |
| 3.1287 | 1.6729 | 1.5658 | 18.7030 | 0.1352 | 0.899 | |
| [0.077] | [0.1960] | [0.2110] | [0.0000] | [0.7130] | [0.343] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.6232 *** | −1.0192 *** | −0.4045 ** | −1.1033 *** | −0.2813 * | −0.2343 * | |
| (0.2298) | (0.1967) | (0.1723) | (0.2288) | (0.1500) | (0.1366) | |
| −0.1056 | −0.0959 | −0.0678 | −0.1104 ** | −0.0692 | −0.0482 | |
| (0.0729) | (0.0731) | (0.0547) | (0.0452) | (0.0531) | (0.0527) | |
| 0.6630 ** | 1.1014 *** | 0.3151 | 1.2664 *** | 0.1618 | 0.1037 | |
| (0.2739) | (0.2369) | (0.2099) | (0.2646) | (0.1801) | (0.1631) | |
| 0.0914 * | 0.1226 ** | 0.0521 | 0.1622 *** | 0.0500 | 0.0340 | |
| (0.0505) | (0.0502) | (0.0452) | (0.0534) | (0.0423) | (0.0455) | |
| −0.4645 *** | −0.4766 *** | −0.4100 *** | −0.3608 *** | −0.4021 *** | −0.3883 *** | |
| (0.0982) | (0.0912) | (0.0636) | (0.0680) | (0.0566) | (0.0560) | |
| Variance Equation | ||||||
| 0.3829 *** | 0.5656 *** | −0.4941 *** | 0.5197 *** | 0.9669 *** | 1.0479 *** | |
| (0.0762) | (0.0811) | (0.1333) | (0.0654) | (0.3132) | (0.4068) | |
| ARCH () | 0.3385 *** | 0.2685 *** | 0.5618 *** | 0.2139 *** | 0.2204 * | 0.2430 |
| (0.0902) | (0.0781) | (0.1903) | (0.0318) | (0.1331) | (0.1615) | |
| GARCH () | 0.2665 ** | −0.0186 *** | 0.6070 *** | 0.2823 *** | −0.0631 | −0.0331 |
| (0.1088) | (0.0888) | (0.1368) | (0.0734) | (0.3172) | (0.3434) | |
| −0.1618 *** | −0.1902 *** | −0.3808 *** | −0.0892 *** | −0.1414 *** | −0.1363 *** | |
| (0.0320) | (0.0223) | (0.1130) | (0.0164) | (0.0469) | (0.0389) | |
| 0.1131 | 0.0857 | 0.1089 | 0.0169 | 0.1348 | 0.1493 | |
| (0.1042) | (0.0908) | (0.1583) | (0.0215) | (0.1561) | (0.1572) | |
| TGARCH () | 0.3171 * | |||||
| (0.1808) | ||||||
| EGARCH () | −0.0788 | |||||
| (0.1228) | ||||||
| APARCH () | −0.1077 | |||||
| (0.1418) | ||||||
| (A)CGARCH () | 0.8328 *** | 0.8829 *** | ||||
| (0.1183) | (0.0847) | |||||
| Variance Equation | ||||||
| (A)CGARCH () | 0.1400 | 0.1309 | ||||
| (0.1092) | (0.0896) | |||||
| ACGARCH () | −0.0529 | |||||
| (0.1951) | ||||||
| AIC | 2.6339 | 2.6134 | 2.5097 | 2.6367 | 2.5085 | 2.5221 |
| SIC | 2.7522 | 2.7436 | 2.6517 | 2.7668 | 2.6622 | 2.6878 |
| LL | −408.79 | −404.54 | −387.05 | −408.23 | −385.84 | −387.02 |
| JB stat | 137.23 | 133.54 | 94.10 | 80.45 | 138.93 | 138.92 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.1644 | 0.1136 | 0.0713 | 0.1375 | 0.1831 | 0.1669 |
| [0.9754] | [0.9893] | [0.9964] | [0.9835] | [0.9689] | [0.9746] | |
| 0.3046 | 0.1472 | 0.0689 | 0.0689 | 0.4737 | 0.3910 | |
| [0.5810] | [0.7010] | [0.7930] | [0.7930] | [0.4910] | [0.5320] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.2591 ** | −0.3346 ** | −0.2956 * | −0.0290 | 0.0143 | −0.0695 | |
| (0.1023) | (0.1305) | (0.1647) | (0.1509) | (0.1212) | (0.0986) | |
| −0.0041 | −0.0641 | −0.1441 *** | −0.0292 | −0.1207 *** | −0.1217 *** | |
| (0.0637) | (0.0622) | (0.0275) | (0.0334) | (0.0399) | (0.0433) | |
| 0.2570 * | 0.3780 ** | 0.1754 | 0.0390 | −0.1744 | −0.0747 | |
| (0.1438) | (0.1828) | (0.1950) | (0.1869) | (0.1460) | (0.1267) | |
| 0.0253 | −0.0189 | −0.1171 ** | −0.1266 ** | −0.0650 | −0.0460 | |
| (0.0801) | (0.0874) | (0.0522) | (0.0573) | (0.0450) | (0.0508) | |
| −0.2611 *** | −0.2991 *** | −0.3790 *** | −0.2443 *** | −0.3271 *** | −0.3104 *** | |
| (0.0809) | (0.0774) | (0.0459) | (0.0825) | (0.0494) | (0.0545) | |
| Variance Equation | ||||||
| 0.0965 *** | 0.1537 *** | −0.6286 *** | 0.0822 *** | 0.6497 *** | 0.5583 *** | |
| (0.0323) | (0.0344) | (0.1741) | (0.0269) | (0.1592) | (0.1470) | |
| ARCH () | 0.2172 *** | 0.3231 *** | 0.3897 ** | 0.1139 *** | 0.0748 | 0.0768 * |
| (0.0530) | (0.0713) | (0.1734) | (0.0280) | (0.0718) | (0.0453) | |
| GARCH () | 0.6795 *** | 0.6257 *** | −0.3831 *** | 0.8302 *** | −0.3088 | 0.6554 *** |
| (0.0667) | (0.0665) | (0.1172) | (0.0458) | (0.7181) | (0.1820) | |
| 0.1961 *** | 0.2489 *** | 0.2828 ** | 0.0649 *** | 0.1090 ** | 0.1565 *** | |
| (0.0395) | (0.0299) | (0.1221) | (0.0100) | (0.0503) | (0.0283) | |
| 0.0853 | 0.0959 | 0.1969 | 0.0597 ** | 0.2085 *** | 0.2068 ** | |
| (0.0888) | (0.0979) | (0.1561) | (0.0261) | (0.0751) | (0.0978) | |
| TGARCH () | −0.2961 *** | |||||
| (0.0833 | ||||||
| EGARCH () | 0.1859 | |||||
| (0.1357) | ||||||
| APARCH () | −0.6354 *** | |||||
| (0.1680) | ||||||
| (A)CGARCH () | 0.9553 *** | 0.9822 *** | ||||
| (0.0248) | (0.0010) | |||||
| (A)CGARCH () | 0.0355 * | −0.0063 | ||||
| (0.0207) | (0.0089) | |||||
| ACGARCH () | 0.1005 | |||||
| (0.1129) | ||||||
| AIC | 2.5709 | 2.5505 | 2.4590 | 2.5828 | 2.4463 | 2.4261 |
| SIC | 2.6791 | 2.6694 | 2.5888 | 2.7018 | 2.5869 | 2.5775 |
| LL | −451.48 | −446.81 | −429.39 | −452.61 | −426.11 | −421.48 |
| JB stat | 163.564 | 144.089 | 1134.740 | 162.583 | 372.786 | 171.846 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.6315 | 0.9938 | 4.6074 | 1.1945 | 0.9658 | 0.8211 |
| [0.6758] | [0.4214] | [0.0004] | [0.3114] | [0.4387] | [0.5353] | |
| 0.1111 | 0.3153 | 0.1323 | 0.1113 | 0.7483 | 0.1809 | |
| [0.7390] | [0.5740] | [0.7160] | [0.7390] | [0.3870] | [0.6710] |
Appendix B. Recovery Period Analyses
| Variable | Bitcoin | Ethereum | Ripple | Bitcoin Cash | Litecoin |
|---|---|---|---|---|---|
| €/$ | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Gold | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| NYSE | 0.00000 | 0.00000 | 0.00000 | −0.01234 | 0.00000 |
| Oil price | 0.00000 | 0.00000 | 0.00000 | −0.01177 | 0.00000 |
| GTrends | 0.12767 | 0.07840 | 0.08463 | 0.10887 | 0.06412 |
| China | 0.00000 | 0.03764 | 0.00000 | 0.00000 | 0.00097 |
| VIX | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| FFR | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| EPU | 0.00000 | 0.00000 | 0.00168 | 0.00000 | 0.03764 |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| 0.4170 *** | 0.2853 * | −0.2034 *** | −0.1562 *** | −0.2102 * | −0.2223 * | |
| (0.1128) | (0.1701) | (0.0447) | (0.0464) | (0.1187) | (0.1182) | |
| −0.0402 | −0.0915 ** | −0.1196 ** | −0.1488 ** | −0.1289 ** | −0.1189 ** | |
| (0.0487) | (0.0455) | (0.0496) | (0.0738) | (0.0542) | (0.0469) | |
| −0.5829 *** | −0.4114 * | 0.2869 *** | 0.1657 | 0.2905 * | 0.2947 * | |
| (0.1413) | (0.2227) | (0.0972) | (0.1109) | (0.1610) | (0.1582) | |
| 0.3929 *** | 0.3087 *** | 0.1316 *** | 0.0774 * | 0.2140 *** | 0.1964 *** | |
| (0.0703) | (0.0753) | (0.0386) | (0.0466) | (0.0493) | (0.0493) | |
| Variance Equation | ||||||
| 0.2883 *** | 0.2987 *** | 0.0164 *** | 0.0061 | 0.6080 *** | 0.5983 *** | |
| (0.0355) | (0.0380) | (0.0061) | (0.0044) | (0.2184) | (0.1820) | |
| ARCH () | 0.1649 *** | 0.1241 *** | −0.0385 *** | 0.0307 *** | −0.0265 | −0.0940 |
| (0.0317) | (0.0340) | (0.0098) | (0.0092) | (0.0927) | (0.0915) | |
| GARCH () | 0.4425 *** | 0.4513 *** | 0.9953 *** | 0.9723 *** | −0.3160 | 0.8987 *** |
| (0.0500) | (0.0467) | (0.0057) | (0.0097) | (2.6136) | (0.3353) | |
| 0.4401 *** | 0.4229 *** | 0.5865 *** | 0.1269 *** | 0.2188 *** | 0.2512 *** | |
| (0.0378) | (0.0314) | (0.0909) | (0.0144) | (0.0618) | (0.0658) | |
| TGARCH () | −0.0374 | |||||
| (0.0534) | ||||||
| EGARCH () | −0.0824 | |||||
| (0.0523) | ||||||
| APARCH () | 0.9463 *** | |||||
| (0.2114) | ||||||
| Variance Equation | ||||||
| (A)CGARCH () | 0.9338 *** | 0.9356 *** | ||||
| (0.0286) | (0.0260) | |||||
| (A)CGARCH () | 0.0751 | 0.0699 | ||||
| (0.0478) | (0.0936) | |||||
| ACGARCH () | 0.0303 | |||||
| (0.0929) | ||||||
| AIC | 2.4232 | 2.4650 | 2.0630 | 2.1581 | 2.2378 | 2.2266 |
| SIC | 2.5406 | 2.5971 | 2.2098 | 2.2902 | 2.3993 | 2.4027 |
| LL | −277.93 | −281.86 | −233.44 | −245.65 | −253.06 | −250.73 |
| JB stat | 16.16 | 35.23 | 297.92 | 11.07 | 22.71 | 24.12 |
| [0.0003] | [0.0000] | [0.0000] | [0.0039] | [0.0000] | [0.0000] | |
| ARCH(5) | 2.6733 | 6.4518 | 0.4024 | 1.0228 | 0.1956 | 1.4488 |
| [0.0227] | [0.0000] | [0.8469] | [0.4050] | [0.9640] | [0.2078] | |
| 0.7854 | 0.3883 | 1.5919 | 0.4933 | 0.1204 | 0.1141 | |
| [0.3760] | [0.5330] | [0.2070] | [0.4820] | [0.7290] | [0.7350] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.2035 *** | −0.2195 *** | −0.1775 ** | −0.1501 | −0.2376 ** | −0.2310 ** | |
| (0.0785) | (0.0427) | (0.0814) | (0.0895) | (0.1130) | (0.1067) | |
| −0.1447 * | −0.1403 * | −0.1867 *** | −0.1609 ** | −0.1786 *** | −0.1743 *** | |
| (0.0791) | (0.0730) | (0.0462) | (0.0662) | (0.0499) | (0.0459) | |
| 0.2071 * | 0.2351 ** | 0.1266 | 0.1640 | 0.2266 | 0.1975 | |
| (0.1105) | (0.0984) | (0.1187) | (0.1365) | (0.1448) | (0.1352) | |
| 0.1189 * | 0.1065 * | 0.0666 | 0.1046 * | 0.1393 *** | 0.1103 ** | |
| (0.0678) | (0.0636) | (0.0436) | (0.0568) | (0.0466) | (0.0469) | |
| Variance Equation | ||||||
| 0.0379 ** | 0.0266 * | 0.0219 * | −0.0117 * | 0.5357 *** | 0.5919 *** | |
| (0.0179) | (0.0152) | (0.0127) | (0.0060) | (0.0836) | (0.2265) | |
| ARCH () | 0.0907 *** | 0.0569 ** | −0.0387 *** | 0.0153 | 0.0805 | 0.0610 |
| (0.0296) | (0.0232) | (0.0141) | (0.0259) | (0.1146) | (0.0938) | |
| GARCH () | 0.8586 *** | 0.8947 *** | 1.0114 *** | 1.0003 *** | 0.2420 | 0.8529 *** |
| (0.0371) | (0.0334) | (0.0064) | (0.0185) | (0.6634) | (0.2367) | |
| 0.2575 *** | 0.2397 *** | 0.3568 *** | 0.0824 *** | 0.1773 *** | 0.2032 *** | |
| (0.0365) | (0.0391) | (0.0660) | (0.0080) | (0.0558) | (0.0787) | |
| TGARCH () | 0.0109 | |||||
| (0.0223) | ||||||
| EGARCH () | 0.0264 | |||||
| (0.0425) | ||||||
| APARCH () | 0.8462 * | |||||
| (0.4909) | ||||||
| (A)CGARCH () | 0.9785 *** | 0.9730 *** | ||||
| (0.0018) | (0.0144) | |||||
| (A)CGARCH () | −0.0123 | −0.0055 | ||||
| (0.0219) | (0.0553) | |||||
| ACGARCH () | −0.0392 | |||||
| (0.0842) | ||||||
| AIC | 2.6108 | 2.6056 | 2.3896 | 2.4999 | 2.4252 | 2.4305 |
| SIC | 2.7282 | 2.7377 | 2.5364 | 2.6320 | 2.5867 | 2.6066 |
| LL | −300.07 | −298.46 | −271.98 | −285.98 | −275.18 | −274.79 |
| JB stat | 54.14 | 52.86 | 191.67 | 13.41 | 34.27 | 40.47 |
| [0.0000] | [0.0000] | [0.0000] | [0.0012] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.2800 | 0.1706 | 2.1382 | 0.3198 | 0.6598 | 0.3411 |
| [0.9238] | [0.9733] | [0.0619] | [0.9008] | [0.6543] | [0.8876] | |
| 0.2520 | 0.0423 | 8.5346 | 0.1539 | 0.0277 | 0.0224 | |
| [0.6160] | [0.8370] | [0.0030] | [0.6950] | [0.8680] | [0.8810] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.1765 *** | −0.2225 *** | −0.1429 *** | −0.1293 *** | −0.2057 * | −0.2234 ** | |
| (0.0671) | (0.0342) | (0.0554) | (0.0463) | (0.1109) | (0.1027) | |
| −0.1838 *** | −0.1641 ** | −0.2038 *** | −0.2528 *** | −0.2280 *** | −0.2265 *** | |
| (0.0692) | (0.0776) | (0.0514) | (0.0442) | (0.0623) | (0.0585) | |
| 0.2086 * | 0.2670 *** | 0.1651 ** | 0.0602 | 0.2838 | 0.3197 * | |
| (0.1123) | (0.0797) | (0.0841) | (0.0438) | (0.1767) | (0.1701) | |
| 0.1014 | 0.0832 | 0.0664 | 0.0131 | 0.1272 *** | 0.1071 ** | |
| (0.0695) | (0.0594) | (0.0434) | (0.0533) | (0.0468) | (0.0469) | |
| Variance Equation | ||||||
| 0.0673 *** | 0.1285 *** | 0.0532 *** | 0.0256 ** | 0.3265 *** | 0.2899 *** | |
| (0.0194) | (0.0296) | (0.0008) | (0.0115) | (0.0714) | (0.0056) | |
| ARCH () | 0.0813 ** | 0.0992 | −0.0952 *** | 0.1123 *** | 0.1259 * | 0.0367 |
| (0.0362) | (0.0666) | (0.0046) | (0.0291) | (0.0698) | (0.0665) | |
| GARCH () | 0.8110 *** | 0.6376 *** | 0.9899 *** | 0.8918 *** | 0.4824 | 0.6058 |
| (0.0467) | (0.0596) | (0.0073) | (0.0260) | (0.3141) | (0.3766) | |
| 0.2843 *** | 0.3420 *** | 0.5179 *** | 0.1591 *** | 0.1469 *** | 0.1366 *** | |
| (0.0317) | (0.0374) | (0.0458) | (0.0164) | (0.0327) | (0.0313) | |
| TGARCH () | 0.1726 * | |||||
| (0.1000) | ||||||
| EGARCH () | −0.1243 *** | |||||
| (0.0447) | ||||||
| APARCH () | 0.7351 *** | |||||
| (0.1863) | ||||||
| (A)CGARCH () | 0.9378 *** | 0.9303 *** | ||||
| (0.0037) | (0.0237) | |||||
| (A)CGARCH () | 0.0327 | 0.0363 | ||||
| (0.0287) | (0.0354) | |||||
| ACGARCH () | 0.0551 | |||||
| (0.0869) | ||||||
| AIC | 2.4175 | 2.4266 | 2.1666 | 2.2814 | 2.3181 | 2.2987 |
| SIC | 2.5349 | 2.5587 | 2.3134 | 2.4135 | 2.4795 | 2.4748 |
| LL | −277.27 | −277.34 | −245.66 | −260.21 | −262.53 | −259.24 |
| JB stat | 79.59 | 70.53 | 362.77 | 6.93 | 147.43 | 173.41 |
| [0.0000] | [0.0000] | [0.0000] | [0.0313] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.6538 | 0.7382 | 3.5939 | 0.8075 | 0.3923 | 0.4899 |
| [0.6589] | [0.5956] | [0.0038] | [0.5453] | [0.8538] | [0.7837] | |
| 0.5331 | 0.0374 | 11.4740 | 0.5719 | 0.0107 | 0.3417 | |
| [0.4650] | [0.8470] | [0.0010] | [0.4490] | [0.9170] | [0.5590] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.2111 | −0.2262 | −0.5563 *** | −0.1677 | −0.4240 *** | −0.4109 *** | |
| (0.1840) | (0.1725) | (0.1284) | (0.1157) | (0.0862) | (0.1056) | |
| −0.1564 * | −0.1327 | −0.1912 *** | −0.1406 *** | −0.1818 *** | −0.1446 *** | |
| (0.0900) | (0.0973) | (0.0240) | (0.0542) | (0.0306) | (0.0379) | |
| 0.1940 | 0.2124 | 0.6017 *** | 0.1159 | 0.3802 *** | 0.4311 *** | |
| (0.2768) | (0.2668) | (0.1799) | (0.1966) | (0.1062) | (0.1458) | |
| 0.1499 *** | 0.1352 *** | −0.0638 | 0.0233 | −0.0005 | 0.0386 | |
| (0.0494) | (0.0500) | (0.0459) | (0.0695) | (0.0173) | (0.0388) | |
| Variance Equation | ||||||
| 0.2277 *** | 0.1930 *** | −0.5416 *** | 0.0575 *** | 0.6733 *** | 0.6241 *** | |
| (0.0436) | (0.0387) | (0.1130) | (0.0121) | (0.2453) | (0.1464) | |
| ARCH () | 0.3782 *** | 0.2911 *** | 0.4422 *** | 0.0406 ** | 0.2773 ** | 0.0662 |
| (0.0804) | (0.0596) | (0.1066) | (0.0217) | (0.1270) | (0.0821) | |
| GARCH () | 0.3272 *** | 0.3941 *** | 0.5845 *** | 0.9059 *** | −0.0356 | −0.1009 |
| (0.0851) | (0.0873) | (0.0846) | (0.0186) | (0.1541) | (0.1195) | |
| 0.2839 *** | 0.2778 *** | 0.6286 *** | 0.1217 *** | 0.2037 *** | 0.1853 *** | |
| (0.0345) | (0.0344) | (0.1053) | (0.0200) | (0.0771) | (0.0631) | |
| TGARCH () | 0.1419 | |||||
| (0.1403) | ||||||
| EGARCH () | −0.0410 | |||||
| (0.0710) | ||||||
| APARCH () | 0.9941 *** | |||||
| (0.0675) | ||||||
| (A)CGARCH () | 0.8414 *** | 0.8337 *** | ||||
| (0.0656) | (0.0674) | |||||
| (A)CGARCH () | 0.0569 | 0.0021 | ||||
| (0.0937) | (0.0319) | |||||
| ACGARCH () | 0.3304 ** | |||||
| (0.1424) | ||||||
| AIC | 2.3033 | 2.3107 | 2.0289 | 2.1924 | 2.0589 | 2.0692 |
| SIC | 2.4207 | 2.4428 | 2.1757 | 2.3245 | 2.2204 | 2.2453 |
| LL | −263.79 | −263.67 | −229.41 | −249.70 | −231.95 | −232.17 |
| JB stat | 43.14 | 46.60 | 126.81 | 50.92 | 93.88 | 114.54 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 1.1687 | 1.2851 | 0.4671 | 0.4418 | 0.7987 | 0.4301 |
| [0.3255] | [0.2712] | [0.8005] | [0.8190] | [0.5516] | [0.8274] | |
| 0.8169 | 0.4563 | 0.2478 | 0.6182 | 1.0492 | 0.3069 | |
| [0.3660] | [0.4990] | [0.6190] | [0.4320] | [0.3060] | [0.5800] |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.0713 | −0.0241 | −0.0111 | −0.0584 | −0.0675 | −0.1011 *** | |
| (0.0611) | (0.0679) | (0.0714) | (0.0484) | (0.0687) | (0.0128) | |
| −0.0973 * | −0.0140 | 0.5668 | −0.0054 | −0.0309 | −0.1239 ** | |
| (0.0526) | (0.0739) | (0.4937) | (0.0455) | (0.0718) | (0.0574) | |
| 0.0871 | 0.0587 | −0.0238 | 0.0402 | 0.0155 | 0.0749 | |
| (0.0586) | (0.0712) | (0.0959) | (0.0680) | (0.0633) | (0.0555) | |
| Variance Equation | ||||||
| 0.2765 | 0.1619 ** | −0.1000 * | 0.0442 *** | 0.9047 *** | 1.0285 *** | |
| (0.1764) | (0.0636) | (0.0525) | (0.0171) | (0.0457) | (0.1838) | |
| ARCH () | 0.1750 | 0.0022 | 0.0915 | −0.0207 | 0.0910 ** | 0.0594 |
| (0.1256) | (0.0199) | (0.0654) | (0.0229) | (0.0367) | (0.0851) | |
| GARCH () | 0.5767 *** | 0.7714 *** | 0.8115 *** | 0.9664 *** | 0.7361 *** | 0.4306 |
| (0.2034) | (0.0808) | (0.0876) | (0.0273) | (0.1177) | (0.2625) | |
| 0.3130 ** | 0.4084 *** | 0.3061 *** | 0.0538 *** | 0.2760 *** | 0.2720 *** | |
| (0.1417) | (0.0825) | (0.0965) | (0.0155) | (0.0561) | (0.0830) | |
| TGARCH () | 0.1343 | |||||
| (0.0874) | ||||||
| EGARCH () | −0.1216 * | |||||
| (0.0678) | ||||||
| APARCH () | −0.7531 | |||||
| (1.1979) | ||||||
| (A)CGARCH () | 0.9192 | 0.9524 *** | ||||
| (0.0102 | (0.0216) | |||||
| (A)CGARCH () | −0.0754 *** | −0.0314 | ||||
| (0.0182) | (0.0269) | |||||
| ACGARCH () | 0.3516 ** | |||||
| (0.1474) | ||||||
| AIC | 2.6401 | 2.7415 | 2.7525 | 2.7384 | 2.6236 | 2.5969 |
| SIC | 2.7575 | 2.8589 | 2.8846 | 2.8558 | 2.7703 | 2.7584 |
| LL | −303.53 | −315.50 | −315.80 | −315.13 | −299.58 | −295.44 |
| JB stat | 456.38 | 180.95 | 296.19 | 233.12 | 141.80 | 135.54 |
| [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | [0.0000] | |
| ARCH(5) | 0.1269 | 0.0971 | 0.1219 | 0.1676 | 0.0445 | 0.1827 |
| [0.9862] | [0.9925] | [0.9874] | [0.9743] | [0.9988] | [0.9689] | |
| 0.1793 | 0.0284 | 0.0187 | 0.0178 | 0.0015 | 0.2114 | |
| [0.6720] | [0.8660] | [0.8910] | [0.8940] | [0.9690] | [0.6460] |
References
- Aalborg, Halvor Aarhus, Peter Molnár, and Jon Erik de Vries. 2019. What can explain the price, volatility and trading volume of bitcoin? Finance Research Letters 29: 255–65. [Google Scholar] [CrossRef]
- Akyildirim, Erdinc, Shaen Corbet, Paraskevi Katsiampa, Neil Kellard, and Ahmet Sensoy. 2019. The development of bitcoin futures: Exploring the interactions between cryptocurrency derivatives. Finance Research Letters. In press. [Google Scholar] [CrossRef]
- Ardia, David, Keven Bluteau, and Maxime Rüede. 2019. Regime changes in bitcoin garch volatility dynamics. Finance Research Letters 29: 266–71. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bouoiyour, Jamal, and Refk Selmi. 2015. What does bitcoin look like? Annals of Economics and Finance 16: 449–92. [Google Scholar]
- Bouoiyour, Jamal, and Refk Selmi. 2016. Bitcoin: A beginning of a new phase. Economics Bulletin 36: 1430–40. [Google Scholar]
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017a. On the hedge and safe haven properties of bitcoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Bouri, Elie, Rangan Gupta, Aviral Kumar Tiwari, and David Roubaud. 2017b. Does bitcoin hedge global uncertainty? Evidence from wavelet-based quantile-in-quantile regressions. Finance Research Letters 23: 87–95. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2019. Volatility estimation for bitcoin: Replication and robustness. International Economics 157: 23–32. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, Maurice Peat, and Samuel Vigne. 2018. Bitcoin futures—What use are they? Economics Letters 172: 23–27. [Google Scholar] [CrossRef]
- Dastgir, Shabbir, Ender Demir, Gareth Downing, Giray Gozgor, and Chi Keung Marco Lau. 2019. The causal relationship between bitcoin attention and bitcoin returns: Evidence from the copula-based granger causality test. Finance Research Letters 28: 160–64. [Google Scholar] [CrossRef]
- Demir, Ender, Giray Gozgor, Chi Keung Marco Lau, and Samuel A. Vigne. 2018. Does economic policy uncertainty predict the bitcoin returns? an empirical investigation. Finance Research Letters 26: 145–49. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W.J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016a. Bitcoin, gold and the dollar—A garch volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016b. Hedging capabilities of bitcoin. Is it the virtual gold? Finance Research Letters 16: 139–44. [Google Scholar] [CrossRef]
- Engle, Robert F., and Gary G.J. Lee. 1993. A Permanent and Transitory Component Model of Stock Return Volatility; Technical report. San Diego: Department of Economics.
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the relation between the expected value and the volatility of the nominal excess return on stocks. The Journal of Finance 48: 1779–1801. [Google Scholar] [CrossRef]
- Hale, Galina, Arvind Krishnamurthy, Marianna Kudlyak, and Patrick Shultz. 2018. How futures trading changed bitcoin prices. FRBSF Economic Letter 12: 1–5. [Google Scholar]
- Katsiampa, Paraskevi. 2017. Volatility estimation for bitcoin: A comparison of garch models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2018. Volatility co-movement between bitcoin and ether. Finance Research Letters 30: 221–27. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2019. An empirical investigation of volatility dynamics in the cryptocurrency market. Research in International Business and Finance 50: 322–35. [Google Scholar] [CrossRef]
- Kim, Wonse, Junseok Lee, and Kyungwon Kang. 2019. The effects of the introduction of bitcoin futures on the volatility of bitcoin returns. Finance Research Letters 33: 101204. [Google Scholar] [CrossRef]
- Köchling, Gerrit, Janis Müller, and Peter N. Posch. 2018. Does the introduction of futures improve the efficiency of bitcoin? Finance Research Letters 30: 367–70. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2013. Bitcoin meets google trends and wikipedia: Quantifying the relationship between phenomena of the internet era. Scientific Reports 3: 3415. [Google Scholar] [CrossRef]
- Liu, Ruozhou, Shanfeng Wan, Zili Zhang, and Xuejun Zhao. 2019. Is the introduction of futures responsible for the crash of bitcoin? Finance Research Letters. In press. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. bitcoin. org. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 21 May 2019).
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica: Journal of the Econometric Society 59: 347–70. [Google Scholar] [CrossRef]
- Pal, Debdatta, and Subrata K Mitra. 2019. Hedging bitcoin with other financial assets. Finance Research Letters 30: 30–36. [Google Scholar] [CrossRef]
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2018. On the determinants of bitcoin returns: A lasso approach. Finance Research Letters 27: 235–40. [Google Scholar] [CrossRef]
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2019. The effects of markets, uncertainty and search intensity on bitcoin returns. International Review of Financial Analysis 63: 220–42. [Google Scholar] [CrossRef]
- Panagiotidis, Theodore, Thanasis Stengos, and Orestis Vravosinos. 2020. A principal component-guided sparse regression approach for the determination of bitcoin returns. Journal of Risk and Financial Management 13: 33. [Google Scholar] [CrossRef]
- Sebastião, Helder, and Pedro Godinho. 2019. Bitcoin futures: An effective tool for hedging cryptocurrencies. Finance Research Letters 33: 101230. [Google Scholar] [CrossRef]
- Stein, Jeremy C. 1987. Informational externalities and welfare-reducing speculation. Journal of Political Economy 95: 1123–45. [Google Scholar] [CrossRef]
- Tay, J. Kenneth, Jerome Friedman, and Robert Tibshirani. 2018. Principal component-guided sparse regression. arXiv, arXiv:1810.04651. [Google Scholar]
- Wu, Shan, Mu Tong, Zhongyi Yang, and Abdelkader Derbali. 2019. Does gold or bitcoin hedge economic policy uncertainty? Finance Research Letters 31: 171–78. [Google Scholar] [CrossRef]
- Yermack, David. 2015. Is bitcoin a real currency? An economic appraisal. In Handbook of Digital Currency. Amsterdam: Elsevier, pp. 31–43. [Google Scholar]
| 1. | There are currently more than 2300 currencies worldwide suggested by coinmarketcap.com as of the date of this study, 18 August 2019. Bitcoin is followed by Ethereum (ETH), Ripple (XRP), Bitcoin Cash (BHC) and Litecoin (LTC), in order, according to market capitalization. |
| 2. | It is constituting more than 65% of the total market capitalization of 250 billion US $, as of 18 August 2019. |
| 3. | This is the listing date of the first Bitcoin futures market by the Chicago Board Options Exchange (CBOE). However, CBOE has announced to stop listing Bitcoin futures by March 2019. Chicago Mercantile Exchange (CME) has launched Bitcoin futures market by 10 December 2017. |
| 4. | The dataset is available on demand. |
| 5. | Top 5 cryptocurrencies are selected according to their market capitalization as of 18 August 2019. |
| 6. | 13 June 2017 to 7 June 2018 is the 360 days of the overall time span. |
| 7. | Hence, . |
| 8. | Unit root test results are available on demand. |
| Variable | Source | Code | Frequency | Type |
|---|---|---|---|---|
| Cryptocurrencies | coinmarketcap.com | - | daily | % change |
| €/$ | quandl.com | FRED/DEXUSEU | daily | % change |
| Gold | quandl.com | WGC/GOLD_DAILY_USD | daily | % change |
| NYSE | quandl.com | BCB/7809 | daily | % change |
| Oil price | quandl.com | FRED/DCOILBRENTEU | daily | % change |
| GTrends | “gtrendsR” R package | - | daily | % change |
| China EPU | policyuncertainty.com | - | monthly | % change |
| VIX | cboe.com | - | daily | % change |
| FFR | quandl.com | FED/RIFSPFF_N_D | daily | levels |
| US EPU | policyuncertainty.com | - | daily | % change |
| BTC | e | Gold | NYSE | Oil Price | GTrends | China EPU | |
|---|---|---|---|---|---|---|---|
| Mean | 0.47 | 0.00 | 0.01 | 0.05 | 0.14 | 1.51 | 0.21 |
| Max. | 25.25 | 0.98 | 2.59 | 2.33 | 4.64 | 100.00 | 2.58 |
| Min. | −18.74 | −1.06 | −1.88 | −4.15 | −4.32 | −38.00 | −3.70 |
| Std. Dev. | 5.44 | 0.31 | 0.46 | 0.59 | 1.13 | 18.84 | 1.26 |
| Skewness | 0.24 | 0.01 | 0.58 | −1.48 | 0.00 | 1.73 | −1.09 |
| Kurtosis | 5.10 | 4.80 | 8.25 | 14.81 | 5.32 | 9.34 | 4.25 |
| JB | 61.63 ** | 43.24 ** | 384.98 ** | 1971.16 ** | 71.84 ** | 693.08 ** | 83.55 ** |
| VIX | FFR | US EPU | ETH | XRP | CASH | LTC | |
| Mean | 0.20 | 1.37 | 16.48 | 0.49 | 0.81 | 0.88 | 0.61 |
| Max. | 115.60 | 1.70 | 564.19 | 26.46 | 83.47 | 53.97 | 47.60 |
| Min. | −22.87 | 1.06 | −79.58 | −22.81 | −29.76 | −35.98 | −32.64 |
| Std. Dev. | 9.35 | 0.22 | 74.56 | 5.99 | 9.83 | 11.05 | 7.81 |
| Skewness | 6.52 | 0.41 | 2.61 | 0.10 | 3.21 | 1.41 | 1.51 |
| Kurtosis | 76.83 | 1.69 | 14.55 | 5.19 | 24.48 | 8.36 | 11.47 |
| JB | 74,722.37 ** | 31.90 ** | 2134.85 ** | 64.48 ** | 6677.14 ** | 486.74 ** | 1074.70 ** |
| Variable | Pre-30 | Post-30 | Pre-60 | Post-60 | Pre-90 | Post-90 |
|---|---|---|---|---|---|---|
| €/$ | 0.00000 | −0.02872 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Gold | −0.00165 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| NYSE | 0.00000 | 0.05370 | 0.00000 | 0.02231 | 0.00000 | 0.00000 |
| Oil price | −0.00669 | 0.00000 | 0.00000 | 0.00000 | −0.08133 | 0.00000 |
| GTrends | 0.08211 | −0.07252 | 0.14020 | −0.14161 | 0.13052 | −0.13083 |
| China | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| VIX | 0.00000 | −0.03311 | 0.00000 | −0.06211 | 0.00000 | −0.05824 |
| FFR | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| EPU | 0.00000 | 0.04333 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Variable | Pre-120 | Post-120 | Pre-150 | Post-150 | Pre-180 | Post-180 |
| €/$ | 0.00000 | 0.00000 | 0.01970 | 0.00000 | 0.00139 | 0.00000 |
| Gold | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| NYSE | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| Oil price | −0.03595 | 0.00000 | −0.01879 | 0.00000 | 0.00000 | 0.00000 |
| GTrends | 0.13613 | −0.10881 | 0.09501 | −0.08957 | 0.08510 | −0.09490 |
| China | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| VIX | 0.00000 | −0.04241 | 0.00000 | −0.04599 | 0.00000 | −0.03787 |
| FFR | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| EPU | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| GARCH | TGARCH | EGARCH | APARCH | CGARCH | ACGARCH | |
|---|---|---|---|---|---|---|
| Mean Equation | ||||||
| −0.3130 * | −0.2056 | −0.3532 | −0.3742 ** | −0.0416 | −0.4107 *** | |
| (0.1679) | (0.2005) | (0.6283) | (0.1508) | (0.1240) | (0.1140) | |
| −0.0685 | −0.0722 | −0.0674 | −0.0499 | −0.0440 | −0.0802 | |
| (0.0624) | (0.0559) | (0.0431) | (0.0562) | (0.0550) | (0.0513) | |
| 0.3772 * | 0.2207 | 0.3676 | 0.4128 ** | 0.0489 | 0.4921 *** | |
| (0.2065) | (0.2474) | (0.6946) | (0.1998) | (0.1583) | (0.1692) | |
| 0.0949 | 0.1363 | 0.0263 | 0.0854 | 0.1892 *** | 0.1227 * | |
| (0.0992) | (0.0954) | (0.1860) | (0.0955) | (0.0610) | (0.0656) | |
| −0.3078 *** | −0.2884 *** | −0.3625 *** | −0.3137 *** | −0.3172 *** | −0.3621 *** | |
| (0.0765) | (0.0781) | (0.1238) | (0.0962) | (0.0809) | (0.0690) | |
| Variance Equation | ||||||
| 0.2285 *** | 0.2020 *** | −0.3394 ** | 0.1320 *** | 0.8275 *** | 0.6977 *** | |
| (0.0663) | (0.0552) | (0.1612) | (0.0414) | (0.1541) | (0.1206) | |
| ARCH () | 0.1172 ** | 0.0547 | 0.0962 | 0.0816 *** | 0.2421 | 0.1115 |
| (0.0467) | (0.0413) | (0.1447) | (0.0232) | (0.7781) | (0.2192) | |
| GARCH () | 0.6147 *** | 0.6530 *** | −0.1126 | 0.8061 *** | 0.6998 | 0.7331 ** |
| (0.0917) | (0.0872) | (0.1403) | (0.0526) | (0.7025) | (0.3045) | |
| 0.4204 *** | 0.4145 *** | 0.6586 *** | 0.1482 *** | 0.1995 *** | 0.2764 *** | |
| (0.0827) | (0.0547) | (0.1612) | (0.0256) | (0.0424) | (0.1016) | |
| 0.1136 | 0.1314 * | 0.3069 ** | 0.0561 * | 0.2625 *** | 0.0811 | |
| (0.0703) | (0.0767) | (0.1553) | (0.0315) | (0.0884) | (0.0931) | |
| TGARCH () | 0.0914 | |||||
| (0.0715) | ||||||
| EGARCH () | −0.0804 | |||||
| (0.0952) | ||||||
| APARCH () | 0.9594 *** | |||||
| (0.1210) | ||||||
| (A)CGARCH () | 0.9601 *** | 0.7914 *** | ||||
| (0.0199) | (0.1124) | |||||
| (A)CGARCH () | −0.1511 | −0.0841 | ||||
| (0.7997) | (0.2323) | |||||
| ACGARCH () | 0.0703 | |||||
| (0.0705) | ||||||
| AIC | 2.5983 | 2.5829 | 2.6158 | 2.5616 | 2.5732 | 2.5839 |
| SIC | 2.7065 | 2.7019 | 2.7456 | 2.6806 | 2.7138 | 2.7353 |
| LL | −456.40 | −452.63 | −457.53 | −448.82 | −448.88 | −449.81 |
| JB stat | 16.5278 | 12.4547 | 16.9623 | 10.3891 | 10.7820 | 15.6510 |
| [0.0003] | [0.0020] | [0.0002] | [0.0055] | [0.0046] | [0.0004] | |
| ARCH(5) | 1.4018 | 1.5379 | 4.3657 | 0.7529 | 1.4881 | 0.7208 |
| [0.2229] | [0.1773] | [0.0007] | [0.5844] | [0.1930] | [0.6082] | |
| 4.3556 | 4.6183 | 7.9512 | 2.5770 | 3.3294 | 5.0435 | |
| [0.9300] | [0.9150] | [0.6340] | [0.9900] | [0.9730] | [0.8880] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deniz, P.; Stengos, T. Cryptocurrency Returns before and after the Introduction of Bitcoin Futures. J. Risk Financial Manag. 2020, 13, 116. https://doi.org/10.3390/jrfm13060116
Deniz P, Stengos T. Cryptocurrency Returns before and after the Introduction of Bitcoin Futures. Journal of Risk and Financial Management. 2020; 13(6):116. https://doi.org/10.3390/jrfm13060116
Chicago/Turabian StyleDeniz, Pinar, and Thanasis Stengos. 2020. "Cryptocurrency Returns before and after the Introduction of Bitcoin Futures" Journal of Risk and Financial Management 13, no. 6: 116. https://doi.org/10.3390/jrfm13060116
APA StyleDeniz, P., & Stengos, T. (2020). Cryptocurrency Returns before and after the Introduction of Bitcoin Futures. Journal of Risk and Financial Management, 13(6), 116. https://doi.org/10.3390/jrfm13060116






