News-Driven Expectations and Volatility Clustering
Abstract
1. Introduction
2. The Empirical Regularities
3. The Model
3.1. A Purely News-Driven Investment Market Model
3.2. A Purely Speculative Trend-Following Market Model
3.3. A More General Model
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Akerlof, George A., and Robert J. Shiller. 2009. Animal Spirits: How Human Psychology Drives the Economy, and why it Matters for Global Capitalism. Princeton: Princeton University Press. [Google Scholar]
- Aoki, Masanao. 2002. Open models of Share Markets with two Dominant Types of Participants. Journal of Economic Behavior & Organization 49: 199–216. [Google Scholar]
- Bachelier, Louis. 1900. Theory of Speculation. In The Random Character of Stock Market Prices. Edited by Paul H. Cootner. Cambridge: MIT Press. (In French) [Google Scholar]
- Barberis, Nicholas, and Richard Thaler. 2003. A Survey of Behavioral Finance. Handbook of the Economics of Finance 1: 1053–128. [Google Scholar]
- Basrak, Bojan, Richard A. Davis, and Thomas Mikosch. 2002. Regular Variation of GARCH Processes. Stochastic Processes and their Applications 99: 95–115. [Google Scholar] [CrossRef]
- Beekhuizen, Paul, and Winfried G. Hallerbach. 2017. Uncovering Trend Rules. The Journal of Alternative Investments 20: 28–38. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized Autoregressive Conditional Heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Ray Y. Chou, and Kenneth F. Kroner. 1992. ARCH Modeling in Finance: A Review of the Theory and Empirical Evidence. Journal of Econometrics 52: 5–59. [Google Scholar] [CrossRef]
- Bouchaud, Jean-Phillippe. 2010. Price Impact. In Encyclopedia of Quantitative Finance. Chichester: Wiley Online Library Press. [Google Scholar]
- Bouchaud, Jean-Philippe. 2011. The Endogenous Dynamics of Markets: Price Impact, Feedback Loops and IInstabilities. In Lessons from the Credit Crisis. London: Risk Publications, pp. 345–74. [Google Scholar]
- Bouchaud, Jean-Philippe, and Damien Challet. 2016. Why Have Asset Price Properties Changed so Little in 200 Years. In Econophysics and Sociophysics: Recent Progress and Future Directions. Cham: Springer, pp. 3–17. [Google Scholar]
- Buraczewski, Dariusz, Ewa Damek, and Thomas Mikosch. 2016. Stochastic Models with Power-Law Tails. New York: Springer. [Google Scholar]
- Caginalp, Gunduz, David Porter, and Vernon L. Smith. 2000. Overreaction, Momentum, Liquidity, And Price Bubbles in Laboratory and Field Asset Markets. Journal of Psychology and Financial Markets 1: 24–48. [Google Scholar] [CrossRef]
- Carvalho, Rui. 2004. The Dynamics of the Linear Random Farmer Model. International Symposia in Economic Theory and Econometrics 14: 411–30. [Google Scholar]
- Clauset, Aaron, Cosma Rohilla Shalizi, and Mark E. J. Newman. 2009. Power-law distributions in empirical data. SIAM Review 51: 661–703. [Google Scholar] [CrossRef]
- Cont, Rama. 2007. Volatility Clustering In Financial Markets: Empirical Facts and Agent-Based Models. In Long Memory In Economics. Berlin and Heidelberg: Springer, pp. 289–309. [Google Scholar]
- Cont, Rama, Arseniy Kukanov, and Sasha Stoikov. 2014. The price impact of order book events. Journal of Financial Econometrics 12: 47–88. [Google Scholar] [CrossRef]
- Cootner, Paul. H. 1964. The Random Character of Stock Market Prices. Edited by Paul H. Cootner. Cambridge: MIT Press. [Google Scholar]
- Cutler, David M., James M. Poterba, and Lawrence H. Summers. 1989. What Moves Stock Prices? The Journal of Portfolio Management 15: 4–12. [Google Scholar] [CrossRef]
- Cutler, David M., James M. Poterba, and Lawrence H. Summers. 1990. Speculative Dynamics and The Role of Feedback Traders. The American Economic Review 80: 63–68. [Google Scholar]
- Dickhaut, John, Shengle Lin, David Porter, and Vernon Smith. 2012. Commodity Durability, Trader Specialization, and Market Performance. Proceedings of the National Academy of Sciences 109: 1425–30. [Google Scholar] [CrossRef] [PubMed]
- Ding, Zhuanxin, Clive W. J. Granger, and Robert F. Engle. 1993. A Long Memory Property of Stock Market Returns and a New Model. Journal of empirical finance 1: 83–106. [Google Scholar] [CrossRef]
- Engle, Robert F. 1982. Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation. Econometrica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Tim Bollerslev. 1986. Modelling the Persistence of Conditional Variances. Econometric Reviews 5: 1–50. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1963. Mandelbrot and the Stable Paretian Hypothesis. Journal of Business 36: 420–29. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1965a. The Behavior of Stock-Market Prices. Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1965b. Random Walks in Stock Market Prices. Financial Analysts Journal 21: 55–59. [Google Scholar] [CrossRef]
- Fisher, Irving. 1933. The debt-deflation theory of great depressions. Econometrica 1: 337–57. [Google Scholar] [CrossRef]
- Gabaix, Xavier. 2009. Power Laws in Economics and Finance. Annual Reviews of Economics 1: 255–94. [Google Scholar] [CrossRef]
- Gabaix, Xaiver. 2016. Power Laws in Economics: An Introduction. The Journal of Economic Perspectives 30: 185–205. [Google Scholar] [CrossRef]
- Gjerstad, Steven D., and Vernon L. Smith. 2014. Rethinking Housing Bubbles: The Role of Household and Bank Balance Sheets in Modeling Economic Cycles. New York: Cambridge University Press. [Google Scholar]
- Gopikrishnan, Parameswaran, Martin Meyer, L. Nunes Amaral, and H. Eugene Stanley. 1998. Inverse Cubic Law for the Distribution of Stock Price Variations. The European Physical Journal B-Condensed Matter and Complex Systems 3: 139–40. [Google Scholar] [CrossRef]
- He, Xue-Zhong, and Kai Li. 2012. Heterogeneous Beliefs and Adaptive Behaviour in A Continuous-Time Asset Price Model. Journal of Economic Dynamics and Control 36: 973–87. [Google Scholar] [CrossRef]
- He, Xue-Zhong, Kai Li, and Chuncheng Wang. 2016. Volatility Clustering: A Nonlinear Theoretical Approach. Journal of Economic Behavior & Organization 130: 274–97. [Google Scholar]
- Inoua, Sabiou M., and Vernon L. Smith. 2020. Classical Economics: Lost and Found. The Independent Review, to be appeared. [Google Scholar]
- Keen, Steve. 2013. A Monetary Minsky Model of the Great Moderation and the Great Recession. Journal of Economic Behavior & Organization 86: 221–35. [Google Scholar]
- Kesten, Harry. 1973. Random Difference Equations and Renewal Theory for Products of Random Matrices. Acta Mathematica 131: 207–48. [Google Scholar] [CrossRef]
- Keynes, John Maynard. 1936. The General Theory of Interest, Employment and Money. London: Macmillan. [Google Scholar]
- Klüppelberg, Claudia, and Serguei Pergamenchtchikov. 2004. The Tail of The Stationary Distribution of a Random Coefficient AR (q) model. Annals of Applied Probability 14: 971–1005. [Google Scholar] [CrossRef]
- Kyle, Albert S. 1985. Continuous Auctions and Insider Trading. Econometrica 53: 1315–35. [Google Scholar] [CrossRef]
- Lux, Thomas. 1998. The Socio-Economic Dynamics of Speculative Markets: Interacting Agents, Chaos, and the Fat Tails of Return Distributions. Journal of Economic Behavior & Organization 33: 143–65. [Google Scholar]
- Lux, Thomas, and Simone Alfarano. 2016. Financial Power Laws: Empirical Evidence, Models, and Mechanisms. Chaos, Solitons & Fractals 88: 3–18. [Google Scholar]
- Lux, Thomas, and Michele Marchesi. 1999. Scaling and Criticality in a Stochastic Multi-Agent Model of a Financial Market. Nature 397: 498–500. [Google Scholar] [CrossRef]
- Lux, Thomas, and Michele Marchesi. 2000. Volatility Clustering in Financial Markets: A Microsimulation of Interacting Agents. International Journal of Theoretical and Applied Finance 3: 675–702. [Google Scholar] [CrossRef]
- Lux, Thomas, and Didier Sornette. 2002. On Rational Bubbles and Fat Tails. Journal of Money, Credit, and Banking 34: 589–610. [Google Scholar] [CrossRef]
- Malkiel, Burton G., and Eugene F. Fama. 1970. Efficient Capital Markets: A Review of Theory and Empirical Work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B. 1963. The Variation of Certain Speculative Prices. The Journal of Business 36: 394–419. [Google Scholar] [CrossRef]
- Mikosch, Thomas, and Catalin Starica. 2000. Limit Theory For The Sample Autocorrelations and Extremes of a GARCH (1, 1) process. Annals of Statistics 28: 1427–51. [Google Scholar]
- Mikosch, Thomas, and Catalin Starica. 2003. Long-Range Dependence Effects and ARCH Modeling. In Long–Range Dependence: Theory and Applications. Edited by Paul Doukhan, George Oppenheim and Murad Taqqu. Boston, Basel and Berlin: Birkhäuser, pp. 439–59. [Google Scholar]
- Milgrom, Paul, and Nancy Stokey. 1982. Information, Trade and Common Knowledge. Journal of Economic Theory 26: 17–27. [Google Scholar] [CrossRef]
- Minsky, Hyman P. 1992. The Financial Instability Hypothesis. Working Paper no. 74. Annandale-on-Hudson: The Levy Economics Institute. [Google Scholar]
- Newman, Mark E. J. 2005. Power Laws, Pareto Distributions and Zipf’s Law. Contemporary Physics 46: 323–51. [Google Scholar] [CrossRef]
- Orléan, André. 1989. Mimetic Contagion and Speculative Bubbles. Theory and Decision 27: 63–92. [Google Scholar] [CrossRef]
- Osborne, Maury F. M. 1959. Brownian Motion in the Stock Market. Operations Research 7: 145–73. [Google Scholar] [CrossRef]
- Palan, Stefan. 2013. A Review of Bubbles and Crashes in Experimental Asset Markets. Journal of Economic Surveys 27: 570–88. [Google Scholar] [CrossRef]
- Plerou, Vasiliki, Xavier Gabaix, H. Eugene Stanley, and Parameswaran Gopikrishnan. 2006. Institutional Investors and Stock Market Volatility. Quaterly Journal of Economics 2: 461–504. [Google Scholar]
- Porter, David P., and Vernon L. Smith. 2003. Stock Market Bubbles in the Laboratory. The Journal of Behavioral Finance 4: 7–20. [Google Scholar] [CrossRef]
- Samanidou, E., Elmar Zschischang, Dietrich Stauffer, and Thomas Lux. 2007. Agent-Based Models of Financial Markets. Reports on Progress in Physics 70: 409. [Google Scholar] [CrossRef]
- Samuelson, Paul. A. 1965. Proof that Properly Anticipated Prices Fluctuate Randomly. Industrial Management Review 6: 41–49. [Google Scholar]
- Sato, Aki-Hiro, and Hideki Takayasu. 1998. Dynamic Numerical Models of Stock Market Price: From Microscopic Determinism to Macroscopic Randomness. Physica A: Statistical Mechanics and its Applications 250: 231–52. [Google Scholar] [CrossRef]
- Shaikh, Anwar. 2010. Reflexivity, Path Dependence, and Disequilibrium Dynamics. Journal of Post Keynesian Economics 33: 3–16. [Google Scholar] [CrossRef]
- Shannon, Claude Elwood. 1948. A Mathematical Theory of Communication. Bell system Technical Journal 27: 379–423. [Google Scholar] [CrossRef]
- Shi, Yu, Qixuan Luo, and Handong Li. 2019. An Agent-Based Model of a Pricing Process with Power Law, Volatility Clustering, and Jumps. Complexity. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1980. Do Stock Prices Move Too Much to Be Justified by Subsequent Changes in Dividends? Cambridge: National Bureau of Economic Research. [Google Scholar]
- Smith, Vernon L., Gerry L. Suchanek, and Arlington W. Williams. 1988. Bubbles, Crashes, and Endogenous Expectations in Experimental Spot Asset Markets. Econometrica 56: 1119–51. [Google Scholar] [CrossRef]
- Soros, George. 2013. Fallibility, Reflexivity, and the Human Uncertainty Principle. Journal of Economic Methodology 20: 309–29. [Google Scholar] [CrossRef]
- Soros, George. 2015. The Alchemy of Finance. Hoboken: John Wiley & Sons. [Google Scholar]
- Tirole, Jean. 1982. On the Possibility of Speculation under Rational Expectations. Econometrica 50: 1163–81. [Google Scholar] [CrossRef]
| 1 | See, e.g., Bouchaud and Challet (2016). |
| 2 | The nuance in this diverse literature on endogenous financial instability, already clearly articulated by the classical economists (Inoua and Smith 2020), lies perhaps in the nature of the ultimate destabilizing force that is specifically emphasized in each tradition, notably human psychology (Keynes and behavioral finance) or the easy bank-issued liquidity that backs or fuels the speculative euphoria, without which this latter would be of no significant, macroeconomic, harm (Fisher, Minsky, Kindleberger, etc., and the classical economists who preceded them). |
| 3 | Other types of models are also suggested for the power law more specifically; one of them, for example, relates the power law of return to the trades of very large institutional investors (Plerou et al. 2006). |
| 4 | Random-coefficient autoregressive (RCAR) processes are also known as Kesten processes, named after H. Kesten whose seminal theorem proves their power-law tail behavior. Kesten’s theorem was perhaps first used in finance to study GARCH processes, which are in fact also Kesten processes. ‘Rational bubbles’ can also be interpreted as first-order RCAR processes assuming a random discount factor (Lux and Sornette 2002); but this model generates a tail exponent smaller than 1. First-order RCAR processes have also been suggested as approximations to complex agent-based mechanisms (Sato and Takayasu 1998; Aoki 2002; Carvalho 2004). In this paper, however, a general RCAR return process holds directly in a competitive market of trend-following speculators. |
| 5 | A more detailed study of the power-law tail of volatility as it emerges from the RCAR model is the subject of a planned follow-up paper. |
| 6 | It may seem paradoxical that GARCH models, being also RCAR processes, could nonetheless generate clustered volatility; but this latter is in reality an ‘IGARCH effect’ (Mikosch and Starica 2000, 2003). It is more the persistence implied by the near-integration in fitted GARCH models that mimics the volatility clusters in these models. This near integration of fitted GARCH models resembles the near integration of speculators’ anticipated return in this paper’s model. |
| 7 | The linear fit is based on a maximum-likelihood algorithm developed by Clauset et al. (2009), which is an important reference for the statistical test of empirical power laws; the program codes are available at http://tuvalu.santafe.edu/~aaronc/powerlaws/. For an introduction to power laws more generally, see, for example, Newman (2005) and Gabaix (2009, 2016). |
| 8 | Because nonlinearity adds no further insight to this theory, we assume these standard linear supply and demand functions, which can be viewed as first-order linear approximations of more general functions; also, since financial supply and demand can be treated symmetrically (by treating supply formally as a negative demand), one can think directly in terms of a trader’s excess demand, which is a demand or a supply, depending on the sign. |
| 9 | The seminal work is Kyle (1985). A distinction may be in order here: a ‘price adjustment function’ models the overall price impact of the competition of buyers and sellers in a market; empirical evidence suggests it is linear in financial markets (Cont et al. 2014); a related but different concept is the ‘price impact’ of a trade or series of trades, which is typically a concave function of trade volume (Bouchaud 2010). The first concept is relevant for a theorist studying a market as a whole; the second, perhaps for a trader wishing to minimize the execution cost of a given trade volume. |
| 10 | We are grateful to a reviewer whose comment makes us aware of the need to emphasize explicitly the difference between a news and a noise. It is common in agent-based models to assume a Gaussian white noise in the fundamental-value dynamics, starting from Lux and Marchesi (1999), who, however, note that this (noise-driven) random walk in their model has nothing to do with the stylized facts. In fact, they assume the Gaussian white noise precisely so that none of the emergent financial regularities in their models can be attributed to this white noise: “In order to ensure that none of the typical characteristics of financial prices can be traced back to exogenous factors, we assume that the relative changes of [fundamental value] are Gaussian random variables.” (Lux and Marchesi 1999, p. 499). In fact, Lux and Marchesi (2000) show that the fat tail and volatility clustering in their model hold even when the fundamental value is constant. This is the case in this paper’s model as well, as emphasized below (Figure 7). The reviewer nonetheless suggests that the white-noise assumption, along with traders’ heterogeneity, may be responsible for clustered volatility in the agent-based model by He and Li (2012). |
| 11 | An arbitrarily general AR model is recently suggested by Shi et al. (2019), which replicates and studies in detail the robustness of an earlier working version of this paper’s model (titled ‘The Random Walk Behind Volatility Clustering, 2016’). However, the choice is crucial for volatility clustering. |
| 12 | For greater visibility, only the first 1000 periods out of 10,000 are shown in the subplots (a), (a′), (b), and (b′). |
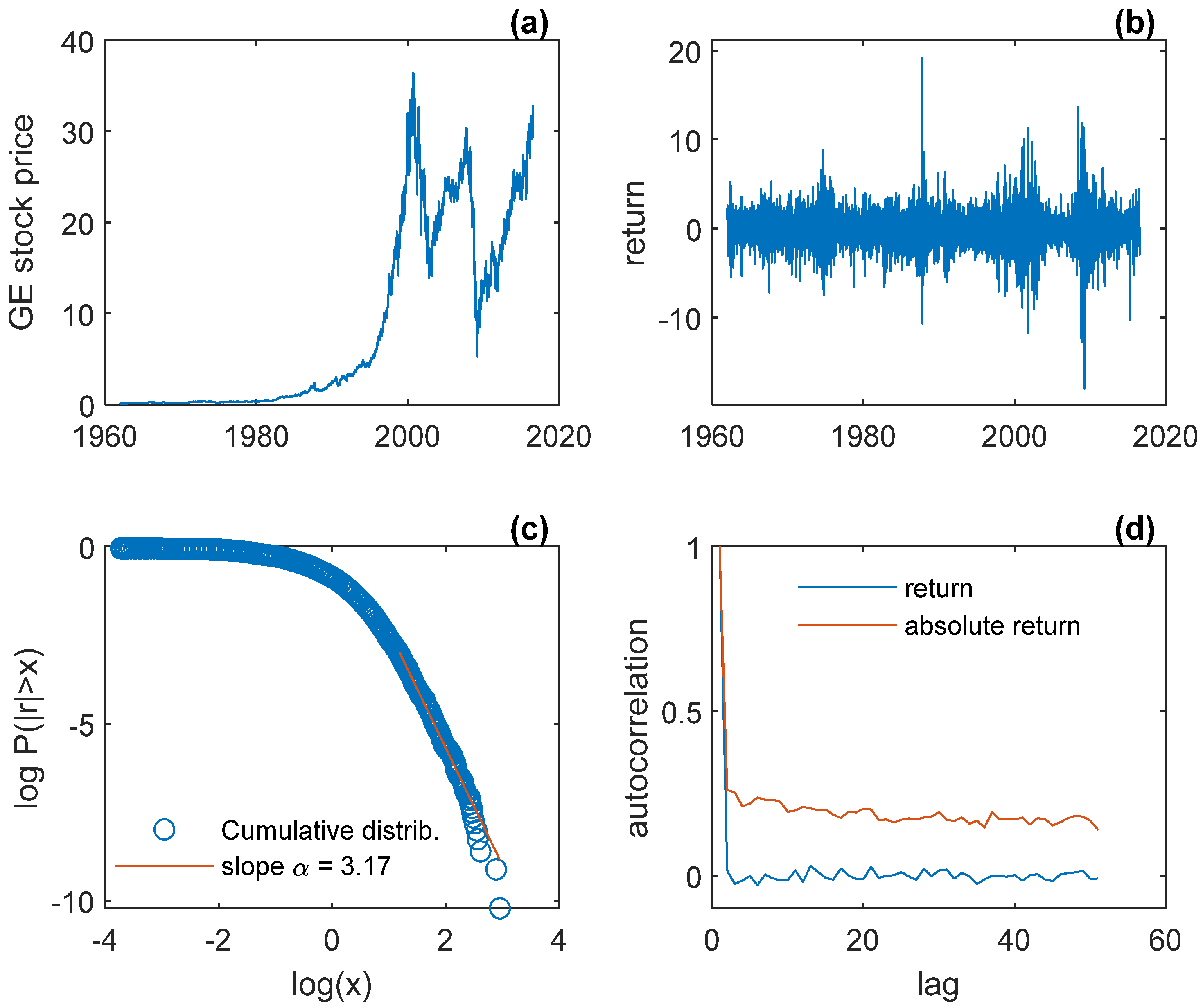
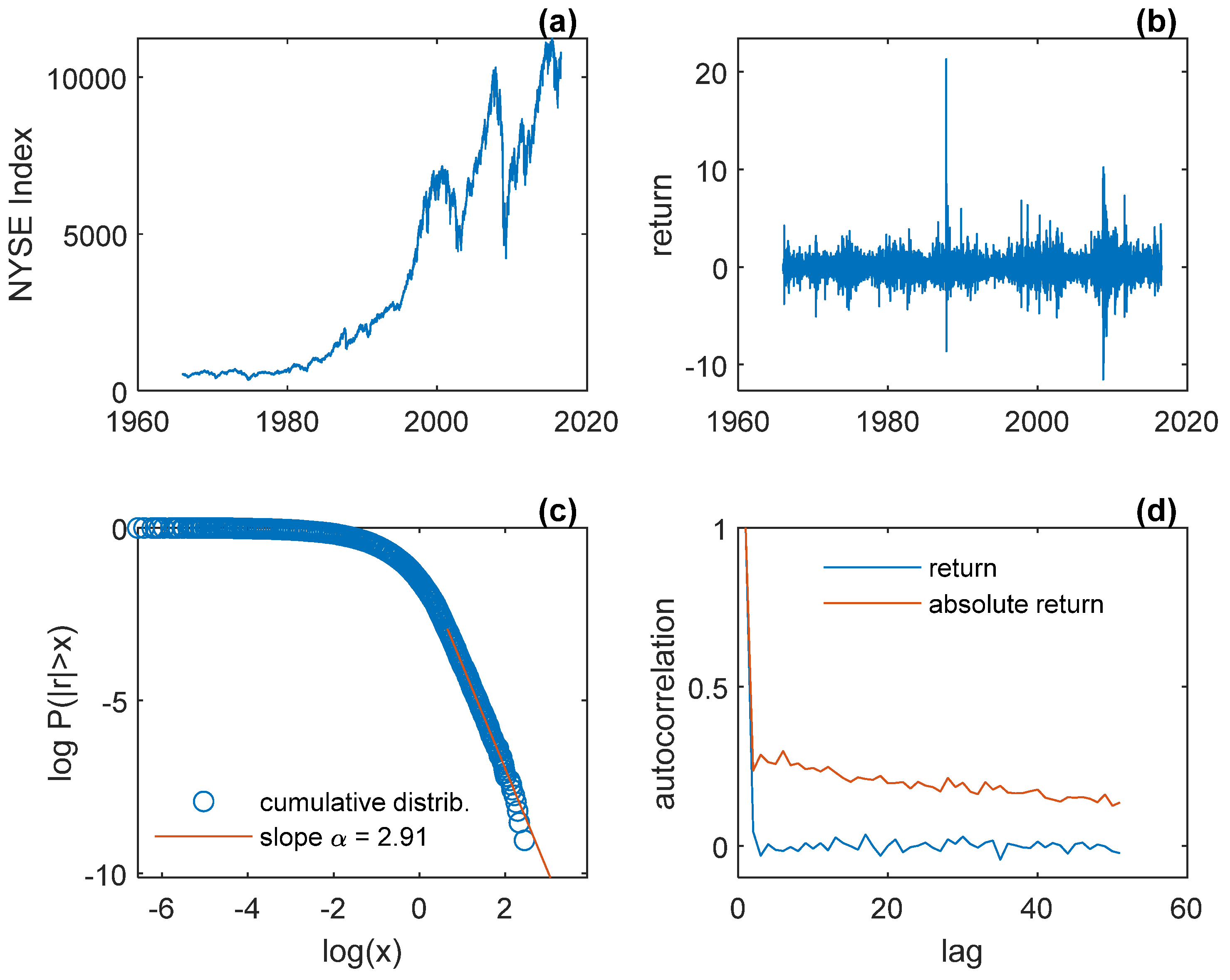
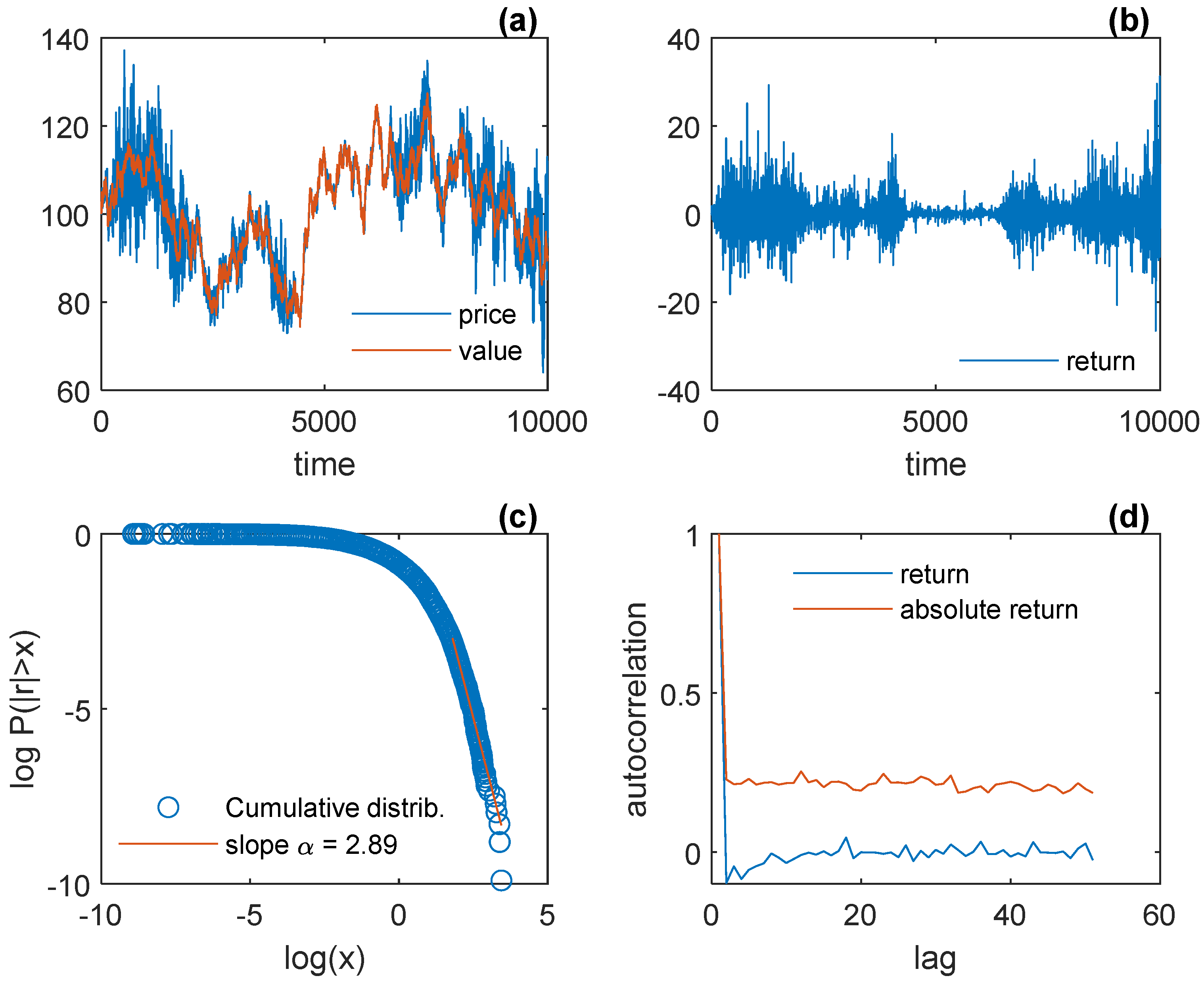
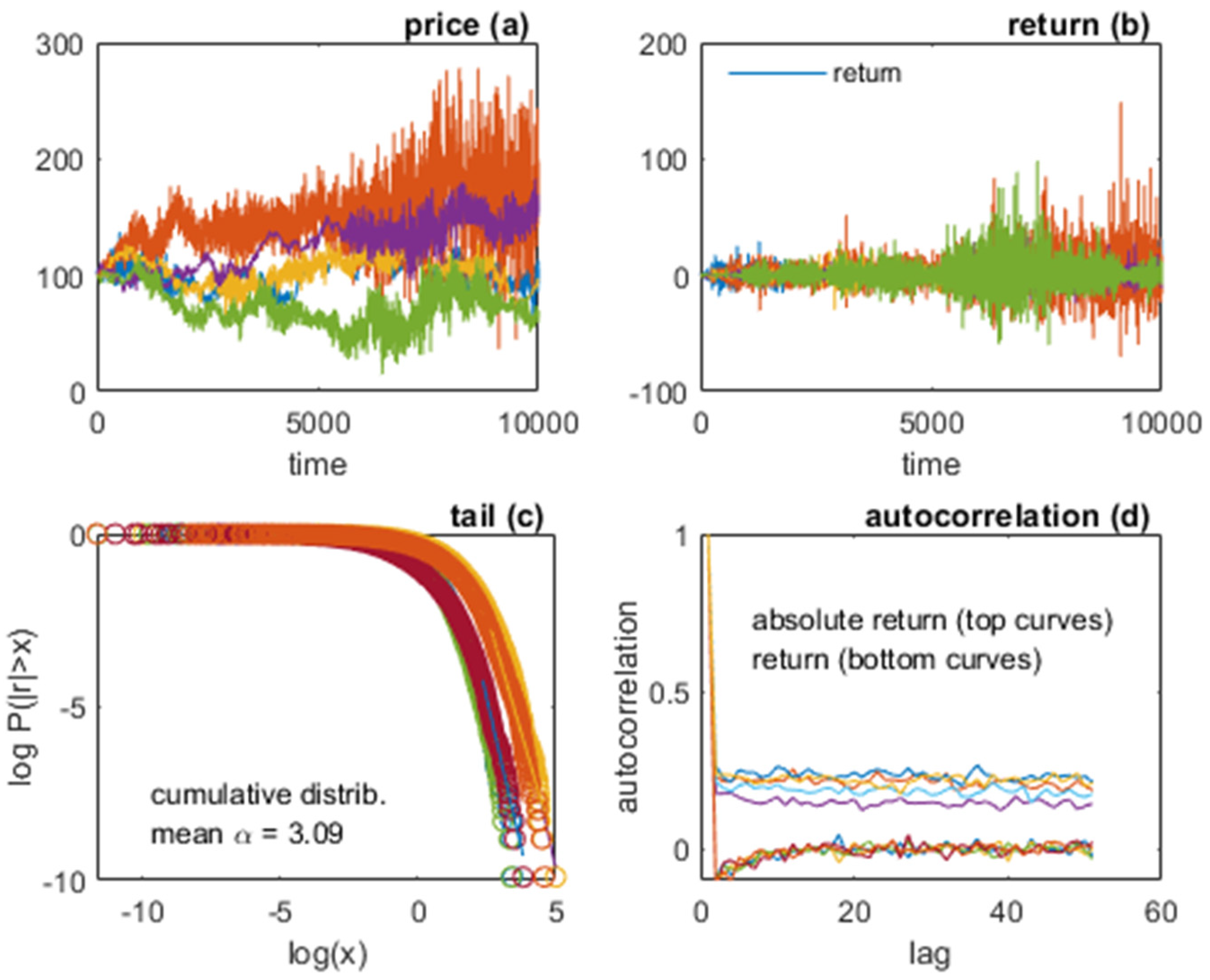
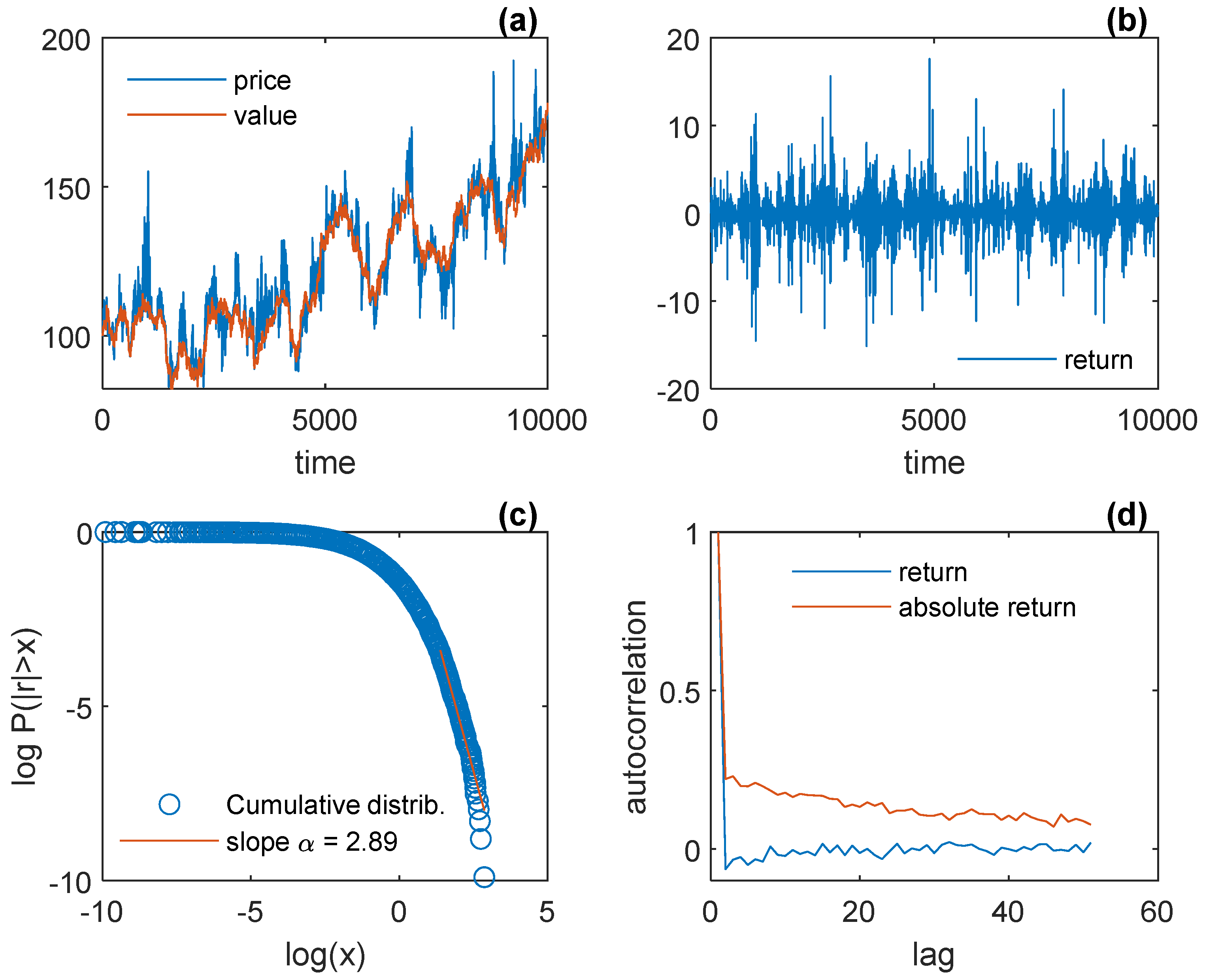
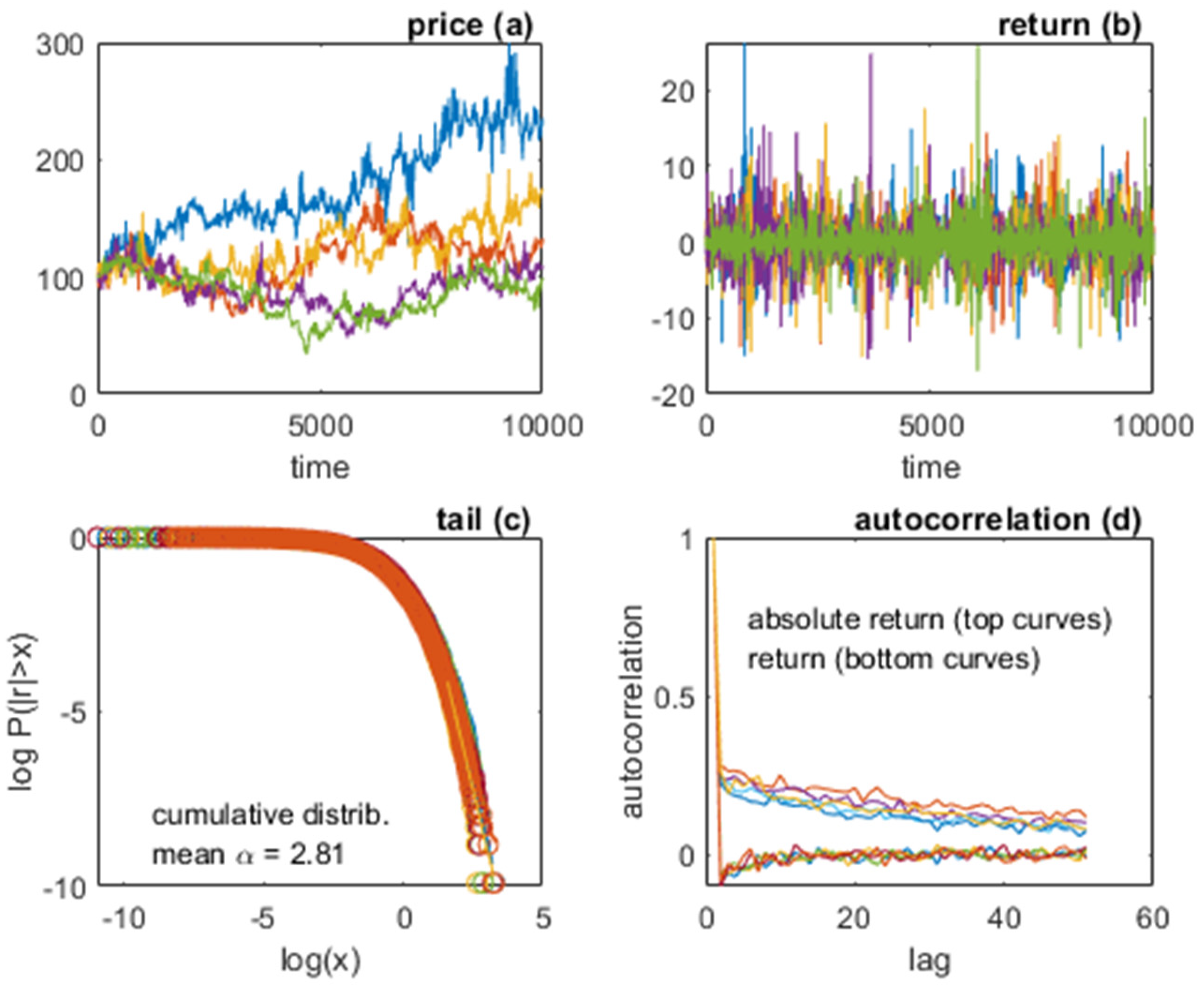
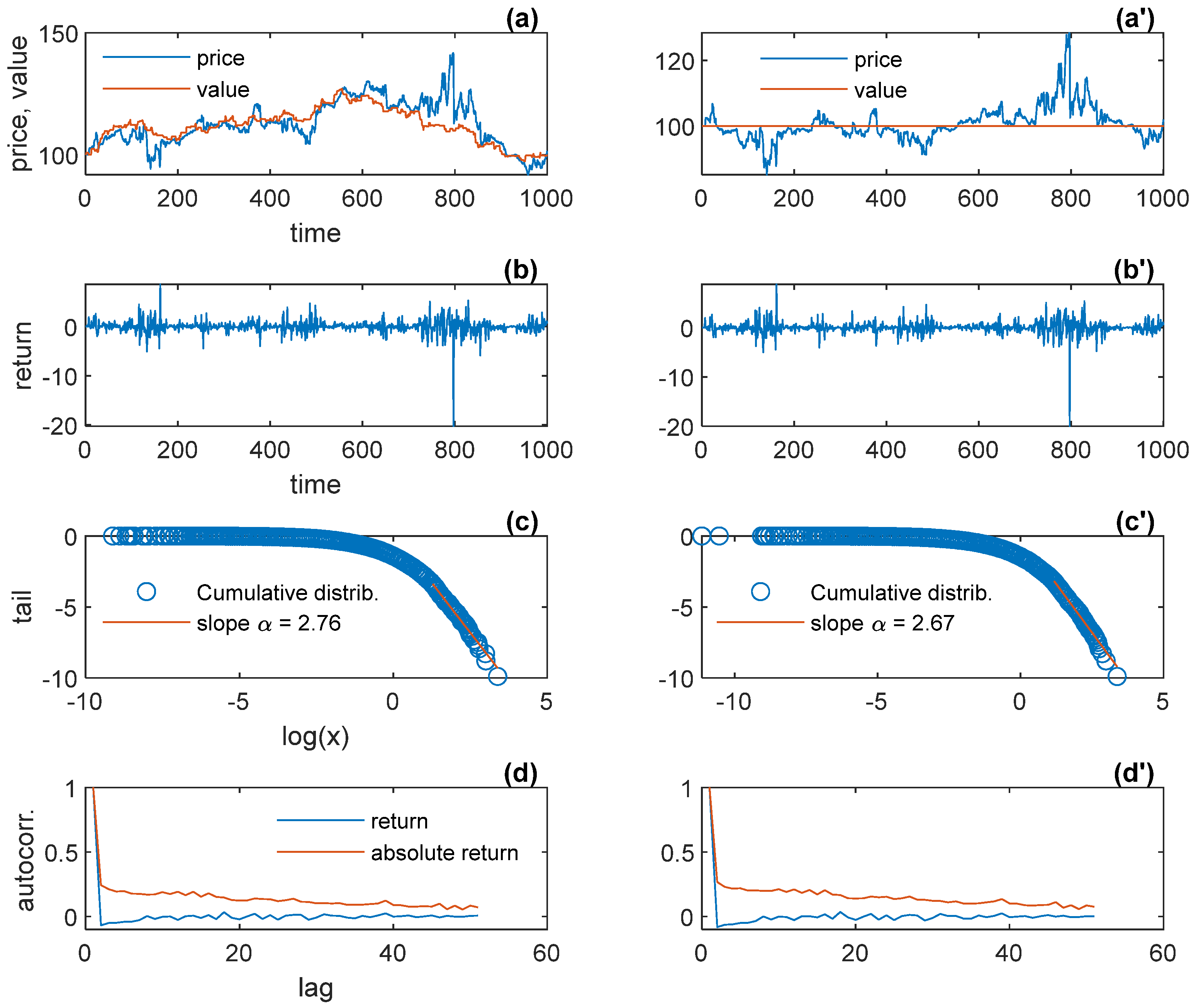
| Figure 1 | Figure 2 | Figure 3 | Figure 41 | Figure 5 | Figure 61 | Figure 7 | |
|---|---|---|---|---|---|---|---|
| GE | NYSE | Model 1 | Model 1 | Model 2 | Model 2 | Model 2 | |
| Parameters | |||||||
| mean (m) | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | ||
| mean (n) | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | ||
| std () | 1 | 1 | 1 | 1 | 1 | ||
| std () | 1 | 1 | 0.04 | 0.04 | 0.04 | ||
| prob (News I) | 0.5 | 0.5 | 0.3 | 0.3 | 0.3 3; 0 4 | ||
| prob (News J) | 0.5 | 0.5 | 0.1 | 0.1 | 0.1 | ||
| a (feedback) | 0.99 | 0.99 | 0.99 | ||||
| mean (r) | −0.04 | −0.02 | 0.04 | 0.16 2 | 0.01 | 0.01 2 | 0.01 3; 0.01 3 |
| std (r) | 1.62 | 1.01 | 2.68 | 4.99 2 | 1.43 | 1.46 2 | 1.48 3; 1.44 3 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoua, S.M. News-Driven Expectations and Volatility Clustering. J. Risk Financial Manag. 2020, 13, 17. https://doi.org/10.3390/jrfm13010017
Inoua SM. News-Driven Expectations and Volatility Clustering. Journal of Risk and Financial Management. 2020; 13(1):17. https://doi.org/10.3390/jrfm13010017
Chicago/Turabian StyleInoua, Sabiou M. 2020. "News-Driven Expectations and Volatility Clustering" Journal of Risk and Financial Management 13, no. 1: 17. https://doi.org/10.3390/jrfm13010017
APA StyleInoua, S. M. (2020). News-Driven Expectations and Volatility Clustering. Journal of Risk and Financial Management, 13(1), 17. https://doi.org/10.3390/jrfm13010017





