Capital Markets Integration and Cointegration: Testing for the Correct Specification of Stock Market Indices
Abstract
1. Introduction
2. Testing for Common Trends in an Integrated Framework
2.1. Treating the Variables as I(1)
2.1.1. Scenario I: One Cointegrating Vector, Four Common Stochastic Trends
2.1.2. Scenario II: Two Cointegrating Vectors, Three Common Stochastic Trends
2.2. Treating Prices as I(2)
2.2.1. Scenario I: One Cointegrating Vector, Three I(1) and One I(2) Common Stochastic Trends
2.2.2. Scenario II: Two Cointegrating Vectors, Two I(1) and One I(2) Common Stochastic Trends
3. Econometric Methodology
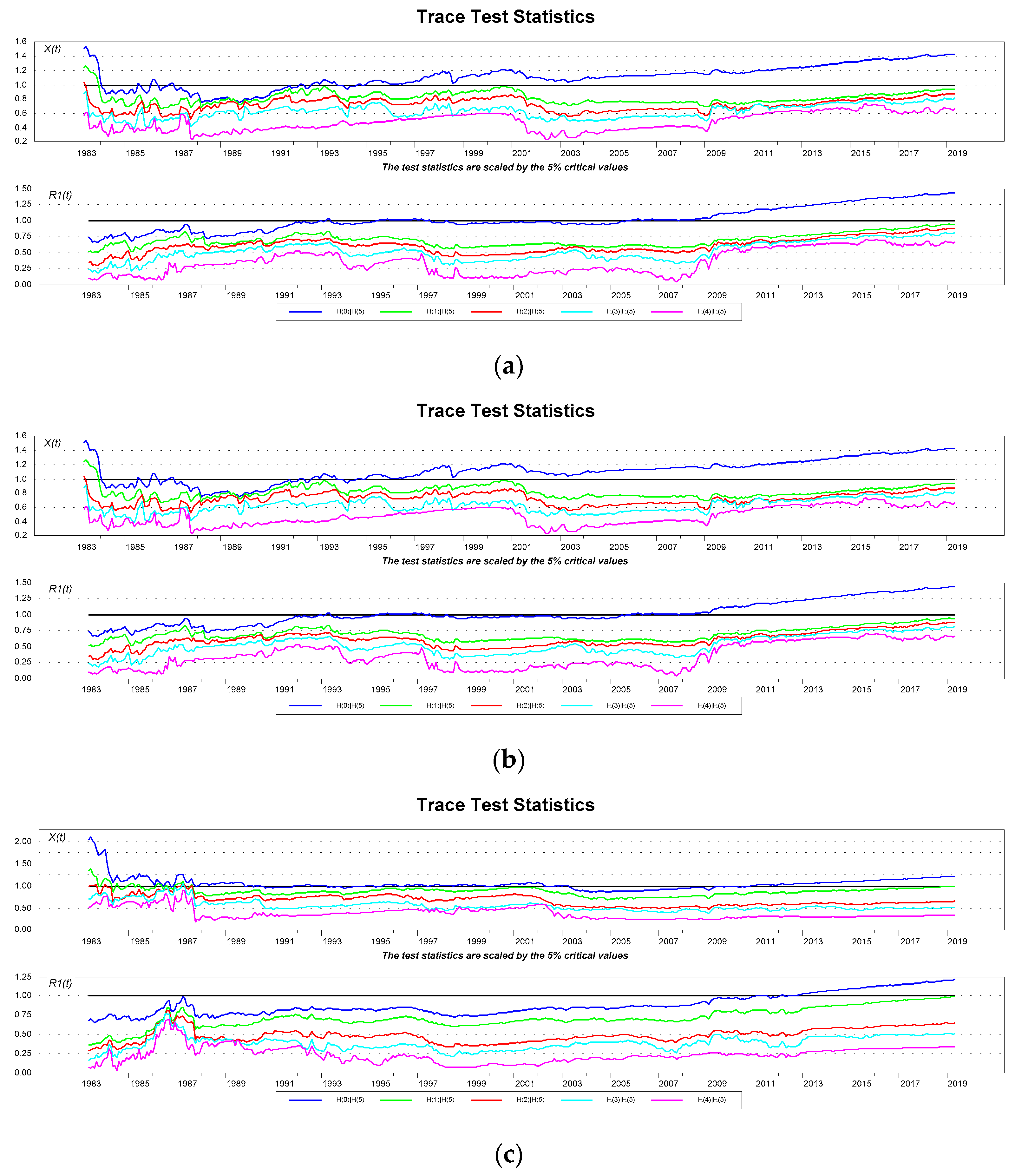
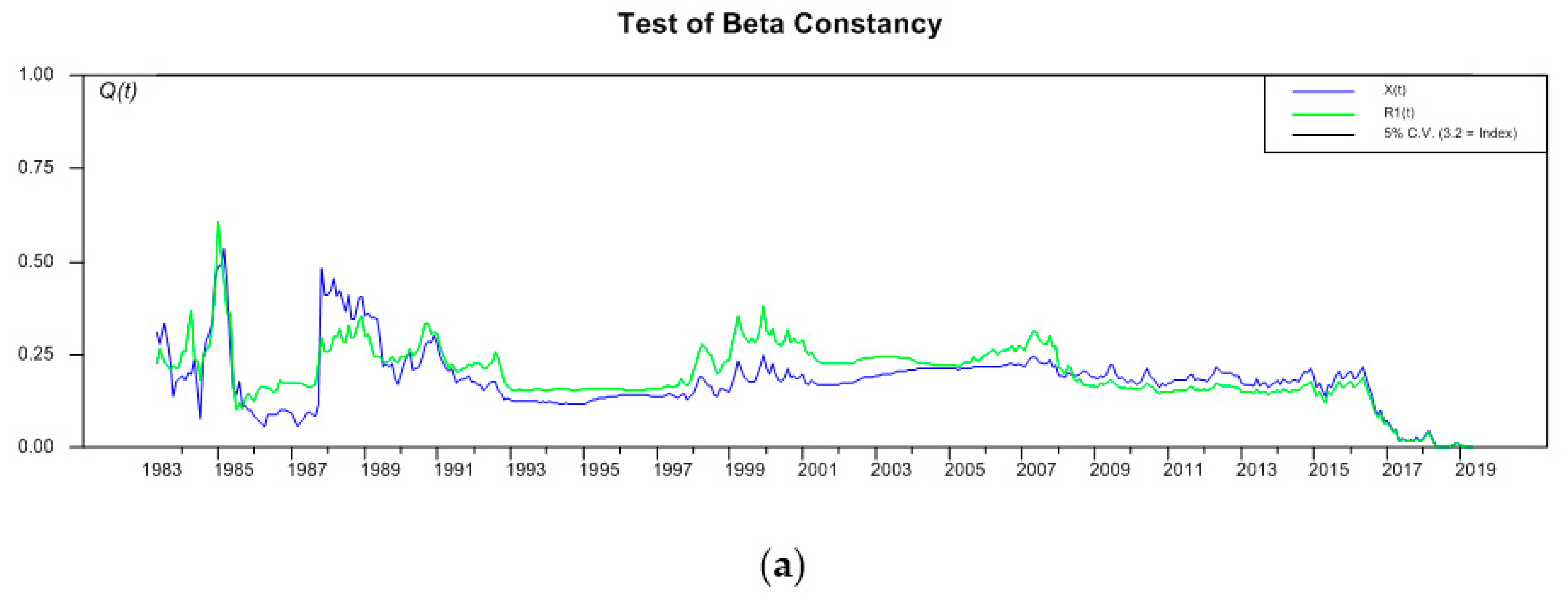
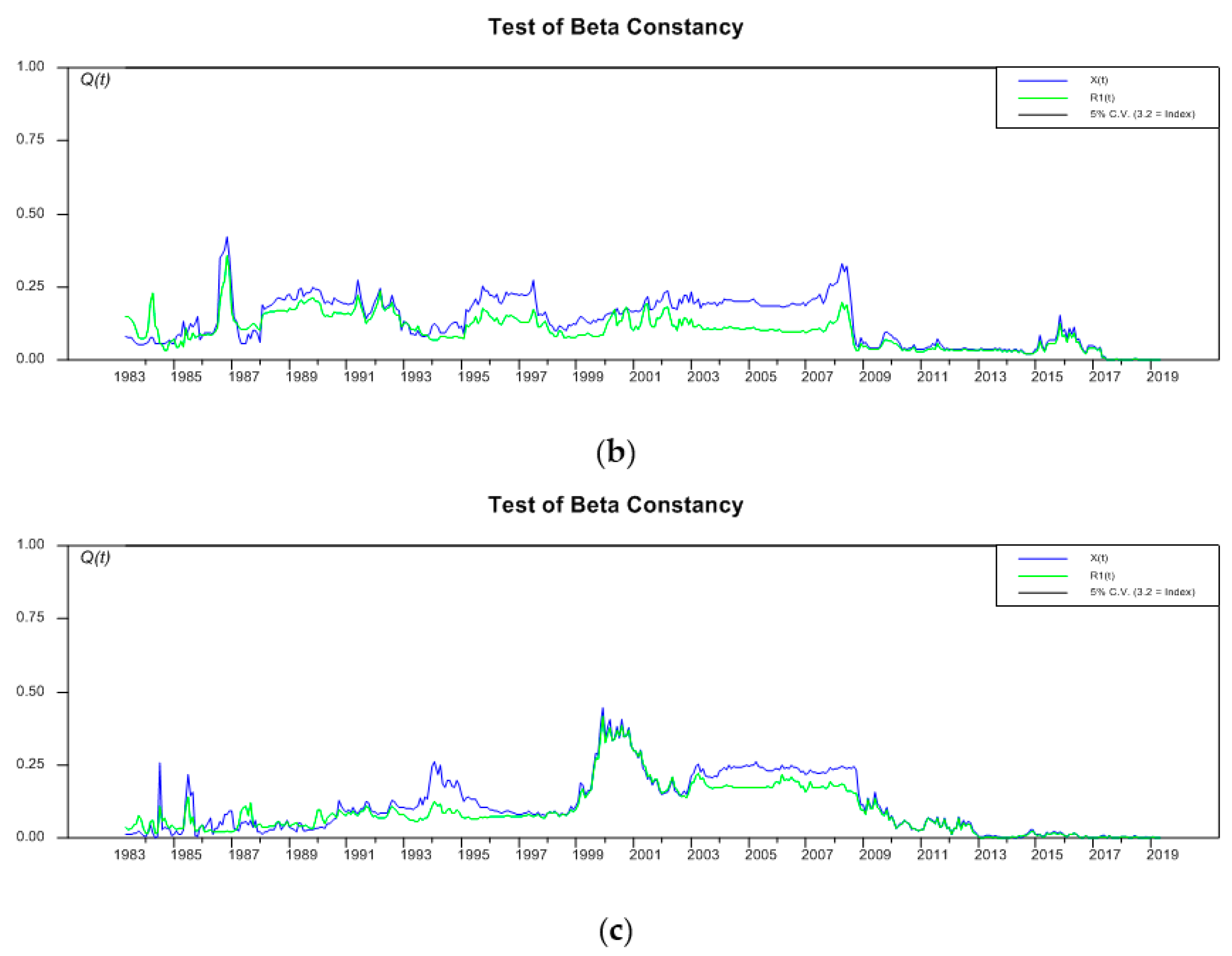
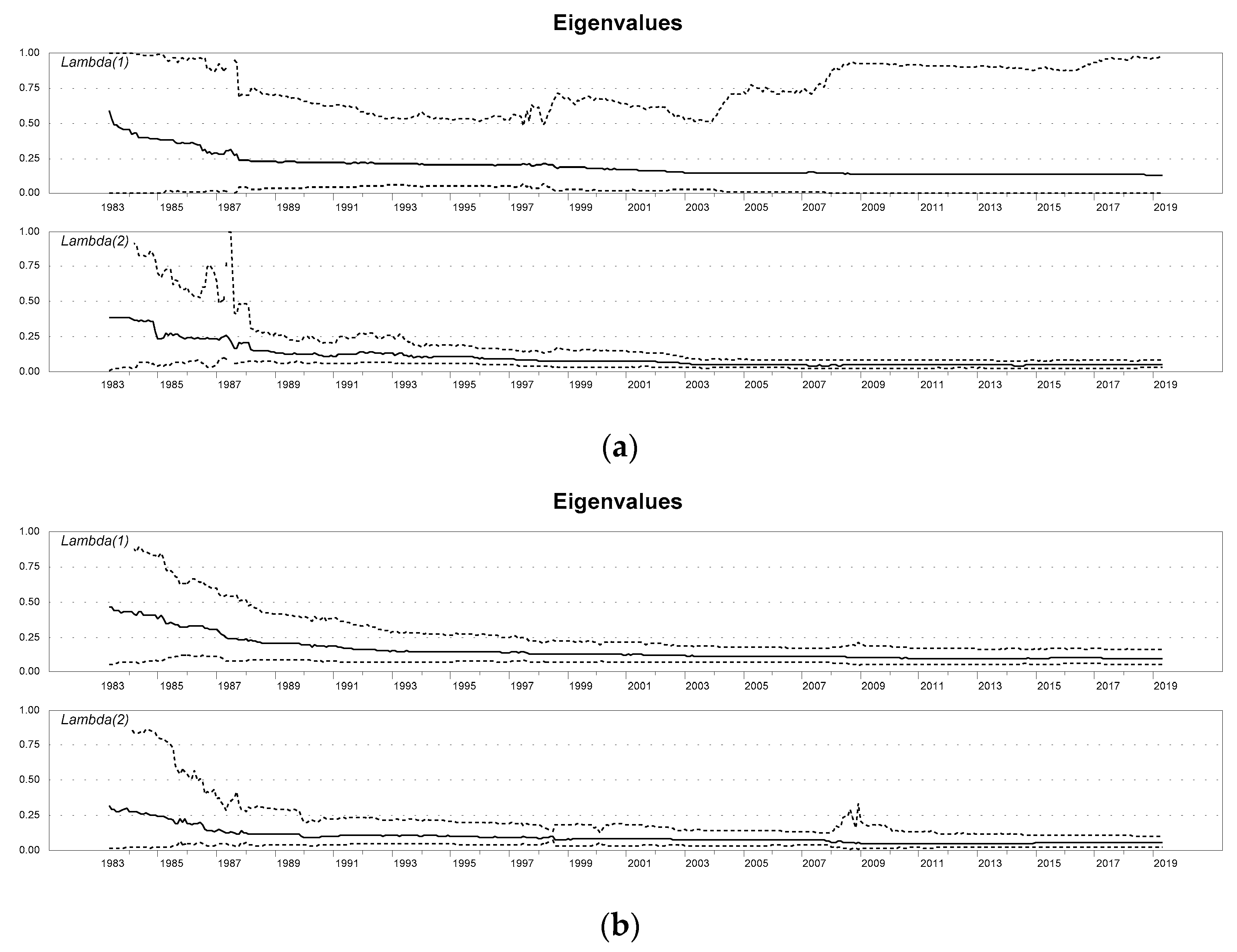
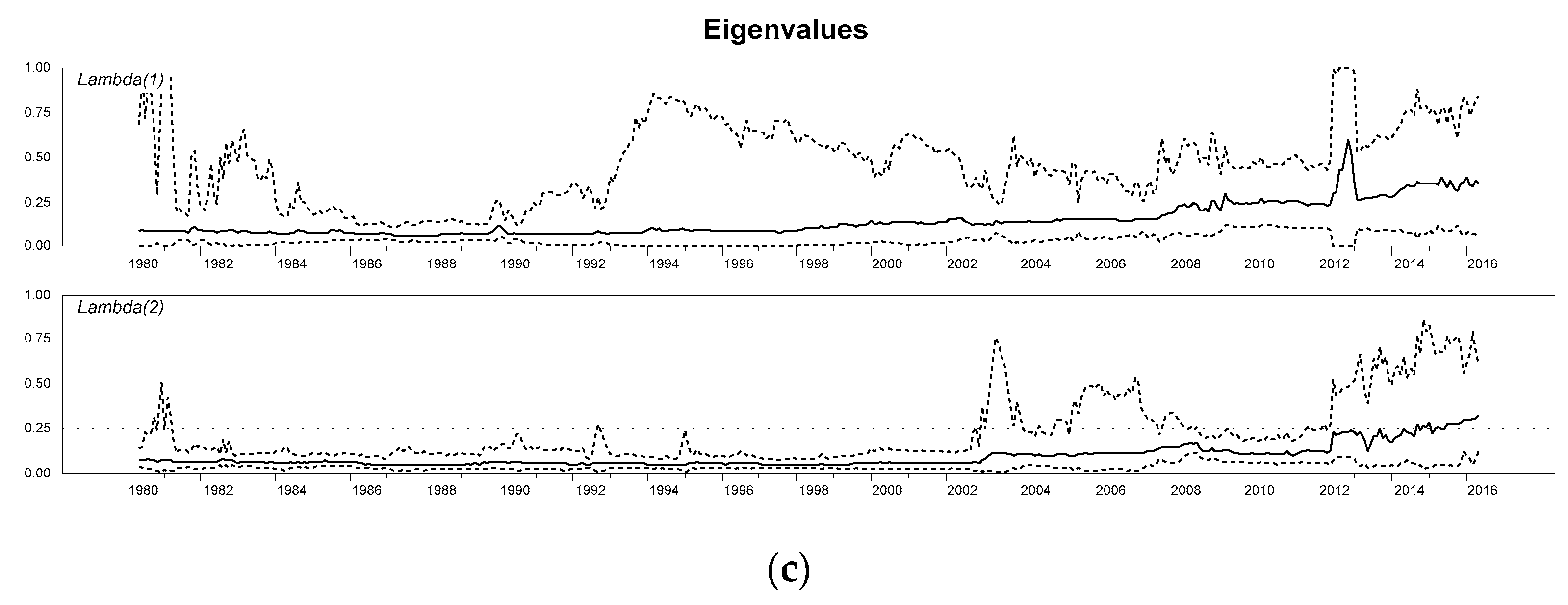
4. Empirical Evidence
Determination of the Cointegration Rank and the Order of Integration
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Arshanapalli, Bala, and John Doukas. 1993. International stock market linkages: Evidence from the pre- and post-October 1987 period. Journal of Banking and Finance 17: 193–208. [Google Scholar] [CrossRef]
- Bracker, Kevin, Diane Scott Docking, and Paul D. Koch. 1999. Economic determinants of evolution in international stock market integration. Journal of Empirical Finance 6: 1–27. [Google Scholar] [CrossRef]
- Calvi, Rossella. 2010. Assessing Financial Integration: A Comparison between Europe and East Asia. Working Paper 423. Brussels: European Economy. [Google Scholar]
- Caporale, Gulglielmo Maria, Luis A. Gil-Alana, and James C. Orlando. 2016. Linkages between the US and European Stock Markets: A Fractional Cointegration Approach. International Journal of Finance and Economics 21: 143–53. [Google Scholar] [CrossRef]
- Ceylan, Onay. 2006. A Co-integration Analysis Approach to European Union Integration: The Case of Acceding and Candidate Countries. European Integration Online Papers 10: 7. [Google Scholar]
- Chan, Kam C., Benton E. Gup, and Ming-Shiun Pan. 1992. An empirical analysis of stock prices in major Asian markets and the United States. The Financial Review 27: 289–307. [Google Scholar] [CrossRef]
- Corhay, A., A. Tourani Rand, and J.-P. Urbain. 1993. Common stochastic trends in european stock markets. Economics Letters 42: 385–90. [Google Scholar] [CrossRef]
- Crowder, William J., and Mark Wohar. 1998. Cointegration, Forecasting and International Stock Prices. Global Finance Journal 9: 181–204. [Google Scholar] [CrossRef]
- Dornbusch, Rudiger. 1989. Real exchange rates and macroeconomics: A selected survey. Scandinavian Journal of Economics 91: 401–32. [Google Scholar] [CrossRef][Green Version]
- Engle, Robert F., and C.W.J. Granger. 1987. Cointegration and error correction: Representation estimation and testing. Econometrica 55: 251–76. [Google Scholar] [CrossRef]
- Francis, Bill B., and Lori L. Leachman. 1998. Superexogeneity and the dynamic linkages among international equity markets. Journal of International Money and Finance 17: 475–92. [Google Scholar] [CrossRef][Green Version]
- Fraser, Patricia, and O. Oyefeso. 2005. US, UK and European stock and market integration. Journal of Business Finance and Accounting 32: 161–81. [Google Scholar] [CrossRef]
- Garcia Pascual, A. 2003. Assessing European stock markets (co)integration. Economics Letters 78: 197–203. [Google Scholar] [CrossRef]
- Gonzalo, Jesus. 1994. Comparison of five alternative methods of estimating long-run equilibrium relationships. Journal of Econometrics 60: 203–33. [Google Scholar] [CrossRef]
- Granger, C.W.J. 1986. Developments in the study of cointegrated economic variables. Oxford Bulletin of Economics and Statistics 48: 213–28. [Google Scholar] [CrossRef]
- Hansen, Henrik, and Soren Johansen. 1993. Recursive Estimation in Cointegrated VAR-Models. Working Paper. Copenhagen: University of Copenhagen, Institute of Mathematical Statistics. [Google Scholar]
- Hansen, Henrik, and Soren Johansen. 1999. Some tests for parameter constancy in cointegrated VAR-models. Econometrics Journal 2: 306–33. [Google Scholar] [CrossRef]
- Jeon, Bang Nam, and Thomas C. Chiang. 1991. A system of stock prices in world stock exchanges: Common stochastic trends for 1975–1990? Journal of Economics and Business 43: 329–38. [Google Scholar] [CrossRef]
- Johansen, Soren. 1988. Statistical analysis of cointegrating vectors. Journal of Economic Dynamics and Control 12: 231–54. [Google Scholar] [CrossRef]
- Johansen, Soren. 1991. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica 59: 1551–80. [Google Scholar] [CrossRef]
- Johansen, Soren. 1992a. A representation of vector autoregressive processes integrated of order 2. Econometric Theory 8: 188–202. [Google Scholar] [CrossRef]
- Johansen, Soren. 1992b. Determination of cointegration rank in the presence of a linear trend. Oxford Bulletin of Economics and Statistics 54: 383–97. [Google Scholar] [CrossRef]
- Johansen, S. 1995a. A statistical analysis of cointegration for I(2) variables. Econometric Theory 11: 25–29. [Google Scholar] [CrossRef]
- Johansen, Soren. 1995b. Identifying restrictions of linear equations with applications to simultaneous equations and cointegration. Journal of Econometrics 69: 111–32. [Google Scholar] [CrossRef]
- Johansen, Soren. 1997. A Likelihood analysis of the I(2) model. Scandinavian Journal of Statistics 24: 433–62. [Google Scholar] [CrossRef]
- Johansen, Soren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—with applications to the demand for money. Oxford Bulletin of Economics and Statistics 52: 169–210. [Google Scholar] [CrossRef]
- Johansen, Soren, and Katarina Juselius. 1992. Testing structural hypotheses in a multivariate cointegration analysis of the PPP and the UIP for UK. Journal of Econometrics 53: 211–44. [Google Scholar] [CrossRef]
- Johansen, Soren, and Katarina Juselius. 1994. Identification of the long-run and the short-run structure: An application to the ISLM model. Journal of Econometrics 63: 7–36. [Google Scholar] [CrossRef]
- Juselius, Katarina. 1995. Do purchasing power parity and uncovered interest rate parity hold in the long-run? An example of likelihood inference in a multivariate time-series model. Journal of Econometrics 69: 211–40. [Google Scholar] [CrossRef]
- Juselius, Katarina. 1999. Models and relations in economics and econometrics. Journal of Economic Methodology 6: 259–90. [Google Scholar] [CrossRef]
- Kasa, Kenneth. 1992. Common stochastic trends in international stock markets. Journal of Monetary Economics 29: 95–124. [Google Scholar] [CrossRef]
- Kasa, Kenneth. 1995. Comovements among national stock markets. In Economic Review. San Francisko: Federal Reserve Bank of San Francisco. [Google Scholar]
- Leachman, Lori L., and Bill B. Francis. 1995. Long run relations among the G-5 and G-7 Equity Markets: Evidence on the Plaza and Louvre Accords. Journal of Macroeconomics 17: 551–77. [Google Scholar] [CrossRef]
- Lee, Tae Hwy, and Yiuman Tse. 1996. Cointegration tests with conditional heteroskedasticity. Journal of Econometrics 73: 401–10. [Google Scholar] [CrossRef]
- Lucas, Robert E. 1982. Interest rates and currency prices in a two-country world. Journal of Monetary Economics 10: 335–59. [Google Scholar] [CrossRef]
- Pantula, Sastry G. 1989. Testing for unit roots in time series data. Econometric Theory 5: 256–71. [Google Scholar] [CrossRef]
- Paruolo, Paolo. 1996. On the determination of integration indices in I(2) Systems. Journal of Econometrics 72: 313–56. [Google Scholar] [CrossRef]
- Rahbek, Anders, Hans Cristian Konsted, and Clara Jorgensen. 1999. Trend-stationarity in the I(2) cointegration model. Journal of Econometrics 90: 265–89. [Google Scholar] [CrossRef]
- Rangvid, Jesper. 2001. Increasing convergence among European stock markets? A recursive common stochastic trends analysis. Economic Letters 71: 383–89. [Google Scholar] [CrossRef]
- Reimers, H.-E. 1992. Comparison of tests for multivariate Co-integration. Statistical Papers 33: 335–59. [Google Scholar] [CrossRef]
- Richards, Anthony J. 1995. Co-movement in national stock market returns: Evidence of predictability but not cointegration. Journal of Monetary Economics 36: 631–54. [Google Scholar] [CrossRef]
- Serletis, Apostolos, and Martin King. 1997. Common stochastic trends and convergence of European union stock markets. The Manchester School 65: 44–57. [Google Scholar] [CrossRef]
- Sims, Christopher A. 1980. Macroeconomics and reality. Econometrica 48: 1–48. [Google Scholar] [CrossRef]
- Taylor, Mark, and Ian Tonks. 1989. The internationalisation of stock markets and the abolition of U.K. exchange control. Review of Economics and Statistics 71: 332–336. [Google Scholar] [CrossRef]
- Worthington, Andrew C., Masaki Katsuura, and Helen Higgs. 2003. Financial Integration in European Equity markets: The Final Stage of Economic and Monetary Union (EMU) and its Impact on Capital Markets. Economia 54: 79–99. [Google Scholar]
| 1 | This argument follows from the evidence linking cointegration and error correction that leads to the predictability of at least one of the asset prices. Those results apply strictly however on total returns (i.e., cum dividend) or otherwise on non-interest/dividend paying assets (Richards 1995). The efficiency hypothesis can still be preserved, in the presence of cointegration, if the error correction is a proxy for a risk premium. |
| 2 | The general tendency is to draw a distinction between tests for capital integration and those for the existence of common trends. The important implication of integrated capital markets is the equalization among countries of marginal rates of substitution in consumption both inter-temporally and across states of nature (Lucas 1982; Kasa 1995). But even then the existence of a common model of required returns is not sufficient to generate cointegrating relationships. The cumulative stochastic errors, if they are found to be I(1), of each one of the assets return series must be cointegrated as well (Richards 1995). |
| 3 | In this paper we focus on results derived from the multivariate cointegration analysis of Johansen (1988). However, the first strand of papers examining cointegration between stock prices employed the Engle and Granger (1987) methodology (see e.g., Arshanapalli and Doukas 1993; Chan et al. 1992). |
| 4 | Serletis and King (1997) have transformed their data into “real deutschemark” units. In other studies, the stock indices are expressed in local, nominal, currency terms (e.g., Calvi 2010). |
| 5 | In this case it might be more realistic to restrict the impact on the U.S. price index and have the exchange rate absorb all of the shock (i.e., ). As a matter of fact, the common trends in (2) are over-identified and up to three restrictions can be imposed without changing the likelihood function. |
| 6 | Since the two prices indices are excluded from the cointegrating vector. Therefore, deviations from PPP have no impact, in the long-run, on the behavior of the two equity market indices. |
| 7 | In general if then the unrestricted linear regressor, , allows for cubic trends while the constant regressor, , allows for quadratic ones. Rahbek et al. (1999) show that to guarantee linear trends in all linear combinations of we must impose restrictions on both and . Finally, Rahbek et al. (1999) provide a likelihood ratio (LR) test, which is asymptotically distributed, to examine whether the linear trend significantly enters the cointegrating vector. |
| 8 | Gonzalo (1994) shows that the performance of the maximum likelihood estimator of the cointegrating vectors is little affected by non-normal errors. Lee and Tse (1996) have shown similar results when conditional heteroskedasticity is present. |
| 9 | The calculations of all tests as well as the estimation of the eigenvectors have been performed using the program CATS 2.0 in RATS 9.0 developed by Katarina Juselius and Henrik Hansen, Estima Inc. Illinois, 1995. |
| 10 | |
| 11 | It should be noted however that the falling number, over time, of the underlying stochastic trends governing the system can be attributed to the convergence of the trace statistics to their long-run values as the sample expands (i.e., the power of the test increases). Garcia Pascual (2003) presented evidence on estimates of the trace statistic obtained from constant sample sizes that are being rolled over each time to the next period. It is shown there that the trace statistics do not present any upward trend and this is interpreted as running against the proposition that an increased number of cointegrating vectors among the stock price indices is an indicator of an increasing integration among the capital markets (Rangvid 2001). |
| Direction | Dimension | Stationary Process |
|---|---|---|
| ~ I(0) | , if | |
| ~ I(1) | ~ I(0) | |
| ~ I(1) | ~ I(0) | |
| ~ I(2) | ~ I(0) |
| USA | UK | GER | JAP | |
|---|---|---|---|---|
| USA | 1.0 | |||
| UK | 0.750 | 1.0 | ||
| GER | 0.705 | 0.709 | 1.0 | |
| JAP | 0.422 | 0.445 | 0.419 | 1.0 |
| U.S.–U.K. | |||||||
|---|---|---|---|---|---|---|---|
| Eq. | LB(36) | ARCH(4) | NORM(4) | ||||
| 0.006 | 28.14 | 9.71 | 0.39 | 1.19 | 100.71 * | 0.703 | |
| 0.054 | 23.12 | 6.43 | −0.68 | 4.19 | 86.44 * | 0.363 | |
| 0.039 | 34.09 | 1.59 | −0.05 | 0.88 | 9.59 * | 0.285 | |
| 0.007 | 24.81 | 2.94 | −0.28 | 1.76 | 102.25 * | 0.603 | |
| 0.045 | 23.65 | 5.22 | −0.71 | 2.15 | 73.61 * | 0.362 | |
| U.S.–Germany | |||||||
| Eq. | LB(36) | ARCH(4) | NORM(4) | ||||
| 0.004 | 31.28 | 3.51 | −0.78 | 6.78 | 59.39 * | 0.446 | |
| 0.024 | 14.31 | 3.37 | −0.76 | 5.87 | 55.79 * | 0.365 | |
| 0.010 | 29.44 | 5.15 | −0.08 | 3.56 | 7.04 | 0.402 | |
| 0.003 | 31.16 | 8.15 | −1.36 | 1.55 | 102.21 * | 0.667 | |
| 0.018 | 30.14 | 10.38 | −0.97 | 5.01 | 73.33 * | 0.209 | |
| U.S.–Japan | |||||||
| Eq. | LB(36) | ARCH(4) | NORM(4) | ||||
| 0.003 | 22.39 | 8.62 | −0.35 | 0.01 | 19.45 * | 0.553 | |
| 0.023 | 31.35 | 11.39 | −0.37 | 0.08 | 18.97 | 0.288 | |
| 0.011 | 28.16 | 7.32 | −0.31 | 0.33 | 8.62 * | 0.346 | |
| 0.003 | 32.11 | 6.73 | −1.37 | 0.01 | 105.22 * | 0.591 | |
| 0.018 | 24.12 | 10.07 | −1.02 | 0.05 | 73.02 * | 0.371 | |
| Testing the Joint Hypothesis U.S.–U.K | |||||||
|---|---|---|---|---|---|---|---|
| p-r | r | ||||||
| 5 | 0 | 901.2 206.1 | 691.0 174.3 | 486.9 146.4 | 346.8 123.1 | 216.5 103.8 | 126.7 88.6 |
| 4 | 1 | 483.6 141.5 | 302.8 115.8 | 166.5 94.2 | 73.4 76.8 | 59.8 63.7 | |
| 3 | 2 | 164.7 89.0 | 68.6 69.4 | 50.9 53.9 | 37.2 42.7 | ||
| 2 | 3 | 49.7 48.5 | 29.7 34.98 | 20.8 25.7 | |||
| 1 | 4 | 18.5 20.0 | 8.28 12.44 | ||||
| s2 | 5 | 4 | 3 | 2 | 1 | 0 | |
| U.S.–Germany | |||||||
| p-r | r | ||||||
| 5 | 0 | 867.1 206.1 | 603.1 174.3 | 493.1 146.4 | 327.2 123.1 | 229.6 103.8 | 112.4 88.6 |
| 4 | 1 | 444.1 141.5 | 299.6 115.8 | 172.3 94.2 | 64.3 76.8 | 64.1 63.7 | |
| 3 | 2 | 171.5 89.0 | 66.4 69.4 | 51.7 53.9 | 38.7 42.7 | ||
| 2 | 3 | 41.2 48.5 | 28.3 34.98 | 17.8 25.7 | |||
| 1 | 4 | 15.3 20.0 | 6.59 12.44 | ||||
| s2 | 5 | 4 | 3 | 2 | 1 | 0 | |
| U.S.–Japan | |||||||
| p-r | r | ||||||
| 5 | 0 | 802.4 206.1 | 598.9 174.3 | 452.2 146.4 | 319.7 123.1 | 208.8 103.8 | 107.7 88.6 |
| 4 | 1 | 426.7 141.5 | 287.1 115.8 | 170.6 94.2 | 68.1 76.8 | 63.3 63.7 | |
| 3 | 2 | 167.1 89.0 | 68.6 69.4 | 35.0 53.9 | 27.9 42.7 | ||
| 2 | 3 | 34.7 48.5 | 25.2 34.98 | 13.2 25.7 | |||
| 1 | 4 | 12.4 20.0 | 4.16 12.44 | ||||
| s2 | 5 | 4 | 3 | 2 | 1 | 0 | |
| (a) Tests for Long-Run Exclusion, Stationarity, and Weak Exogeneity | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Long-Run Exclusion | Stationarity | Weak Exogeneity | |||||||
| US/UK US/GE | US/JP | US/UK | US/GE US/JP | US/UK | US/GE | US/JP | |||
| 3.39 * | 15.32 * | * | 20.60 * | 22.47 * | 11.71 * | 2.77 | 4.69 * | 0.62 | |
| 0.97 * | 11.61 * | 6.63 * | 14.77 * | 23.01 * | 24.11 * | 9.08 * | 4.43 * | 14.78 * | |
| 5.84 * | 0.05 * | 14.02 * | 40.83 * | 25.88 * | 15.52 * | 3.30 | 7.27 * | 1.52 | |
| 1.08 * | 16.73 * | 7.22 * | 11.76 * | 18.50 * | 12.72 * | 13.33 * | 9.43 * | * | |
| 2.47 * | 0.16 * | 9.29 * | 25.16 * | 19.525 * | 14.73 * | 1.67 | 3.49 | 8.72 * | |
| (b) Multivariate Residuals Diagnostics | ||||
|---|---|---|---|---|
| Case | L-B(117) | LM(1) | LM(4) | |
| U.S–U.K | 1960.46(0.00) | 34.39(0.69) | 40.92(0.26) | 1023.49(0.00) |
| U.S.–Germany | 1784.33(0.00) | 36.95(0.41) | 38.12(0.31) | 490.69(0.00) |
| U.S.–Japan | 1000.49(0.00) | 35.19(0.62) | 29.84(0.46) | 351.53(0.00) |
| U.S.–U.K. | |
|---|---|
| Q(5) = 53.91(0.0000) | |
| Q(5) = 54.31(0.0000) | |
| Q(5) = 9.51 (0.0642) | |
| Q(5) = 8.46 (0.1752) | |
| U.S.–Germany | |
| Q(5) = 29.83 (0.0000) | |
| Q(5) = 33.35 (0.0000) | |
| Q(5) = 7.31 (0.0941) | |
| Q(5) = 9.02 (0.0833) | |
| U.S.–Japan | |
| Q(5) = 44.18(0.0000) | |
| Q(5) = 41.29(0.0000) | |
| Q(5) = 6.38 (0.1348) | |
| Q(5) = 10.28 (0.057) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agoraki, M.-E.K.; Georgoutsos, D.A.; Kouretas, G.P. Capital Markets Integration and Cointegration: Testing for the Correct Specification of Stock Market Indices. J. Risk Financial Manag. 2019, 12, 186. https://doi.org/10.3390/jrfm12040186
Agoraki M-EK, Georgoutsos DA, Kouretas GP. Capital Markets Integration and Cointegration: Testing for the Correct Specification of Stock Market Indices. Journal of Risk and Financial Management. 2019; 12(4):186. https://doi.org/10.3390/jrfm12040186
Chicago/Turabian StyleAgoraki, Maria-Eleni K., Dimitris A. Georgoutsos, and Georgios P. Kouretas. 2019. "Capital Markets Integration and Cointegration: Testing for the Correct Specification of Stock Market Indices" Journal of Risk and Financial Management 12, no. 4: 186. https://doi.org/10.3390/jrfm12040186
APA StyleAgoraki, M.-E. K., Georgoutsos, D. A., & Kouretas, G. P. (2019). Capital Markets Integration and Cointegration: Testing for the Correct Specification of Stock Market Indices. Journal of Risk and Financial Management, 12(4), 186. https://doi.org/10.3390/jrfm12040186




