1. Introduction
The idea of cryptocurrency and the related technology, Blockchain, was suggested in 2009 by an anonymous user known as Satoshi Nakamoto. He posted a paper to a cryptographic mailing list introducing a new electronic cash system with very low transaction costs able to avoid the presence of a central bank: the Bitcoin, see
Nakamoto (
2009). In the last ten years, cryptocurrencies have become more and more popular among researchers and investors, with around 2000 cryptocurrencies available at the time of writing. In recent months, the Bitcoin has experienced a dramatic price increase and consequently, the global interest in cryptocurrencies has spiked substantially. Despite the price increase, there are other numerous reasons for this intensified interest, just to mention a few: Japan and South Korea have recognised Bitcoin as a legal method of payment (
Bloomberg 2017a;
Cointelegraph 2017); some central banks are exploring the use of the cryptocurrencies (
Bloomberg 2017b); a large number of companies and banks created the Enterprise Ethereum Alliance
1 to make use of the cryptocurrencies and the related technology called blockchain (
Forbes 2017). Finally, the Chicago Mercantile Exchange (CME) started the Bitcoin futures on 18 December 2017, see
Group (
2017), Nasdaq and the Tokyo Financial Exchange will follow, see
Bloomberg (
2017b).
Although Bitcoin is a relatively new currency, there have already been some studies on this topic:
Hencic and Gourieroux (
2015) applied a non-causal autoregressive model to detect the presence of bubbles in the Bitcoin/USD exchange rate. The study of
Cheah and Fry (
2015) focused on the same issue.
Fernández-Villaverde and Sanches (
2016) analysed the existence of price equilibria among privately issued fiat currencies and
Yermack (
2015) wondered whether the cryptocurrency can be considered a real currency.
Sapuric and Kokkinaki (
2014) measured the volatility of the Bitcoin exchange rate against six major currencies.
Chu et al. (
2015) provided a statistical analysis of the log–returns of the exchange rate of Bitcoin versus the USD.
Catania and Grassi (
2018) analysed the main characteristics of cryptocurrency volatility.
Moreover
Bianchi (
2018) tried to investigate some of the key features of cryptocurrency returns and volatilities, such as their relationship with traditional asset classes, as well as the main driving factors behind the market activity. He found that returns on cryptocurrencies are moderately correlated with commodities and a few more assets.
Other studies have analyzed cryptocurrency manipulation and predictability. For instance,
Hotz-Behofsits et al. (
2018) applied a time-varying parameter VAR with t-distributed measurement errors and stochastic volatility.
Griffin and Shams (
2018) investigated whether Tether (another cryptocurrency backed by USD) is directly manipulating the price of Bitcoin, increasing its predictability.
Catania et al. (
2019) studied cryptocurrencies’ predictability using several alternative univariate and multivariate models. They found statistically significant improvements in point forecasting when using combinations of univariate models and in density forecasting when relying on a selection of multivariate models.
Many institutions tried to investigate the relationship between Bitcoin and the stock market. In some articles, it was speculated that the Bitcoin can improve stock market’s predictability, in this case, Bitcoin could be used as a leading indicator. In an article by
Bloomberg (
2018), Morgan Stanley’s analysts stated that “big investors may be dragging Bitcoin toward Market correlation”: the increasing risk of this cryptocurrency may have had an attraction for investors who were seeking for high gains.
Stavroyiannis and Babalos (
2019) examine the dynamic properties of Bitcoin and the Standard & Poor’s 500 (S&P500) index. They study whether Bitcoin can be classified as a possible hedge, diversifier, or safe-haven with respect to the US markets. They found that it does not hold any of the hedge, diversifier, or safe-haven properties and it exhibits intrinsic attributes not related to US markets.
To the best of our knowledge, there are still no studies to confirm that Bitcoin is a good stock market predictor. This paper tries to fill this gap, analyzing whether Bitcoin could be used as a leading indicator for the S&P500.
To answer this question, we allow for parameter and model uncertainty, avoiding Markov Chain Monte Carlo (MCMC) estimation at the same time. This is accomplished using the forgetting factors methodology (also known as discount factors) which have been recently proposed by
Raftery et al. (
2010) and found to be useful in economic and financial applications, see
Dangl and Halling (
2012) and
Koop and Korobilis (
2012) (KK). Another advantage of this methodology is to provide, in close form, both the marginal and predictive likelihood (PL), which are useful in model selection.
The rest of the paper proceeds as follows:
Section 2 presents the general model and the estimation strategy;
Section 3 presents the Dataset;
Section 4 discusses the empirical results; finally,
Section 5 reports some conclusions.
2. Models and Estimation Strategy
Let
denote the time series of interest and
the series of exogenous variables, then the model can be written as:
where
is a scalar representing the observed time series at time
t,
is a
vector (
) stacking all the lags of the series of interest and of the exogenous variable;
is an
vector containing the time varying states
s, which are assumed to follow a random-walk dynamic. Finally, the errors,
and
, are assumed to be mutually independent at all leads and lags. The
contains the time-varying volatilities of the series. The state space model (SSM) of Equation (
1) has been used in several recent papers, see among others,
Primiceri (
2005) and
Koop and Korobilis (
2012).
In order to estimate the quantities of interest, maximum likelihood or Bayesian estimation based on MCMC can be used. However, these two estimation approaches end up being computationally complex and, most of the time, infeasible. To reduce the computational burden, KK proposed two main adjustments to the usual MCMC.
The first is to replace the variance-covariance matrix
with an approximation. Latent states—
—can then be obtained with a closed-form expression avoiding maximum likelihood or MCMC, see
Supplementary Materials. The second adjustment is to replace the measurement error variance matrix
with an Exponential Weighted Moving Average (EWMA) type filter.
As discussed in
Supplementary Materials, this methodology requires the specification of the hyperparameters
,
and
and the specification of the initial condition of the states
and
. Refer to KK for an extensive discussion of the problem.
3. Dataset Description
Table 1 reports the dataset used for the analysis, with the transformation and the data source. The sample goes from 11 August 2015 to 19 July 2018 and consists of 740 daily observations. The crypto–market is open 24 h a day, seven days a week; hence, for computing returns we use the closing price at midnight (UTC). As discussed in
Catania et al. (
2019), the data are available from
https://coinmarketcap.com/ with daily frequency; unfortunately, hourly data that could allow for a more precise analysis are not freely available. To investigate non-stationary issues, three Unit-Root tests have been performed: Augmented Dickey-Fuller (ADF) Test, Philips-Perron (PP) Test and Kwiatkowsky, Phillips, Schmidt and Shin (KPSS) Test. All of them confirm the stationarity of each transformed series, results are available from the authors upon request.
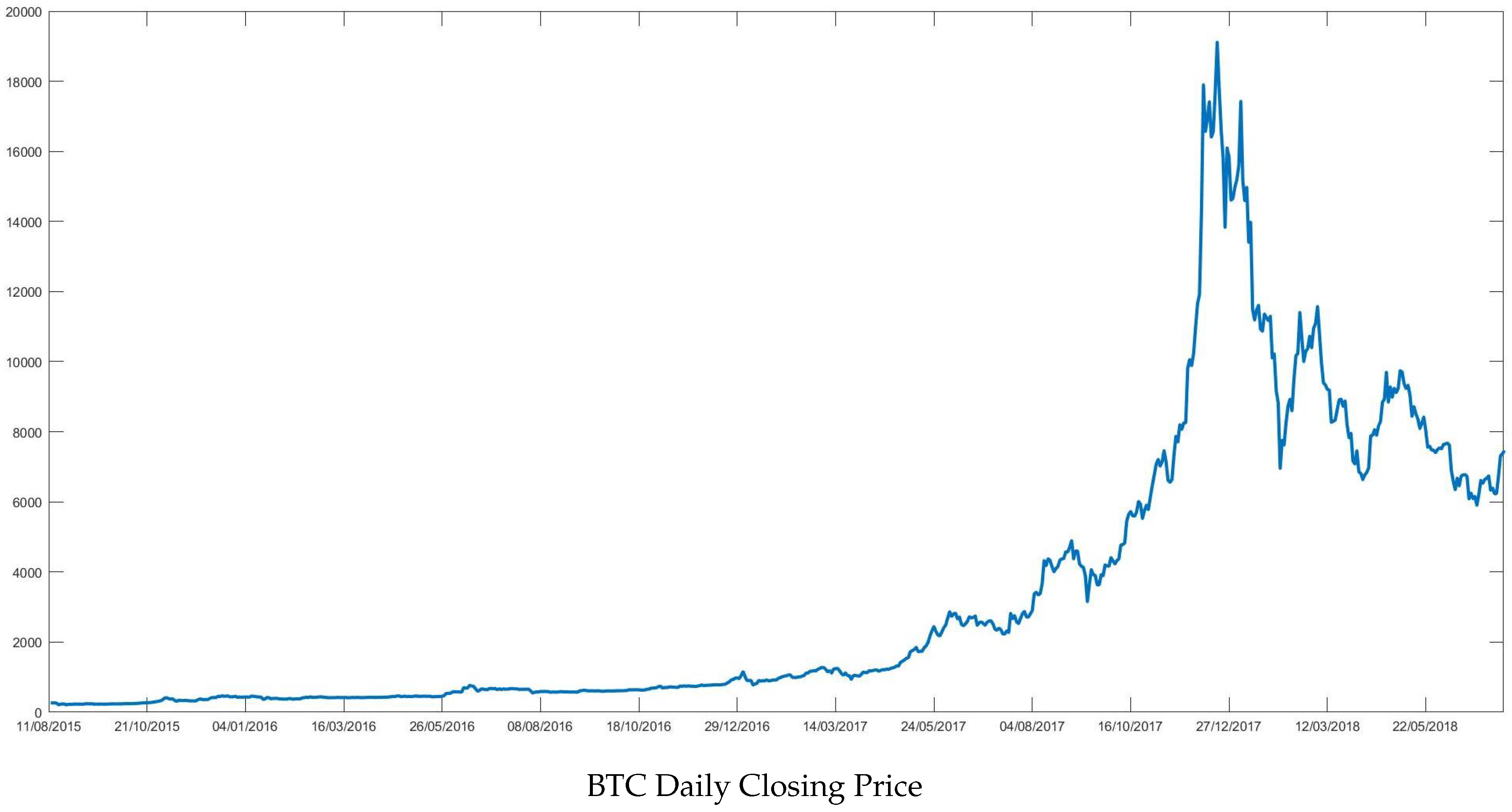
Figure 1 reports Bitcoin closing price (BTC) which shows a steep rise in 2017 reaching the value of almost 20,000 US dollars in December 2017. This ascending trend was severely interrupted at the beginning of 2018, when price quickly dropped down to
$6000. At the time of writing, BTC’s price is fluctuating between 5000 and 6000 dollars.
The series reported in
Table 1 are divided in: financial predictors, such as VIX; commodity predictors, such as GOLD and crypto predictors such as BTC. Among the financial predictors, the VIX, see
Figure S1 in Supplementary Materials (Panel (c)), is the most volatile, as expected. It displays a very steep peak between January and February 2018, the same period in which BTC’s price started to fall.
Table S1 in Supplementary Materials reports the correlation matrix of the predictors. As the table shows the BTC appears to be highly positively correlated with all the financial indexes: S&P500, EF300 and NASDAQ.
4. Analysis
The out-of-sample period begins on 1st September 2016 and the forecast horizon ranges from
to
days ahead. The analysis compares the performances of two models: the first—
—includes all the predictors: financial, commodity and crypto predictors, see
Table 1. The second,
, excludes crypto predictors. The benchmark model, denoted with
, is an ARMA(1,1)-GARCH(1,1) model.
and
can suffer from massive model uncertainty due to the number of possible predictor’s combination at each time point
t. For example,
has
models at each point in time. To mitigate this fact, we use the DMA and DMS as described in
Koop and Korobilis (
2012) and reported in
Supplementary Materials. As already mentioned, the methodology requires fixing three hyperparameters: the forgetting factor
for the parameter variation; the decay factor
for the EWMA; and, finally, the discount weight
that weights each model based on forecast performances.
The results reported in this section are based on
. This value suits daily data, see
Riskmetrics (
1996) and
Prado and West (
2010). The other parameters are set to
and
, coherently with
Raftery et al. (
2010). In
Section 4.2 a robustness analysis for the forgetting factors
and
is carried out. Moreover, we also tried to optimize at each time point
using a standard data-driven approach minimizing the expected prediction error. Unfortunately, the optimized
with crypto time series seems to be very unstable; we leave this issue as a topic of further research.
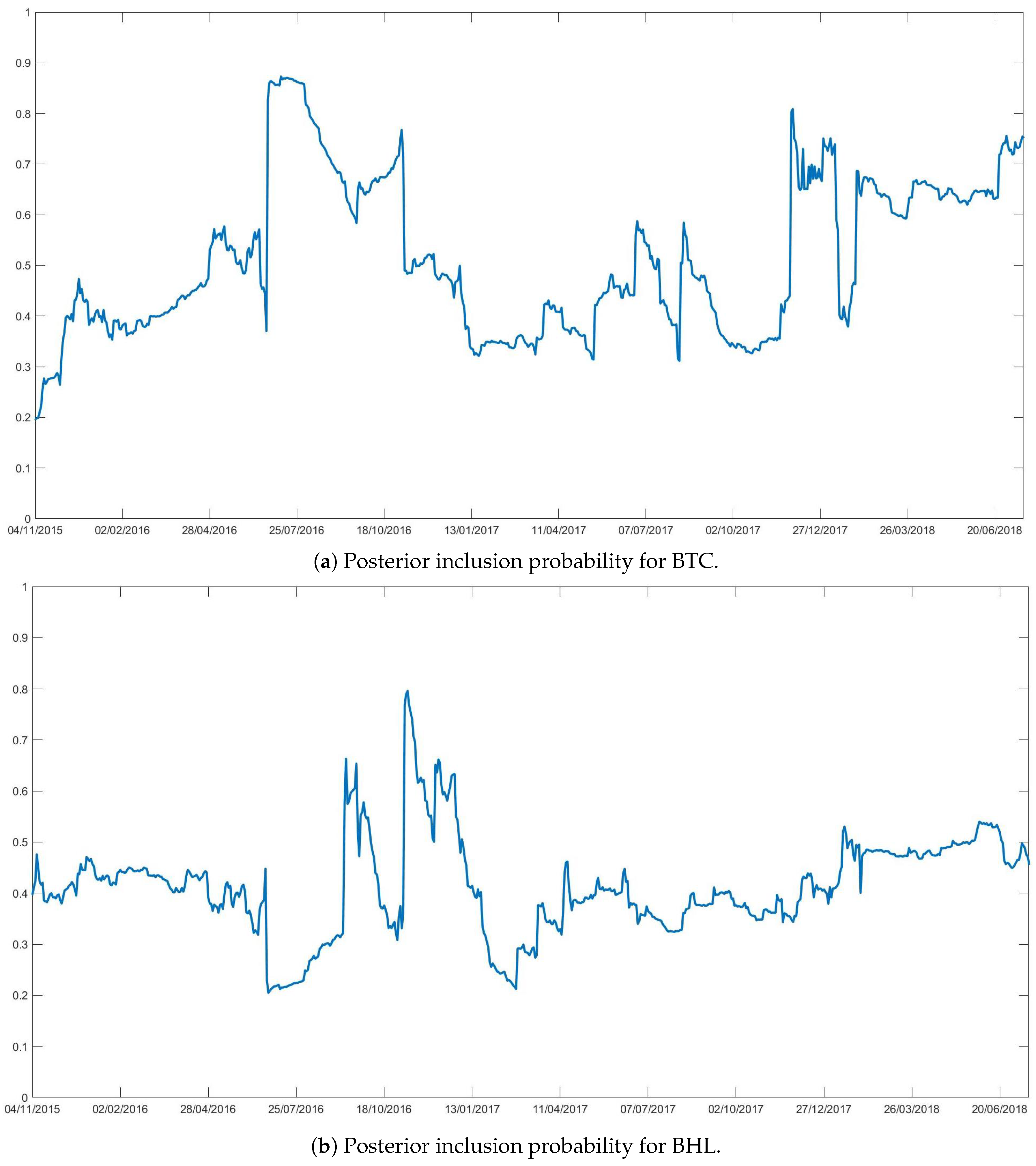
The analysis begins with the investigation of the posterior inclusion probabilities of each predictor: the higher the probability the higher the predictor’s influence over the dependent variable.
Figure 2 depicts the posterior probabilities of BTC (Panel (a)), and of BHL (Panel (b)). Time-varying posterior probabilities of inclusion for the other exogenous variables are reported in
Supplementary Materials.
The figures show that the importance of each predictor switches rapidly over time, with a high inclusion probability of BTC in some specific periods. One important change is in 2016 when the inclusion probability suddenly jumped from 0.5 to 0.9 increasing the correlation with the S&P500 and potentially its role as a leading indicator.
After a calm period during 2017, the BTC gained importance once again at the end of the same year with a steep rise in price. During this period, a lot of articles pointed out a correlation between BTC and financial markets.
Bloomberg (
2018) stated that “big investors may be dragging Bitcoin toward market correlation” and see BTC as an asset which guarantees the highest potential risk/return combination in the market. This may have attracted the interest of big investors able to move huge amounts of funds and consequently correlate BTC to the USA stock market. Another article by
Cointelegraph (
2018) asserted that BTC might be correlated with VIX, but there is no evidence that it may influence the S&P500 index. An extensive analysis of the latter issue is carried out in the next sections using point and density forecast.
4.1. Forecast Metrics
To assess the leading property of BTC we use point and density forecast. For the point forecasts, we use the mean absolute forecast error (MAFE) for each forecast horizon,
:
where
T is the number of observations,
R is the length of the rolling window,
is the S&P500 forecast made at time
t for horizon
h and
is the realization.
To evaluate the density forecasts, we use predictive log score (LS) that is commonly viewed as the broadest measure of density accuracy, see
Geweke and Amisano (
2010). As for the MAFE, we compute the LS for each horizon:
where
is the predictive density for
constructed using information up to time
t.
We report the MAFEs and the LSs as a ratio of each model’s with respect to the baseline. Entries smaller than 1 indicate that a given model yields forecasts that are more accurate than those from the baseline and differences in score relative to the baseline, such as a negative number, indicates a model that beats the baseline. In order to statistically assess the differences between alternative models, we apply the
Diebold and Mariano (
1995) test for equality of the average loss (with loss defined as squared error and negative log score) of each model versus the ARMA(1,1)-GARCH(1,1) benchmark and we also employ the Model Confidence Set procedure of
Hansen et al. (
2011) using the R package MCS detailed in
Bernardi and Catania (
2016) to jointly compare all predictions. Differences are tested separately for each forecast horizon.
4.2. Point Forecast
Point forecast is evaluated through MAFE for both DMA and DMS as well as for their special case, Bayesian Model Averaging (BMA). For each forecast horizon, the errors are calculated using the following combination of forgetting and discount factors: , , and , and , and finally . In all the cases, the decay factor is fixed to .
Table 2 compares point forecast for
and
as a ratio
(top) and against
(bottom). From the upper table, it emerges that the errors are increasing in accordance with the forecast horizon. Moreover, when
h increases, the ratio increases, meaning that the benchmark model displays better results than DMA and DMS.
Table S8 in Supplementary Materials B shows that increasing the forecasting horizon to
does not improve the forecasting performance of
and
. However,
Section 4.3, which analyses density forecasts results, reveals different outcomes.
Another peculiarity is that forecasts improve when and tend to 1. When we get the worst forecast performance for DMA and DMS, while the best results are obtained with BMA. This may be due to the nature of the series: the presence of outliers and high peaks in BTC series may distort the point forecast.
To see if BTC improves predictability over the S&P 500 a DM test is performed with a level of significance equal to
. Results are reported in
Supplementary Materials Table S2. There is no evidence of an improvement in prediction when the BTC is added to the set of predictors. Further results for different forecast horizons are reported in
Supplementary Materials.
Using point forecast it seems that BTC does not improve predictability over the S&P 500 index.
4.3. Density Forecast
Density forecast is more informative than point forecast, as it is a measure of the prediction uncertainty. The PL, which is the basis of density forecast, comes as a by-product of the adopted estimation strategy.
Table 3 reports the LS: the evidence is striking and the results are almost opposite to those in
Section 4.2. Both
and
provide statistically superior forecasts with respect to
.
The first column reports the PL for the benchmark model (
), and the other columns report the differences of
and
with respect to the benchmark. Among the three models,
shows the worst results in contrast with the results of
Section 4.2. The best forecast result is obtained for
when
; however, the difference between
and
is almost irrelevant. Following the same strategy previously adopted the DM test is carried out, with a significance level of
.
The DM statistics, equal to
, suggest that the null hypothesis of equal forecasting ability is rejected. As discussed in
Harvey et al. (
1997), the DM test could be over-sized when the forecast horizon is greater than one, so in those cases, we used the modified test given by:
where
is the original statistics,
h is the forecast horizon,
P is the forecast evaluation period. The modified version of DM test maintains the same null hypothesis of equal forecasting ability. Whereas, the alternative is that model
is more accurate than model
.
is accepted in this case since the test shows a very high p-value (0.987). In other words, model is performing better than in terms of forecasting. Finally, the MCS indicates that DMS and DMA has similar performance across horizons and they are both superior to the benchmark.
Therefore, the density forecast shows a different outcome to that of the point forecast. While the benchmark model performs better than DMA and DMS in terms of MAFEs, the opposite is true when the density forecast is considered. DMA and DMS give much better predictions for the S&P 500 when the PL is considered.
The main goal of the paper is to understand whether BTC can be assumed to be a good predictor for the S&P 500. Point forecast does not give any contribution to answering this question. A more precise result is reached when the density forecast is used. Even though the PL are close to each other, it has been found that the model that excludes the BTC related series outperforms the one that includes them at lag one. For the other lags, the results are mixed and almost all the models are included in the MCS without a clear superior model. This indicates that BTC does not seem to improve the predictability of the S&P 500 index.
Table S9 in Supplementary Materials reports the results for
and
when the Dow Jones (DJ) index is substituted to S&P500. It emerges that, using DJ, the BTC improves the result of both point and density forecast for shorter horizon (one or two days ahead). These results are promising and carrying out an extensive analysis for different markets is a topic for further research.
5. Conclusions
This work investigates whether BTC can be used as a leading indicator for the S&P500 index. We use the methodologies recently introduced by
Raftery et al. (
2010), which allow the predictor’s weight to change dynamically over time. The study is based on two distinct models: the first—
—includes all the predictors; the second—
—excludes the crypto-predictors. The benchmark model—
—is estimated using an ARMA(1,1)-GARCH(1,1).
The forecasting analysis is based on both point and density forecast. Results coming from the point forecast are not very satisfactory: the outperforms both and . Density forecast provides a totally different outcome: and strongly outperform . Unfortunately, in this case, the DM and the MCS do not give clear evidence about which of the two models is the best. Accordingly, from our results we can conclude that BTC does not show any predictive power over the S&P500 index. In the coming years, cryptocurrencies will surely receive more and more consideration and there is the possibility that our result may be disavowed.