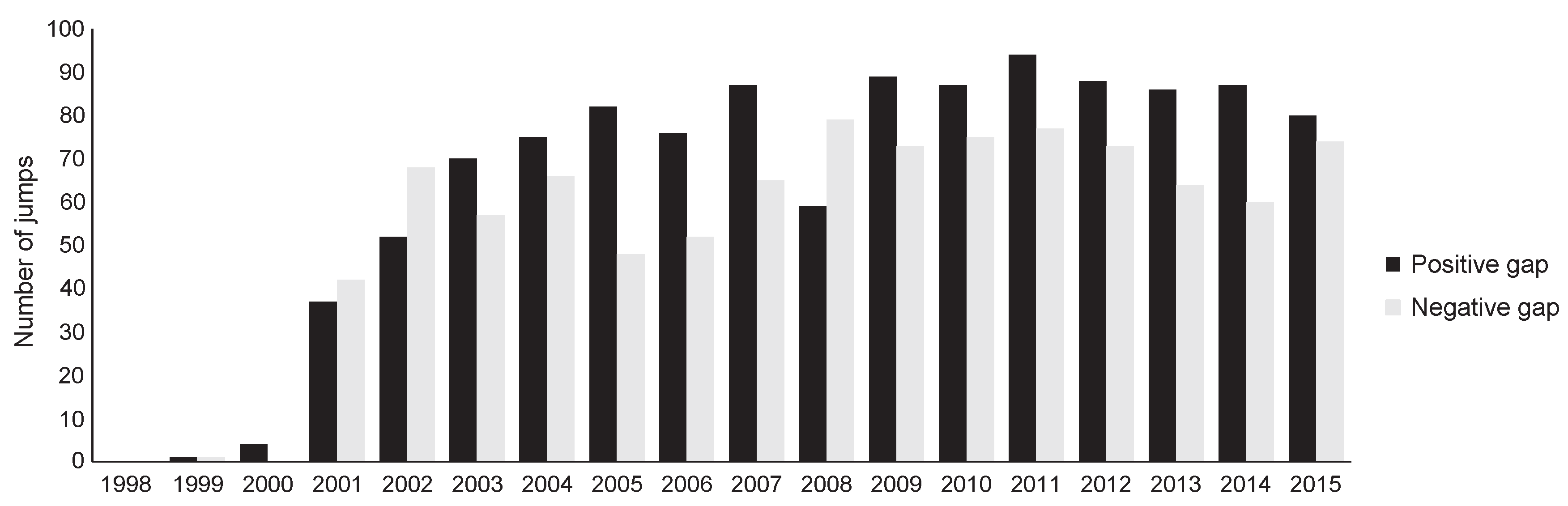1. Introduction
Statistical arbitrage is a market-neutral strategy developed by a quantitative group at Morgan Stanley in the mid-1980s (
Pole 2011). Following
Hogan et al. (
2004), the self-financing strategy describes a long-term trading opportunity that exploits persistent capital market anomalies to draw positive expected profits with a Sharpe ratio that increases steadily over time. Arbitrage situations are identified with the aid of data-driven techniques ranging from plain vanilla approaches to state-of-the-art models. In the event of a temporary anomaly, an arbitrageur goes long in the undervalued stock and short in the overvalued stock (see
Vidyamurthy (
2004),
Gatev et al. (
2006)). If history repeats itself, prices converge to their long-term equilibrium and an investor makes a profit. Key contributions are provided by
Vidyamurthy (
2004),
Gatev et al. (
2006),
Avellaneda and Lee (
2010),
Bertram (
2010),
Do and Faff (
2012), and
Chen et al. (
2017).
The available literature divides statistical arbitrage into five sub-streams, including the time-series approach, which concentrates on mean-reverting price dynamics. Since financial data are exposed to more than one source of uncertainty, it is surprising that there exist only a few academic studies that use a jump-diffusion model (see
Larsson et al. (
2013),
Göncü and Akyildirim (
2016),
Stübinger and Endres (
2018),
Endres and Stübinger (
2019a,
2019b)). In addition to mean-reversion, volatility clusters, and drifts, this general and flexible stochastic model is able to capture jumps and fat tails. First,
Larsson et al. (
2013) used jump-diffusion models to formulate an optimal stopping theory.
Göncü and Akyildirim (
2016) presented a stochastic model for the daily trading of commodity pairs in which the noise-term is driven by a Lévy process.
Stübinger and Endres (
2018) introduce a holistic pair selection and trading strategy based on a jump-diffusion model. Recently,
Endres and Stübinger (
2019a,
2019b) derived an optimal pairs trading framework based on a flexible Lévy-driven Ornstein–Uhlenbeck process and applied it to high-frequency data. All these studies deal with intraday price dynamics and are therefore not in a position to take into account the impact of overnight price changes, an apparent deficit as information is published in media platforms 24 h a day, seven days a week.
This paper enhances the existing research in several aspects. First, our manuscript contributes to the literature by developing a fully-fledged statistical arbitrage framework based on a jump–diffusion model, which is able to capture intraday and overnight high-frequency price dynamics. Specifically, we detect overnight price gaps based on the jump test of
Barndorff-Nielsen and Shephard (
2004) and
Andersen et al. (
2010) and exploit temporary market anomalies during the first minutes of a trading day. The existence of the assumed mean-reverting property is confirmed by a preliminary analysis on the S&P 500 index; this characteristic is particularly significant 120 min after market opening. Second, the value-add of the proposed trading framework is evaluated by benchmarking it against well-known quantitative strategies in the same research area. In particular, we consider the naive S&P 500 buy-and-hold strategy, fixed threshold strategy, general volatility strategy, as well as reverting volatility strategy. Third, we perform a large-scale empirical study on the sophisticated back-testing framework of high-frequency data of the S&P 500 constituents from January 1998–December 2015. Our jump-based strategy produces statistically- and economically-significant returns of 51.47 percent p.a. appropriate after transaction costs. The results outperform the benchmarks ranging from −6.56 percent for the fixed threshold strategy to 38.85 percent for the reverting volatility strategy; complexity pays off. Fourth, a deep-dive analysis shows that our results are consistently profitable and robust against drawdowns even in the last part of our sample period, which is noteworthy as almost all statistical arbitrage strategies have suffered from negative returns in recent years (see
Do and Faff (
2010),
Stübinger and Endres (
2018)). The results pose a major challenge to the semi-strong form of market efficiency.
The remainder of this research study is structured as follows.
Section 2 provides the theoretical framework applied in this study. In
Section 3, we discuss the event study of the S&P 500 index. After describing the empirical back-testing framework in
Section 4, we analyze our results and present key findings in
Section 5. Finally,
Section 6 gives final remarks and an outlook on future work.
3. Event Study of the S&P 500 Index
This section uses the outlined methodology of
Section 2 to identify and analyze overnight price gaps in the S&P 500 index. Following the approaches of
Fung et al. (
2000) and
Grant et al. (
2005), we conducted the following four steps.
At first, the data were filtered according to the event of interest, the presence of overnight gaps. To identify overnight gaps, we conducted daily the BNS jump tests, as introduced in
Section 2.1. For the test, we used high-frequency intraday returns of the previous day and the overnight return and a significance level of 0.1 percent. The timing of jumps was determined by the jump detection procedure of
Andersen et al. (
2010) (see
Section 2.2). If the timing of the jump corresponded with the overnight return, the day was marked as an event day and included in our study.
Second, for every event day, the cumulative return of the S&P 500 index at minute
t after the market opening was computed by:
where
denotes the index price on event day
i at minute
t after the beginning of the trading day. Respectively,
represents the market opening.
Third, the average cumulative return (
) at time
t:
was computed for all event days. This figure is available for any minute
t after the start of the trading day.
N is defined as the total number of days fulfilling the event day properties.
Fourth,
t-tests were conducted to determine whether a given price movement after a specified event was significant. Specifically, we calculated the corresponding test statistic to examine if the
at time
t was significantly distinct from zero. The test statistic had the following form:
where
and
denotes the mean of the sample. Furthermore,
represents its standard deviation, and
N defines the total numbers of days in the filtered dataset. Under the null hypothesis of no distinction from zero, the test statistic follows a
t-distribution with
degrees of freedom.
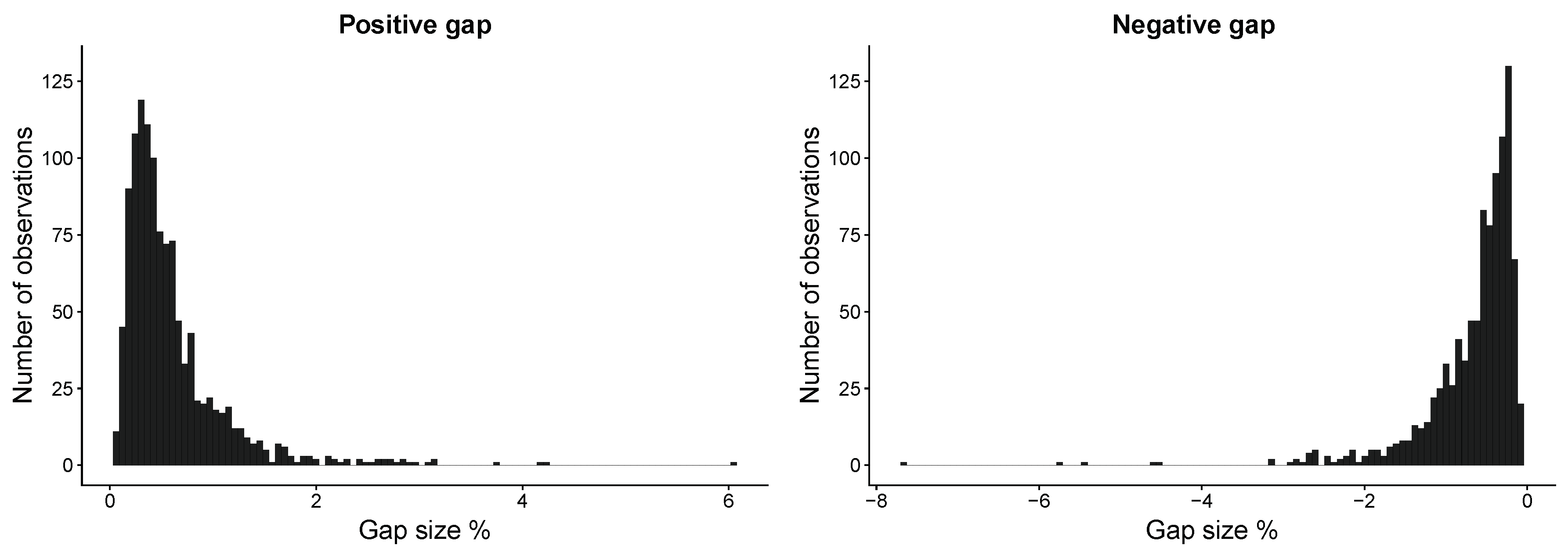
Table 1 shows the characteristics of the overnight price gaps detected by our jump test procedure. In total, we observed 2128 overnight gaps during the sample period: 1154 of those gaps were positive, while 974 were negative. On average, the S&P 500 index faced positive (negative) overnight gaps of 0.60 percent (−0.67 percent). The largest overnight gaps occurred during the global financial crisis with 6.02 percent and −7.64 percent. The fact that both the range and the standard deviation of negative gaps were higher than those of positive overnight movements confirms the existing literature: market participants tend to react stronger to bad news rather than to good headlines (
Suleman 2012). Concluding,
Table 1 shows that there was a sufficient number of overnight price gaps leading to temporary market inefficiencies. As a result, this jump behavior generated high-frequency stock price dynamics that created major trading opportunities. In stark contrast to the approach of
Fung et al. (
2000) and
Grant et al. (
2005), the gaps identified by our jump-test scheme were both flexible and data-driven.
Figure 1 illustrates the detected jumps in a more detailed way. We observe a higher variation of negative overnight gaps, which is not surprising since financial data possess an asymmetric distribution (
Cont 2001). Interestingly, the interval with the highest number of observations for both positive and negative overnight gaps was about
.
Figure 2 presents the number of detected overnight gaps over time. With rising volatility in financial markets, the number of overnight gaps also increased; fluctuations in the market imply jumps. Thus, it is not surprising that we observed almost no jumps in the first years of our sample period. In stark contrast, the number of overnight price gaps increased in times of high market turmoil. In general, more positive than negative gaps affect the S&P 500 index. As expected, this pattern changes during crises such as the dot-com crash in the early 2000s and the financial crisis in 2008. This also demonstrates the flexibility of the approach used to identify overnight gaps.
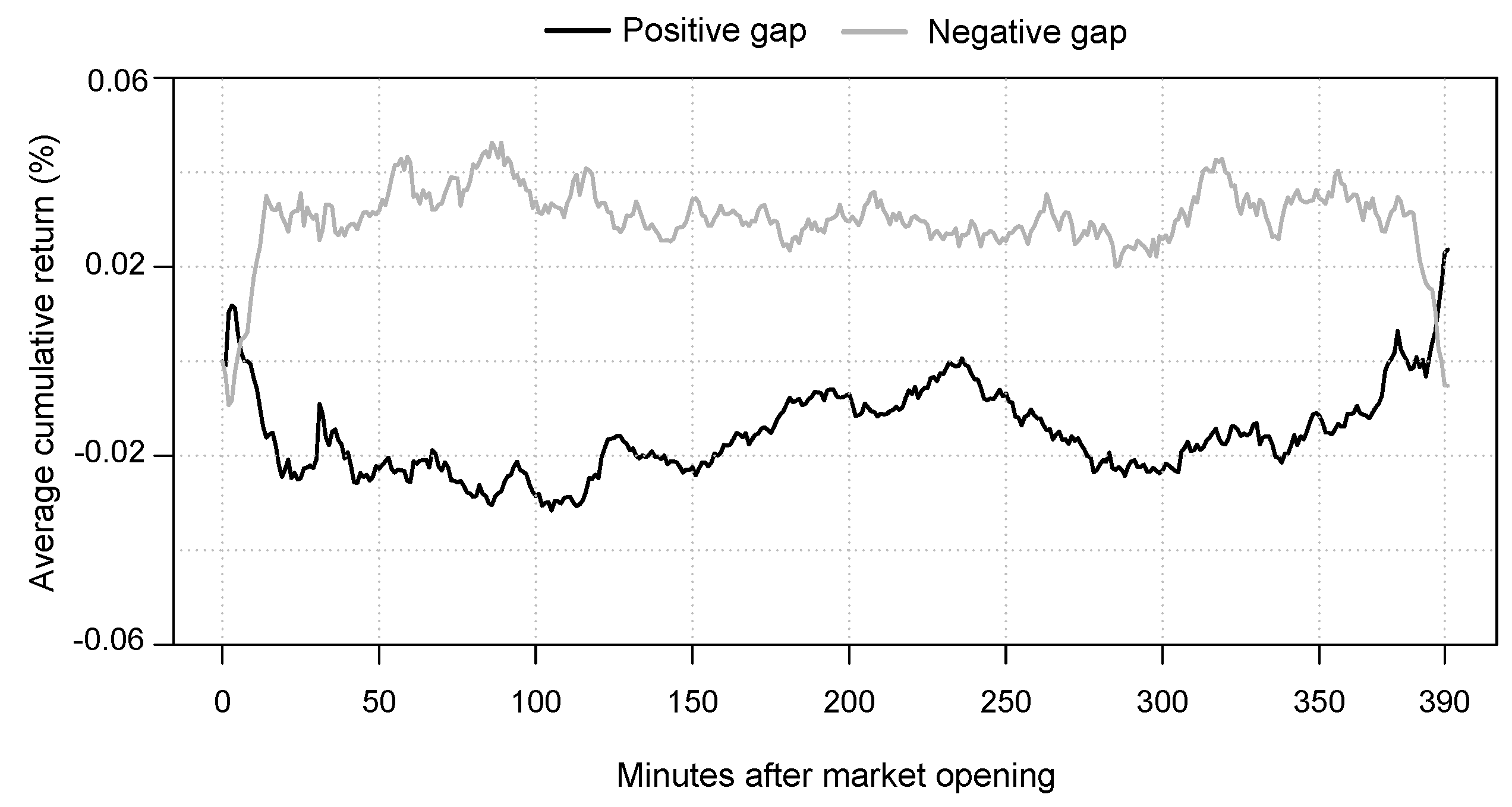
Figure 3 depicts the average cumulative returns after overnight gaps identified by the BNS jump test. The detailed development of the
for positive and negative price gaps is reported in
Table A1. The typical price pattern after overnight gaps is still persistent in modern financial markets, despite that markets should become more efficient in the course of digitalization and improved information flow (see
Fung et al. (
2000) and
Grant et al. (
2005)). In the case of a positive overnight gap, the average cumulative returns rose for a brief period before reverting to the minimum at −0.0316 percent. After reaching the lowest
105 min after market opening, it began to rise until it crossed the zero percent line. From this point, the returns almost fell close to the minimum before increasing again. The upswing accelerated towards market closing, reaching 0.0236 percent at the end of the trading day. Following a negative overnight gap, the
move inverted. Starting with a brief continuation of the initial overnight movement, which marked the minimum of −0.0093 percent two minutes after the stock exchange opens, the
began to reverse to its maximum of 0.0463 percent after approximately one and a half hours. The
remained relatively stable between 0.0200 and 0.0400 percent subsequent to hitting the upper limit. During the last ten minutes, the
rapidly decreased until the end of the trading day. Noticeable is that the magnitude of the variation of the
was stronger after negative price gaps. This is in line with stronger expected reactions of market participants to bad information that was also observable in the represented gap characteristics (
Table 1). The
p-values for both
realizations indicated that the returns were statistically different from zero on a 10 percent significance level for most of the time before the 115-min mark. After that threshold has passed,
p-values well exceeded 10 percent; this fact is not surprising since many professional day traders stop trading after two trading hours because volatility and volume tend to decrease (see
Balance (
2019)). Furthermore, we recognized that the
for positive overnight gaps were not significant for a target time of 5, 35, 65, and 95 min based on a 10% significance level; it seems that the pattern is systematically repeated at 30-min intervals. This statement is confirmed by
Business Insider (
2015), which shows that the trading volume increases in the first minutes of every trading hour. Furthermore,
Bedowska-Sojka (
2013) demonstrated that this volatility is influenced by macroeconomic releases, which are typically published at 9:30, 10:00, 10:30, and 11:00. As a result, the test-statistic decreased, leading to non-significant
p-values.
Concluding, our event study confirms the overreaction hypothesis and supports the results of
Fung et al. (
2000) and
Grant et al. (
2005). The findings of the event study further suggest that we are in a position to develop a statistical arbitrage strategy that exploits the mean-reversion characteristic of stocks after statistically-significant overnight price gaps (see
Poterba and Summers (
1988),
Leung and Li (
2015),
Lubnau and Todorova (
2015)). Specifically, it seems profitable to open trades after overnight gaps and close them after 2 h, i.e., we should set a target time of 120 min.
5. Results
Following the high-frequency research studies of
Mitchell (
2010) and
Knoll et al. (
2018), we conducted a fully-fledged performance evaluation for the top 10 stocks of JDS from January 1998–December 2015 compared to the benchmarks BHS, FTS, GVS, and RVS. In particular, we evaluated the return characteristics and risk metrics (
Section 5.1), examined the performance over time (
Section 5.2), and analyzed the robustness of the strategies (
Section 5.3). According to
Gatev et al. (
2006) and
Avellaneda and Lee (
2010), this paper calculated the total return based on committed capital, i.e., we divided the sum of daily net profits at the current day by the deployed capital.
5.1. Risk-Return Characteristics
Table 3 shows the daily return characteristics and risk metrics before and after transaction costs for the top 10 stocks per strategy from January 1998–December 2015. We observed statistically-significant returns for FTS, GVS, RVS, and JDS with Newey–West (NW)
t-statistics above 15 prior to transaction costs. From an economical point of view, daily returns ranged between 0.17 percent for FTS and 0.36 percent for JDS. If we considered transaction costs, only the mean-reverting strategies RVS and JDS produced positively significant daily returns of 0.13 percent (RVS) and 0.17 percent (JDS). As expected, BHS generated statistically non-significant returns of 0.02 percent per day (see
Endres and Stübinger (
2019b)). The range, i.e., the difference of the maximum and minimum, was vastly different for JDS (approximately 0.30 percentage points), compared to BHS, FTS, GVS, and RVS (approximately 0.15 percentage points); this dissimilarity is potentially driven by the jump-diffusion term. The same argument explains the increased standard deviation of JDS. All individual strategy variants depicted favorable characteristics for any potential investor due to the fact that the underlying returns showed right skewness and followed a leptokurtic distribution (
Cont 2001). We found that the maximum drawdown was quite different for FTS (87.84 percent) and GVS (89.47 percent), in contrast to RVS (55.91 percent), BHS (64.33 percent), and JDS (68.17 percent); the difference between non-reverting and reverting top stocks is clearly pointed out. The hit rate of JDS, i.e., the percentage of days with non-negative returns, outperformed with 58.41 percent after transactions costs, compared to the benchmarks, ranging between 41.79 percent for FTS and 55.92 percent for RVS.
In
Table 4, we depict annualized risk-return measures before transaction costs (left side) and after transaction costs (right side). After transaction costs, JDS produced returns of 51.47 percent p.a., compared to 38.85 percent for RVS, −4.07 percent for GVS, and −6.59 percent for FTS. Thus, the first two strategies achieved meaningfully better results than the naive buy-and-hold strategy (BHS) with an average return of 1.81 percent p.a. Across all strategies, the mean excess return was similar to the mean return because the risk-free rate was very close to zero, especially in the last years. Our jump-based strategy JDS generated approximately the standard deviation of the market, resulting in a Sharpe ratio of 2.38 after transaction costs. This value confirmed the results of the high-frequency studies of
Knoll et al. (
2018) and
Stübinger (
2018). The lower partial moment risk of JDS led to a Sortino ratio of 4.76, compared to the benchmarks ranging between −1.03 (FTS) and 4.67 (RVS). We summarized that JDS outperformed the classic approaches in a large number of comparisons; complexity pays off. Our task was still to evaluate the performance over time, as well as the robustness of the strategies.
5.2. Sub-Period Analysis
Motivated by the time-varying returns of
Liu et al. (
2017) and
Stübinger and Knoll (
2018), we analyzed the stability and potential of the strategies over time.
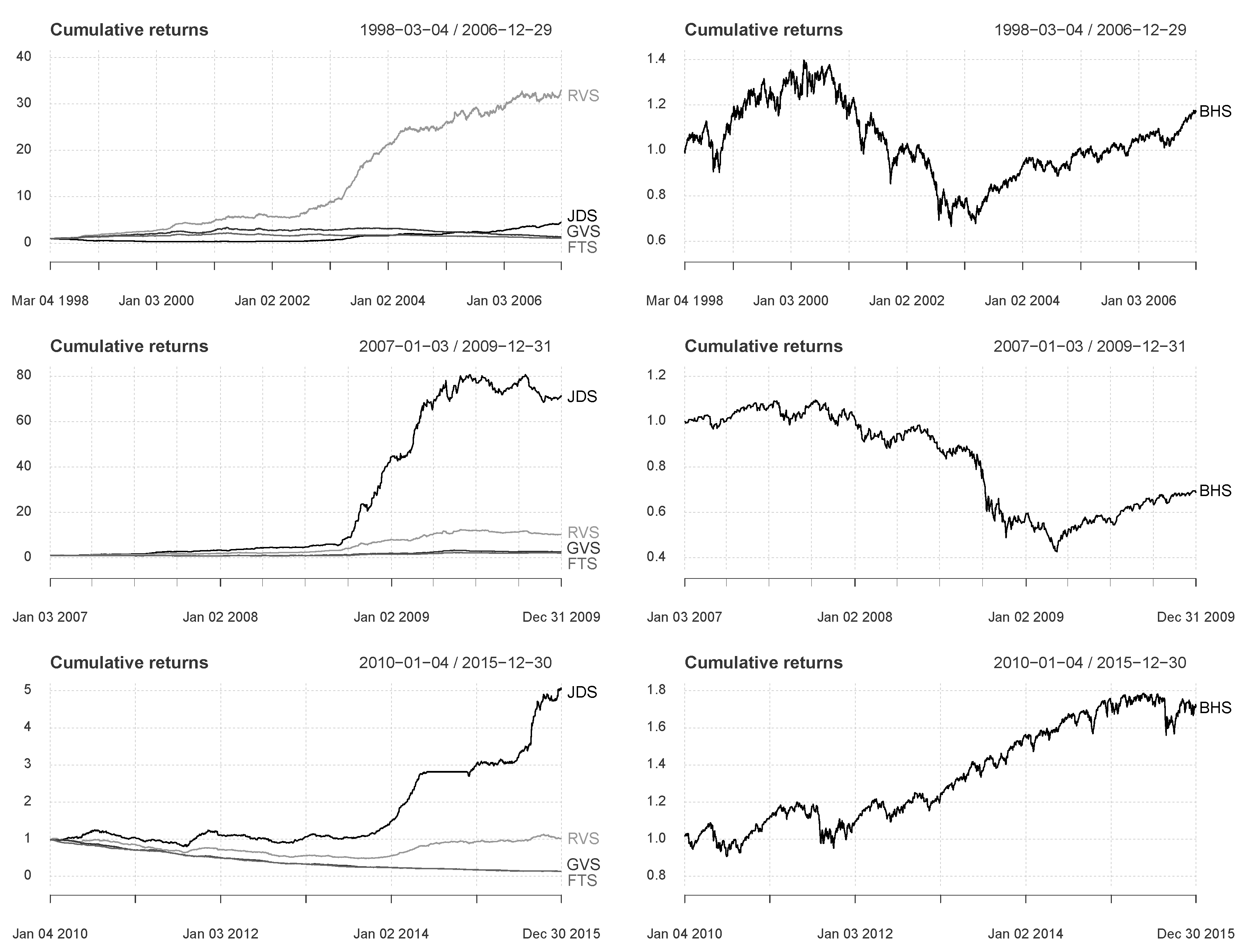
Figure 4, therefore, presents the development of an investment of USD 1 after transaction costs for FTS, GVS, RVS, JDS (first column), and the S&P 500 buy-and-hold strategy BHS (second column) over three partial periods.
Table A2 provides a detailed overview of the corresponding annualized risk-return ratios for sub-periods of three years.
The first sub-period ran from 1998–2006 and described the bursting of the Internet bubble and the start of the Iraq war, as well as the subsequent bull market. We observed meaningful differences in performance between the mean-reverting and non-mean-reverting strategies: the average annual returns after transaction costs of up to 73.76 percent for RVS and up to 64.08 percent for JDS were well above those of BHS (7.87 percent), FTS (27.31 percent), and GVS (42.26 percent). As a typical feature in the financial context, the baseline methods were nevertheless successful in this period due to market inefficiencies and a lack of transparency.
The second sub-period ranged from 2007–2009 and was characterized by the global financial crisis and its consequences. In the course of the sub-prime crisis, the overall market showed strong fluctuations and substantial declines. In contrast, the other strategies generated positive returns, ranging from 27.35 percent for FTS to 315.02 percent for JDS. This strong performance was not astonishing as
Avellaneda and Lee (
2010) and
Rad et al. (
2016) demonstrated that statistical arbitrage trading strategies achieved abnormal returns during bear markets.
The third sub-period extends from 2010–2015 and covered a period of comebacks and restarts. The benchmarks FTS and GVS showed declining trends compared to the overall market, caused by the increasing public availability of these methods. RVS achieved an almost constant cumulative return of one, i.e., this strategy generated exactly the costs that were incurred. For JDS, we observed that 1 USD invested in January 2010 grew to 5 USD after transaction costs; performance did not decline across time and seemed to be robust against drawdowns.
5.3. Robustness Check
As mentioned above, we motivated the target time of 120 min based both on the available literature and the results of our event study; see
Section 3. Since data snooping is a major problem in many financial applications, this subsection examines the sensitivity of our strategies to deviations from their parameter value. In
Table 5, we vary the target time in two directions and report the annualized returns before and after transaction costs for BHS, FTS, GVS, RVS, and JDS.
First of all, we see that our results were robust in the face of parameter variations and always led to statements similar to those in
Section 5.1. As expected, the results of a target time of 120 were identical to those of
Table 3. Furthermore, the annualized returns for each strategy converged as the relative change decreased with increasing target time. The naive S&P 500 buy-and-hold strategy (BHS) always led to an annualized return of 1.81 percent, which is not surprising, since this approach is completely independent of the target time (
Section 4). Furthermore, the performance of FTS increased slightly with ascending target time, e.g., the annualized return after transaction costs was −9.37 percent if we closed the trade at 9:50 and −8.36 percent if we closed it at 13:10. The same statement applies to GVS (−9.70 percent vs. −4.28 percent). Due to their mean-reverting component, RVS and JDS showed a slightly declining performance. For each target time, JDS remained the best variant with annualized returns between 49.65 percent and 62.61 percent, after transaction costs. Obviously, we were not on an optimum, but we found robust trading results, regardless of fluctuations in our parameter setting.
Motivated by the findings in
Section 3,
Table 6 examines the annualized returns for a target time of 5, 35, 65, and 95 min. Most interestingly, annual returns were substantially lower for a target time of 5 min for FTS, GVS, RVS, and JDS because high market turmoil during the opening minutes reduced the results. For a target time of 35, 65, and 95 min, increasing market efficiency during the first minutes of each trading hour did not affect yearly returns before and after transaction costs; our strategies seem to be robust against this effect.
Next, we take a closer look at our S&P 500 buy-and-hold strategy (BHS). The S&P 500 index was purchased in January 1998 and was held for the entire sample period. Of course, BHS is only a baseline approach for betting on the market. Therefore, we followed
Endres and Stübinger (
2019b) and developed a more realistic benchmark: The S&P 500 strategy buys the index at 9:30 and reverses it after 120 min. We observed an annualized return of 1.03% compared to 1.81% for BHS (see also
Table 4). This insufficient performance is not surprising, as it is a baseline approach without modeling.
Finally, this manuscript supposed a high-turnover strategy of an institutional trader on high-frequency prices. Motivated by the literature, our back-testing framework assumed transaction costs of five basis points per share per half-turn, resulting in 20 basis points per round-trip per pair. However, other traders may be less aggressive in implementing this strategy. Therefore, we analyzed the breakeven point of the statistical arbitrage strategy since investors are exposed to different market conditions. We found that the breakeven point of JDS was between 35 basis points and 40 basis points. Concluding, this strategy generated promising results, even for investors that are exposed to different market conditions and thus higher transaction costs.