Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model?
Abstract
:1. Introduction
2. Filtered Historical Simulation Models
- √
- Let denotes the daily log-returns. The benchmark GARCH(1,1) model, introduced by Bollerslev (1986), is defined bywhere , ,, and are the conditional mean and variance, respectively, and is the innovation distribution with zero mean and unit variance. Maximum Likelihood Estimation (MLE) method is widely used to estimate parameters of GARCH models. Under the assumption of independently and identically distributed (iid) innovations with density function, the log-likelihood function of for a sample of T observations is given bywhere is the parameter vector of GARCH model, is the shape parameter(s) of and .The standardized residuals of estimated GARCH(1,1) model are extracted as follows:where is the estimated residual and is the corresponding daily estimated volatility.Now, we can generate the first simulated residual by randomly (with replacement) draw standardized residuals from the dataset with multiplying the one-day ahead volatility forecast:The first simulated return for period can be obtained as follows:where is the first simulated residual for period .
2.1. Normal Distribution
2.2. Skew-Normal Distribution
2.3. Student’s-t Distribution
2.4. Skew-T Distribution
2.5. Generalized Error Distribution
2.6. Skewed Generalized Error Distribution
3. Evaluation of VaR Forecasts
4. Empirical Results
4.1. Data Description
4.2. Backtesting Results
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Angelidis, Timotheos, Alexandros Benos, and Stavros Degiannakis. 2007. A robust VaR model under different time periods and weighting schemes. Review of Quantitative Finance and Accounting 28: 187–201. [Google Scholar] [CrossRef]
- Azzalini, Adelchi. 1985. A class of distributions which includes the normal ones. Scandinavian Journal of Statistics 12: 171–78. [Google Scholar]
- Azzalini, Adelchi, and Antonella Capitanio. 2003. Distributions generated by perturbation of symmetry with emphasis on a multivariate skew t-distribution. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 65: 367–89. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, Kostas Giannopoulos, and Les Vosper. 1999. VaR without correlations for nonlinear portfolios. Journal of Futures Markets 19: 583–602. [Google Scholar] [CrossRef]
- Barone-Adesi, Giovanni, and Kostas Giannopoulos. 2001. Non parametric var techniques. myths and realities. Economic Notes 30: 167–81. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A conditionally heteroskedastic time series model for speculative prices and rates of return. The Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Christoffersen, Peter F. 1998. Evaluating interval forecasts. International Economic Review 39: 841–62. [Google Scholar] [CrossRef]
- Dumitrescu, Elena-Ivona, Christophe Hurlin, and Vinson Pham. 2012. Backtesting value-at-risk: from dynamic quantile to dynamic binary tests. Finance 33: 79–112. [Google Scholar]
- Engle, Robert F., and Simone Manganelli. 2004. CAViaR: Conditional autoregressive value at risk by regression quantiles. Journal of Business & Economic Statistics 22: 367–81. [Google Scholar]
- Hull, John, and Alan White. 1998. Incorporating volatility updating into the historical simulation method for value-at-risk. Journal of Risk 1: 5–19. [Google Scholar] [CrossRef]
- Kupiec, Paul H. 1995. Techniques for verifying the accuracy of risk measurement models. The Journal of Derivatives 3: 73–84. [Google Scholar] [CrossRef]
- Kuester, Keith, Stefan Mittnik, and Marc S. Paolella. 2006. Value-at-risk prediction: A comparison of alternative strategies. Journal of Financial Econometrics 4: 53–89. [Google Scholar] [CrossRef]
- Lee, Ming-Chih, Jung-Bin Su, and Hung-Chun Liu. 2008. Value-at-risk in US stock indices with skewed generalized error distribution. Applied Financial Economics Letters 4: 425–31. [Google Scholar] [CrossRef]
- Mögel, Benjamin, and Benjamin R. Auer. 2017. How accurate are modern Value-at-Risk estimators derived from extreme value theory? Review of Quantitative Finance and Accounting, 1–52. [Google Scholar]
- Nelson, Daniel B. 1991. Conditional heteroscedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Omari, Cyprian Ondieki. 2017. A Comparative Performance of Conventional Methods for Estimating Market Risk Using Value at Risk. International Journal of Econometrics and Financial Management 5: 22–32. [Google Scholar]
- Roy, Indrajit. 2011. Estimating Value at Risk (VaR) using Filtered Historical Simulation in the Indian capital market. Reserve Bank of India Occasional Papers 32: 81–98. [Google Scholar]
- Sarma, Mandira, Susan Thomas, and Ajay Shah. 2003. Selection of Value-at-Risk models. Journal of Forecasting 22: 337–58. [Google Scholar] [CrossRef]
- Ziggel, Daniel, Tobias Berens, Gregor N. F. Weiß, and Dominik Wied. 2014. A new set of improved Value-at-Risk backtests. Journal of Banking & Finance 48: 29–41. [Google Scholar]
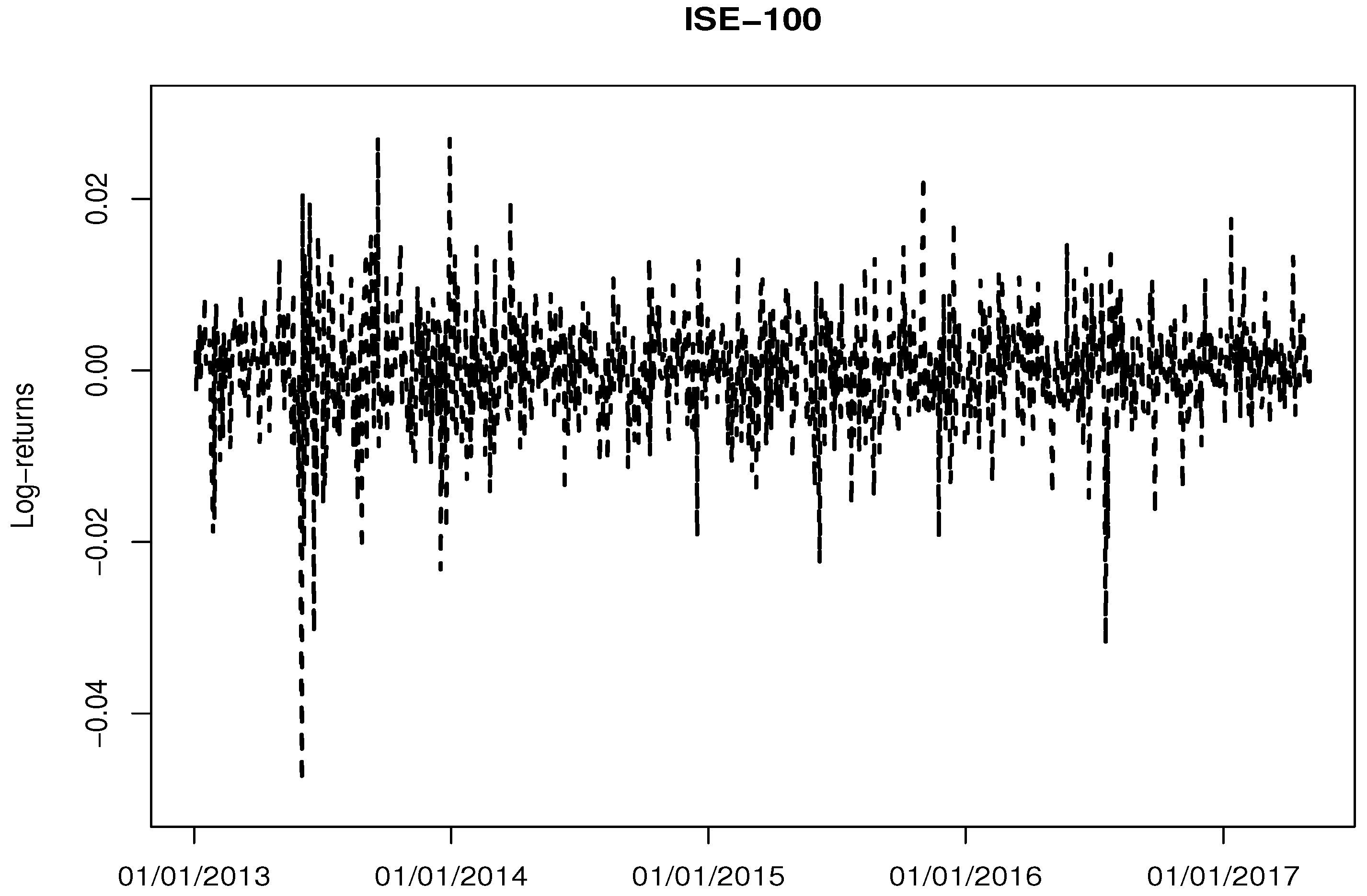
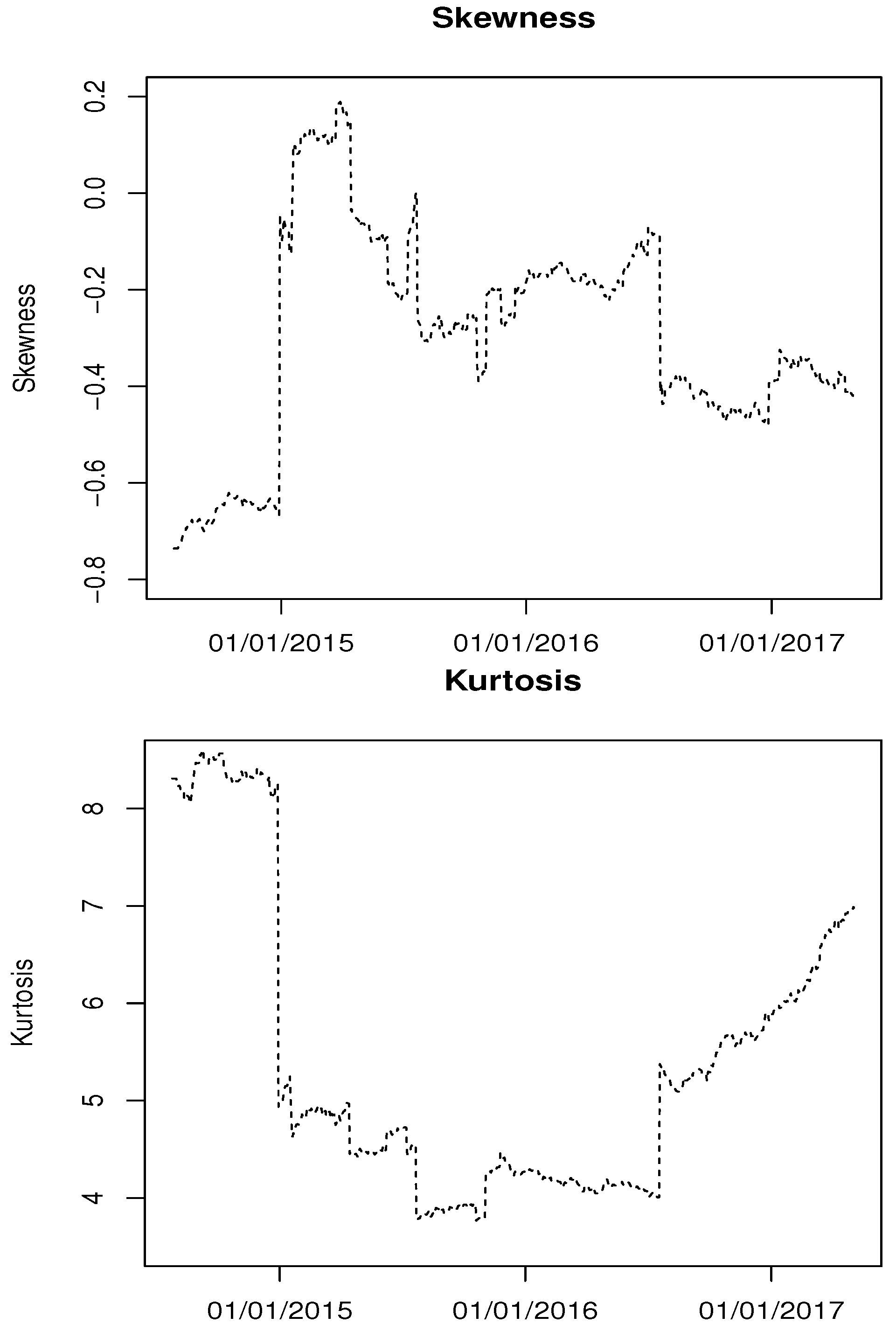
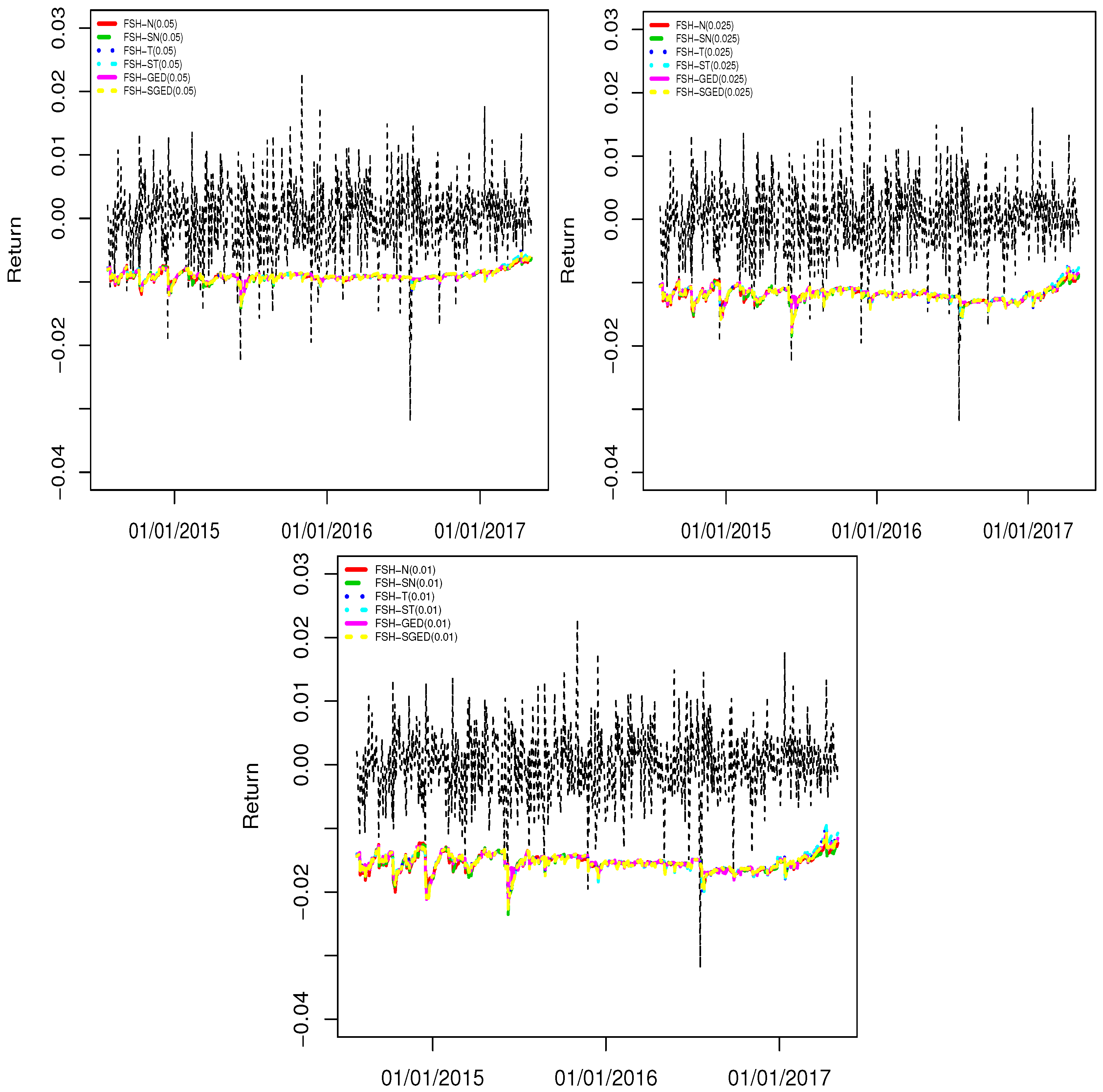
| ISE-100 | |
|---|---|
| Number of observations | 1092 |
| Minimum | −0.048 |
| Maximum | 0.027 |
| Mean | |
| Median | |
| Std. Deviation | 0.006 |
| Skewness | −0.603 |
| Kurtosis | 4.957 |
| Jarque-Bera | 1190.970 (p <0.001) |
| Parameters | Normal | Student-T | ST | SN | GED | SGED |
|---|---|---|---|---|---|---|
| 0.1194 | 0.0759 | 0.1510 | 0.1460 | 0.0930 | 0.0873 | |
| 0.0413 | 0.0336 | 0.2940 | 0.0560 | 0.0393 | 0.0353 | |
| 0.8234 | 0.8908 | 0.8240 | 0.7950 | 0.8600 | 0.8650 | |
| 0.0449 | 0.0485 | 0.3130 | 0.0662 | 0.0518 | 0.0486 | |
| - | 4.7490 | 4.8760 | - | 1.2020 | - | |
| - | 1.1600 | 0.5620 | - | 0.1040 | - | |
| - | - | −0.2750 | −1.5050 | - | 0.8860 | |
| - | - | 2.4260 | 0.2630 | - | 0.0440 | |
| - | - | - | - | - | 1.2200 | |
| - | - | - | - | - | 0.1093 | |
| −1381.1100 | −1405.003 | −1402.2630 | −1388.1800 | −1401.0600 | −1402.7300 |
| p = 0.05 | ||||||
| Models | Mean VaR (%) | N. Of Vio. | Failure Rate | LR-uc | LR-cc | DQ |
| FSH-N | −0.910 | 29 | 0.041 | 1.146 (0.284) | 1.186 (0.552) | 4.586 (0.710) |
| FSH-SN | −0.911 | 29 | 0.041 | 1.146 (0.284) | 1.186 (0.552) | 4.545 (0.715) |
| FSH-T | −0.897 | 32 | 0.046 | 0.278 (0.597) | 0.459 (0.794) | 2.996 (0.885) |
| FSH-GED | −0.899 | 30 | 0.043 | 0.788 (0.374) | 0.863 (0.649) | 4.041 (0.775) |
| FSH-SGED | −0.904 | 30 | 0.043 | 0.788 (0.374) | 0.863 (0.649) | 4.255 (0.749) |
| FSH-ST | −0.897 | 32 | 0.046 | 0.278 (0.597) | 0.459 (0.794) | 3.187 (0.867) |
| p = 0.025 | ||||||
| Models | Mean VaR (%) | N. Of Vio. | Failure Rate | LR-uc | LR-cc | DQ |
| FSH-N | −1.193 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 6.820 (0.448) |
| FSH-SN | −1.196 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 6.805 (0.449) |
| FSH-T | −1.177 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 4.056 (0.773) |
| FSH-GED | −1.179 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 4.579 (0.711) |
| FSH-SGED | −1.187 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 5.102 (0.647) |
| FSH-ST | −1.177 | 20 | 0.029 | 0.350 (0.554) | 0.630 (0.729) | 4.051 (0.774) |
| Models | Mean VaR (%) | N. Of Vio. | Failure Rate | LR-uc | LR-cc | DQ |
| FSH-N | −1.546 | 9 | 0.013 | 0.529 (0.466) | 0.764 (0.682) | 15.479 (0.030) |
| FSH-SN | −1.549 | 9 | 0.013 | 0.529 (0.466) | 0.764 (0.682) | 16.338 (0.022) |
| FSH-T | −1.526 | 9 | 0.013 | 0.529 (0.466) | 0.764 (0.682) | 13.185 (0.067) |
| FSH-GED | −1.530 | 8 | 0.011 | 0.137 (0.710) | 0.323 (0.851) | 16.115 (0.024) |
| FSH-SGED | −1.538 | 9 | 0.013 | 0.529 (0.466) | 0.764 (0.682) | 14.620 (0.041) |
| FSH-ST | −1.526 | 9 | 0.013 | 0.529 (0.466) | 0.764 (0.682) | 12.893 (0.075) |
| p = 0.05 | ||||||
| Models | ARLF | Min.-Max. ARLF | UL | Min.-Max. UL | FLF | Min.-Max. FLF |
| FSH-N | 0.0172063 | (, 5.133) | −0.0179110 | (−2.265, −0.010) | 0.0283988 | (, 5.133) |
| FSH-SN | 0.0171900 | (, 5.121) | −0.0178643 | (−2.263, −0.011) | 0.0283877 | (, 5.121) |
| FSH-T | 0.0173740 | (, 5.150) | −0.0181385 | (−2.269, ) | 0.0284271 | (, 5.150) |
| FSH-GED | 0.0172983 | (, 5.135) | −0.0180858 | (−2.266, −0.001) | 0.0283820 | (, 5.135) |
| FSH-SGED | 0.0173162 | (, 5.145) | −0.0179867 | (−2.268, −0.004) | 0.0284463 | (, 5.145) |
| FSH-ST | 0.0173437 | (, 5.127) | −0.0181591 | (−2.264, −0.003) | 0.0283897 | (, 5.127) |
| p = 0.025 | ||||||
| Models | ARLF | Min.-Max. ARLF | UL | Min.-Max. UL | FLF | Min.-Max. FLF |
| FSH-N | 0.0097984 | (0.003, 3.896) | −0.0108364 | (−1.974, −0.058) | 0.0228029 | (0.003, 3.896) |
| FSH-SN | 0.0097622 | (0.001, 3.863) | −0.0107498 | (−1.965, −0.033) | 0.0227883 | (0.001, 3.863) |
| FSH-T | 0.0098350 | (0.002, 3.886) | −0.0108600 | (−1.971, −0.049) | 0.0226889 | (0.002, 3.886) |
| FSH-GED | 0.0097898 | (0.004, 3.876) | −0.0108694 | (−1.968, −0.063) | 0.0226529 | (0.004, 3.876) |
| FSH-SGED | 0.0098099 | (0.002, 3.893) | −0.0107848 | (−1.973, −0.040) | 0.0227502 | (0.002, 3.893) |
| FSH-ST | 0.0098287 | (0.002, 3.884) | −0.0108752 | (−1.971, −0.049) | 0.0226755 | (0.002, 3.884) |
| p = 0.01 | ||||||
| Models | ARLF | Min.-Max. ARLF | UL | Min.-Max. UL | FLF | Min.-Max. FLF |
| FSH-N | 0.0052475 | (, 2.885) | −0.0051635 | (−1.698, −0.008) | 0.0212668 | (, 2.885) |
| FSH-SN | 0.0052483 | ( , 2.893) | −0.0051776 | (−1.700, −0.009) | 0.0213011 | (, 2.893) |
| FSH-T | 0.0052399 | (, 2.914) | −0.0051979 | (−1.707, −0.011) | 0.0210625 | (, 2.914) |
| FSH-GED | 0.0052125 | (, 2.882) | −0.0051546 | (−1.697, −0.017) | 0.0210964 | (, 2.882) |
| FSH-SGED | 0.0052148 | (, 2.883) | −0.0051849 | ( −1.697, −0.019) | 0.0211543 | (, 2.883) |
| FSH-ST | 0.0052135 | (, 2.895) | −0.0051634 | (−1.701, −0.006) | 0.0210319 | (, 2.895) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Altun, E.; Tatlidil, H.; Ozel, G.; Nadarajah, S. Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model? J. Risk Financial Manag. 2018, 11, 7. https://doi.org/10.3390/jrfm11010007
Altun E, Tatlidil H, Ozel G, Nadarajah S. Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model? Journal of Risk and Financial Management. 2018; 11(1):7. https://doi.org/10.3390/jrfm11010007
Chicago/Turabian StyleAltun, Emrah, Huseyin Tatlidil, Gamze Ozel, and Saralees Nadarajah. 2018. "Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model?" Journal of Risk and Financial Management 11, no. 1: 7. https://doi.org/10.3390/jrfm11010007
APA StyleAltun, E., Tatlidil, H., Ozel, G., & Nadarajah, S. (2018). Does the Assumption on Innovation Process Play an Important Role for Filtered Historical Simulation Model? Journal of Risk and Financial Management, 11(1), 7. https://doi.org/10.3390/jrfm11010007




