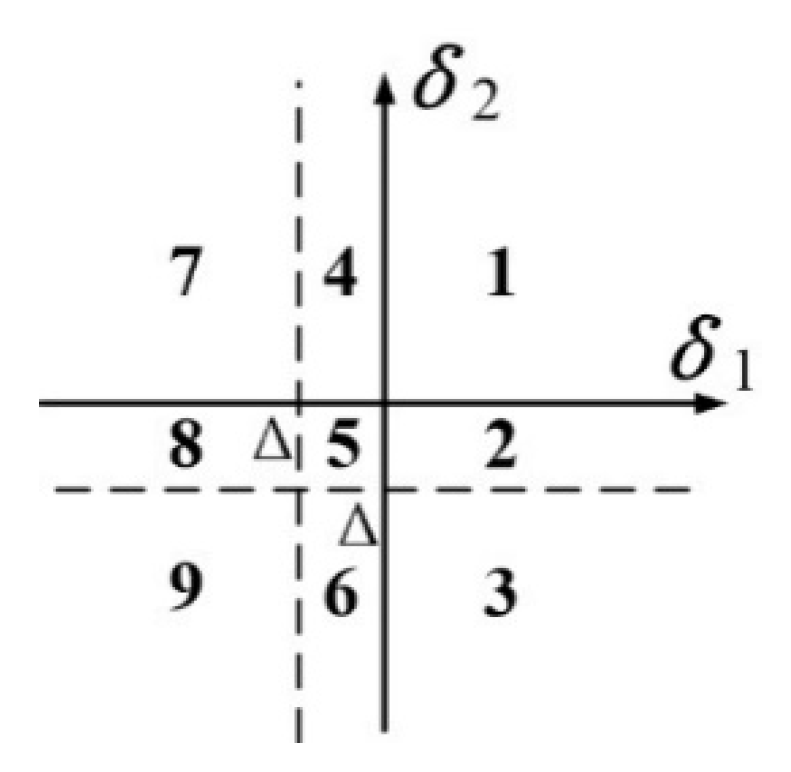
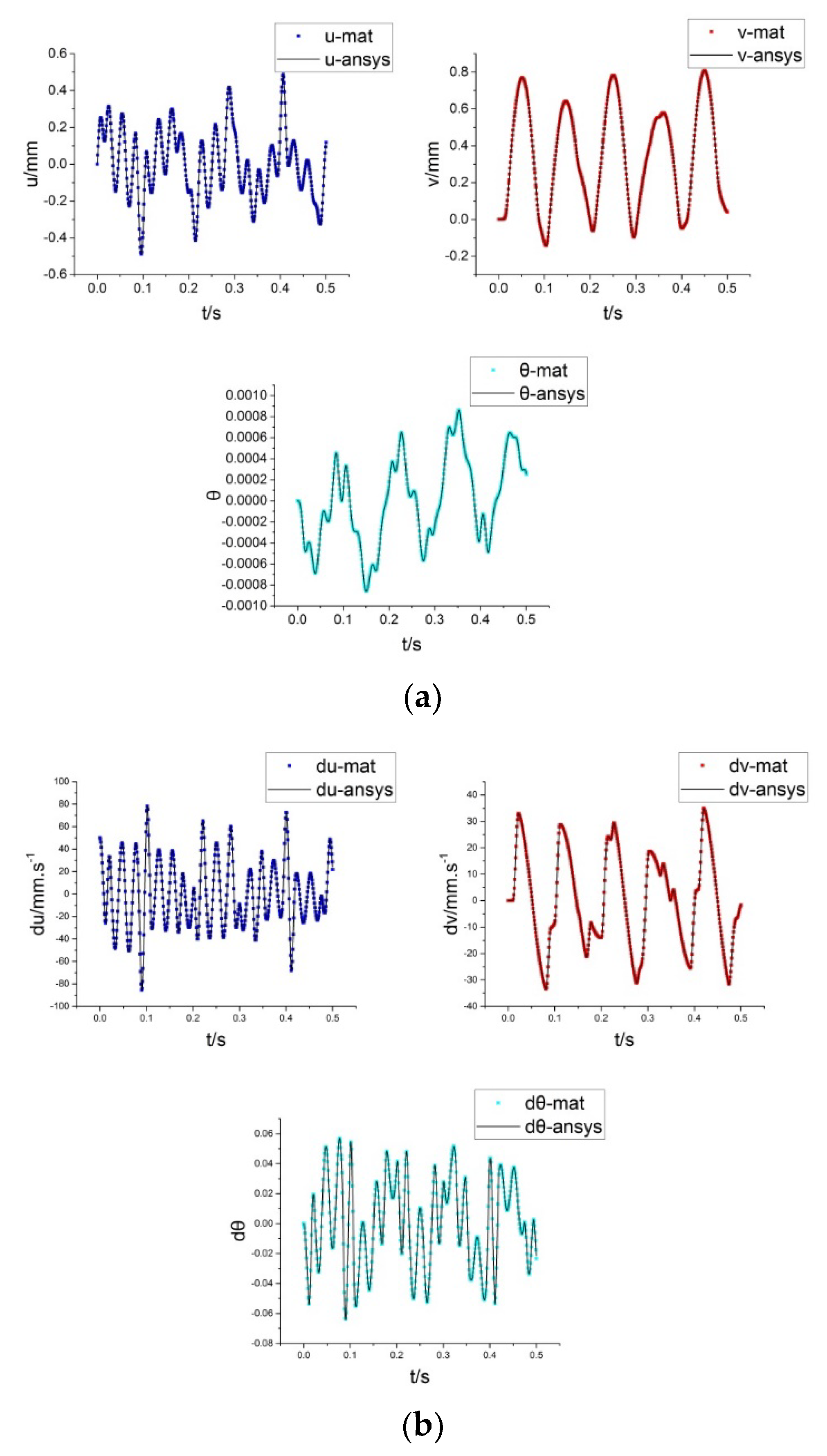
3.3.1. Response under Axial Impact Loading
For a 3-dof trilinear system, the system generates an initial velocity along the axial direction under an axial shock, ignoring the time effect of the shock load, and directly assigning the system initial conditions , , where , and the system response is calculated by the half-numerical analysis method.
Take
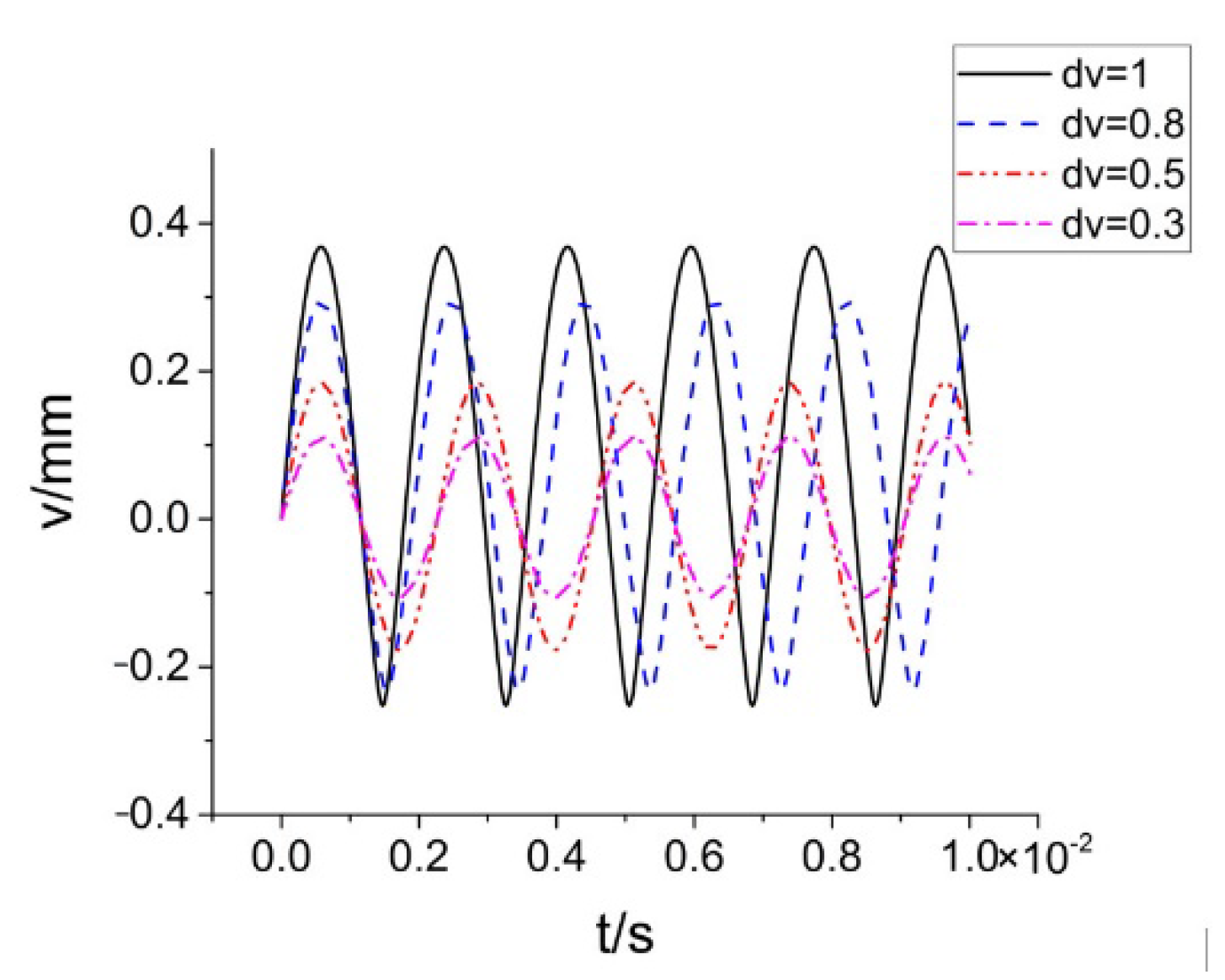
, the system only vibrates along the axial direction. Its axial displacement curve is shown in
Figure 10, and dv is the axial initial velocity in the legend. The 0.1 s response time of the system is intercepted, and the motion time of each region of the system is counted, as shown in
Table 6. Under the condition that the initial displacement of the system is zero, when the system is subjected to a small axial shock, the system only moves in region 1 and region 5, and the axial response frequency of the system is fixed. When the system is subjected to a large axial shock, the system moves in regions 1, 5, and 9, and the axial response frequency of the system increases with the increase in the shock load.
The first-order response frequency of the system is shown in
Figure 11, conducting the fast Fourier transform. Under the condition that the initial displacement is zero, the axial response frequency of the system is 441 Hz when the initial axial velocity satisfies
. Combined with
Figure 10 and
Table 6, it can be seen that the system only moves in regions 1 and 5 at this time, and its axial response frequency is independent of the magnitude of the impact load. With initial axial velocity
, the axial response frequency of the system increases with the increase of the impact load magnitude, which is due to the fact that the system starts to move in region 9.
In fact, by substituting the frequencies and vibration shapes of the system in
Table A4 into Equations (46) and (48), we can learn that the system has only axial displacement response in region 1, region 5, and region 9, and its response frequencies are
,
and
. When the axial impact load is small, the system moves only in regions 1 and 5, and within one vibration cycle, the system moves in region 1 with time of
and in region 5 with time of
. Let the system’s motion frequency be
f and period 1/
f, and then, the theoretical response frequency of the system satisfies:
Calculation by substitution gives f = 441 Hz, which is consistent with the fast Fourier transform results.
When the axial shock load is large, the system moves in regions 1, 5, and 9. Region 5 is the region formed by the assembly gap; when the axial shock is large enough, the system moves in region 5 for a short time, and this part of time can be ignored in the limit state, when the theoretical response frequency of the system satisfies:
Then, we can get f = 722.3 Hz.
Since the actual shock load cannot be very large, region 5 still affects the response frequency of the system, the magnitude of which depends on the magnitude of the shock load, and the response frequency should be between 441 and 722.3 Hz. The system response is highly sensitive to the magnitude of the load, which is one of the typical characteristics of nonlinear systems.
3.3.2. Response under Lateral Impact Loading
Similar to the axial shock, for a 3-dof trilinear system, the system generates an initial velocity along the lateral direction under the lateral shock, neglecting the time effect of the shock load, and directly assigning the system initial conditions , where ; the system response is calculated by the half-numerical analysis method.
The displacement response of the system is shown in
Figure 12, by taking
and
, respectively. When the initial displacement of the system is zero, the system will produce axial displacement and turning angle in bending direction under the lateral impact load, and the three directions of system motion are completely coupled. When the lateral impact load is small (e.g.,
), the axial displacement of the system is not significant, and the main motion is rotation and translation along the lateral direction; when the lateral impact load is large (e.g.,
), it will produce a large axial displacement response, of which the magnitude is close to the lateral displacement.
The displacement response of the system was intercepted within 1 s, and the motion time of the system in each division was counted, as shown in
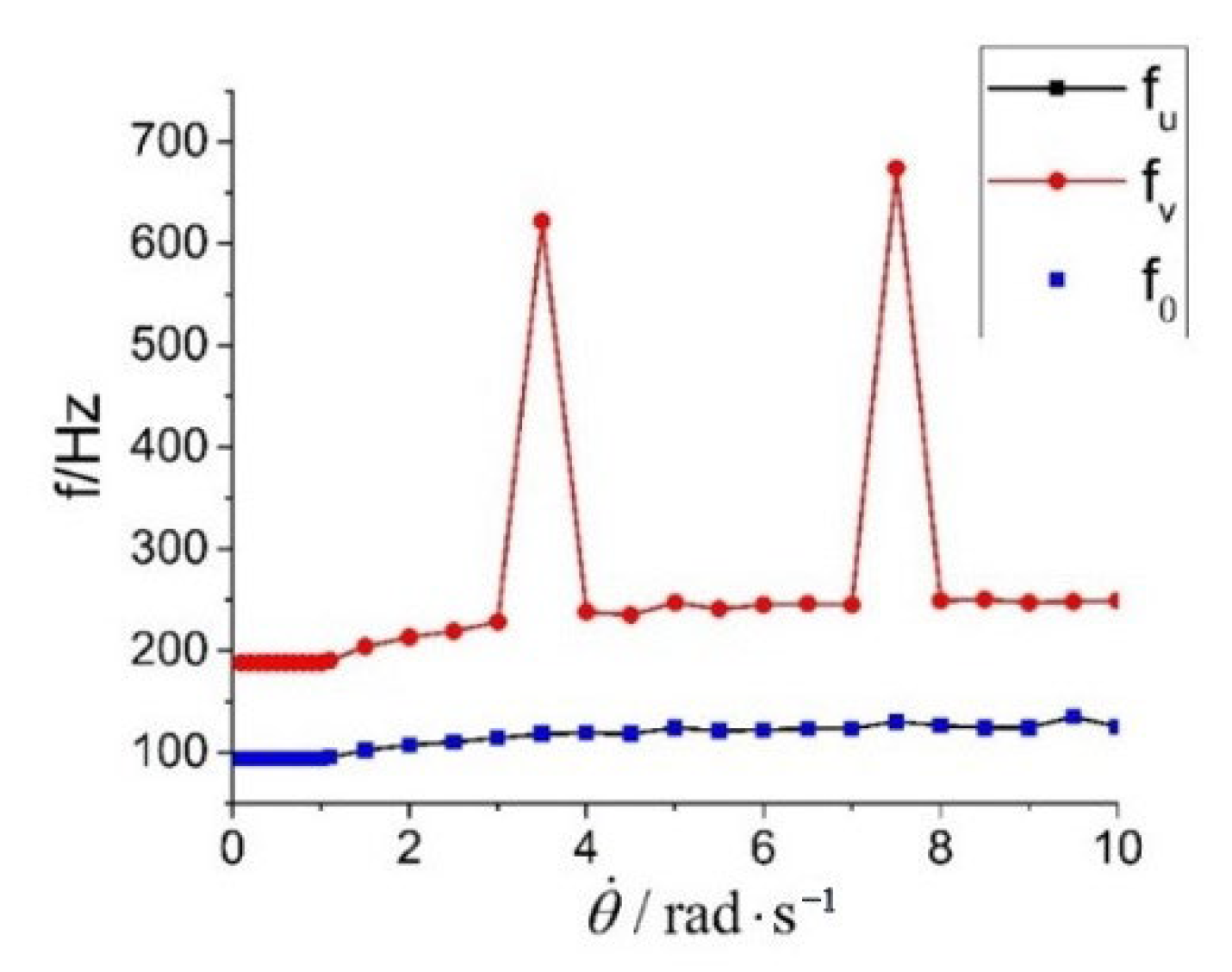
Table 7. The response is very sensitive to the magnitude of the impact load, and the first-order response frequencies of the system in each degree of freedom under different lateral impact conditions are shown in
Figure 13, by performing the fast Fourier transform. It can be seen that the first-order response frequencies in the lateral and bending directions under the impact conditions are identical, while the first-order response frequency in the axial direction is twice as high as that in the lateral and bending directions in most cases. Due to the nonlinear characteristics of the system, the axial direction produces a higher first-order response frequency under certain impact conditions.
(1) System response under small lateral impact loads.
When the lateral impact load is small, the first-order response frequencies of the system in the lateral, axial, and corner directions are approximately 94 Hz, 188 Hz, and 94 Hz, respectively, and remain constant.
Table 7 shows that the main motion regions of the system at this time are regions 2 and 4, and the spring states on the left and right sides are tensile on one side and compressive on the other side, and the compression is less than the assembly gap
. The tensile stiffness of the tri-linear spring is
, and the compression stiffness with clearance is
; the stiffness values are close to each other, so the symmetry of the system motion is good. Considering only the motion of the system in regions 2 and 4, and substituting the frequencies and vibration patterns of the two regions and the initial conditions of the system into Equation (46), the system response can be approximately resolved. With initial conditions of
, the system response in region 2 is:
When the system enters region 4 from region 2, the initial condition is approximated as
; then, the response in region 4 is:
Combining Equation (61) and Equation (62) yields an approximate analytical expression for the displacement response of the system as:
When
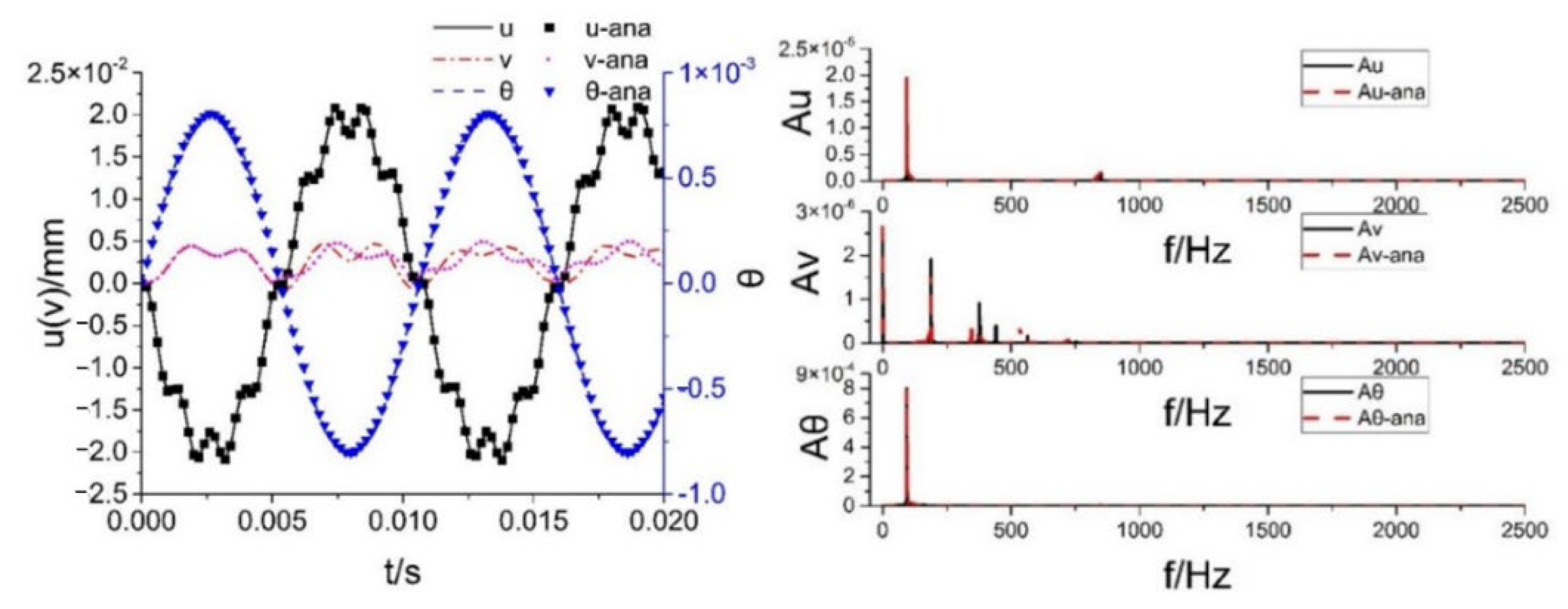
, the displacement response of the system obtained by the half-value analytical calculation method and the approximate analytical expression is shown in
Figure 14; “-ana” represents the result of the approximate analytical expression, and the lateral displacement and rotation angle of both are basically the same. The two axial displacements are basically the same in magnitude, but the specific values are slightly different, which is due to the fact that when the system enters region 4 from region 2 during the approximate analytical calculation, the system state is assumed to be
, which is different from the actual situation.
The amplitude frequency curves obtained from the displacement responses of the two methods are shown in
Figure 14. It can be seen that the displacement response frequencies of the lateral and bending directions of the system obtained by the two methods are basically the same, both being 94.1 Hz and 849.4 Hz, and the magnitude of the displacement response of 441.3 Hz in Equation (63) is very small and can be ignored. The first-order response frequencies of axial displacements are consistent, both being 188 Hz, but the response frequencies of higher orders are significantly different.
In summary, when the lateral impact load is small, the lateral and bending direction displacement response of the system can be solved by Equation (63), and its axial displacement response is small in magnitude and can be neglected.
(2) System response under large lateral impact loads
When the lateral impact load is large (as the resulting lateral initial velocity
), as can be seen from
Table 7, the motion time of the system in region 2 and region 4 is significantly reduced. When the lateral impact is large enough, its motion trajectory is spread over all nine regions, and the response is more complex and difficult to analytically calculate, which can only be solved by the semi-numerical analytical calculation method.
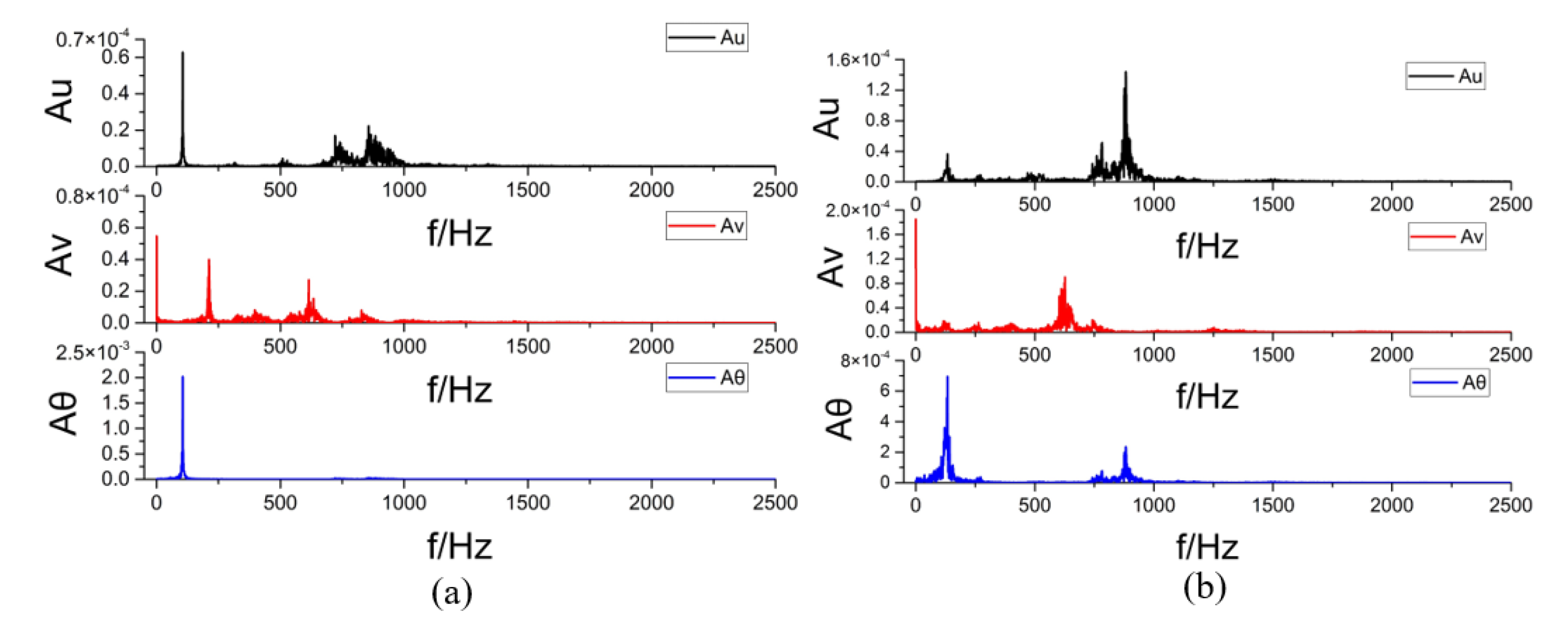
The amplitude frequencies of the system are shown in
Figure 15, taking
and
. Compared with the small impact load condition, the amplitude spectrum under a large impact load has more local peaks, and the amplitude spectrum will change with the impact load. When
, the first-order response frequency of the system in both lateral and bending directions is 106 Hz, the higher-order response frequency amplitude is smaller, and the axial first-order response frequency is 212 Hz, which is twice that of the lateral and bending directions. When
, the first-order response frequency of the system in both lateral and bending directions is 133 Hz, the higher-order response frequency amplitude is significantly higher, and the axial first-order response frequency is about 627 Hz, which is no longer two times that of the lateral and bending directions. Therefore, in the design of the connection structure, attention should be paid to the change in response frequency due to structural nonlinearity to avoid frequency peaks.
In fact, in the axial response plot in
Figure 15b, there is also a local peak near 212 Hz. However, due to its small amplitude, the response characteristics are not obvious, defining the more pronounced peak at 627 Hz as the axial first-order frequency. This is also the reason for the jump in the axial first-order frequency in
Figure 13.
3.3.3. System Response under Bending Moment Impact Loading
For a 3-dof trilinear system, the system generates angular velocity under the bending moment impact load, neglecting the time effect of the impact load, and directly assigning the system initial conditions , where ; the system response is calculated by the semi-numerical value resolution method.
The displacement response of the system was intercepted within 1 s, and the motion duration of the system in each division was counted, as shown in
Table A5. The system response was very sensitive to the magnitude of the impact load, and the first-order response frequencies of each degree of freedom of the system under different lateral impact conditions were obtained by doing the fast Fourier transform on the system response, as shown in
Figure 16.
Since the top side of the cabin is the free end and the bottom side of the cabin is the bound end, the lateral motion of the bottom side always causes the cabin to rotate, and the first-order response frequencies of the system in the lateral and bending directions are exactly the same. Due to the symmetry of the motion, the first-order response frequency in the axial direction is twice as high as that in the lateral direction. However, in specific cases, the amplitude of this multiplier frequency in the axial direction is small, and its first-order frequency migrates to high frequencies. Under small impact loads (i.e., the angular velocity generated is less than or equal to 1 rad/s), the displacement response frequency of the system does not vary with the load, and the first-order displacement response frequencies in the lateral, axial, and bending directions remain at 94 Hz, 188 Hz, and 94 Hz, respectively.
From
Table A5, it can be seen that the system mainly moves in regions 2 and 4 under small impact loads, and the motion time in region 5 is short and can be neglected in the approximate analytical calculation. Substituting the vibration type, frequency, and initial conditions of the system into Equation (46), the response of the system in region 4 is:
When the system enters region 2 from region 4, the initial condition is approximated by
, then the response in region 2 is:
Combining Equations (64) and (65) yields an approximate analytical expression for the displacement response of the system as:
The displacement responses and amplitude frequencies of the half-value semi-analytic calculation method and the approximate analytical method are shown in
Figure 17. It can be seen that the displacement responses and amplitude frequencies of the system in the lateral and bending directions obtained by the two methods are basically the same. The axial displacement response is consistent in the initial stage, but when the system enters region 2 from region 4, the approximate analytical method ignores the small amount of system displacement and velocity, which leads to the difference in the later stage.
When the bending impact load is large (i.e., the resulting angular velocity is greater than or equal to 1.1 rad/s), the system motion is no longer confined to regions 2 and 4, and it is difficult to analytically calculate the system response because the motion state of the system cannot be judged when the motion region changes. The displacement response and the amplitude frequency of the system at the initial angular velocity are shown in
Figure 18. It can be seen that the response frequency of the system changes slightly under different impact loads, especially the axial displacement response, whose first-order response frequency corresponds to a significant decrease in amplitude under a specific impact load. Due to the nonlinearity of the system, the influence of load magnitude should be considered when analyzing its dynamic characteristics.