Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review
Abstract
1. Introduction
2. Materials and Methods
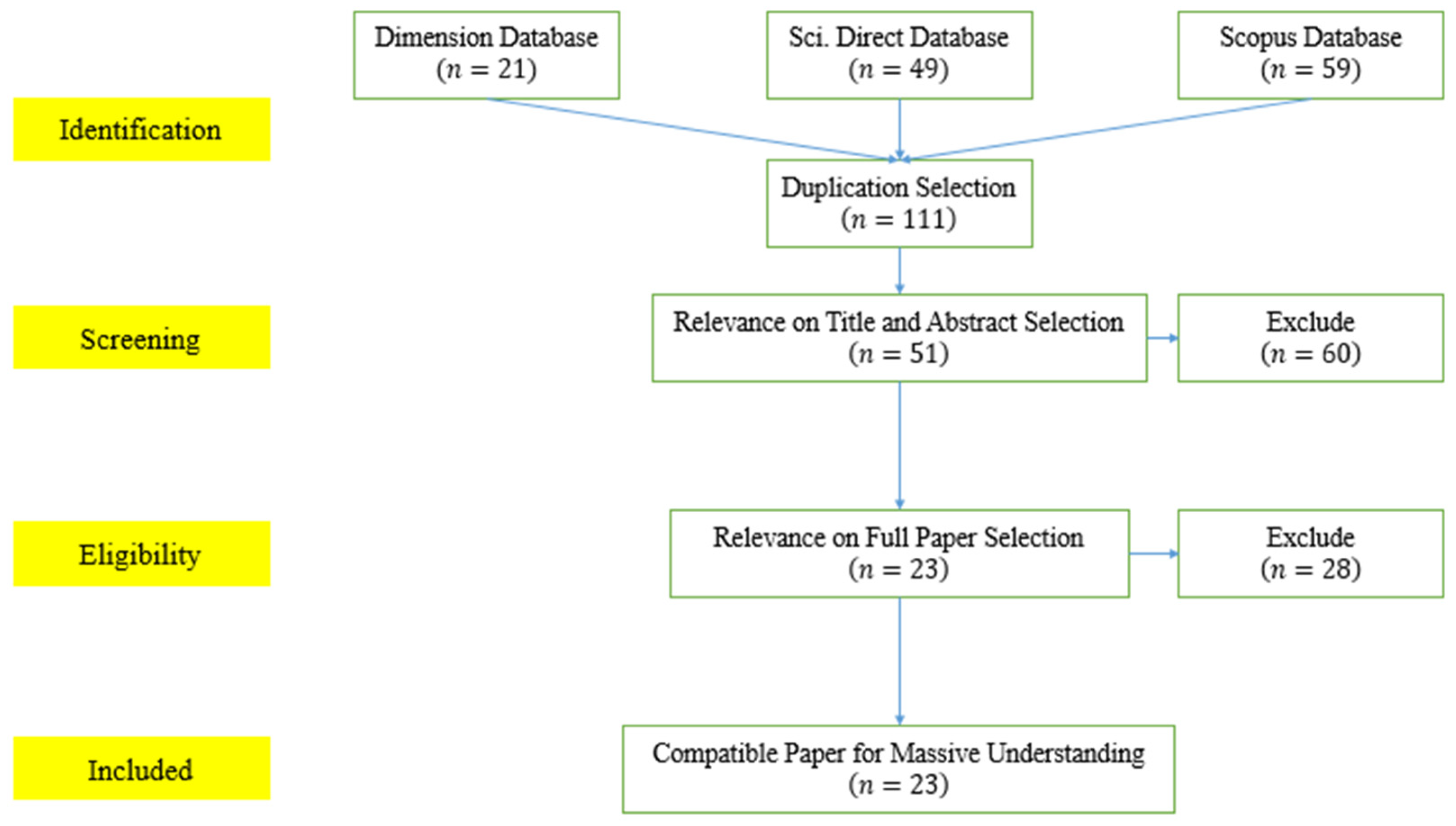
2.1. The PRISMA Method
2.2. Bibliometric Analsysis
3. Results and Discussion
3.1. Bibliometric Analysis Results
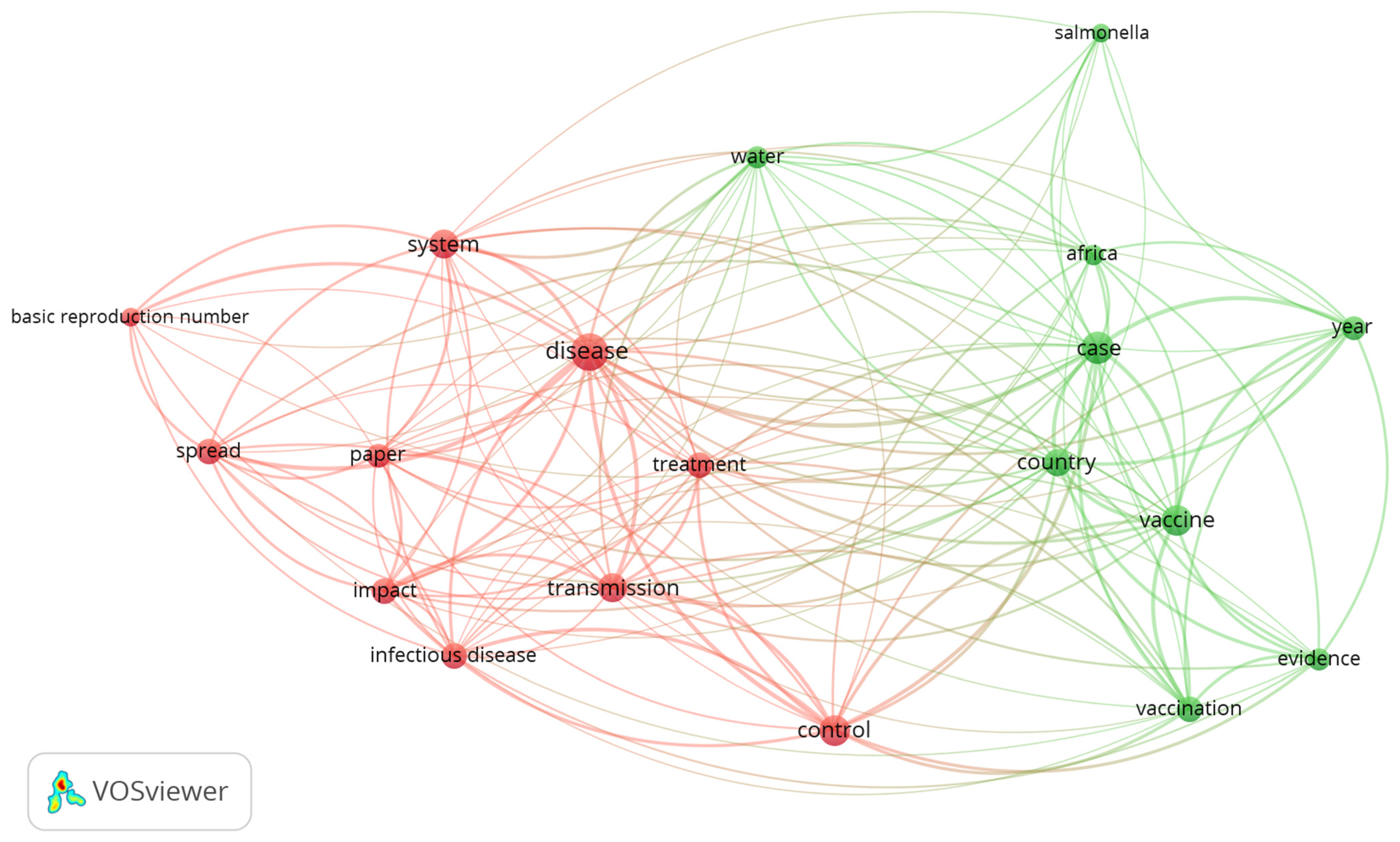
3.1.1. Visualization of the Occurrence–Word Relation in Dataset 1
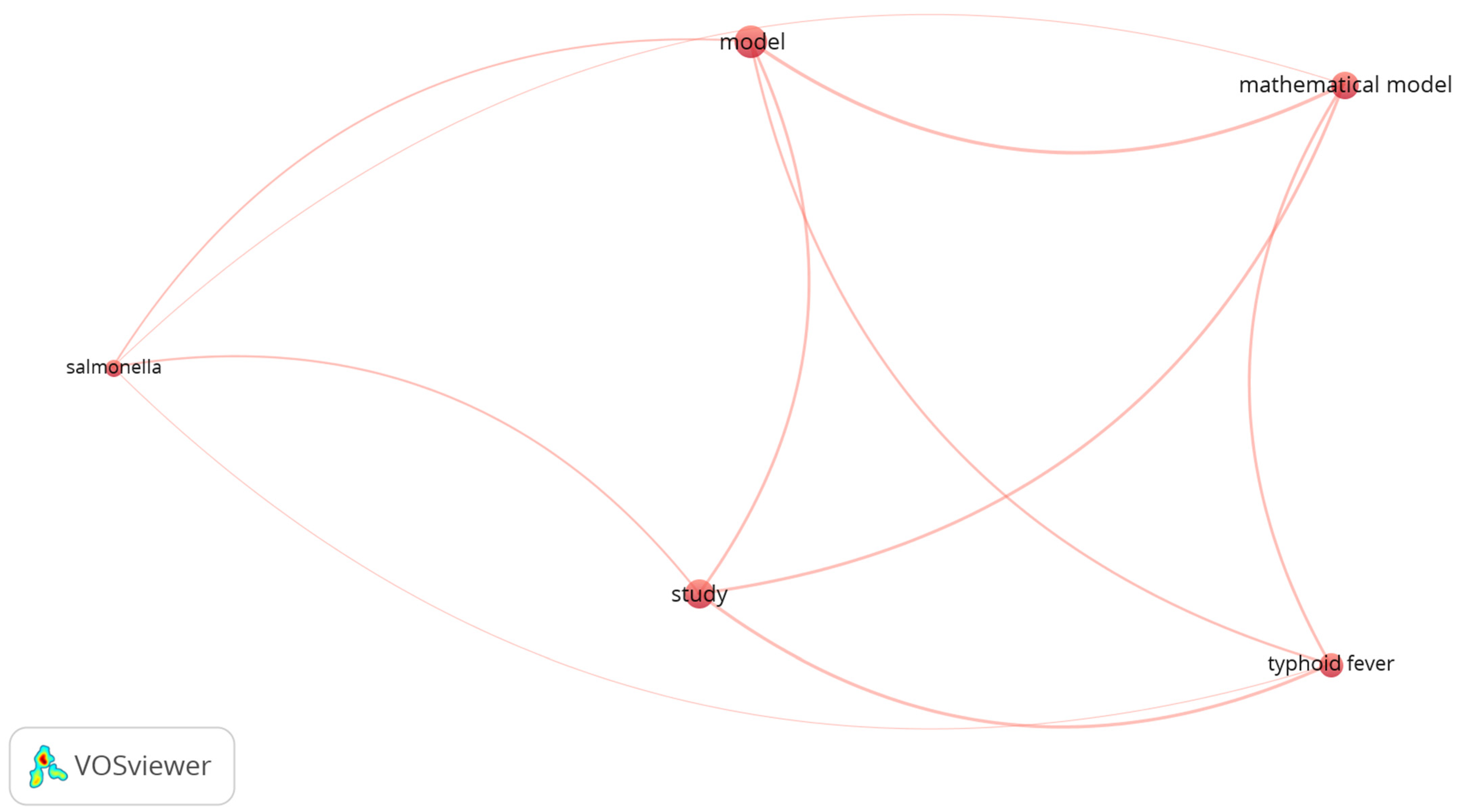
3.1.2. Visualization of the Occurrence–Word Relation in Dataset 2
3.2. Systematic Literature Review Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crump, J.A. Progress in Typhoid Fever Epidemiology. Clin. Infect. Dis. 2019, 68, 4–9. [Google Scholar] [CrossRef] [PubMed]
- House, D.; Bishop, A.; Parry, C.; Dougan, G.; Wain, J. Typhoid fever: Pathogenesis and disease. Curr. Opin. Infect. Dis. 2001, 14, 573–578. [Google Scholar] [CrossRef] [PubMed]
- Edward, S. A Deterministic Mathematical Model for Direct and Indirect Transmission Dynamics of Typhoid Fever. Open Access Libr. J. 2017, 4, 75873. [Google Scholar] [CrossRef]
- Mogasale, V.; Maskery, B.; Ochiai, R.L.; Lee, J.S.; Mogasale, V.V.; Ramani, E.; Kim, Y.E.; Park, J.K.; Wierzba, T.F. Burden of typhoid fever in low-income and middle-income countries: A systematic, literature-based update with risk-factor adjustment. Lancet Glob. Health 2014, 2, 570–580. [Google Scholar] [CrossRef]
- Moyer, C.A.; Johnson, C.; Kaselitz, E.; Aborigo, R. Using social autopsy to understand maternal, newborn, and child mortality in low-resource settings: A systematic review of the literature. Glob. Health Action 2017, 10, 1413917. [Google Scholar] [CrossRef]
- Snavely, M.E.; Maze, M.J.; Muiruri, C.; Ngowi, L.; Mboya, F.; Beamesderfer, J.; Makupa, G.F.; Mwingwa, A.G.; Lwezaula, B.F.; Mmbaga, B.T.; et al. Sociocultural and health system factors associated with mortality among febrile inpatients in Tanzania: A prospective social biopsy cohort study. BMJ Glob. Health 2018, 3, e000507. [Google Scholar] [CrossRef]
- Snavely, M.E.; Oshosen, M.; Msoka, E.F.; Karia, F.P.; Maze, M.J.; Blum, L.S.; Rubach, M.P.; Mmbaga, B.T.; Maro, V.P.; Crump, J.A.; et al. “If you have no money, you might die”: A qualitative study of sociocultural and health system barriers to care for decedent febrile inpatients in Northern Tanzania. Am. J. Trop. Med. Hyg. 2020, 103, 494–500. [Google Scholar] [CrossRef]
- Matsebula, L.; Nyabadza, F.; Mushanyu, J. Mathematical analysis of typhoid fever transmission dynamics with seasonality and fear. Commun. Math. Biol. Neurosci. 2021, 2021, 36. [Google Scholar] [CrossRef]
- Crump, J.A.; Sjölund-Karlsson, M.; Gordon, M.A.; Parry, C.M. Epidemiology, clinical presentation, laboratory diagnosis, antimicrobial resistance, and antimicrobial management of invasive Salmonella infections. Clin. Microbiol. Rev. 2015, 28, 901–937. [Google Scholar] [CrossRef]
- Pitzer, V.E.; Feasey, N.A.; Msefula, C.; Mallewa, J.; Kennedy, N.; Dube, Q.; Denis, B.; Gordon, M.A.; Heyderman, R.S. Mathematical modeling to assess the drivers of the recent emergence of typhoid fever in Blantyre, Malawi. Clin. Infect. Dis. 2015, 61, 251–258. [Google Scholar] [CrossRef]
- Watson, C.H.; Edmunds, W.J. A review of typhoid fever transmission dynamic models and economic evaluations of vaccination. Vaccine 2015, 33, 42–54. [Google Scholar] [CrossRef] [PubMed]
- Lofgren, E.T.; Halloran, M.E.; Rivers, C.M.; Drake, J.M.; Porco, T.C.; Lewis, B.; Yang, W.; Vespignani, A.; Shaman, J.; Eisenberg, J.N.S.; et al. Opinion: Mathematical models: A key tool for outbreak response. Proc. Natl. Acad. Sci. USA 2014, 111, 18095–18096. [Google Scholar] [CrossRef] [PubMed]
- Bakach, I.; Just, M.; Gambhir, M.; Fung, I. Typhoid transmission: A historical perpective on mathematical model development. Trans. R. Soc. Trop. Med. Hyg. 2015, 109, 775–782. [Google Scholar] [CrossRef]
- Brauer, F. Mathematical epidemiology: Past, present, and future. Infect. Dis. Model. 2017, 2, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics, part II—The problem of endemicity. Proc. R. Soc. Lond. A 1932, 138, 55–83. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics, part III—Further studies of the problem of endemicity. Proc. R. Soc. Lond. A 1933, 141, 94–112. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Nyaberi, H.O.; Musaili, J.S. Mathematical modeling of the impact of treatment on the dynamics of typhoid. J. Egypt Math. Soc. 2021, 29, 15. [Google Scholar] [CrossRef]
- Peter, O.J.; Ibrahim, M.O.; Edogbanya, H.O.; Oguntolu, F.A.; Oshinubi, K.; Ibrahim, A.A.; Ayoola, T.A.; Lawal, J.O. Direct and indirect transmission of typhoid fever model with optimal control. Results Phys. 2021, 27, 104463. [Google Scholar] [CrossRef]
- Side, S.; Badwi, N.; Abdy, M.; Sanusi, W. SEIR Model and Simulation for Typus Disease. In Journal of Physics: Conference Series, Proceedings of the 3rd International Conference on Statistics, Mathematics, Teaching and Research 2019, Makassar, Indonesia, 9–10 October 2019; IOP Publishing: Bristol, UK, 2021; Volume 1752, pp. 1–7. [Google Scholar] [CrossRef]
- Irena, T.K.; Gakkhar, S. Modelling the dynamics of antimicrobial-resistant typhoid infection with environmental transmission. Appl. Math. Comput. 2021, 401, 126081. [Google Scholar] [CrossRef]
- Cvjetanović, B.B. Field trial of typhoid vaccines. Am. J. Public Health 1957, 47, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G. Preferred Reporting Items for Systematic Reviews and Meta-Analyses: The PRISMA statement. Ann. Intern. Med. 2009, 151, 264–269. [Google Scholar] [CrossRef] [PubMed]
- Stovold, E.; Beecher, D.; Foxlee, R.; Noel-Storr, A. Study flow diagrams in Cochrane systematic review updates: An adapted PRISMA flow diagram. Syst. Rev. 2014, 3, 54. [Google Scholar] [CrossRef] [PubMed]
- Haidong, Q.; ur Rahman, M.; Arfan, M.; Salimi, M.; Salahshour, S.; Ahmadian, A. Fractal–fractional dynamical system of Typhoid disease including protection from infection. Eng. Comput. 2021. [Google Scholar] [CrossRef]
- Abboubakar, H.; Regonne, R.K.; Nisar, K.S. Fractional dynamics of typhoid fever transmission models with mass vaccination perspectives. Fractal Fract. 2021, 5, 149. [Google Scholar] [CrossRef]
- Sinan, M.; Shah, K.; Kumam, P.; Mahariq, I.; Ansari, K.J.; Ahmad, Z.; Shah, Z. Fractional order mathematical modeling of typhoid fever disease. Results Phys. 2022, 32, 105044. [Google Scholar] [CrossRef]
- Shah, K.; Ali, A.; Zeb, S.; Khan, A.; Alqudah, M.A.; Abdeljawad, T. Study of fractional order dynamics of nonlinear mathematical model. Alex. Eng. J. 2022, 61, 11211–11224. [Google Scholar] [CrossRef]
- López-Quílez, A. Spatio-temporal analysis of infectious diseases. Int. J. Environ. Res. Public Health 2019, 16, 669. [Google Scholar] [CrossRef]
- Tanui, C.K.; Karanth, S.; Njage, P.M.K.; Meng, J.; Pradhan, A.K. Machine learning-based predictive modeling to identify genotypic traits associated with Salmonella enterica disease endpoints in isolates from ground chicken. LWT 2022, 154, 112701. [Google Scholar] [CrossRef]
- Lo, N.C.; Gupta, R.; Stanaway, J.D.; Garrett, D.O.; Bogoch, I.I.; Luby, S.P.; Andrews, J.R. Comparison of Strategies and Incidence Thresholds for VI Conjugate Vaccines Against Typhoid Fever: A Cost-effectiveness Modeling Study. J. Infect. Dis. 2018, 218, S232–S242. [Google Scholar] [CrossRef]
- Hagedorn, B.L.; Gauld, J.; Feasey, N.; Hu, H. Cost-effectiveness of using environmental surveillance to target the roll-out typhoid conjugate vaccine. Vaccine 2020, 38, 1661–1670. [Google Scholar] [CrossRef] [PubMed]
- Gauld, J.S.; Hu, H.; Klein, D.J.; Levine, M.M. Typhoid fever in Santiago, Chile: Insights from a mathematical model utilizing venerable archived data from a successful disease control program. PLoS Negl. Trop. Dis. 2018, 12, e0006759. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Ou, L.; Chen, X.; Zhang, X.; Tan, X. The Application of the Grey Disaster Model to Forecast Epidemic Peaks of Typhoid and Paratyphoid Fever in China. PLoS ONE 2013, 8, e60601. [Google Scholar] [CrossRef][Green Version]
- Avram, F.; Adenane, R.; Bianchin, G.; Halanay, A. Stability Analysis of an Eight Parameter SIR-Type Model Including Loss of Immunity, and Disease and Vaccination Fatalities. Mathematics 2022, 10, 402. [Google Scholar] [CrossRef]
- Do, T.S.; Lee, Y.S. Modeling the Spread of Ebola. Osong Public Health Res. Perspect. 2016, 7, 43–48. [Google Scholar] [CrossRef]
- Ahn, I.; Baek, S.; Lin, Z. The spreading fronts of an infective environment in a man–environment–man epidemic model. Appl. Math. Model. 2016, 40, 7082–7101. [Google Scholar] [CrossRef]
- Rai, R.K.; Misra, A.K.; Takeuchi, Y. Modeling the impact of sanitation and awareness on the spread of infectious diseases. Math. Biosci. Eng. 2019, 16, 667–700. [Google Scholar] [CrossRef]
- Ellegaard, O.; Wallin, J.A. The bibliometric analysis of scholarly production: How great is the impact? Scientometrics 2015, 105, 1809–1831. [Google Scholar] [CrossRef]
- Van Eck, N.J.; Waltman, L. Manual for VOSviewer; Version 1.5.2; Leiden University: Leiden, The Netherlands, 2012; pp. 1–28. [Google Scholar]
- Cvjetanović, B.; Grab, B.; Uemura, K. Epidemiological model of typhoid fever and its use in the planning and evaluation of antityphoid immunization and sanitation programmes. Bull. World Health Organ. 1971, 45, 53–75. [Google Scholar]
- Karunditu, J.W.; Kimathi, G.; Osman, S. Mathematical Modeling of Typhoid Fever Disease Incorporating Unprotected Humans in the Spread Dynamics. J. Adv. Math. Comput. Sci. 2019, 32, 1–11. [Google Scholar] [CrossRef]
- Mushanyu, J.; Nyabadza, F.; Muchatibaya, G.; Mafuta, P.; Nhawu, G. Assessing the potential impact of limited public health resources on the spread and control of typhoid. J. Math. Biol. 2018, 77, 647–670. [Google Scholar] [CrossRef] [PubMed]
- Mushayabasa, S.; Bhunu, C.P.; Ngarakana-Gwasira, E.T. Assessing the Impact of Drug Resistance on the Transmission Dynamics of Typhoid Fever. Comput. Biol. J. 2013, 2013, 303645. [Google Scholar] [CrossRef]
- Oluwafemi, T.J.; Azuaba, E.; Kura, Y.M. Stability Analysis of the Disease Free Equilibrium of Malaria, Dengue and Typhoid Triple Infection Model. Asian Res. J. Math. 2020, 16, 15–23. [Google Scholar] [CrossRef]
- Peter, O.J.; Folasade, A.A.; Ajisope, M.O.; Ajibade, F.O.; Abioye, A.I.; Oguntolu, F.A. Global stability analysis of typhoid fever model. Adv. Syst. Sci. Appl. 2020, 20, 20–31. [Google Scholar] [CrossRef]
- Mondal, J. Influence of awareness programs by media in the typhoid fever: A study based on mathematial modeling. J. Math. Model. 2018, 6, 1–26. [Google Scholar]
- Pitzer, V.E.; Bowles, C.C.; Baker, S.; Kang, G.; Balaji, V.; Farrar, J.J.; Grenfell, B.T. Predicting the Impact of Vaccination on the Transmission Dynamics of Typhoid in South Asia: A Mathematical Modeling Study. PLoS Negl. Trop. Dis. 2014, 8, 40. [Google Scholar] [CrossRef]
- Shukla, J.B.; Goyal, A.; Singh, S.; Chandra, P. Effects of habitat characteristics on the growth of carrier population leading to increased spread of typhoid fever: A model. J. Epidemiol. Glob. Health 2014, 4, 107–114. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Makinde, O.D.; Malonza, D. Modelling and Optimal Control of Typhoid Fever Disease with Cost-Effective Strategies. Comput. Math. Methods Med. 2017, 2017, 2324518. [Google Scholar] [CrossRef]
- Irena, T.K.; Gakkhar, S. A dynamical model for HIV-typhoid co-infection with typhoid vaccine. J. Appl. Math. Comput. 2021, 67, 641–670. [Google Scholar] [CrossRef]
- Akinyi, O.C.; Mugisha, J.Y.T.; Manyonge, A.; Ouma, C. A model on the impact of treating typhoid with anti-malarial: Dynamics of malaria concurrent and co-infection with typhoid. Int. J. Math. Anal. 2015, 9, 541–551. [Google Scholar] [CrossRef]
- Tilahun, G.T.; Makinde, O.D.; Malonza, D. Co-dynamics of Pneumonia and Typhoid fever diseases with cost effective optimal control analysis. Appl. Math. Comput. 2018, 316, 438–459. [Google Scholar] [CrossRef]
- Musa, S.S.; Zhao, S.; Hussaini, N.; Usaini, S.; He, D. Dynamics analysis of typhoid fever with public health education programs and final epidemic size relation. Results Appl. Math. 2021, 10, 100153. [Google Scholar] [CrossRef]
- Abboubakar, H.; Racke, R. Mathematical modeling, forecasting, and optimal control of typhoid fever transmission dynamics. Chaos Solitons Fractals 2021, 149, 111074. [Google Scholar] [CrossRef]
- Mutua, J.M.; Wang, F.-B.; Vaidya, N.K. Modeling malaria and typhoid fever co-infection dynamics. Math. Biosci. 2015, 264, 128–144. [Google Scholar] [CrossRef]
- Mushayabasa, S. Modeling the impact of optimal screening on typhoid dynamics. Int. J. Dyn. Control 2016, 4, 330–338. [Google Scholar] [CrossRef]
| (Name, Year) | Cited | Compartments | Data Type | Analyzed Mathematically | Citation Number | Interventions |
|---|---|---|---|---|---|---|
| (Edward, 2017) | 7 | Secondary | Yes | [3] | Clean Water, Sanitation Vaccination, and Treatment. | |
| (Karunditu et al., 2019) | 12 | Secondary | Yes | [42] | - | |
| (Mushanyu et al., 2018) | 12 | Secondary | Yes | [43] | Treatment. | |
| (Mushayabasa et al., 2013) | 4 | Secondary | Yes | [44] | - | |
| (Nyaberi and Musaili, 2021) | 3 | Secondary | Yes | [18] | Treatment. | |
| (Oluwafemi et al., 2020) | 1 | Secondary | Yes | [45] | - | |
| (Peter et al., 2020) | 5 | Secondary | Yes | [46] | - | |
| (Mondal, 2018) | - | Secondary | Yes | [47] | Treatment, and Media Awareness. | |
| (Peter et al., 2021) | 4 | Secondary | Yes | [19] | Educational Campaign, Sanitation, and Combined Educational and Sanitation. | |
| (Pitzer et al., 2014) | 103 | Primer and Secondary | No | [48] | Vaccination. | |
| (Pitzer et al., 2015) | 55 | Primer and Secondary | No | [10] | - | |
| (Shukla et al., 2014) | 7 | Secondary | Yes | [49] | - | |
| (Side et al., 2021) | 1 | Secondary | Yes | [20] | Screening. | |
| (Tilahun et al., 2017) | 70 | Secondary | Yes | [50] | Prevention, Screening, and Treatment. | |
| (Irena et al., 2021) | - | Secondary | Yes | [51] | Vaccination. | |
| (Akinyi et al., 2015) | 8 | Secondary | Yes | [52] | - | |
| (Tilahun et al., 2018) | 39 | Secondary | Yes | [53] | Prevention, Treatment, and Mass Cleaning of Environments. | |
| (Musa et al., 2021) | 1 | Secondary | Yes | [54] | Education. | |
| (Matsebula et al., 2021) | - | Secondary | Yes | [8] | - | |
| (Abboubakar et al., 2021) | 6 | Secondary | Yes | [55] | Vaccination, Sanitation, and Treatment. | |
| (Mutua et al., 2015) | 52 | Secondary | Yes | [56] | - | |
| (Mushayabasa, 2016) | 22 | Secondary | Yes | [57] | Detection and Treatment. | |
| (Irena et al., 2021) | 2 | Secondary | Yes | [21] | - |
| Notations | Description | Additional |
|---|---|---|
| Susceptible population. | - | |
| Susceptible human. | - | |
| Susceptible vector. | - | |
| Susceptible food. | - | |
| Susceptible flies. | - | |
| Fully susceptible. | Fully susceptible is a subpopulation that has never gotten infected yet. | |
| Partially susceptible. | Partially susceptible is a subpopulation that is possible to get reinfection. | |
| Exposed population. | Infected but not yet infectious. | |
| Infected population. | - | |
| Asymptomatically infected. | Asymptotically infected is a subpopulation that has no symptoms despite being infected. | |
| Carrier infected. | ||
| Drug-resistant infected. | Drug-resistant infection is a subpopulation that cannot be cured through drug consumption. | |
| Carriers of the typhoid bacteria who do not show the typhoid symptoms. | - | |
| Infected with typhoid but are misdiagnosed for malaria. | - | |
| Malaria-infected human. | - | |
| Dengue-infected human. | - | |
| Human-typhoid infected. | - | |
| Malaria and dengue-infected human. | - | |
| Malaria and typhoid-infected human. | - | |
| Dengue and typhoid-infected human. | - | |
| Malaria, dengue, and typhoid-infected human. | - | |
| HIV-infected human. | - | |
| HIV and typhoid-infected human. | - | |
| AIDS-infected human. | - | |
| AIDS and typhoid-infected human. | - | |
| Pneumonia-infected human. | - | |
| Typhoid and pneumonia-infected human. | - | |
| Malaria-infected vector. | - | |
| Dengue-infected vector. | - | |
| Infected food. | - | |
| Infected flies. | - | |
| Primary infected. | Primary infected is a subpopulation that is infected for the first. | |
| Partially infected. | Short-term infected whose infectivity is not as long as the infection period. | |
| Carrier population. | - | |
| Asymptomatic infectious carriers with a sensitive strain. | - | |
| Asymptomatic infectious carriers with a resistant strain | - | |
| Fraction of carrier. | Fraction of carrier is a subpopulation of carrier population that has some special characteristics. | |
| Recovered. | - | |
| Recovered from pneumonia. | The population that recovered from pneumonia but still infected by the typhoid. | |
| Recovered from typhoid. | The population that recovered from typhoid but still infected by pneumonia. | |
| Recovered from pneumonia and typhoid. | - | |
| Bacteria. | - | |
| Vaccinated population. | - | |
| Density of public health education. | - | |
| Total of each population. | The population of humans, bacteria, and food/water, respectively. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tresna, S.T.; Subiyanto; Supian, S. Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review. Mathematics 2022, 10, 2506. https://doi.org/10.3390/math10142506
Tresna ST, Subiyanto, Supian S. Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review. Mathematics. 2022; 10(14):2506. https://doi.org/10.3390/math10142506
Chicago/Turabian StyleTresna, Sanubari Tansah, Subiyanto, and Sudradjat Supian. 2022. "Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review" Mathematics 10, no. 14: 2506. https://doi.org/10.3390/math10142506
APA StyleTresna, S. T., Subiyanto, & Supian, S. (2022). Mathematical Models for Typhoid Disease Transmission: A Systematic Literature Review. Mathematics, 10(14), 2506. https://doi.org/10.3390/math10142506







