Tracking an Underwater Object with Unknown Sensor Noise Covariance Using Orthogonal Polynomial Filters
Abstract
:1. Introduction
- (i)
- With bearings-only measurements, the system is unobservable until the ownship executes a maneuver.
- (ii)
- In certain TMA applications, fast convergence of the solution is important, which is challenging with passive measurements.
- (iii)
- The measurement equation is highly nonlinear, which limits the ability of the estimator to provide reliable tracking performance.
- (iv)
- Sometimes, the measurement noise covariance is time-varying and unknown.
2. Problem Formulation
2.1. System Model
2.1.1. Constant Velocity Model
2.1.2. Constant Turn Model
2.2. Measurement Model
2.2.1. Case I—Bearings-Only Measurement
2.2.2. Case II—Doppler-Bearing Measurement
3. Tracking Methodology
3.1. Orthogonal Polynomial Filter
Measurement Update
3.2. Estimation of Measurement Noise Covariance
| Algorithm 1: Pseudo code for adaptive polynomial filter for target tracking |
Step 1: Initialisation 1 Initialise the filter with , , and . 2 Compute the sample points , and their respective weights . Step 2: Time update 3 Compute the predicted mean and covariance as
Step 3: Measurement update 5 Calculate the Kalman gain, . 6 Estimate the posterior state,
7 Compute the posterior error covariance,
Step 4: Estimate unknown 8 Calculate the posterior estimate of the measurement, using Equation (29). 9 Calculate the residual of measurement as . 10 Calculate the covariance of measurement residual () using Equation (34). 11 Estimate using Equation (35). |
3.3. Computational Advantage
3.3.1. Alternative to the Square Root Filters
3.3.2. Flops Count
4. Simulation Results
4.1. Tracking Scenarios
4.2. Performance Metrics
4.2.1. Root Mean Square Error
4.2.2. Normalised (State) Estimation Error Squared
4.2.3. Bias Norm
4.2.4. Track Loss
4.3. Initialisation of the Filters
4.4. Performance Comparison
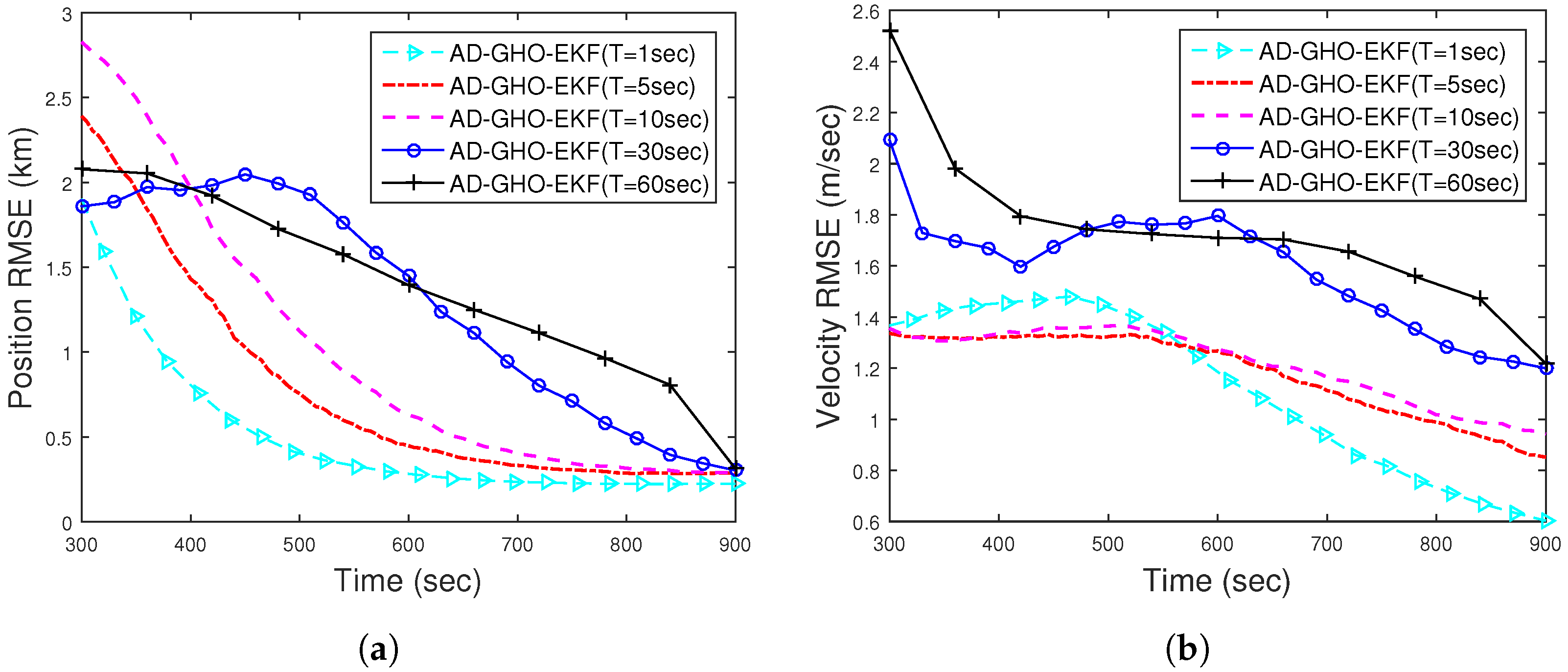
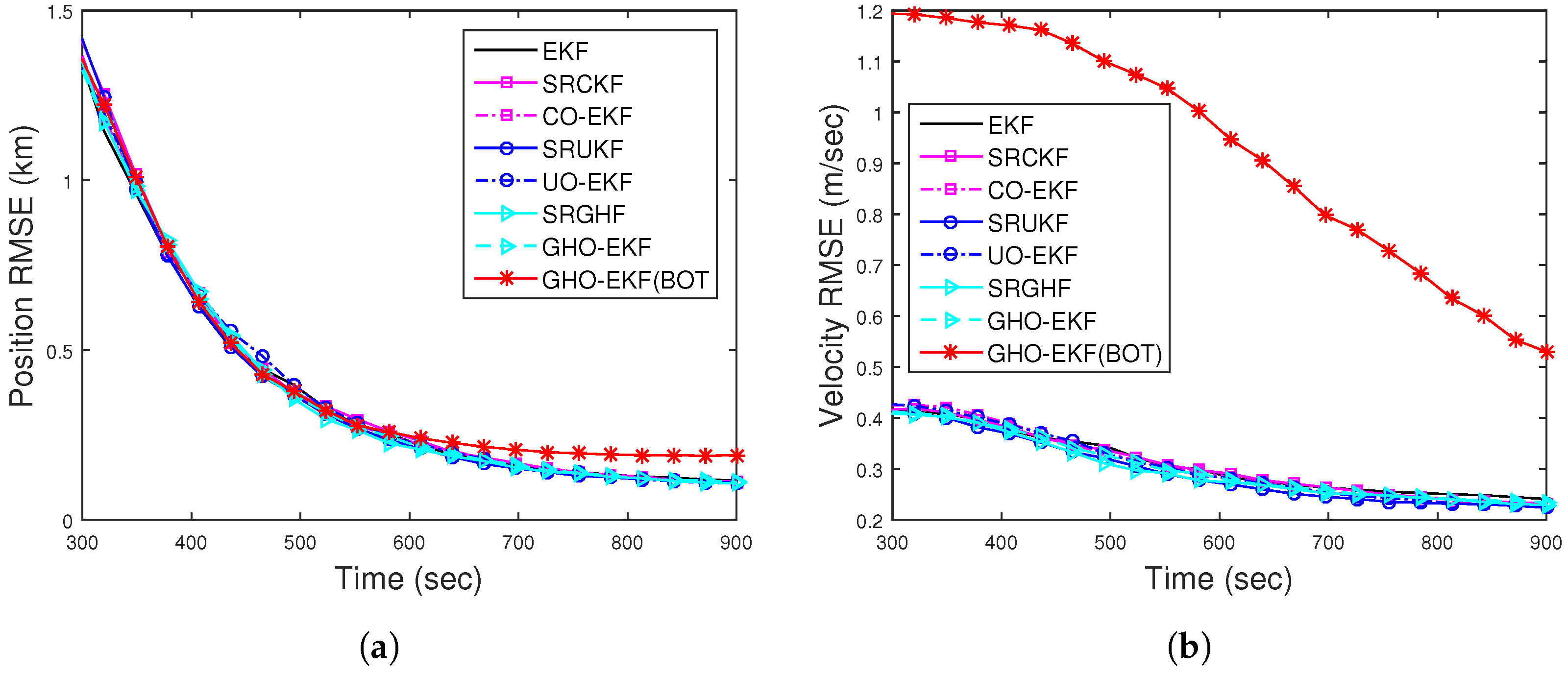
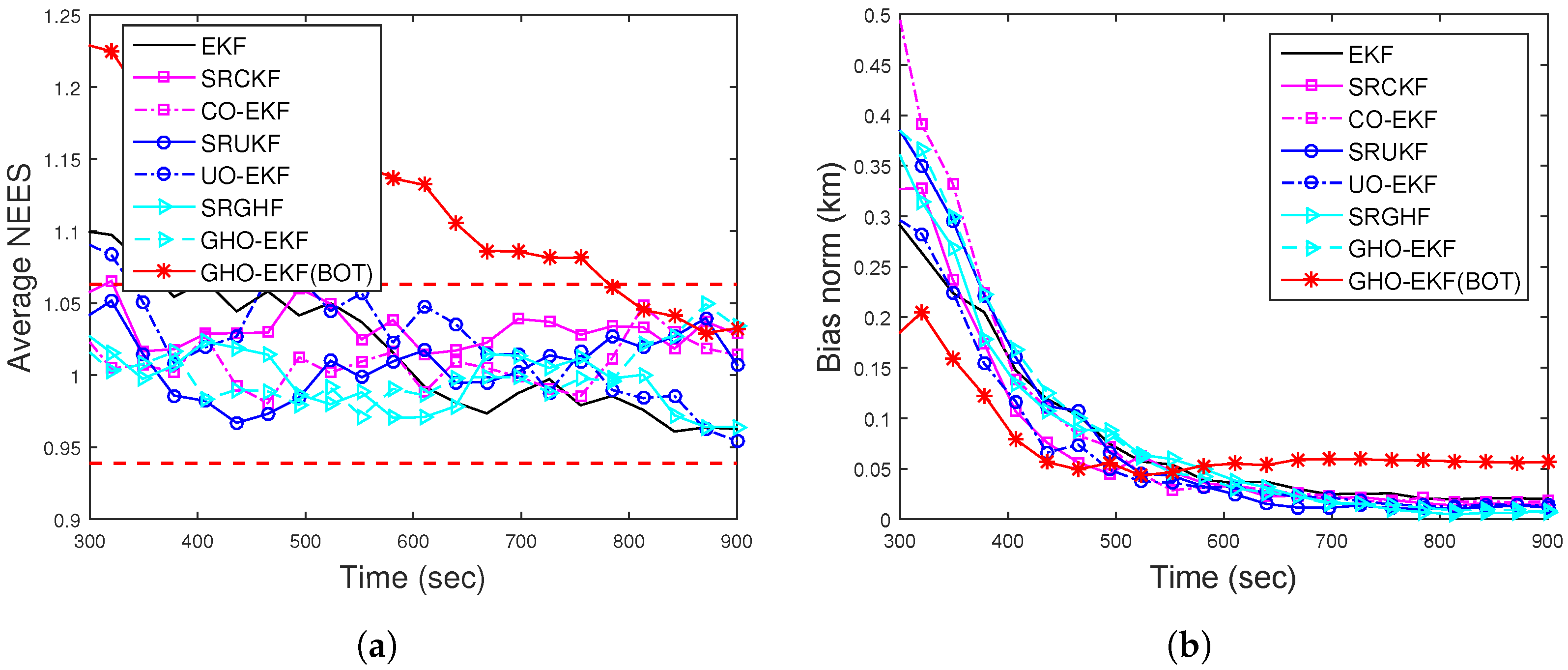
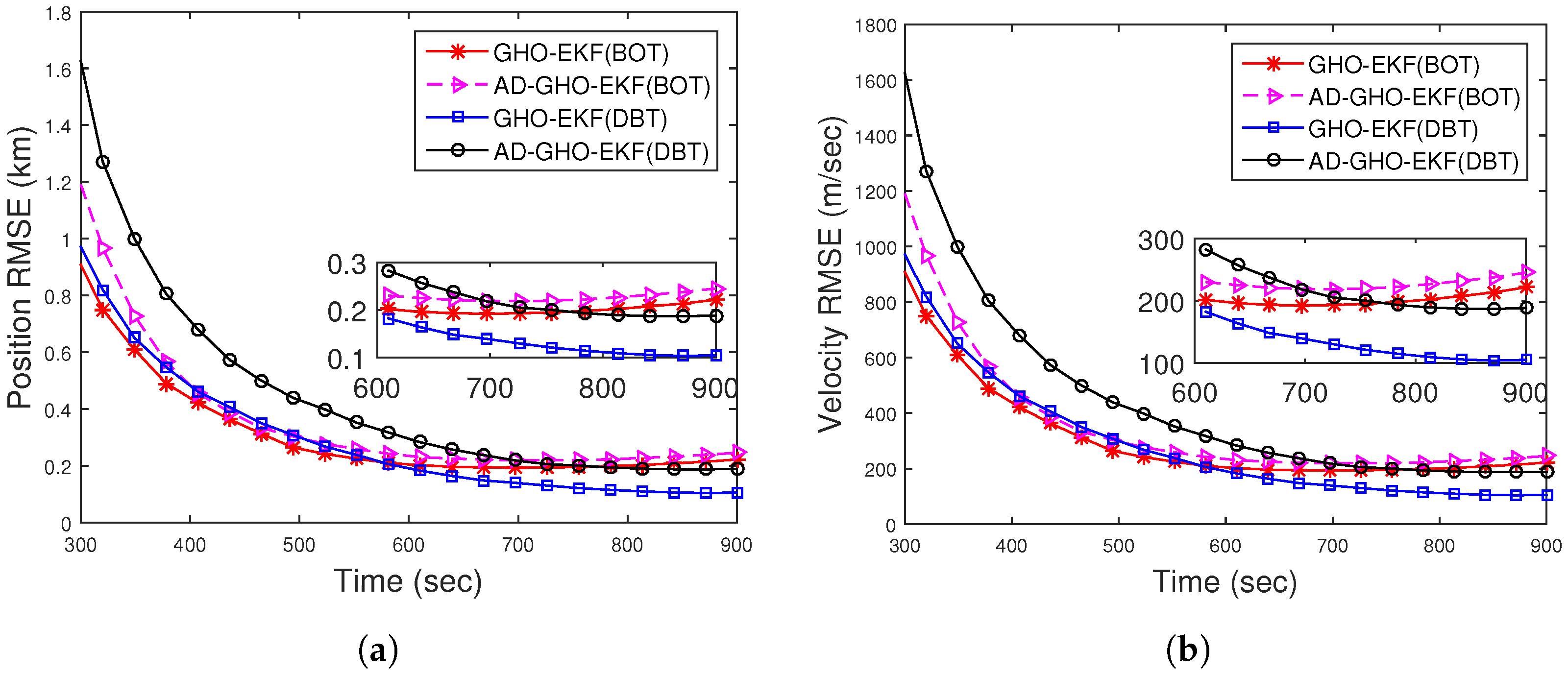
4.4.1. Scenario I: Case I—Bearings-Only Tracking
4.4.2. Scenario I: Case II—Doppler-Bearing Tracking
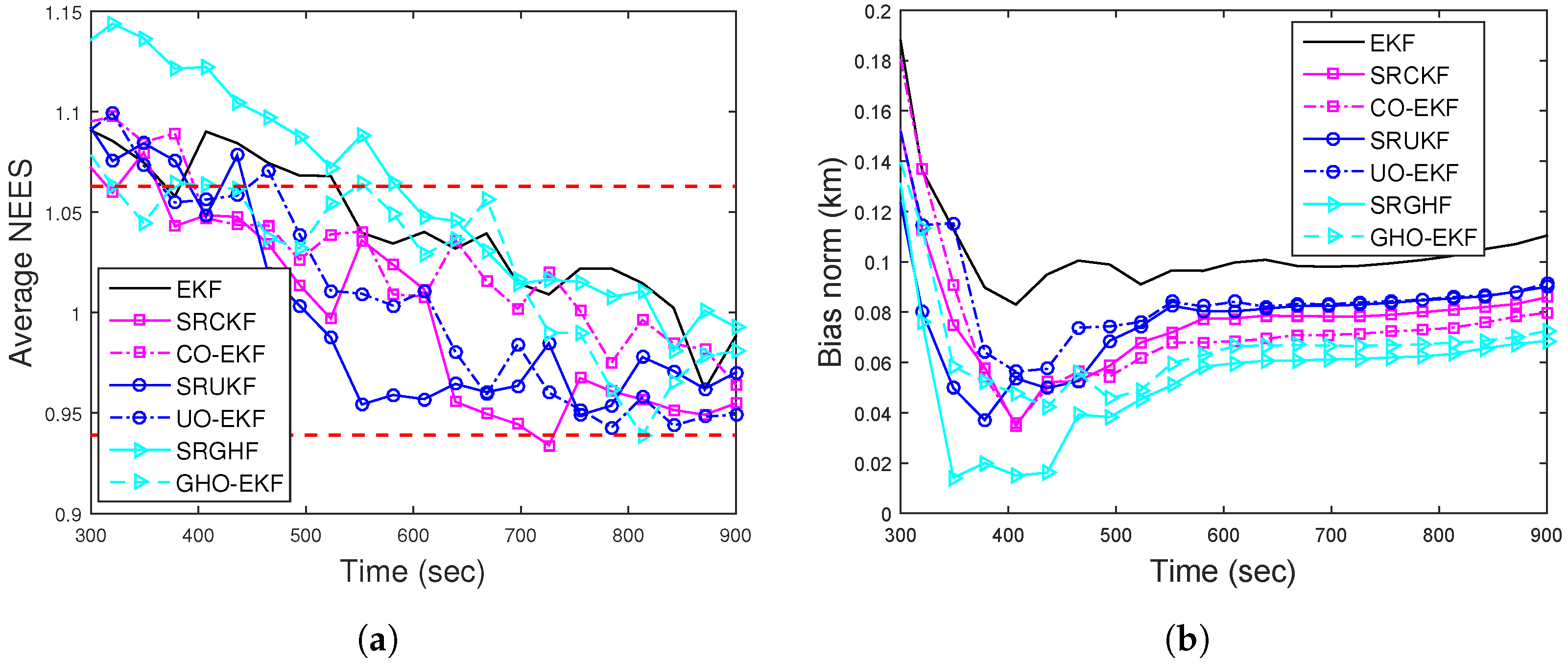
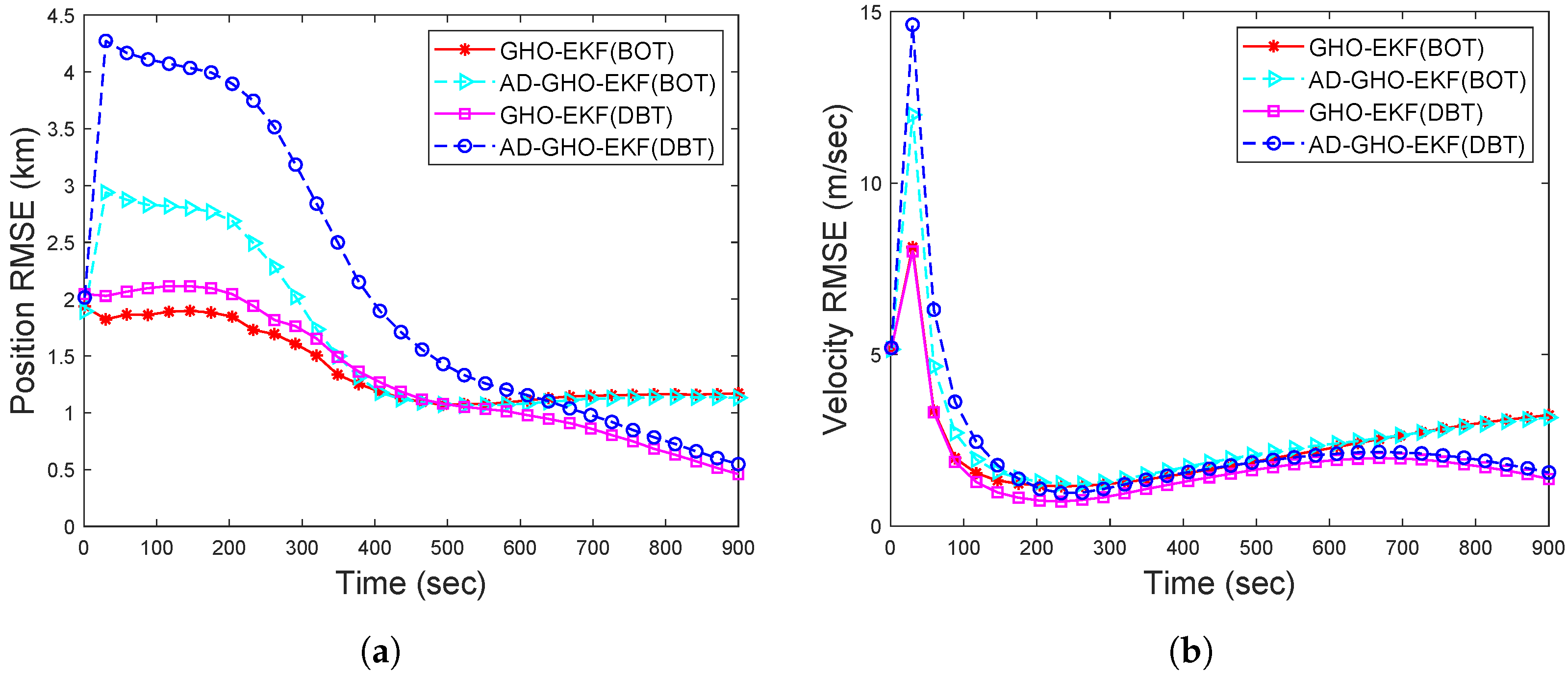
4.4.3. Scenario II: Case I—Bearings-Only Tracking
4.4.4. Scenario II: Case II—Doppler-Bearing Tracking
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arulampalam, S.; Ristic, B. Comparison of the particle filter with range-parameterized and modified polar EKFs for angle-only tracking. In Proceedings of the AeroSense 2000 Signal and Data Processing of Small Targets 2000, Orlando, FL, USA, 24–28 April 2000; Volume 4048, pp. 288–299. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters For Tracking Applications; Artech House: London, UK, 2003. [Google Scholar]
- Ho, K.; Chan, Y.T. An asymptotically unbiased estimator for bearings-only and Doppler-bearing target motion analysis. IEEE Trans. Signal Process. 2006, 54, 809–822. [Google Scholar] [CrossRef]
- Guo, Y.; Tharmarasa, R.; Rajan, S.; Song, T.L.; Kirubarajan, T. Passive tracking in heavy clutter with sensor location uncertainty. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1536–1554. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Bhaumik, S.; Tomar, N.K. Gaussian sum shifted Rayleigh filter for underwater bearings-only target tracking problems. IEEE J. Ocean. Eng. 2018, 44, 492–501. [Google Scholar] [CrossRef]
- Luo, J.; Han, Y.; Fan, L. Underwater acoustic target tracking: A review. Sensors 2018, 18, 112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leong, P.H.; Arulampalam, S.; Lamahewa, T.A.; Abhayapala, T.D. A Gaussian-sum based cubature Kalman filter for bearings-only tracking. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 1161–1176. [Google Scholar] [CrossRef]
- Yang, L.; Sun, M.; Ho, K. Doppler-bearing tracking in the presence of observer location error. IEEE Trans. Signal Process. 2008, 56, 4082–4087. [Google Scholar] [CrossRef]
- Rao, S.K. Doppler-bearing passive target tracking using a parameterized unscented Kalman filter. IETE J. Res. 2010, 56, 69–75. [Google Scholar] [CrossRef]
- Li, X.; Zhao, C.; Yu, J.; Wei, W. Underwater bearing-only and bearing-Doppler target tracking based on square root unscented Kalman filter. Entropy 2019, 21, 740. [Google Scholar] [CrossRef] [Green Version]
- Borisov, A.; Bosov, A.; Miller, B.; Miller, G. Passive underwater target tracking: Conditionally minimax nonlinear filtering with bearing-Doppler observations. Sensors 2020, 20, 2257. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Anderson, B.D.; Moore, J.B. Optimal Filtering; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Karaman, S. Fixed point smoothing algorithm to the torpedo tracking problem. Master’s Thesis, Naval Postgraduate School Monterey, Monterey, CA, USA, 1986. [Google Scholar]
- Karlsson, R. Various Topics on Angle-Only Tracking Using Particle Filters; Linköping University: Linköping, Sweden, 2002. [Google Scholar]
- Karlsson, R. Simulation based methods for target tracking. Ph.D. Thesis, Linköpings University, Linköpings, Sweden, 2002. [Google Scholar]
- Kumar, D.R.; Rao, S.K.; Raju, K.P. A novel estimation algorithm for torpedo tracking in undersea environment. J. Cent. South Univ. 2019, 26, 673–683. [Google Scholar] [CrossRef]
- Reif, K.; Gunther, S.; Yaz, E.; Unbehauen, R. Stochastic stability of the discrete-time extended Kalman filter. IEEE Trans. Autom. Control 1999, 44, 714–728. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of the AeroSense ’97, Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–25 April 1991; Volume 3068, pp. 182–193. [Google Scholar]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef] [Green Version]
- Ito, K.; Xiong, K. Gaussian filters for nonlinear filtering problems. IEEE Trans. Autom. Control 2000, 45, 910–927. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, R.; Singh, A.K.; Bhaumik, S.; Tomar, N.K. Multiple sparse-grid Gauss–Hermite filtering. Appl. Math. Model. 2016, 40, 4441–4450. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef] [Green Version]
- Bhaumik, S.; Swati. Cubature quadrature Kalman filter. IET Signal Process. 2013, 7, 533–541. [Google Scholar] [CrossRef] [Green Version]
- Van Der Merwe, R.; Wan, E.A. The square-root unscented Kalman filter for state and parameter-estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing. Proceedings (Cat. No. 01CH37221), Salt Lake City, UT, USA, 7–11 May 2001; Volume 6, pp. 3461–3464. [Google Scholar]
- Arasaratnam, I.; Haykin, S. Square-root quadrature Kalman filtering. IEEE Trans. Signal Process. 2008, 56, 2589–2593. [Google Scholar] [CrossRef]
- Bhaumik, S.; Swati. Square-root cubature-quadrature Kalman filter. Asian J. Control 2014, 16, 617–622. [Google Scholar] [CrossRef]
- Kumar, K.; Bhaumik, S.; Date, P. Extended Kalman filter using orthogonal polynomials. IEEE Access 2021, 9, 59675–59691. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I: Dynamic models. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 1333–1364. [Google Scholar]
- Hou, X.; Yang, L.; Yang, Y.; Zhou, J.; Qiao, G. Bearing-only underwater uncooperative target tracking for non-Gaussian environment using fast particle filter. IET Radar Sonar Navig. 2022, 16, 501–514. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1964; Volume 55.
- Holmquist, B. The d-variate vector Hermite polynomial of order k. Linear Algebra Its Appl. 1996, 237, 155–190. [Google Scholar] [CrossRef]
- Buet-Golfouse, F. A multinomial theorem for Hermite polynomials and financial applications. Appl. Math. 2015, 6, 1017. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Hu, D.; Wu, M.; Hu, X. A numerical-integration perspective on Gaussian filters. IEEE Trans. Signal Process. 2006, 54, 2910–2921. [Google Scholar] [CrossRef]
- Jia, B.; Xin, M.; Cheng, Y. High-degree cubature Kalman filter. Automatica 2013, 49, 510–518. [Google Scholar] [CrossRef]
- Singh, A.K.; Bhaumik, S. Higher degree cubature quadrature Kalman filter. Int. J. Control Autom. Syst. 2015, 13, 1097–1105. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S.; Elliott, R.J. Discrete-time nonlinear filtering algorithms using Gauss-Hermite quadrature. Proc. IEEE 2007, 95, 953–977. [Google Scholar] [CrossRef]
- Chalasani, G.; Bhaumik, S. Bearing only tracking using Gauss-Hermite filter. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1549–1554. [Google Scholar]
- Zhang, X.; Ying, W.; Yang, P.; Sun, M. Parameter estimation of underwater impulsive noise with the class B model. IET Radar Sonar Navig. 2020, 14, 1055–1060. [Google Scholar] [CrossRef]
- Mahmood, A.; Chitre, M. Modeling colored impulsive noise by Markov chains and alpha-stable processes. In Proceedings of the OCEANS 2015-Genova, Genova, Italy, 18–21 May 2015; pp. 1–7. [Google Scholar]
- Zhou, H.; Xu, L.; Chen, W.; Guo, K.; Shen, F.; Guo, Z. A novel robust filtering strategy for systems with non-Gaussian noises. AEU Int. J. Electron. Commun. 2018, 97, 154–164. [Google Scholar] [CrossRef]
- Mohamed, A.; Schwarz, K. Adaptive Kalman filtering for INS/GPS. J. Geod. 1999, 73, 193–203. [Google Scholar] [CrossRef]
- Wang, J. Stochastic modeling for real-time kinematic GPS/GLONASS positioning. Navigation 1999, 46, 297–305. [Google Scholar] [CrossRef]
- Almagbile, A.; Wang, J.; Ding, W. Evaluating the performances of adaptive Kalman filter methods in GPS/INS integration. J. Glob. Position. Syst. 2010, 9, 33–40. [Google Scholar] [CrossRef] [Green Version]
- Soken, H.E.; Sakai, S.I. Adaptive tuning of the unscented Kalman filter for satellite attitude estimation. J. Aerosp. Eng. 2015, 28, 04014088. [Google Scholar] [CrossRef]
- Dey, A.; Sadhu, S.; Ghoshal, T.K. Adaptive Gauss–Hermite filter for non-linear systems with unknown measurement noise covariance. IET Sci. Meas. Technol. 2015, 9, 1007–1015. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE Trans. Autom. Control 2017, 63, 594–601. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Sidoti, D.; Bienkowski, A.; Pattipati, K.R.; Bar-Shalom, Y.; Kleinman, D.L. On the identification of noise covariances and adaptive Kalman filtering: A new look at a 50 year-old problem. IEEE Access 2020, 8, 59362–59388. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, C.; Zhang, Y.; Zhang, J. A new adaptive square-root unscented Kalman filter for nonlinear systems with additive noise. Int. J. Aerosp. Eng. 2015, 2015, 381478. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Zheng, L.; Li, Y.; Wu, H.; Liang, Y.; Qiao, X. Correction adaptive square-root cubature Kalman filter with application to autonomous vehicle target tracking. Meas. Sci. Technol. 2021, 32, 115101. [Google Scholar] [CrossRef]
- Ristic, B.; Wang, X.; Arulampalam, S. Target motion analysis with unknown measurement noise variance. In Proceedings of the 2017 20th International Conference on Information Fusion (Fusion), Xi’an, China, 10–13 July 2017; pp. 1–8. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Wang, X. Measurement variance ignorant target motion analysis. Inf. Fusion 2018, 43, 27–32. [Google Scholar] [CrossRef]
- Karlsson, R.; Schon, T.; Gustafsson, F. Complexity analysis of the marginalized particle filter. IEEE Trans. Signal Process. 2005, 53, 4408–4411. [Google Scholar] [CrossRef] [Green Version]
- Li, X.R.; Zhao, Z.; Jilkov, V.P. Estimator’s credibility and its measures. In Proceedings of the IFAC 15th World Congress, Barcelona, Spain, 21–26 July 2002. [Google Scholar]
- Li, X.R.; Zhao, Z.; Jilkov, V.P. Practical measures and test for credibility of an estimator. In Proceedings Workshop on Estimation, Tracking, and Fusion: A Tribute to Yaakov Bar-Shalom; Citeseer: Princeton, NJ, USA, 2001; pp. 481–495. [Google Scholar]
- Arulampalam, S.; Ristic, B.; Kirubarajan, T. Analysis of propagation delay effects on bearings-only fusion of heterogeneous sensors. IEEE Trans. Signal Process. 2021, 69, 6488–6503. [Google Scholar] [CrossRef]

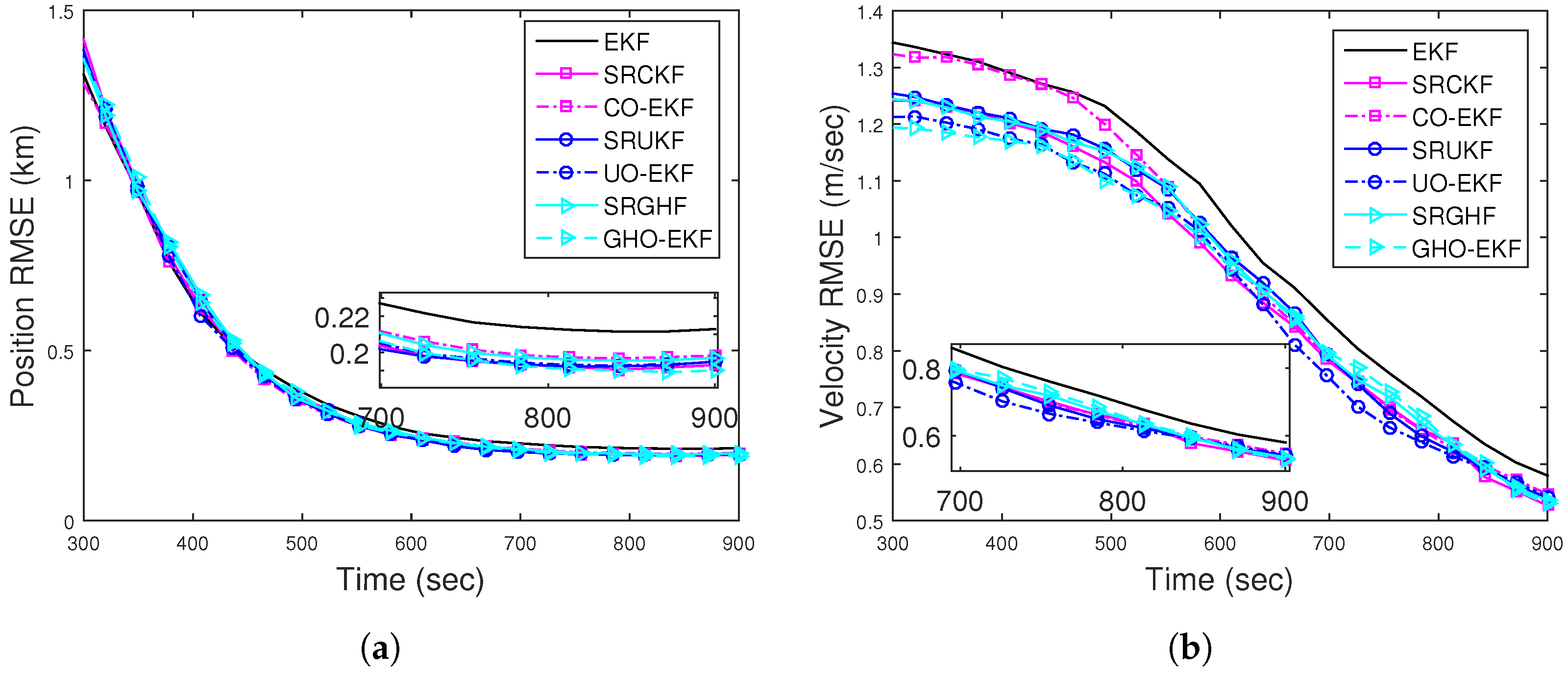
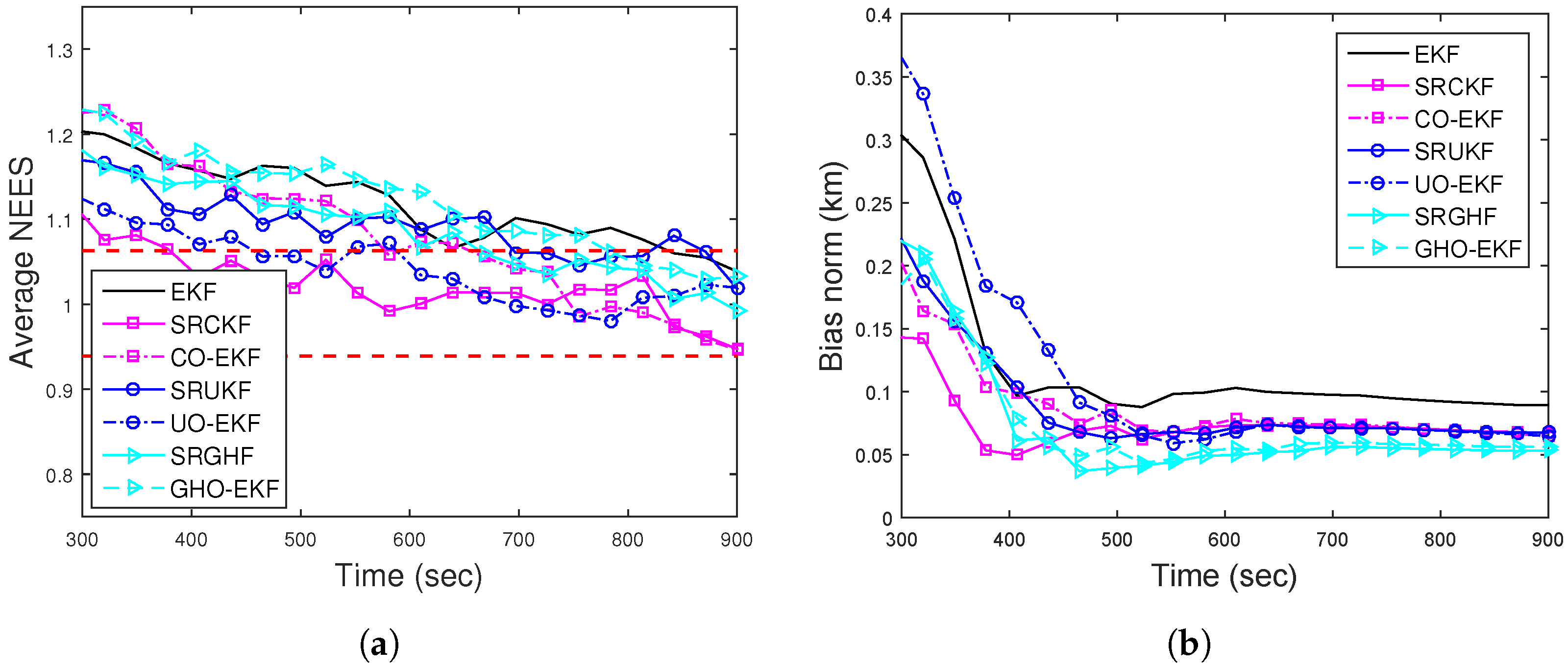

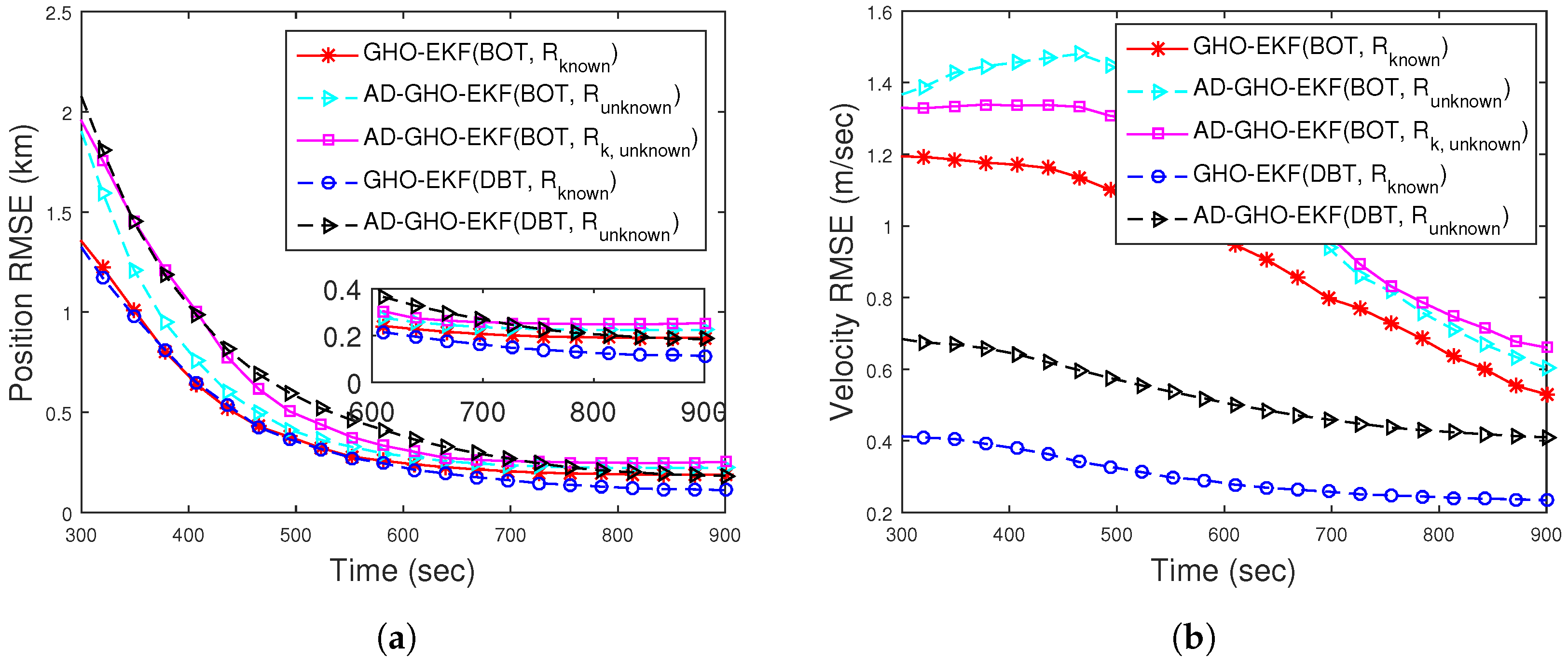
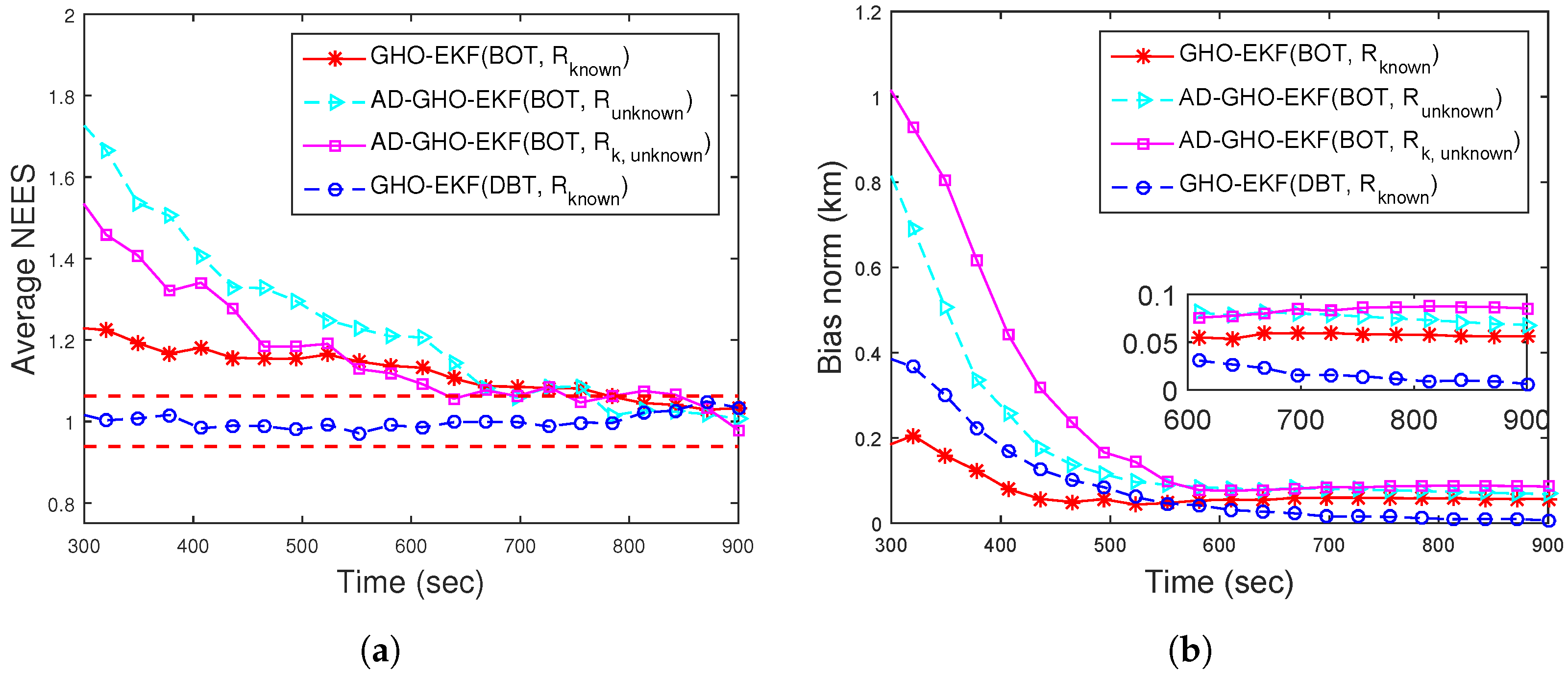


| Filter | BOT | DBT | ||
|---|---|---|---|---|
| Ordinary | Adaptive | Ordinary | Adaptive | |
| EKF | 409 | 516 | 589 | 914 |
| SRCKF | 1197 | 1548 | 1475 | 2053 |
| CO-EKF | 775 | 966 | 1011 | 1440 |
| SRUKF | 1323 | 1711 | 1659 | 2282 |
| UO-EKF | 817 | 1008 | 1065 | 1444 |
| SRGHF | 8090 | 11,142 | 10,299 | 14,162 |
| GHO-EKF | 3913 | 4104 | 4953 | 5382 |
| Parameters | Scenario I | Scenario II |
|---|---|---|
| Initial range | 16.1 km | 16.1 km |
| Target speed | 35 knots | 35 knots |
| Target course | −° | −° |
| Observer speed | 18 knots | 18 knots |
| Observer initial course | ° | ° |
| Observer maneuver | 61th to 420th s | 181th s |
| 2 km | 2 km | |
| 2 knots | 2 knots | |
| ° | ° | |
| 1 Hz | 1 Hz | |
| (km/s) | ||
| T | 1 s | 1 s |
| Scenario I | Scenario II | |||
|---|---|---|---|---|
| Filter | BOT | DBT | BOT | DBT |
| EKF | 2.30 | 0 | 6.73 | 0 |
| AD-EKF | 9.86 | 2.27 | 17.35 | 2.09 |
| SRCKF | 2.25 | 0 | 5.72 | 0 |
| CO-EKF | 2.03 | 0 | 6.17 | 0 |
| AD-SRCKF | 8.28 | 1.3 | 16.51 | 0.91 |
| AD-CO-EKF | 8.78 | 1.35 | 16.23 | 1.01 |
| SRUKF | 2.16 | 0 | 6.12 | 0 |
| UO-EKF | 2.22 | 0 | 6.26 | 0 |
| AD-SRUKF | 8.48 | 1.41 | 17.73 | 1.05 |
| AD-UO-EKF | 8.69 | 1.38 | 15.61 | 0.95 |
| SRGHF | 1.86 | 0 | 6.35 | 0 |
| GHO-EKF | 2.24 | 0 | 6.27 | 0 |
| AD-SRGHF | 8.20 | 0.72 | 16.96 | 0.74 |
| AD-GHO-EKF | 8.35 | 0.80 | 16.41 | 0.80 |
| Filter | BOT | DBT | ||
|---|---|---|---|---|
| Ordinary | Adaptive | Ordinary | Adaptive | |
| EKF | 1.00 | 2.14 | 1.28 | 2.40 |
| SRCKF | 1.84 | 3.72 | 2.14 | 4.02 |
| CO-EKF | 1.51 | 2.70 | 1.95 | 2.92 |
| SRUKF | 1.88 | 3.80 | 2.28 | 4.09 |
| UO-EKF | 1.53 | 2.78 | 2.03 | 2.99 |
| SRGHF | 6.53 | 10.35 | 10.52 | 14.13 |
| GHO-EKF | 4.16 | 5.97 | 5.64 | 7.75 |
| Filter | BOT | DBT | ||
|---|---|---|---|---|
| Ordinary | Adaptive | Ordinary | Adaptive | |
| EKF | 13.34 | 29.72 | 0 | 0.35 |
| SRCKF | 12.30 | 26.95 | 0 | 0.25 |
| CO-EKF | 12.40 | 26.94 | 0 | 0.26 |
| SRUKF | 12.62 | 26.80 | 0 | 0.28 |
| UO-EKF | 12.04 | 27.08 | 0 | 0.25 |
| SRGHF | 11.55 | 26.57 | 0 | 0.20 |
| GHO-EKF | 11.53 | 26.62 | 0 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, K.; Bhaumik, S.; Arulampalam, S. Tracking an Underwater Object with Unknown Sensor Noise Covariance Using Orthogonal Polynomial Filters. Sensors 2022, 22, 4970. https://doi.org/10.3390/s22134970
Kumar K, Bhaumik S, Arulampalam S. Tracking an Underwater Object with Unknown Sensor Noise Covariance Using Orthogonal Polynomial Filters. Sensors. 2022; 22(13):4970. https://doi.org/10.3390/s22134970
Chicago/Turabian StyleKumar, Kundan, Shovan Bhaumik, and Sanjeev Arulampalam. 2022. "Tracking an Underwater Object with Unknown Sensor Noise Covariance Using Orthogonal Polynomial Filters" Sensors 22, no. 13: 4970. https://doi.org/10.3390/s22134970








