Momentum Distribution Functions and Pair Correlation Functions of Unpolarized Uniform Electron Gas in Warm Dense Matter Regime
Abstract
:1. Introduction
2. Theoretical Part
2.1. Uniform Electron Gas
2.2. Single Momentum Approach
2.3. Path Integrals
3. Simulation Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPIMC | Configuration Path Integral Monte Carlo |
| DFT | Density Functional Theory |
| IFG | Ideal Fermi Gas |
| MDF | Momentum Distribution Function |
| PBC | Periodic Boundary Conditions |
| PCF | Pair Correlation Function |
| SMPIMC | Single Momentum Path Integral Monte Carlo |
| UEG | Uniform Electron Gas |
| WDM | Warm Dense Matter |
Appendix A. Numerical Method SMPIMC
Appendix A.1. Basic Idea of Path Integral Monte Carlo Methods
Appendix A.2. Periodic Boundary Conditions
Appendix A.3. Smpimc Algorithm for PCFs
- Set the run number and the initial state : the coordinates are uniformly distributed in the simulation box, the coordinates are equal to zero (, ).
- Set the step number and the first state .
- Select the particle number randomly, then select the type of the step: –step with the probability or –step with the probability . If –step has been chosen, modify with uniformly distributed in the volume . If –step has been chosen, select the bead number randomly and modify with uniformly distributed in the volume . In both cases, take into account the PBC. The resulting state has to be set as the proposed state .
- Accept the proposed state with the probability (A4) or reject it. In the case of acceptance—set , in the case of rejection—set .
- Calculate the distances between each pair of electrons and build the related histograms: , and , where is the cell number with the length , so .
- Repeat steps (3)–(5) for .
- Calculate the average histograms for the obtained sample of states via averaging of , and with as the weight function:
- Repeat steps (2)–(7) for , but instead of initialization use the last state from the previous run: .
- As a result, the sample of average histograms , is obtained. Considering the 0-th run as idle and omitting it to eliminate the influence of the initial state, calculate the resulting average histograms over the sample and the statistical errors as follows:
- To obtain the final histograms of the PCFs with the statistical errors one takes into account the angular distribution and the numbers of electron pairs for different spin projections:where , is equal to , and for , equal to u,u; d,d and u,d, respectively.
Appendix A.4. Smpimc Algorithm for MDFs
- Set the run number and the initial state : the coordinates are uniformly distributed in the simulation box, while the relative coordinates and the differential coordinate are equal to zero.
- Set the step number and the first state .
- Select the type of step: –step with the probability , –step with the probability or –step with the probability . If –step has been chosen, modify with uniformly distributed in the volume . Otherwise, select the particle number randomly; if –step has been chosen, modify with uniformly distributed in the volume ; if –step has been chosen, select the “bead” number randomly and modify with uniformly distributed in the volume . Take into account the PBC. The resulting state has to be set as the proposed state .
- Accept the proposed state with the probability (A4) or reject it. In the case of acceptance, set , in the case of rejection, set .
- Calculate the absolute value and build the related histogram , where is the number of the cell with the length , so .
- Repeat steps (3)–(5) for .
- Calculate the average histogram for the obtained sample of states via the averaging of with as the weight function:
- To obtain the histogram of the -distribution on the l-th run take into account the angular distribution:
- Repeat steps (2)–(8) for , but instead of the initialization use the last state from the previous run: .
- As a result, the sample of average histograms of -distribution , is obtained. Considering the 0-th run as idle and omitting it to eliminate the influence of the initial state, calculate the resulting average histogram over the sample with the statistical error as follows:
- To obtain the histogram of the MDF perform the discrete sine transform of the lattice function :for the lattice values of p. The statistical error can be easily calculated via a similar procedure.
References
- Knudson, M.D.; Desjarlais, M.P.; Lemke, R.W.; Mattsson, T.R.; French, M.; Nettelmann, N.; Redmer, R. Probing the Interiors of the Ice Giants: Shock Compression of Water to 700 GPa and 3.8 g/cm3. Phys. Rev. Lett. 2012, 108, 091102. [Google Scholar] [CrossRef] [PubMed]
- Nettelmann, N.; Becker, A.; Holst, B.; Redmer, R. Jupiter models with Improved ab initio hydrogen equation of state (H-REOS.2). Astrophys. J. 2012, 750, 52. [Google Scholar] [CrossRef] [Green Version]
- Mazevet, S.; Licari, A.; Chabrier, G.; Potekhin, A.Y. Ab initio based equation of state of dense water for planetary and exoplanetary modeling. Astron. Astrophys. 2019, 621, A128. [Google Scholar] [CrossRef] [Green Version]
- Hubbard, W.B.; Guillot, T.; Lunine, J.I.; Burrows, A.; Saumon, D.; Marley, M.S.; Freedman, R.S. Liquid metallic hydrogen and the structure of brown dwarfs and giant planets. Phys. Plasmas 1997, 4, 2011–2015. [Google Scholar] [CrossRef] [Green Version]
- Chabrier, G.; Brassard, P.; Fontaine, G.; Saumon, D. Cooling Sequences and Color-Magnitude Diagrams for Cool White Dwarfs with Hydrogen Atmospheres. Astrophys. J. 2000, 543, 216–226. [Google Scholar] [CrossRef]
- Haensel, P.; Potekhin, A.Y.; Yakovlev, D.G. Neutron Stars 1: Equation of State and Structure; Astrophysics and Space Science Library; Springer: New York, NY, USA, 2007. [Google Scholar] [CrossRef]
- Sharma, B.K.; Centelles, M.; Viñas, X.; Baldo, M.; Burgio, G.F. Unified equation of state for neutron stars on a microscopic basis. Astron. Astrophys. 2015, 584, A103. [Google Scholar] [CrossRef]
- Schmit, P.F.; Knapp, P.F.; Hansen, S.B.; Gomez, M.R.; Hahn, K.D.; Sinars, D.B.; Peterson, K.J.; Slutz, S.A.; Sefkow, A.B.; Awe, T.J.; et al. Understanding Fuel Magnetization and Mix Using Secondary Nuclear Reactions in Magneto-Inertial Fusion. Phys. Rev. Lett. 2014, 113, 155004. [Google Scholar] [CrossRef] [Green Version]
- Nora, R.; Theobald, W.; Betti, R.; Marshall, F.J.; Michel, D.T.; Seka, W.; Yaakobi, B.; Lafon, M.; Stoeckl, C.; Delettrez, J.; et al. Gigabar Spherical Shock Generation on the OMEGA Laser. Phys. Rev. Lett. 2015, 114, 045001. [Google Scholar] [CrossRef]
- Roozehdar Mogaddam, R.; Sepehri Javan, N.; Javidan, K.; Mohammadzadeh, H. Modulation instability and soliton formation in the interaction of X-ray laser beam with relativistic quantum plasma. Phys. Plasmas 2019, 26, 062112. [Google Scholar] [CrossRef]
- Edwards, M.R.; Shi, Y.; Mikhailova, J.M.; Fisch, N.J. Laser amplification in strongly magnetized plasma. Phys. Rev. Lett. 2019, 123, 025001. [Google Scholar] [CrossRef] [Green Version]
- Ebeling, W.; Fortov, V.; Filinov, V. Quantum Statistics of Dense Gases and Nonideal Plasmas; Springer: Berlin, Germany, 2017. [Google Scholar]
- Savchenko, V.I. Quantum, multibody effects and nuclear reaction rates in plasmas. Phys. Plasmas 2001, 8, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Salpeter, E.E.; van Horn, H.M. Nuclear Reaction Rates at High Densities. Astrophys. J. 1969, 155, 183. [Google Scholar] [CrossRef]
- Ichimaru, S. Nuclear fusion in dense plasmas. Rev. Mod. Phys. 1993, 65, 255–299. [Google Scholar] [CrossRef]
- Dewitt, H.; Slattery, W. Screening Enhancement of Thermonuclear Reactions in High Density Stars. Contrib. Plasma Phys. 1999, 39, 97–100. [Google Scholar] [CrossRef] [Green Version]
- Starostin, A.; Mironov, A.; Aleksandrov, N.; Fisch, N.; Kulsrud, R. Quantum corrections to the distribution function of particles over momentum in dense media. Physica A 2002, 305, 287–296. [Google Scholar] [CrossRef]
- Starostin, A.; Leonov, A.; Petrushevich, Y. Quantum corrections to the particle distribution function and reaction rates in dense media. Plasma Phys. Rep. 2005, 31, 123–132. [Google Scholar] [CrossRef]
- Starostin, A.; Gryaznov, V.; Petrushevich, Y. Development of the theory of momentum distribution of particles with regard to quantum phenomena. J. Exp. Theor. Phys. 2017, 125, 940–947. [Google Scholar] [CrossRef]
- Larkin, A.S.; Filinov, V.S.; Fortov, V.E. Path Integral Representation of the Wigner Function in Canonical Ensemble. Contrib. Plasma Phys. 2016, 56, 187–196. [Google Scholar] [CrossRef]
- Larkin, A.; Filinov, V. Phase Space Path Integral Representation for Wigner Function. J. Appl. Math. Phys. 2017, 5, 392–411. [Google Scholar] [CrossRef] [Green Version]
- Larkin, A.; Filinov, V. Quantum tails in the momentum distribution functions of non-ideal Fermi systems. Contrib. Plasma Phys. 2018, 58, 107–113. [Google Scholar] [CrossRef]
- Larkin, A.; Filinov, V.; Fortov, V. Peculiarities of the momentum distribution functions of strongly correlated charged fermions. J. Phys. A Math. Theor. 2017, 51, 035002. [Google Scholar] [CrossRef] [Green Version]
- Larkin, A.; Filinov, V.; Fortov, V. Pauli blocking by effective pair pseudopotential in degenerate Fermi systems of particles. Contrib. Plasma Phys. 2017, 57, 506–511. [Google Scholar] [CrossRef]
- Larkin, A.S.; Filinov, V.S. Monte Carlo simulation of the thermodynamic properties of hydrogen plasma with the Wigner function. High Temp. 2019, 57, 651–659. [Google Scholar] [CrossRef]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef] [Green Version]
- Karasiev, V.V.; Sjostrom, T.; Dufty, J.; Trickey, S.B. Accurate Homogeneous Electron Gas Exchange-Correlation Free Energy for Local Spin-Density Calculations. Phys. Rev. Lett. 2014, 112, 076403. [Google Scholar] [CrossRef]
- Chachiyo, T. Communication: Simple and accurate uniform electron gas correlation energy for the full range of densities. J. Chem. Phys. 2016, 145, 021101. [Google Scholar] [CrossRef]
- Loos, P.F.; Gill, P.M.W. The uniform electron gas. WIREs Comput. Mol. Sci. 2016, 6, 410–429. [Google Scholar] [CrossRef]
- Mahan, G. Many-Particle Physics; Physics of Solids and Liquids; Springer: New York, NY, USA, 2000. [Google Scholar]
- Yasuhara, H.; Kawazoe, Y. A note on the momentum distribution function for an electron gas. Phys. A 1976, 85, 416–424. [Google Scholar] [CrossRef]
- Kimball, J.C. Short-range correlations and the structure factor and momentum distribution of electrons. J. Phys. A Math. Gen. 1975, 8, 1513–1517. [Google Scholar] [CrossRef]
- Hunger, K.; Schoof, T.; Dornheim, T.; Bonitz, M.; Filinov, A. Momentum distribution function and short-range correlations of the warm dense electron gas: Ab initio quantum Monte Carlo results. Phys. Rev. E 2021, 103, 053204. [Google Scholar] [CrossRef]
- Larkin, A.S.; Filinov, V.S.; Levashov, P.R. Single-momentum path integral Monte Carlo simulations of uniform electron gas in warm dense matter regime. Phys. Plasmas 2021, 28, 122712. [Google Scholar] [CrossRef]
- Toukmaji, A.Y.; Board, J.A. Ewald summation techniques in perspective: A survey. Comput. Phys. Commun. 1996, 95, 73–92. [Google Scholar] [CrossRef]
- Dornheim, T.; Groth, S.; Bonitz, M. The uniform electron gas at warm dense matter conditions. Phys. Rep. 2018, 744, 1–86. [Google Scholar] [CrossRef] [Green Version]
- Tatarskiĭ, V.I. The Wigner representation of quantum mechanics. PHYS-USP+ 1983, 26, 311–327. [Google Scholar] [CrossRef]
- Feynman, R.; Hibbs, A. Quantum Mechanics and Path-Integral; Physics of Solids and Liquids; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Filinov, V.S.; Bonitz, M.; Levashov, P.; Fortov, V.E.; Ebeling, W.; Schlanges, M.; Koch, S.W. Plasma phase transition in dense hydrogen and electron–hole plasmas. J. Phys. A Math. Gen. 2003, 36, 6069–6076. [Google Scholar] [CrossRef] [Green Version]
- Kleinert, H. Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets; World Scientific: Singapore, 2004. [Google Scholar]
- Dornheim, T.; Groth, S.; Schoof, T.; Hann, C.; Bonitz, M. Ab initio quantum Monte Carlo simulations of the uniform electron gas without fixed nodes: The unpolarized case. Phys. Rev. B 2016, 93, 205134. [Google Scholar] [CrossRef] [Green Version]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Allen, M.; Tildesley, D. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1988. [Google Scholar]

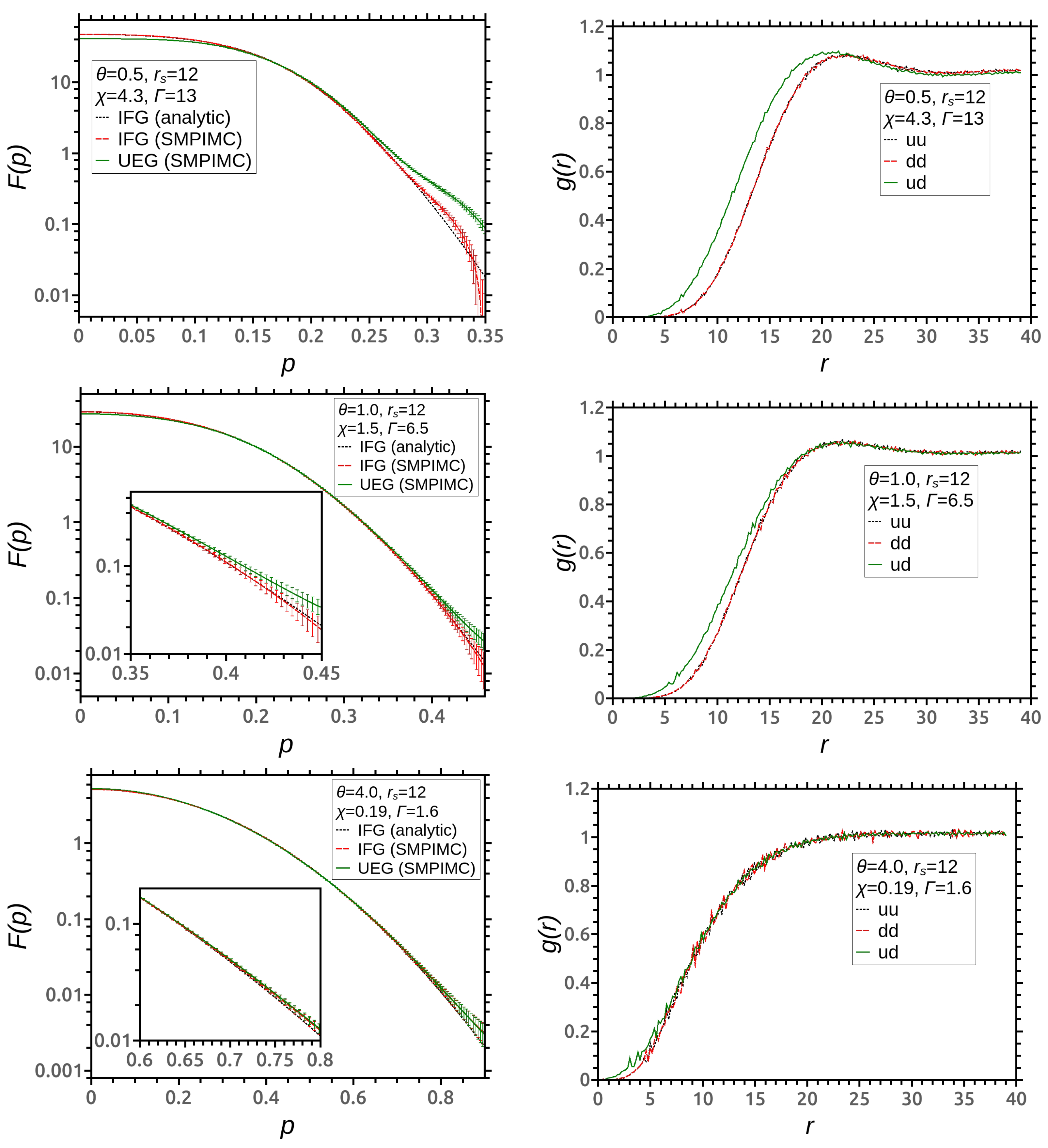
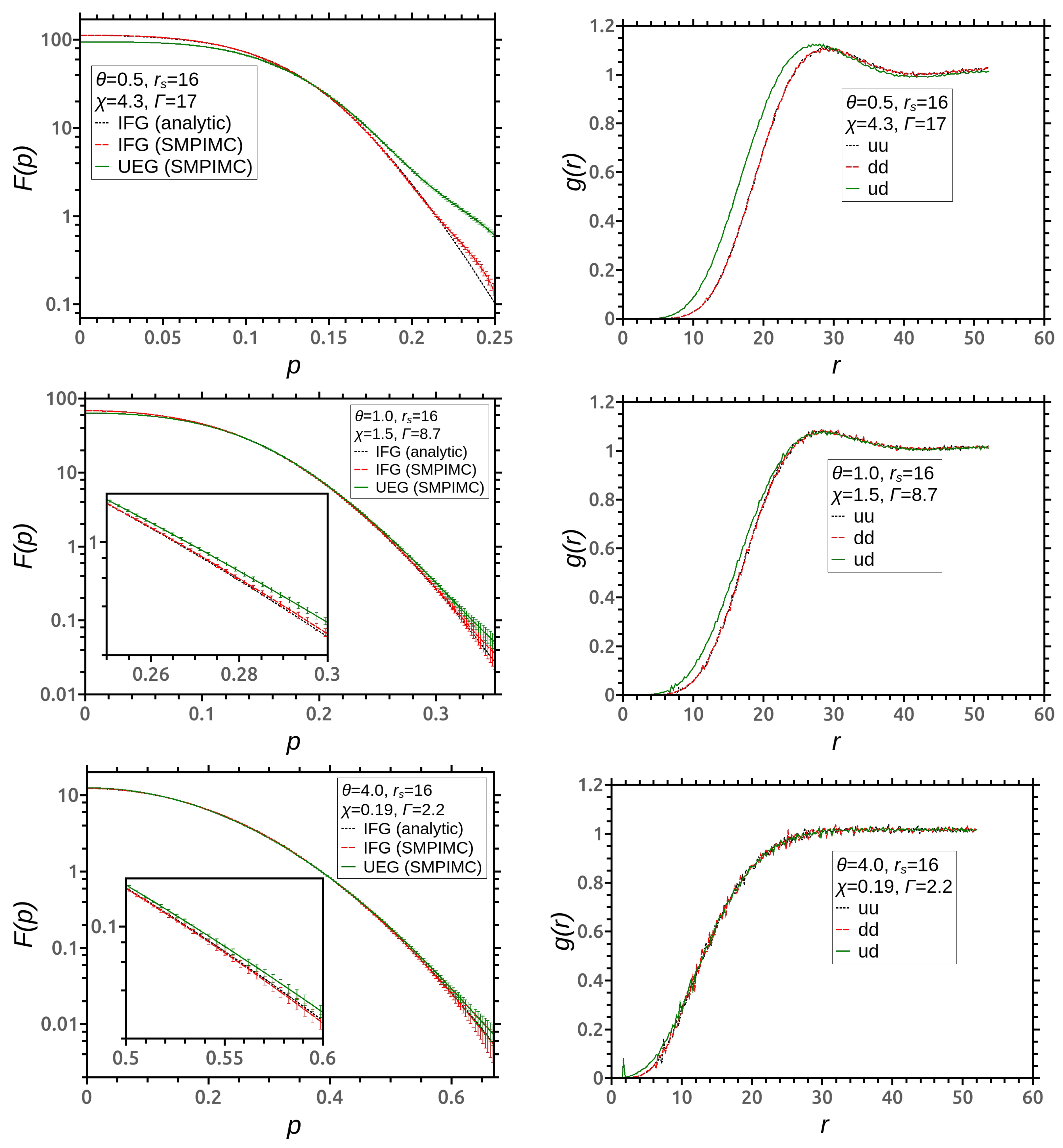
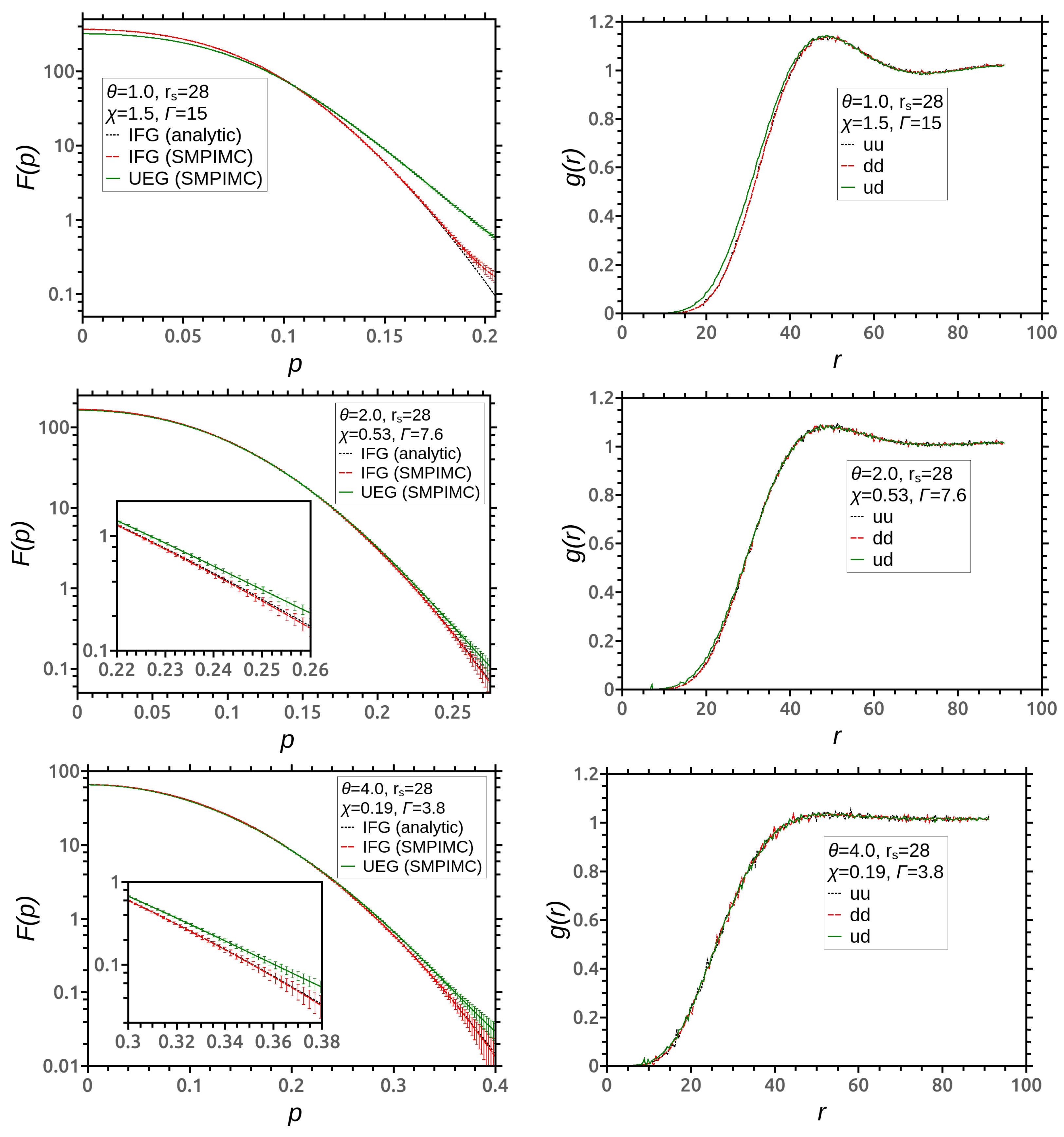
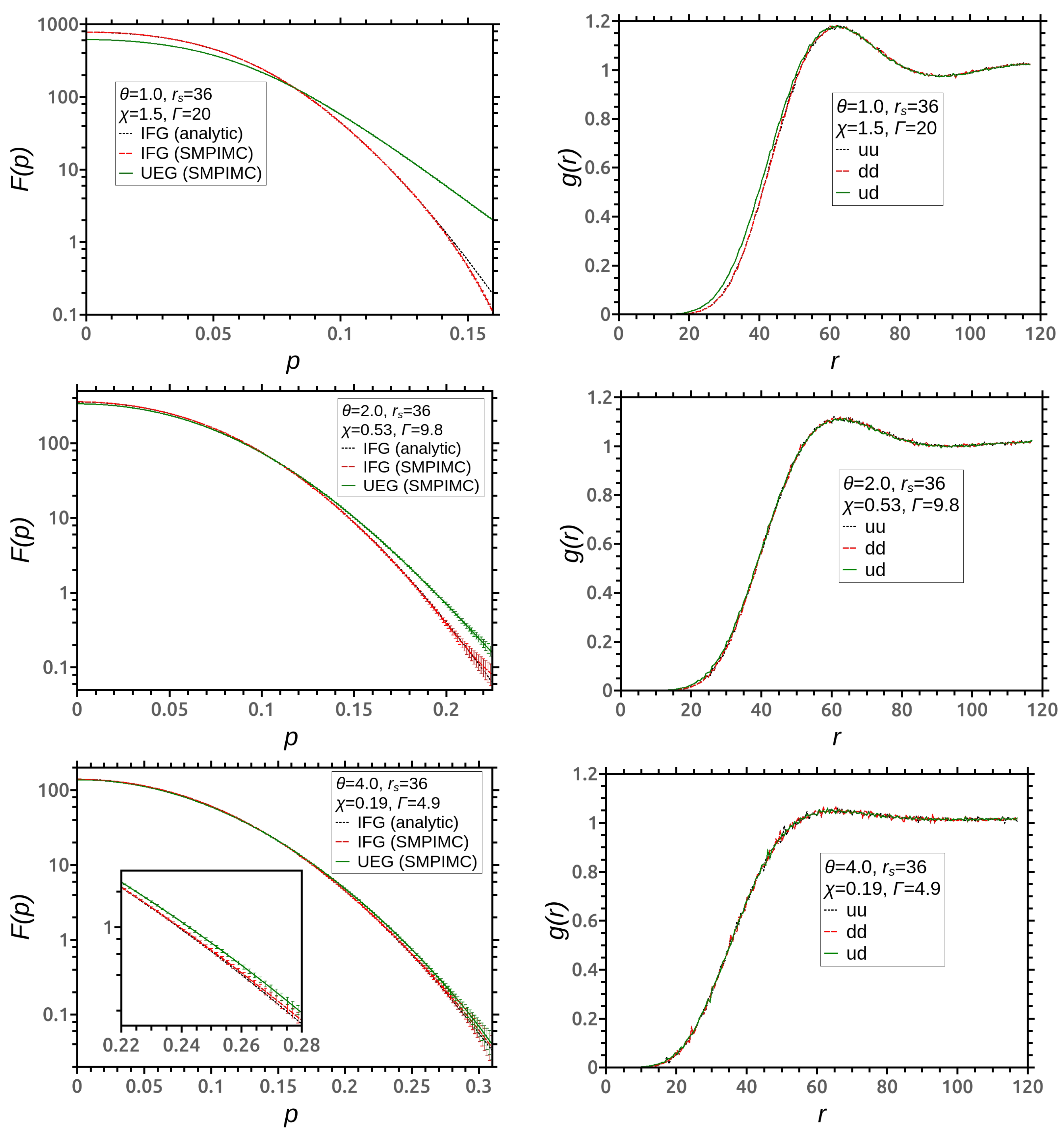

| 10 | 26 | — | — | |||||
| 26 | — | — | ||||||
| 26 | >1.9 | — | — | |||||
| 12 | 13 | 31 | 78 | 20–22 | 30–32 | |||
| 12 | 22 | 78 | 20–22 | — | ||||
| 12 | 11 | 78 | — | — | ||||
| 16 | 17 | 42 | 100 | 26–28 | 40–42 | |||
| 16 | 30 | 100 | 26–28 | — | ||||
| 16 | 15 | 100 | — | — | ||||
| 28 | 15 | 52 | 180 | 45–50 | 70 | |||
| 28 | 37 | 180 | 45–50 | 70–75 | ||||
| 28 | 26 | 180 | 50 | — | ||||
| 36 | 20 | 66 | 230 | 60–65 | 90 | |||
| 36 | 47 | 230 | 60–65 | 90–95 | ||||
| 36 | 33 | 230 | 60–65 | — |
| , Ha | , Ha | , Ha | , Ha | ||
|---|---|---|---|---|---|
| 12 | |||||
| 12 | |||||
| 12 | |||||
| 16 | |||||
| 16 | |||||
| 16 | |||||
| 28 | |||||
| 28 | |||||
| 28 | |||||
| 36 | |||||
| 36 | |||||
| 36 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larkin, A.; Filinov, V.; Levashov, P. Momentum Distribution Functions and Pair Correlation Functions of Unpolarized Uniform Electron Gas in Warm Dense Matter Regime. Mathematics 2022, 10, 2270. https://doi.org/10.3390/math10132270
Larkin A, Filinov V, Levashov P. Momentum Distribution Functions and Pair Correlation Functions of Unpolarized Uniform Electron Gas in Warm Dense Matter Regime. Mathematics. 2022; 10(13):2270. https://doi.org/10.3390/math10132270
Chicago/Turabian StyleLarkin, Alexander, Vladimir Filinov, and Pavel Levashov. 2022. "Momentum Distribution Functions and Pair Correlation Functions of Unpolarized Uniform Electron Gas in Warm Dense Matter Regime" Mathematics 10, no. 13: 2270. https://doi.org/10.3390/math10132270
APA StyleLarkin, A., Filinov, V., & Levashov, P. (2022). Momentum Distribution Functions and Pair Correlation Functions of Unpolarized Uniform Electron Gas in Warm Dense Matter Regime. Mathematics, 10(13), 2270. https://doi.org/10.3390/math10132270







