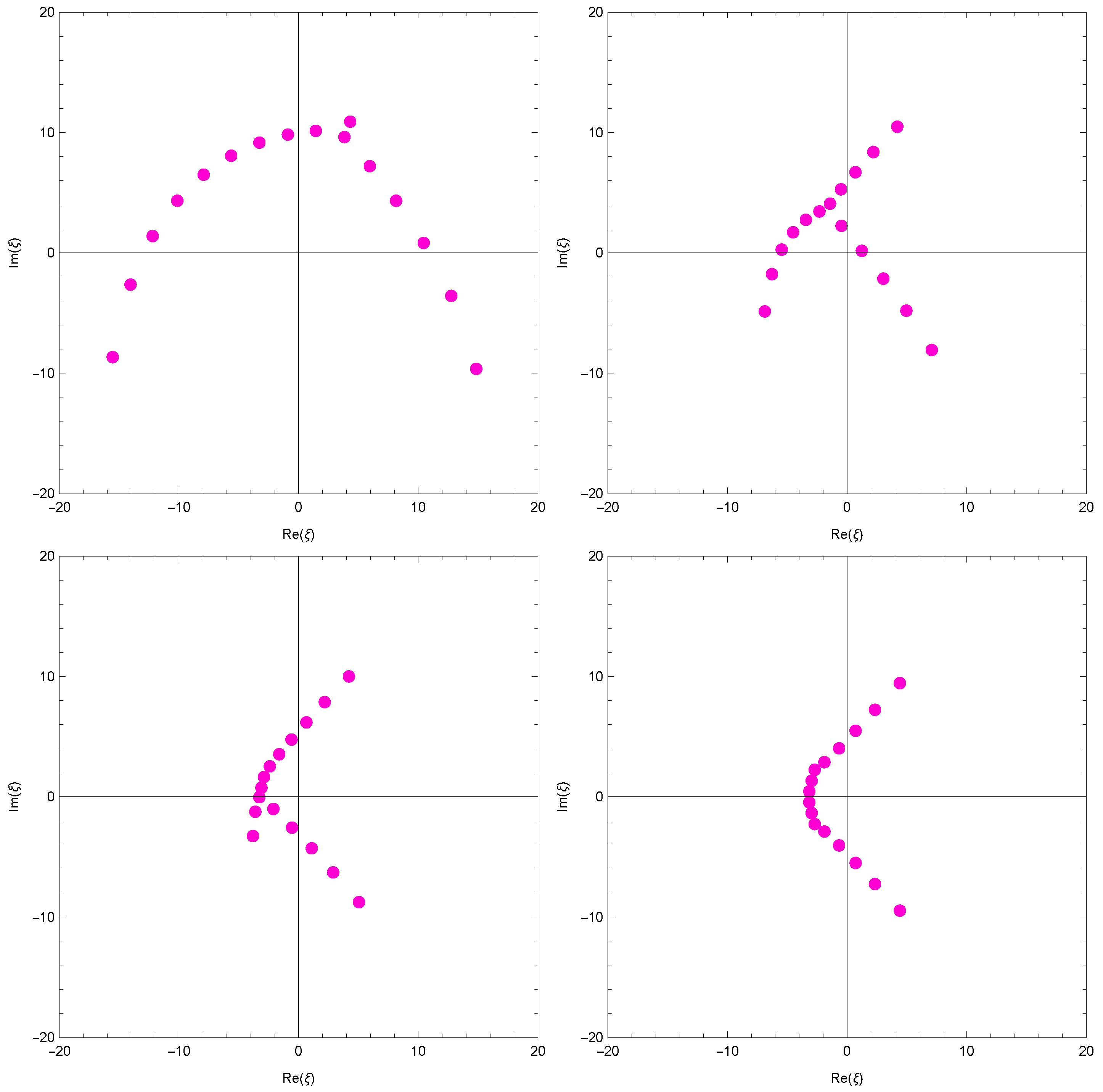A Note on Bell-Based Apostol-Type Frobenius-Euler Polynomials of Complex Variable with Its Certain Applications

Abstract

In this paper, we introduce new class of Bell-based Apostol-type Frobenius–Euler polynomials and investigate some properties of these polynomials. We derive some explicit and implicit summation formulas and their symmetric identities by using different analytical means and applying generating functions of generalized Apostol-type Frobenius-Euler polynomials and Bell-based Apostol-type Frobenius-Euler polynomials. In particular, parametric kinds of the Bell-based Apostol-type Frobenius-Euler polynomials are introduced and some of their algebraic and analytical properties are established. In addition, illustrative examples of these families of polynomials are shown, focusing on their numerical values and piloting some beautiful computer-aided graphs of them.

1. Introduction

Nowadays, an increasing number of authors [1,2,3,4] have considered the use of generating functions method in order to introduce new families of special polynomials, including two parametric kinds of polynomials, such as Bernoulli, Euler, Genocchi, etc.

With a such work methodology, it is possible to establish novel properties for these families of polynomials, which include relations between trigonometric functions, as well as parametric kinds of special polynomials. By applying the partial derivative operator to the generating functions involved, it is possible to deduce some derivative formulae, and finite combinatorial sums related with aforementioned polynomials and their associated numbers. Moreover, these special polynomials allow for the derivation of different useful identities in a fairly straightforward way. The so-called Apostol-type Frobenius-Euler polynomials appear in combinatorial mathematics and play an important role in the theory and applications of mathematics, leading to a great number of theories; combinatorics experts have extensively studied their properties, obtaining a series of interesting results (cf., e.g., [5,6,7,8,9,10] and the references therein).

The Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )$ of order $\alpha$ are defined by (see [7,8]):

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )\frac{z^j}{j!},$$

(1)

$$\left(\alpha ,\xi ,\lambda \in \mathbb{C},u\in \mathbb{C}\backslash \left\{1\right\},\lambda \ne u,\mid z\mid <\left|\mathrm{Log}\left(\frac{u}{\lambda }\right)\right|\right),$$

and $e^{\xi z}$ is an entire function of z for any $\xi \in \mathbb{C}$.

At the point $\xi =0$, ${\mathbb{H}}_j^{\left(\alpha \right)}(u;\lambda )={\mathbb{H}}_j^{\left(\alpha \right)}(0;u;\lambda )$ are called the Apostol-type Frobenius-Euler numbers of order $\alpha$. From (1), we find

$${\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )=\sum _{\nu =0}^j\left(\begin{array}{c}j\hfill \\ \nu \hfill \end{array}\right){\mathbb{H}}_{\nu }^{\left(\alpha \right)}(u;\lambda ){\xi }^{j-\nu },$$

(2)

and

$${\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;-1;\lambda )={\mathbb{E}}_j^{\left(\alpha \right)}(\xi ;\lambda ),$$

(3)

where ${\mathbb{E}}_j^{\left(\alpha \right)}(\xi ;\lambda )$ are the jth Apostol–Euler polynomials of order $\alpha$.

For $j\ge 0$, the Stirling numbers of the first kind are defined by

$${\left(\xi \right)}_j=\sum _{p=0}^j{S}_1(j,p){\xi }^p,$$

(4)

where ${\left(\xi \right)}_0=1$, and ${\left(\xi \right)}_j=\xi (\xi -1)\cdots (\xi -j+1),(j\ge 1)$. From (4), we obtain

$$\frac{1}{r!}{\left(\mathrm{Log}(1+z)\right)}^r=\sum _{j=r}^{\infty }{S}_1(j,r)\frac{z^j}{j!},(r\ge 0).$$

(5)

For $j\ge 0$, the Stirling numbers of the second kind are defined by

$${\xi }^j=\sum _{q=0}^j{S}_2(j,q){\left(\xi \right)}_q.$$

(6)

From (6), we see that

$$\frac{1}{r!}{(e^z-1)}^r=\sum _{j=r}^{\infty }{S}_2(j,r)\frac{z^j}{j!}.$$

(7)

For any nonnegative integer r, the r-Stirling numbers $S_r(j,k)$ of the second kind are defined by (see [11])

$$\frac{1}{k!}{e}^{rz}{(e^z-1)}^k=\sum _{j=k}^{\infty }{S}_r(j+r,k+r)\frac{z^j}{j!}.$$

(8)

For any positive integer m, the r-Whitney numbers $W_{m,r}(j,k)$ of the second kind are defined by (see [12,13])

$$\frac{1}{m^{k}k!}{e}^{rz}{(e^{mz}-1)}^k=\sum _{j=k}^{\infty }{W}_{m,r}(j,k)\frac{z^j}{j!}.$$

(9)

The Apostol-type Bernoulli polynomials ${\mathbb{B}}_j^{\left(\alpha \right)}(\xi ;\lambda )$ of order $\alpha$, the Apostol-type Euler polynomials ${\mathbb{E}}_j^{\left(\alpha \right)}(\xi ;\lambda )$ of order $\alpha$ and the Apostol-type Genocchi polynomials ${\mathbb{G}}_j^{\left(\alpha \right)}(\xi ;\lambda )$ of order $\alpha$ are defined by (see [1,2,12]):

$${\left(\frac{z}{\lambda e^z-1}\right)}^{\alpha }{e}^{\xi z}=\sum _{j=0}^{\infty }{\mathbb{B}}_j^{\left(\alpha \right)}(\xi ;\lambda )\frac{z^j}{j!},$$

(10)

where $\mid z\mid <2\pi$ when $\lambda =1$; $\mid z\mid <\mid \mathrm{Log}\left(\lambda \right)\mid$ when $\lambda \ne 1$.

$${\left(\frac{2}{\lambda e^z+1}\right)}^{\alpha }{e}^{\xi z}=\sum _{j=0}^{\infty }{\mathbb{E}}_j^{\left(\alpha \right)}(\xi ;\lambda )\frac{z^j}{j!},$$

(11)

where $\mid z\mid <\pi$ when $\lambda =1$; $\mid z\mid <\mid \mathrm{Log}(-\lambda )\mid$ when $\lambda \ne 1$.

and

$${\left(\frac{2z}{\lambda e^z+1}\right)}^{\alpha }{e}^{\xi z}=\sum _{j=0}^{\infty }{\mathbb{G}}_j^{\left(\alpha \right)}(\xi ;\lambda )\frac{z^j}{j!},$$

(12)

where $\mid z\mid <\pi$ when $\lambda =1$; $\mid z\mid <\mid \mathrm{Log}(-\lambda )\mid$ when $\lambda \ne 1$, respectively.

Clearly, we have

$${\mathbb{B}}_j^{\left(\alpha \right)}\left(\lambda \right)={\mathbb{B}}_j^{\left(\alpha \right)}(0;\lambda ),{\mathbb{E}}_j^{\left(\alpha \right)}\left(\lambda \right)={\mathbb{E}}_j^{\left(\alpha \right)}(0;\lambda ),{\mathbb{G}}_j^{\left(\alpha \right)}\left(\lambda \right)={\mathbb{G}}_j^{\left(\alpha \right)}(0;\lambda ).$$

The Bell polynomials $Be{l}_j\left(\xi \right)$ are defined by the generating function (see [14,15])

$$e^{\xi (e^z-1)}=\sum _{j=0}^{\infty }Be{l}_j\left(\xi \right)\frac{z^j}{j!}.$$

(13)

When $\xi =1$, $Be{l}_j=Be{l}_j\left(1\right),(j\ge 0)$ are called the Bell numbers. From (7) and (13), we note that

$$Be{l}_j\left(\xi \right)=\sum _{k=0}^j{S}_2(j,k){\xi }^k(j\ge 0).$$

(14)

Recently, Duran et al. [12], introduced the Bell polynomials $Be{l}_j(\xi ;\eta )$ of two variable defined by the generating function

$$e^{\xi z+\eta (e^z-1)}=\sum _{j=0}^{\infty }Be{l}_j(\xi ;\eta )\frac{z^j}{j!}.$$

(15)

Furthermore, they introduced the generalized Bell-based Bernoulli polynomials ${}_{Bel}{\mathbb{B}}_j^{\left(\alpha \right)}(\xi ;\eta )$ defined by

$${\left(\frac{z}{e^z-1}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{B}}_j^{\left(\alpha \right)}(\xi ;\eta )\frac{z^j}{j!},$$

(16)

so that

$${}_{Bel}{\mathbb{B}}_j^{\left(\alpha \right)}(\xi ;\eta )=\sum _{r=0}^j\left(\genfrac{}{}{0pt}{}{j}{r}\right){\mathbb{B}}_{j-r}^{\left(\alpha \right)}\left(\xi \right)Be{l}_r\left(\eta \right).$$

(17)

Kim and Ryoo [16] and Jamei et al. [1] introduced the Bernoulli and Euler polynomials of complex variable defined by

$$\frac{z}{e^z-1}{e}^{\xi z}cos\eta z=\sum _{j=0}^{\infty }\frac{{\mathbb{B}}_j(\xi +i\eta )+{\mathbb{B}}_j(\xi -i\eta )}{2}\frac{z^j}{j!}=\sum _{j=0}^{\infty }{\mathbb{B}}_j^{\left(c\right)}(\xi ,\eta )\frac{z^j}{j!},$$

(18)

$$\frac{z}{e^z-1}{e}^{\xi z}sin\eta z=\sum _{j=0}^{\infty }\frac{{\mathbb{B}}_j(\xi +i\eta )-{\mathbb{B}}_j(\xi -i\eta )}{2i}\frac{z^j}{j!}=\sum _{j=0}^{\infty }{\mathbb{B}}_j^{\left(s\right)}(\xi ,\eta )\frac{z^j}{j!},$$

(19)

and

$$\frac{2}{e^z+1}{e}^{\xi z}cos\eta z=\sum _{j=0}^{\infty }\frac{{\mathbb{E}}_j(\xi +i\eta )+{\mathbb{E}}_j(\xi -i\eta )}{2}\frac{z^j}{j!}=\sum _{j=0}^{\infty }{\mathbb{E}}_j^{\left(c\right)}(\xi ,\eta )\frac{z^j}{j!},$$

(20)

$$\frac{2}{e^z+1}{e}^{\xi z}sin\eta z=\sum _{j=0}^{\infty }\frac{{\mathbb{E}}_j(\xi +i\eta )-{\mathbb{E}}_j(\xi -i\eta )}{2i}\frac{z^j}{j!}=\sum _{j=0}^{\infty }{\mathbb{E}}_j^{\left(s\right)}(\xi ,\eta )\frac{z^j}{j!},$$

(21)

respectively.

Furthermore, they have proven that (see [13,17,18,19]):

$$e^{\xi z}cos\eta z=\sum _{r=0}^{\infty }{C}_r(\xi ,\eta )\frac{z^r}{r!},$$

(22)

and

$$e^{\xi z}sin\eta z=\sum _{r=0}^{\infty }{S}_r(\xi ,\eta )\frac{z^r}{r!},$$

(23)

where

$$C_r(\xi ,\eta )=\sum _{j=0}^{\left[\frac{r}{2}\right]}{(-1)}^j\left(\begin{array}{c}r\hfill \\ 2j\hfill \end{array}\right){\xi }^{r-2j}{\eta }^{2j},$$

(24)

and

$$S_r(\xi ,\eta )=\sum _{j=0}^{\left[\frac{r-1}{2}\right]}\left(\begin{array}{c}r\hfill \\ 2j+1\hfill \end{array}\right){(-1)}^j{\xi }^{r-2j-1}{\eta }^{2j+1}.$$

(25)

The manuscript of this paper is arranged as follows: In Section 2, we introduce Bell-based Apostol-type Frobenius-Euler numbers and polynomials and investigate some properties of these numbers and polynomials. In Section 3, we derive summation formulas of Apostol-type Frobenius-Euler numbers and polynomials, connected with Apostol-type Bernoulli, Euler, and Genocchi polynomials. In Section 4, we prove several identities of Apostol-type Frobenius-Euler polynomials by using different analytical means and applying generating functions. In the last Section 5, we establish parametric kinds of Apostol-type Frobenius-Euler polynomials and investigate some identities of these polynomials.

2. Bell-Based Apostol-Type Frobenius-Euler Polynomials ${}_{\mathit{Bel}}{\mathbb{H}}_{\mathit{j}}^{\left(\mathit{\alpha }\right)}(\mathit{\xi },\mathit{\eta };\mathit{u};\mathit{\lambda })$

In this section, we define Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;\lambda )$ and explicit formula for the Apostol-type Frobenius-Euler polynomials and investigate its properties. First, we start with the following definition:

Definition 1.

The Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ of order α are defined by means of the following generating function:

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!},$$

(26)

where

$$\left(\alpha ,\xi ,\eta ,\lambda \in \mathbb{C},u\in \mathbb{C}\backslash \left\{1\right\},\lambda \ne u,\mid z\mid <\left|\mathrm{Log}\left(\frac{u}{\lambda }\right)\right|\right).$$

A few of them are

$$\begin{array}{ll}{}_{Bel}{\mathbb{H}}_0^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha },\\ {}_{Bel}{\mathbb{H}}_1^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{u\eta +\alpha \lambda -\eta \lambda +u\xi -\lambda \xi }{u-\lambda }}\right),\\ {}_{Bel}{\mathbb{H}}_2^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{u^2\eta +u^2{\eta }^2+u\alpha \lambda -2u\eta \lambda +2u\alpha \eta \lambda -2u{\eta }^2\lambda }{{(u-\lambda )}^2}}\right)\\ & +{\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{{\alpha }^2{\lambda }^2+\eta {\lambda }^2-2\alpha \eta {\lambda }^2+{\eta }^2{\lambda }^2+2u^2\eta \xi +2u\alpha \lambda \xi }{{(u-\lambda )}^2}}\right)\\ & +{\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{-4u\eta \lambda \xi -2\alpha {\lambda }^2\xi +2\eta {\lambda }^2\xi +u^2{\xi }^2-2u\lambda {\xi }^2+{\lambda }^2{\xi }^2}{{(u-\lambda )}^2}}\right).\end{array}$$

Remark 1.

On taking $\xi =0$ in (26), we obtain new type Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\eta ;u;\lambda )$ of order α as follows:

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\eta ;u;\lambda )\frac{z^j}{j!}.$$

(27)

Remark 2.

Upon setting $\eta =0$ in (26), the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ of order α reduces to familiar Frobenius-Euler polynomials ${\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )$ of order α in (1).

Remark 3.

When $\eta =0$ and $\alpha =1$, the polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ reduce to the usual Frobenius-Euler polynomials ${\mathbb{H}}_j(\xi ;u;\lambda )$.

We note that

$${}_{Bel}{\mathbb{H}}_j^{\left(1\right)}(\xi ,\eta ;u;\lambda )={}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda ).$$

(28)

Theorem 1.

For $j\ge 0$, we have

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){\mathbb{H}}_s^{\left(\alpha \right)}(u;\lambda )Be{l}_{j-s}(\xi ;\eta ),$$

(29)

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){\mathbb{H}}_s^{\left(\alpha \right)}(\xi ;u;\lambda )Be{l}_{j-s}\left(\eta \right),$$

(30)

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){}_{Bel}{\mathbb{A}}_s^{\left(\alpha \right)}(\eta ;u;\lambda ){\xi }^{j-s}.$$

(31)

Proof. 

Using (1), (13), (15) and (26), we obtain representation (29)–(31). □

Theorem 2.

$j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha +\beta )}(\xi +w,\eta +v;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_s^{\left(\beta \right)}(v,w;u;\lambda ){}_{Bel}{\mathbb{H}}_{j-s}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda ),$$

(32)

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +\zeta ,\eta ;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){\mathbb{H}}_{j-s}^{\left(\alpha \right)}(\xi ;u;\lambda ){Bel}_s(\eta ;\zeta ).$$

(33)

Proof. 

In view of (15) and (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha +\beta )}(\xi +\eta ,\zeta +w;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha +\beta }{e}^{(\xi +w)z+(\eta +v)(e^z-1)}$$

$$=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{s=0}^{\infty }{}_{Bel}{\mathbb{H}}_s^{\left(\beta \right)}(v,w;u;\lambda )\frac{z^s}{s!}$$

$$=\sum _{j=0}^{\infty }\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_s^{\left(\beta \right)}(v,w;u;\lambda ){}_{Bel}{\mathbb{H}}_{j-s}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}.$$

Now equating the coefficients of the like powers of t in the above equation, we obtain the result (32). Again by using (15) and (26), we have

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{(\xi +\zeta )z+\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +\zeta ,\eta ;u;\lambda )\frac{z^j}{j!},$$

(34)

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}{e}^{\zeta z+\eta (e^z-1)}=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )\frac{z^j}{j!}\sum _{s=0}^{\infty }Be{l}_s(\zeta ;\eta )\frac{z^s}{s!}.$$

(35)

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +\zeta ,\eta ;u;\lambda )\frac{z^j}{j!}=\sum _{j=0}^{\infty }\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){\mathbb{H}}_{j-s}^{\left(\alpha \right)}(\xi ;u;\lambda )Be{l}_s(\zeta ;\eta )\frac{z^j}{j!},$$

yields the formula (33). □

Theorem 3.

The following differentiation formulas for the Bell-based Apostol-type Frobenius-Euler polynomials of order α hold true:

$$\frac{\partial {}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )}{\partial \xi }=j{}_{Bel}{\mathbb{H}}_{j-1}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda ),$$

(36)

$$\frac{\partial {}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )}{\partial \eta }={}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )-{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda ).$$

(37)

Proof. 

The proof follows from (26), we have

$$\sum _{j=1}^{\infty }\frac{\partial }{\partial \xi }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}=\frac{\partial }{\partial \xi }{\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }\frac{\partial }{\partial \xi }{e}^{\xi z+\eta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }z{e}^{\xi z+\eta (e^z-1)}$$

$$=\sum _{j=1}^{\infty }{}_{Bel}{\mathbb{H}}_{j-1}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!},$$

(38)

the proof is completed. Again, using (26), we note that

$$\sum _{j=0}^{\infty }\frac{\partial }{\partial \eta }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}=\frac{\partial }{\partial \eta }{\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }\frac{\partial }{\partial \eta }{e}^{\xi z+\eta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}(e^z-1)$$

$$=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )\frac{z^j}{j!}-\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}.$$

(39)

Equating the coefficients of z, we obtain (37). □

Theorem 4.

Let $j\ge 0$. Then,

$$(2u-1)\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right){\mathbb{H}}_k(\xi ;u;\lambda ){}_{Bel}{\mathbb{H}}_{j-k}(\xi ,\eta ;1-u;\lambda )$$

$$=u{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda )-(1-u){}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;1-u;\lambda ).$$

(40)

Proof. 

We set

$$\frac{(2u-1)}{(\lambda e^z-\lambda )(\lambda e^z-(1-u))}=\frac{1}{\lambda e^z-u}-\frac{1}{\lambda e^z-(1-u)}.$$

We see that

$$(2u-1)\frac{(1-u)e^{\xi z}(1-(1-u))e^{\eta (e^z-1)}}{(\lambda e^z-u)(\lambda e^z-(1-u))}=\frac{(1-u)e^{\eta (e^z-1)}u{e}^{\xi z}}{\lambda e^z-u}-\frac{(1-u)e^{\eta (e^z-1)}u{e}^{\xi z}(1-(1-u))}{\lambda e^z-(1-u)},$$

$$(2u-1)\left(\sum _{k=0}^{\infty }{\mathbb{H}}_k(\xi ;u;\lambda )\frac{z^k}{k!}\right)\left(\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j(\eta ;1-u;\lambda )\frac{z^j}{j!}\right)$$

$$=u\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}-(1-u)\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;1-u;\lambda )\frac{z^j}{j!}.$$

In view of the above equation, we obtain (40). □

Theorem 5.

For $j\ge 0$, we have

$$u{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda )=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)\lambda {}_{Bel}{\mathbb{H}}_{j-k}(\xi ,\eta ;u;\lambda )-(1-u)Be{l}_j(\xi ;\eta ).$$

(41)

Proof. 

Consider

$$\frac{u}{\lambda (\lambda e^z-u)e^z}=\frac{1}{\lambda e^z-u}-\frac{1}{\lambda e^z}.$$

We find

$$\frac{u(1-u)e^{\xi z+\eta (e^z-1)}}{\lambda (\lambda e^z-u)e^z}=\frac{(1-u)e^{\xi z+\eta (e^z-1)}}{\lambda e^z-u}-\frac{(1-u)e^{\xi z+\eta (e^z-1)}}{\lambda e^z}$$

$$u\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}=\lambda \sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }\frac{z^k}{k!}-(1-u)\sum _{j=0}^{\infty }Be{l}_j(\xi ;\eta )\frac{z^j}{j!}.$$

(42)

Therefore, by (42), we obtain (41). □

Theorem 6.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$$

$$=\frac{1}{1-u}\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)\left[\lambda {\mathbb{H}}_{j-k}(u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )-u{\mathbb{H}}_{j-k}(u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\right].$$

(43)

Proof. 

In (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}=\left(\frac{1-u}{\lambda e^z-u}\right)\left(\frac{\lambda e^z-u}{1-u}\right){\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}$$

$$=\frac{\lambda }{1-u}\left[\left(\frac{1-u}{\lambda e^z-u}\right)e^z{\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}\right.$$

$$\left.-u\left(\frac{1-u}{\lambda e^z-u}\right){\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}\right]$$

$$=\frac{1}{1-u}\left[\sum _{j=0}^{\infty }\lambda {\mathbb{H}}_j(u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )\frac{z^k}{k!}-u\sum _{j=0}^{\infty }{\mathbb{H}}_j(u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^k}{k!}\right].$$

(44)

By (26) and (44), we obtain (43). □

Theorem 7.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{s=0}^j\sum _{k=0}^s\left(\genfrac{}{}{0pt}{}{j}{s}\right){\left(\xi \right)}_k{S}_2(s,k){}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\eta ;u;\lambda ).$$

(45)

Proof. 

By (26), we note that

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\eta (e^z-1)}{[e^z-1+1]}^{\xi }$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\eta (e^z-1)}\sum _{k=0}^{\infty }{\left(\xi \right)}_k\frac{{(e^z-1)}^k}{k!}$$

$$=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\eta ;u;\lambda )\frac{z^j}{j!}\sum _{s=0}^{\infty }\sum _{k=0}^s{\left(\xi \right)}_k{S}_2(s,k)\frac{z^s}{s!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{s=0}^j\sum _{k=0}^s\left(\genfrac{}{}{0pt}{}{j}{s}\right){\left(\xi \right)}_k{S}_2(s,k){}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\eta ;u;\lambda )\right)\frac{z^j}{j!}.$$

(46)

In view of (26) and (46), we obtain (45). □

3. Summation Formulas for Bell-Based Apostol-Type Frobenius-Euler Polynomials

In this section, we derive some implicit formulas for Bell-based Apostol-type Frobenius-Euler polynomials of order $\alpha$ related to Apostol-type Bernoulli polynomials, Apostol-type Euler polynomials, Apostol-type Genocchi polynomials and Stirling numbers of the second kind. Now, we begin with the following theorem.

Theorem 8.

The following formula holds true:

$${}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{j,s=0}^{h,f}\left(\begin{array}{c}f\hfill \\ s\hfill \end{array}\right)\left(\begin{array}{c}h\hfill \\ j\hfill \end{array}\right){(\xi -\zeta )}^{j+s}{}_{Bel}{\mathbb{H}}_{h+f-j-s}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda ).$$

(47)

Proof. 

By changing z with $z+w$ in (26), we have

$${\left(\frac{1-u}{\lambda e^{(z+w)}-u}\right)}^{\alpha }{e}^{\eta (e^{z+w}-1)}=e^{-\xi (z+w)}\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}.$$

(48)

Again changing $\xi$ with $\zeta$ in the above equation, we obtain

$$e^{-\zeta (z+w)}\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}={\left(\frac{1-u}{\lambda e^{(z+w)}-u}\right)}^{\alpha }{e}^{\eta (e^{z+w}-1)}.$$

(49)

By the last equations, we obtain

$$e^{(\xi -\zeta )(z+w)}\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}=\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}.$$

(50)

On expanding exponential function (50) provides

$$\sum _{N=0}^{\infty }\frac{{\left[(\xi -\zeta )(z+w)\right]}^N}{N!}\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}$$

$$=\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!},$$

(51)

which on using formula [4]

$$\sum _{N=0}^{\infty }f\left(N\right)\frac{{(\zeta +\eta )}^N}{N!}=\sum _{j,s=0}^{\infty }f(j+s)\frac{{\zeta }^j}{j!}\frac{{\eta }^s}{s!},$$

(52)

$$\sum _{j,s=0}^{\infty }\frac{{(\xi -\zeta )}^{j+s}{z}^j{w}^s}{j!s!}\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}$$

$$=\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}.$$

(53)

$$\sum _{h,f=0}^{\infty }\sum _{j,s=0}^{h,f}\frac{{(\xi -\zeta )}^{j+s}}{j!s!}{}_{Bel}{\mathbb{H}}_{h+f-j-s}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda )\frac{z^h}{(h-j)!}\frac{w^f}{(f-s)!}$$

$$=\sum _{h,f=0}^{\infty }{}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^h}{h!}\frac{w^f}{f!}.$$

(54)

In view of above equation, we obtain the required result. □

Remark 4.

Letting $f=0$ in Theorem 8, we obtain.

$${}_{Bel}{\mathbb{H}}_h^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{j=0}^h\left(\begin{array}{c}h\hfill \\ j\hfill \end{array}\right){(\xi -\zeta )}^j{}_{Bel}{\mathbb{H}}_{h-j}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda ),(j\ge 0).$$

(55)

Remark 5.

On changing ξ with $\xi +\zeta$ and setting $\eta =0$ in Theorem 8, we obtain

$${}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\xi +\zeta ;u;\lambda )=\sum _{j,s=0}^{h,f}\left(\begin{array}{c}f\hfill \\ s\hfill \end{array}\right)\left(\begin{array}{c}h\hfill \\ j\hfill \end{array}\right){\xi }^{j+s}{}_{Bel}{\mathbb{H}}_{h+f-j-s}^{\left(\alpha \right)}(\zeta ;u;\lambda ),$$

(56)

whereas by setting $\xi =0$ in Theorem 8, we obtain another result involving Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ of one and two variables

$${}_{Bel}{\mathbb{H}}_{h+f}^{\left(\alpha \right)}(\eta ;u;\lambda )=\sum _{j,s=0}^{h,f}\left(\begin{array}{c}f\hfill \\ s\hfill \end{array}\right)\left(\begin{array}{c}h\hfill \\ j\hfill \end{array}\right){(-\zeta )}^{j+s}{}_{Bel}{\mathbb{H}}_{h+f-j-s}^{\left(\alpha \right)}(\zeta ,\eta ;u;\lambda ).$$

Theorem 9.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha +1)}(\xi ,\eta ;u;\lambda )=\sum _{d=0}^j\left(\begin{array}{c}j\hfill \\ d\hfill \end{array}\right){\mathbb{H}}_{j-d}(u;\lambda ){}_{Bel}{\mathbb{H}}_d^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda ).$$

(57)

Proof. 

By (26), we have

$$\frac{1-u}{\lambda e^z-u}{\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}=\frac{1-u}{e^z-u}\sum _{d=0}^{\infty }{}_{Bel}{\mathbb{H}}_d^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^d}{d!}$$

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha +1}{e}^{\xi z+\eta (e^z-1)}=\frac{1-u}{\lambda e^z-u}\sum _{d=0}^{\infty }{}_{Bel}{\mathbb{H}}_d^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^d}{d!}$$

$$=\sum _{j=0}^{\infty }{\mathbb{H}}_j(u;\lambda )\frac{z^j}{j!}\sum _{d=0}^{\infty }{}_{Bel}{\mathbb{H}}_d^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^d}{d!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{d=0}^j\left(\genfrac{}{}{0pt}{}{j}{d}\right){\mathbb{H}}_{j-d}(u;\lambda ){}_{Bel}{\mathbb{H}}_d^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\right)\frac{z^j}{j!}.$$

Therefore, by above equation, we obtain (57). □

Theorem 10.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )=\sum _{p=0}^j\left(\begin{array}{c}j\hfill \\ p\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_p^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda ).$$

(58)

Proof. 

Using Definition 1, we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +1,\eta ;u;\lambda )\frac{z^j}{j!}-\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}(e^z-1)$$

$$=\left(\sum _{p=0}^{\infty }{}_{Bel}{\mathbb{H}}_p^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^p}{p!}\right)\left(\sum _{j=0}^{\infty }\frac{z^j}{j!}\right)-\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\zeta ;u;\lambda )\frac{z^j}{j!}$$

$$=\sum _{j=0}^{\infty }\sum _{p=0}^j\left(\genfrac{}{}{0pt}{}{j}{p}\right){}_{Bel}{\mathbb{H}}_p^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}-\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}.$$

In view of above equation, we obtain (58). □

Theorem 11.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{s=0}^j\sum _{l=s}^j\left(\begin{array}{c}\alpha +s-1\hfill \\ s\hfill \end{array}\right)s!\left(\begin{array}{c}j\hfill \\ l\hfill \end{array}\right)S_2(l,s;\lambda ){(1-u)}^{-s}Be{l}_{j-l}(\xi ;\eta ).$$

(59)

Proof. 

In (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}$$

$$=e^{\xi z+\eta (e^z-1)}{\left(1+\frac{\lambda e^z-1}{1-u}\right)}^{-\alpha }$$

$$=\sum _{s=0}^{\infty }\left(\begin{array}{c}-\alpha \hfill \\ s\hfill \end{array}\right){\left(\frac{\lambda e^z-1}{1-u}\right)}^s\sum _{j=0}^{\infty }Be{l}_j(\xi ;\eta )\frac{z^j}{j!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{s=0}^j\sum _{l=s}^j\left(\begin{array}{c}\alpha +s-1\hfill \\ s\hfill \end{array}\right)s!\left(\begin{array}{c}j\hfill \\ l\hfill \end{array}\right)S_2(l,s;\lambda ){(1-u)}^{-s}Be{l}_{j-l}(\xi ;\eta )\right)\frac{z^j}{j!},$$

yields the result (59). □

Theorem 12.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{l=0}^j\sum _{k=0}^l\left(\genfrac{}{}{0pt}{}{j}{l}\right){\left(\alpha \right)}_k{(u-1)}^{-k}{S}_l^k(\xi ;\lambda )Be{l}_{j-l}\left(\eta \right).$$

(60)

Proof. 

By (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}$$

$$=e^{\xi z+\eta (e^z-1)}{\left(1-\frac{\lambda e^z-1}{1-u}\right)}^{-\alpha }=e^{\xi z+\eta (e^z-1)}{\left(\frac{u-e^z}{u-1}\right)}^{-\alpha }$$

$$=e^{\xi z+\eta (e^z-1)}\sum _{k=0}^{\infty }{\left(\alpha \right)}_k\frac{1}{k!}{\left(\frac{\lambda e^z-1}{u-1}\right)}^k$$

$$=e^{\eta (e^z-1)}\sum _{l=0}^{\infty }\sum _{k=0}^l{\left(\alpha \right)}_k{(u-1)}^{-k}{S}_l^k(\xi ;\lambda )\frac{z^l}{l!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{l=0}^j\sum _{k=0}^l\left(\genfrac{}{}{0pt}{}{j}{l}\right){\left(\alpha \right)}_k{(u-1)}^{-k}{S}_l^k(\xi ;\lambda )Be{l}_{j-l}\left(\eta \right)\right)\frac{z^j}{j!},$$

yield the required result (60). □

Remark 6.

For $\eta =0$, Theorem 12 reduces to

$${\mathbb{H}}_l^{\left(\alpha \right)}(\xi ;u;\lambda )=\sum _{k=0}^l{\left(\alpha \right)}_k{(u-1)}^{-k}{S}_l^k(\xi ;\lambda ).$$

Remark 7.

For $\xi =r$ and $u=s$ in Theorem 12, we obtain

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(r,\eta ;s;\lambda )=\sum _{l=0}^j\sum _{k=0}^l\left(\genfrac{}{}{0pt}{}{j}{l}\right){\left(\alpha \right)}_k{W}_{s-1,r;\lambda }(l,k)Be{l}_{j-l}\left(\eta \right).$$

In particular, for $s=2$ in the above equation, we obtain

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(r,\eta ;2;\lambda )=\sum _{l=0}^j\sum _{k=0}^l\left(\genfrac{}{}{0pt}{}{j}{l}\right){\left(\alpha \right)}_k{S}_r(l+r,k+r;\lambda )Be{l}_{j-l}\left(\eta \right).$$

Theorem 13.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\sum _{k=0}^{j+1}\left(\begin{array}{c}j+1\hfill \\ k\hfill \end{array}\right)\left(\lambda \sum _{r=0}^k\left(\begin{array}{c}k\hfill \\ r\hfill \end{array}\right){\mathbb{B}}_{k-r}(\xi ;\lambda )-{\mathbb{B}}_k(\xi ;\lambda )\right){}_{Bel}{\mathbb{H}}_{j-k+1}^{\left(\alpha \right)}(0,\eta ;u;\lambda ).$$

(61)

Proof. 

In view of (10) and (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}\left(\frac{z}{\lambda e^z-1}\right)\left(\frac{\lambda e^z-1}{z}\right)$$

$$=\frac{1}{z}\left(\lambda \sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{B}}_k(\xi ;\lambda )\frac{z^k}{k!}\sum _{r=0}^{\infty }\frac{z^r}{r!}-\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{B}}_k(\xi ;\lambda )\frac{z^k}{k!}\right).$$

(62)

On equating the coefficients of same powers of z after using Cauchy product rule in (62), assertion (61) follows. □

Theorem 14.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\frac{1}{2}\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)\left(\lambda \sum _{r=0}^k\left(\begin{array}{c}k\hfill \\ r\hfill \end{array}\right){\mathbb{E}}_{k-r}(\xi ;\lambda )+{\mathbb{E}}_k(\xi ;\lambda )\right){}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(0,\eta ;u;\lambda ).$$

(63)

Proof. 

From (11) and (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}\left(\frac{2}{\lambda e^z+1}\right)\left(\frac{\lambda e^z+1}{2}\right)$$

$$=\frac{1}{2}\left(\lambda \sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{E}}_k(\xi ;\lambda )\frac{z^k}{k!}\sum _{r=0}^{\infty }\frac{z^r}{r!}+\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{A}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{E}}_k(\xi ;\lambda )\frac{z^k}{k!}\right).$$

(64)

On equating the coefficients of same powers of z after using Cauchy product rule in (64), assertion (63) follows. □

Theorem 15.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=\frac{1}{2}\sum _{k=0}^{j+1}\left(\begin{array}{c}j+1\hfill \\ k\hfill \end{array}\right)\left(\lambda \sum _{r=0}^k\left(\begin{array}{c}k\hfill \\ r\hfill \end{array}\right){\mathbb{G}}_{k-r}(\xi ;\lambda )+{\mathbb{G}}_k(\xi ;\lambda )\right){}_{Bel}{\mathbb{H}}_{j-k+1}^{\left(\alpha \right)}(0,\eta ;u;\lambda ).$$

(65)

Proof. 

By (12) and (26), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z+\eta (e^z-1)}\left(\frac{2z}{\lambda e^z+1}\right)\left(\frac{\lambda e^z+1}{2z}\right)$$

$$=\frac{1}{2z}\left(\lambda \sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{G}}_k(\xi ;\lambda )\frac{z^k}{k!}\sum _{r=0}^{\infty }\frac{z^r}{r!}+\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(0,\eta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }{\mathbb{G}}_k(\xi ;\lambda )\frac{z^k}{k!}\right).$$

On equating the coefficients of same powers of z after using Cauchy product rule in above equation, we obtain (65). □

4. Identities for Bell-Based Apostol-Type Frobenius-Euler Polynomials

In this section, we provide general symmetry identities for the Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ and generalized Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda )$ by applying the generating functions (5) and (26).

Theorem 16.

Let $a,b,>0$ with $a\ne b$ and $j\ge 0$. Then,

$$\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)b^k{a}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )$$

$$=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)a^k{b}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda ).$$

(66)

Proof. 

Let

$$A\left(z\right)={\left(\frac{{(1-u)}^2}{(\lambda e^{az}-u)(\lambda e^{bz}-u)}\right)}^{\alpha }{e}^{2ab\xi z+\eta (e^{az}-1)+\eta (e^{bz}-1)}.$$

(67)

Then, the expression for $A\left(z\right)$ is symmetric in a and b; we obtain

$$A\left(z\right)=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda )\frac{{\left(az\right)}^j}{j!}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\frac{{\left(bz\right)}^k}{k!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)b^k{a}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\right)\frac{z^j}{j!}.$$

Similarly, we can show that

$$A\left(z\right)=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\frac{{\left(bz\right)}^j}{j!}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda )\frac{{\left(az\right)}^k}{k!}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)a^k{b}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda )\right)\frac{z^j}{j!}.$$

On comparing the coefficients of $z^j$ on the right-hand sides of the last two equations, we arrive at the desired result (66). □

Remark 8.

For $\alpha =1$ in Theorem 16, the result reduces to

$$\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)b^k{a}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}(b\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k(a\xi ,\eta ;u;\lambda )$$

$$=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right)a^k{b}^{j-k}{}_{Bel}{\mathbb{H}}_{j-k}(a\xi ,\eta ;u;\lambda ){}_{Bel}{\mathbb{H}}_k(b\xi ,\eta ;u;\lambda ).$$

(68)

Theorem 17.

Let $a,b,>0$ with $a\ne b$ and $s\ge 0$. Then,

$$\sum _{k=0}^s\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)\sum _{i=0}^{a-1}\sum _{j=0}^{b-1}{(-\lambda )}^{i+j}{a}^{s-k}{b}^k{}_{Bel}{\mathbb{H}}_{s-k}^{\left(\alpha \right)}\left(b\xi +\frac{b}{a}i+j,\eta ;u;\lambda \right){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )$$

$$=\sum _{k=0}^s\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)\sum _{i=0}^{b-1}\sum _{j=0}^{a-1}{(-\lambda )}^{i+j}{b}^{s-k}{a}^k{}_{Bel}{\mathbb{H}}_{s-k}^{\left(\alpha \right)}\left(a\xi +\frac{a}{b}i+j,\eta ;u;\lambda \right){}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda ).$$

(69)

Proof. 

Consider the identity

$$B\left(z\right)={\left(\frac{{(1-u)}^2}{(\lambda e^{az}-u)(\lambda e^{bz}-u)}\right)}^{\alpha }\frac{1+\lambda {(-1)}^{a+1}{e}^{abz}}{(\lambda e^{az}+1)(\lambda e^{bz}+1)}{e}^{2ab\xi z+\eta (e^{az}-1)+\eta (e^{bz}-1)}$$

$$B\left(z\right)={\left(\frac{1-u}{\lambda e^{az}-u}\right)}^{\alpha }{e}^{ab\xi z+\eta (e^{az}-1)}\left(\frac{1-\lambda {(-e^{-bz})}^a}{\lambda e^{bz}+1}\right){\left(\frac{1-u}{\lambda e^{bz}-u}\right)}^{\alpha }$$

$$\times \left(\frac{1-\lambda {(-e^{-az})}^b}{\lambda e^{az}+1}\right)e^{ab\xi z+\eta (e^{bz}-1)}$$

$$={\left(\frac{1-u}{\lambda e^{az}-u}\right)}^{\alpha }{e}^{ab\xi z+\eta (e^{az}-1)}\sum _{i=0}^{a-1}{(-\lambda )}^i{e}^{bzi}{\left(\frac{1-u}{\lambda e^{bz}-u}\right)}^{\alpha }{e}^{ab\xi z+\eta (e^{bz}-1)}\sum _{j=0}^{b-1}{(-\lambda )}^j{e}^{azj}$$

$$={\left(\frac{1-u}{\lambda e^{az}-u}\right)}^{\alpha }{e}^{\eta (e^{az}-1)}\sum _{i=0}^{a-1}\sum _{j=0}^{b-1}{(-\lambda )}^{i+j}{e}^{(b\xi +\frac{b}{a}i+j)at}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\frac{{\left(bz\right)}^k}{k!}$$

$$=\sum _{s=0}^{\infty }\sum _{i=0}^{a-1}\sum _{j=0}^{b-1}{(-\lambda )}^{i+j}{}_{Bel}{\mathbb{H}}_s^{\left(\alpha \right)}\left(b\xi +\frac{b}{a}i+j,\eta ;u;\lambda \right)\frac{{\left(az\right)}^s}{s!}\sum _{k=0}^{\infty }{}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\frac{{\left(bz\right)}^k}{\left(k\right)!}$$

$$=\sum _{s=0}^{\infty }\sum _{k=0}^s\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)\sum _{i=0}^{a-1}\sum _{j=0}^{b-1}{(-\lambda )}^{i+j}{a}^{s-k}{b}^k{}_{Bel}{\mathbb{H}}_{s-k}^{\left(\alpha \right)}\left(b\xi +\frac{b}{a}i+j,\eta ;u;\lambda \right)$$

$$\times {}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(a\xi ,\eta ;u;\lambda )\frac{z^s}{s!}.$$

(70)

On the other hand, we have

$$B\left(z\right)=\sum _{s=0}^{\infty }\sum _{k=0}^s\left(\begin{array}{c}s\hfill \\ k\hfill \end{array}\right)\sum _{i=0}^{b-1}\sum _{j=0}^{a-1}{(-\lambda )}^{i+j}{b}^{s-k}{a}^k{}_{Bel}{\mathbb{H}}_{s-k}^{\left(\alpha \right)}\left(a\xi +\frac{a}{b}i+j,\eta ;u;\lambda \right)$$

$$\times {}_{Bel}{\mathbb{H}}_k^{\left(\alpha \right)}(b\xi ,\eta ;u;\lambda )\frac{z^s}{s!}.$$

(71)

By (70) and (71), we arrive at the desired result (69). □

5. Bell-Based Apostol-Type Frobenius-Euler Polynomials of Complex Variable

In this section, we consider the Bell-based Apostol-type Frobenius-Euler polynomials of complex variable and deduce some identities of these polynomials. First, we begin with the following definition.

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{(\xi +i\eta )z}{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}.$$

(72)

On the other hand, we suppose that

$$e^{(\xi +i\eta )z}=e^{\xi z}{e}^{i\eta z}=e^{\xi z}(cos\eta z+isin\eta z).$$

(73)

Thus, by (72) and (73), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{(\xi +i\eta )z}{e}^{\zeta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}(cos\eta z+isin\eta z)e^{\zeta (e^z-1)},$$

(74)

and

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{(\xi -i\eta )z}{e}^{\zeta (e^z-1)}$$

$$={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}(cos\eta z-isin\eta z)e^{\zeta (e^z-1)}.$$

(75)

From (74) and (75), we obtain

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }\left(\frac{{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )+{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )}{2}\right)\frac{z^j}{j!},$$

(76)

and

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}sin\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }\left(\frac{{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )-{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )}{2i}\right)\frac{z^j}{j!}.$$

(77)

Definition 2.

Let $j\ge 0$. We define two parametric kinds of cosine Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ and sine Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )$, for non negative integer j are defined by

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!},$$

(78)

and

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}sin\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!},$$

(79)

respectively.

Note that ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,0,0;u;\lambda )={\mathbb{H}}_j^{\left(\alpha \right)}(\xi ;u;\lambda ),{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(0,0,0;u;\lambda )=0,(j\ge 0)$.

From (76)–(79), we have

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=\frac{{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )+{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )}{2},$$

(80)

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=\frac{{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )-{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )}{2i}.$$

(81)

Remark 9.

For $\xi =\zeta =0$ in (78) and (79), we obtain new types of cosine Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{(\alpha ,c)}(\eta ;u;\lambda )$ and sine Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{(\alpha ,s)}(\eta ;u;\lambda )$ as

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }cos\eta z=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{(\alpha ,c)}(\eta ;u;\lambda )\frac{z^j}{j!},$$

(82)

and

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }sin\eta z=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{(\alpha ,s)}(\eta ;u;\lambda )\frac{z^j}{j!},$$

(83)

respectively.

It is clear that

$${\mathbb{H}}_j^{(\alpha ,c)}(0;u;\lambda )={\mathbb{H}}_j^{(\alpha ,c)}(u;\lambda ),{\mathbb{H}}_j^{(\alpha ,s)}(0;u;\lambda )=0,(j\ge 0).$$

Remark 10.

Letting $\zeta =0$ in (78) and (79), we obtain two parametric kinds of cosine Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ;u;\lambda )$ and sine Apostol-type Frobenius-Euler polynomials ${\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ;u;\lambda )$ as

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\eta z=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!},$$

(84)

and

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}sin\eta z=\sum _{j=0}^{\infty }{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ;u;\lambda )\frac{z^j}{j!},$$

(85)

respectively.

Remark 11.

On setting $\xi =0$ in (78) and (79), we obtain new type of cosine Bell-based Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda )$ and sine Bell-based Apostol-type Frobenius-Euler polynomials as ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda )$

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }cos\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda )\frac{z^j}{j!},$$

(86)

and

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }sin\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda )\frac{z^j}{j!},$$

(87)

respectively.

Theorem 18.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda )=\sum _{v=0}^{\left[\frac{j}{2}\right]}\left(\begin{array}{c}j\hfill \\ 2v\hfill \end{array}\right){(-1)}^v{\eta }^{2v}{}_{Bel}{\mathbb{H}}_{j-2v}^{\left(\alpha \right)}(\zeta ;u;\lambda ),$$

(88)

and

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda )=\sum _{v=0}^{\left[\frac{j-1}{2}\right]}\left(\begin{array}{c}j\hfill \\ 2v+1\hfill \end{array}\right){(-1)}^v{\eta }^{2v+1}{}_{Bel}{\mathbb{H}}_{j-2v-1}^{\left(\alpha \right)}(\zeta ;u;\lambda ).$$

(89)

Proof. 

By (82) and (83), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }cos\eta z{e}^{\zeta (e^z-1)}$$

$$=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\zeta ;u;\lambda )\frac{z^j}{j!}\sum _{v=0}^{\infty }{(-1)}^v{\eta }^{2v}\frac{z^v}{2v!}.$$

$$=\sum _{j=0}^{\infty }\left(\sum _{v=0}^{\left[\frac{j}{2}\right]}\left(\begin{array}{c}j\hfill \\ 2v\hfill \end{array}\right){(-1)}^v{\eta }^{2v}{}_{Bel}{\mathbb{H}}_{j-2v}^{\left(\alpha \right)}(\zeta ;u;\lambda )\right)\frac{z^j}{j!},$$

(90)

and

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }sin\eta z{e}^{\zeta (e^z-1)}$$

$$=\sum _{j=0}^{\infty }\left(\sum _{v=0}^{\left[\frac{j-1}{2}\right]}\left(\begin{array}{c}j\hfill \\ 2v+1\hfill \end{array}\right){(-1)}^v{\eta }^{2v+1}{}_{Bel}{\mathbb{H}}_{j-2v-1}^{\left(\alpha \right)}(\zeta ;u;\lambda )\right)\frac{z^j}{j!}.$$

(91)

Therefore, by (90) and (91), we obtain (88). Similarly, we can easily obtain (89). □

Theorem 19.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi +i\eta ,\zeta ;u;\lambda )=\sum _{s=0}^j\left(\genfrac{}{}{0pt}{}{j}{s}\right){(\xi +i\eta )}^{j-s}{}_{Bel}{\mathbb{H}}_s^{\left(\alpha \right)}(\zeta ;u;\lambda )$$

$$=\sum _{s=0}^j\left(\genfrac{}{}{0pt}{}{j}{s}\right){\left(i\eta \right)}^{j-s}{}_{Bel}{\mathbb{H}}_s^{\left(\alpha \right)}(\xi ,\zeta ;u;\lambda ),$$

(92)

and

$${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi -i\eta ,\zeta ;u;\lambda )=\sum _{s=0}^j\left(\genfrac{}{}{0pt}{}{j}{s}\right){(\xi -i\eta )}^{j-s}{}_{Bel}{\mathbb{H}}_s^{\left(\alpha \right)}(\zeta ;u;\lambda )$$

$$=\sum _{s=0}^j\left(\genfrac{}{}{0pt}{}{j}{s}\right){(-1)}^{j-s}{\left(i\eta \right)}^{j-s}{}_{Bel}{\mathbb{H}}_s^{\left(\alpha \right)}(\xi ,\zeta ;u;\lambda ).$$

(93)

Proof. 

By using (74) and (75), we obtain (92) and (93). So we omit the proof. □

Theorem 20.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{s=0}^j\left(\begin{array}{c}j\hfill \\ s\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_{j-s}^{\left(\alpha \right)}(\zeta ;u;\lambda )C_s(\xi ,\eta ),$$

(94)

and

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,k)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_{j-k}^{\left(\alpha \right)}(\zeta ;u;\lambda )S_k(\xi ,\eta ).$$

(95)

Proof. 

Consider

$$\left(\sum _{j=0}^{\infty }{a}_j\frac{z^j}{j!}\right)\left(\sum _{v=0}^{\infty }{b}_v\frac{z^v}{v!}\right)=\sum _{j=0}^{\infty }\left(\sum _{v=0}^j{a}_{j-v}{b}_v\right)\frac{z^j}{j!}.$$

Now,

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\eta z{e}^{\zeta (e^z-1)}$$

$$=\left(\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\zeta ;u;\lambda )\frac{z^j}{j!}\right)\left(\sum _{v=0}^{\infty }{C}_v(\xi ,\eta )\frac{z^j}{j!}\right)$$

$$=\sum _{j=0}^{\infty }\left(\sum _{v=0}^j\left(\begin{array}{c}j\hfill \\ v\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_{j-v}^{\left(\alpha \right)}(\zeta ;u;\lambda )C_v(\xi ,\eta )\right)\frac{z^j}{j!},$$

which proves (94). The proof of (95) is similar. □

Theorem 21.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j{\mathbb{H}}_k^{(\alpha ,c)}(\xi ,\eta ;u;\lambda )Be{l}_{j-k}\left(\zeta \right),$$

(96)

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j{\mathbb{H}}_k^{(\alpha ,s)}(\xi ,\eta ;u;\lambda )Be{l}_{j-k}\left(\zeta \right),$$

(97)

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j{}_{Bel}{\mathbb{H}}_k^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda ){\xi }^{j-k},$$

(98)

and

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j{}_{Bel}{\mathbb{H}}_k^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda ){\xi }^{j-k}.$$

(99)

Proof. 

Using (78) and (79), we obtain (96)–(99). Here, we omit the proof of the theorem. □

Theorem 22.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi +s,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_k^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )s^{j-k},$$

(100)

and

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi +s,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_k^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )s^{j-k}.$$

(101)

Proof. 

By changing $\xi$ with $\xi +s$ in (78), we have

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi +s,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\eta z{e}^{sz}{e}^{\zeta (e^z-1)}$$

$$=\left(\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}\right)\left(\sum _{k=0}^{\infty }{s}^k\frac{z^k}{k!}\right)$$

$$=\sum _{j=0}^{\infty }\left(\sum _{k=0}^j\left(\begin{array}{c}j\hfill \\ k\hfill \end{array}\right){}_{Bel}{\mathbb{H}}_k^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )s^{j-k}\right)\frac{z^j}{j!},$$

which complete the proof (100). The result (101) can be similarly proved. □

Theorem 23.

Let $j\ge 1$. Then,

$$\frac{\partial }{\partial \xi }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=j{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda ),$$

(102)

$$\frac{\partial }{\partial \eta }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=-j{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda ),$$

(103)

and

$$\frac{\partial }{\partial \xi }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=j{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda ),$$

(104)

$$\frac{\partial }{\partial \eta }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=j{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda ).$$

(105)

Proof. 

Equation (78) yields

$$\sum _{j=1}^{\infty }\frac{\partial }{\partial \xi }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }z{e}^{\xi z}cos\eta z{e}^{\zeta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^{j+1}}{j!}$$

$$=\sum _{j=1}^{\infty }{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{(j-1)!}=\sum _{j=1}^{\infty }j{}_{Bel}{\mathbb{H}}_{j-1}^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!},$$

proving (102). Other (103)–(105) can be similarly derived. □

Theorem 24.

Let $j\ge 0$. Then,

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j\sum _{m=0}^k\left(\genfrac{}{}{0pt}{}{j}{k}\right){}_{Bel}{\mathbb{H}}_{j-k}^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda ){\left(\xi \right)}_m{S}_2(k,m),$$

(106)

and

$${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )=\sum _{k=0}^j\sum _{m=0}^k\left(\genfrac{}{}{0pt}{}{j}{k}\right){}_{Bel}{\mathbb{H}}_{j-k}^{(\alpha ,s)}(\eta ,\zeta ;u;\lambda ){\left(\xi \right)}_m{S}_2(k,m).$$

(107)

Proof. 

Using (7) and (78), we find

$$\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}={\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }cos\eta z{e}^{\zeta (e^z-1)}{(e^z-1+1)}^{\xi }$$

$$={\left(\frac{1-u}{e^z-u}\right)}^{\alpha }cos\eta z{e}^{\zeta (e^z-1)}\sum _{m=0}^{\infty }{\left(\xi \right)}_m\frac{{(e^z-1)}^m}{m!}$$

$$={\left(\frac{1-u}{e^{\lambda z}-u}\right)}^{\alpha }cos\eta z{e}^{\zeta (e^z-1)}\sum _{m=0}^{\infty }{\left(\xi \right)}_m\sum _{k=m}^{\infty }{S}_2(k,m)\frac{z^k}{k!}$$

$$=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\eta ;\zeta ;u;\lambda )\frac{z^j}{j!}\sum _{k=0}^{\infty }\sum _{m=0}^k{\left(\xi \right)}_m{S}_2(k,m)\frac{z^k}{k!}$$

$$=\sum _{j=0}^{\infty }\sum _{k=0}^j\sum _{m=0}^k\left(\genfrac{}{}{0pt}{}{j}{k}\right){}_{Bel}{\mathbb{H}}_{j-k}^{(\alpha ,c)}(\eta ,\zeta ;u;\lambda ){\left(\xi \right)}_m{S}_2(k,m)\frac{z^j}{j!}.$$

(108)

In view of (78) and (108), we obtain (106). Similarly, we can easily obtain (107). □

6. Numerical Values and Graphical Representations of Bell-Based Apostol-Type Frobenius-Euler Polynomials

In this section, we find some numerical values of the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ and, beautifully, graphical representations are shown.

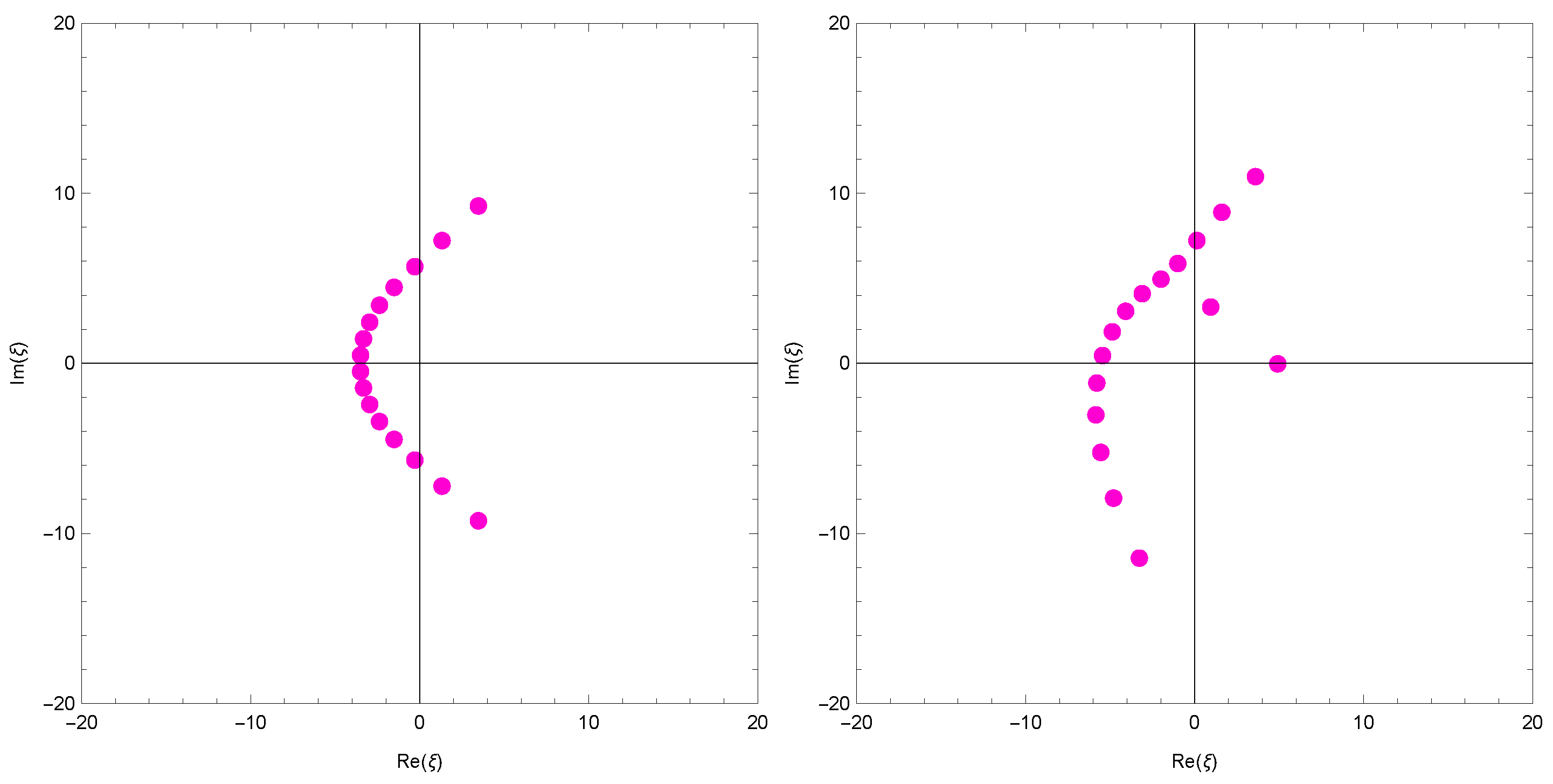
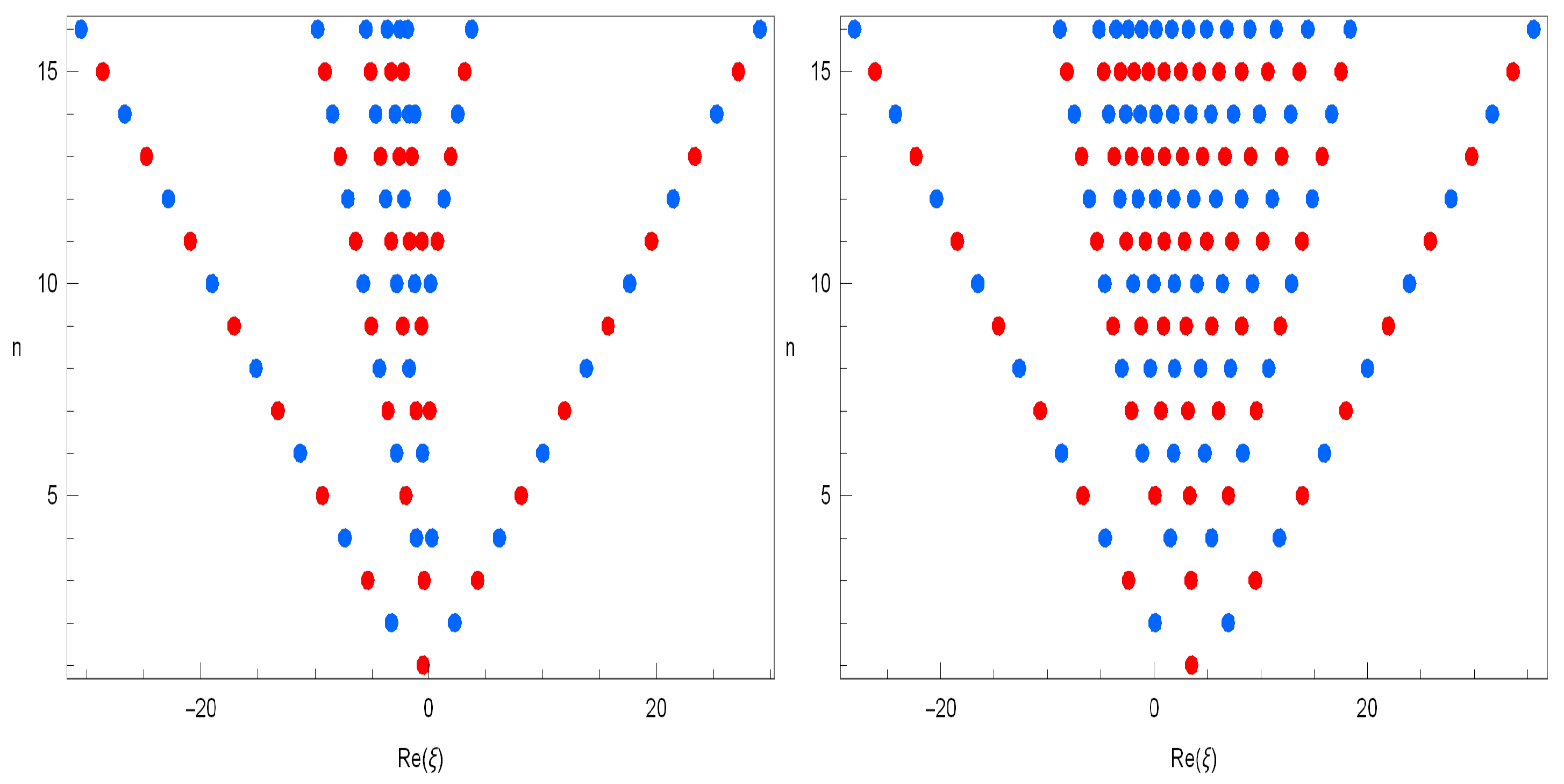
We investigated the beautiful zeros of the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$ using a computer. We plotted the zeros of Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=0$ for $j=16$ (Figure 1).

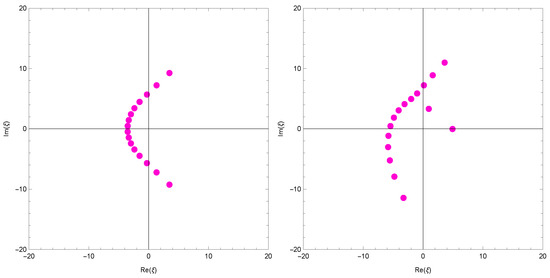
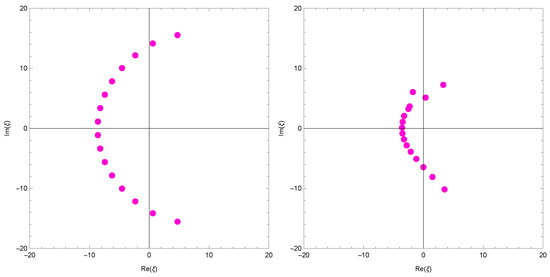
Figure 1. Zeros of ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$.

In Figure 1 (top left), we choose $\alpha =3,\eta =2,u=5,$ and $\lambda =-2$. In Figure 1 (top right), we choose $\alpha =3,\eta =2,u=5,$ and $\lambda =-2e^{\frac{2\pi i}{3}}$. In Figure 1 (bottom left), we choose $\alpha =3,\eta =2,u=5,$ and $\lambda =2$. In Figure 1 (bottom right), we choose $\alpha =3,\eta =2,u=5,$ and $\lambda =2e^{\frac{2\pi i}{3}}$.

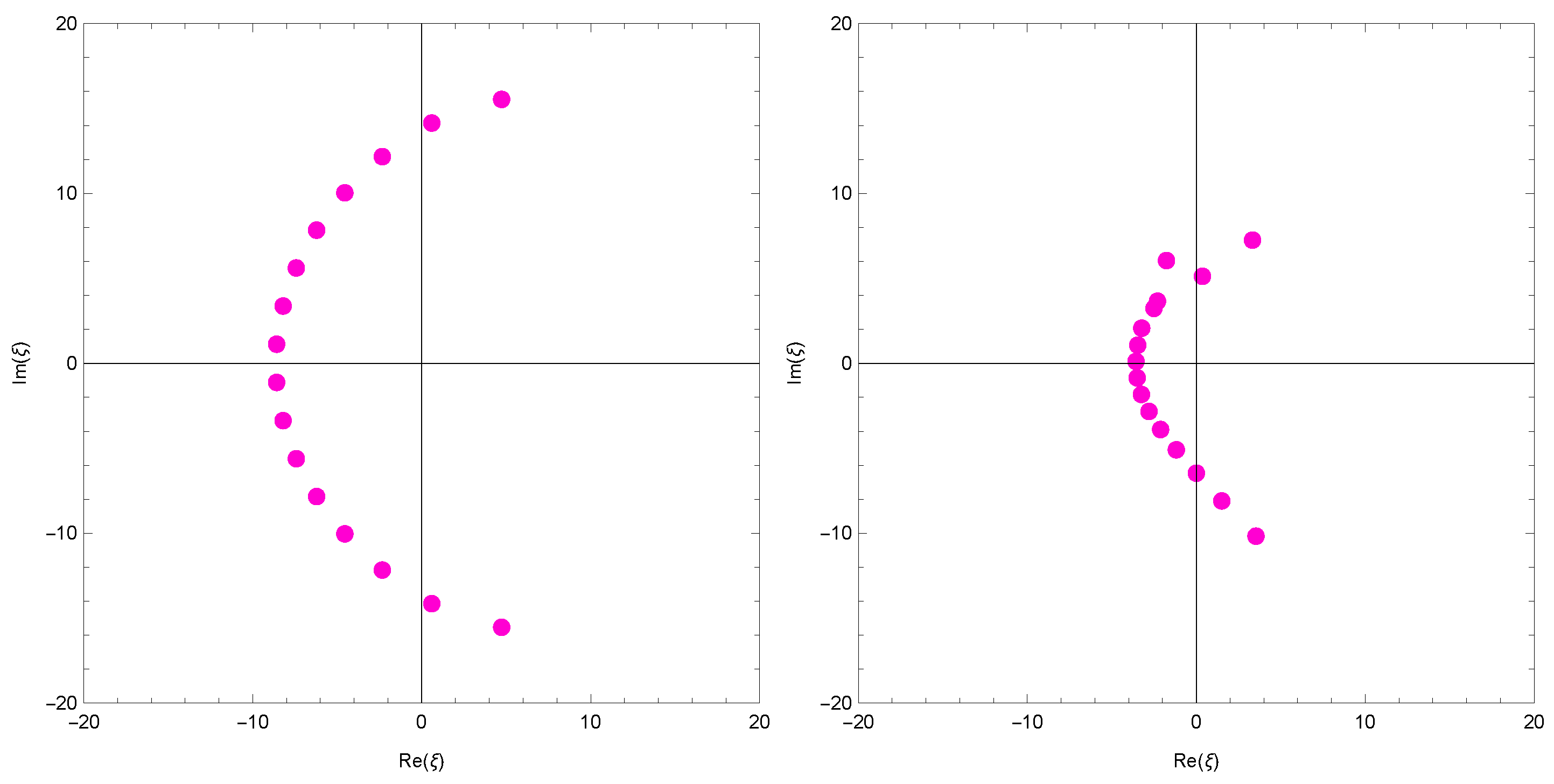
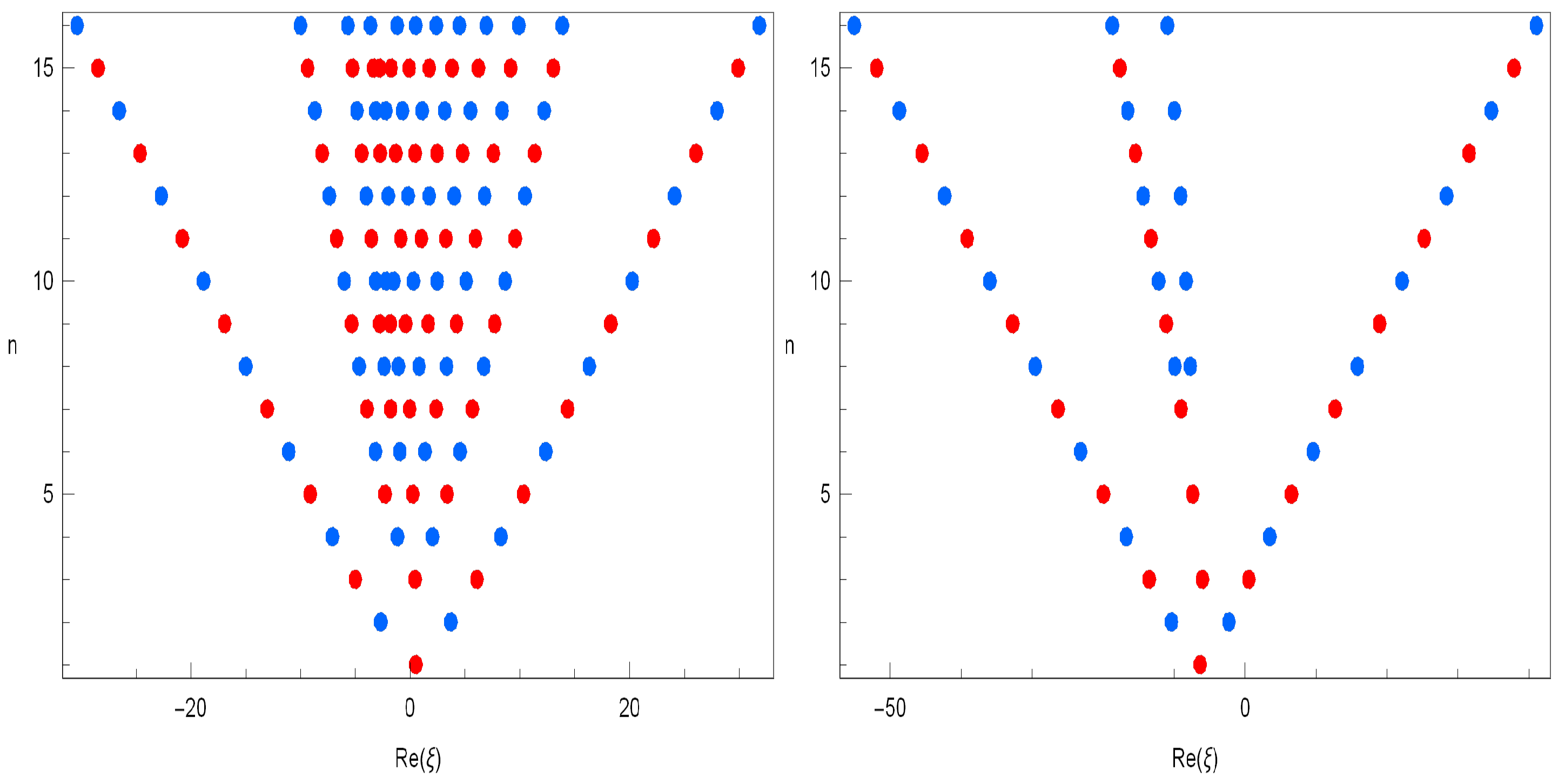
In Figure 2 (top left), we choose $\alpha =3,\eta =2,u=2e^{\frac{\pi i}{4}},$ and $\lambda =2$. In Figure 2 (top right), we choose $\alpha =3,\eta =2,u=2e^{\frac{2\pi i}{4}},$ and $\lambda =2$. In Figure 2 (bottom left), we choose $\alpha =3,\eta =2,u=2e^{\frac{3\pi i}{4}},$ and $\lambda =2$. In Figure 2 (bottom right), we choose $\alpha =3,\eta =2,u=2e^{\frac{4\pi i}{4}},$ and $\lambda =2$.

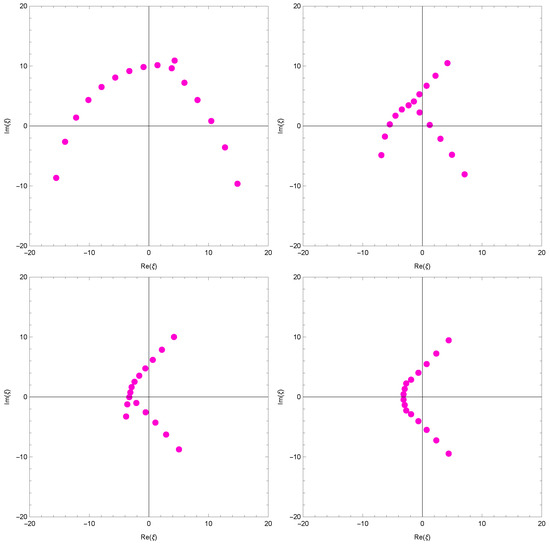
Figure 2. Zeros of ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$.

Next, we calculated an approximate solution satisfying the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )=0$. The results are displayed in Table 1.

Table 1. Approximate solutions of ${}_{Bel}{\mathbb{H}}_j^{\left(3\right)}(\xi ,2;5;2)=0$.

Degree j	$\mathit{\xi }$
1	−4.0000
2	−4.0000 − 2.3094i,    −4.0000 + 2.3094i
3	−4.5978,    −3.7011 − 4.0334i,    −3.7011 + 4.0334i
4	−4.7318 − 1.7816i,    −4.7318 + 1.7816i,
	−3.2682 − 5.4678i,    −3.2682 + 5.4678i
5	−5.2066,    −4.6389 − 3.2957i,    −4.6389 + 3.2957i,
	−2.7578 − 6.7195i,    −2.7578 + 6.7195i
6	−5.3949 − 1.5358i,    −5.3949 + 1.5358i,    −4.4091 − 4.6403i,
	−4.4091 + 4.6403i,    −2.1959 − 7.8407i,    −2.1959 + 7.8407i
7	−5.8232,    −5.4043 − 2.9141i,    −5.4043 + 2.9141i,    −4.0873 − 5.8644i,
	−4.0873 + 5.8644 i,    −1.5968 − 8.8619i,    −1.5968 + 8.8619i

7. Computational Values and Graphical Representations of Cosine Bell-Based Apostol-Type Frobenius-Euler Polynomials of Complex Variable

In this section, certain zeros of the cosine Bell-based Apostol-type Frobenius-Euler polynomials of complex variable ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ and, beautifully, graphical representations are shown.

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}cos\zeta z{e}^{\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}.$$

A few of them are

$$\begin{array}{ll}{}_{Bel}{\mathbb{H}}_0^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha },\\ {}_{Bel}{\mathbb{H}}_1^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{u\eta +\alpha \lambda -\eta \lambda +u\xi -\lambda \xi }{u-\lambda }}\right),\\ {}_{Bel}{\mathbb{H}}_2^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )& ={\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{u^2{\zeta }^2-u^2\eta -u^2{\eta }^2-u\alpha \lambda -2u{\zeta }^2\lambda +2u\eta \lambda -2u\alpha \eta \lambda }{{(u-\lambda )}^2}}\right)\\ & +{\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{2u{\eta }^2\lambda -{\alpha }^2{\lambda }^2+{\zeta }^2{\lambda }^2-\eta {\lambda }^2+2\alpha \eta {\lambda }^2-{\eta }^2{\lambda }^2-2u^2\eta \xi }{{(u-\lambda )}^2}}\right)\\ & +{\left({\displaystyle \frac{-1+u}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{-2u\alpha \lambda \xi +4u\eta \lambda \xi +2\alpha {\lambda }^2\xi -2\eta {\lambda }^2\xi -u^2{\xi }^2+2u\lambda {\xi }^2-{\lambda }^2{\xi }^2}{{(u-\lambda )}^2}}\right).\end{array}$$

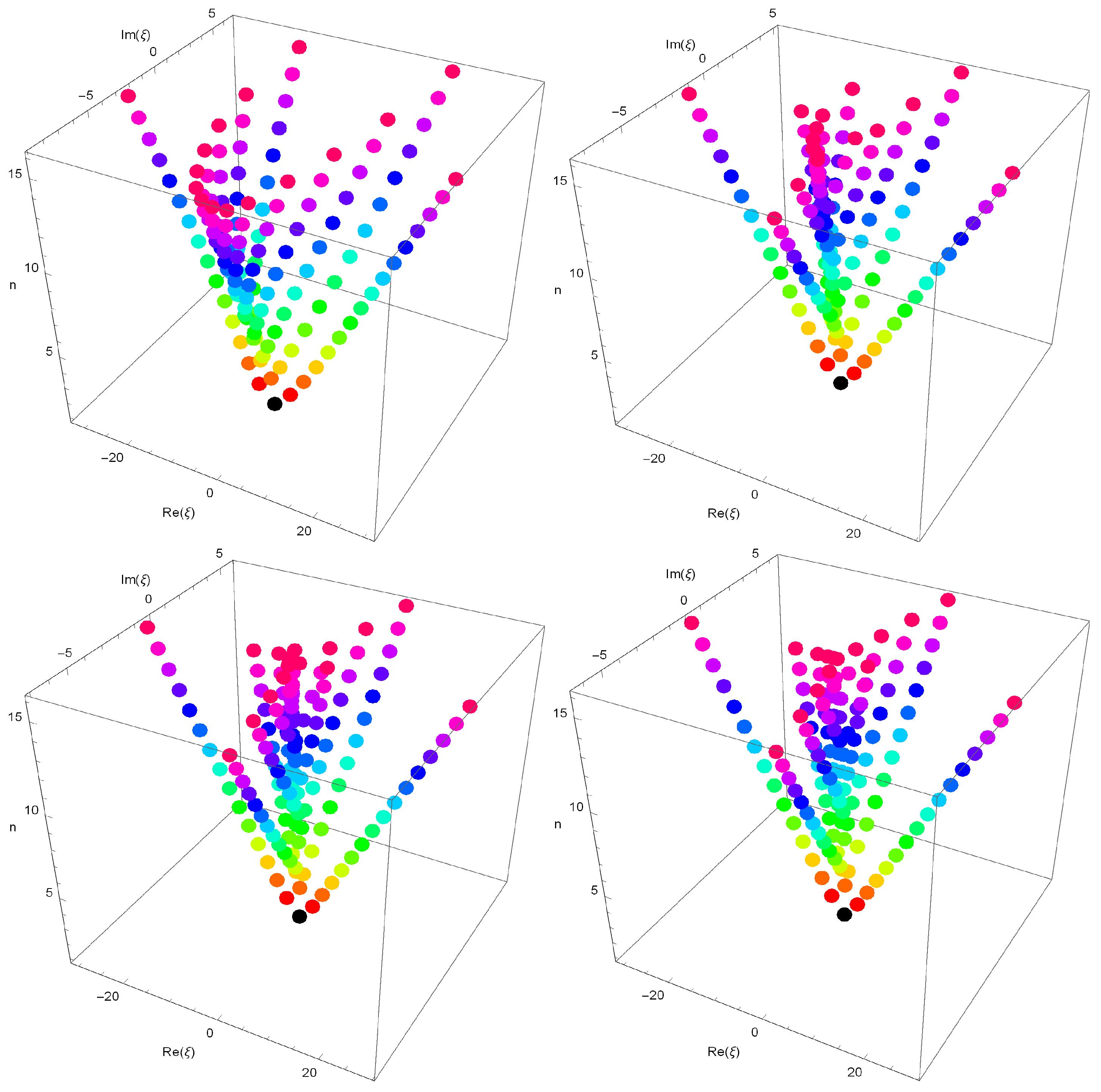
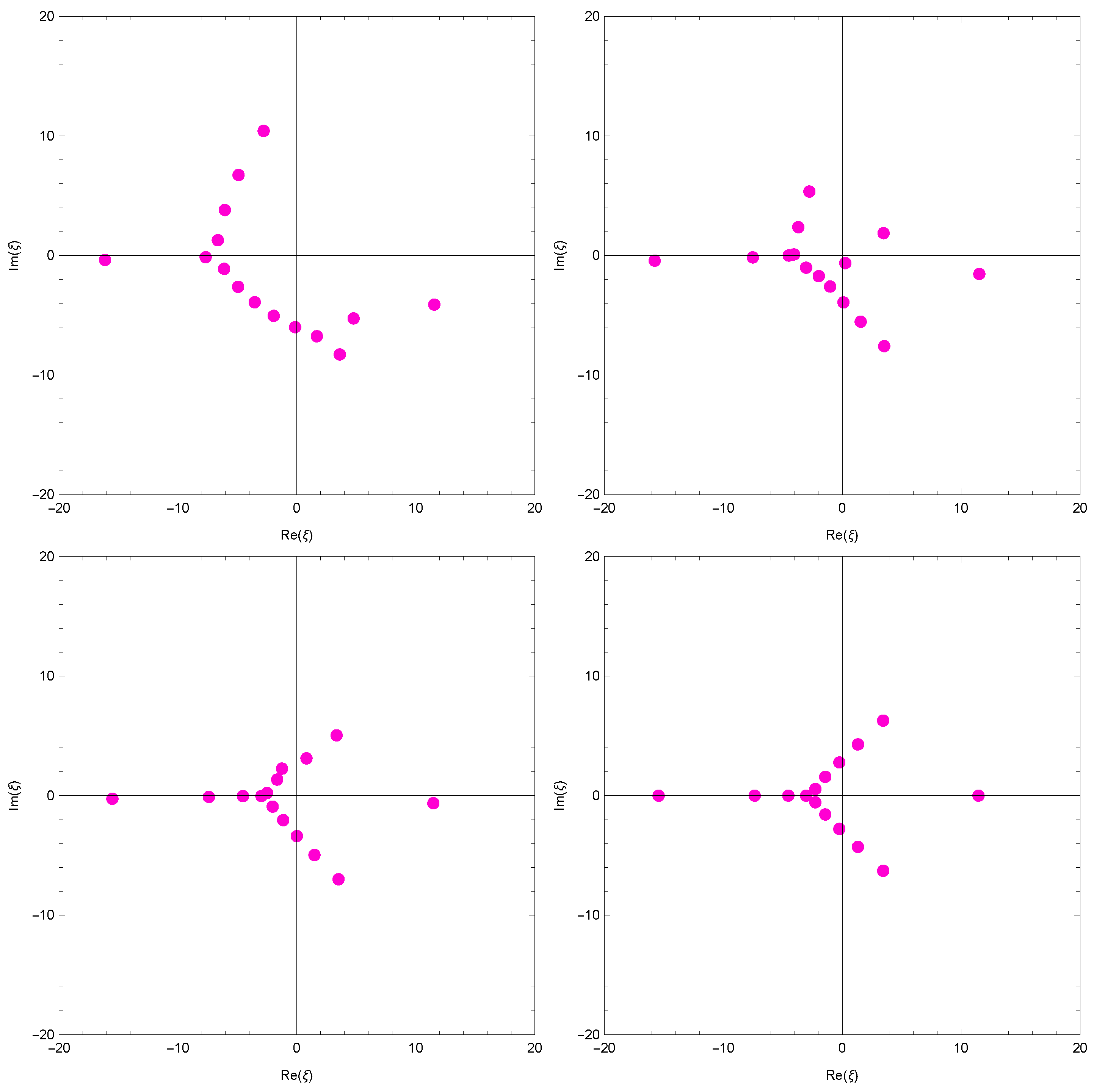
Stacks of zeros of ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ for $1\le j\le 16$ from a 3D structure are presented (Figure 3).

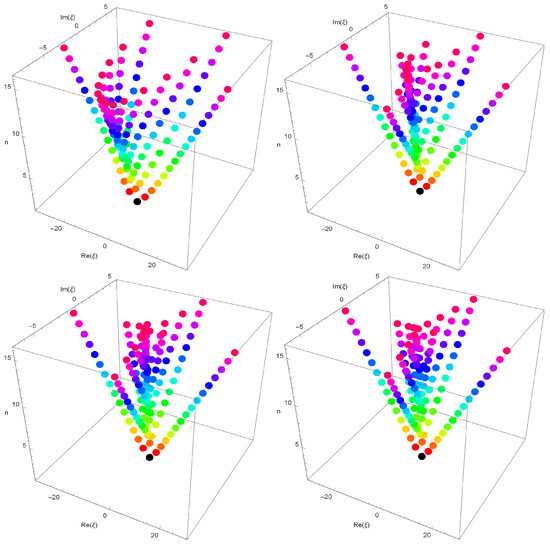
Figure 3. Stacks of zeros of ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ for $1\le j\le 16$.

In Figure 3 (top left), we choose $\alpha =3,\eta =2,u=2,\zeta =3,$ and $\lambda =e^{\frac{\pi i}{4}}$. In Figure 3 (top right), we choose $\alpha =3,\eta =2,u=2,\zeta =3,$ and $\lambda =e^{\frac{2\pi i}{4}}$. In Figure 3 (bottom left), we choose $\alpha =3,\eta =2,u=2,\zeta =3,$ and $\lambda =e^{\frac{3\pi i}{4}}$. In Figure 3 (bottom right), we choose $\alpha =3,\eta =2,u=2,\zeta =3,$ and $\lambda =e^{\frac{4\pi i}{4}}$.

The plots of real zeros of ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ for $1\le j\le 16$ structure are presented (Figure 4).

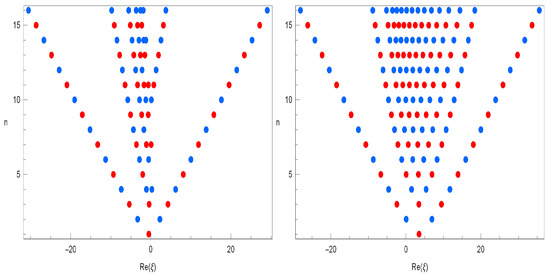
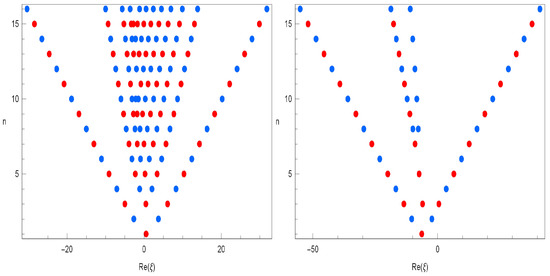
Figure 4. Stacks of zeros of ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )$ for $1\le j\le 16$.

In Figure 4 (top left), we choose $\alpha =3,\eta =2,u=2,\zeta =3,$ and $\lambda =-2$. In Figure 4 (top right), we choose $\alpha =3,\eta =-2,u=2,\zeta =3,$ and $\lambda =-2$. In Figure 4 (bottom left), we choose $\alpha =-3,\eta =-2,u=2,\zeta =3,$ and $\lambda =-2$. In Figure 4 (bottom right), we choose $\alpha =5,\eta =3,u=-5,\zeta =5,$ and $\lambda =-2$.

Next, we calculated an approximate solution satisfying the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,c)}(\xi ,\eta ,\zeta ;u;\lambda )=0$ for $\xi \in \mathbb{R}$. The results are displayed in Table 2.

Table 2. Approximate solutions of ${}_{Bel}{\mathbb{H}}_j^{(5,c)}$$(\xi ,3,5;-5;-2)=0$.

Degree j	$\mathit{\xi }$
1	−6.3333
2	−10.389,    −2.2782
3	−13.514,    −6.0091,    0.52269
4	−16.746,    3.4770
5	−19.963,    −7.3858,    6.5149
6	−23.173,    9.5956
7	−26.376,    −9.0287,    12.702
8	−29.576,    −9.9040,    −7.7419,    15.825
9	−32.772,    −11.095,    18.960
10	−35.967,    −12.179,    −8.3216,    22.103

Finally, certain zeros of the sine Bell-based Apostol-type Frobenius-Euler polynomials of complex variable ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )$ and, beautifully, graphical representations are shown.

$${\left(\frac{1-u}{\lambda e^z-u}\right)}^{\alpha }{e}^{\xi z}sin\zeta z{e}^{\eta (e^z-1)}=\sum _{j=0}^{\infty }{}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )\frac{z^j}{j!}$$

A few of them are as follows:

$$\begin{array}{ll}{}_{Bel}{\mathbb{H}}_0^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )& =0,\\ {}_{Bel}{\mathbb{H}}_1^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )& =\zeta {\left({\displaystyle \frac{u-1}{u-\lambda }}\right)}^{\alpha },\\ {}_{Bel}{\mathbb{H}}_2^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )& =2\zeta {\left({\displaystyle \frac{u-1}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{u\eta +\alpha \lambda -\eta \lambda +u\xi -\lambda \xi }{u-\lambda }}\right),\\ {}_{Bel}{\mathbb{H}}_3^{(\alpha ,s)}(\xi ,\eta ,\zeta ;u;\lambda )& =\zeta {\left({\displaystyle \frac{u-1}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{-u^2{\zeta }^2+3u^2\eta +3u^2{\eta }^2+3u\alpha \lambda +2u{\zeta }^2\lambda -6u\eta \lambda +6u\alpha \eta \lambda }{{(u-\lambda )}^2}}\right)\\ & +\zeta {\left({\displaystyle \frac{u-1}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{-6u{\eta }^2\lambda +3{\alpha }^2{\lambda }^2-{\zeta }^2{\lambda }^2+3\eta {\lambda }^2-6\alpha \eta {\lambda }^2+3{\eta }^2{\lambda }^2+6u^2\eta \xi }{{(u-\lambda )}^2}}\right)\\ & +\zeta {\left({\displaystyle \frac{u-1}{u-\lambda }}\right)}^{\alpha }\left({\displaystyle \frac{6u\alpha \lambda \xi -12u\eta \lambda \xi -6\alpha {\lambda }^2\xi +6\eta {\lambda }^2\xi +3u^2{\xi }^2-6u\lambda {\xi }^2+3{\lambda }^2{\xi }^2}{{(u-\lambda )}^2}}\right).\end{array}$$

We investigated the beautiful zeros of the Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ;u;\lambda )$ using a computer. We plotted the zeros of Apostol-type Frobenius-Euler polynomials ${}_{Bel}{\mathbb{H}}_j^{(\alpha ,s)}(\xi ,\eta ;u;\lambda )=0$ for $j=16$ (Figure 5).

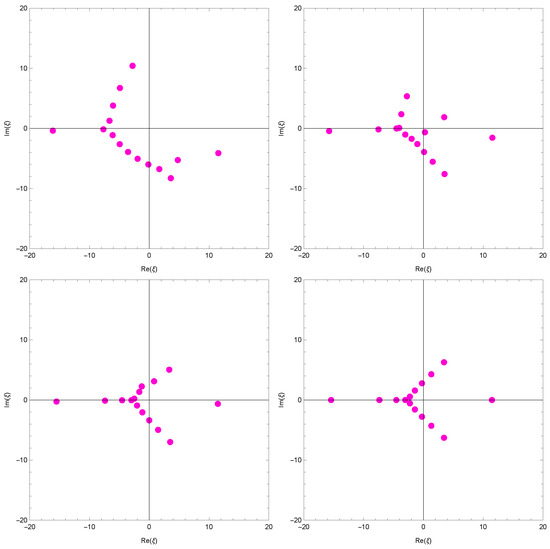
Figure 5. Zeros of ${}_{Bel}{\mathbb{H}}_j^{\left(\alpha \right)}(\xi ,\eta ;u;\lambda )$.

In Figure 5 (top left), we choose $\alpha =3,\eta =2,\zeta =3,u=5,$ and $\lambda =2e^{\frac{\pi i}{4}}$. In Figure 5 (top right), we choose $\alpha =3,\eta =2,\zeta =3,u=5,$ and $\lambda =2e^{\frac{2\pi i}{4}}$. In Figure 5 (bottom left), we choose $\alpha =3,\eta =2,\zeta =3,u=5,$ and $\lambda =2e^{\frac{3\pi i}{4}}$. In Figure 5 (bottom right), we choose $\alpha =3,\eta =2,\zeta =3,u=5,$ and $\lambda =2e^{\frac{4\pi i}{4}}$.

8. Conclusions

In this paper, we introduced the Bell-based Apostol-type Frobenius-Euler numbers and polynomials and the properties of these numbers and polynomials. We derived summation formulas of Bell-based Apostol-type Frobenius-Euler numbers and polynomials, connected with Apostol-type Bernoulli, Euler, Genocchi polynomials and Stirling numbers. Furthermore, we proved several identities of Bell-based Apostol-type Frobenius-Euler polynomials by using different analytical means and applying generating functions. Furthermore, we established parametric kinds of Bell-based Apostol-type Frobenius-Euler polynomials and investigate some identities of these polynomials. We derived some numerical values of Bell-based Apostol-type Frobenius-Euler polynomials and drew some graphs of these polynomials using Mathematica. Consequently, the results of this article have potential applications in mathematics, mathematical physics, and engineering.