Designing a Resilient–Sustainable Supply Chain Network of Age-Differentiated Blood Platelets Using Vertical–Horizontal Transshipment and Grey Wolf Optimizer
Abstract
1. Introduction
2. Literature Review
- Scarcity of blood: The human body is the sole supply channel of blood. The required blood in hospitals should be extracted from voluntary donors and cannot be replaced by other materials.
- Shortage: Blood products are critical to ensure health and the saving of lives. Blood shortage may lead to serious consequences, especially in the case of critical illness patients.
- Wastage: Blood products, especially platelets, are highly perishable. If platelets spoil because of infection or expiration, they must be disposed by stipulated protocols. Excessive discarding of infected and outdated platelets leads to extra costs and negative environmental impacts.
- Age-differentiated demands: Some treatments need high blood platelet freshness, while less critical patients can be treated via older platelets.
2.1. Inventory Management Methods
2.2. Supply Chain Management Methods
2.3. Transshipment Methods
2.4. Research Gaps and Our Contributions
3. Problem Statement
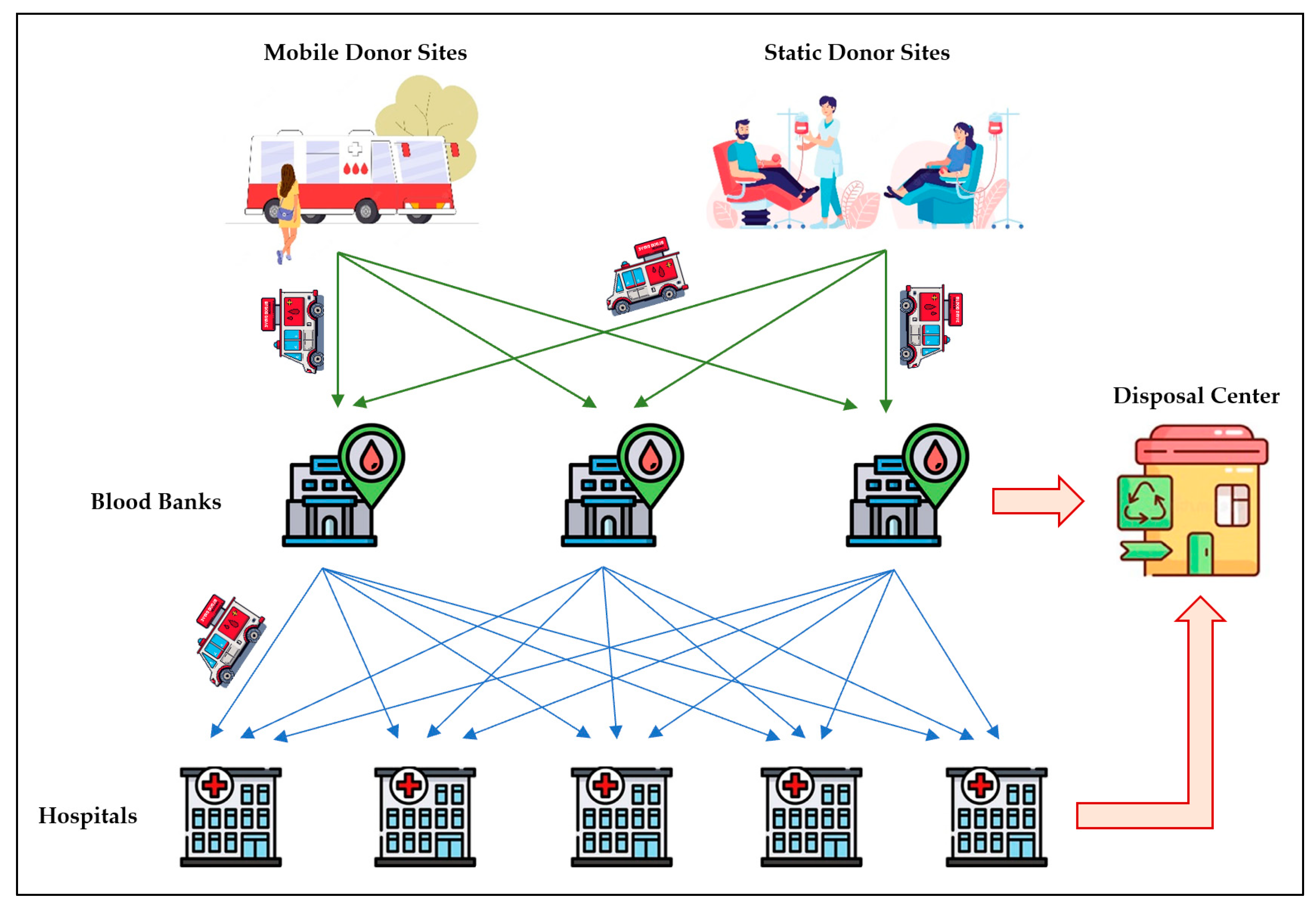
3.1. Blood Platelet Supply Chain Network Design
- Each donor site has a limited capacity for supplying platelets to the blood bank.
- On average, of the received samples in each blood bank j are useful.
- Every day, each hospital faces two types of demands for each platelet age: planned (scheduled) demand and emergency (unscheduled) demand.
- Each hospital is supplied by a specific blood bank.
- Each blood bank may support one or more hospitals.
- In the case of shortage for emergency orders and/or disruptions, each hospital can interchange with other hospitals for any platelet age.
- The received blood samples are processed and tested in blood banks in two days.
- The received platelets in hospitals are considered with a shelf life of three days.
- Platelets and demands are grouped into three categories: young, mature, and old.
- The shelf life of fresh (young) platelets received by a hospital is three days.
- Young products become mature in one day.
- Mature products become old in one day.
- Old platelets are expired in one day.
- The issuing policy is considered as First Input First Output (FIFO) in both blood banks and hospitals.
- Hospitals request young platelets from the associated blood banks.
- Hospitals can request any ages of platelets from other hospitals.
- Lead time of transportation from donor sites to blood banks is zero.
- Lead time of transportation from blood banks to hospitals is one day, i.e., the blood bank delivers the received orders to hospitals early in the morning of the next day.
- Lead time of horizontal exchange between hospitals is neglected.
3.2. Notations
3.3. Reactive Resilient Model
3.4. Inventory Management Model
3.5. Objective Function
3.5.1. Economic Objective Function
- Cost of ordering from blood banks:
- Cost of lateral transshipments:
- Cost of transportation:
- Cost of inventory holding:
3.5.2. Social Objective Function
3.5.3. Environmental Objective Function
3.5.4. Integration of Objective Functions
3.5.5. Mathematical Model Constraints
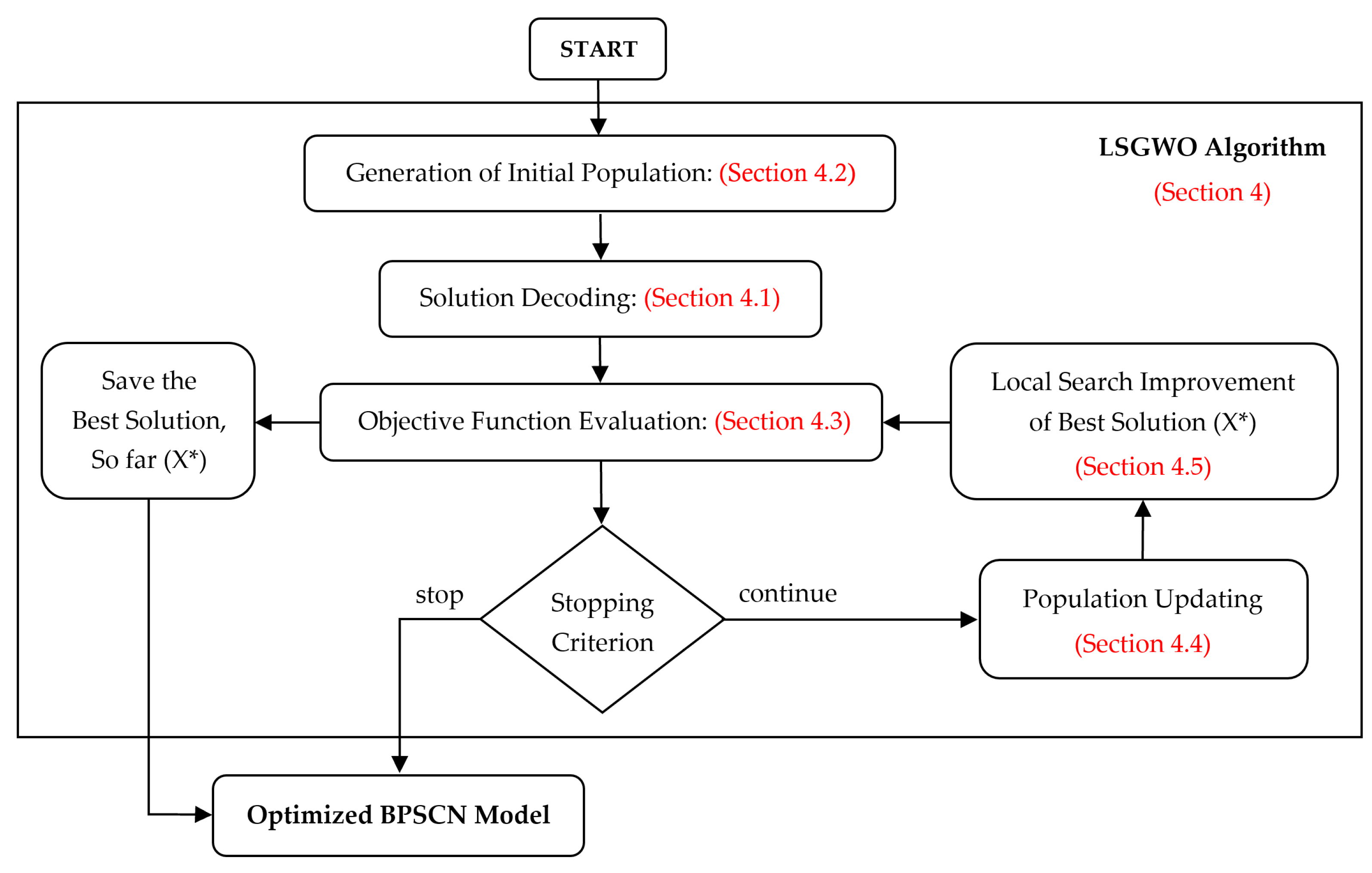
4. Solution Method
| Algorithm 1. Local Search empowered Grey Wolf Optimizer (LSGWO) |
| Inputs: |
| Number of donor sites (D), blood banks (M), hospitals (N), and time periods (T) |
| Controllable parameters of LSGWO: PopSize, MaxIter, and local search operators |
| Output: |
| Optimized BPSCN model: Xij, XLTik, Yijlt, YLTiklt, Rijl, Qijl, RLTikl, and QLTikl |
| LSGWO algorithm: |
| 1. Initialize a population of grey wolves (feasible solutions) |
| 2. Evaluate OBJP for each grey wolf using Equation (29) |
| 3. Update Xα (best solution), Xβ (second best solution), and Xδ (third best solution) |
| 4. it = 0; |
| 5. while (it ≤ MaxIter) |
| 6. Update a |
| 7. for each grey wolf |
| 8. Update A, C, r1, and r2 for alpha, beta, and delta |
| 9. if (|A| < 1) |
| 10. Update the position of grey wolf g by attacking prey using Equation (30) |
| 11. else if (|A| > 1) |
| 12. Update the position of grey wolf g by search for prey using Equation (30) |
| 13. end if |
| 14. end for |
| 15. Evaluate OBJP for each grey wolf using Equation (29) |
| 16. Update Xα, Xβ, and Xδ, and global best solution X* |
| 17. Perform local search improvement on X* to generate X*new |
| 18. Replace X* with X*new, if OBJP*new < OBJP* |
| 19. it = it + 1; |
| 20. end while |
| Return X* as the best solution of the BPSCN model |
4.1. Solution Representation (Encoding and Decoding)
4.2. Initial Population Generation
4.3. Evaluation of Objective Function
4.4. Population Updating
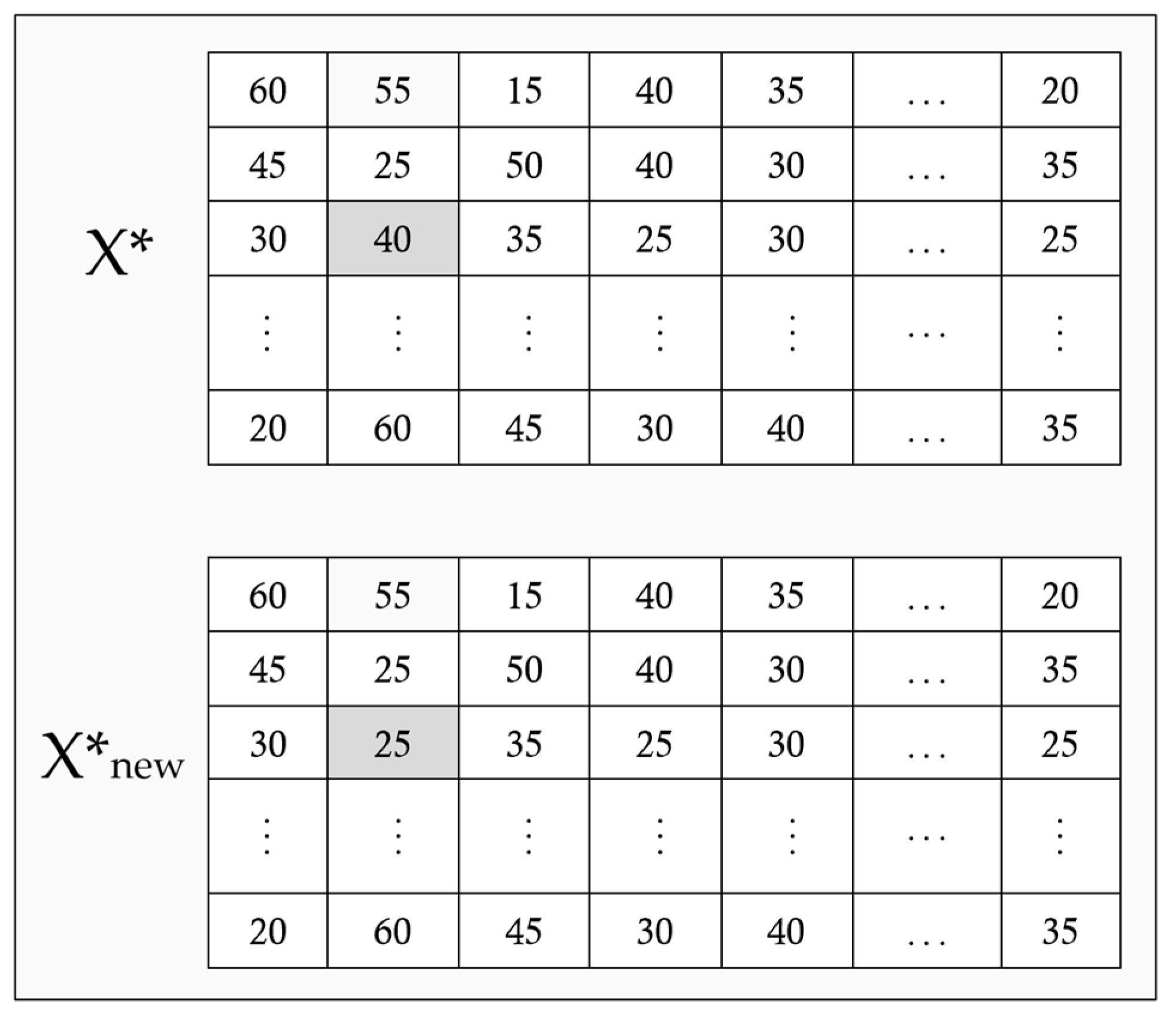
4.5. Local Search Improvement
5. Numerical Results
5.1. Simulation Settings
5.2. Simulation Results
5.3. Sensitivity Analysis
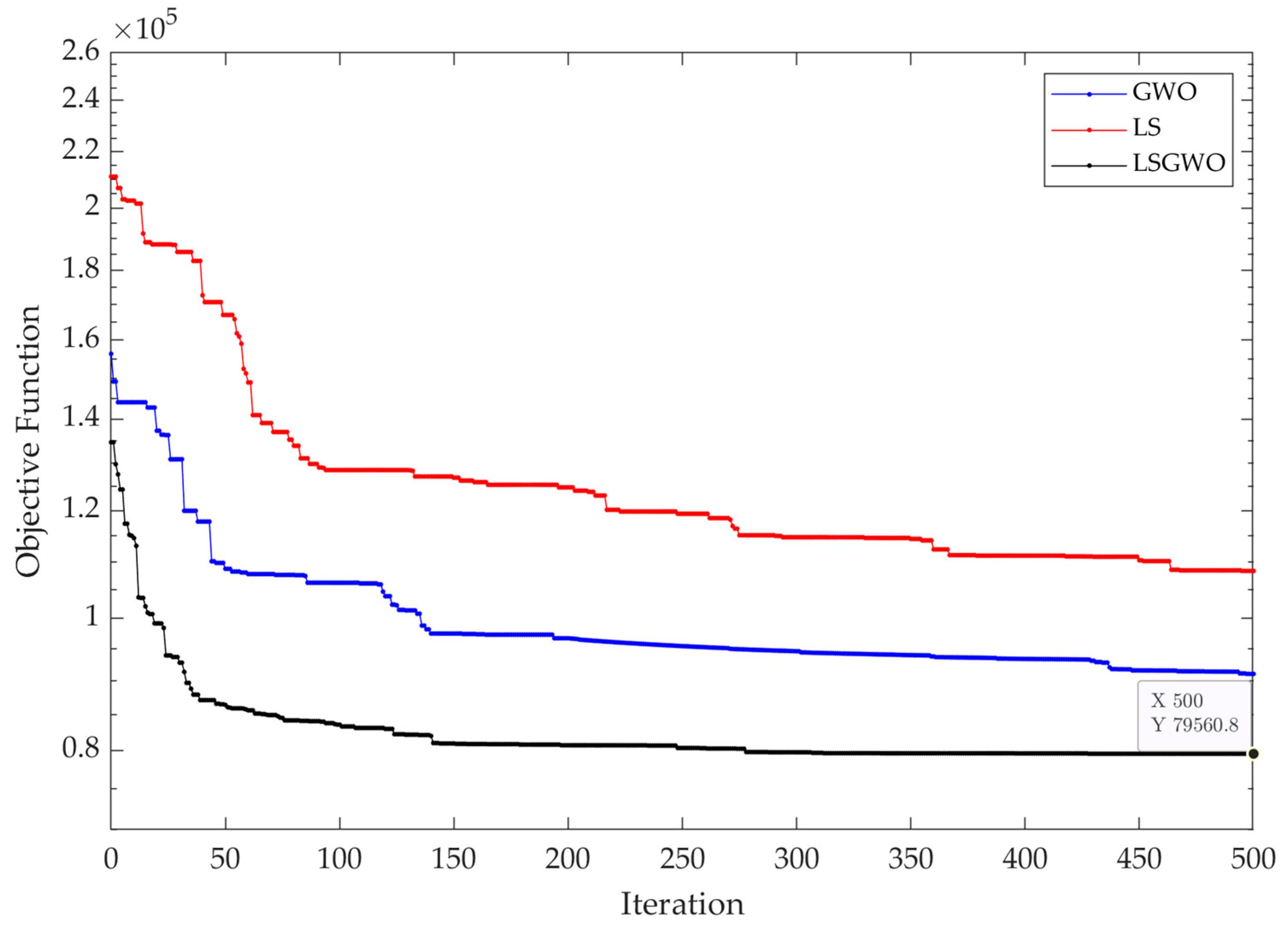
5.4. Comparison with Other Metaheuristics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Zou, T.; Liu, C.; Yu, H.; Chen, L.; Su, J. Blood supply chain operation considering lifetime and transshipment under uncertain environment. Appl. Soft Comput. 2021, 106, 107364. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Sabbaghi, M.M.; Pilevari, N. Inventory management in blood supply chain considering fuzzy supply/demand uncertainties and lateral transshipment. Transfus. Apher. Sci. 2021, 60, 103103. [Google Scholar] [CrossRef]
- Pirabán, A.; Guerrero, W.J.; Labadie, N. Survey on blood supply chain management: Models and methods. Comput. Oper. Res. 2019, 112, 104756. [Google Scholar] [CrossRef]
- Stroncek, D.F.; Rebulla, P. Platelet transfusions. Lancet 2007, 370, 427–438. [Google Scholar] [CrossRef] [PubMed]
- Abbaspour, A.; Jahan, A.; Rezaiee, M. A simple empirical model for blood platelet production and inventory management under uncertainty. J. Ambient. Intell. Humaniz. Comput. 2021, 12, 1783–1799. [Google Scholar] [CrossRef]
- Civelek, I.; Karaesmen, I.; Scheller-Wolf, A. Blood platelet inventory management with protection levels. Eur. J. Oper. Res. 2015, 243, 826–838. [Google Scholar] [CrossRef]
- Wang, K.M.; Ma, Z.J. Age-based policy for blood transshipment during blood shortage. Transp. Res. Part E Logist. Transp. Rev. 2015, 80, 166–183. [Google Scholar] [CrossRef]
- Aubron, C.; Flint, A.W.; Ozier, Y.; McQuilten, Z. Platelet storage duration and its clinical and transfusion outcomes: A systematic review. Crit. Care 2018, 22, 185. [Google Scholar] [CrossRef]
- Zhang, M.; Yang, X.; Cheng, T.E.; Chang, C. Inventory Management of Perishable Goods with Overconfident Retailers. Mathematics 2022, 10, 1716. [Google Scholar] [CrossRef]
- Noble, J.; John, K.; Paul, B. A new (q*, S) policy to manage inventory for low shelf life products facing deterioration in quality and age differentiated requirements. Comput. Ind. Eng. 2022, 173, 108706. [Google Scholar] [CrossRef]
- Liu, W.; Ke, G.Y.; Chen, J.; Zhang, L. Scheduling the distribution of blood products: A vendor-managed inventory routing approach. Transp. Res. Part E Logist. Transp. Rev. 2020, 140, 101964. [Google Scholar] [CrossRef]
- Sohrabi, M.; Zandieh, M.; Nadjafi, B.A. Dynamic demand-centered process-oriented data model for inventory management of hemovigilance systems. Healthc. Inform. Res. 2021, 27, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Sohrabi, M.; Zandieh, M.; Afshar-Nadjafi, B. A simple empirical inventory model for managing the processed corneal tissue equitably in hospitals with demand differentiation. Comput. Appl. Math. 2021, 40, 1–38. [Google Scholar] [CrossRef]
- Shokouhifar, M.; Ranjbarimesan, M. Multivariate time-series blood donation/demand forecasting for resilient supply chain management during COVID-19 pandemic. Clean. Logist. Supply Chain. 2022, 5, 100078. [Google Scholar] [CrossRef]
- Matin, R.K.; Azadi, M.; Saen, R.F. Measuring the sustainability and resilience of blood supply chains. Decis. Support Syst. 2022, 161, 113629. [Google Scholar] [CrossRef]
- Mehrjerdi, Y.Z.; Shafiee, M. A resilient and sustainable closed-loop supply chain using multiple sourcing and information sharing strategies. J. Clean. Prod. 2021, 289, 125141. [Google Scholar] [CrossRef]
- Sibevei, A.; Azar, A.; Zandieh, M.; Khalili, S.M.; Yazdani, M. Developing a Risk Reduction Support System for Health System in Iran: A Case Study in Blood Supply Chain Management. Int. J. Environ. Res. Public Health 2022, 19, 2139. [Google Scholar] [CrossRef]
- Fong, I.W. Blood transfusion-associated infections in the twenty-first century: New challenges. In Current Trends and Concerns in Infectious Diseases; Springer: Berlin/Heidelberg, Germany, 2020; pp. 191–215. [Google Scholar]
- Nagurney, A.; Masoumi, A.H.; Yu, M. Supply chain network operations management of a blood banking system with cost and risk minimization. Comput. Manag. Sci. 2012, 9, 205–231. [Google Scholar] [CrossRef]
- Rajendran, S.; Ravindran, A.R. Inventory management of platelets along blood supply chain to minimize wastage and shortage. Comput. Ind. Eng. 2019, 130, 714–730. [Google Scholar] [CrossRef]
- Wu, S.; Tyler, L.K.; Henson, R.N.; Rowe, J.B.; Tsvetanov, K.A. Cerebral blood flow predicts multiple demand network activity and fluid intelligence across the adult lifespan. Neurobiol. Aging 2023, 121, 1–14. [Google Scholar] [CrossRef]
- Hosseinifard, Z.; Abbasi, B. The inventory centralization impacts on sustainability of the blood supply chain. Comput. Oper. Res. 2018, 89, 206–212. [Google Scholar] [CrossRef]
- Lowalekar, H.; Ravi, R.R. Revolutionizing blood bank inventory management using the TOC thinking process: An Indian case study. Int. J. Prod. Econ. 2017, 186, 89–122. [Google Scholar] [CrossRef]
- Blake, J.T.; Hardy, M.; Delage, G.; Myhal, G. Déjà-vu all over again: Using simulation to evaluate the impact of shorter shelf life for red blood cells at H éma-Q uébec. Transfusion 2013, 53, 1544–1558. [Google Scholar] [CrossRef]
- Baron, O.; Berman, O.; Perry, D. Continuous review inventory models for perishable items ordered in batches. Math. Methods Oper. Res. 2010, 72, 217–247. [Google Scholar] [CrossRef]
- Broekmeulen, R.A.; Van Donselaar, K.H. A heuristic to manage perishable inventory with batch ordering, positive lead-times, and time-varying demand. Comput. Oper. Res. 2009, 36, 3013–3018. [Google Scholar] [CrossRef]
- Dillon, M.; Oliveira, F.; Abbasi, B. A two-stage stochastic programming model for inventory management in the blood supply chain. Int. J. Prod. Econ. 2017, 187, 27–41. [Google Scholar] [CrossRef]
- Abdulwahab, U.; Wahab, M.I.M. Approximate dynamic programming modeling for a typical blood platelet bank. Comput. Ind. Eng. 2014, 78, 259–270. [Google Scholar] [CrossRef]
- Abbasi, B.; Hosseinifard, S.Z. On the issuing policies for perishable items such as red blood cells and platelets in blood service. Decis. Sci. 2014, 45, 995–1020. [Google Scholar] [CrossRef]
- Simonetti, A.; Forshee, R.A.; Anderson, S.A.; Walderhaug, M. A stock-and-flow simulation model of the US blood supply. Transfusion 2014, 54, 828–838. [Google Scholar] [CrossRef]
- Pahlevan, S.M.; Hosseini, S.M.S.; Goli, A. Sustainable supply chain network design using products’ life cycle in the aluminum industry. In Environmental Science and Pollution Research; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1–25. [Google Scholar]
- Becerra, P.; Mula, J.; Sanchis, R. Sustainable Inventory Management in Supply Chains: Trends and Further Research. Sustainability 2022, 14, 2613. [Google Scholar] [CrossRef]
- Gunpinar, S.; Centeno, G. Stochastic integer programming models for reducing wastages and shortages of blood products at hospitals. Comput. Oper. Res. 2015, 54, 129–141. [Google Scholar] [CrossRef]
- Mousavi, R.; Salehi-Amiri, A.; Zahedi, A.; Hajiaghaei-Keshteli, M. Designing a supply chain network for blood decomposition by utilizing social and environmental factor. Comput. Ind. Eng. 2021, 160, 107501. [Google Scholar] [CrossRef]
- Hamdan, B.; Diabat, A. Robust design of blood supply chains under risk of disruptions using Lagrangian relaxation. Transp. Res. Part E Logist. Transp. Rev. 2020, 134, 101764. [Google Scholar] [CrossRef]
- Sohrabi, M.; Zandieh, M.; Shokouhifar, M. Sustainable inventory management in blood banks considering health equity using a combined metaheuristic-based robust fuzzy stochastic programming. Socio-Econ. Plan. Sci. 2023; in press. [Google Scholar]
- Thomas, A.V.; Mahanty, B. Dynamic assessment of control system designs of information shared supply chain network experiencing supplier disruption. Oper. Res. 2021, 21, 425–451. [Google Scholar] [CrossRef]
- Wang, C.; Chen, S. A distributionally robust optimization for blood supply network considering disasters. Transp. Res. Part E Logist. Transp. Rev. 2020, 134, 101840. [Google Scholar] [CrossRef]
- Ivanov, D. Revealing interfaces of supply chain resilience and sustainability: A simulation study. Int. J. Prod. Res. 2018, 56, 3507–3523. [Google Scholar] [CrossRef]
- Pavlov, A.; Ivanov, D.; Pavlov, D.; Slinko, A. Optimization of network redundancy and contingency planning in sustainable and resilient supply chain resource management under conditions of structural dynamics. In Annals of Operations Research; Springer: Berlin/Heidelberg, Germany, 2019; pp. 1–30. [Google Scholar]
- Elluru, S.; Gupta, H.; Kaur, H.; Singh, S.P. Proactive and reactive models for disaster resilient supply chain. Ann. Oper. Res. 2019, 283, 199–224. [Google Scholar] [CrossRef]
- Ash, C.; Diallo, C.; Venkatadri, U.; VanBerkel, P. Distributionally robust optimization of a Canadian healthcare supply chain to enhance resilience during the COVID-19 pandemic. Comput. Ind. Eng. 2022, 168, 108051. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Soltanzadeh, S.; Weber, G.W.; Roy, S.K. Designing an efficient blood supply chain network in crisis: Neural learning, optimization and case study. Ann. Oper. Res. 2020, 289, 123–152. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Golpîra, H.; Javanmardan, A.; Maihami, R. A socio-economic optimization model for blood supply chain network design during the COVID-19 pandemic: An interactive possibilistic programming approach for a real case study. Socio-Econ. Plan. Sci. 2023, 85, 101439. [Google Scholar] [CrossRef]
- Wang, K.; Ma, Z.; Zhou, Y. Age-based transshipment strategy for overstock blood in emergency relief. Adv. Inf. Sci. Serv. Sci. 2012, 4, 633–642. [Google Scholar]
- Zu-jun, M.A. Optimization of multi-stage emergency blood transferring. Syst. Eng.—Theory Pract. 2014, 34, 7. [Google Scholar]
- Puranam, K.; Novak, D.C.; Lucas, M.T.; Fung, M. Managing blood inventory with multiple independent sources of supply. Eur. J. Oper. Res. 2017, 259, 500–511. [Google Scholar] [CrossRef]
- Tirkolaee, E.B.; Goli, A.; Ghasemi, P.; Goodarzian, F. Designing a sustainable closed-loop supply chain network of face masks during the COVID-19 pandemic: Pareto-based algorithms. J. Clean. Prod. 2022, 333, 130056. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Abualigah, L.; Yousri, D.; Abd Elaziz, M.; Ewees, A.A.; Al-Qaness, M.A.; Gandomi, A.H. Aquila optimizer: A novel meta-heuristic optimization algorithm. Comput. Ind. Eng. 2021, 157, 107250. [Google Scholar] [CrossRef]

| Indices | Definition |
| j | Blood bank index, j = 1, 2, …, M |
| i, k | Hospital index, i, k = 1, 2, …, N |
| d | Donor site (supplier) index, d = 1, 2, …, D |
| l | Platelet age (young, mature, old) index, l = 1, 2, …, L |
| t | Time period (day) index, t = 1, 2, …, T |
| Parameters | Definition |
| fj | Fixed cost of ordering from blood bank j |
| cjl | Unit procurement cost by blood bank j for platelet age l |
| cLTkl | Unit interchange cost between hospitals for platelet age l provided by hospital k |
| qj | Percentage of platelets with acceptable quality in blood bank j |
| hil | Unit holding cost for platelet age l in hospital i |
| pij | Fixed transportation cost per order to hospital i from blood bank j |
| rij | Variable mileage cost per order to hospital i from blood bank j |
| dij | Distance between hospital i and blood bank j |
| pLTik | Fixed transportation cost per lateral transshipment to hospital i from hospital k |
| rLTik | Variable mileage cost per lateral transshipment to hospital i from hospital k |
| dLTik | Distance between hospital i and hospital k |
| Ldj | Lead time between donor site d and blood bank j |
| Lij | Lead time between hospital i and blood bank j |
| LLTik | Lead time between hospital i and hospital k |
| sil | Unit shortage cost for platelets with age l in hospital i |
| wi | Unit wastage cost in hospital i |
| wj | Unit wastage cost in blood bank j |
| DPilt | Planned (scheduled) demand for platelets with age l in hospital i on day t |
| DEilt | Emergency (unscheduled) demand for platelets with age l in hospital i on day t |
| Dilt | Total demand for platelets with age l in hospital i on day t, Dilt = DPilt + DEilt. |
| I0ilt | Inventory of platelet age l in hospital i at the beginning (morning) of day t |
| Iilt | Inventory of platelets with age l in hospital i at the end (night) of day t |
| Sjdt | Quantity of blood platelets donated from donor site d to blood bank j at time t |
| TPTj | Testing and producing time in blood bank j |
| IBjlt | Inventory of platelets age l in blood bank j at time t |
| Zjd | Binary parameter and equal to 1 if blood bank j is sourced by donor site d; 0, otherwise |
| Eilt | Binary parameter and equal to 1 if total demand Dilt is more than the inventory I0ilt; 0, otherwise |
| Decision Variables | Definition |
| Xij | Binary variable and equal to 1 if hospital i is supplied by blood bank j; 0, otherwise |
| XLTik | Binary variable and equal to 1 if hospital i is supplied by hospital k; 0, otherwise |
| Yijlt | Binary variable and equal to 1 if hospital i is sourced by blood bank j for platelets with age l at time t; 0, otherwise |
| YLTiklt | Binary variable and equal to 1 if hospital i is sourced by hospital k for platelets with age l at time t; 0, otherwise |
| Rijl | Reorder point of hospital i for platelets with age l from blood bank j |
| Qijl | Order quantity of hospital i for platelets with age l from blood bank j |
| RLTikl | Reorder point of hospital i for platelets with age l from hospital k |
| QLTikl | Order quantity of hospital i for platelets with age l from hospital k |
| Parameter | Value/Description |
|---|---|
| Maximum number of iterations (MaxIter) | 500 |
| Population size of grey wolves (PopSize) | 200 |
| Multiple local search operators | Binary Swap/Exchange, Integer Swap |
| Weight of economic objective (wEC) | 0.5 |
| Weight of social objective (wSC) | 0.25 |
| Weight of environmental objective (wEN) | 0.25 |
| Lower and upper bounds of reorder point from blood banks | [5, 30] |
| Lower and upper bounds of order quantity from blood banks | [20, 100] |
| Lower and upper bounds of reorder point for lateral transshipment | [2, 10] |
| Lower and upper bounds of order quantity for lateral transshipment | [5, 20] |
| Parameter | Value | Parameter | Value |
| fj | 20 | Sjdt | (20–60) |
| qj () | 0.85 | DPilt | (50–100) |
| sil () | 0.5 | DEilt | (0–30) |
| wi | 0.3 | TPTj | 2 |
| pij | 3 | Ldj | 0 |
| rij | 1.5 | Lij | 1 |
| pLTik | 2 | LLTik | 0 |
| rLTik | 2 | I0ilt (t = 0) | 30 |
| Parameter | Value for Young (l = 1) | Value for Mature (l = 2) | Value for Old (l = 3) |
| cjl | 2.5 | 2 | 1.5 |
| cLTkl | 0.3 | 0.25 | 0.15 |
| hil | 0.1 | 0.075 | 0.05 |
| Demand % | 50 | 30 | 20 |
| Objective Function | GWO | LS | LSGWO | Improvement of LSGWO | |
|---|---|---|---|---|---|
| Against GWO | Against LS | ||||
| Cost of ordering from Blood banks | 120 | 141.4 | 102.8 | 14.3% | 27.3% |
| Cost of lateral Transshipment | 8.51 | 8.99 | 9.33 | −9.64% | −3.78% |
| Cost of transportation | 22.6 | 29.3 | 22.3 | 1.33% | 23.9% |
| Cost of inventory holding | 17.8 | 18.6 | 14.4 | 19.1% | 22.6% |
| Economic objective (total cost) | 168.91 | 198.29 | 148.83 | 11.9% | 24.9% |
| Social objective (shortage) | 14.7 | 19.1 | 11.4 | 22.4% | 40.3% |
| Environmental objective (wastage) | 11.6 | 17.9 | 9.17 | 20.9% | 48.8% |
| Overall objective function | 91.03 | 108.4 | 79.56 | 12.6% | 26.6% |
| Percentage of Demand for | Shortage Rate | Wastage Rate | ||
|---|---|---|---|---|
| Young | Mature | Old | ||
| 50% | 30% | 20% | 6.87% | 10.31% |
| 40% | 30% | 30% | 6.53% | 10.87% |
| 30% | 20% | 50% | 5.2% | 12.3% |
| 20% | 30% | 50% | 5.48% | 11.92% |
| 60% | 30% | 10% | 7.46% | 9.41% |
| 70% | 20% | 10% | 8.12% | 8.8% |
| wEC | wSC | wEN | Economic Cost | Social Cost | Environmental Cost |
|---|---|---|---|---|---|
| 0.5 | 0.25 | 0.25 | 148.83 | 11.4 | 9.17 |
| 1 | 0 | 0 | 113.7 | 22.8 | 13.76 |
| 0 | 1 | 0 | 162.49 | 5.31 | 16.11 |
| 0 | 0 | 1 | 145.54 | 23.7 | 4.35 |
| 0.25 | 0.5 | 0.25 | 157.21 | 8.1 | 9.82 |
| 0.25 | 0.25 | 0.5 | 153.8 | 12.6 | 7.86 |
| Cost | Without LT | With LT | % Improvement of LT |
|---|---|---|---|
| Cost of ordering from Blood banks | 118.7 | 102.8 | 13.4% |
| Cost of lateral Transshipment | 0 | 9.33 | N/A |
| Cost of transportation | 18.4 | 22.3 | −21.2% |
| Cost of inventory holding | 17.3 | 14.4 | 16.8% |
| Economic objective (total cost) | 154.4 | 148.83 | 3.61% |
| Social objective (shortage) | 16.3 | 11.4 | 30.1% |
| Environmental objective (wastage) | 11.3 | 9.17 | 18.8% |
| Overall objective function | 84.3 | 79.56 | 5.62% |
| Objective Function | GA | AO [50] | GASA [36] | LSGWO |
|---|---|---|---|---|
| Economic objective (total cost) | 163.45 | 156.9 | 153.61 | 148.83 |
| Social objective (shortage) | 13.6 | 11.1 | 12.8 | 11.4 |
| Environmental objective (wastage) | 12.5 | 12.8 | 10.3 | 9.17 |
| Overall objective function | 88.25 | 84.43 | 82.58 | 79.56 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokouhifar, M.; Goli, A. Designing a Resilient–Sustainable Supply Chain Network of Age-Differentiated Blood Platelets Using Vertical–Horizontal Transshipment and Grey Wolf Optimizer. Int. J. Environ. Res. Public Health 2023, 20, 4078. https://doi.org/10.3390/ijerph20054078
Shokouhifar M, Goli A. Designing a Resilient–Sustainable Supply Chain Network of Age-Differentiated Blood Platelets Using Vertical–Horizontal Transshipment and Grey Wolf Optimizer. International Journal of Environmental Research and Public Health. 2023; 20(5):4078. https://doi.org/10.3390/ijerph20054078
Chicago/Turabian StyleShokouhifar, Mohammad, and Alireza Goli. 2023. "Designing a Resilient–Sustainable Supply Chain Network of Age-Differentiated Blood Platelets Using Vertical–Horizontal Transshipment and Grey Wolf Optimizer" International Journal of Environmental Research and Public Health 20, no. 5: 4078. https://doi.org/10.3390/ijerph20054078
APA StyleShokouhifar, M., & Goli, A. (2023). Designing a Resilient–Sustainable Supply Chain Network of Age-Differentiated Blood Platelets Using Vertical–Horizontal Transshipment and Grey Wolf Optimizer. International Journal of Environmental Research and Public Health, 20(5), 4078. https://doi.org/10.3390/ijerph20054078







