Risk Perception Influence on Vaccination Program on COVID-19 in Chile: A Mathematical Model
Abstract
:1. Introduction
2. Materials and Methods
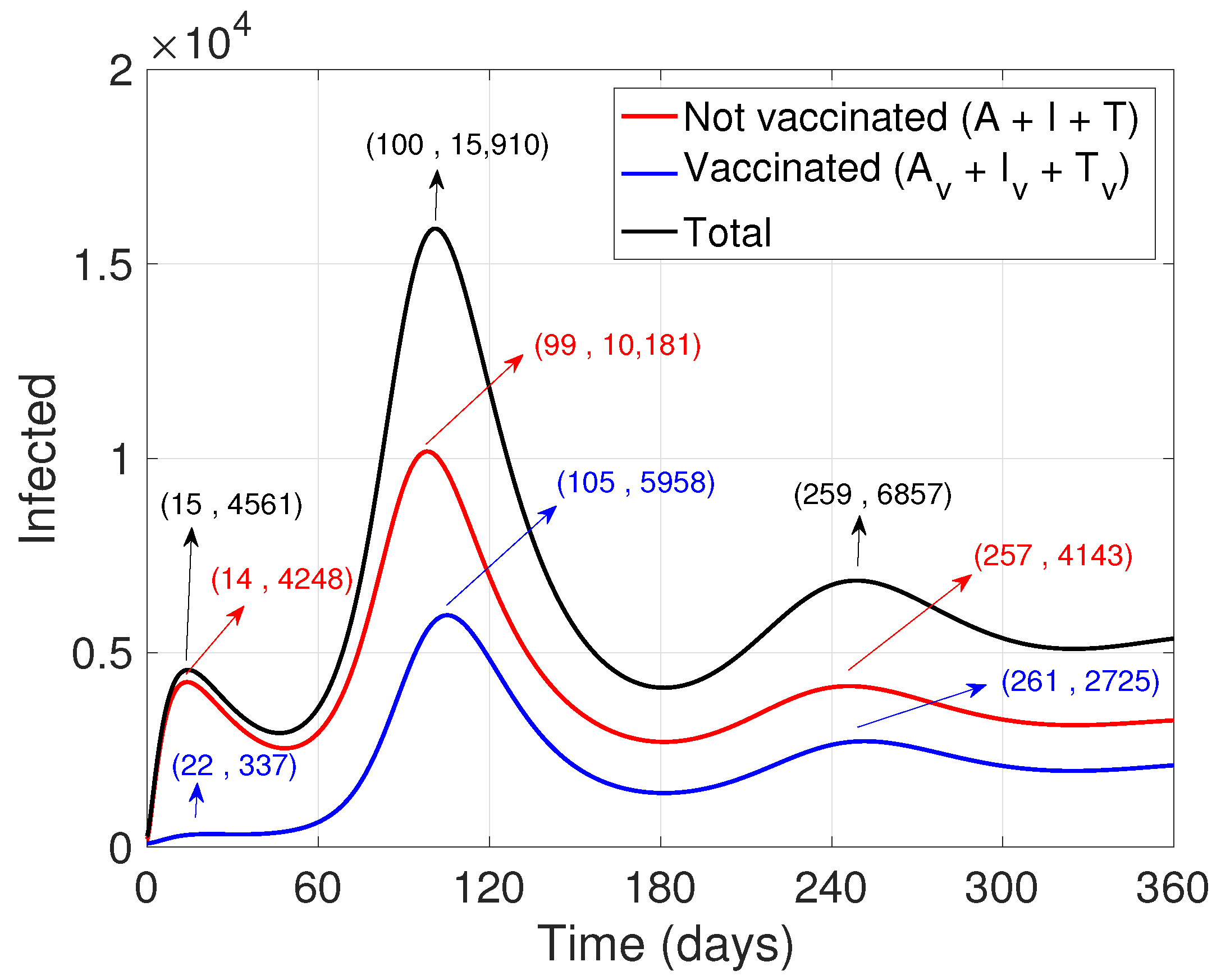
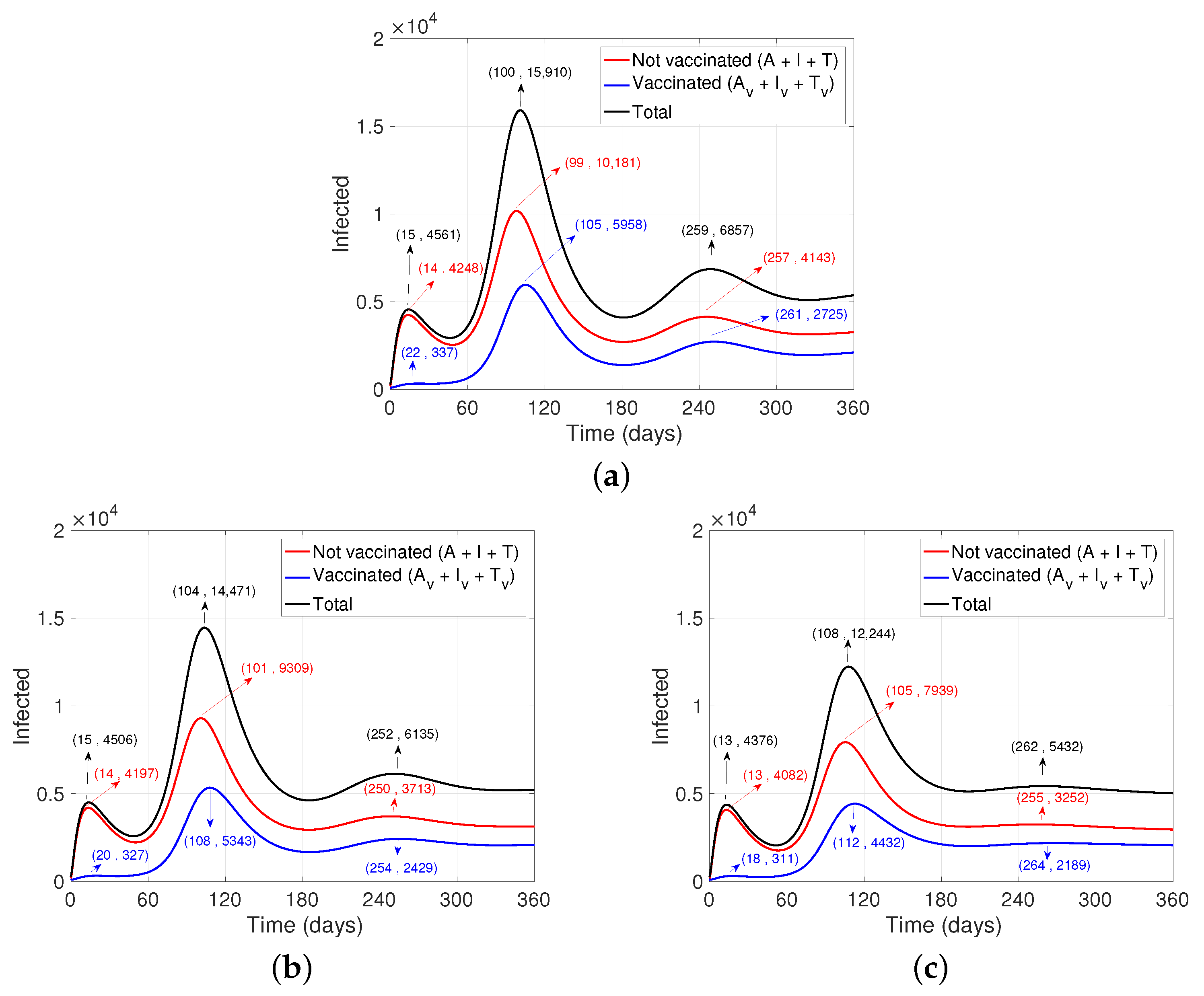
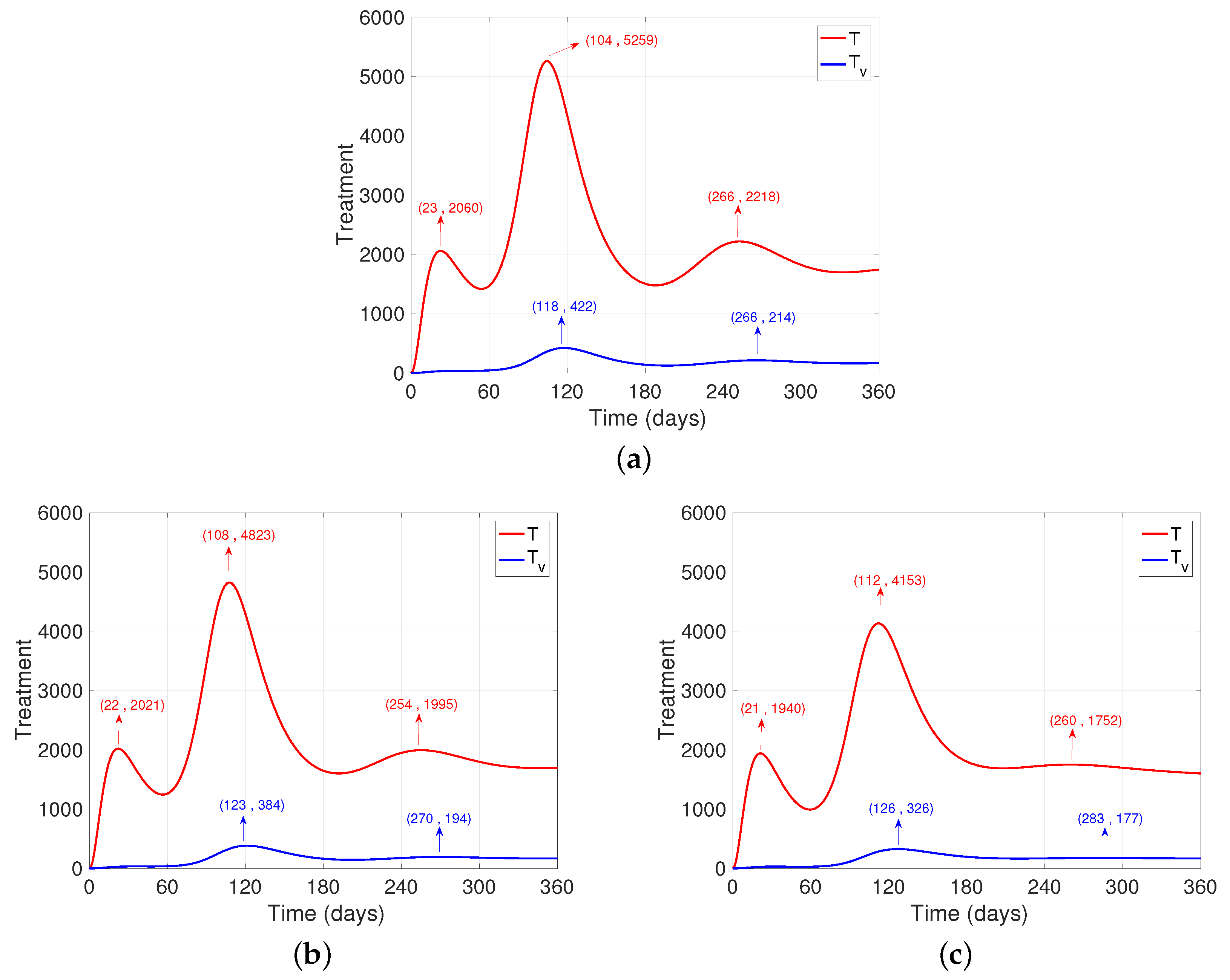
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PPEs | Personal Protective Elements |
Appendix A
| Parameters | Units | Baseline | Reference |
|---|---|---|---|
| b (d) | D | 0 | Author chosen |
| f | D | 0.012 | [20] |
| D | 1/360 | Author chosen | |
| () | D | () | [17,35,36] |
| () | UN | 0.35 | [20,21,35] |
| () | D | 1/5 | [17,21,35] |
| () | UN | 0.2 (0.653) | [17,21] |
| () | UN | 0.8 (0.347) | [17,21] |
| () | D | 1/7 (1/14) | [20,35] |
| () | D | 0.1 ( 0.13) | [17,21,35] |
| m () | D | 0.001 ( 0.14) | [20,35] |
| () | D | 1/10 | [17,20,21,35] |
| () | D | 1/10 | [17,20,21,35] |
| () | D | 1/14 | [17,20,21,35] |
| () | D | 1/90 | Author chosen |
| () | D | Author chosen | |
| () | D | Author chosen | |
| () | UN | Author chosen | |
| () | UN | Author chosen |
References
- Liu, Y.C.; Kuo, R.L.; Shih, S.R. COVID-19: The first documented coronavirus pandemic in history. Biomed. J. 2020, 43, 328–333. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.; Weiss, A.; Schwarzenberg, A.; Nelson, M.; Sutter, K.; Sutherland, M. Global Economic Effects of COVID-19. Congressional Research Service. Updated 4 October 2021. CRS Reports. Available online: https://sgp.fas.org/crs/row/R46270.pdf (accessed on 4 October 2021).
- Balanzá-Martínez, V.; Kapczinski, F.; de Azevedo Cardoso, T.; Atienza-Carbonell, B.; Rosa, A.R.; Mota, J.C.; De Boni, R.B. The assessment of lifestyle changes during the COVID-19 pandemic using a multidimensional scale. Rev. Psiquiatr. Salud Ment. 2021, 14, 16–26. [Google Scholar] [CrossRef] [PubMed]
- Stanton, R.; To, Q.G.; Khalesi, S.; Williams, S.L.; Alley, S.J.; Thwaite, T.L.; Fenning, A.S.; Vandelanotte, C. Depression, anxiety and stress during COVID-19: Associations with changes in physical activity, sleep, tobacco and alcohol use in Australian adults. Int. J. Environ. Res. Public Health 2020, 17, 4065. [Google Scholar] [CrossRef] [PubMed]
- Feter, N.; Caputo, E.; Doring, I.; Leite, J.; Cassuriaga, J.; Reichert, F.; da Silva, M.; Coombes, J.; Rombaldi, A. Sharp increase in depression and anxiety among Brazilian adults during the COVID-19 pandemic: Findings from the PAMPA cohort. Public Health 2021, 190, 101–107. [Google Scholar] [CrossRef]
- Zhou, J.; Zogan, H.; Yang, S.; Jameel, S.; Xu, G.; Chen, F. Detecting community depression dynamics due to COVID-19 pandemic in australia. IEEE Trans. Comput. Soc. Syst. 2021, 8, 982–991. [Google Scholar] [CrossRef]
- Fegert, J.M.; Vitiello, B.; Plener, P.L.; Clemens, V. Challenges and burden of the Coronavirus 2019 (COVID-19) pandemic for child and adolescent mental health: A narrative review to highlight clinical and research needs in the acute phase and the long return to normality. Child Adolesc. Psychiatry Ment. Health 2020, 14, 20. [Google Scholar] [CrossRef]
- Mansfield, K.E.; Mathur, R.; Tazare, J.; Henderson, A.D.; Mulick, A.R.; Carreira, H.; Matthews, A.A.; Bidulka, P.; Gayle, A.; Forbes, H.; et al. Indirect acute effects of the COVID-19 pandemic on physical and mental health in the UK: A population-based study. Lancet Digit. Health 2021, 3, e217–e230. [Google Scholar] [CrossRef]
- Wong, C.K.; Wong, J.Y.; Tang, E.H.; Au, C.H.; Lau, K.T.; Wai, A.K. Impact of national containment measures on decelerating the increase in daily new cases of COVID-19 in 54 countries and 4 epicenters of the pandemic: Comparative observational study. J. Med. Internet Res. 2020, 22, e19904. [Google Scholar] [CrossRef]
- Ge, Y.; Zhang, W.; Liu, H.; Ruktanonchai, C.W.; Hu, M.; Wu, X.; Song, Y.; Ruktanonchai, N.; Yan, W.; Feng, L.; et al. Effects of worldwide interventions and vaccination on COVID-19 between waves and countries. medrxiv 2021. [Google Scholar] [CrossRef]
- van den Driessche, P.; Watmought, J. Reproduction numbers and subthreshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematicals Tools for Understanding Infectious Diseases Dynamics; Princeton Series in Theoretical and Computational Biology; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Gumel, A.B.; Iboi, E.A.; Ngonghala, C.N.; Elbasha, E.H. A primer on using mathematics to understand COVID-19 dynamics: Modeling, analysis and simulations. Infect. Dis. Model. 2021, 6, 148–168. [Google Scholar] [CrossRef] [PubMed]
- Harjule, P.; Tiwari, V.; Kumar, A. Mathematical models to predict COVID-19 outbreak: An interim review. J. Interdiscip. Math. 2021, 24, 259–284. [Google Scholar] [CrossRef]
- D’angelo, D.; Sinopoli, A.; Napoletano, A.; Gianola, S.; Castellini, G.; Del Monaco, A.; Fauci, A.J.; Latina, R.; Iacorossi, L.; Salomone, K.; et al. Strategies to exiting the COVID-19 lockdown for workplace and school: A scoping review. Saf. Sci. 2020, 134, 105067. [Google Scholar] [CrossRef] [PubMed]
- Bhadauria, A.S.; Pathak, R.; Chaudhary, M. A SIQ mathematical model on COVID-19 investigating the lockdown effect. Infect. Dis. Model. 2021, 6, 244–257. [Google Scholar] [CrossRef] [PubMed]
- Epstein, J.M.; Hatna, E.; Crodelle, J. Triple contagion: A two-fears epidemic model. J. R. Soc. Interface 2021, 18, 20210186. [Google Scholar] [CrossRef]
- Mathieu, E.; Ritchie, H.; Ortiz-Ospina, E.; Roser, M.; Hasell, J.; Appel, C.; Giattino, C.; Rodés-Guirao, L. A global database of COVID-19 vaccinations. Nat. Hum. Behav. 2021, 5, 947–953. [Google Scholar] [CrossRef]
- Taylor, L. Covid-19: Spike in cases in Chile is blamed on people mixing after first vaccine shot. Br. Med. J. (Online) 2021, 373, n1023. [Google Scholar] [CrossRef]
- GitHub. MinCienias/Datos-COVID19. Updated 4 September 2021. COVID-19 Reports. 2021. Available online: https://github.com/MinCiencia/Datos-COVID19 (accessed on 4 September 2021).
- Jara, A.; Undurraga, E.A.; González, C.; Paredes, F.; Fontecilla, T.; Jara, G.; Pizarro, A.; Acevedo, J.; Leo, K.; Leon, F.; et al. Effectiveness of an inactivated SARS-CoV-2 vaccine in Chile. N. Engl. J. Med. 2021, 385, 875–884. [Google Scholar] [CrossRef]
- Maftei, A.; Holman, A.C. SARS-CoV-2 threat perception and willingness to vaccinate: The mediating role of conspiracy beliefs. Front. Psychol. 2021, 3371. [Google Scholar] [CrossRef]
- Poletti, P.; Ajelli, M.; Merler, S. Risk perception and effectiveness of uncoordinated behavioral responses in an emerging epidemic. Math. Biosci. 2012, 238, 80–89. [Google Scholar] [CrossRef]
- Poletti, P.; Ajelli, M.; Merler, S. The effect of risk perception on the 2009 H1N1 pandemic influenza dynamics. PLoS ONE 2011, 6, e16460. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smith, R.D. Responding to global infectious disease outbreaks: Lessons from SARS on the role of risk perception, communication and management. Soc. Sci. Med. 2006, 63, 3113–3123. [Google Scholar] [CrossRef] [PubMed]
- Majid, U.; Wasim, A.; Bakshi, S.; Truong, J. Knowledge,(mis-) conceptions, risk perception, and behavior change during pandemics: A scoping review of 149 studies. Public Underst. Sci. 2020, 29, 777–799. [Google Scholar] [CrossRef] [PubMed]
- Wise, T.; Zbozinek, T.D.; Michelini, G.; Hagan, C.C.; Mobbs, D. Changes in risk perception and self-reported protective behaviour during the first week of the COVID-19 pandemic in the United States. R. Soc. Open Sci. 2020, 7, 200742. [Google Scholar] [CrossRef] [PubMed]
- Bagnoli, F.; Lio, P.; Sguanci, L. Risk perception in epidemic modeling. Phys. Rev. E 2007, 76, 061904. [Google Scholar] [CrossRef] [Green Version]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics. II.—The problem of endemicity. Proc. R. Soc. Lond. Ser. A Contain. Pap. Math. Phys. Character 1932, 138, 55–83. [Google Scholar]
- Cabrera, M.; Córdova-Lepe, F.; Gutiérrez-Jara, J.P.; Vogt Geisse, K. An SIR type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 2021, 11, 10170. [Google Scholar] [CrossRef]
- Muñoz-Quezada, M.T.; Lucero, B.; Gutiérrez-Jara, J.P.; Buralli, R.J.; Zúñiga-Venegas, L.; Muñoz, M.P.; Ponce, K.V.; Iglesias, V. Longitudinal exposure to pyrethroids (3-PBA and trans-DCCA) and 2,4-D herbicide in rural schoolchildren of Maule region, Chile. Sci. Total Environ. 2020, 749, 141512. [Google Scholar] [CrossRef]
- The Mathworks, I. MATLAB Version 9.1 (R2016b). Natick, Massachusetts. 2016. Available online: https://www.mathworks.com (accessed on 4 September 2021).
- Fisayo, T.; Tsukagoshi, S. Three waves of the COVID-19 pandemic. Postgrad. Med. J. 2021, 97, 332. [Google Scholar] [CrossRef]
- Minsal. Casos confirmados en Chile COVID-19. Updated 5 September 2021. Ministerio de Salud de Chile. 2021. Available online: https://www.minsal.cl/nuevo-coronavirus-2019-ncov/casos-confirmados-en-chile-covid-19/ (accessed on 5 September 2021).
- Mossong, J.; Hens, N.; Jit, M.; Beutels, P.; Auranen, K.; Mikolajczyk, R.; Massari, M.; Salmaso, S.; Tomba, G.S.; Wallinga, J.; et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008, 5, e74. [Google Scholar] [CrossRef] [PubMed]
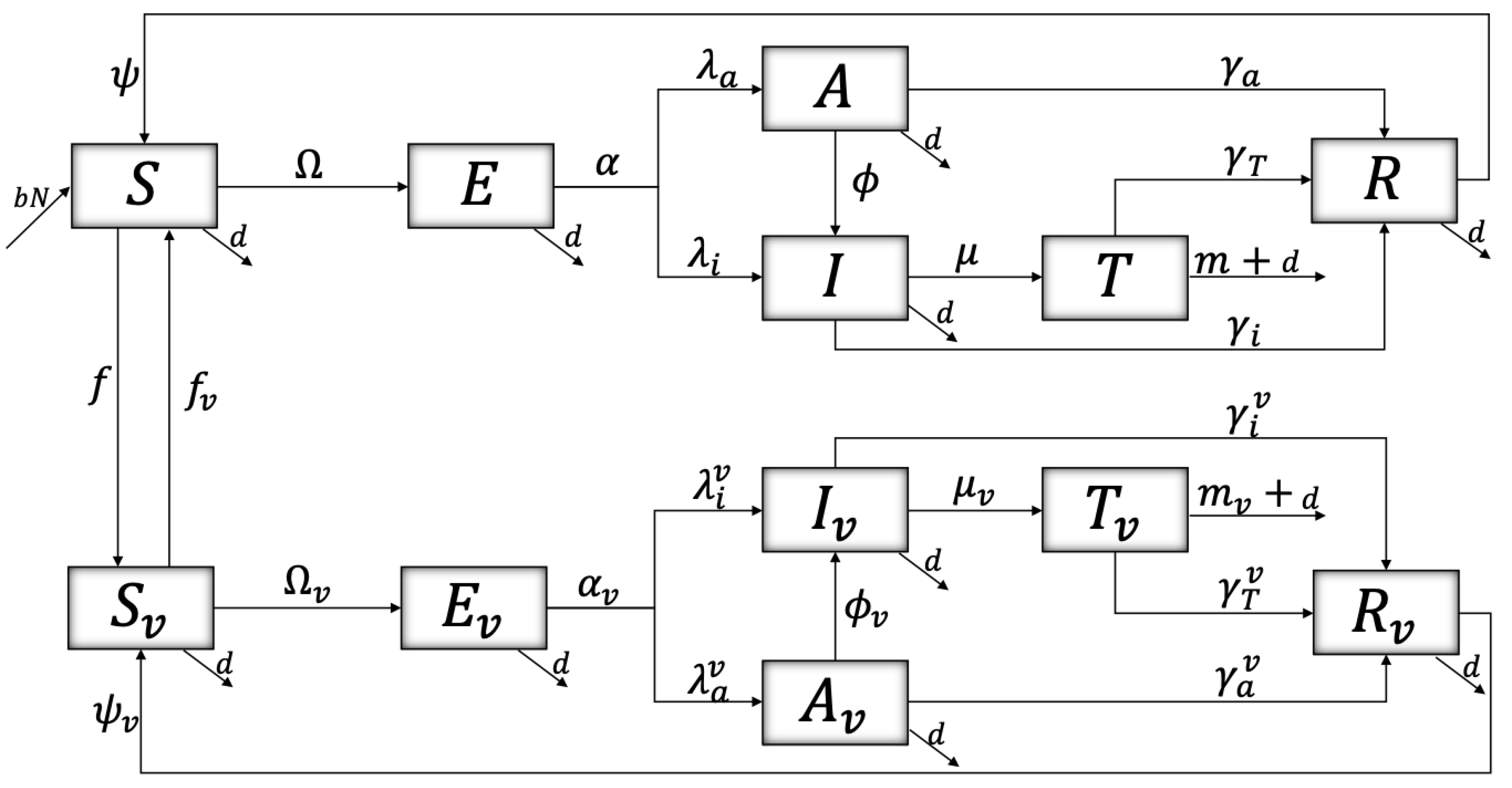


| Susceptible | Exposed | Asymptomatic | Infected | Treatment | Recovered | |
|---|---|---|---|---|---|---|
| NVac. | S | E | A | I | T | R |
| Vac. |
| Parameters | Description | Units |
|---|---|---|
| b (d) | Birth (Mortality) rate | D |
| f | Vaccination rate | D |
| Loss of immunity of vaccinated | D | |
| () | Transmission rate of asymptomatic (infectious) | D |
| () | Susceptibility (Infectivity) reduction factor | UN |
| () | Exit rate from latent unvaccinated (vaccinated) | D |
| to infectious unvaccinated (vaccinated) | ||
| () | Proportion of latent unvaccinated (vaccinated) | UN |
| that transit to asymptomatic unvaccinated | ||
| (vaccinated) | ||
| () | Proportion of latent unvaccinated (vaccinated) | UN |
| that transit to infectious unvaccinated | ||
| (vaccinated) | ||
| () | Transition rate from asymptomatic unvaccinated | D |
| (vaccinated) to infectious unvaccinated (vaccinated) | ||
| () | Transition rate of people unvaccinated (vaccinated) | D |
| needing medical intervention | ||
| m () | Disease induced death rate of unvaccinated (vaccinated) | D |
| () | Recovered rate of asymptomatic unvaccinated (vaccinated) | D |
| () | Recovered rate of infectious unvaccinated (vaccinated) | D |
| () | Recovery rate from treatment of people | D |
| unvaccinated (vaccinated) | ||
| () | Natural immunity loss rate of people | D |
| unvaccinated (vaccinated) | ||
| () | Rate of resistance to behavioral change those | D |
| unvaccinated (vaccinated) | ||
| () | Reaction rate to behavior change those | D |
| unvaccinated (vaccinated) | ||
| () | quantified average risk perception of those | UN |
| unvaccinated (vaccinated) | ||
| () | Unvaccinated (vaccinated) population | UN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez-Jara, J.P.; Saracini, C. Risk Perception Influence on Vaccination Program on COVID-19 in Chile: A Mathematical Model. Int. J. Environ. Res. Public Health 2022, 19, 2022. https://doi.org/10.3390/ijerph19042022
Gutiérrez-Jara JP, Saracini C. Risk Perception Influence on Vaccination Program on COVID-19 in Chile: A Mathematical Model. International Journal of Environmental Research and Public Health. 2022; 19(4):2022. https://doi.org/10.3390/ijerph19042022
Chicago/Turabian StyleGutiérrez-Jara, Juan Pablo, and Chiara Saracini. 2022. "Risk Perception Influence on Vaccination Program on COVID-19 in Chile: A Mathematical Model" International Journal of Environmental Research and Public Health 19, no. 4: 2022. https://doi.org/10.3390/ijerph19042022
APA StyleGutiérrez-Jara, J. P., & Saracini, C. (2022). Risk Perception Influence on Vaccination Program on COVID-19 in Chile: A Mathematical Model. International Journal of Environmental Research and Public Health, 19(4), 2022. https://doi.org/10.3390/ijerph19042022







