Evaluation and Prediction of Low-Carbon Economic Efficiency in China, Japan and South Korea: Based on DEA and Machine Learning
Abstract
:1. Introduction
2. Literature Review
2.1. Economic Efficiency Evaluation Studies
2.1.1. Low-Carbon Economic Efficiency Evaluation Indicators
| Authors/Year | Inputs | Outputs |
|---|---|---|
| Hu and Kao (2007) [3] | Labor input, capital input, energy input | Gross domestic product |
| Zhou and Ang (2008) [4] | Capital stock, labor force | Gross domestic product, CO2 emissions |
| Wang et al. (2012) [5] | Capital input, labor input, energy input | The gross product value of industrial enterprises above a designated size |
| Wang et al. (2013) [6] | Energy consumption, labor input, capital input | Gross domestic product, CO2 emissions |
| Wang and Wei (2014) [7] | Labor input, capital input, energy input | Total volume of industrial sulfur dioxide emissions, total volume of industrial carbon dioxide emissions |
| Wang et al. (2014) [8] | Capital stock, energy consumption, labor | Gross domestic product, environmental pollutants |
| Wang and Feng (2014) [9] | Capital stock, labor, energy consumption | Gross domestic product, positive environmental indicator |
| Zhang et al. (2017) [10] | Labor employment, capital stock, total energy consumption | Gross domestic product, CO2 emissions |
| Dong et al. (2017) [11] | Capital stock, labor, CO2 emissions | Gross domestic product |
| Cheng et al. (2019) [12] | Labor, capital stock, energy consumption | Gross domestic product, CO2 emissions |
| Li et al. (2020) [13] | Labor, capital stock, energy consumption | Gross domestic product, CO2 emissions |
| Wang et al. (2021) [14] | Labor, capital stock, energy consumption | Gross domestic product, CO2 emissions |
| Xue et al. (2022) [15] | Manpower input, capital investment, energy input | Gross domestic product, CO2 emissions |
| Niu et al. (2022) [16] | Labor force, capital stock, total energy consumption | Gross regional product, carbon dioxide emissions |
2.1.2. Low-Carbon Economy Efficiency Evaluation Methods
2.2. Low-Carbon Economic Efficiency Predicting Studies
3. Modeling Method
3.1. SBM Model with Undesirable Output Based on Global Covariance
3.1.1. SBM Model with Undesirable Output
3.1.2. Global Covariance Method
3.2. Machine Learning Models
3.2.1. Linear Regression (LR)
3.2.2. Support Vector Machine (SVM)
3.2.3. Back Propagation Neural Network (BPNN)
3.2.4. Decision Tree (DT)
3.2.5. Random Forest (RF), Gradient Boosting Decision Tree (GBDT), Extreme Gradient Boosting (XGBoost) and Light Gradient Boosting Machine (LightGBM)
3.2.6. Adaptive Boosting (AdaBoost) and Bootstrap Aggregating (Bagging)
3.2.7. GridSearchCV
4. Evaluation Index System and Research Data
4.1. Decision-Making Unit
4.2. Low-Carbon Economic Efficiency Evaluation Index System
4.3. Data Sources and Descriptive Statistics
| Input-Output Indicators | China | Japan | South Korea | |
|---|---|---|---|---|
| Input indicator 1 | Labor | The Bureau of Statistics of provinces, municipalities and autonomous regions [56] | Portal Site of Official Statistics of Japan [57] | Korean Statistical Information Service [58] |
| Input indicator 2 | Capital Stock | National Bureau of Statistics of China [56] | Cabinet Office, Economic and Social Research Institute [59] | Korean Statistical Information Service [58] |
| Input indicator 3 | Total Energy Consumption | The Bureau of Statistics of provinces, municipalities and autonomous regions [56] | Agency for Natural Resources and Energy [60] | Korea Energy Statistical Information System [61] |
| Desirable output indicator | GDP | National Bureau of Statistics of China [56] | Cabinet Office, Economic and Social Research Institute [59] | Korean Statistical Information Service [58] |
| Undesirable output indicator | Carbon Dioxide Emission | China Emission Accounts and Datasets (CEADs) [62] | Agency for Natural Resources and Energy [60] | Korea Energy Statistical Information System [61] |
- The average value of labor, capital stock, and total energy consumption in Chinese PLADs is 2.87, 2.75, and 2.69 times the average of the full sample. The average GDP as an indicator of desirable output is 1.99 times the average of the full sample, and the average carbon dioxide emission as an indicator of undesirable output is 2.86 times the average of the full sample. The average value of labor, capital stock, and total energy consumption in the PLADs of Japan are 0.11, 0.17 and 0.16 times the average of the full sample, respectively. The average GDP of the output indicator is 0.56 times that of the full sample, and the average value of carbon dioxide emissions is 0.10 times that of the full sample. The average value of labor, capital stock, and total energy consumption in the PLADs of South Korea is 0.16, 0.19 and 0.33 times the average of the full sample. The average GDP is 0.47 times the average of the full sample, and the average of carbon dioxide emissions is 0.21 times the average of the full sample. The multiple of the mean of labor force in Chinese PLADs/the mean of full sample is 26.38 and 17.70 times that of Japan and South Korea, respectively. The multiple of the mean of capital stock in Chinese PLADs/the mean of full sample is 15.91 and 14.56 times that of Japan and South Korea, respectively. The multiple of the mean of total energy consumption in Chinese PLADs/the mean of full sample mean is 16.33 and 8.16 times that of Japan and South Korea. The multiple of the average of GDP in Chinese PLADs/the mean of full sample is 3.56 and 4.23 times that of Japan and South Korea. In addition, the multiple of the mean of carbon dioxide emissions in Chinese PLADs/the mean of full sample is 28.18 times that of Japan and 13.93 times that of South Korea. It can be seen that the multiple of the overall mean of PLADs in China/the mean of full sample is much higher than that of Japan and South Korea in terms of input and undesirable output indicators, while the GDP as an indicator of desirable output is only 3.56 and 4.23 times higher than that of Japan and South Korea. Higher input costs and undesirable outputs, as well as lower desirable outputs, will lead to inefficiencies in a low-carbon economy.
- The standard deviation, minimum value and maximum value show the data distribution of the PLADs of China, Japan, and South Korea, also the full sample.
- The coefficient of variation is used as a relative index to measure the degree of dispersion of data, which can compare the degree of dispersion among several samples under variables with the same dimension but greatly different mean values. Statistics show that among the five input-output indicators, the PLADs of China is smaller than Japan and South Korea, indicating that the distribution difference of various input-output indicators among China is smaller than that of Japan and South Korea. The coefficient of variation of Japanese PLADs is larger than that of South Korea in terms of labor force, capital stock, total energy consumption, and GDP. As for carbon dioxide emissions, the coefficient of variation of Japanese PLADs is smaller than that of South Korea, but the difference between the two is small, only 0.04.
4.4. Data Pre-Processing
4.4.1. China
- The capital stock and GDP collected in this paper are nominal values, which have not been adjusted for inflation and cannot accurately measure the actual level of the indicators. Therefore, this paper uses 2015 as the base period for constant prices and calculates the actual value in other years. The reason for choosing 2015 is that the data of Japan and South Korea on these two indicators are the actual values obtained by deflating 2015 as the base period. To facilitate the calculation, those two indicators in China are also deflated with 2015 as the base period. The specific calculation method is that the data value in 2015 × the GDP deflator in 2016 compared with 2015, and the actual value in 2016 can be obtained. The calculation method is also used for 2017–2019. For the real values in 2014, derived from 2015 data values/the GDP deflator in 2015 compared with 2014, and the same for 2013. Among them, the GDP deflator measures the current price level relative to the price in base year, and the data comes from the website of the National Bureau of Statistics of China [56].
- China no longer publishes capital stock data after 2018, so the average growth rate of the previous three years is used, that is, the growth rate in 2015 compared with 2014, the growth rate in 2016 compared with 2015, and the growth rate in 2017 compared with 2016. The average growth rate is used as the growth rate of 2018 compared with 2017, to supply data for this indicator in 2018. Take the growth rate of 2016 compared with 2015, the growth rate of 2017 compared with 2016, and the growth rate of 2018 compared with 2017 to calculate the average value. The average growth rate is used as the growth rate of 2019 compared with 2018, and the data requirement for this indicator in 2019 is fulfilled.
4.4.2. Japan
- Convert the unit of labor force from thousand to ten thousand.
- Complete the missing data of capital stock. In terms of capital stock indicators, Aomori, Fukui, Nara, Okinawa and Tokushima lack data in 2019, so the average growth rate of the previous three years is used, that is, the growth rate in 2016 compared with 2015, the growth rate in 2017 compared with 2016, and the average growth rate in 2018 compared with 2017. The average growth rate is used as the growth rate in 2019 compared with 2018, so as to supply data for this indicator in 2019.
- Complete the missing data of GDP. In terms of GDP indicators, Aomori, Fukui, Nara, Okinawa, and Tokushima still lack data for 2019.The filling method of the indicator data in 2019 is consistent with the method of the capital stock indicator.
- Convert the unit of capital stock and GDP. The unit of capital stock and regional gross domestic product, one million yen is converted into one hundred million yuan, and is converted by the standard price in the foreign exchange rate announced by the Bank of China on December 31 of that year. The data comes from the Bank of China [63].
- Convert the unit of total energy consumption. The unit of total energy consumption, converting trillion Joules to ten thousand tons of coal equivalent. According to the International Energy Agency conversion standard [64], 1 trillion joules = 34.12 tonne(s) of coal equivalent (tce); after conversion to tce, divide by 10,000 to convert to ten thousand tons of coal equivalent.
- Convert the unit of carbon dioxide emissions. The molecular weight of carbon is 12, and the molecular weight of carbon dioxide is 44. 44/12 = 3.67, which means that 1 ton of carbon can produce about 3.67 tons of carbon dioxide after burning in oxygen. The carbon emissions in Japan (unit: 103 t) is converted into carbon dioxide emissions (unit: ton t), the indicator needs to be multiplied by 3.67 and then divided by 103 to complete the conversion.
4.4.3. South Korea
- Convert the unit of labor force from thousand to ten thousand.
- Convert the unit of capital stock and regional GDP indicators. One million won is converted into one hundred million yuan. The standard price in the foreign exchange rate announced by the Bank of China on December 31 of that year is used for conversion. The data comes from the Bank of China [63].
- Complete the data of Sejong in 2013. Among the indicators of total energy consumption and carbon dioxide emissions, Sejong lacks data in 2013. In 2013, the two indicators of Sejong were collected by Chungcheongnam-do. This paper calculates the growth rate of 2015 compared with 2014, the growth rate of 2016 compared with 2015, and the growth rate of 2017 compared with 2016. The three-year average growth rate is calculated as the growth rate of 2014 compared with 2013, so as to calculate the data of Sejong in 2013, and deduct the corresponding data from Chungcheongnam-do to correct the 2013 data of this indicator for Chungcheongnam-do.
- Convert the unit of total energy consumption. According to the conversion standard of the International Energy Agency [64], 1 toe= 1.429 tce, and the unit of total energy consumption is 103 tonne(s) of oil equivalent (toe), which is 1429 tce, and divided by 10,000 after conversion to tce. The result obtained is ten thousand tons of coal equivalent.
- Convert the unit of carbon dioxide emissions. Since there is no published data on carbon dioxide emissions, this paper calculates CO2 emissions based on CO2 emission factors from the combustion of different energy sources published by the Intergovernmental Panel on Climate Change [65]. First, convert the energy unit, and 1000 toe is converted into 41.87 TJ [64], then multiplied by the CO2 emission factor (unit: Kg/TJ) to obtain the kilogram carbon dioxide emission value. According to the standard 1 ton = 1000 Kg, it is converted into ten thousand tons of carbon dioxide emissions.
5. Empirical Research
5.1. Analysis of Low-Carbon Economic Efficiency Evaluation Results
5.2. Analysis of Low-Carbon Economic Efficiency Prediction Results
5.3. Discussion
6. Conclusions and Recommendations
- From the evaluation results, Japan had the highest average national low-carbon economic efficiency from 2013 to 2019, followed by South Korea and China. The low-carbon economic efficiency of Japan from 2013 to 2019 has steadily improved, with an average value of 0.533. The low-carbon economic efficiency value of Tokyo, Tokushima and Nara reached an effective value of 1.000 in 2019, and 20 of 47 PLADs reached the national average efficiency value and above. From 2013 to 2019, the low-carbon economy efficiency value of South Korea decreased, with an average value of 0.337. From the perspective of the PLADs, none reached the effective value of 1.000, and only 5 of 17 PLADs in the country reached the national average. The low-carbon economic efficiency of China from 2013 to 2019 shows a clear upward trend, with an average value of 0.094. Guangdong and Jiangsu achieved an effective value of 1 in 2019. Among the 30 PLADs in the country, only 4 divisions reached the national average efficiency value. From a country perspective, the low-carbon economic efficiency of China, Japan and South Korea show obvious regional differences. From a domestic perspective, only a small number of PLADs in China have reached the national average efficiency.
- From the perspective of input-output indicators, the input indicators of China have serious problems of excessive input and low utilization efficiency. In China, the redundancy rate of total energy consumption is the largest, and most of the PLADs have reached 90%. There are also problems of excessive investment in labor and capital stock. Most divisions in China have a high redundancy rate of CO2 emission, which may reach more than 90%, and there is much room for improvement. Among the input indicators in Japan, the redundancy rate of total energy consumption is the largest, followed by redundancy rate of labor input, and redundancy rate of capital stock is the lowest. Undesirable output, CO2 emission, is a significant factor affecting the low-carbon economic efficiency of most Japanese PLADs. The labor, total energy consumption, and carbon dioxide emissions of Korea have a great impact on the low-carbon economic efficiency.
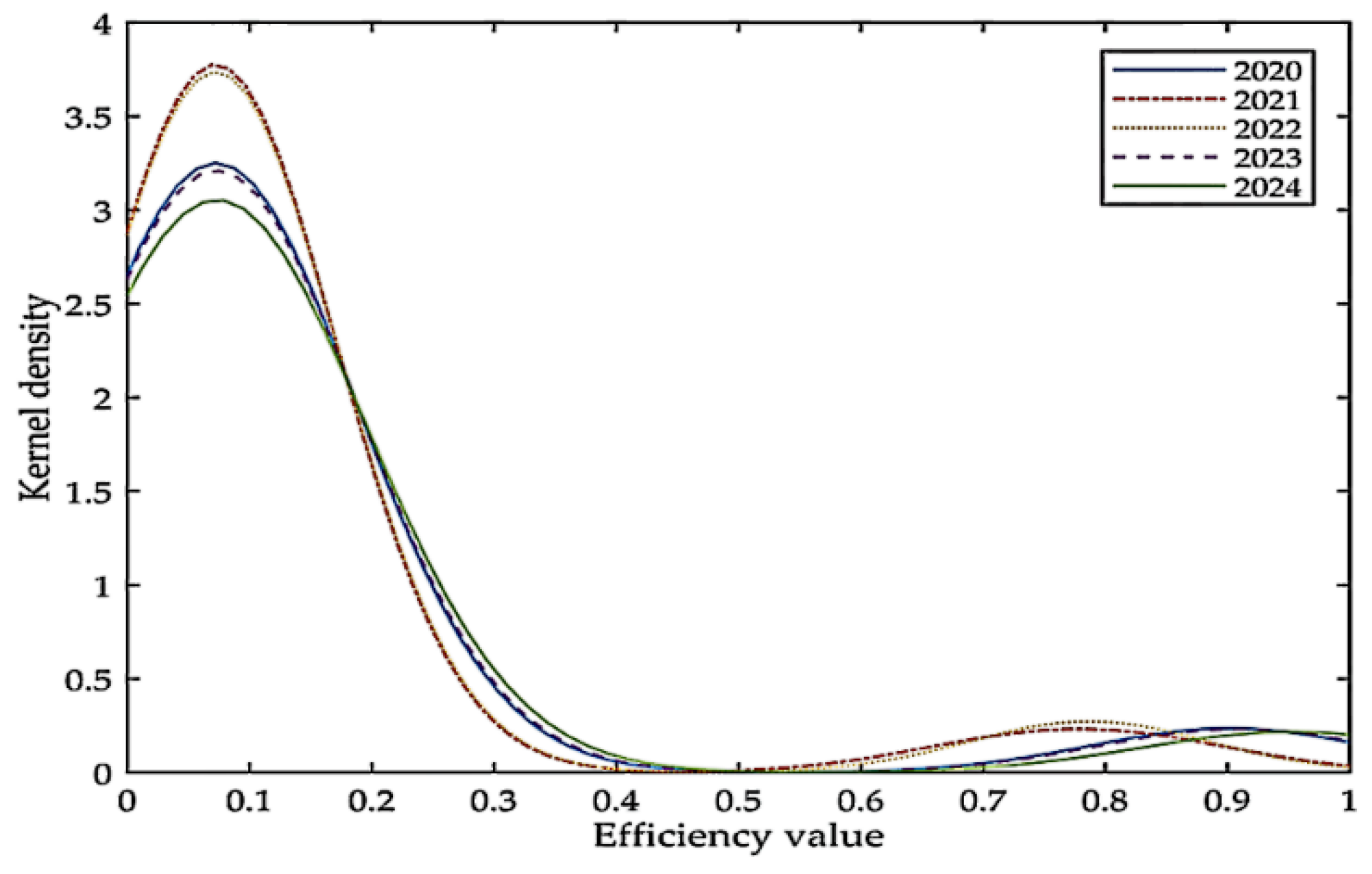
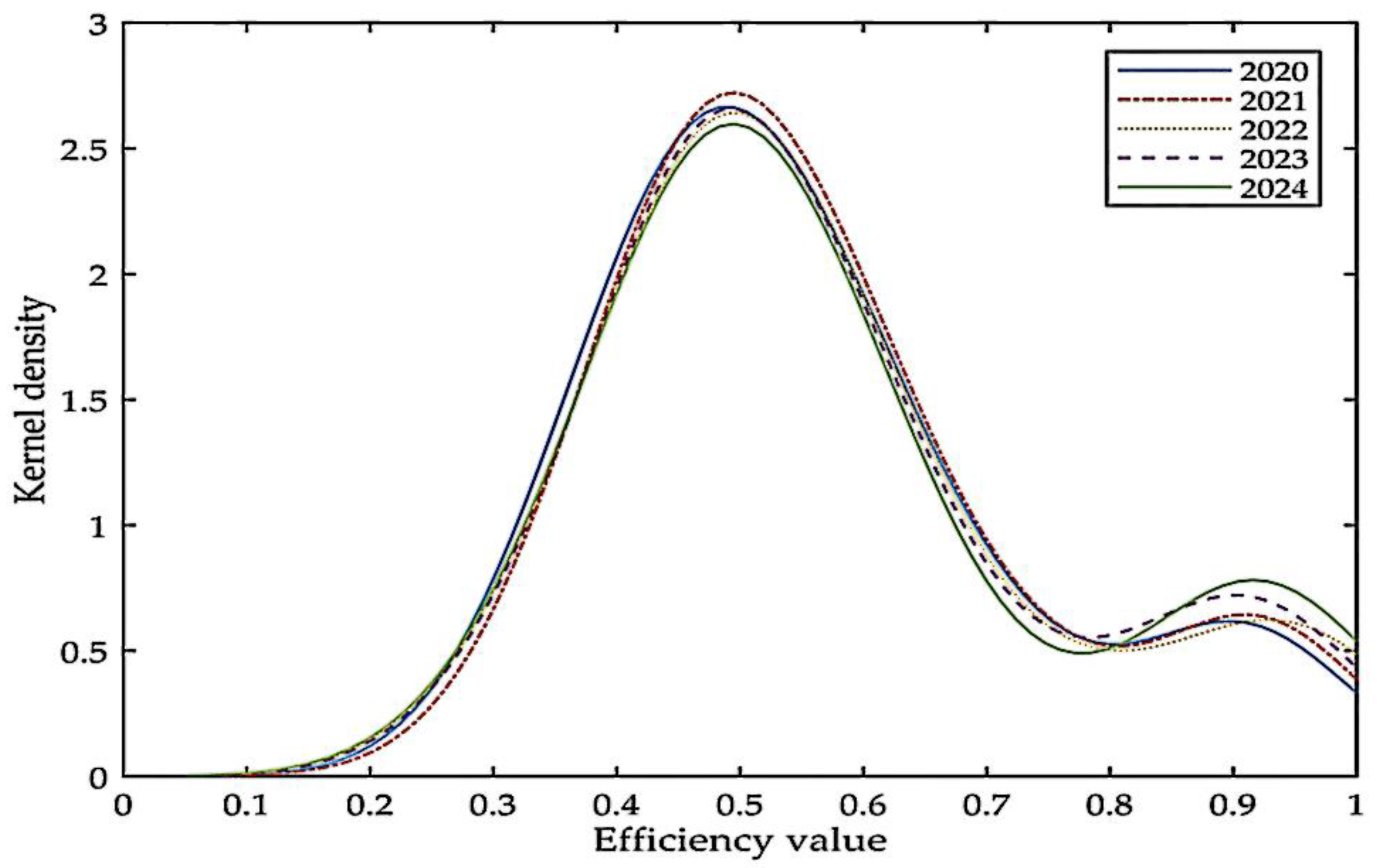
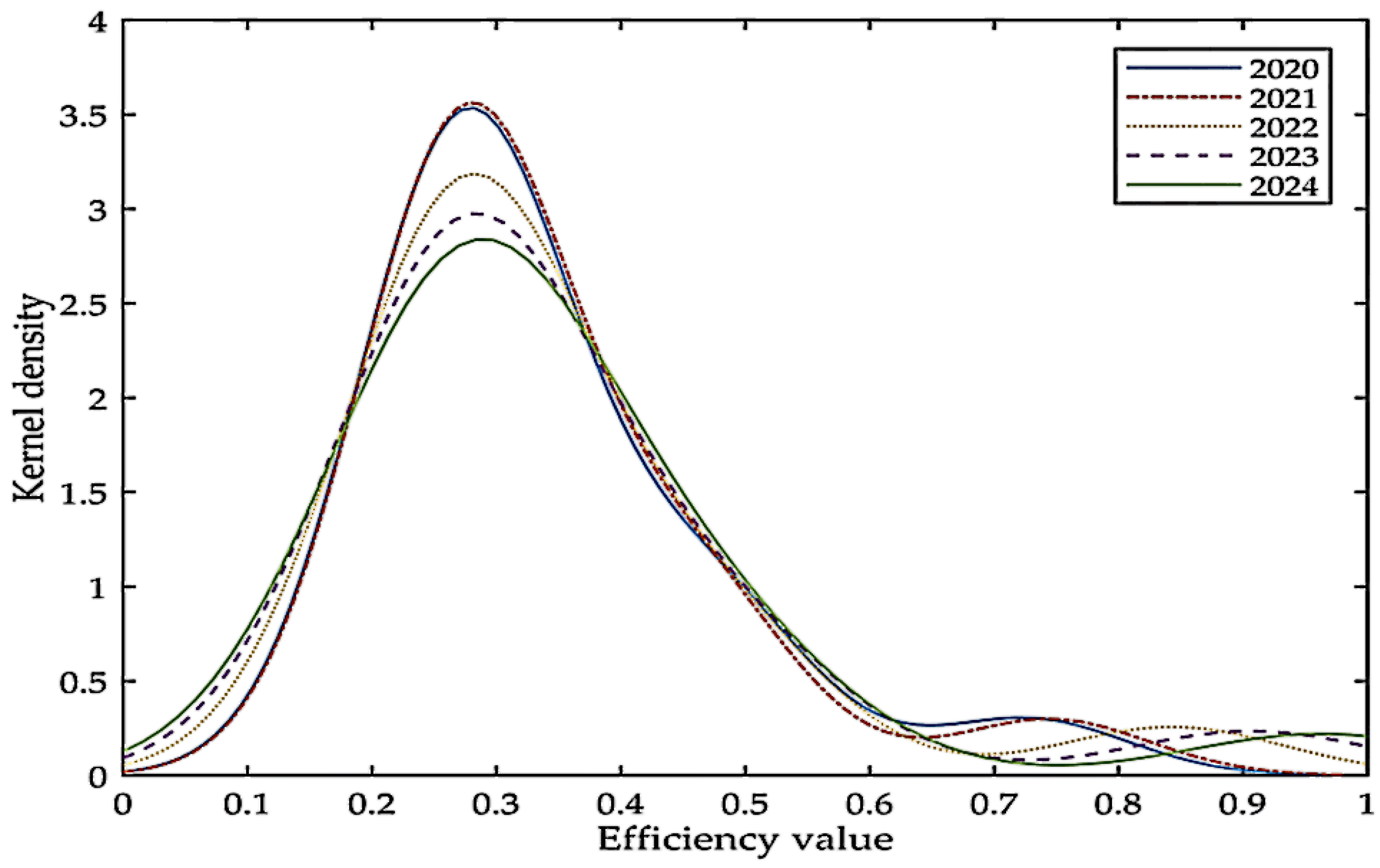
- From the prediction results, the overall low-carbon economic efficiency value of China will drop slightly from 2020 to 2021, and will rise steadily after 2022. The number of divisions that achieve low-carbon economic efficiency improvement is increasing year by year. Among them, the efficiency value of the divisions in the coastal areas where low-carbon technologies and markets are more developed will increase greatly, while the low-carbon economic efficiency values of the divisions in the western and northeastern regions, which are subject to regional resources and industrial structure, will decrease slightly. The national low-carbon economic efficiency value of Japan will show a steady upward trend from 2020 to 2024, and the average value will rise to 0.576 in 2024. The number of high-efficiency PLADs will increase significantly. The low-carbon efficiency of the divisions in Japan shows non-equilibrium characteristics, and divisions that use clean energy represented by nuclear energy have significantly higher efficiency values than the divisions that use coal and crude oil. The low-carbon economic efficiency value of South Korea from 2020 to 2024 will increase year by year, and the overall average value will reach 0.353 in 2024. Both the number of high-efficiency and low-efficiency PLADs will increase, and the GDP will continue to expand. In South Korea, the efficiency values of divisions that are dominated by the primary and tertiary industries are generally high, while the efficiency values of some industrial cities show a clear downward trend.
- Focus on inter-regional differences and make full use of the endowment advantages of each country. From the evaluation results, it can be seen that there are large differences in the low-carbon economic efficiency values between China and Japan and South Korea, and there is still a significant gap in the predicted values after five years. In response to the different development situations of the three countries, it is necessary to make full use of their own advantages to develop differentiated low-carbon economic development strategies. China is a major energy producer and consumer, especially in the development of natural gas, solar energy, wind energy and other clean and new energy sources, and has a unique advantage. China should seize the opportunity to take advantage of its vast territory and abundant energy resources to increase the research, development and promotion of new energy technologies. Japan and South Korea are small energy producing and consuming countries, with high external energy dependence. As developed countries, both these two countries have high domestic carbon reduction costs. Japan and South Korea have the advantage of leading international energy-saving and emission reduction technologies, have mastered key technologies in waste treatment, soot desulfurization and other fields, and have accumulated rich experience in the field of energy utilization. China, Japan and South Korea have strong complementarities in energy-saving technologies and energy resources, and it is necessary for the three countries to form a collaboration on emission reduction to achieve emission reduction outside at a lower cost.
- Optimize the energy structure and drive industrial development with new energy sources. Based on the empirical results of this paper, a high redundancy rate of CO2 emissions is common in China, Japan and South Korea, which significantly affects the improvement of low-carbon economic efficiency in each country, and they need to further adjust the energy structure and reduce the proportion of fossil energy consumption. The energy consumption of China is dominated by coal, and its energy structure, which is determined by resource endowment, is the root cause of the high energy carbon intensity in China. In the energy structure of Japan, the reliance on oil is decreasing, and the use of natural gas and nuclear energy is increasing. Japan is also focusing on clean technologies for fossil energy in order to reduce the environmental problems caused by fossil energy. Similar to Japan, South Korea is focusing on diversification of energy outcomes by developing nuclear energy and importing liquefied natural gas to meet energy demand. Although China, Japan and South Korea are in different processes of restructuring their energy institutions, renewable energy is the focus of attention in all three countries. China is currently a global leader in the field of renewable energy, especially in the solar photovoltaic, wind power, hydroelectric power and other industries. While Japan and South Korea have world-class R&D and technological advantages, their domestic resources and environment place a non-negligible constraint on the development of the low-carbon economy. China, Japan and South Korea should effectively integrate technical and new energy resources and cooperate with each other, so they can achieve a diverse low-carbon energy portfolio and obtain multi-win results.
- Focus on international cooperation and drive regional cooperation with business cooperation. From the prediction results, the low-carbon economic efficiency in the eastern coastal regions of China, in Japan and South Korea, with developed science and technology industries is generally higher; this is inseparable from international cooperation. Especially in the context of addressing climate change, whether from the perspective of national interests or global environmental interests, regional environmental cooperation among China, Japan, and South Korea will play a positive role in promoting national economic development and achieving global common interests. However, influenced by regional politics, rights, and perceptions, there are also difficulties in regional environmental cooperation between the governments of China, Japan, and South Korea. Thus, business-to-business cooperation is expected to be the main vehicle for regional environmental cooperation. At present, Japan has developed corresponding projects in China through the Clean Development Mechanism (CDM). Enterprise cooperation has become a major component of China-Japan low-carbon economic cooperation, and is expected to become the main body of regional low-carbon economic cooperation among China, Japan and South Korea. In the future, enterprises in these three countries should continue to deepen their cooperation in the fields of low-carbon technology transformation, green direct investment and low-carbon technology trading, and then promote the low-carbon economic development worldwide and build a community of green destiny for mankind.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Machine Learning Model | Optimal Parameter Combination |
|---|---|
| Linear Regression | normalize = True |
| SVR | C = 19, gamma = 0.3 |
| BPNN | hidden_layer_sizes = [5], max_iter = 100, solver = ‘lbfgs’ |
| Decision Tree | max_depth = 8, max_features = 2 |
| Random Forest | max_depth = 9, n_estimators = 500 |
| GBDT | max_depth = 5, n_estimators = 500 |
| XGBoost | learning_rate = 0.01, n_estimators = 500, max_depth = 5, subsample = 0.6 |
| LightGBM | max_depth = 6, subsample = 0.6) |
| AdaBoost | learning_rate = 0.001, n_estimators = 100 |
| Bagging | base_estimator = Decision Tree Regressor (max_depth = 7), n_estimators = 500 |
References
- Department of Trade and Industry (DTI). UK Energy White Paper: Our Energy Future–Creating a Low Carbon Economy; The Stationery Office: London, UK, 2003.
- Bp. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy/co2-emissions.html (accessed on 15 July 2022).
- Hu, J.L.; Kao, C.H. Effificient energy-saving targets for APEC economies. Energy Policy 2007, 35, 373–382. [Google Scholar] [CrossRef]
- Zhou, P.; Ang, B.W. Linear programming models for measuring economy-wide energy effificiency performance. Energy Policy 2008, 38, 2911–2916. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zeng, H.L.; Wei, Y.M.; Zhang, Y.X. Regional total factor energy efficiency: An empirical analysis of industrial sector in China. Appl. Energy 2012, 97, 115–123. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.M.; Zhang, X. Energy and emissions efficiency patterns of Chinese regions: A multi-directional efficiency analysis. Appl. Energy 2013, 104, 105–116. [Google Scholar] [CrossRef]
- Wang, K.; Wei, Y.M. China’s regional industrial energy efficiency and carbon emissions abatement costs. Appl. Energy 2014, 130, 617–631. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, C.; Zhang, B. An empirical analysis of China’s energy efficiency from both static and dynamic perspectives. Energy 2014, 74, 322–330. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, C. The impact and economic cost of environmental regulation on energy utilization in China. Appl. Econ. 2014, 46, 3362–3376. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, W.; Wang, J.; Yang, F.; Jiang, H. Regional low-carbon economy efficiency in China: Analysis based on the Super-SBM model with CO2 emissions. J. Clean. Prod. 2017, 163, 202–211. [Google Scholar] [CrossRef]
- Dong, F.; Long, R.; Bian, Z.; Xu, X.; Yu, B.; Wang, Y. Applying a Ruggiero three-stage super-efficiency DEA model to gauge regional carbon emission efficiency: Evidence from China. Nat. Hazards 2017, 87, 1453–1468. [Google Scholar] [CrossRef]
- Cheng, Y.; Lv, K.; Wang, J.; Xu, H. Energy efficiency, carbon dioxide emission efficiency, and related abatement costs in regional China: A synthesis of input–output analysis and DEA. Energy Effic. 2019, 12, 863–877. [Google Scholar] [CrossRef]
- Li, J.; Ma, J.; Wei, W. Analysis and Evaluation of the Regional Characteristics of Carbon Emission Efficiency for China. Sustainability 2020, 12, 3138. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Wang, Q.; Yao, S. Evaluation and difference analysis of regional energy efficiency in China under the carbon neutrality targets: Insights from DEA and Theil models. J. Environ. Manag. 2021, 293, 112958. [Google Scholar] [CrossRef]
- Xue, L.M.; Zheng, Z.X.; Meng, S.; Li, M.; Li, H.; Chen, J.M. Carbon emission efficiency and spatio-temporal dynamic evolution of the cities in Beijing-Tianjin-Hebei Region, China. Environ. Dev. Sustain. 2022, 24, 7640–7664. [Google Scholar] [CrossRef]
- Niu, H.; Zhang, Z.; Xiao, Y.; Luo, M.; Chen, Y. A Study of Carbon Emission Efficiency in Chinese Provinces Based on a Three-Stage SBM-Undesirable Model and an LSTM Model. Int. J. Environ. Res. Public Health 2022, 19, 5395. [Google Scholar] [CrossRef] [PubMed]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Xi, X.Y.; Li, J. An Assessment of Low-Carbon Efficiency Evaluation in the Prospect of Environmental Optimization. Adv. Mater. Res. 2011, 160, 1187–1192. [Google Scholar] [CrossRef]
- Fan, Y.; Fang, C. Circular economy development in China-current situation, evaluation and policy implications. Environ. Impact Asses. 2020, 84, 106441. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, G.; Zhao, Y. An analysis of Chinese provincial carbon dioxide emission efficiencies based on energy consumption structure. Energy Policy 2016, 96, 524–533. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Liang, L.; Wang, D.; Cui, X.; Wei, W. Spatial-temporal pattern evolution and driving factors of China’s energy efficiency under low-carbon economy. Sci. Total Environ. 2020, 739, 140197. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Han, Y. Low Carbon Economy Assessment in China Using the Super-SBM Model. Discret. Dyn. Nat. Soc. 2022, 2022, 4690140. [Google Scholar] [CrossRef]
- Iftikhar, Y.; He, W.; Wang, Z. Energy and CO2 emissions efficiency of major economies: A non-parametric analysis. J. Clean. Prod. 2016, 139, 779–787. [Google Scholar] [CrossRef]
- Yang, W.C.; Lee, Y.M.; Hu, J.L. Urban sustainability assessment of Taiwan based on data envelopment analysis. Renew. Sustain. Energy Rev. 2016, 61, 341–353. [Google Scholar] [CrossRef]
- Sueyoshi, T.; Yuan, Y.; Li, A.; Wang, D. Social sustainability of provinces in China: A data envelopment analysis (DEA) window analysis under the concepts of natural and managerial disposability. Sustainability 2017, 9, 2078. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.Q.; Li, B.L. Energy Consumer Demand Predict of Hebei Province in the Domain of Low-Carbon Economy-Analysis Based on Gray Model GM (1,1). Appl. Mech. Mater. 2013, 380–384, 4456–4460. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C.; Tseng, C.L. Forecasting of CO2 emissions, energy consumption and economic growth in China using an improved grey model. Energy 2012, 40, 400–409. [Google Scholar] [CrossRef]
- Nyoni, T.; Bonga, W.G. Prediction of CO2 emissions in India using arima models. DRJ-J. Econ. Financ. 2019, 4, 1–10. [Google Scholar]
- Ning, L.; Pei, L.; Li, F. Forecast of China’s carbon emissions based on Arima method. Discret. Dyn. Nat. Soc. 2021, 2021, 1441942. [Google Scholar] [CrossRef]
- Lotfalipour, M.R.; Falahi, M.A.; Bastam, M. Prediction of CO2 emissions in Iran using grey and ARIMA models. Int. J. Energy Econ. Policy 2013, 3, 229–237. [Google Scholar]
- Rehman, H.U.; Rafique, R.; Nasir, M.; Chudhery, M.A.Z. Forecasting CO2 Emissions from Energy, Manufacturing and Transport Sectors in Pakistan: Statistical vs. Machine Learning Methods. SSRN J. 2018. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3292279 (accessed on 19 July 2022). [CrossRef]
- Ma, Z.; Ye, C.; Li, H.; Ma, W. Applying support vector machines to predict building energy consumption in China. Energy Procedia 2018, 152, 780–786. [Google Scholar] [CrossRef]
- Bakay, M.S.; Ağbulut, Ü. Electricity production based forecasting of greenhouse gas emissions in Turkey with deep learning, support vector machine and artificial neural network algorithms. J. Clean. Prod. 2021, 285, 125324. [Google Scholar] [CrossRef]
- Homaira, M.; Hassan, R. Prediction of agricultural emissions in Malaysia using the arima, LSTM, and regression models. Int. J. Perceptive Cogn. Comput. 2021, 7, 33–40. [Google Scholar]
- Bousqaoui, H.; Slimani, I.; Achchab, S. Comparative analysis of short-term demand predicting models using ARIMA and deep learning. Int. J. Electr. Comput. 2021, 11, 3319. [Google Scholar] [CrossRef]
- Kumari, S.; Singh, S.K. Machine learning-based time series models for effective CO2 emission prediction in India. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef] [PubMed]
- Sun, W.; Liu, M. Prediction and analysis of the three major industries and residential consumption CO2 emissions based on least squares support vector machine in China. J. Clean. Prod. 2016, 122, 144–153. [Google Scholar] [CrossRef]
- Sun, W.; Sun, J. Prediction of carbon dioxide emissions based on principal component analysis with regularized extreme learning machine: The case of China. Environ. Eng. Res. 2017, 22, 302–311. [Google Scholar] [CrossRef] [Green Version]
- Meng, Z.; Sun, H.; Wang, X. Forecasting Energy Consumption Based on SVR and Markov Model: A Case Study of China. Front. Env. Sci. 2022, 10, 883711. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Tone, K. Dealing with undesirable outputs in DEA: A slacks-based measure (SBM) approach. Present. NAPW III 2004, 2004, 44–45. [Google Scholar]
- Pastor, J.T.; Lovell, C.K. A global Malmquist productivity index. Econ. Lett. 2005, 88, 266–271. [Google Scholar] [CrossRef]
- Bishop, C.M.; Nasrabadi, N.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Vapnik, V.N. The nature of statistical learning theory. Nat. Stat. Learn. Theory 1995, 20, 273–297. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Breiman, L.I.; Friedman, J.H.; Olshen, R.A. Classification and Regression Trees Wadsworth. Biometrics 1984, 40, 358. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13 August 2016. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiao, Y.; Niu, H. DEA and Machine Learning for Performance Prediction. Mathematics 2022, 10, 1776. [Google Scholar] [CrossRef]
- National Bureau of Statistics. Available online: http://www.stats.gov.cn/ (accessed on 24 July 2022).
- E-Stat. Available online: https://www.e-stat.go.jp/stat-search/files?page=1&layout=dataset&cycle_facet=%3Acycle&metadata=1&data=1 (accessed on 26 July 2022).
- KOSIS. Available online: https://kosis.kr/statisticsList/statisticsListIndex.do?vwcd=MT_ZTITLE&menuId=M_01_01 (accessed on 31 July 2022).
- Cabinet Office. Available online: https://www.esri.cao.go.jp/jp/sna/sonota/kenmin/todouhukensi/todouhukensi.html (accessed on 28 July 2022).
- Agency for Natural Resources and Energy. Available online: https://www.enecho.meti.go.jp/statistics/energy_consumption/ec002/results.html#headline2 (accessed on 29 July 2022).
- KESIS. Available online: http://www.kesis.net/sub/sub_LastPubctList.jsp (accessed on 2 August 2022).
- China Emission Accounts and Datasets. Available online: https://www.ceads.net/data/province/ (accessed on 25 July 2022).
- Bank of China. Available online: https://www.boc.cn/sourcedb/whpj/ (accessed on 4 August 2022).
- IEA Unit Converter. Available online: https://www.iea.org/data-and-statistics/data-tools/unit-converter (accessed on 4 August 2022).
- Publications-IPCC-TFI. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/vol2.html (accessed on 5 August 2022).
- Wang, L.-W.; Le, K.-D.; Nguyen, T.-D. Assessment of the Energy Efficiency Improvement of Twenty-Five Countries: A DEA Approach. Energies 2019, 12, 1535. [Google Scholar] [CrossRef]
| Input-Output Indicator | Measurement | Unit | |
|---|---|---|---|
| Input indicator 1 | Labor | Number of employed population at the end of the year in PLADs | ten thousand people |
| Input indicator 2 | Capital Stock | Real Gross Fixed Capital in PLADs (deflated with 2015 as the base period) | RMB 100 Million Yuan |
| Input indicator 3 | Total Energy Consumption | Total energy consumption in PLADs | Ten thousand ton of Standard Coal Equivalent |
| Desirable output indicator | GDP | Real GDP in PLADs (deflated with 2015 as the base period) | RMB 100 Million Yuan |
| Undesirable output indicator | Carbon Dioxide Emission | Carbon dioxide emissions in PLADs | Million Tons |
| Input-Output Indicators | Sample | Mean | Standard Deviation | Minimum | Maximum | Coefficient of Variation |
|---|---|---|---|---|---|---|
| Labor (ten thousand person) | PLADs of China | 2755.57 | 1772.51 | 314.20 | 6995.00 | 0.64 |
| PLADs of Japan | 104.45 | 149.05 | 9.91 | 1071.46 | 1.43 | |
| PLADs of South Korea | 155.69 | 165.87 | 6.01 | 704.30 | 1.07 | |
| Full Sample | 959.82 | 1590.51 | 6.01 | 6995.00 | —— | |
| Capital Stock (RMB 100 Million Yuan) | PLADs of China | 26,144.13 | 19,876.77 | 2045.71 | 97,440.07 | 0.76 |
| PLADs of Japan | 1643.43 | 1981.59 | 265.66 | 13,826.07 | 1.21 | |
| PLADs of South Korea | 1796.19 | 1850.10 | 291.74 | 9813.82 | 1.03 | |
| Full Sample | 9490.43 | 16,076.81 | 265.66 | 97,440.07 | —— | |
| Total Energy Consumption (Ten thousand ton of Standard Coal Equivalent) | PLADs of China | 15,205.01 | 8863.27 | 1720.33 | 41,390.00 | 0.58 |
| PLADs of Japan | 931.17 | 945.00 | 143.38 | 4810.90 | 1.01 | |
| PLADs of South Korea | 1862.99 | 1722.99 | 61.94 | 5995.70 | 0.92 | |
| Full Sample | 5655.17 | 8300.57 | 61.94 | 41,390.00 | —— | |
| GDP (RMB 100 Million Yuan) | PLADs of China | 24,927.67 | 19,916.15 | 1702.01 | 97,953.88 | 0.80 |
| PLADs of Japan | 7001.23 | 10,155.97 | 909.19 | 72,968.51 | 1.45 | |
| PLADs of South Korea | 5886.29 | 6578.05 | 395.10 | 27,885.23 | 1.12 | |
| Full Sample | 12,520.79 | 16,058.50 | 395.10 | 97,953.88 | —— | |
| Carbon Dioxide Emission (Million tons) | PLADs of China | 384.67 | 320.51 | 44.05 | 1700.04 | 0.83 |
| PLADs of Japan | 13.65 | 15.83 | 1.19 | 83.67 | 1.16 | |
| PLADs of South Korea | 27.62 | 33.04 | 0.41 | 120.45 | 1.20 | |
| Full Sample | 134.59 | 249.78 | 0.41 | 1700.04 | —— |
| 2013 | 2015 | 2017 | 2019 | 7-Year Average | Redundancy Rate of Labor | Redundancy Rate of Capital Stock | Redundancy Rate of Total Energy Consumption | Deficiency Rate of Regional GDP | Redundancy Rate of CO2 Emissions | |
|---|---|---|---|---|---|---|---|---|---|---|
| Guangdong | 0.082 | 0.148 | 0.527 | 1.000 | 0.417 | 52.63% | 47.04% | 56.51% | 0.00% | 58.42% |
| Jiangsu | 0.086 | 0.095 | 0.424 | 1.000 | 0.366 | 50.17% | 54.16% | 63.81% | 0.00% | 69.80% |
| Beijing | 0.115 | 0.122 | 0.130 | 0.138 | 0.126 | 77.11% | 79.38% | 88.42% | 0.00% | 91.34% |
| Shanghai | 0.100 | 0.108 | 0.117 | 0.125 | 0.113 | 78.31% | 79.91% | 91.91% | 0.00% | 95.11% |
| Fujian | 0.079 | 0.082 | 0.094 | 0.100 | 0.088 | 87.60% | 80.65% | 92.57% | 0.00% | 96.64% |
| Zhejiang | 0.080 | 0.085 | 0.090 | 0.094 | 0.087 | 87.10% | 81.08% | 93.02% | 0.00% | 96.99% |
| Hainan | 0.087 | 0.086 | 0.087 | 0.087 | 0.087 | 92.75% | 80.09% | 88.75% | 0.00% | 96.05% |
| Chongqing | 0.075 | 0.079 | 0.089 | 0.089 | 0.083 | 89.27% | 81.00% | 92.99% | 0.00% | 95.93% |
| Hubei | 0.069 | 0.073 | 0.079 | 0.084 | 0.076 | 90.56% | 81.82% | 93.77% | 0.00% | 96.63% |
| Shaanxi | 0.070 | 0.073 | 0.077 | 0.080 | 0.075 | 90.38% | 81.26% | 94.58% | 0.00% | 98.97% |
| Jiangxi | 0.070 | 0.073 | 0.077 | 0.080 | 0.075 | 92.71% | 81.11% | 92.81% | 0.00% | 96.82% |
| Hunan | 0.067 | 0.071 | 0.077 | 0.083 | 0.074 | 91.66% | 81.51% | 93.70% | 0.00% | 96.74% |
| Anhui | 0.069 | 0.072 | 0.076 | 0.078 | 0.074 | 93.78% | 79.74% | 93.42% | 0.00% | 98.15% |
| Yunnan | 0.067 | 0.070 | 0.073 | 0.075 | 0.071 | 94.24% | 79.27% | 94.78% | 0.00% | 97.26% |
| Sichuan | 0.065 | 0.068 | 0.072 | 0.076 | 0.070 | 92.94% | 81.09% | 94.82% | 0.00% | 96.63% |
| Henan | 0.063 | 0.066 | 0.070 | 0.074 | 0.068 | 93.68% | 81.30% | 94.54% | 0.00% | 98.03% |
| Shandong | 0.062 | 0.065 | 0.070 | 0.076 | 0.068 | 90.34% | 83.70% | 95.46% | 0.00% | 98.68% |
| Guizhou | 0.062 | 0.064 | 0.068 | 0.070 | 0.066 | 93.95% | 81.12% | 95.44% | 0.00% | 98.64% |
| Xinjiang | 0.064 | 0.065 | 0.066 | 0.067 | 0.066 | 91.84% | 81.25% | 97.46% | 0.00% | 99.02% |
| Tianjin | 0.064 | 0.067 | 0.062 | 0.063 | 0.065 | 89.23% | 87.46% | 94.54% | 0.00% | 97.15% |
| Guangxi | 0.059 | 0.062 | 0.064 | 0.065 | 0.063 | 94.19% | 83.40% | 94.55% | 0.00% | 97.41% |
| Qinghai | 0.060 | 0.061 | 0.063 | 0.065 | 0.062 | 93.91% | 83.41% | 95.14% | 0.00% | 95.33% |
| Gansu | 0.059 | 0.060 | 0.062 | 0.063 | 0.061 | 95.51% | 81.61% | 95.62% | 0.00% | 98.08% |
| Shanxi | 0.057 | 0.059 | 0.060 | 0.064 | 0.060 | 93.17% | 82.41% | 97.55% | 0.00% | 99.70% |
| Hebei | 0.056 | 0.058 | 0.060 | 0.063 | 0.059 | 93.06% | 83.43% | 97.02% | 0.00% | 98.68% |
| Inner Mongolia | 0.054 | 0.056 | 0.061 | 0.064 | 0.059 | 89.99% | 86.26% | 97.49% | 0.00% | 99.44% |
| Ningxia | 0.058 | 0.058 | 0.058 | 0.059 | 0.058 | 94.88% | 82.60% | 96.31% | 0.00% | 98.78% |
| Liaoning | 0.053 | 0.056 | 0.058 | 0.063 | 0.057 | 90.73% | 86.49% | 96.76% | 0.00% | 98.87% |
| Jilin | 0.051 | 0.054 | 0.059 | 0.060 | 0.056 | 92.69% | 87.72% | 94.63% | 0.00% | 98.18% |
| Heilongjiang | 0.053 | 0.054 | 0.057 | 0.060 | 0.056 | 93.65% | 85.38% | 96.01% | 0.00% | 98.74% |
| China | 0.069 | 0.074 | 0.101 | 0.139 | 0.094 | 88.40% | 80.22% | 92.15% | 0.00% | 95.21% |
| 2013 | 2015 | 2017 | 2019 | 7-Year Average | Redundancy Rate of Labor | Redundancy Rate of Capital Stock | Redundancy Rate of Total Energy Consumption | Deficiency Rate of Regional GDP | Redundancy Rate of CO2 Emissions | |
|---|---|---|---|---|---|---|---|---|---|---|
| Tokushima | 1.000 | 1.000 | 0.844 | 1.000 | 0.939 | 6.17% | 0.00% | 4.04% | 0.00% | 6.30% |
| Tottori | 0.856 | 1.000 | 0.833 | 0.955 | 0.932 | 8.02% | 0.00% | 9.34% | 0.00% | 2.49% |
| Tokyo | 1.000 | 0.758 | 0.848 | 1.000 | 0.875 | 19.35% | 0.08% | 7.67% | 0.00% | 9.59% |
| Yamanashi | 0.700 | 0.829 | 0.904 | 0.907 | 0.837 | 10.23% | 1.39% | 11.52% | 0.00% | 21.85% |
| Nara | 0.623 | 0.700 | 0.697 | 1.000 | 0.779 | 25.39% | 0.00% | 18.07% | 0.00% | 21.38% |
| Saga | 0.645 | 0.740 | 0.741 | 0.751 | 0.715 | 25.72% | 0.00% | 23.77% | 0.00% | 33.73% |
| Kochi | 0.599 | 0.681 | 0.679 | 0.733 | 0.709 | 14.46% | 0.05% | 24.28% | 0.00% | 48.90% |
| Shimane | 0.601 | 0.664 | 0.736 | 0.647 | 0.676 | 34.00% | 0.00% | 24.22% | 0.00% | 38.95% |
| Yamagata | 0.570 | 0.634 | 0.684 | 0.675 | 0.644 | 38.84% | 0.00% | 27.97% | 0.00% | 41.84% |
| Nagasaki | 0.577 | 0.603 | 0.634 | 0.638 | 0.625 | 24.51% | 0.76% | 37.89% | 0.00% | 52.88% |
| Fukui | 0.533 | 0.648 | 0.571 | 0.600 | 0.604 | 25.73% | 1.24% | 42.17% | 0.00% | 54.83% |
| Kyoto | 0.534 | 0.556 | 0.618 | 0.622 | 0.577 | 23.67% | 1.43% | 49.73% | 0.00% | 60.67% |
| Nagano | 0.439 | 0.552 | 1.000 | 0.514 | 0.571 | 21.14% | 12.05% | 49.18% | 0.00% | 61.88% |
| Shiga | 0.494 | 0.586 | 0.603 | 0.585 | 0.559 | 14.54% | 9.14% | 54.65% | 0.00% | 64.87% |
| Ishikawa | 0.523 | 0.579 | 0.613 | 0.551 | 0.556 | 35.35% | 3.20% | 45.24% | 0.00% | 59.65% |
| Gunma | 0.491 | 0.559 | 0.590 | 0.594 | 0.547 | 10.71% | 14.78% | 54.96% | 0.00% | 68.08% |
| Tochigi | 0.515 | 0.529 | 0.622 | 0.589 | 0.545 | 17.08% | 6.72% | 56.95% | 0.00% | 68.77% |
| Kagawa | 0.518 | 0.521 | 0.551 | 0.562 | 0.542 | 32.03% | 7.13% | 45.54% | 0.00% | 64.74% |
| Kagoshima | 0.487 | 0.498 | 0.545 | 0.599 | 0.541 | 37.32% | 0.00% | 49.72% | 0.00% | 62.58% |
| Okinawa | 0.530 | 0.523 | 0.543 | 0.624 | 0.537 | 42.01% | 1.84% | 44.65% | 0.00% | 63.21% |
| Toyama | 0.402 | 0.530 | 0.504 | 0.586 | 0.510 | 22.49% | 7.74% | 61.87% | 0.00% | 72.17% |
| Akita | 0.499 | 0.532 | 0.508 | 0.539 | 0.509 | 45.52% | 1.69% | 51.46% | 0.00% | 63.56% |
| Miyagi | 1.000 | 0.396 | 0.411 | 0.477 | 0.507 | 24.79% | 23.30% | 56.87% | 0.00% | 67.54% |
| Miyazaki | 0.499 | 0.464 | 0.557 | 0.508 | 0.507 | 35.76% | 6.43% | 54.14% | 0.00% | 67.89% |
| Kumamoto | 0.507 | 0.516 | 0.488 | 0.504 | 0.507 | 28.09% | 8.57% | 57.67% | 0.00% | 70.68% |
| Hokkaido | 0.434 | 0.402 | 0.398 | 0.473 | 0.506 | 32.65% | 1.79% | 66.45% | 0.00% | 74.55% |
| Wakayama | 0.413 | 0.424 | 0.432 | 0.426 | 0.498 | 19.35% | 23.00% | 62.92% | 0.00% | 72.73% |
| Shizuoka | 0.467 | 0.470 | 0.473 | 0.499 | 0.471 | 33.28% | 14.08% | 62.40% | 0.00% | 69.62% |
| Gifu | 0.409 | 0.466 | 0.502 | 0.469 | 0.463 | 30.59% | 14.42% | 64.82% | 0.00% | 74.26% |
| Fukushima | 0.463 | 0.437 | 0.488 | 0.478 | 0.461 | 22.33% | 27.47% | 60.74% | 0.00% | 73.86% |
| Osaka | 0.438 | 0.430 | 0.484 | 0.489 | 0.457 | 34.33% | 10.90% | 65.70% | 0.00% | 76.24% |
| Saitama | 0.425 | 0.427 | 0.439 | 0.482 | 0.453 | 40.10% | 16.38% | 60.78% | 0.00% | 69.00% |
| Iwate | 0.444 | 0.436 | 0.479 | 0.496 | 0.452 | 26.06% | 27.11% | 59.68% | 0.00% | 76.45% |
| Niigata | 0.411 | 0.417 | 0.438 | 0.475 | 0.440 | 29.18% | 18.77% | 68.72% | 0.00% | 77.46% |
| Aomori | 0.423 | 0.457 | 0.414 | 0.419 | 0.432 | 55.39% | 15.87% | 54.40% | 0.00% | 69.04% |
| Aichi | 0.428 | 0.382 | 0.421 | 0.445 | 0.418 | 32.30% | 21.14% | 69.60% | 0.00% | 82.23% |
| Fukuoka | 0.432 | 0.378 | 0.413 | 0.426 | 0.408 | 39.34% | 17.08% | 70.46% | 0.00% | 83.11% |
| Hyogo | 0.403 | 0.370 | 0.399 | 0.438 | 0.407 | 30.43% | 19.15% | 75.20% | 0.00% | 86.96% |
| Ibaraki | 0.374 | 0.374 | 0.441 | 0.415 | 0.397 | 22.89% | 22.32% | 82.28% | 0.00% | 89.76% |
| Mie | 0.420 | 0.413 | 0.375 | 0.365 | 0.387 | 37.19% | 12.32% | 82.43% | 0.00% | 89.16% |
| Kanagawa | 0.378 | 0.373 | 0.367 | 0.406 | 0.383 | 40.27% | 15.76% | 78.68% | 0.00% | 87.87% |
| Chiba | 0.403 | 0.379 | 0.403 | 0.395 | 0.379 | 20.63% | 22.26% | 89.71% | 0.00% | 94.68% |
| Ehime | 0.360 | 0.370 | 0.403 | 0.367 | 0.370 | 45.00% | 21.31% | 75.98% | 0.00% | 84.12% |
| Yamaguchi | 0.372 | 0.366 | 0.375 | 0.372 | 0.369 | 30.21% | 20.45% | 87.28% | 0.00% | 93.27% |
| Hiroshima | 0.358 | 0.364 | 0.383 | 0.346 | 0.367 | 34.26% | 27.19% | 79.16% | 0.00% | 89.99% |
| Oita | 0.375 | 0.357 | 0.397 | 0.331 | 0.358 | 44.84% | 10.41% | 87.37% | 0.00% | 93.27% |
| Okayama | 0.337 | 0.341 | 0.342 | 0.338 | 0.340 | 37.38% | 23.87% | 88.69% | 0.00% | 94.21% |
| Japan | 0.513 | 0.520 | 0.544 | 0.556 | 0.533 | 28.96% | 10.86% | 54.40% | 0.00% | 64.91% |
| 2013 | 2015 | 2017 | 2019 | 7-Year Average | Redundancy Rate of Labor | Redundancy Rate of Capital Stock | Redundancy Rate of Total Energy Consumption | Deficiency Rate of Regional GDP | Redundancy Rate of CO2 Emissions | |
|---|---|---|---|---|---|---|---|---|---|---|
| Sejong | 1.000 | 0.772 | 0.696 | 0.686 | 0.796 | 27.87% | 6.39% | 15.96% | 0.00% | 10.35% |
| Jeju | 0.517 | 0.450 | 0.381 | 0.427 | 0.442 | 66.41% | 4.32% | 51.33% | 0.00% | 69.94% |
| Seoul | 0.439 | 0.420 | 0.439 | 0.468 | 0.436 | 54.73% | 3.15% | 66.64% | 0.00% | 68.56% |
| Gwangju | 0.412 | 0.434 | 0.423 | 0.438 | 0.426 | 69.99% | 0.00% | 62.25% | 0.00% | 62.33% |
| Daejeon | 0.377 | 0.368 | 0.374 | 0.377 | 0.374 | 67.41% | 8.29% | 70.29% | 0.00% | 74.90% |
| Daegu | 0.325 | 0.309 | 0.331 | 0.343 | 0.327 | 76.41% | 26.70% | 67.46% | 0.00% | 64.14% |
| Ulsan | 0.335 | 0.327 | 0.309 | 0.318 | 0.324 | 31.02% | 31.40% | 93.58% | 0.00% | 96.29% |
| Busan | 0.299 | 0.313 | 0.303 | 0.305 | 0.304 | 70.39% | 27.97% | 74.70% | 0.00% | 78.32% |
| Gyeongsangnam-do | 0.295 | 0.281 | 0.278 | 0.302 | 0.290 | 64.98% | 37.83% | 76.61% | 0.00% | 77.31% |
| Chungcheongbuk-do | 0.272 | 0.281 | 0.268 | 0.281 | 0.277 | 64.08% | 42.76% | 76.47% | 0.00% | 80.82% |
| Gyeonggi-do | 0.278 | 0.263 | 0.262 | 0.278 | 0.270 | 62.77% | 41.27% | 81.56% | 0.00% | 82.23% |
| Jeollabuk-do | 0.245 | 0.245 | 0.282 | 0.287 | 0.263 | 76.28% | 40.96% | 75.05% | 0.00% | 73.02% |
| Gyeongsangbuk-do | 0.245 | 0.244 | 0.247 | 0.259 | 0.251 | 59.17% | 40.25% | 89.85% | 0.00% | 94.55% |
| Gangwon-do | 0.246 | 0.237 | 0.251 | 0.260 | 0.249 | 72.66% | 44.87% | 76.71% | 0.00% | 83.71% |
| Incheon | 0.250 | 0.245 | 0.244 | 0.248 | 0.245 | 70.37% | 37.55% | 85.23% | 0.00% | 90.19% |
| Chungcheongnam-do | 0.241 | 0.226 | 0.228 | 0.255 | 0.237 | 50.21% | 50.57% | 93.84% | 0.00% | 96.96% |
| Jeollanam-do | 0.212 | 0.221 | 0.234 | 0.220 | 0.226 | 59.27% | 44.13% | 95.69% | 0.00% | 97.90% |
| South Korea | 0.352 | 0.332 | 0.326 | 0.338 | 0.337 | 61.41% | 28.73% | 73.72% | 0.00% | 76.56% |
| Machine Learning Models | R2 |
|---|---|
| Linear Regression | 0.791 |
| SVR | 0.803 |
| BPNN | 0.832 |
| Decision Tree | 0.837 |
| Random Forest | 0.848 |
| GBDT | 0.813 |
| XGBoost | 0.869 |
| LightGBM | 0.789 |
| AdaBoost | 0.855 |
| Bagging | 0.847 |
| Average Value | 0.828 |
| 2020 | 2021 | 2022 | 2023 | 2024 | |
|---|---|---|---|---|---|
| Guangdong | 0.901 | 0.721 | 0.791 | 0.896 | 0.927 |
| Jiangsu | 0.901 | 0.835 | 0.783 | 0.921 | 0.978 |
| Beijing | 0.129 | 0.129 | 0.129 | 0.129 | 0.129 |
| Shanghai | 0.122 | 0.128 | 0.129 | 0.129 | 0.129 |
| Fujian | 0.093 | 0.094 | 0.105 | 0.115 | 0.115 |
| Zhejiang | 0.093 | 0.091 | 0.088 | 0.087 | 0.093 |
| Hainan | 0.080 | 0.080 | 0.080 | 0.080 | 0.080 |
| Chongqing | 0.085 | 0.082 | 0.080 | 0.080 | 0.080 |
| Hubei | 0.078 | 0.079 | 0.080 | 0.080 | 0.080 |
| Shaanxi | 0.078 | 0.079 | 0.079 | 0.080 | 0.080 |
| Jiangxi | 0.077 | 0.078 | 0.078 | 0.080 | 0.080 |
| Hunan | 0.077 | 0.077 | 0.077 | 0.078 | 0.080 |
| Anhui | 0.076 | 0.076 | 0.077 | 0.077 | 0.078 |
| Yunnan | 0.072 | 0.072 | 0.071 | 0.072 | 0.075 |
| Sichuan | 0.071 | 0.072 | 0.072 | 0.072 | 0.074 |
| Henan | 0.069 | 0.069 | 0.069 | 0.067 | 0.067 |
| Shandong | 0.069 | 0.069 | 0.071 | 0.070 | 0.073 |
| Guizhou | 0.067 | 0.064 | 0.062 | 0.061 | 0.059 |
| Xinjiang | 0.063 | 0.060 | 0.059 | 0.059 | 0.059 |
| Tianjin | 0.060 | 0.060 | 0.058 | 0.058 | 0.058 |
| Guangxi | 0.060 | 0.059 | 0.058 | 0.058 | 0.058 |
| Qinghai | 0.060 | 0.059 | 0.058 | 0.058 | 0.058 |
| Gansu | 0.059 | 0.058 | 0.058 | 0.058 | 0.058 |
| Shanxi | 0.059 | 0.058 | 0.058 | 0.058 | 0.058 |
| Hebei | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| Inner Mongolia | 0.059 | 0.058 | 0.058 | 0.058 | 0.058 |
| Ningxia | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| Liaoning | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| Jilin | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| Heilongjiang | 0.058 | 0.058 | 0.058 | 0.058 | 0.058 |
| China | 0.128 | 0.120 | 0.121 | 0.129 | 0.132 |
| 2020 | 2021 | 2022 | 2023 | 2024 | |
|---|---|---|---|---|---|
| Tokushima | 0.887 | 0.909 | 0.976 | 0.911 | 0.907 |
| Tottori | 0.948 | 0.902 | 0.923 | 0.934 | 0.926 |
| Tokyo | 0.902 | 0.916 | 0.940 | 0.929 | 0.912 |
| Yamanashi | 0.922 | 0.949 | 0.937 | 0.910 | 0.916 |
| Nara | 0.924 | 0.929 | 0.931 | 0.932 | 0.930 |
| Saga | 0.859 | 0.915 | 0.975 | 0.933 | 0.916 |
| Kochi | 0.741 | 0.746 | 0.784 | 0.852 | 0.970 |
| Shimane | 0.707 | 0.744 | 0.801 | 0.795 | 0.928 |
| Yamagata | 0.688 | 0.710 | 0.728 | 0.742 | 0.796 |
| Nagasaki | 0.683 | 0.674 | 0.654 | 0.665 | 0.694 |
| Fukui | 0.606 | 0.609 | 0.609 | 0.608 | 0.600 |
| Kyoto | 0.612 | 0.606 | 0.606 | 0.600 | 0.606 |
| Nagano | 0.579 | 0.575 | 0.535 | 0.567 | 0.577 |
| Shiga | 0.600 | 0.593 | 0.596 | 0.608 | 0.603 |
| Ishikawa | 0.592 | 0.601 | 0.580 | 0.607 | 0.607 |
| Gunma | 0.602 | 0.598 | 0.601 | 0.610 | 0.598 |
| Tochigi | 0.601 | 0.581 | 0.602 | 0.606 | 0.602 |
| Kagawa | 0.555 | 0.538 | 0.584 | 0.569 | 0.564 |
| Kagoshima | 0.563 | 0.599 | 0.602 | 0.601 | 0.597 |
| Okinawa | 0.556 | 0.539 | 0.576 | 0.572 | 0.568 |
| Toyama | 0.541 | 0.552 | 0.587 | 0.568 | 0.572 |
| Akita | 0.521 | 0.487 | 0.490 | 0.502 | 0.495 |
| Miyagi | 0.460 | 0.478 | 0.471 | 0.464 | 0.467 |
| Miyazaki | 0.550 | 0.522 | 0.501 | 0.525 | 0.514 |
| Kumamoto | 0.499 | 0.484 | 0.474 | 0.481 | 0.472 |
| Hokkaido | 0.496 | 0.542 | 0.566 | 0.520 | 0.532 |
| Wakayama | 0.500 | 0.531 | 0.493 | 0.483 | 0.491 |
| Shizuoka | 0.488 | 0.472 | 0.478 | 0.477 | 0.469 |
| Gifu | 0.474 | 0.477 | 0.473 | 0.466 | 0.472 |
| Fukushima | 0.480 | 0.466 | 0.470 | 0.467 | 0.467 |
| Osaka | 0.477 | 0.473 | 0.476 | 0.474 | 0.470 |
| Saitama | 0.462 | 0.476 | 0.478 | 0.462 | 0.471 |
| Iwate | 0.486 | 0.463 | 0.476 | 0.483 | 0.463 |
| Niigata | 0.462 | 0.474 | 0.480 | 0.459 | 0.471 |
| Aomori | 0.434 | 0.451 | 0.450 | 0.460 | 0.458 |
| Aichi | 0.456 | 0.452 | 0.456 | 0.467 | 0.457 |
| Fukuoka | 0.433 | 0.453 | 0.447 | 0.463 | 0.458 |
| Hyogo | 0.466 | 0.453 | 0.463 | 0.464 | 0.469 |
| Ibaraki | 0.416 | 0.437 | 0.449 | 0.458 | 0.456 |
| Mie | 0.402 | 0.399 | 0.452 | 0.441 | 0.456 |
| Kanagawa | 0.414 | 0.435 | 0.425 | 0.435 | 0.429 |
| Chiba | 0.398 | 0.615 | 0.486 | 0.469 | 0.499 |
| Ehime | 0.372 | 0.389 | 0.360 | 0.375 | 0.364 |
| Yamaguchi | 0.367 | 0.369 | 0.336 | 0.362 | 0.365 |
| Hiroshima | 0.368 | 0.386 | 0.383 | 0.347 | 0.359 |
| Oita | 0.322 | 0.353 | 0.334 | 0.324 | 0.324 |
| Okayama | 0.336 | 0.324 | 0.324 | 0.322 | 0.321 |
| Japan | 0.558 | 0.567 | 0.571 | 0.570 | 0.576 |
| 2020 | 2021 | 2022 | 2023 | 2024 | |
|---|---|---|---|---|---|
| Sejong | 0.728 | 0.745 | 0.843 | 0.907 | 0.963 |
| Jeju | 0.468 | 0.455 | 0.466 | 0.497 | 0.473 |
| Seoul | 0.458 | 0.46 | 0.468 | 0.455 | 0.458 |
| Gwangju | 0.498 | 0.477 | 0.483 | 0.479 | 0.487 |
| Daejeon | 0.368 | 0.371 | 0.372 | 0.373 | 0.370 |
| Daegu | 0.325 | 0.320 | 0.308 | 0.302 | 0.303 |
| Ulsan | 0.305 | 0.303 | 0.297 | 0.287 | 0.301 |
| Busan | 0.298 | 0.295 | 0.296 | 0.296 | 0.296 |
| Gyeongsangnam-do | 0.283 | 0.283 | 0.282 | 0.283 | 0.295 |
| Chungcheongbuk-do | 0.280 | 0.282 | 0.282 | 0.282 | 0.282 |
| Gyeonggi-do | 0.275 | 0.274 | 0.273 | 0.273 | 0.273 |
| Jeollabuk-do | 0.279 | 0.28 | 0.281 | 0.281 | 0.283 |
| Gyeongsangbuk-do | 0.264 | 0.266 | 0.266 | 0.267 | 0.267 |
| Gangwon-do | 0.249 | 0.264 | 0.260 | 0.265 | 0.266 |
| Incheon | 0.252 | 0.242 | 0.243 | 0.243 | 0.243 |
| Chungcheongnam-do | 0.225 | 0.231 | 0.229 | 0.242 | 0.238 |
| Jeollanam-do | 0.222 | 0.224 | 0.227 | 0.214 | 0.210 |
| South Korea | 0.340 | 0.340 | 0.346 | 0.350 | 0.353 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, H.; Zhang, Z.; Luo, M. Evaluation and Prediction of Low-Carbon Economic Efficiency in China, Japan and South Korea: Based on DEA and Machine Learning. Int. J. Environ. Res. Public Health 2022, 19, 12709. https://doi.org/10.3390/ijerph191912709
Niu H, Zhang Z, Luo M. Evaluation and Prediction of Low-Carbon Economic Efficiency in China, Japan and South Korea: Based on DEA and Machine Learning. International Journal of Environmental Research and Public Health. 2022; 19(19):12709. https://doi.org/10.3390/ijerph191912709
Chicago/Turabian StyleNiu, Huayong, Zhishuo Zhang, and Manting Luo. 2022. "Evaluation and Prediction of Low-Carbon Economic Efficiency in China, Japan and South Korea: Based on DEA and Machine Learning" International Journal of Environmental Research and Public Health 19, no. 19: 12709. https://doi.org/10.3390/ijerph191912709
APA StyleNiu, H., Zhang, Z., & Luo, M. (2022). Evaluation and Prediction of Low-Carbon Economic Efficiency in China, Japan and South Korea: Based on DEA and Machine Learning. International Journal of Environmental Research and Public Health, 19(19), 12709. https://doi.org/10.3390/ijerph191912709






