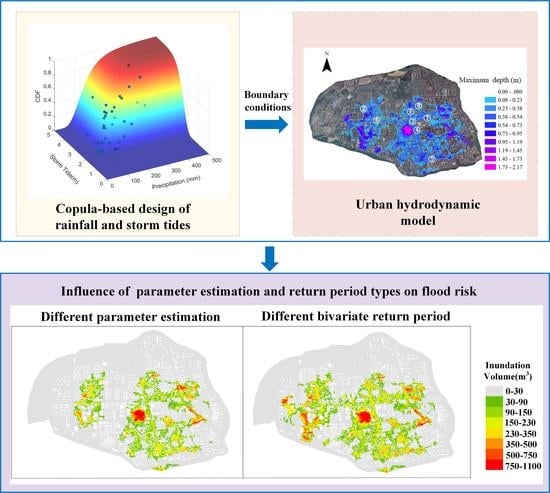
Investigating Flood Risks of Rainfall and Storm Tides Affected by the Parameter Estimation Coupling Bivariate Statistics and Hydrodynamic Models in the Coastal City
Abstract
:1. Introduction
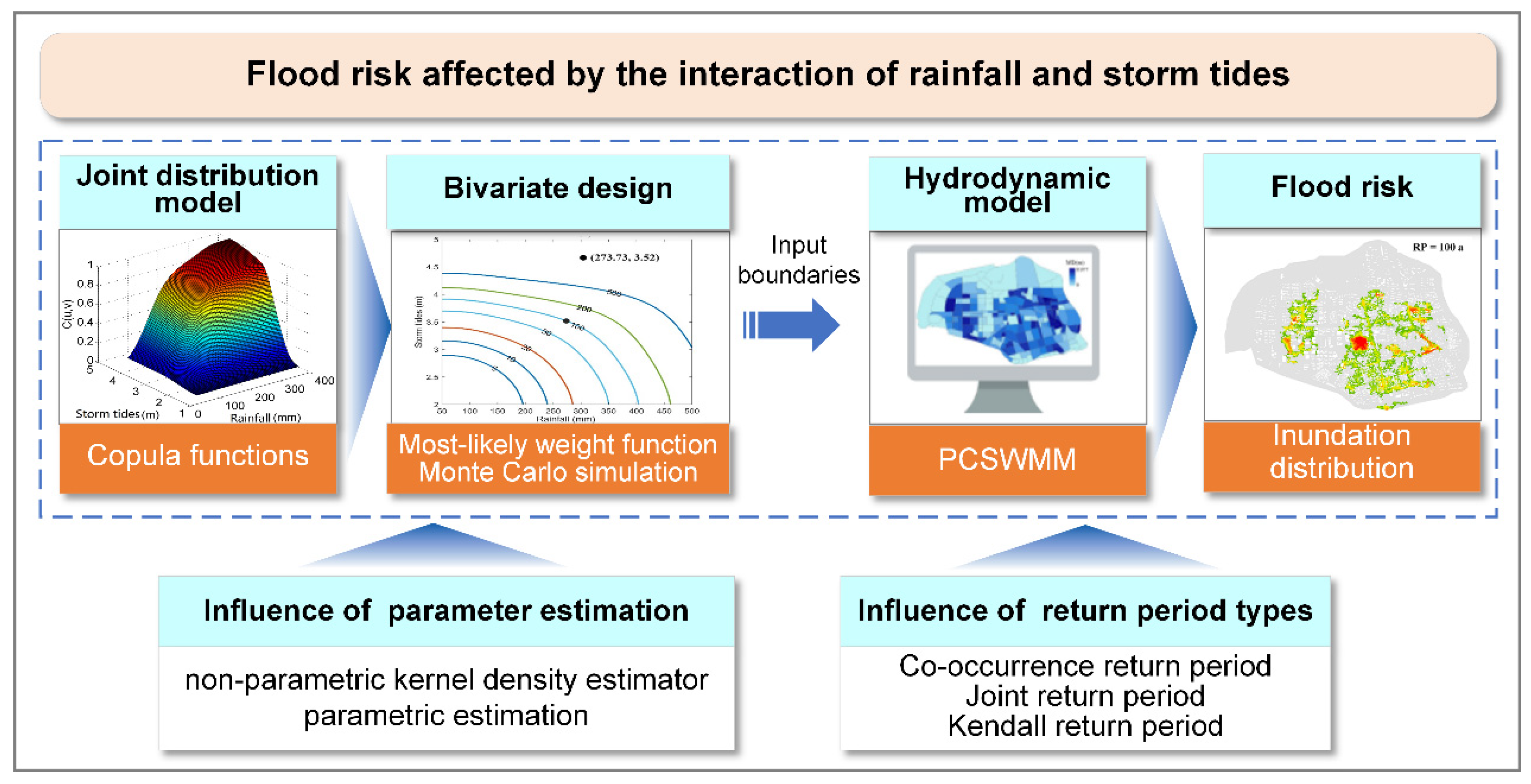
2. Methods
2.1. Copula Model of Rainfall and Storm Tides
2.2. Parameter Estimation Methods
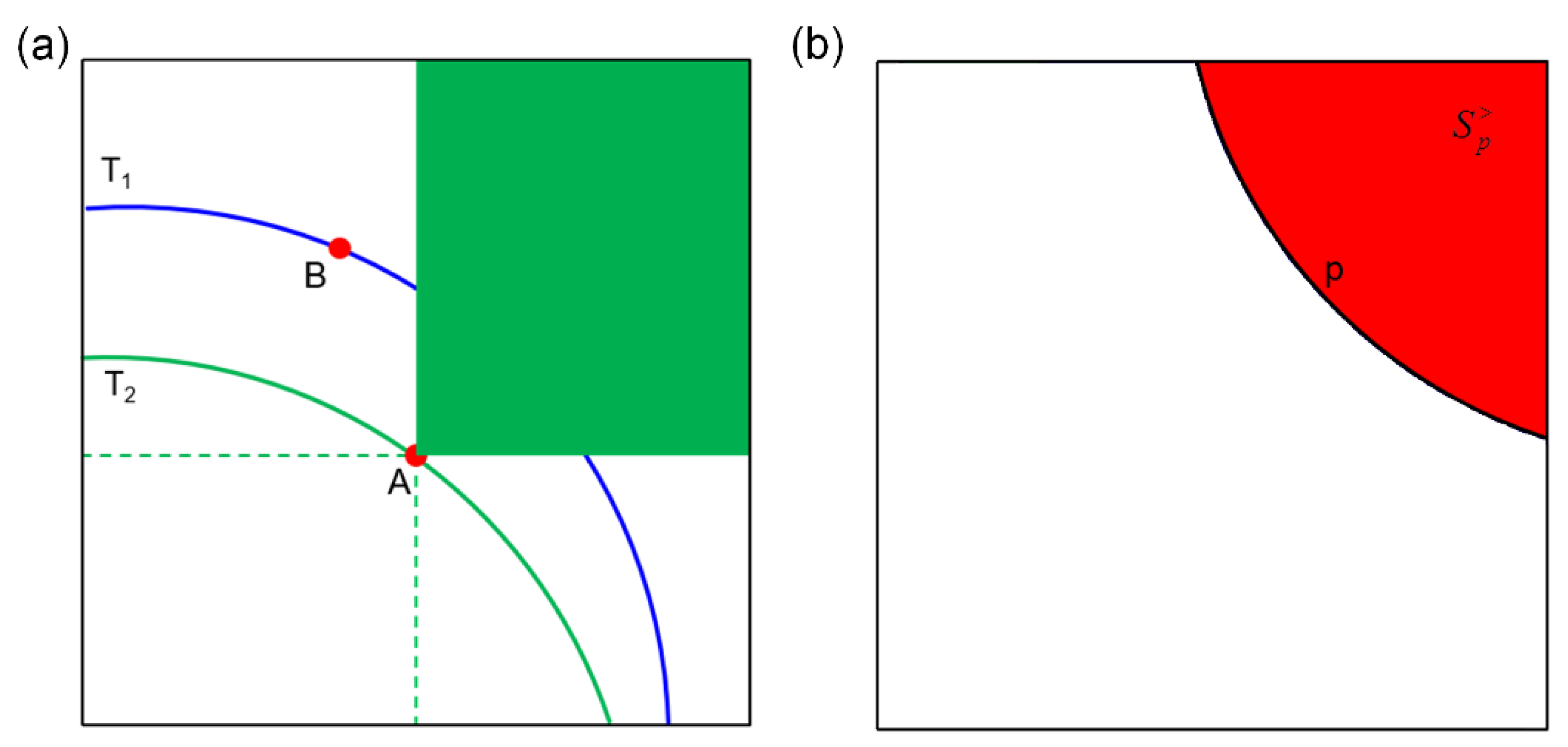
2.3. Bivariate Return Period
2.3.1. Joint Return Period
2.3.2. Co-Occurrence Return Period
2.3.3. Kendall Return Period
2.4. Most-Likely Weight Function Method
- (1)
- When the marginal and joint distributions of rainfall–storm tides are determined, the Monte Carlo simulation method is adopted to simulate n1 sets of rainfall–storm tide combinations, and n1 is greater than 10,000 to ensure that the number of samples is large enough;
- (2)
- Use Equations (7)–(9) to calculate the return period of each combination. For a given return period T, select all combinations with the return period of T;
- (3)
- Calculate a combination that makes reach the maximum by Equation (13);
- (4)
- Finally, calculate the combined design of rainfall and storm tides (hm, zm) based on the inverse function of the marginal distribution (Equations (14) and (15)).
2.5. Urban Hydrodynamic Model
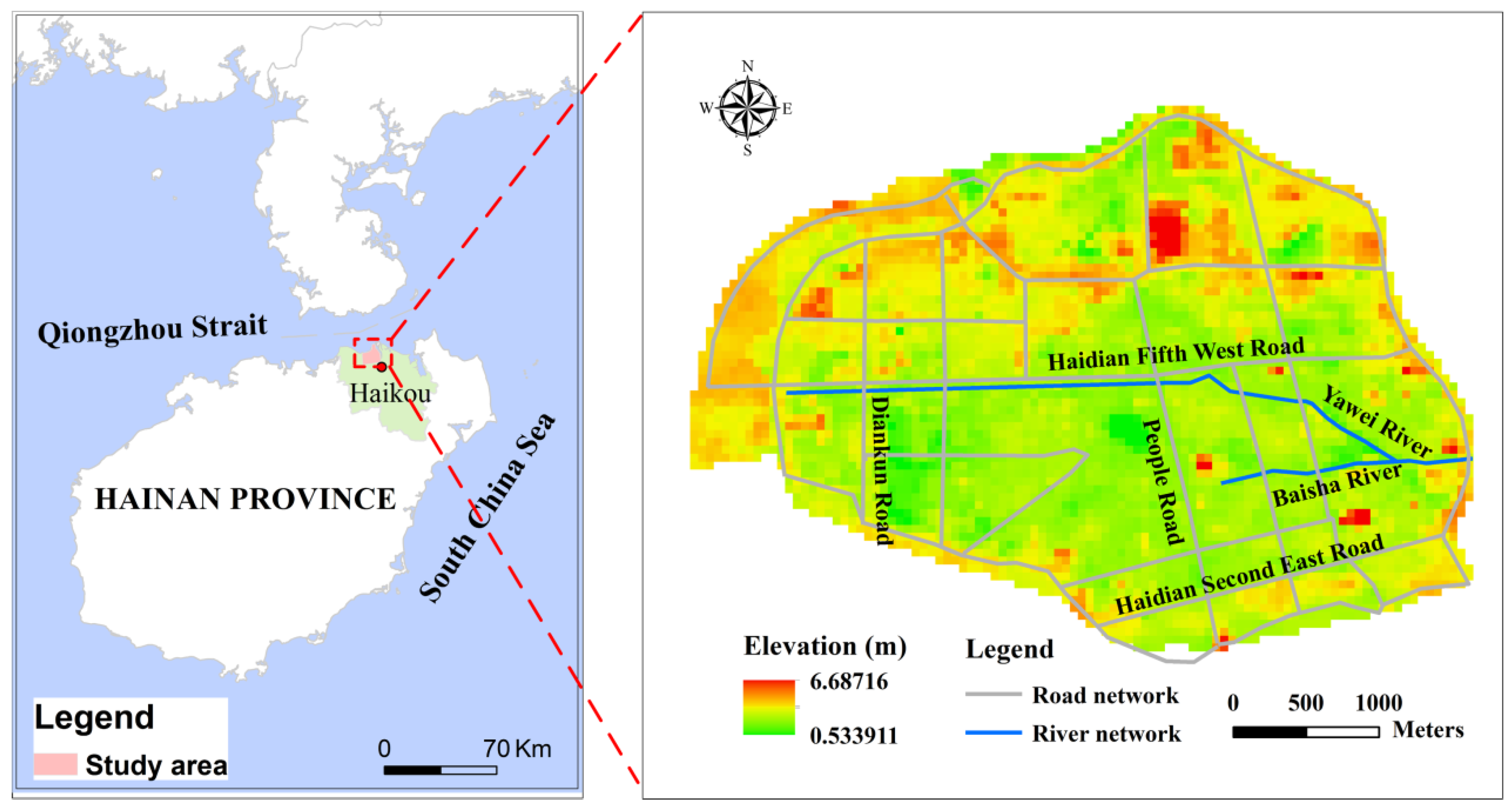
3. Study Area and Data
4. Results and Discussion
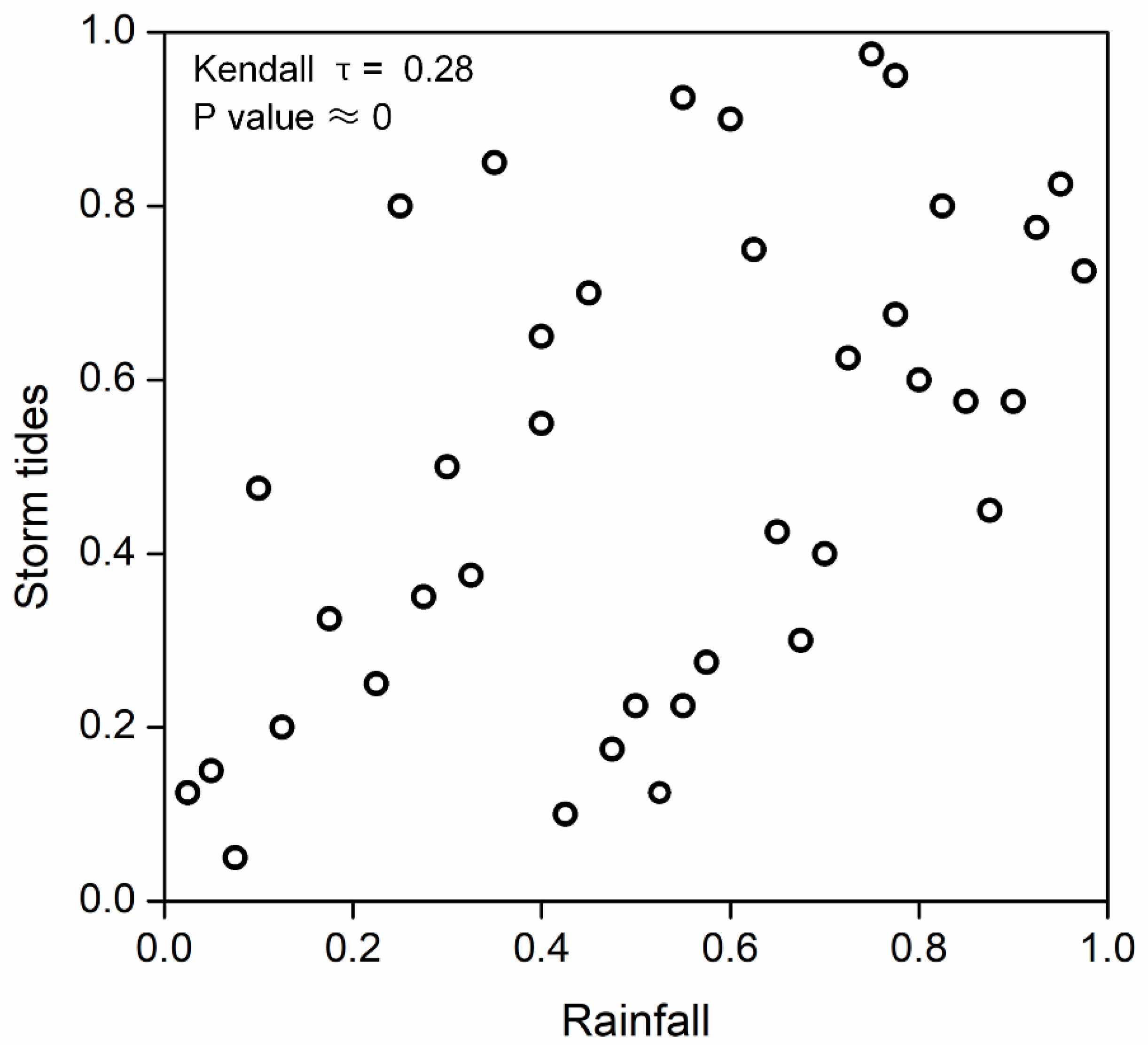
4.1. Bivariate Joint Distribution Model of Rainfall and Storm Tides
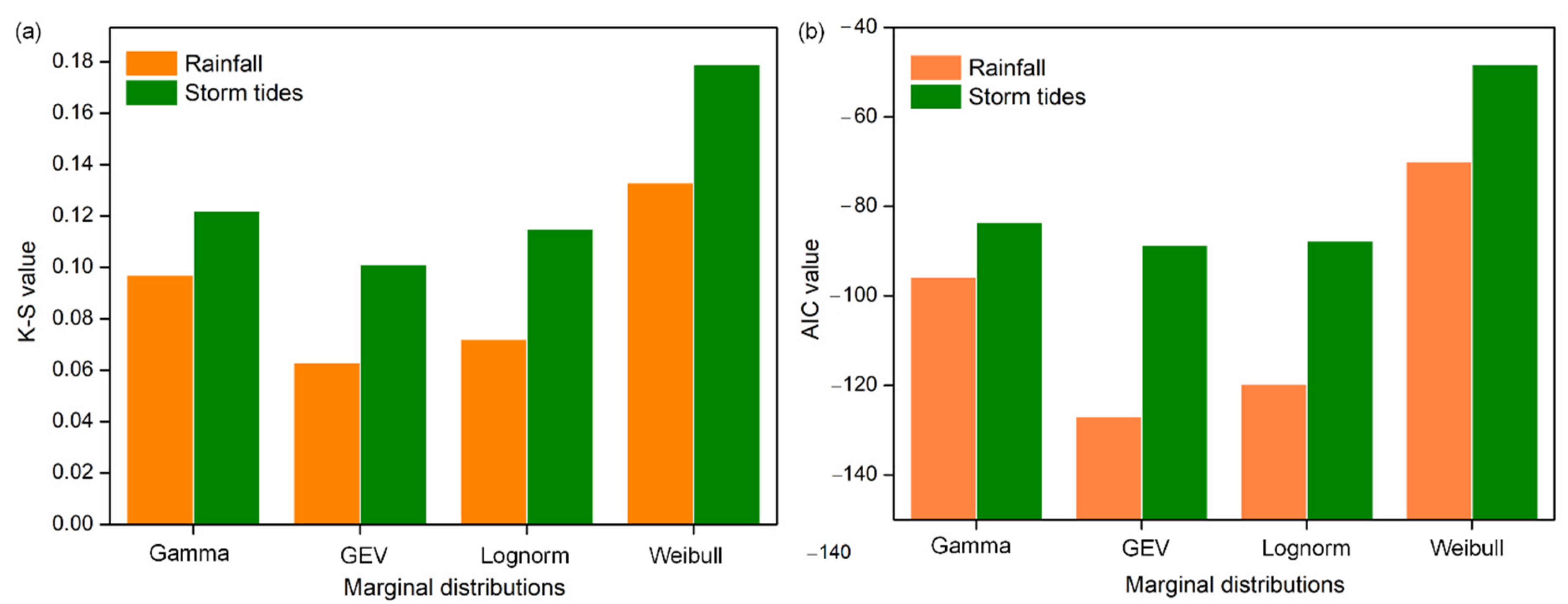
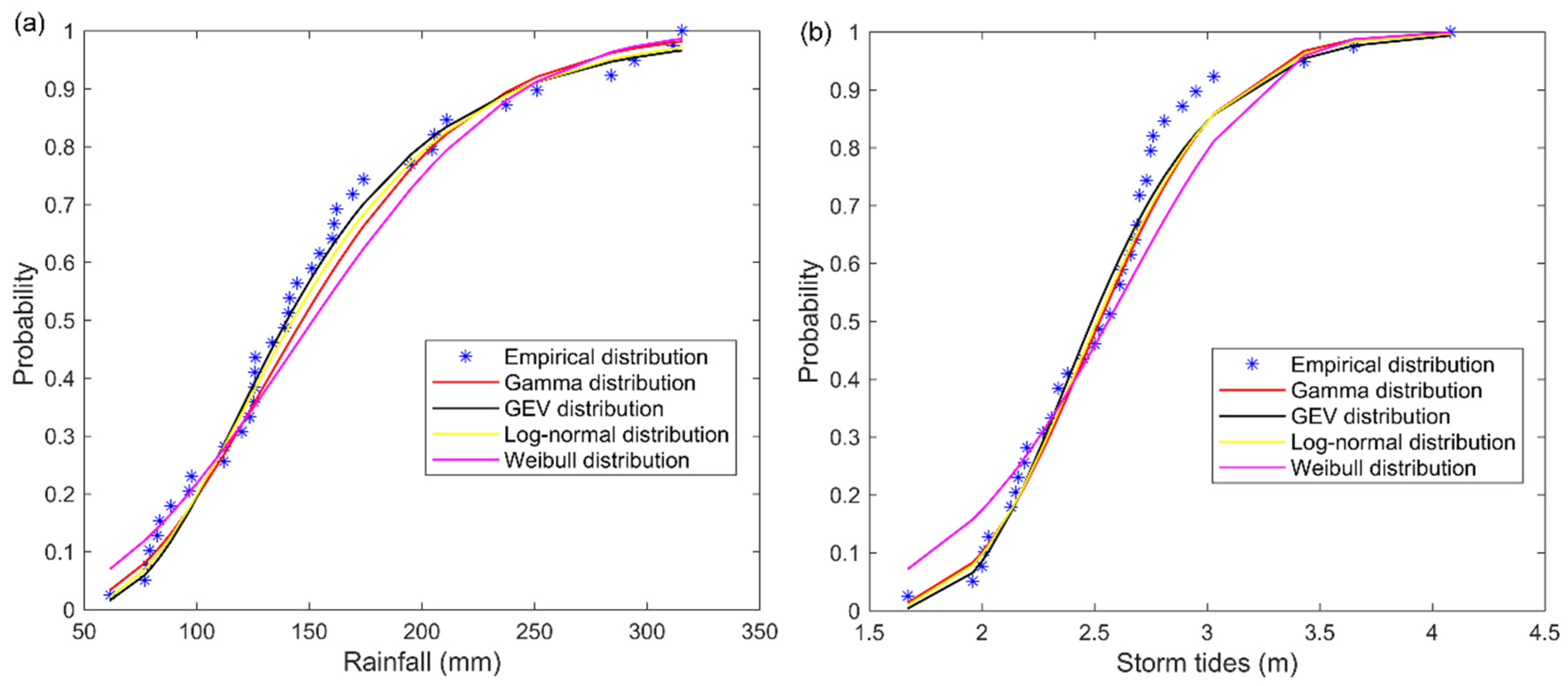
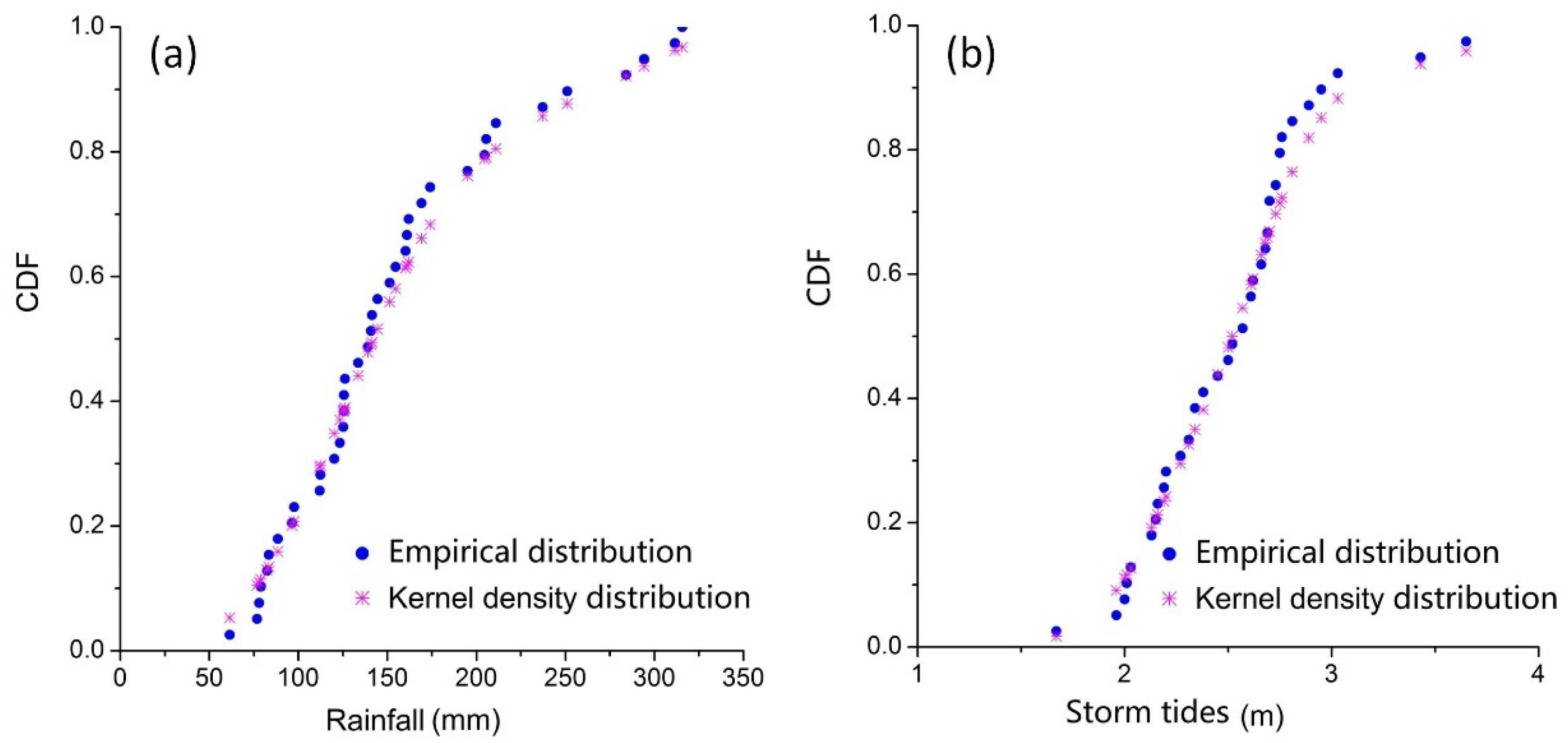
4.1.1. Marginal Distribution Model
4.1.2. Bivariate Joint Distribution Model
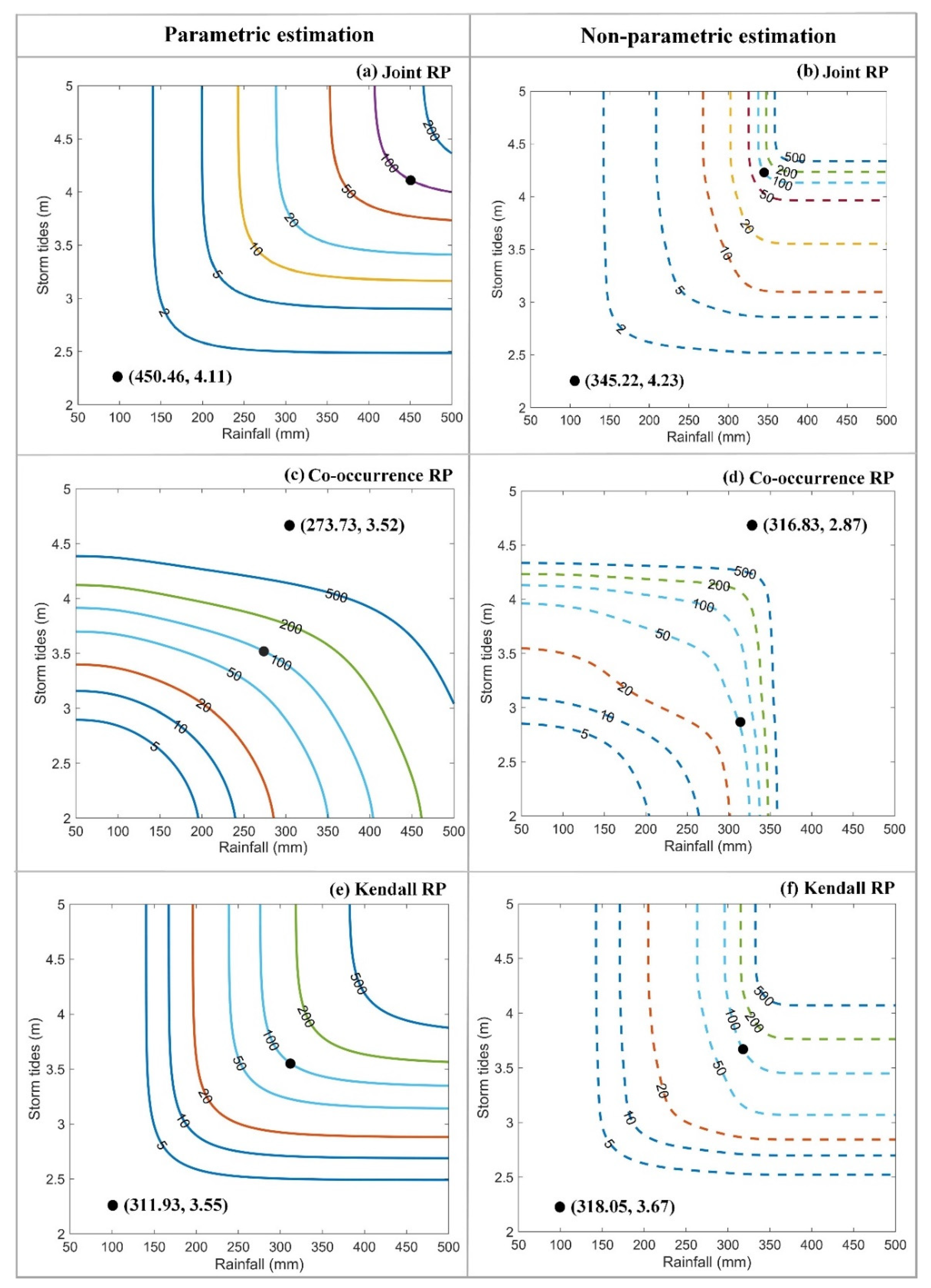
4.2. Influence of Parameter Estimation and RP Types on Bivariate Designs of Rainfall and Storm Tides
4.2.1. The Influence of Parameter Estimation Methods
4.2.2. The Influence of RP Types
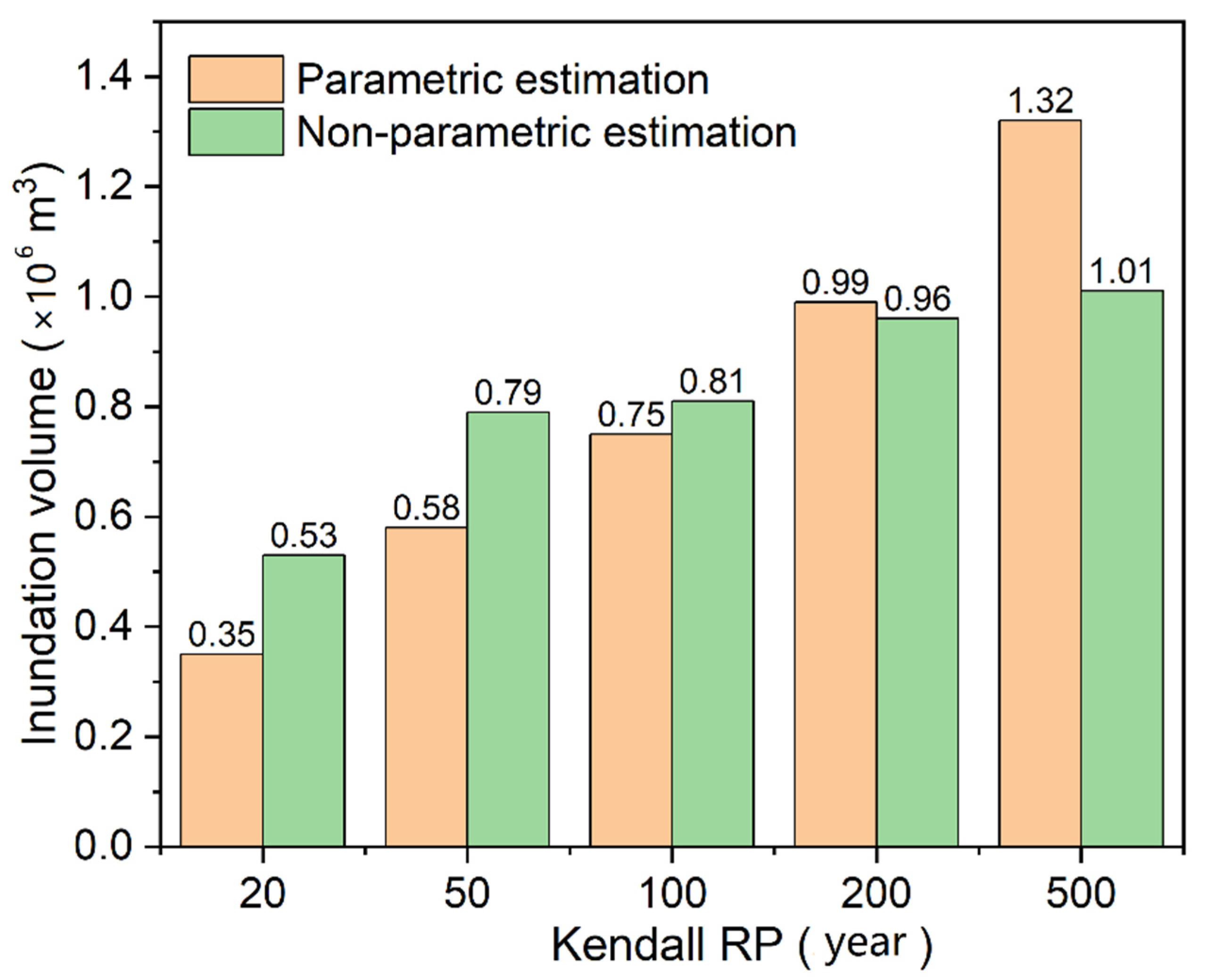
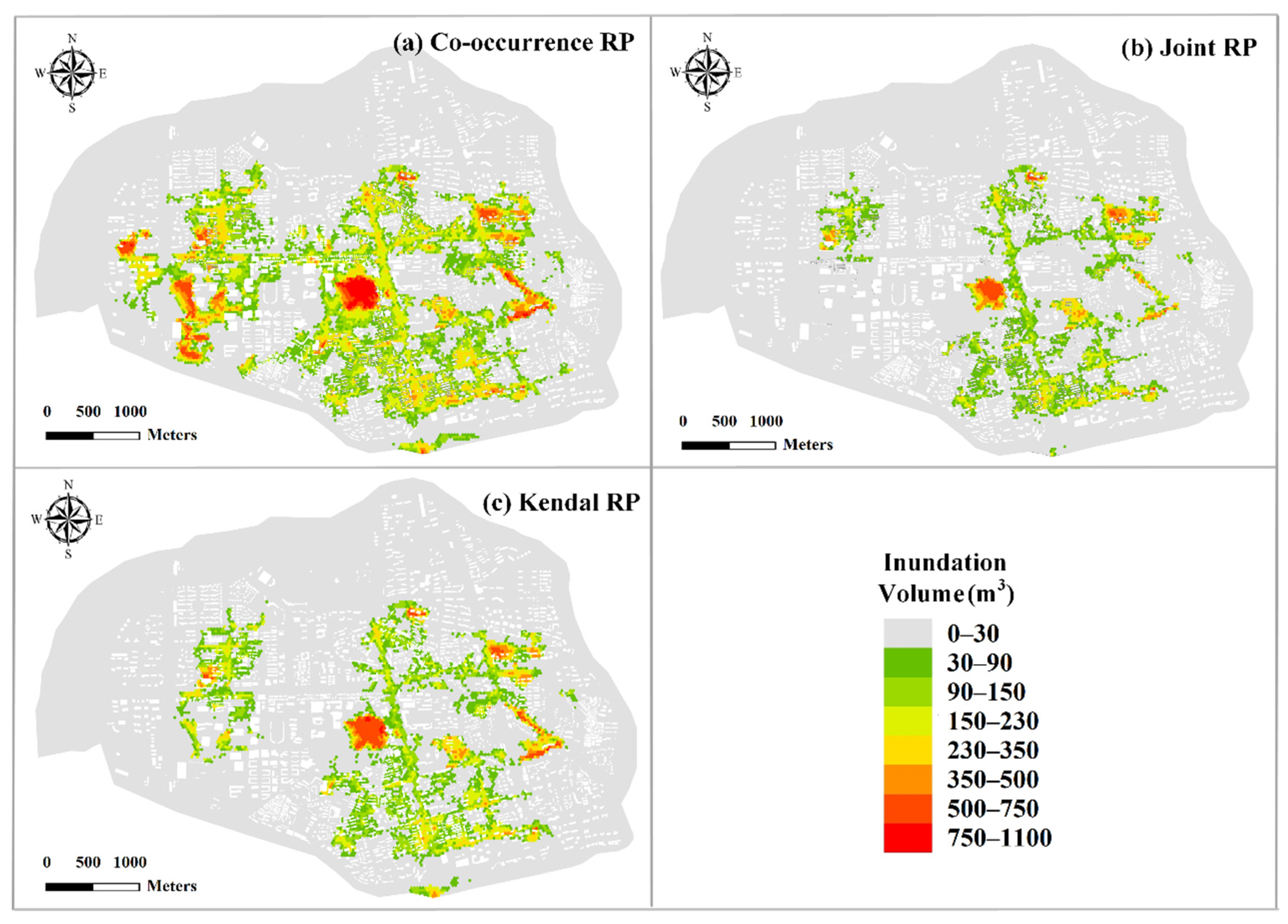
4.3. Compound Flood Risks with Different Designs of Rainfall and Storm Tides
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Didovets, I.; Krysanova, V.; Bürger, G.; Snizhko, S.; Balabukh, V.; Bronstert, A. Climate change impact on regional floods in the Carpathian region. J. Hydrol. Reg. Stud. 2019, 22, 100590. [Google Scholar] [CrossRef]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite imaging reveals increased proportion of population exposed to floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Archetti, R.; Bolognesi, A.; Casadio, A.; Maglionico, M. Development of flood probability charts for urban drainage network in coastal areas through a simplified joint assessment approach. Hydrol. Earth Syst. Sci. 2011, 15, 3115–3122. [Google Scholar] [CrossRef] [Green Version]
- Lian, J.; Xu, H.; Xu, K.; Ma, C. Optimal management of the flooding risk caused by the joint occurrence of extreme rainfall and high tide level in a coastal city. Nat. Hazards 2017, 89, 183–200. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, X.; Guan, X.; Wang, T.; Ma, C.; Yan, D. Amplification of Flood Risks by the Compound Effects of Precipitation and Storm Tides Under the Nonstationary Scenario in the Coastal City of Haikou, China. Int. J. Disaster Risk Sci. 2022, 13, 602–620. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (2021) The Sixth Assessment Report, Climate Change 2021: The Physical Science Basis. Available online: https://www.ipcc.ch/report/ar6/wg1/ (accessed on 10 July 2022).
- Jongman, B.; Ward, P.; Aerts, J. Global exposure to river and coastal flooding: Long term trends and changes. Glob Environ. Chang. 2013, 22, 823–835. [Google Scholar] [CrossRef]
- Almar, R.; Ranasinghe, R.; Bergsma, E.W.J.; Diaz, H.; Melet, A.; Papa, F.; Vousdoukas, M.; Athanasiou, P.; Dada, O.; Almeida, L.P.; et al. A global analysis of extreme coastal water levels with implications for potential coastal overtopping. Nat. Commun. 2021, 12, 3775. [Google Scholar] [CrossRef]
- Ward, P.J.; Couasnon, A.; Eilander, D.; Haigh, I.D.; Hendry, A.; Muis, S.; Veldkamp, T.I.E.; Winsemius, H.C.; Wahl, T. Dependence between high sea-level and high river discharge increases flood hazard in global deltas and estuaries. Environ. Res. Lett. 2018, 13, 084012. [Google Scholar] [CrossRef]
- Zheng, F.; Westra, S.; Sisson, S.A. Quantifying the dependence between extreme rainfall and storm surge in the coastal zone. J. Hydrol. 2013, 505, 172–187. [Google Scholar] [CrossRef]
- Wahl, T.; Jain, S.; Bender, J.; Meyers, S.; Luther, M.E. Increasing risk of compound flooding from storm surge and rainfall for major US cities. Nat. Clim. Chang. 2015, 5, 1093–1097. [Google Scholar] [CrossRef]
- Lian, J.; Xu, K.; Ma, C. Joint impact of rainfall and tidal level on flood risk in a coastal city with a complex river network: A case study of Fuzhou City, China. Hydrol. Earth Syst. Sci. 2013, 17, 679–689. [Google Scholar] [CrossRef] [Green Version]
- Zellou, B.; Rahali, H. Assessment of the joint impact of extreme rainfall and storm surge on the risk of flooding in a coastal area. J. Hydrol. 2019, 569, 647–665. [Google Scholar] [CrossRef]
- Bevacqua, E.; Maraun, D.; Vousdoukas, M.I.; Voukouvalas, E.; Vrac, M.; Mentaschi, L.; Widmann, M. Higher probability of compound flooding from precipitation and storm surge in Europe under anthropogenic climate change. Sci. Adv. 2019, 5, eaaw5531. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, H.; Xu, K.; Lian, J.; Ma, C. Compound effects of rainfall and storm tides on coastal flooding risk. Stoch. Env. Res. Risk A 2019, 33, 1249–1261. [Google Scholar] [CrossRef]
- Jane, R.; Cadavid, L.; Obeysekera, J.; Wahl, T. Multivariate statistical modelling of the drivers of compound flood events in south Florida. Nat. Hazards Earth Syst. Sci. 2020, 20, 2681–2699. [Google Scholar] [CrossRef]
- Wu, W.; McInnes, K.; O’Grady, J.; Hoeke, R.; Leonard, M.; Westra, S. Mapping Dependence Between Extreme Rainfall and Storm Surge. J. Geophys. Res. Oceans 2018, 123, 2461–2474. [Google Scholar] [CrossRef]
- Vittal, H.; Singh, J.; Kumar, P.; Karmakar, S. A framework for multivariate data-based at-site flood frequency analysis: Essentiality of the conjugal application of parametric and nonparametric approaches. J. Hydrol. 2015, 525, 658–675. [Google Scholar] [CrossRef]
- Xu, H.; Xu, K.; Bin, L.L.; Lian, J. Joint risk of rainfall and storm surges during typhoons in a coastal city of Haidian Island, China. Int. J. Environ. Res. Pub. Health 2018, 15, 1377. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santos, V.M.; Wahl, T.; Jane, R.; Misra, S.K.; White, K.D. Assessing compound flooding potential with multivariate statistical models in a complex estuarine system under data constraints. J. Flood Risk Manag. 2021, 14, 12749. [Google Scholar] [CrossRef]
- Francisco-Fernandez, M.; Quintela-Del-Rio, A. Nonparametric analysis of high wind speed data. Clim. Dynam. 2011, 40, 429–441. [Google Scholar] [CrossRef]
- Rauf, U.; Zeephongsekul, P. Analysis of rainfall severity and duration in Victoria, Australia using non-parametric copulas and marginal distributions. Water Resour. Manag. 2014, 28, 4835–4856. [Google Scholar] [CrossRef]
- Lai, Y.; Li, J.; Gu, X.; Liu, C.; Chen, Y.D. Global compound floods from precipitation and storm surge: Hazards and the roles of cyclones. J. Clim. 2021, 34, 8319–8339. [Google Scholar] [CrossRef]
- Salvadori, G.; Durante, F.; De Michele, C.; Bernardi, M.; Petrella, L. A multivariate copula-based framework for dealing with hazard scenarios and failure probabilities. Water Resour. Res. 2016, 52, 3701–3721. [Google Scholar] [CrossRef] [Green Version]
- Moftakhari, H.R.; Salvadori, G.; AghaKouchak, A.; Sanders, B.F.; Matthew, R.A. Compounding effects of sea level rise and fluvial flooding. Proc. Natl. Acad. Sci. USA 2017, 114, 9785–9790. [Google Scholar] [CrossRef] [Green Version]
- Salvadori, G.; Michele, C.; Durante, F. On the return period and design in a multivariate framework. Hydrol. Earth Syst. Sci. 2011, 15, 3293–3305. [Google Scholar] [CrossRef] [Green Version]
- Sklar, A. Fonctions de Re´Partition a´n Dimensions et Leurs Marges; Publications de l’Institut de Statistique de l’Universite´ de Paris: Paris, France, 1959; pp. 229–231. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Zhang, L.; Singh, V.P. Bivariate Flood Frequency Analysis Using the Copula Method. J. Hydrol. Eng. 2006, 11, 150–164. [Google Scholar] [CrossRef]
- Balbhadra, T.; Ajay, K.; Sajjad, A.; Lamb, K.W.; Lakshmi, V. Bringing statistical learning machines together for hydro-climatological predictions—Case study for Sacramento San Joaquin River Basin, California. J. Hydrol. Reg. Stud. 2020, 27, 100651. [Google Scholar] [CrossRef]
- Kim, K.D.; Heo, J.H. Comparative study of flood quantiles estimation by nonparametric models. J. Hydrol. 2002, 260, 176–193. [Google Scholar] [CrossRef]
- Merz, B.; Nguyen, V.D.; Vorogushyn, S. Temporal clustering of floods in Germany: Do flood-rich and flood-poor periods exist? J. Hydrol. 2016, 541, 824–838. [Google Scholar] [CrossRef]
- Mohanty, M.P.; Sherly, M.A.; Karmakar, S.; Ghosh, S. Regionalized Design Rainfall Estimation: An Appraisal of Inundation Mapping for Flood Management Under Data-Scarce Situations. Water Resour. Manag. 2018, 32, 4725–4746. [Google Scholar] [CrossRef]
- Adamowski, K. Nonparametric Estimation of Low-Flow Frequencies. J. Hydraul. Eng. 1996, 122, 46–49. [Google Scholar] [CrossRef]
- Huang, Q.; Chen, Z. Multivariate flood risk assessment based on the secondary return period. J. Lake Sci. 2015, 27, 352–360. (In Chinese) [Google Scholar]
- Genest, C.; Quessy, J.; Re´millard, B. Goodness-of-fit procedures for Copula models based on the probability integral trans-formation. Scand. J. Stat. 2006, 33, 337–366. [Google Scholar] [CrossRef]
- Tu, X.; Du, Y.; Singh, V.P.; Chen, X. Joint distribution of design precipitation and tide and impact of sampling in a coastal area. Int. J. Clim. 2017, 38, e290–e302. [Google Scholar] [CrossRef]
- Tu, X.; Wu, H.; Singh, V.P.; Chen, X.; Lin, K.; Xie, Y. Multivariate design of socioeconomic drought and impact of water reservoirs. J. Hydrol. 2018, 566, 192–204. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Wang, Y.; Qiu, J.; Singh, V.P.; Ju, X.; Zhang, A.; Wu, J.; Zhang, C. Time-varying copula and average annual reliability-based nonstationary hazard assessment of extreme rainfall events. J. Hydrol. 2021, 603, 126792. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Fang, H. Study on Urban Rainstorms Design Based on Multivariate Secondary Return Period. Water Resour. Manag. 2022, 36, 2293–2307. [Google Scholar] [CrossRef]
- Hu, Y.; Liang, Z.; Huang, Y.; Yao, Y.; Wang, J.; Li, B. A nonstationary bivariate design flood estimation approach coupled with the most likely and expectation combination strategies. J. Hydrol. 2022, 605, 127325. [Google Scholar] [CrossRef]
- Feng, Y.; Shi, P.; Qu, S.; Mou, S.; Chen, C.; Dong, F. Nonstationary flood coincidence risk analysis using time-varying copula functions. Sci. Rep. 2020, 10, 3395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ju, X.; Wang, Y.; Wang, D.; Singh, V.P.; Xu, P.; Wu, J.; Ma, T.; Liu, J.; Zhang, J. A time-varying drought identification and frequency analyzation method: A case study of Jinsha River Basin. J. Hydrol. 2021, 603, 126864. [Google Scholar] [CrossRef]
- Xu, H.; Ma, C.; Lian, J.; Xu, K.; Chaima, E. Urban flooding risk assessment based on an integrated k-means cluster algorithm and improved entropy weight method in the region of Haikou, China. J. Hydrol. 2018, 563, 975–986. [Google Scholar] [CrossRef]
- Xu, H.; Ma, C.; Xu, K.; Lian, J.; Long, Y. Staged optimization of urban drainage systems considering climate change and hydrological model uncertainty. J. Hydrol. 2020, 587, 124959. [Google Scholar] [CrossRef]
- Qi, W.; Ma, C.; Xu, H.; Chen, Z.; Zhao, K.; Han, H. Low Impact Development Measures Spatial Arrangement for Urban Flood Mitigation: An Exploratory Optimal Framework based on Source Tracking. Water Resour. Manag. 2021, 35, 3755–3770. [Google Scholar] [CrossRef]
- Mattos, T.; Oliveira, P.; Bruno, L.; de Oliveira, N.D.; Vasconcelos, J.G. Improving Urban Flood Resilience under Climate Change Scenarios in a Tropical Watershed Using Low-Impact Development Practices. J. Hydrol. Eng. 2021, 26, 05021031. [Google Scholar] [CrossRef]
- Rosenberger, L.; Leandro, J.; Pauleit, S.; Erlwein, S. Sustainable stormwater management under the impact of climate change and urban densification. J. Hydrol. 2021, 596, 126137. [Google Scholar] [CrossRef]
- Rossman, L.A. Storm Water Management Model User’s Manual, Version 5.1; EPA: Washington, DC, USA, 2015. [Google Scholar]
- Gräler, B.; Berg, M.J.V.D.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N.E.C. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef] [Green Version]
- Zheng, F.; Seth, W.; Michael, L.; Sisson, S.A. Modeling dependence between extreme rainfall and storm surge to estimate coastal flooding risk. Water Resour. Res. 2014, 50, 2050–2071. [Google Scholar] [CrossRef]
- Seaman, D.E.; Millspaugh, J.J.; Kernohan, B.J.; Brundige, G.C.; Raedeke, K.J.; Gitzen, R. Effects of Sample Size on Kernel Home Range Estimates. J. Wildl. Manag. 1999, 63, 739. [Google Scholar] [CrossRef]
- Bender, J.; Wahl, T.; Müller, A.; Jensen, J. A multivariate design framework for river confluences. Hydrol. Sci. J. 2016, 61, 471–482. [Google Scholar] [CrossRef]
- Ghanbari, M.; Arabi, M.; Kao, S.; Obeysekera, J.; Sweet, W. Climate change and changes in compound coastal-riverine flooding hazard along the U.S. coasts. Earth’s Future 2021, 9, e2021EF002055. [Google Scholar]
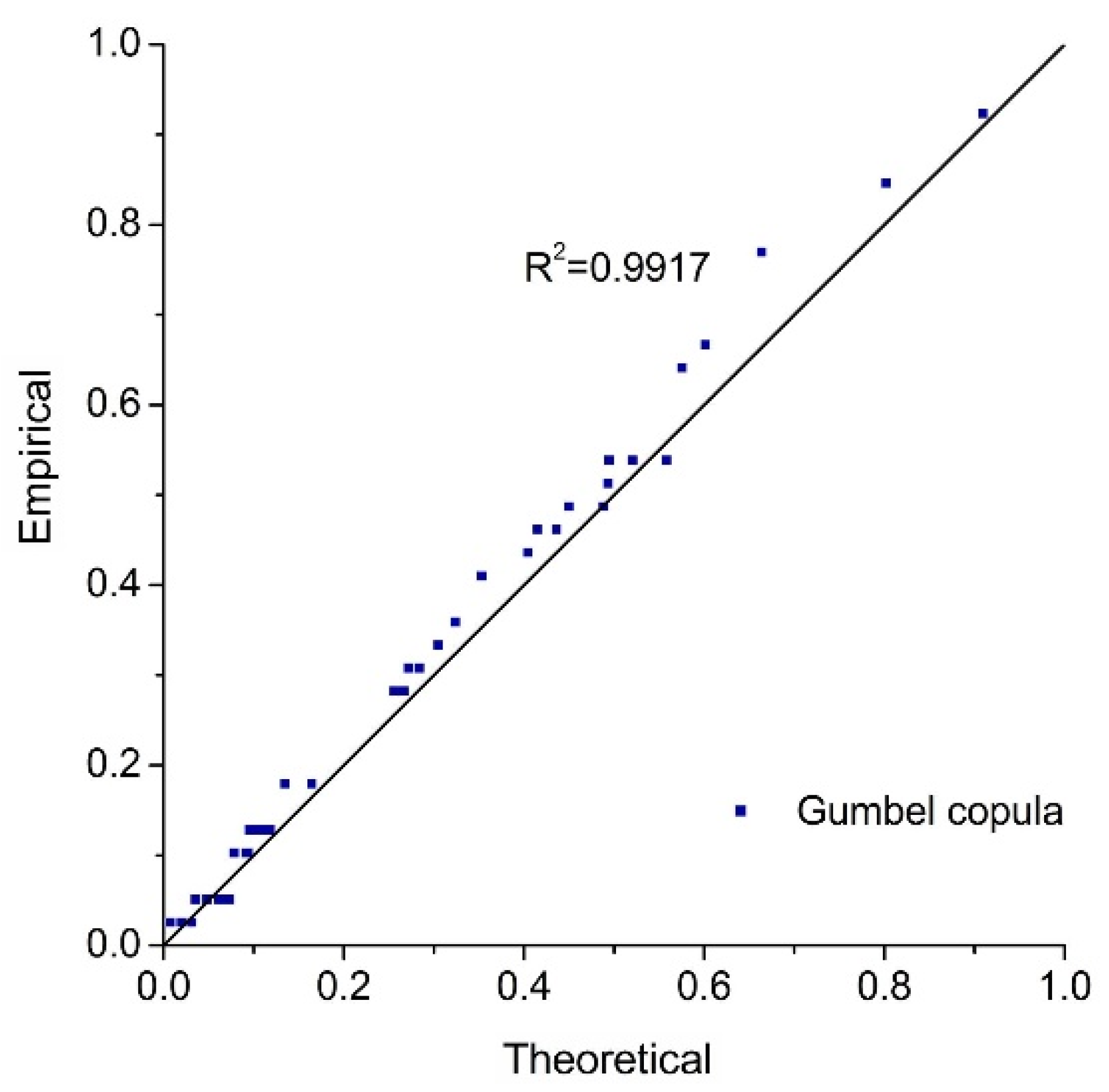
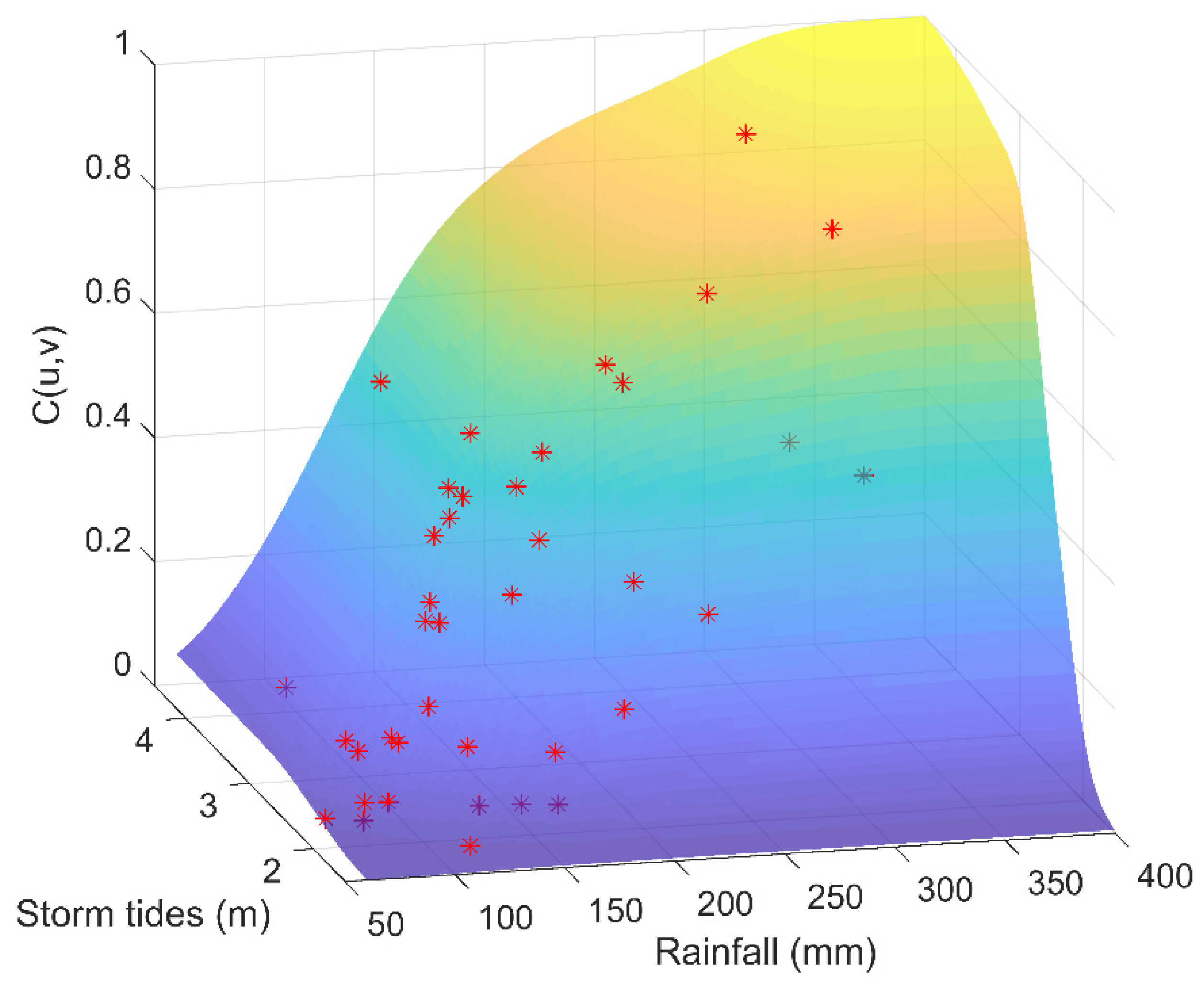

| Copulas | C(u,v) | |
|---|---|---|
| Gumbel Copula | ||
| Clayton Copula | ||
| Frank Copula |
| Functions | F(x) | Parameters |
|---|---|---|
| Lognorm | μ, σ | |
| Gamma | α, β | |
| Weibull | m, a, b | |
| Generalized Extreme Value (GEV) | μ, α, k |
| Distribution | Rainfall | Storm Tides | ||||
|---|---|---|---|---|---|---|
| Shape Parameter k | Scale Parameter σ | Location Parameter μ | Shape Parameter k | Scale Parameter σ | Location Parameter μ | |
| GEV | 0.115 | 46.784 | 122.513 | −0.048 | 0.380 | 2.349 |
| Copula Function | K–S | AIC | OLS |
|---|---|---|---|
| Clayton Copula | 0.123 | −100.108 | 0.043 |
| Frank Copula | 0.113 | −110.317 | 0.038 |
| Gumbel Copula | 0.106 | −110.773 | 0.037 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Xu, K.; Wang, T.; Xue, W. Investigating Flood Risks of Rainfall and Storm Tides Affected by the Parameter Estimation Coupling Bivariate Statistics and Hydrodynamic Models in the Coastal City. Int. J. Environ. Res. Public Health 2022, 19, 12592. https://doi.org/10.3390/ijerph191912592
Xu H, Xu K, Wang T, Xue W. Investigating Flood Risks of Rainfall and Storm Tides Affected by the Parameter Estimation Coupling Bivariate Statistics and Hydrodynamic Models in the Coastal City. International Journal of Environmental Research and Public Health. 2022; 19(19):12592. https://doi.org/10.3390/ijerph191912592
Chicago/Turabian StyleXu, Hongshi, Kui Xu, Tianye Wang, and Wanjie Xue. 2022. "Investigating Flood Risks of Rainfall and Storm Tides Affected by the Parameter Estimation Coupling Bivariate Statistics and Hydrodynamic Models in the Coastal City" International Journal of Environmental Research and Public Health 19, no. 19: 12592. https://doi.org/10.3390/ijerph191912592
APA StyleXu, H., Xu, K., Wang, T., & Xue, W. (2022). Investigating Flood Risks of Rainfall and Storm Tides Affected by the Parameter Estimation Coupling Bivariate Statistics and Hydrodynamic Models in the Coastal City. International Journal of Environmental Research and Public Health, 19(19), 12592. https://doi.org/10.3390/ijerph191912592