Early Prediction of Diabetes Using an Ensemble of Machine Learning Models
Abstract
:1. Introduction
- Introducing a new Diabetes Diseases Classification (DDC) dataset from the northeastern part of South Asia (Bangladesh).
- Recommending a DDC pipeline by proposing a weighted ensemble classifier using various ML frameworks for classifying this DDC dataset.
- Fine-tuning the hyperparameters of various ML-based models using the grid search optimization approach.
- Incorporating extensive preprocessing in the DDC pipeline, which comprises outlier rejection, missing value imputation, and feature selection techniques.
- Conducting extensive research for comprehensive ablation studies using various combinations of ML models to achieve the best ensemble classifier model, incorporating the best preprocessing from previous experiments.
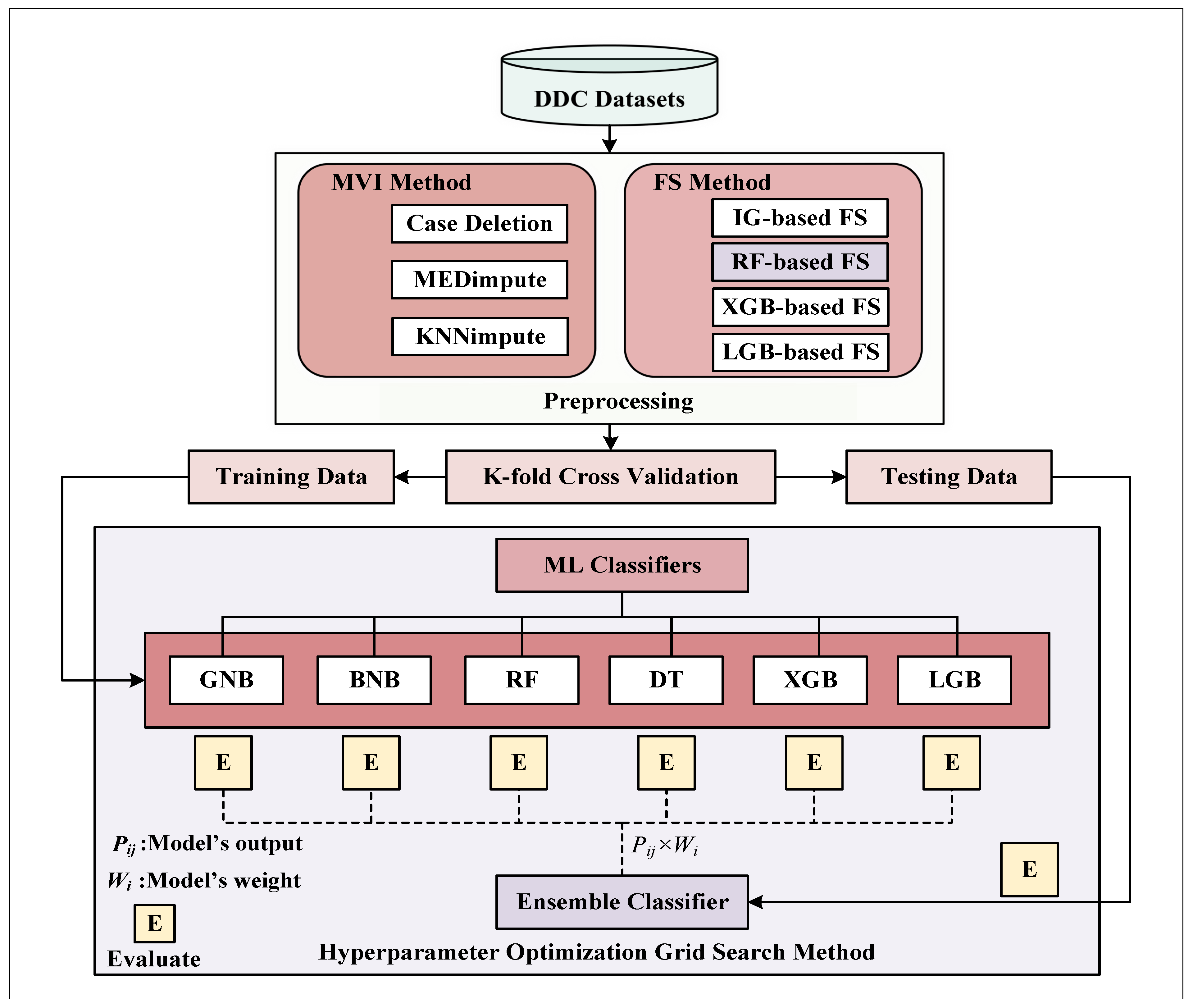
2. Materials and Methods
2.1. Proposed Datasets
2.1.1. Data Source
2.1.2. Study Variables
2.2. Proposed Methodologies
2.2.1. Missing Value Imputation (MVI)
| Algorithm 1: The procedure for applying the MVI method |
|
Input: An uncurated column vector with n-samples (), where Result: A curated column vector with n-samples (), where 1 Impute the missing values using the following equation position for jth attribute |
2.2.2. Feature Selection (FS)
RF-Based FS
| Algorithm 2: The procedure for applying RF-based FS method |
|
Input: The d-dimensional data, and result, Result: The reduced m-dimensional data, , where m < d 1 Calculate a tree’s Out of Bag (OOB) error. 2 When primary node i is separated in , allocate per adherence with to minor nodes at random, where the comparative frequency of occurrences is , that previously followed the tree in the same direction. 3 Recalculate tree’s OOB error (follow step 2). 4 Determine the contrast in OOB errors between the initial and recalculated errors. 5 Reapply previous steps (1 to 4) for each tree, the total importance score (F) is then calculated employing the average deviation across all trees. 6 Choose the high scores (F) of top-m features as well as preserve them in . |
IG-Based FS
| Algorithm 3: The procedure for applying the IG-based FS method |
 |
XGB- and LGB-Based FS
| Algorithm 4: The procedure for applying the XGB diabetes detection model |
 |
| Algorithm 5: The procedure for applying the LGB diabetes detection model |
 |
2.2.3. K-Fold Cross-Validation
2.2.4. Hyperparameter Optimization
2.2.5. ML Classifiers
GNB and BNB Classifier
| Algorithm 6: The procedure for applying the GNB and BNB diabetes detection model |
|
Input: Input feature vector with n-samples and d-dimension and true label Result: The posterior 1 Calculate the prior as , and is the sample in class. 2 Determine the posterior probability of the output as follows: , which is the predictor’s likelihood for a given class . |
RF Classifier
| Algorithm 7: The procedure for applying the RF diabetes detection model |
 |
DT Classifier
| Algorithm 8: The procedure for applying the DT diabetes detection model |
|
Input: Input feature vector with n-samples and d-dimension and true label Result: The posterior 1 Divide into and subsets, where consisting of a feature, j and threshold, . 2 Use an impurity function (H), which are given below, to calculate the impurity at the node, , where or and 3 Reduce the impurity by selecting the parameters, . 4 Reapply the preceding steps for subsets and until depth reach to or . |
XGB Classifier
LGB Classifier
Proposed Ensemble Classifier
2.3. Evaluation Metrics
3. Results and Discussion
3.1. Results for Missing Imputation
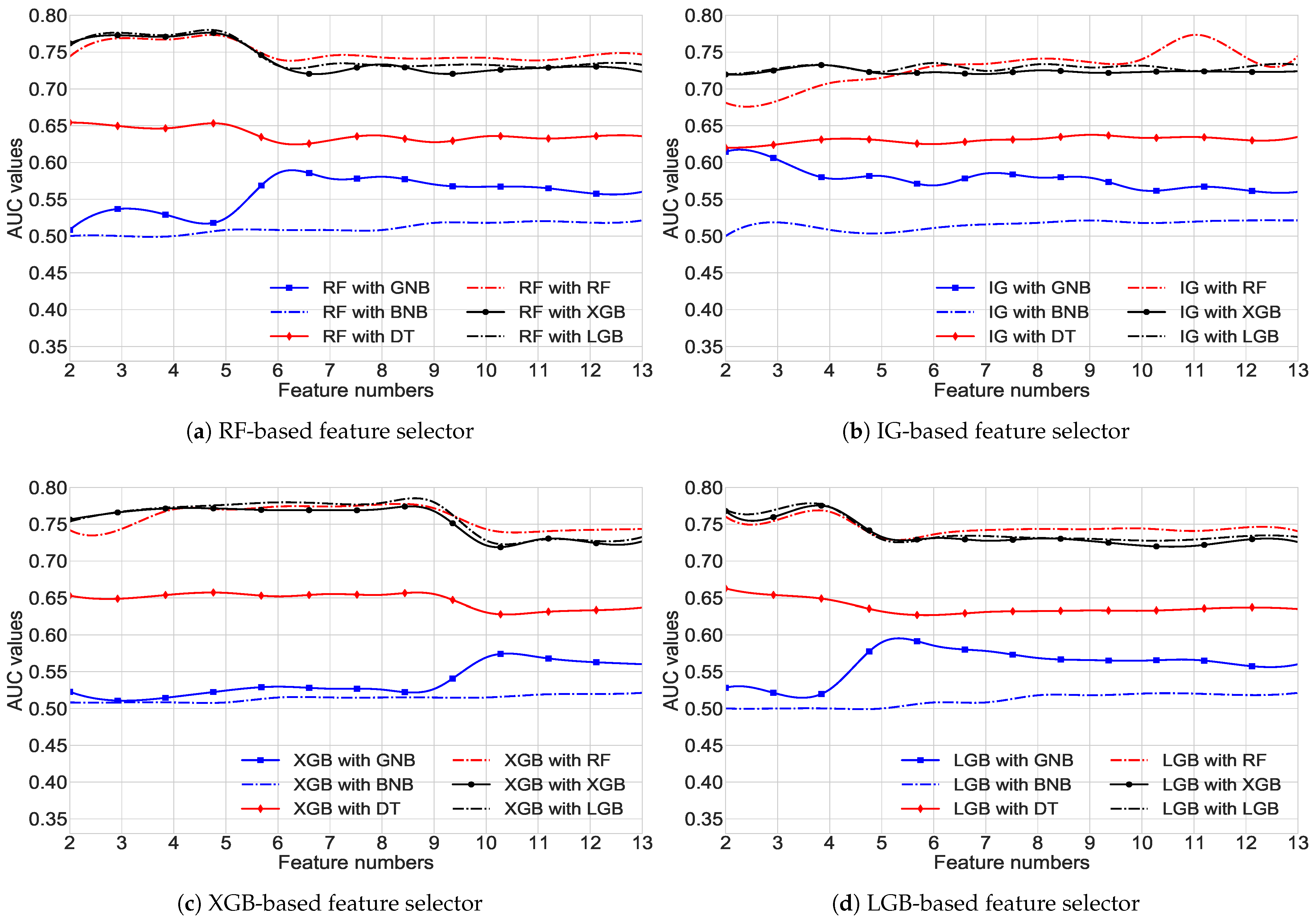
3.2. FS Results
3.3. Optimization Results
3.4. Classifiers’ Results
3.4.1. Single ML Model’s Results
3.4.2. Proposed Ensemble Models’ Results
3.4.3. Year-Wise Cross-Fold Validation
3.4.4. Comparative Studies
3.4.5. Strengths and Drawbacks of Our Proposed Ensemble Classifier
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| AB | AdaBoost |
| Acc | Accuracy |
| ANOVA | Analysis of Variance |
| BWA | Boruta Wrapper Algorithm |
| BPC | Best Performing Classifier |
| CRB | Correlation-Based |
| DDC | Diabetes Diseases Classification |
| DT | Decision Tree |
| DM | Diabetes Mellitus |
| FBS | Fasting Blood Sugar |
| FS | Feature Selection |
| GI | Gini Impurity |
| GOSS | Gradient-based One-side Sampling |
| GSO | Grid Search Optimization |
| KNN | K-Nearest Neighborhood |
| KCV | K-fold Cross-Validation |
| LDA | Linear Discriminant Analysis |
| LR | Logistic Regression |
| ML | Machine Learning |
| MI | Mutual Information |
| MVI | Missing Value Imputation |
| mRMR | Minimum Redundancy Maximum Relevance |
| NHANES | National Health and Nutrition Examination Survey |
| NSF | Number of Selected Feature |
| NB | Naive Bayes |
| PIDD | PIMA Indian Dataset |
| QDA | Quadratic Discriminant Analysis |
| RT | Random Tree |
| RF | Random Forest |
| SVM | Support Vector Machine |
| Sn | Sensitivity |
| Sp | Specificity |
| WHO | World Health Organization |
| XGB | XGBoost |
References
- Misra, A.; Gopalan, H.; Jayawardena, R.; Hills, A.P.; Soares, M.; Reza-Albarrán, A.A.; Ramaiya, K.L. Diabetes in developing countries. J. Diabetes 2019, 11, 522–539. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. Diagnosis and classification of diabetes mellitus. Diabetes Care 2009, 32, S62–S67. [Google Scholar] [CrossRef] [PubMed]
- Fitzmaurice, C.; Allen, C.; Barber, R.M.; Barregard, L.; Bhutta, Z.A.; Brenner, H.; Dicker, D.J.; Chimed-Orchir, O.; Dandona, R.; Dandona, L.; et al. Global, regional, and national cancer incidence, mortality, years of life lost, years lived with disability, and disability-adjusted life-years for 32 cancer groups, 1990 to 2015: A systematic analysis for the global burden of disease study. JAMA Oncol. 2017, 3, 524–548. [Google Scholar] [PubMed]
- Saeedi, P.; Petersohn, I.; Salpea, P.; Malanda, B.; Karuranga, S.; Unwin, N.; Colagiuri, S.; Guariguata, L.; Motala, A.A.; Ogurtsova, K.; et al. Global and regional diabetes prevalence estimates for 2019 and projections for 2030 and 2045: Results from the International Diabetes Federation Diabetes Atlas. Diabetes Res. Clin. Pract. 2019, 157, 107843. [Google Scholar] [CrossRef] [PubMed]
- Bharath, C.; Saravanan, N.; Venkatalakshmi, S. Assessment of knowledge related to diabetes mellitus among patients attending a dental college in Salem city-A cross sectional study. Braz. Dent. Sci. 2017, 20, 93–100. [Google Scholar]
- Akter, S.; Rahman, M.M.; Abe, S.K.; Sultana, P. Prevalence of diabetes and prediabetes and their risk factors among Bangladeshi adults: A nationwide survey. Bull. World Health Organ. 2014, 92, 204A–213A. [Google Scholar] [CrossRef]
- Danaei, G.; Finucane, M.M.; Lu, Y.; Singh, G.M.; Cowan, M.J.; Paciorek, C.J.; Lin, J.K.; Farzadfar, F.; Khang, Y.H.; Stevens, G.A.; et al. National, regional, and global trends in fasting plasma glucose and diabetes prevalence since 1980: Systematic analysis of health examination surveys and epidemiological studies with 370 country-years and 2.7 million participants. Lancet 2011, 378, 31–40. [Google Scholar] [CrossRef]
- Islam, M.; Raihan, M.; Akash, S.R.I.; Farzana, F.; Aktar, N. Diabetes Mellitus Prediction Using Ensemble Machine Learning Techniques. In Proceedings of the International Conference on Computational Intelligence, Security and Internet of Things, Agartala, India, 13–14 December 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 453–467. [Google Scholar]
- Chiang, J.L.; Kirkman, M.S.; Laffel, L.M.; Peters, A.L. Type 1 diabetes through the life span: A position statement of the American Diabetes Association. Diabetes Care 2014, 37, 2034–2054. [Google Scholar] [CrossRef]
- Begum, S.; Afroz, R.; Khanam, Q.; Khanom, A.; Choudhury, T. Diabetes mellitus and gestational diabetes mellitus. J. Paediatr. Surg. Bangladesh 2014, 5, 30–35. [Google Scholar] [CrossRef]
- Canadian Diabetes Association. Diabetes: Canada at the Tipping Point: Charting a New Path; Canadian Diabetes Association: Winnipeg, MB, Canada, 2011. [Google Scholar]
- Shi, Y.; Hu, F.B. The global implications of diabetes and cancer. Lancet 2014, 383, 1947–1948. [Google Scholar] [CrossRef]
- Centers for Disease Control and Prevention. National Diabetes Fact Sheet: National Estimates and General Information on Diabetes and Prediabetes in the United States, 2011; US Department of Health and Human Services, Centers for Disease Control and Prevention: Atlanta, GA, USA, 2011; Volume 201, pp. 2568–2569.
- Maniruzzaman, M.; Kumar, N.; Abedin, M.M.; Islam, M.S.; Suri, H.S.; El-Baz, A.S.; Suri, J.S. Comparative approaches for classification of diabetes mellitus data: Machine learning paradigm. Comput. Methods Programs Biomed. 2017, 152, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.K.; Alam, M.A.; Roy, S.; Dutta, A.; Jawad, M.T.; Das, S. Missing value imputation affects the performance of machine learning: A review and analysis of the literature (2010–2021). Inform. Med. Unlocked 2021, 27, 100799. [Google Scholar] [CrossRef]
- Mitteroecker, P.; Bookstein, F. Linear discrimination, ordination, and the visualization of selection gradients in modern morphometrics. Evol. Biol. 2011, 38, 100–114. [Google Scholar] [CrossRef]
- Tharwat, A. Linear vs. quadratic discriminant analysis classifier: A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 145–180. [Google Scholar] [CrossRef]
- Webb, G.I.; Keogh, E.; Miikkulainen, R. Naïve Bayes. Encycl. Mach. Learn. 2010, 15, 713–714. [Google Scholar]
- Hasan, M.K.; Aleef, T.A.; Roy, S. Automatic mass classification in breast using transfer learning of deep convolutional neural network and support vector machine. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; pp. 110–113. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef]
- Song, Y.Y.; Ying, L. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar]
- Mathuria, M. Decision tree analysis on j48 algorithm for data mining. Int. J. Adv. Res. Comput. Sci. Softw. Eng. 2013, 3, 1114–1119. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Kégl, B. The return of AdaBoost. MH: Multi-class Hamming trees. arXiv 2013, arXiv:1312.6086. [Google Scholar]
- Hasan, M.; Ahamed, M.; Ahmad, M.; Rashid, M. Prediction of epileptic seizure by analysing time series EEG signal using k-NN classifier. Appl. Bionics Biomech. 2017, 2017, 6848014. [Google Scholar] [CrossRef]
- Bashir, S.; Qamar, U.; Khan, F.H. IntelliHealth: A medical decision support application using a novel weighted multi-layer classifier ensemble framework. J. Biomed. Inform. 2016, 59, 185–200. [Google Scholar] [CrossRef] [PubMed]
- Maniruzzaman, M.; Rahman, M.J.; Al-MehediHasan, M.; Suri, H.S.; Abedin, M.M.; El-Baz, A.; Suri, J.S. Accurate diabetes risk stratification using machine learning: Role of missing value and outliers. J. Med. Syst. 2018, 42, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Dutta, D.; Paul, D.; Ghosh, P. Analysing feature importances for diabetes prediction using machine learning. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 924–928. [Google Scholar]
- Sisodia, D.; Sisodia, D.S. Prediction of diabetes using classification algorithms. Procedia Comput. Sci. 2018, 132, 1578–1585. [Google Scholar] [CrossRef]
- Hasan, M.K.; Alam, M.A.; Das, D.; Hossain, E.; Hasan, M. Diabetes prediction using ensembling of different machine learning classifiers. IEEE Access 2020, 8, 76516–76531. [Google Scholar] [CrossRef]
- Orabi, K.M.; Kamal, Y.M.; Rabah, T.M. Early predictive system for diabetes mellitus disease. In Proceedings of the Industrial Conference on Data Mining; Springer: Berlin/Heidelberg, Germany, 2016; pp. 420–427. [Google Scholar]
- Rallapalli, S.; Suryakanthi, T. Predicting the risk of diabetes in big data electronic health Records by using scalable random forest classification algorithm. In Proceedings of the 2016 International Conference on Advances in Computing and Communication Engineering (ICACCE), Durban, South Africa, 28–29 November 2016; pp. 281–284. [Google Scholar]
- Perveen, S.; Shahbaz, M.; Guergachi, A.; Keshavjee, K. Performance analysis of data mining classification techniques to predict diabetes. Procedia Comput. Sci. 2016, 82, 115–121. [Google Scholar] [CrossRef]
- Rashid, T.A.; Abdullah, S.M.; Abdullah, R.M. An intelligent approach for diabetes classification, prediction and description. In Innovations in Bio-Inspired Computing and Applications; Springer: Berlin/Heidelberg, Germany, 2016; pp. 323–335. [Google Scholar]
- Raihan, M.; Islam, M.M.; Ghosh, P.; Shaj, S.A.; Chowdhury, M.R.; Mondal, S.; More, A. A comprehensive Analysis on risk prediction of acute coronary syndrome using machine learning approaches. In Proceedings of the 2018 21st International Conference of Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 21–23 December 2018; pp. 1–6. [Google Scholar]
- Zou, Q.; Qu, K.; Luo, Y.; Yin, D.; Ju, Y.; Tang, H. Predicting diabetes mellitus with machine learning techniques. Front. Genet. 2018, 9, 515. [Google Scholar] [CrossRef]
- Kaur, H.; Kumari, V. Predictive modelling and analytics for diabetes using a machine learning approach. Appl. Comput. Inform. 2020, 18, 90–100. [Google Scholar] [CrossRef]
- Wang, Q.; Cao, W.; Guo, J.; Ren, J.; Cheng, Y.; Davis, D.N. DMP_MI: An effective diabetes mellitus classification algorithm on imbalanced data with missing values. IEEE Access 2019, 7, 102232–102238. [Google Scholar] [CrossRef]
- Sneha, N.; Gangil, T. Analysis of diabetes mellitus for early prediction using optimal features selection. J. Big Data 2019, 6, 1–19. [Google Scholar] [CrossRef]
- Mohapatra, S.K.; Swain, J.K.; Mohanty, M.N. Detection of diabetes using multilayer perceptron. In Proceedings of the International Conference on Intelligent Computing and Applications, Tainan, Taiwan, 30 August–1 September 2019; Springer: Berlin/Heidelberg, Germany, 2019; pp. 109–116. [Google Scholar]
- Maniruzzaman, M.; Rahman, M.; Ahammed, B.; Abedin, M. Classification and prediction of diabetes disease using machine learning paradigm. Health Inf. Sci. Syst. 2020, 8, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Chatrati, S.P.; Hossain, G.; Goyal, A.; Bhan, A.; Bhattacharya, S.; Gaurav, D.; Tiwari, S.M. Smart home health monitoring system for predicting type 2 diabetes and hypertension. J. King Saud Univ. -Comput. Inf. Sci. 2020, 34, 862–870. [Google Scholar] [CrossRef]
- Prakasha, A.; Vignesh, O.; Suneetha Rani, R.; Abinayaa, S. An Ensemble Technique for Early Prediction of Type 2 Diabetes Mellitus–A Normalization Approach. Turk. J. Comput. Math. Educ. 2021, 12, 2136–2143. [Google Scholar]
- Yang, H.; Luo, Y.; Ren, X.; Wu, M.; He, X.; Peng, B.; Deng, K.; Yan, D.; Tang, H.; Lin, H. Risk prediction of diabetes: Big data mining with fusion of multifarious physical examination indicators. Inf. Fusion 2021, 75, 140–149. [Google Scholar] [CrossRef]
- Jo, T.; Japkowicz, N. Class imbalances versus small disjuncts. ACM Sigkdd Explor. Newsl. 2004, 6, 40–49. [Google Scholar] [CrossRef]
- Buda, M.; Maki, A.; Mazurowski, M.A. A systematic study of the class imbalance problem in convolutional neural networks. Neural Netw. 2018, 106, 249–259. [Google Scholar] [CrossRef] [Green Version]
- Ali, H.; Salleh, M.N.M.; Saedudin, R.; Hussain, K.; Mushtaq, M.F. Imbalance class problems in data mining: A review. Indones. J. Electr. Eng. Comput. Sci. 2019, 14, 1560–1571. [Google Scholar] [CrossRef]
- Al-Stouhi, S.; Reddy, C.K. Transfer learning for class imbalance problems with inadequate data. Knowl. Inf. Syst. 2016, 48, 201–228. [Google Scholar] [CrossRef]
- Islam, M.S.; Awal, M.A.; Laboni, J.N.; Pinki, F.T.; Karmokar, S.; Mumenin, K.M.; Al-Ahmadi, S.; Rahman, M.A.; Hossain, M.S.; Mirjalili, S. HGSORF: Henry Gas Solubility Optimization-based Random Forest for C-Section prediction and XAI-based cause analysis. Comput. Biol. Med. 2022, 147, 105671. [Google Scholar] [CrossRef]
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R. Pattern classification with missing data: A review. Neural Comput. Appl. 2010, 19, 263–282. [Google Scholar] [CrossRef]
- Bermingham, M.L.; Pong-Wong, R.; Spiliopoulou, A.; Hayward, C.; Rudan, I.; Campbell, H.; Wright, A.F.; Wilson, J.F.; Agakov, F.; Navarro, P.; et al. Application of high-dimensional feature selection: Evaluation for genomic prediction in man. Sci. Rep. 2015, 5, 10312. [Google Scholar] [CrossRef] [PubMed]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Volume 112. [Google Scholar]
- Jović, A.; Brkić, K.; Bogunović, N. A review of feature selection methods with applications. In Proceedings of the IEEE 2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, 25–29 May 2015; pp. 1200–1205. [Google Scholar]
- Lei, S. A feature selection method based on information gain and genetic algorithm. In Proceedings of the IEEE 2012 International Conference on Computer Science and Electronics Engineering, Hangzhou, China, 23–25 March 2012; Volume 2, pp. 355–358. [Google Scholar]
- Chen, C.; Zhang, Q.; Yu, B.; Yu, Z.; Lawrence, P.J.; Ma, Q.; Zhang, Y. Improving protein-protein interactions prediction accuracy using XGBoost feature selection and stacked ensemble classifier. Comput. Biol. Med. 2020, 123, 103899. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.; Liu, C.; Zemiti, N.; Yang, C. Optimal feature selection for EMG-based finger force estimation using lightGBM model. In Proceedings of the 2019 28th IEEE International Conference on Robot and Human Interactive Communication (RO-MAN), New Delhi, India, 14–18 October 2019; pp. 1–7. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Awal, M.A.; Masud, M.; Hossain, M.S.; Bulbul, A.A.M.; Mahmud, S.H.; Bairagi, A.K. A novel bayesian optimization-based machine learning framework for COVID-19 detection from inpatient facility data. IEEE Access 2021, 9, 10263–10281. [Google Scholar] [CrossRef]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 2017, 18, 6765–6816. [Google Scholar]
- Ustuner, M.; Balik Sanli, F. Polarimetric target decompositions and light gradient boosting machine for crop classification: A comparative evaluation. ISPRS Int. J. Geo. -Inf. 2019, 8, 97. [Google Scholar] [CrossRef] [Green Version]
- Taha, A.A.; Malebary, S.J. An intelligent approach to credit card fraud detection using an optimized light gradient boosting machine. IEEE Access 2020, 8, 25579–25587. [Google Scholar] [CrossRef]
- Hasan, M.K.; Jawad, M.T.; Dutta, A.; Awal, M.A.; Islam, M.A.; Masud, M.; Al-Amri, J.F. Associating Measles Vaccine Uptake Classification and its Underlying Factors Using an Ensemble of Machine Learning Models. IEEE Access 2021, 9, 119613–119628. [Google Scholar] [CrossRef]
- Harangi, B. Skin lesion classification with ensembles of deep convolutional neural networks. J. Biomed. Inform. 2018, 86, 25–32. [Google Scholar] [CrossRef]
- Hsieh, S.L.; Hsieh, S.H.; Cheng, P.H.; Chen, C.H.; Hsu, K.P.; Lee, I.S.; Wang, Z.; Lai, F. Design ensemble machine learning model for breast cancer diagnosis. J. Med. Syst. 2012, 36, 2841–2847. [Google Scholar] [CrossRef] [PubMed]
- Sikder, N.; Masud, M.; Bairagi, A.K.; Arif, A.S.M.; Nahid, A.A.; Alhumyani, H.A. Severity Classification of Diabetic Retinopathy Using an Ensemble Learning Algorithm through Analyzing Retinal Images. Symmetry 2021, 13, 670. [Google Scholar] [CrossRef]
- Masud, M.; Bairagi, A.K.; Nahid, A.A.; Sikder, N.; Rubaiee, S.; Ahmed, A.; Anand, D. A Pneumonia Diagnosis Scheme Based on Hybrid Features Extracted from Chest Radiographs Using an Ensemble Learning Algorithm. J. Healthc. Eng. 2021, 2021, 8862089. [Google Scholar] [CrossRef] [PubMed]
- Cheng, N.; Li, M.; Zhao, L.; Zhang, B.; Yang, Y.; Zheng, C.H.; Xia, J. Comparison and integration of computational methods for deleterious synonymous mutation prediction. Briefings Bioinform. 2020, 21, 970–981. [Google Scholar] [CrossRef]
- Dai, R.; Zhang, W.; Tang, W.; Wynendaele, E.; Zhu, Q.; Bin, Y.; De Spiegeleer, B.; Xia, J. BBPpred: Sequence-based prediction of blood-brain barrier peptides with feature representation learning and logistic regression. J. Chem. Inf. Model. 2021, 61, 525–534. [Google Scholar] [CrossRef]
- Chowdhury, M.A.B.; Uddin, M.J.; Khan, H.M.; Haque, M.R. Type 2 diabetes and its correlates among adults in Bangladesh: A population based study. BMC Public Health 2015, 15, 1070. [Google Scholar] [CrossRef]
- Sathi, N.J.; Islam, M.A.; Ahmed, M.S.; Islam, S.M.S. Prevalence, trends and associated factors of hypertension and diabetes mellitus in Bangladesh: Evidence from BHDS 2011 and 2017–18. PLoS ONE 2022, 17, e0267243. [Google Scholar] [CrossRef]
- Islam, M.M.; Rahman, M.J.; Tawabunnahar, M.; Abedin, M.M.; Maniruzzaman, M. Investigate the Effect of Diabetes on Hypertension Based on Bangladesh Demography and Health Survey, 2017–2018; Research Square: Durham, NC, USA, 2021. [Google Scholar]
- Rahman, M.A. Socioeconomic Inequalities in the Risk Factors of Noncommunicable Diseases (Hypertension and Diabetes) among Bangladeshi Population: Evidence Based on Population Level Data Analysis. PLoS ONE 2022, 17, e0274978. [Google Scholar] [CrossRef]
- Islam, M.M.; Rahman, M.J.; Roy, D.C.; Maniruzzaman, M. Automated detection and classification of diabetes disease based on Bangladesh demographic and health survey data, 2011 using machine learning approach. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 217–219. [Google Scholar] [CrossRef]


| Years | Dataset | MVI 1 | FS | NSF | BPC | Performance |
|---|---|---|---|---|---|---|
| 2016 [32] | ENRC | None | None | 9 | DT | : 0.840 |
| 2018 [37] | LMHC | None | None | All | RF | : 0.808 : 0.849 : 0.767 |
| 2018 [37] | PIDD | None | mRMR | 7 | RF | : 0.772 : 0.746 : 0.799 |
| 2018 [30] | PIDD | None | None | 8 | NB | : 0.819 : 0.763 : 0.763 |
| 2018 [38] | PIDD | KNN impute | BWA | 4 | Linear Kernel SVM | : 0.920 |
| 2019 [39] | PIDD | NB | None | 8 | RF | : 0.928 : 0.871 : 0.857 |
| 2019 [40] | PIDD | None | CRB | 11 | NB | : 0.823 |
| 2019 [41] | PIDD | None | None | 8 | MLP | : 0.775 : 0.85 : 0.68 |
| 2020 [31] | PIDD | Mean | CRB | 6 | Ensemble of AB, XGB | : 0.950 : 0.789 : 0.789 |
| 2020 [42] | NHANES | None | LR | 7 | RF | : 0.95 : 0.943 |
| 2020 [43] | PIDD | Case deletion | None | 2 | SVM | : 0.700 : 0.750 |
| 2021 [44] | PIDD | None | None | 8 | Ensemble of J48, NBT, RF, Simple CART, RT | : 0.832 : 0.792 : 0.786 |
| 2021 [45] | LMHC | Case deletion | ANOVA, GI | 16 | XGB | : 0.876 : 0.727 : 0.738 |
| Dataset | Diabetes Patient | Non-Diabetes Patient |
| DDC-2011 | 4751 | 2814 |
| DDC-2017 | 3492 | 4073 |
| Features | Different Features with Short Descriptions | Categorical? | Continuous? | -Test or Mean ± Std | |
|---|---|---|---|---|---|
| DDC-2011 | DDC-2017 | ||||
| Division (the respondents’ residence place) | Yes | No | 144.689 (0.000) | 383.774 (0.000) | |
| Location of respondents’ residence area (urban/rural) | Yes | No | 463.00 (0.496) | 93.958 (0.000) | |
| Wealth index (respondent’s financial situation) | Yes | No | 16.104 (0.003) | 482.139 (0.000) | |
| Household’s head sexuality (gender of the household head) | Yes | No | 5.858 (0.016) | 4.298 (0.117) | |
| Age of household members | No | Yes | 54.87 ± 12.94 | 39.53 ± 16.21 | |
| Respondent’s current educational status | Yes | No | 6.041 (0.110) | 6.960 (0.541) | |
| Occupation type of the respondent | Yes | No | 30.430 (0.063) | 185.659 (0.000) | |
| Eaten anything | Yes | No | 0.663 (0.416) | 3.065 (0.216) | |
| Had caffeinated drink | Yes | No | 1.590 (0.207) | 20.738 (0.000) | |
| Smoked | Yes | No | 0.001 (0.985) | 7.781 (0.020) | |
| Average of systolic | No | Yes | 77.59 ± 12.05 | 122.63 ± 21.95 | |
| Average of diastolic | No | Yes | 119.93 ± 21.93 | 80.52 ± 13.67 | |
| Body mass index (BMI) for respondent | No | Yes | 2065.63 ± 369.25 | 2239.43 ± 416.47 | |
| Dataset | MVI Techniques | Different ML Classifiers | |||||
|---|---|---|---|---|---|---|---|
| GNB | BNB | RF | DT | XGB | LGB | ||
| DDC-2017 | Case Deletion | ||||||
| MEDimpute | |||||||
| KNNimpute | |||||||
| DDC-2011 | Case Deletion | ||||||
| MEDimpute | |||||||
| KNNimpute | |||||||
| FS Methods | Feature Importance Score | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F4 | F5 | F6 | F7 | F8 | F9 | F10 | F11 | F12 | F13 | |
| RF | |||||||||||||
| IG | |||||||||||||
| XGB | |||||||||||||
| LGB | |||||||||||||
| Classifiers | Tuned Hyperparameters | AUC (W/ GSO) | AUC (W/O GSO) |
|---|---|---|---|
| GNB | The classes’ prior probabilities (=None) and features’ largest variance portion for stability guesstimate (=). | ||
| BNB | Additive Laplace smoothing parameter (=1.0), classes’ prior probabilities (=None), and to learn or not class priors (=True). | ||
| RF | Bootstrap samples or not (=True), split quality function (=gini), the best split feature numbers (=auto), leaf node number for grow trees (=3), leaf node’s samples (=0.4), the samples required to split an internal node (), tree numbers in the forest (=100), out-of-bag samples to calculate the generalization score (=False), and the bootstrapping samples’ randomness control with feature sampling for node’ split (=100). | ||
| DT | Split quality function (=entropy), the best split feature numbers (=auto), leaf node’s samples required (=0.5), samples required to split an internal node (=0.1), the bootstrapping samples’ randomness control with feature sampling for node’ split (=100), and node’s partition strategy (=best). | ||
| XGB | Initial prediction score (), used booster (gbtree), each levels’ subsample ratio (=1), each nodes’ subsample ratio (=1), evaluation metrics for validation data (=error), minimum loss reduction for a further partition on a leaf node (=1.5), weights’ L2 regularization (=1.5), tree depth (=5), child’s hessian sum (=5), trees in the forest (=100), parallel trees built during each iteration (=1), the bootstrapping samples’ randomness control with feature sampling for node’ split (=100), control the unbalance classes (=1), and training subsample ratio (=1.0). | ||
| LGB | Boosting method (=gbdt), class weight (=True), tree construction’s columns subsample ratio (=1.0), base learner tree depth (=), trees in the forest (=50), the bootstrapping samples’ randomness control with feature sampling for node’ split (=100), base learner tree leaves (=25), and training instance subsample ratio (=0.25). |
| Datasets | Different Classifiers | Sn ↑ | Sp ↑ | Acc ↑ | AUC ↑ |
|---|---|---|---|---|---|
| DDC-2011 | GNB | ||||
| BNB | |||||
| RF | |||||
| DT | |||||
| XGB | |||||
| LGB | |||||
| GNB + BNB | |||||
| RF + DT | |||||
| LGB + XGB | |||||
| GNB + BNB + DT + RF | |||||
| GNB + BNB + XGB + LGB | |||||
| DT + RF + XGB + LGB | |||||
| GNB + BNB + DT + RF + XGB + LGB | |||||
| DDC-2017 | GNB | ||||
| BNB | |||||
| RF | |||||
| DT | |||||
| XGB | |||||
| LGB | |||||
| GNB + BNB | |||||
| RF + DT | |||||
| LGB + XGB | |||||
| GNB + BNB + DT + RF | |||||
| GNB + BNB + XGB + LGB | |||||
| DT + RF + XGB + LGB | |||||
| GNB + BNB + DT + RF + XGB + LGB |
| Cases | Different Classifiers | Sn ↑ | Sp ↑ | Acc ↑ | AUC ↑ |
|---|---|---|---|---|---|
| Merged datasets (Case-1) | GNB | ||||
| BNB | |||||
| RF | |||||
| DT | |||||
| XGB | |||||
| LGB | |||||
| GNB + BNB | |||||
| RF + DT | |||||
| LGB + XGB | |||||
| GNB + BNB + DT + RF | |||||
| GNB + BNB + XGB + LGB | |||||
| DT + RF + XGB + LGB | |||||
| GNB + BNB + DT + RF + XGB + LGB | |||||
| Merged datasets (Case-2) | GNB | ||||
| BNB | |||||
| RF | |||||
| DT | |||||
| XGB | |||||
| LGB | |||||
| GNB + BNB | |||||
| RF + DT | |||||
| LGB + XGB | |||||
| GNB + BNB + DT + RF | |||||
| GNB + BNB + XGB + LGB | |||||
| DT + RF + XGB + LGB | |||||
| GNB + BNB + DT + RF + XGB + LGB | |||||
| Merged datasets (Case-3) | GNB | ||||
| BNB | |||||
| RF | |||||
| DT | |||||
| XGB | |||||
| LGB | |||||
| GNB + BNB | |||||
| RF + DT | |||||
| LGB + XGB | |||||
| GNB + BNB + DT + RF | |||||
| GNB + BNB + XGB + LGB | |||||
| DT + RF + XGB + LGB | |||||
| GNB + BNB + DT + RF + XGB + LGB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, A.; Hasan, M.K.; Ahmad, M.; Awal, M.A.; Islam, M.A.; Masud, M.; Meshref, H. Early Prediction of Diabetes Using an Ensemble of Machine Learning Models. Int. J. Environ. Res. Public Health 2022, 19, 12378. https://doi.org/10.3390/ijerph191912378
Dutta A, Hasan MK, Ahmad M, Awal MA, Islam MA, Masud M, Meshref H. Early Prediction of Diabetes Using an Ensemble of Machine Learning Models. International Journal of Environmental Research and Public Health. 2022; 19(19):12378. https://doi.org/10.3390/ijerph191912378
Chicago/Turabian StyleDutta, Aishwariya, Md. Kamrul Hasan, Mohiuddin Ahmad, Md. Abdul Awal, Md. Akhtarul Islam, Mehedi Masud, and Hossam Meshref. 2022. "Early Prediction of Diabetes Using an Ensemble of Machine Learning Models" International Journal of Environmental Research and Public Health 19, no. 19: 12378. https://doi.org/10.3390/ijerph191912378
APA StyleDutta, A., Hasan, M. K., Ahmad, M., Awal, M. A., Islam, M. A., Masud, M., & Meshref, H. (2022). Early Prediction of Diabetes Using an Ensemble of Machine Learning Models. International Journal of Environmental Research and Public Health, 19(19), 12378. https://doi.org/10.3390/ijerph191912378










