Fuzzy Optimization for the Remediation of Ammonia: A Case Study Based on Electrochemical Oxidation
Abstract
1. Introduction
2. Materials and Methods
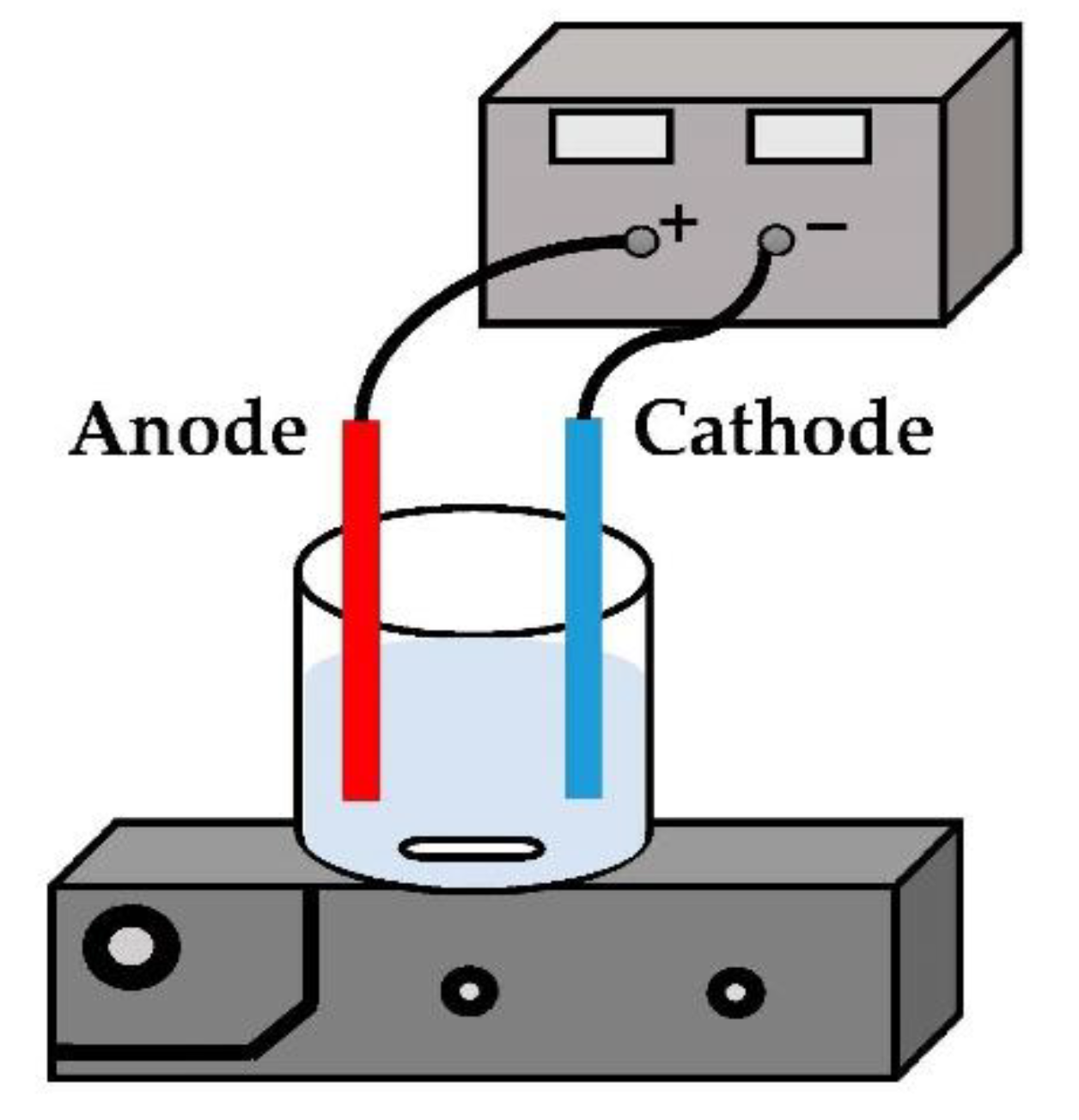
2.1. Experimental Method
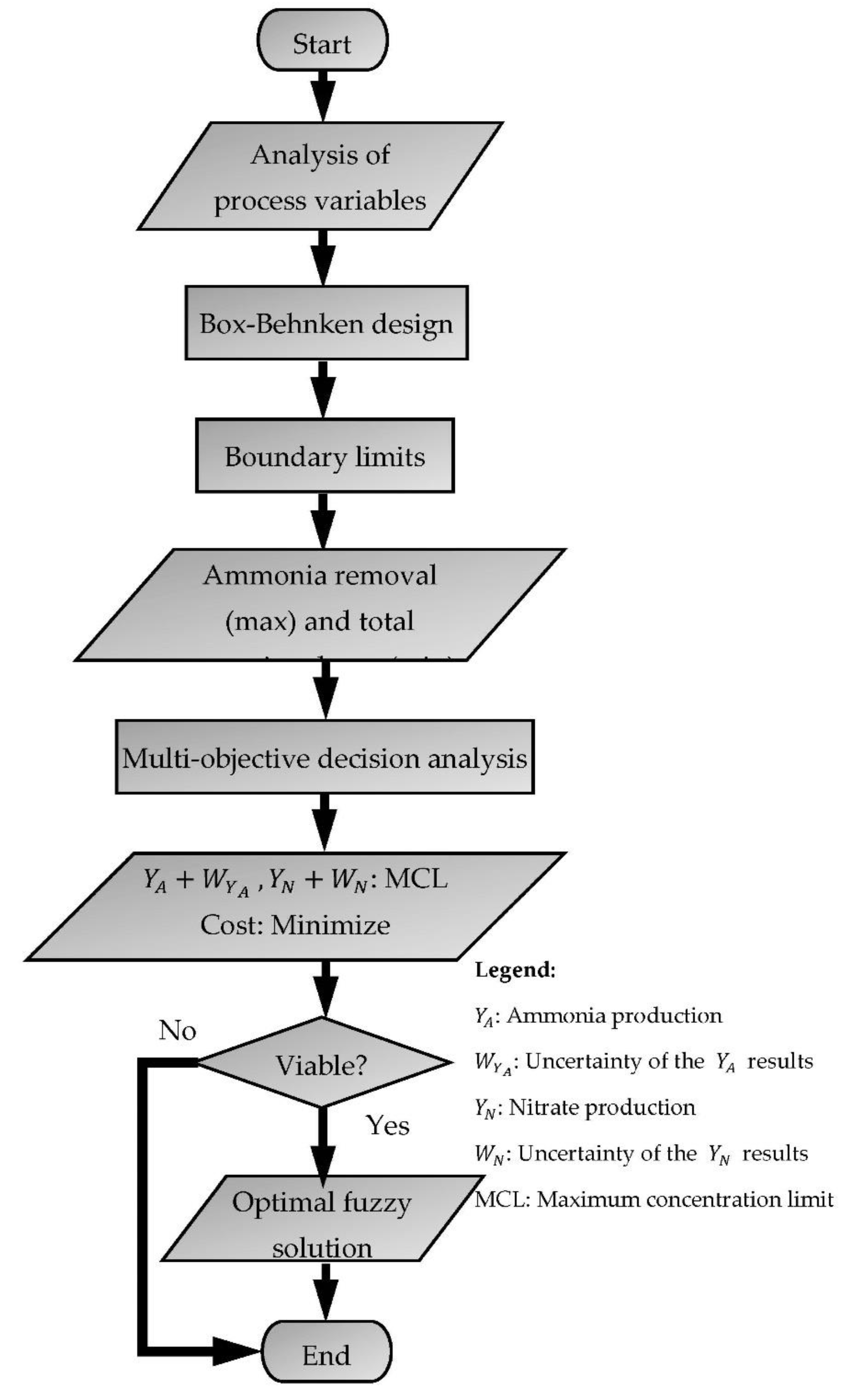
2.2. Fuzzy Multi-Objective Optimization Method
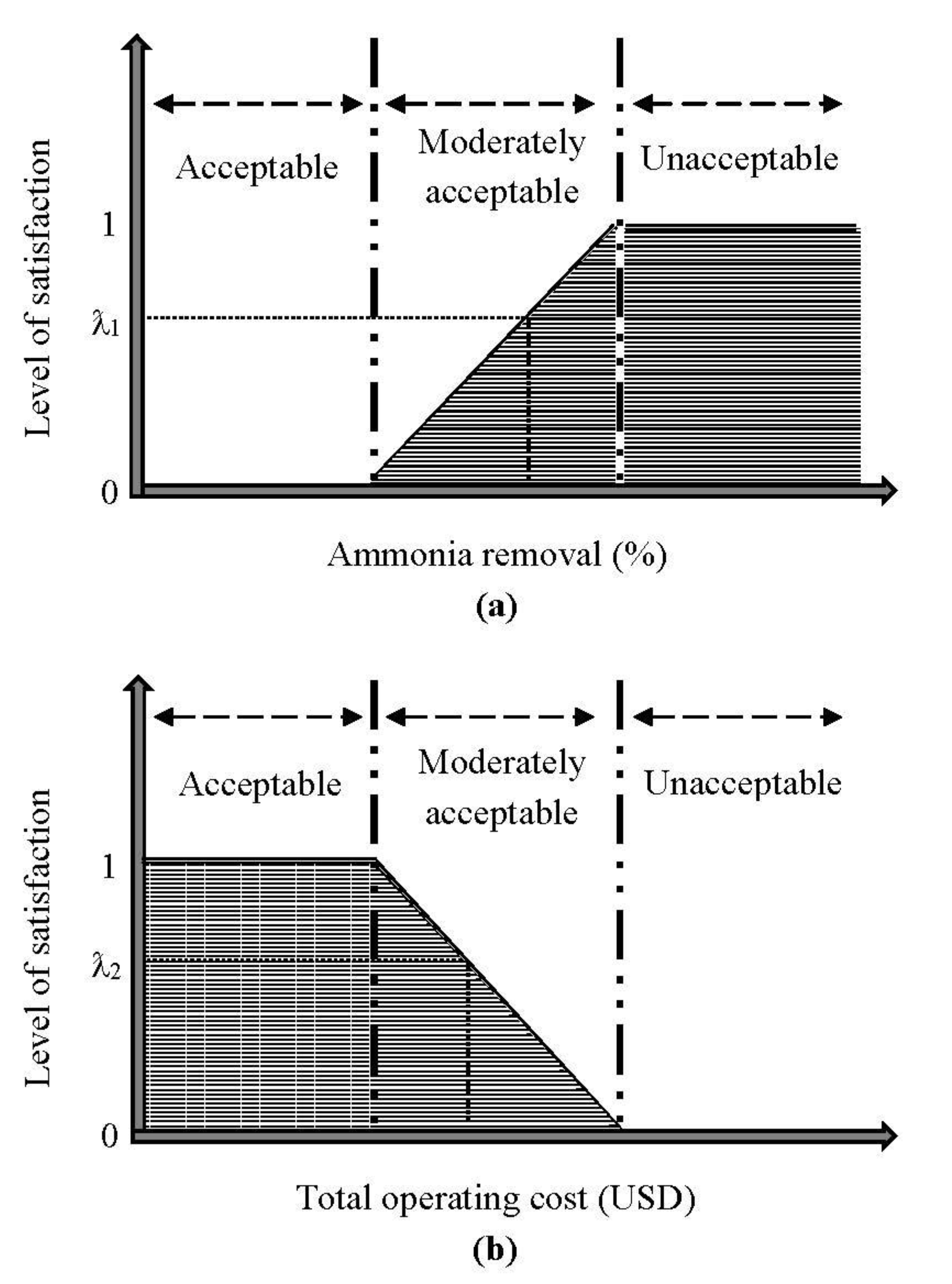
2.2.1. Determination of Boundary Limits
2.2.2. Multi-Objective Decision-Making through Fuzzy Optimization
3. Results and Discussion
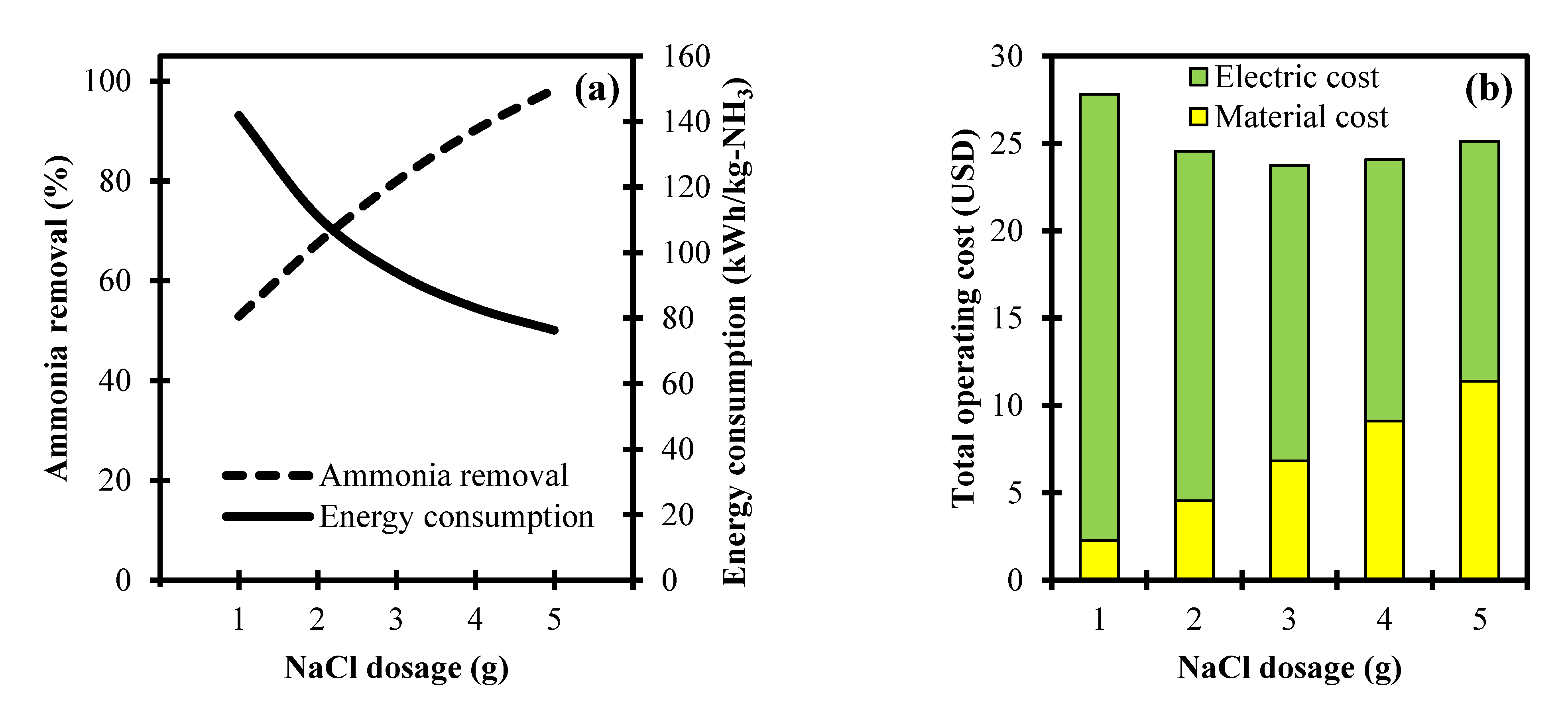
3.1. Analysis of NaCl Dosage towards Ammonia Removal and Its Operating Cost
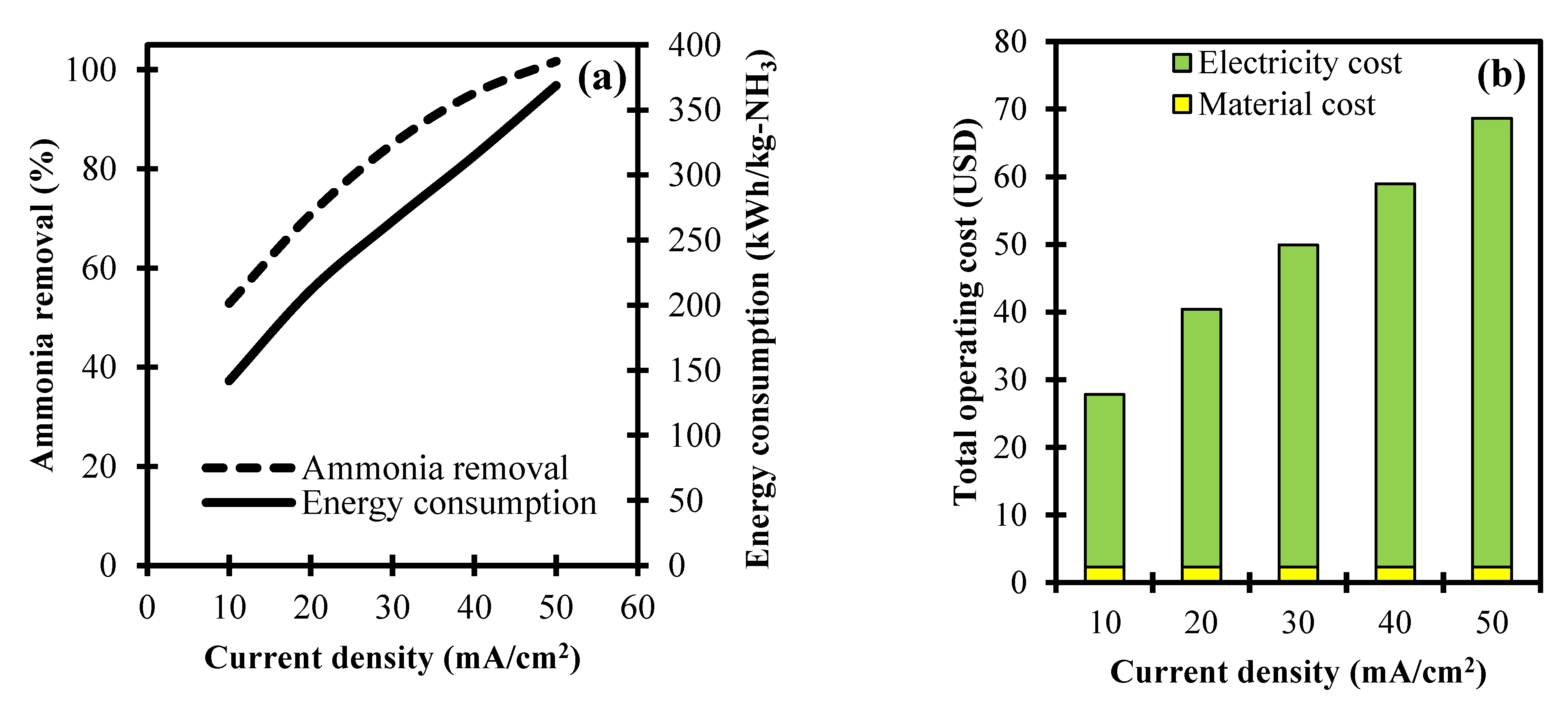
3.2. Analysis of Current Density towards Ammonia Removal and Its Operating Cost
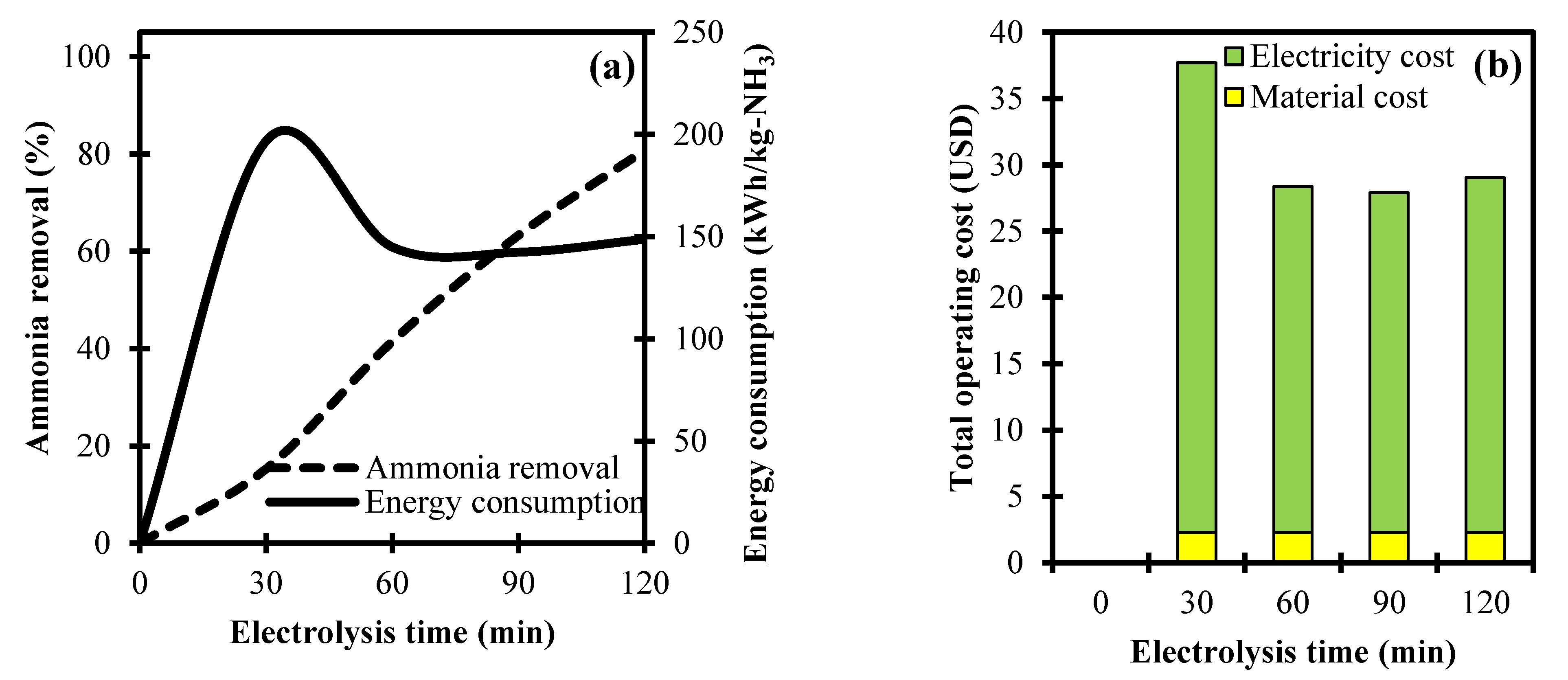
3.3. Analysis of Electrolysis Time towards Ammonia Removal and Its Operating Cost
3.4. Boundary Limits Identification of Ammonia Removal and Operating Cost
3.5. Multi-Objective Decision Analysis: Fuzzy Optimization
3.6. Summary of Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Du, Y.; Ma, T.; Deng, Y.; Shen, S.; Lu, Z. Sources and fate of high levels of ammonium in surface water and shallow groundwater of the Jianghan Plain, Central China. Environ. Sci. Process. Impacts 2017, 19, 161–172. [Google Scholar] [CrossRef]
- Abu-Elala, N.M.; Abd-Elsalam, R.M.; Marouf, S.; Abdelaziz, M.; Moustafa, M. Eutrophication, Ammonia Intoxication, and Infectious Diseases: Interdisciplinary Factors of Mass Mortalities in Cultured Nile Tilapia. J. Aquat. Anim. Health 2016, 28, 187–198. [Google Scholar] [CrossRef]
- Ward, M.H.; Jones, R.R.; Brender, J.D.; De Kok, T.M.; Weyer, P.J.; Nolan, B.T.; Villanueva, C.M.; Van Breda, S.G. Drinking Water Nitrate and Human Health: An Updated Review. Int. J. Environ. Res. Public Health 2018, 15, 1557. [Google Scholar] [CrossRef]
- Hauck, M.; Maalcke-Luesken, F.A.; Jetten, M.S.M.; Huijbregts, M.A.J. Removing nitrogen from wastewater with side stream anammox: What are the trade-offs between environmental impacts? Resour. Conserv. Recycl. 2016, 107, 212–219. [Google Scholar] [CrossRef]
- Huff, L.; Delos, C.; Gallagher, K.; Beaman, J. Aquatic Life Ambient Water Quality Criteria for Ammonia—Freshwater; US Environmental Protection Agency: Washington, DC, USA, 2013.
- Karri, R.R.; Sahu, J.N.; Chimmiri, V. Critical review of abatement of ammonia from wastewater. J. Mol. Liq. 2018, 261, 21–31. [Google Scholar] [CrossRef]
- López De Mishima, B.A.; Lescano, D.; Molina Holgado, T.; Mishima, H.T. Electrochemical oxidation of ammonia in alkaline solutions: Its application to an amperometric sensor. Electrochim. Acta 1998, 43, 395–404. [Google Scholar] [CrossRef]
- Lan, R.; Tao, S. Ammonia as a Suitable Fuel for Fuel Cells. Front. Energy Res. 2014, 2, 35. [Google Scholar] [CrossRef]
- Yao, J.; Mei, Y.; Xia, G.; Lu, Y.; Xu, D.; Sun, N.; Wang, J.; Chen, J. Process Optimization of Electrochemical Oxidation of Ammonia to Nitrogen for Actual Dyeing Wastewater Treatment. Int. J. Environ. Res. Public Health 2019, 16, 2931. [Google Scholar] [CrossRef]
- Li, M.; Feng, C.; Zhang, Z.; Liu, X.; Ma, W.; Xue, Q.; Sugiura, N. Optimization of electrochemical ammonia removal using Box-Behnken design. J. Electroanal. Chem. 2011, 657, 66–73. [Google Scholar] [CrossRef]
- Deng, Y.; Englehardt, J.D. Electrochemical oxidation for landfill leachate treatment. Waste Manag. 2007, 27, 380–388. [Google Scholar] [CrossRef]
- Szpyrkowicz, L.; Kaul, S.N.; Neti, R.N.; Satyanarayan, S. Influence of anode material on electrochemical oxidation for the treatment of tannery wastewater. Water Res. 2005, 39, 1601–1613. [Google Scholar] [CrossRef]
- Meng, X.; Khoso, S.A.; Jiang, F.; Zhang, Y.; Yue, T.; Gao, J.; Lin, S.; Liu, R.; Gao, Z.; Chen, P.; et al. Removal of chemical oxygen demand and ammonia nitrogen from lead smelting wastewater with high salts content using electrochemical oxidation combined with coagulation–flocculation treatment. Sep. Purif. Technol. 2020, 235, 116233. [Google Scholar] [CrossRef]
- Zhang, C.; He, D.; Ma, J.; Waite, T.D. Active chlorine mediated ammonia oxidation revisited: Reaction mechanism, kinetic modelling and implications. Water Res. 2018, 145, 220–230. [Google Scholar] [CrossRef]
- Kim, K.W.; Kim, Y.J.; Kim, I.T.; Park, G.I.; Lee, E.H. The electrolytic decomposition mechanism of ammonia to nitrogen at an IrO2 anode. Electrochim. Acta 2005, 50, 4356–4364. [Google Scholar] [CrossRef]
- Vanlangendonck, Y.; Corbisier, D.; Van Lierde, A. Influence of operating conditions on the ammonia electro-oxidation rate in wastewaters from power plants (ELONITATM technique). Water Res. 2005, 39, 3028–3034. [Google Scholar] [CrossRef]
- Charab, A.A.; Movahedirad, S.; Norouzbeigi, R. Thermal conductivity of Al2O3 + TiO2/water nanofluid: Model development and experimental validation. Appl. Therm. Eng. 2017, 119, 42–51. [Google Scholar] [CrossRef]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef]
- Xie, H.; Lee, Y.C.; Mahajan, R.L.; Su, R. Process Optimization Using a Fuzzy Logic Response Surface Method. IEEE Trans. Components Packag. Manuf. Technol. Part A 1994, 17, 202–211. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Inuiguchi, M.; Ramík, J. Possibilistic linear programming: A brief review of fuzzy mathematical programming and a comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst. 2000, 111, 3–28. [Google Scholar] [CrossRef]
- Rommelfanger, H.J. The Advantages of Fuzzy Optimization Models in Practical Use. Fuzzy Optim. Decis. Mak. 2004, 3, 295–309. [Google Scholar] [CrossRef]
- Bernardelli, A.; Marsili-Libelli, S.; Manzini, A.; Stancari, S.; Tardini, G.; Montanari, D.; Anceschi, G.; Gelli, P.; Venier, S. Real-time model predictive control of a wastewater treatment plant based on machine learning. Water Sci. Technol. 2020, 81, 2391–2400. [Google Scholar] [CrossRef] [PubMed]
- Choi, A.E.S.; Park, H.S. Fuzzy multi-objective optimization case study based on an anaerobic co-digestion process of food waste leachate and piggery wastewater. J. Environ. Manag. 2018, 223, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Choi, A.E.S.; Futalan, C.C.M.; Yee, J.J. Fuzzy optimization for the removal of uranium from mine water using batch electrocoagulation: A case study. Nucl. Eng. Technol. 2020, 52, 1471–1480. [Google Scholar] [CrossRef]
- Choi, A.E.S.; Roces, S.; Dugos, N.; Wan, M.W. Operating cost study through a Pareto-optimal fuzzy analysis using commercial ferrate (VI) in an ultrasound-assisted oxidative desulfurization of model sulfur compounds. Clean Technol. Environ. Policy 2016, 18, 1433–1441. [Google Scholar] [CrossRef]
- Choi, A.E.S.; Futalan, C.M.; Yee, J.-J. Fuzzy Optimization on the Synthesis of Chitosan-Graft-Polyacrylic Acid with Montmorillonite as Filler Material: A Case Study. Polymers 2019, 11, 738. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy mathematical programming. Comput. Oper. Res. 1983, 10, 291–298. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Zhang, F.; Cheng, J. Verification of fuzzy UML models with fuzzy Description Logic. Appl. Soft Comput. J. 2018, 73, 134–152. [Google Scholar] [CrossRef]
- Sun, Y. Fuzzy Approaches and Simulation-Based Reliability Modeling to Solve a Road–Rail Intermodal Routing Problem with Soft Delivery Time Windows When Demand and Capacity are Uncertain. Int. J. Fuzzy Syst. 2020, 22, 2119–2148. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, W.; Wang, W.; Quadrifoglio, L. A multimodal location and routing model for hazardous materials transportation. J. Hazard. Mater. 2012, 227–228, 135–141. [Google Scholar] [CrossRef]
- Aviso, K.B.; Tan, R.R.; Culaba, A.B.; Cruz, J.B. Bi-level fuzzy optimization approach for water exchange in eco-industrial parks. Process Saf. Environ. Prot. 2010, 88, 31–40. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y. Ammonia removal in electrochemical oxidation: Mechanism and pseudo-kinetics. J. Hazard. Mater. 2009, 161, 1010–1016. [Google Scholar] [CrossRef]
- Hansen, H.K.; Peña, S.F.; Gutiérrez, C.; Lazo, A.; Lazo, P.; Ottosen, L.M. Selenium removal from petroleum refinery wastewater using an electrocoagulation technique. J. Hazard. Mater. 2019, 364, 78–81. [Google Scholar] [CrossRef]
- Verma, A.K. Treatment of textile wastewaters by electrocoagulation employing Fe-Al composite electrode. J. Water Process Eng. 2017, 20, 168–172. [Google Scholar] [CrossRef]
- Kim, K.W.; Kim, Y.J.; Kim, I.T.; Park, G.I.; Lee, E.H. Electrochemical conversion characteristics of ammonia to nitrogen. Water Res. 2006, 40, 1431–1441. [Google Scholar] [CrossRef] [PubMed]
- Lim, S.; Zhu, J. Integrated data envelopment analysis: Global vs. local optimum. Eur. J. Oper. Res. 2013, 229, 276–278. [Google Scholar] [CrossRef]
- Wen, B.; Li, H. An approach to formulation of FNLP with complex piecewise linear membership functions. Chin. J. Chem. Eng. 2014, 22, 411–417. [Google Scholar] [CrossRef]
| (a) Process factors and Scale | |||
|---|---|---|---|
| Variables | Scale of the Experiment | ||
| Unit | Range | ||
| Sodium chloride (X1) | g | 1–5 | |
| Current density (X2) | mA/cm2 | 10–50 | |
| Electrolysis time (X3) | min | 30–120 | |
| (b) Cost factors | Unit | Price | Source |
| Material cost (sodium chloride) | USD/g | 2.28 | Sigma-Aldrich |
| Energy consumption cost | USD/kWh | 0.18 | Meralco (December 2020) |
| Run | Sodium Chloride (X1: g) | Current Density (X2: mA/cm2) | Electrolysis Time (X3: min) | Unit: % | |
|---|---|---|---|---|---|
| Ammonia Removal | Cumulative Uncertainty * | ||||
| 1 | 1 | 10 | 75 | 52.86 | ±2.36 |
| 2 | 1 | 30 | 30 | 59.99 | ±2.15 |
| 3 | 1 | 30 | 120 | 100.27 | ±0.76 |
| 4 | 1 | 50 | 75 | 101.69 | ±0.55 |
| 5 | 3 | 10 | 30 | 51.55 | ±2.40 |
| 6 | 3 | 10 | 120 | 98.58 | ±1.01 |
| 7 | 3 | 30 | 75 | 100.00 | ±0.80 |
| 8 | 3 | 30 | 75 | 100.00 | ±0.80 |
| 9 | 3 | 30 | 75 | 100.00 | ±0.80 |
| 10 | 3 | 30 | 75 | 100.00 | ±0.80 |
| 11 | 3 | 30 | 75 | 100.00 | ±0.80 |
| 12 | 3 | 50 | 30 | 101.42 | ±0.59 |
| 13 | 3 | 50 | 120 | 98.06 | ±0.80 |
| 14 | 5 | 50 | 75 | 98.84 | ±0.76 |
| 15 | 5 | 30 | 30 | 99.74 | ±0.84 |
| 16 | 5 | 30 | 120 | 103.12 | ±0.55 |
| 17 | 5 | 10 | 75 | 98.31 | ±1.05 |
| Parameters | Unit | MCL: 10 mg/L NH3-N | MCL: 1.9 mg/L NH3-N |
|---|---|---|---|
| % | 80.3 | 76.1 | |
| % | 80.3 | 86.7 | |
| % | 85.9 | 76.1 | |
| % | 94.8 | 99.1 | |
| % | 1.2 | 0.9 | |
| Energy consumption | kWh/kg-NH3 | 68.3 | 114.7 |
| Material cost | USD | 11.4 | 7.7 |
| Electric cost | USD | 12.3 | 20.6 |
| Total operating cost | USD | 23.7 | 28.3 |
| mg/L | 9.8 | 9.5 | |
| mg/L | 0.2 | 0.5 | |
| Sodium chloride | g | 5.0 | 3.36 |
| Current density | mA/cm2 | 10.0 | 10.0 |
| Electrolysis time | min | 64.7 | 113.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, A.E.S.; Ensano, B.M.B.; Yee, J.-J. Fuzzy Optimization for the Remediation of Ammonia: A Case Study Based on Electrochemical Oxidation. Int. J. Environ. Res. Public Health 2021, 18, 2986. https://doi.org/10.3390/ijerph18062986
Choi AES, Ensano BMB, Yee J-J. Fuzzy Optimization for the Remediation of Ammonia: A Case Study Based on Electrochemical Oxidation. International Journal of Environmental Research and Public Health. 2021; 18(6):2986. https://doi.org/10.3390/ijerph18062986
Chicago/Turabian StyleChoi, Angelo Earvin Sy, Benny Marie B. Ensano, and Jurng-Jae Yee. 2021. "Fuzzy Optimization for the Remediation of Ammonia: A Case Study Based on Electrochemical Oxidation" International Journal of Environmental Research and Public Health 18, no. 6: 2986. https://doi.org/10.3390/ijerph18062986
APA StyleChoi, A. E. S., Ensano, B. M. B., & Yee, J.-J. (2021). Fuzzy Optimization for the Remediation of Ammonia: A Case Study Based on Electrochemical Oxidation. International Journal of Environmental Research and Public Health, 18(6), 2986. https://doi.org/10.3390/ijerph18062986







