The Geography of the Covid-19 Pandemic: A Data-Driven Approach to Exploring Geographical Driving Forces
Abstract
1. Introduction
1.1. Related Work
2. Data and Methods
2.1. Data
2.2. Methods
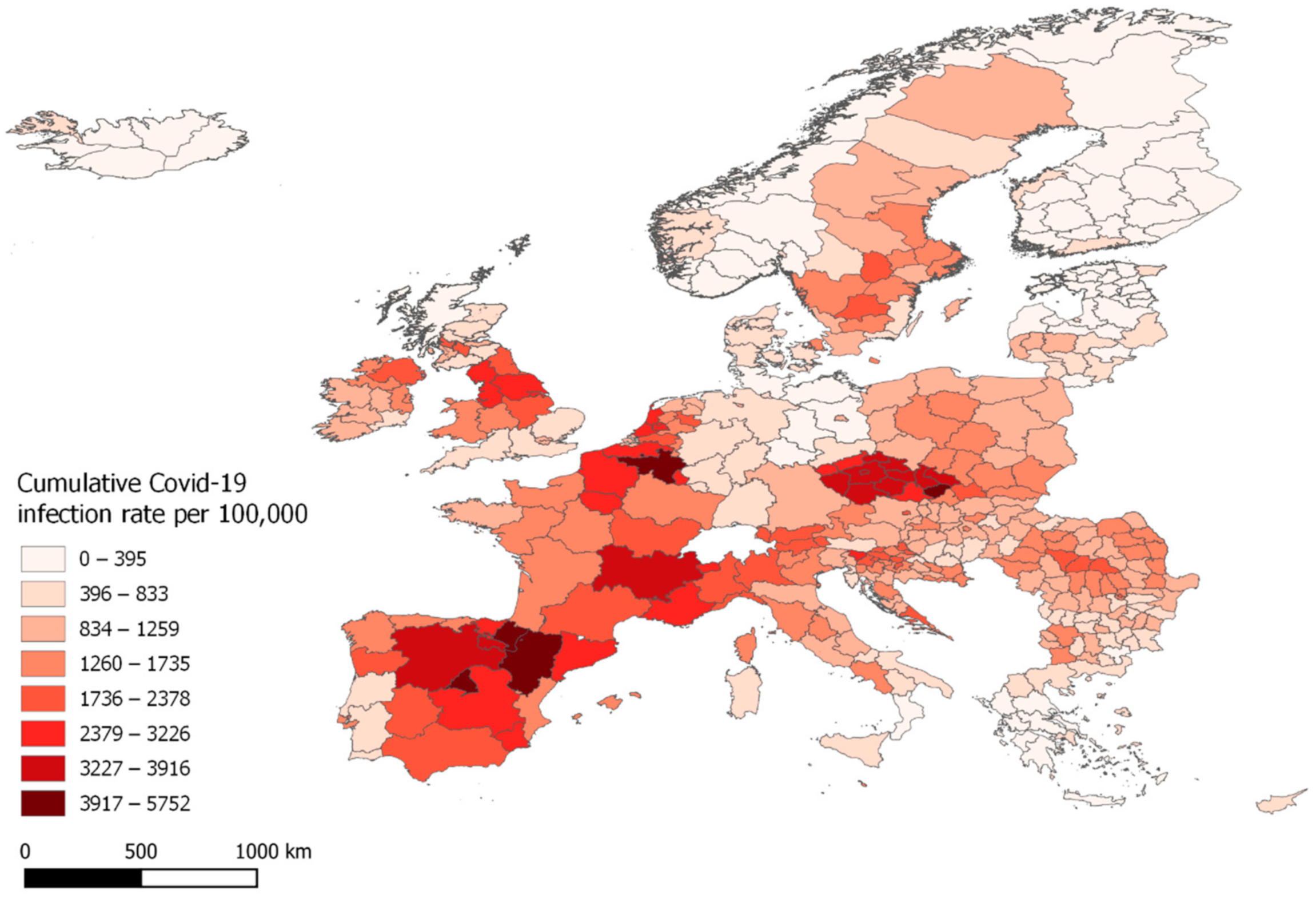
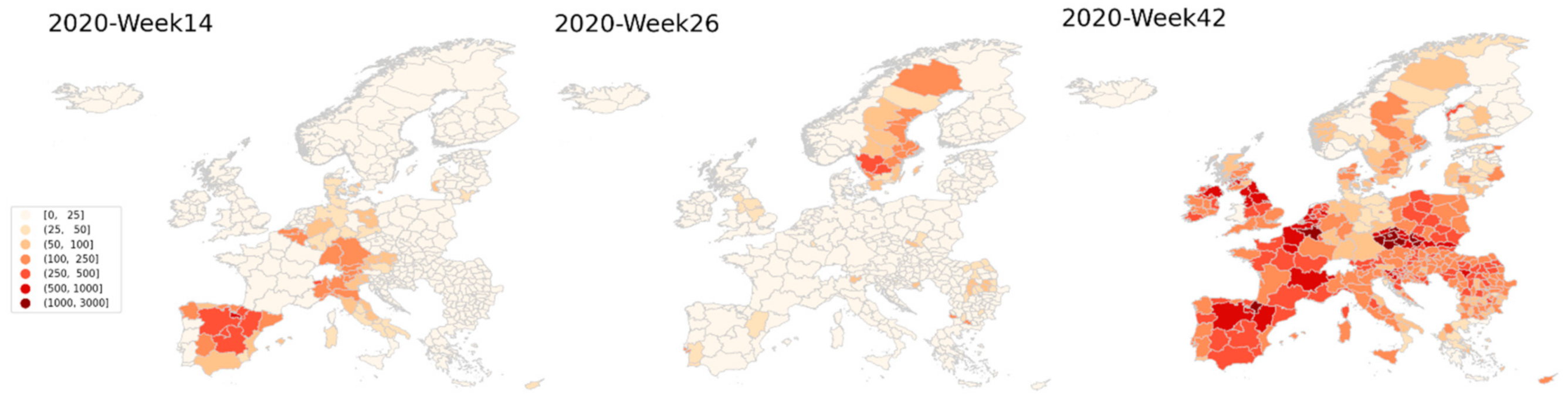
2.2.1. Exploratory Data Analysis
2.2.2. Space Time Patterns
2.2.3. Statistical Models: OLS & Geographically Weighted Regression
OLS
GWR
2.2.4. Machine Learning Prediction
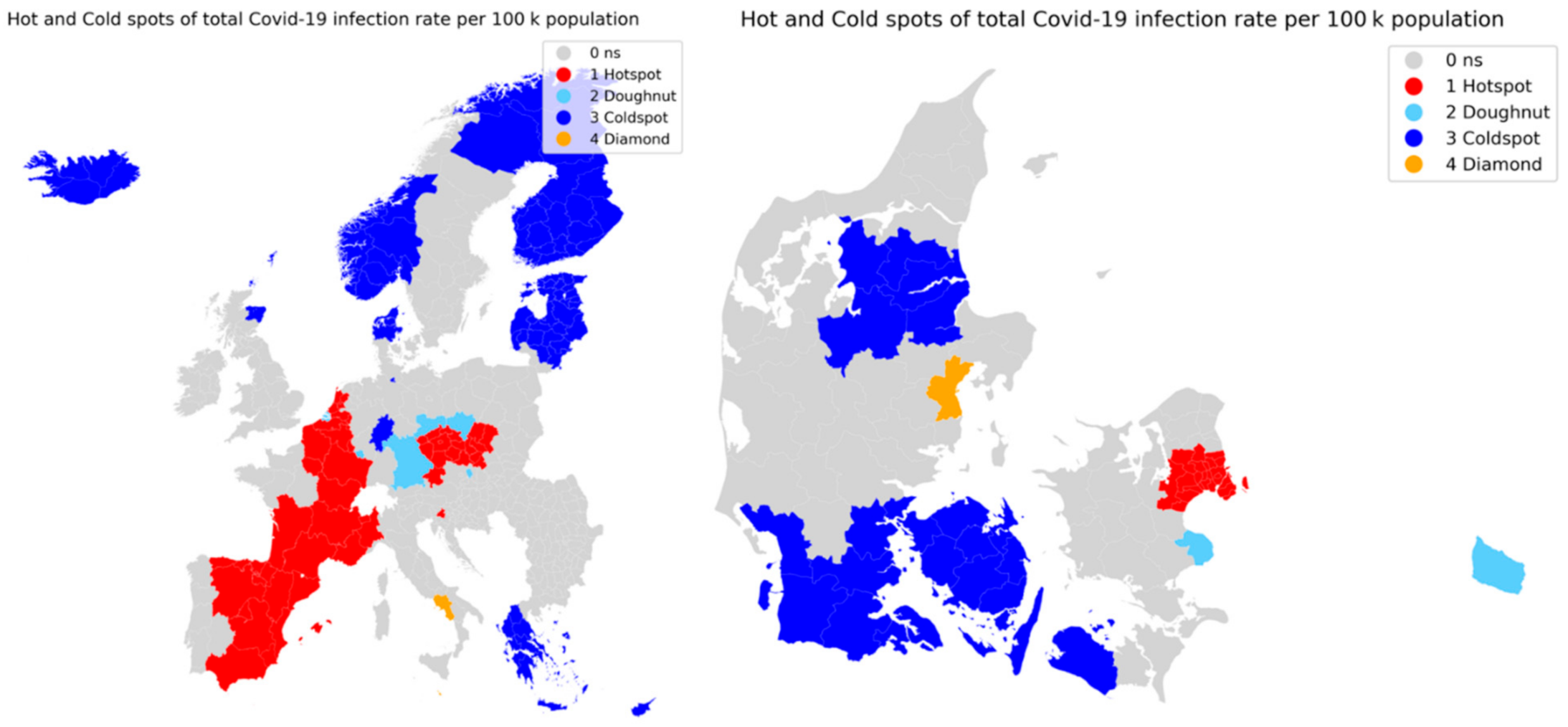
3. Results
3.1. Spatial Autocorrelation, EU and DK
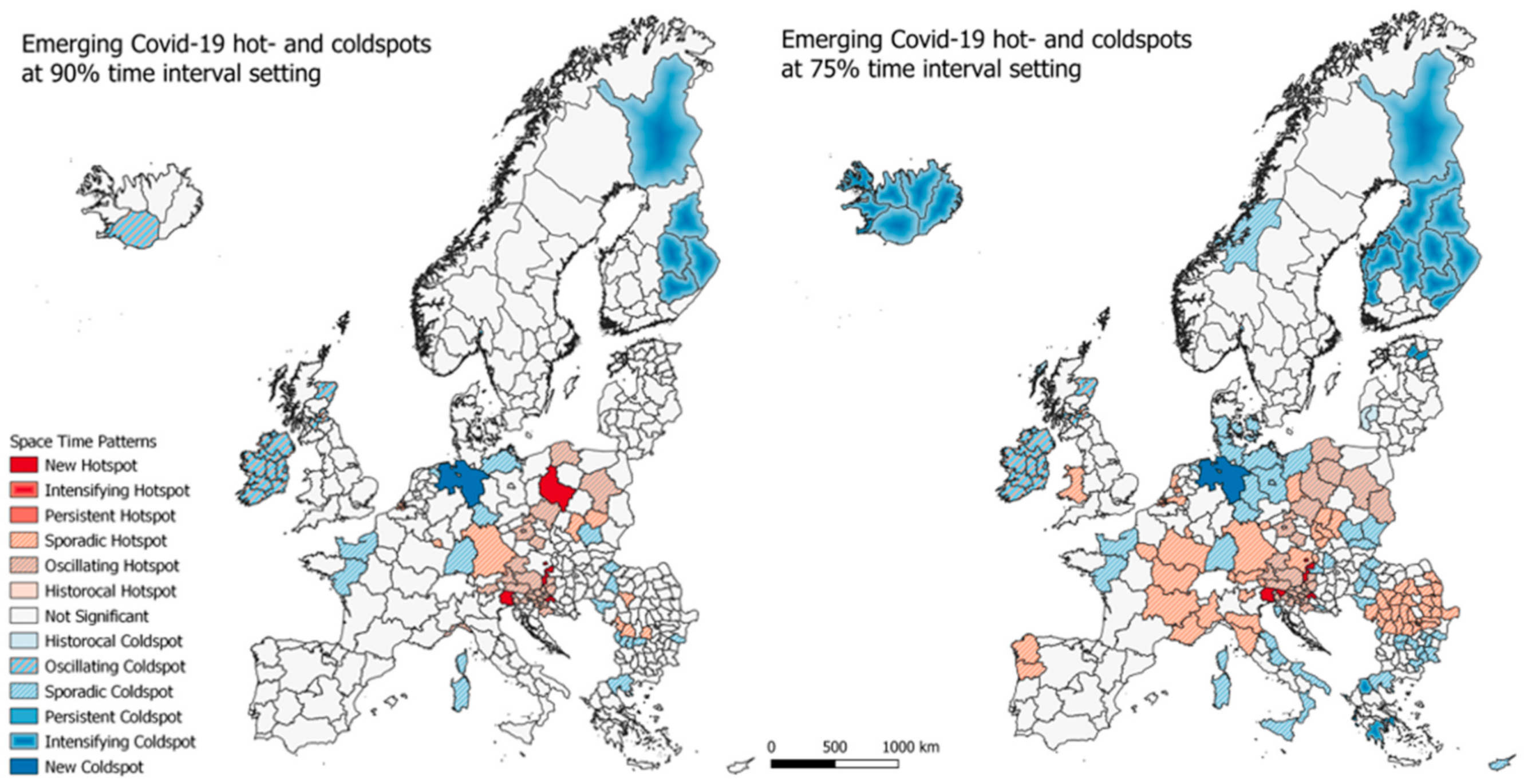
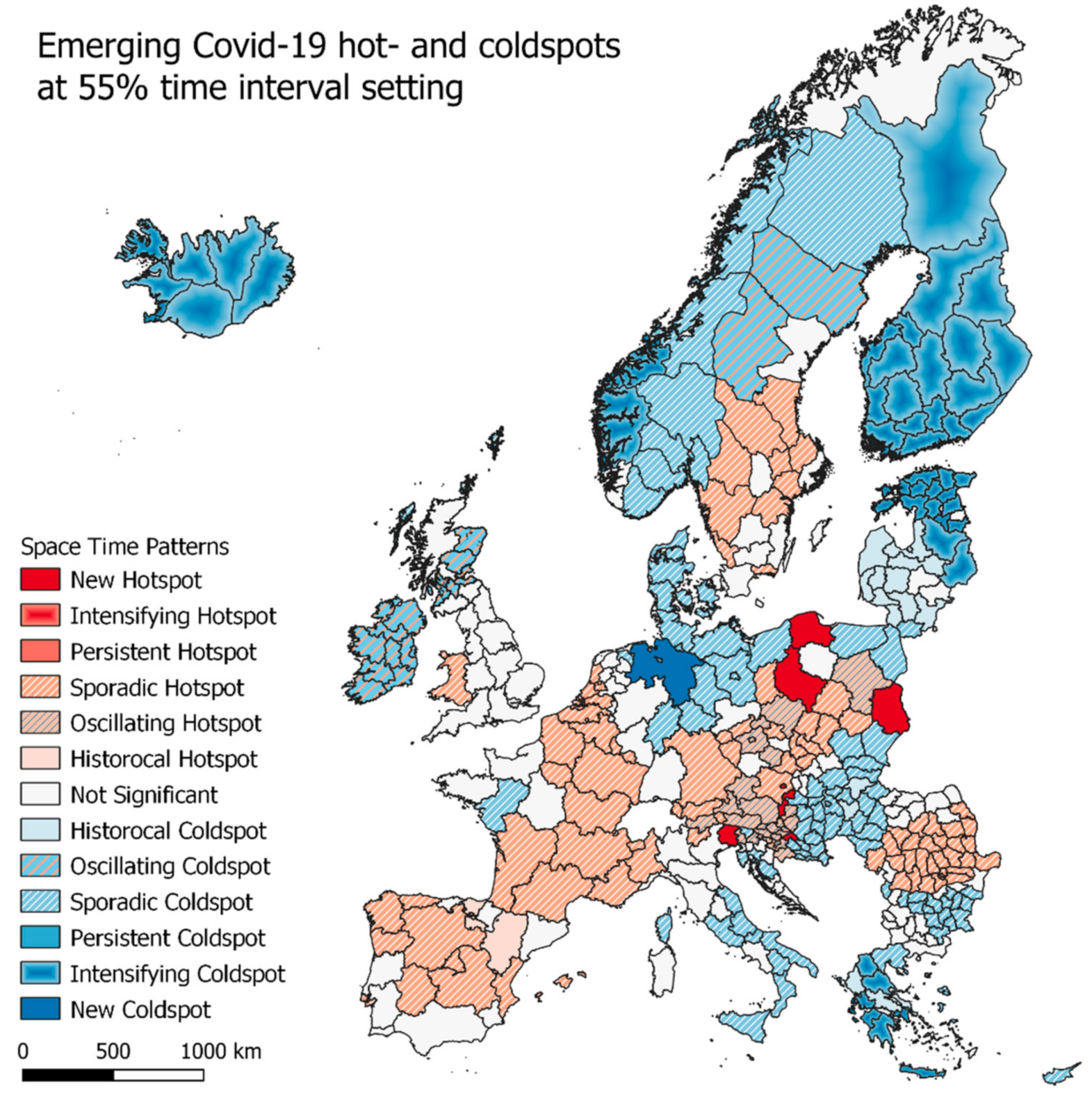
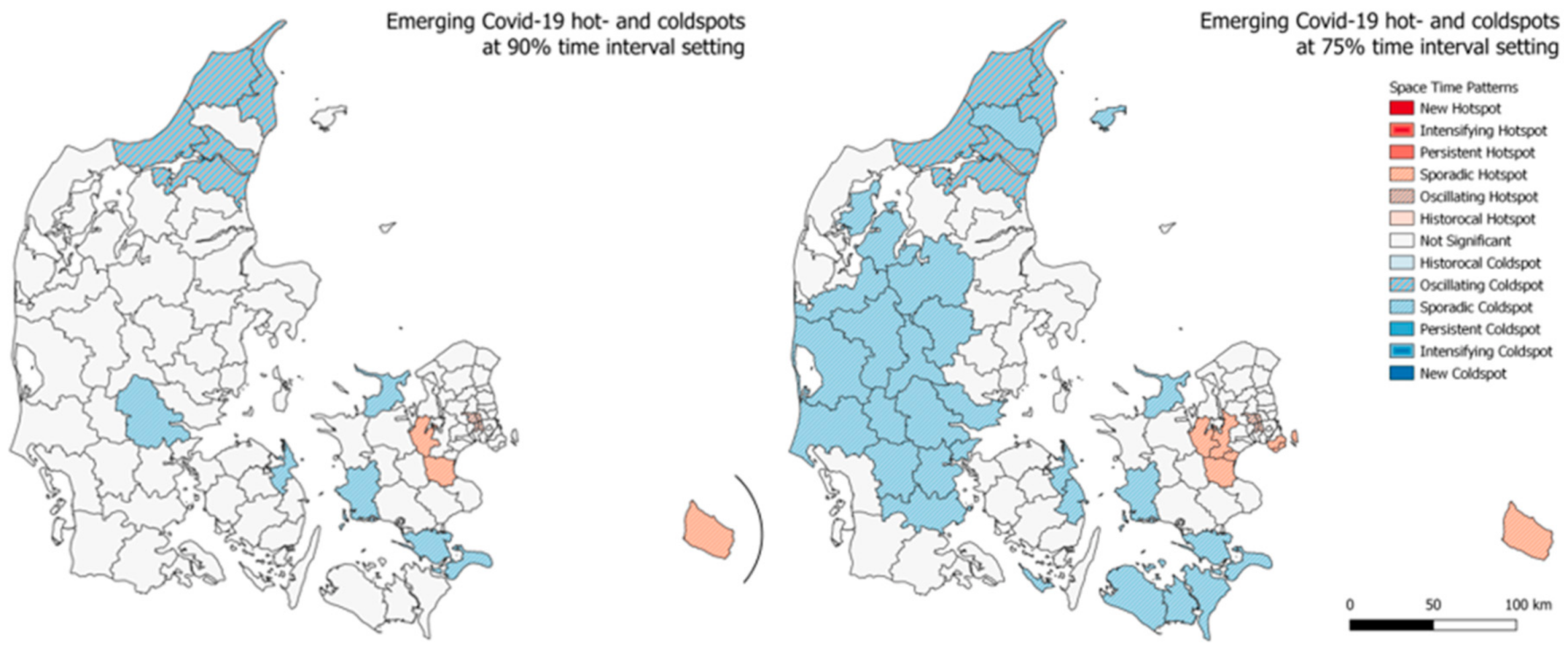
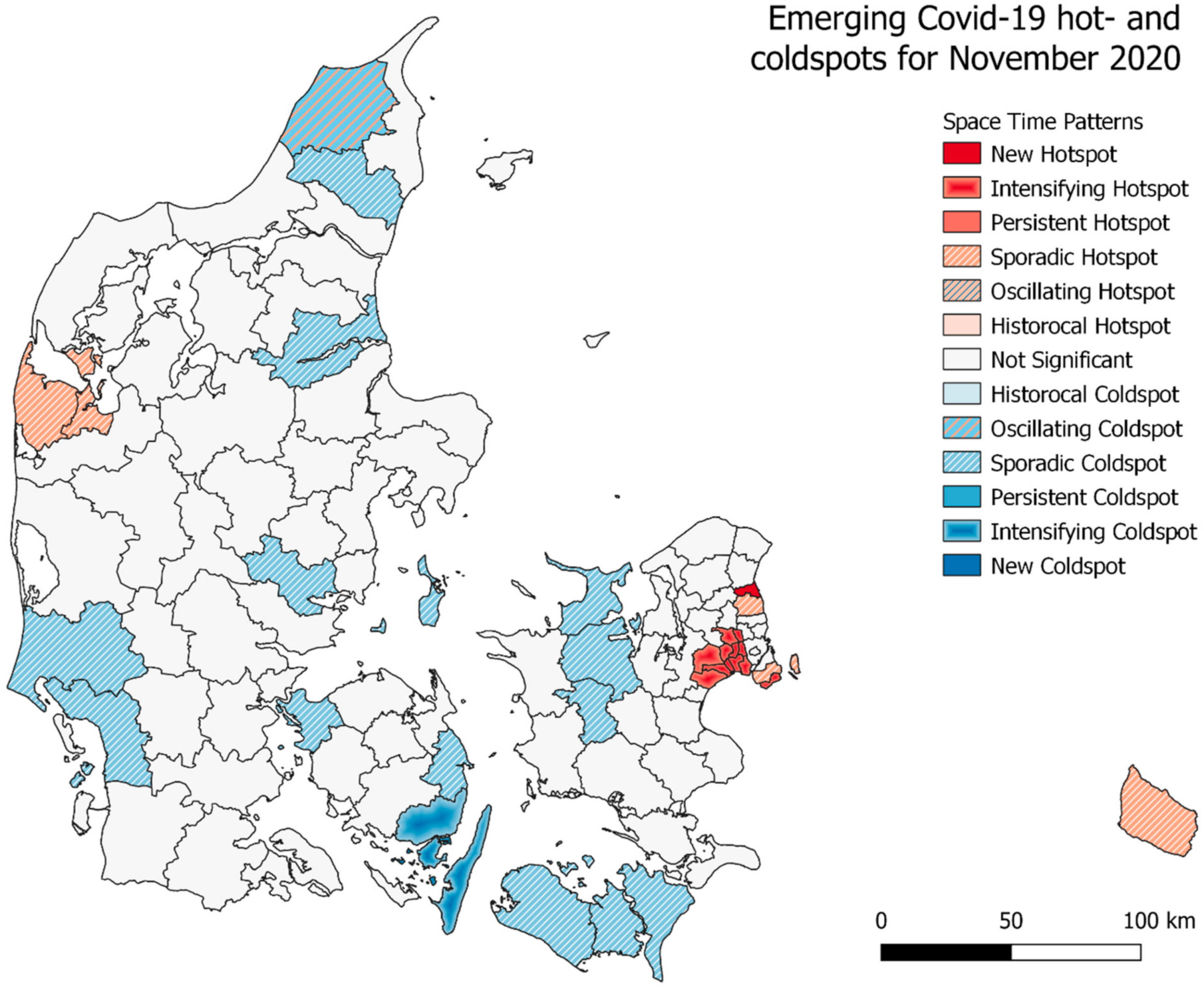
3.2. Space Time Patterns—Emerging Hotspot Analysis
3.2.1. Emerging Hotspots—Europe
3.2.2. Emerging Hotspots—Denmark
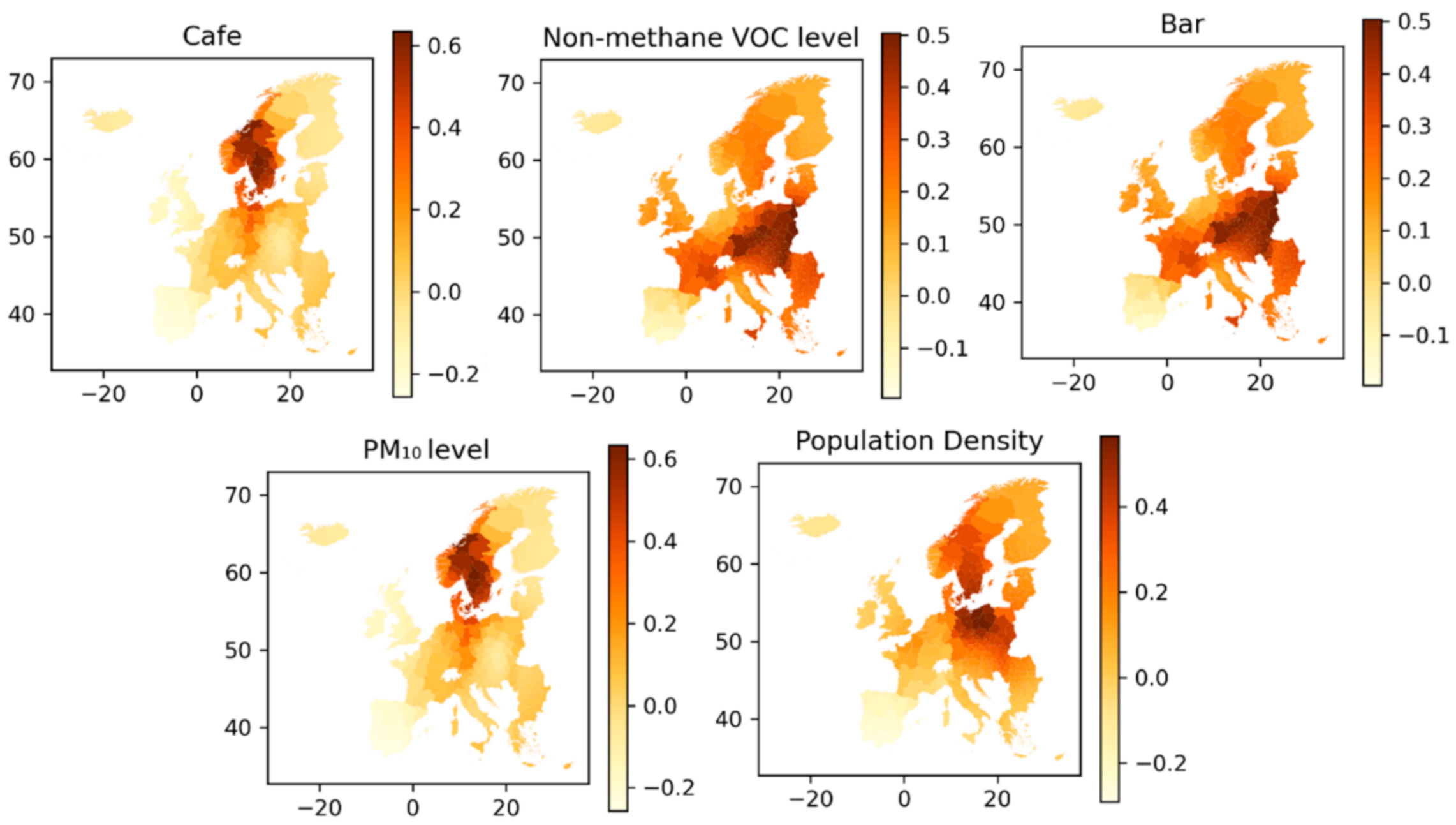
3.3. Geographically Weighted Regression—EU
3.4. Machine Learning Prediction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Weekly Epidemiological Update 29 December 2020. 2020. Available online: https://www.who.int/publications/m/item/weekly-epidemiological-update (accessed on 1 March 2021).
- UN-Habitat. UN-Habitat COVID-19 Response Plan. 2020. Available online: https://unhabitat.org/sites/default/files/2020/04/final_un-habitat_covid-19_response_plan.pdf (accessed on 11 July 2020).
- Adiga, A.; Chen, J.; Marathe, M.; Mortveit, H.; Venkatramanan, S.; Vullikanti, A. Data-Driven Modeling for Different Stages of Pandemic Response. J. Indian Inst. Sci. 2020, 100, 901–915. [Google Scholar] [CrossRef]
- Sharifi, A.; Khavarian-Garmsir, A.R. The COVID-19 pandemic: Impacts on cities and major lessons for urban planning, design, and management. Sci. Total Environ. 2020, 749, 142391. [Google Scholar] [CrossRef]
- Rose-Redwood, R.; Kitchin, R.; Apostolopoulou, E.; Rickards, L.; Blackman, T.; Crampton, J.; Rossi, U.; Buckley, M. Geographies of the COVID-19 pandemic. Dialog Hum. Geogr. 2020, 10, 97–106. [Google Scholar] [CrossRef]
- Kim, S.; Castro, M.C. Spatiotemporal pattern of COVID-19 and government response in South Korea (as of May 31, 2020). Int. J. Infect. Dis. 2020, 98, 328–333. [Google Scholar] [CrossRef]
- Giachino, M.; Valera, C.B.G.; Velásquez, S.R.; Dohrendorf-Wyss, M.A.; Rozanova, L.; Flahault, A. Understanding the Dynamics of the COVID-19 Pandemic: A Real-Time Analysis of Switzerland’s First Wave. Int. J. Environ. Res. Public Heal. 2020, 17, 8825. [Google Scholar] [CrossRef]
- Briz-Redón, Á.; Serrano-Aroca, Á. A spatio-temporal analysis for exploring the effect of temperature on COVID-19 early evolution in Spain. Sci. Total Environ. 2020, 728, 138811. [Google Scholar] [CrossRef]
- Malki, Z.; Atlam, E.-S.; Hassanien, A.E.; Dagnew, G.; Elhosseini, M.A.; Gad, I. Association between weather data and COVID-19 pandemic predicting mortality rate: Machine learning approaches. Chaos Solitons Fractals 2020, 138, 110137. [Google Scholar] [CrossRef] [PubMed]
- Sannigrahi, S.; Pilla, F.; Basu, B.; Basu, A.S. The overall mortality caused by COVID-19 in the European region is highly associated with demographic composition: A spatial regression-based approach. arXiv 2020, arXiv:2005.04029. [Google Scholar]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total. Environ. 2020, 728, 138884. [Google Scholar] [CrossRef] [PubMed]
- Kraemer, M.U.G.; Yang, C.-H.; Gutierrez, B.; Wu, C.-H.; Klein, B.; Pigott, D.M.; Du Plessis, L.; Faria, N.R.; Li, R.; Hanage, W.P.; et al. The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 2020, 368, 493–497. [Google Scholar] [CrossRef]
- Kapoor, A.; Ben, X.; Liu, L.; Perozzi, B.; Barnes, M.; Blais, M.; O’Banion, S. Examining COVID-19 Forecasting using Spatio-Temporal Graph Neural Networks. arXiv 2020, arXiv:2007.03113. [Google Scholar]
- Wang, P.; Zheng, X.; Li, J.; Zhu, B. Prediction of epidemic trends in COVID-19 with logistic model and machine learning technics. Chaos Solitons Fractals 2020, 139, 110058. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.; Gharehgozli, A. Developing a Machine Learning Framework to Determine the Spread of COVID-19. SSRN Electron. J. 2020, 1, 1–19. [Google Scholar] [CrossRef]
- Bao, R.; Zhang, A. Does lockdown reduce air pollution? Evidence from 44 cities in northern China. Sci. Total Environ. 2020, 731, 139052. [Google Scholar] [CrossRef]
- Collivignarelli, M.C.; Abbà, A.; Bertanza, G.; Pedrazzani, R.; Ricciardi, P.; Miino, M.C. Lockdown for CoViD-2019 in Milan: What are the effects on air quality? Sci. Total Environ. 2020, 732, 139280. [Google Scholar] [CrossRef]
- Girres, J.-F.; Touya, G. Quality Assessment of the French OpenStreetMap Dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Haklay, M. How Good is Volunteered Geographical Information? A Comparative Study of OpenStreetMap and Ordnance Survey Datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar] [CrossRef]
- Almendros-Jiménez, J.M.; Becerra-Terón, A. Analyzing the Tagging Quality of the Spanish OpenStreetMap. ISPRS Int. J. Geo-Inf. 2018, 7, 323. [Google Scholar] [CrossRef]
- Zheng, S.; Jianghua, Z. Assessing the completeness and positional accuracy of OpenStreetMap in China. In Thematic Cartography for the Society; Springer: Cham, Switzerland, 2014; pp. 171–189. [Google Scholar]
- Barrington-Leigh, C.; Millard-Ball, A. The world’s user-generated road map is more than 80% complete. PLoS ONE 2017, 12, e0180698. [Google Scholar] [CrossRef]
- Mazzulla, G.; Forciniti, C. Spatial association techniques for analysing trip distribution in an urban area. Eur. Transp. Res. Rev. 2012, 4, 217–233. [Google Scholar] [CrossRef]
- ESRI. How Emerging Hot Spot Analysis Works. 2020. Available online: https://pro.arcgis.com/en/pro-app/latest/tool-reference/space-time-pattern-mining/learnmoreemerging.htm (accessed on 14 December 2020).
- Wheeler, D.C. Geographically Weighted Regression. Handb. Reg. Sci. 2013, 47, 1435–1459. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Support Vector Machines for classification and regression. Analyst 2010, 135, 230–267. [Google Scholar] [CrossRef] [PubMed]
- Hepağuşlar, H.; Ozzeybek, D.; Ozkardeşler, S.; Taşdöğen, A.; Duru, S.; Elar, Z. Propofol and sevoflurane during epidural/general anesthesia: Comparison of early recovery characteristics and pain relief. Middle East J. Anaesthesiol. 2004, 17, 819–832. [Google Scholar]
- Brunsdon, C.; Fotheringsham, S.; Charlton, M. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 1996, 28, 381–398. [Google Scholar] [CrossRef]
- Lin, C.-H.; Wen, T.-H. Using Geographically Weighted Regression (GWR) to Explore Spatial Varying Relationships of Immature Mosquitoes and Human Densities with the Incidence of Dengue. Int. J. Environ. Res. Public Heal. 2011, 8, 2798–2815. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Cummings, D.A.T.; Fraser, C.; Cajka, J.C.; Cooley, P.C.; Burke, D.S. Strategies for mitigating an influenza pandemic. Nat. Cell Biol. 2006, 442, 448–452. [Google Scholar] [CrossRef] [PubMed]
- Holko, A.; Mȩdrek, M.; Pastuszak, Z.; Phusavat, K. Epidemiological modeling with a population density map-based cellular automata simulation system. Expert Syst. Appl. 2016, 48, 1–8. [Google Scholar] [CrossRef]
- Coşkun, H.; Yıldırım, N.; Gündüz, S. The spread of COVID-19 virus through population density and wind in Turkey cities. Sci. Total Environ. 2021, 751, 141663. [Google Scholar] [CrossRef]
- Pequeno, P.; Mendel, B.; Rosa, C.; Bosholn, M.; Souza, J.L.; Baccaro, F.; Barbosa, R.; Magnusson, W. Air transportation, population density and temperature predict the spread of COVID-19 in Brazil. PeerJ 2020, 8, e9322. [Google Scholar] [CrossRef] [PubMed]
- Rashed, E.A.; Kodera, S.; Gomez-Tames, J.; Hirata, A. Influence of Absolute Humidity, Temperature and Population Density on COVID-19 Spread and Decay Durations: Multi-Prefecture Study in Japan. Int. J. Environ. Res. Public Heal. 2020, 17, 5354. [Google Scholar] [CrossRef] [PubMed]
- Kodera, S.; Rashed, E.A.; Hirata, A. Correlation between COVID-19 Morbidity and Mortality Rates in Japan and Local Population Density, Temperature, and Absolute Humidity. Int. J. Environ. Res. Public Heal. 2020, 17, 5477. [Google Scholar] [CrossRef] [PubMed]

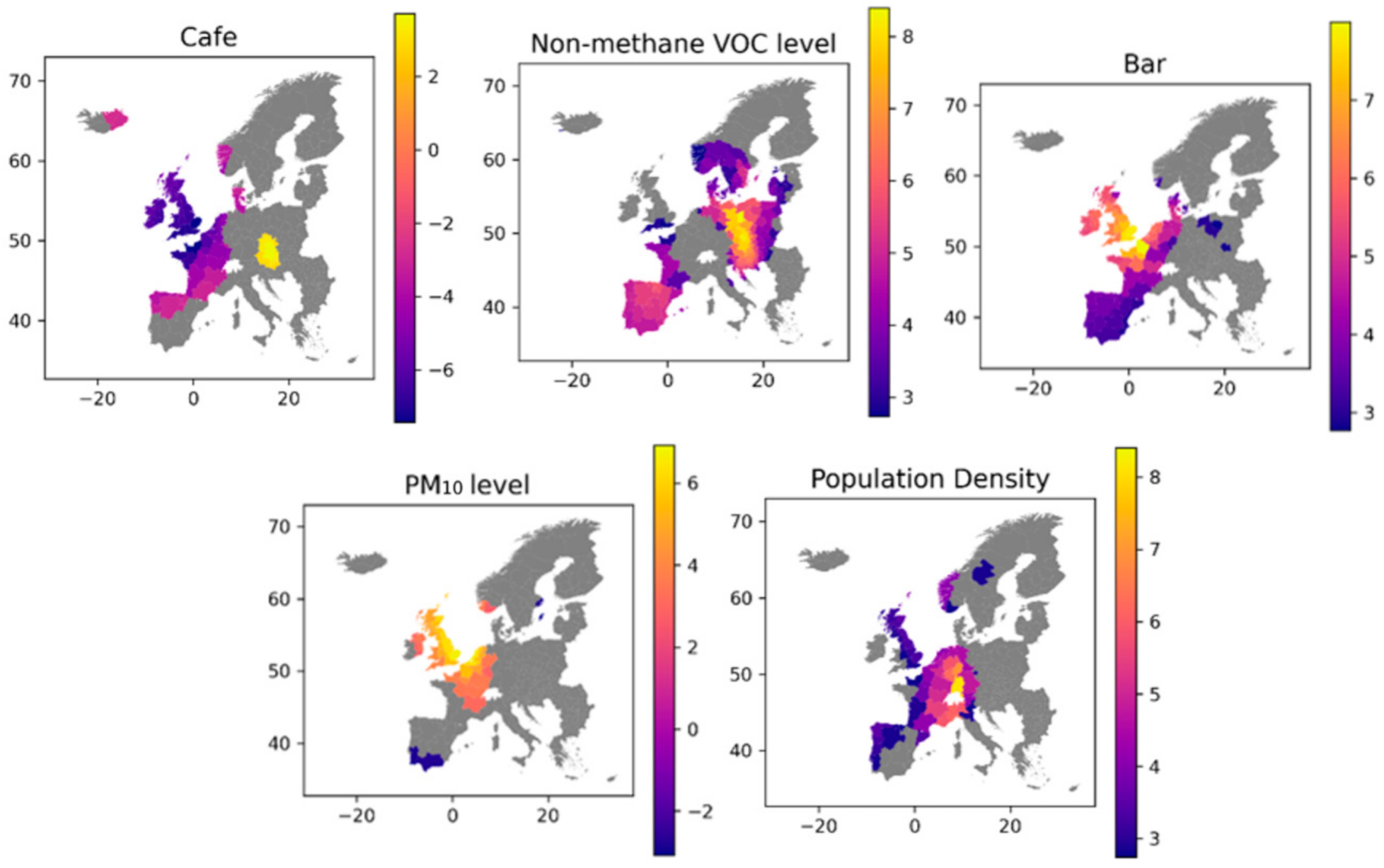
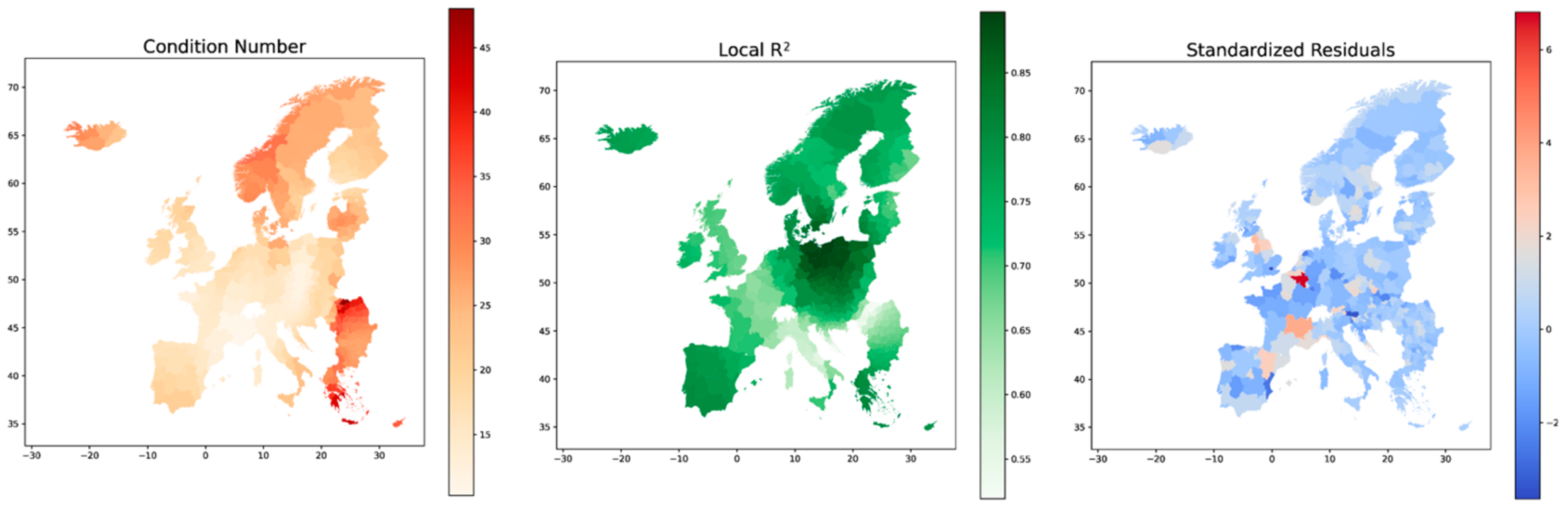
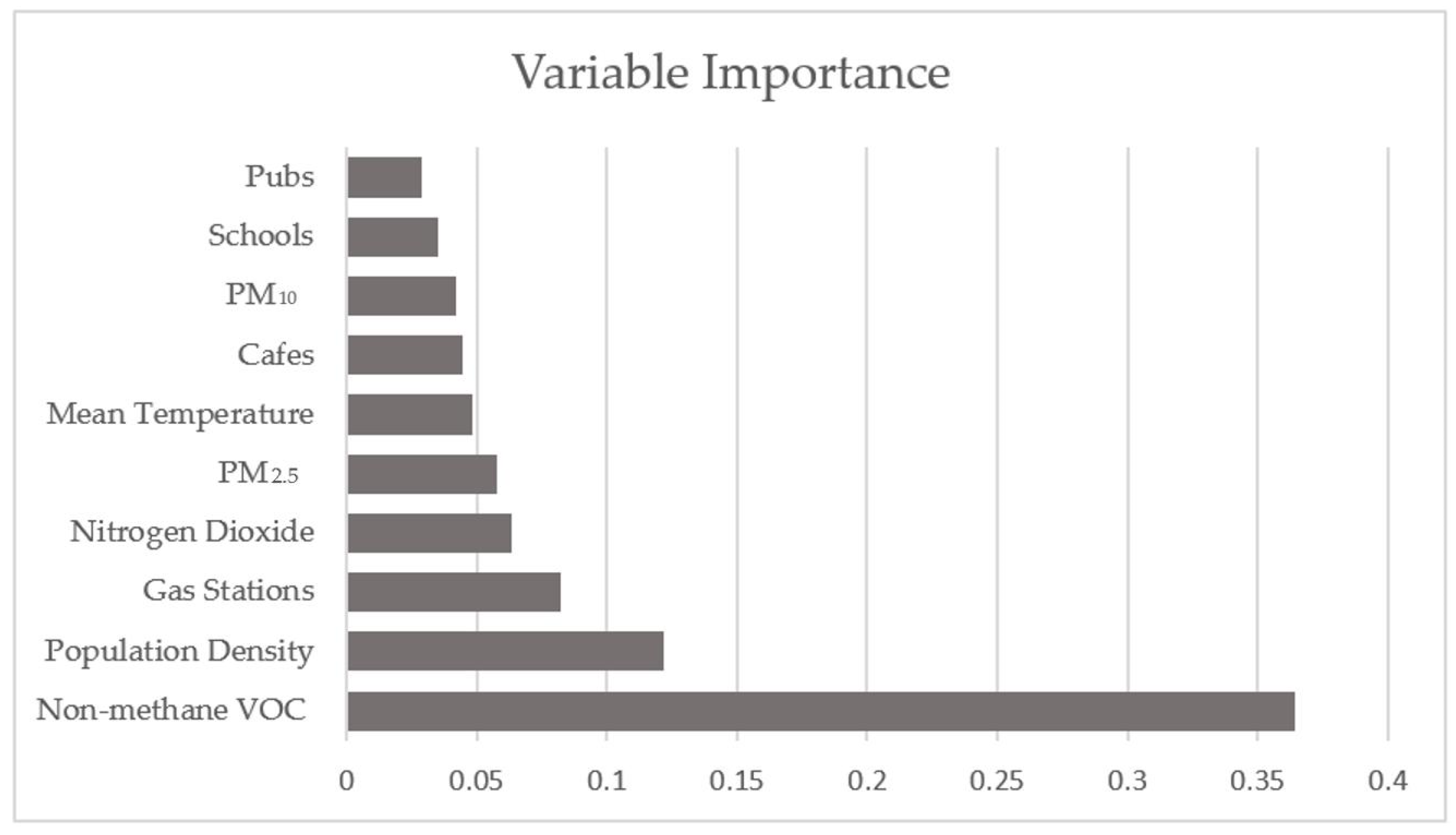
| Variable | Argument |
|---|---|
| Total infected [dependent variable] | X0 |
| Population Density | X1 |
| Restaurants per cap. | X2 |
| Cafes per cap. | X3 |
| Fast Food Places per cap. | X4 |
| Pubs per cap. | X5 |
| Bars per cap. | X6 |
| Gas Stations per cap. | X7 |
| Schools per cap. | X8 |
| Doctors’ Offices per cap. | X9 |
| Kinder gardens per cap. | X10 |
| Annual mean temperature | X11 |
| Nitrogen dioxide, year-over-year change | X12 |
| Particulate matter < 2.5 µm (PM2.5, year-over-year change | X13 |
| Non-methane VOCs (volatile organic compounds), year-over-year change | X14 |
| Particulate matter < 10 µm (PM10), year-over-year change | X15 |
| Space Time Category | Definition (tmax = 90%, tmin = 10%) |
|---|---|
| New Hotspot | Region identified as hotspot in the last time step that has not been a hotspot before |
| Sporadic Hotspot | Region identified as a hot spot at least once but in less than 10% of the time steps that also has not been a cold spot |
| Oscillating Hotspot | Region identified as hotspot in the last time step and been a hotspot in less than 90% of the time steps that also been a coldspot at least once |
| Historical Hotspot | Region that is not identified as hot spot in the last time step but has been a hot spot in more than 90% of the time steps |
| Intensifying Hotspot | Region identified as a hotspot in the last time step that has also been a hotspot in more than 90% of the time steps |
| Persistent Hotspot | Region identified as a hotspot in at least 90% of the time steps |
| New Coldspot | Region identified as a coldspot in the last time step that has not been a coldspot before |
| Sporadic Coldspot | Region identified as a coldspot at least once but in less than 10% of the time steps that also has not been a hotspot |
| Oscillating Coldspot | Region identified as a cold spot in the last time step and been a coldspot in less than 90% of the time steps that also been a hotspot at least once |
| Historical Coldspot | Region that is not identified as coldspot in the last time step but has been a coldspot in more than 90% of the time steps |
| Intensifying Coldspot | Region identified as a coldspot in the last time step that has also been a coldspot in more than 90% of the time steps |
| Persistent Coldspot | Region identified as a coldspot in at least 90% of the time steps |
| Not Significant | None of the above |
| Model | Res Sum Squares | AIC | AICc | R2 | Adjusted R2 |
|---|---|---|---|---|---|
| OLS | 219.230 | 927.850 | 931.448 | 0.453 | 0.432 |
| GWR | 66.922 | 654.585 | 752.719 | 0.833 | 0.765 |
| Variable | OLS | p-Value | GWR | ||||
|---|---|---|---|---|---|---|---|
| Est | SE | STD | Min | Median | Max | ||
| X0 | 0.000 | 0.038 | 1.000 | 0.380 | −0.909 | −0.010 | 0.805 |
| X1 | 0.111 | 0.043 | 0.009 | 0.137 | −0.110 | 0.113 | 0.676 |
| X2 | 0.109 | 0.063 | 0.084 | 0.222 | −0.246 | 0.167 | 1.122 |
| X3 | −0.264 | 0.056 | 0.000 | 0.412 | −1.612 | −0.184 | 0.279 |
| X4 | 0.007 | 0.049 | 0.893 | 0.306 | −0.784 | 0.119 | 0.683 |
| X5 | −0.071 | 0.045 | 0.116 | 0.197 | −0.761 | −0.113 | 0.487 |
| X6 | 0.195 | 0.054 | 0.000 | 0.359 | −0.598 | 0.112 | 1.312 |
| X7 | 0.011 | 0.051 | 0.828 | 0.441 | −0.629 | −0.018 | 1.487 |
| X8 | 0.048 | 0.046 | 0.297 | 0.208 | −0.568 | −0.028 | 0.355 |
| X9 | −0.102 | 0.044 | 0.021 | 0.306 | −1.074 | −0.200 | 1.349 |
| X10 | −0.087 | 0.045 | 0.056 | 0.225 | −0.610 | 0.010 | 0.780 |
| X11 | −0.134 | 0.052 | 0.010 | 0.322 | −1.135 | −0.280 | 0.640 |
| X12 | −0.115 | 0.049 | 0.019 | 0.353 | −1.257 | −0.022 | 0.794 |
| X13 | 0.144 | 0.057 | 0.011 | 0.298 | −0.997 | 0.039 | 0.500 |
| X14 | 0.506 | 0.050 | 0.000 | 0.279 | −0.124 | 0.372 | 0.956 |
| X15 | −0.142 | 0.050 | 0.004 | 0.376 | −0.697 | −0.069 | 1.360 |
| Area | Nr. of Regions | Model | Accuracy | MAE |
|---|---|---|---|---|
| Europe | Random Forest | 52% | 0.079 | |
| 401 | Lasso | 36% | 0.153 | |
| Support Vector Regression | 51% | 0.151 | ||
| Europe—Hot- & Coldspots | Random Forest | 76% | 0.099 | |
| 128 | Lasso | 74% | 0.285 | |
| Support Vector Regression | 73% | 0.256 | ||
| Europe—Hotspots | Random Forest | 19% | 0.177 | |
| 56 | Lasso | - % | 0.217 | |
| Support Vector Regression | - % | 0.221 | ||
| Denmark | Random Forest | 61% | 0.095 | |
| 98 | Lasso | 35% | 0.233 | |
| Support Vector Regression | 41% | 0.232 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hass, F.S.; Jokar Arsanjani, J. The Geography of the Covid-19 Pandemic: A Data-Driven Approach to Exploring Geographical Driving Forces. Int. J. Environ. Res. Public Health 2021, 18, 2803. https://doi.org/10.3390/ijerph18062803
Hass FS, Jokar Arsanjani J. The Geography of the Covid-19 Pandemic: A Data-Driven Approach to Exploring Geographical Driving Forces. International Journal of Environmental Research and Public Health. 2021; 18(6):2803. https://doi.org/10.3390/ijerph18062803
Chicago/Turabian StyleHass, Frederik Seeup, and Jamal Jokar Arsanjani. 2021. "The Geography of the Covid-19 Pandemic: A Data-Driven Approach to Exploring Geographical Driving Forces" International Journal of Environmental Research and Public Health 18, no. 6: 2803. https://doi.org/10.3390/ijerph18062803
APA StyleHass, F. S., & Jokar Arsanjani, J. (2021). The Geography of the Covid-19 Pandemic: A Data-Driven Approach to Exploring Geographical Driving Forces. International Journal of Environmental Research and Public Health, 18(6), 2803. https://doi.org/10.3390/ijerph18062803







