Next Article in Journal
A Comprehensive Assessment of the Associations Between Season of Conception and Birth Defects, Texas, 1999–2015
Next Article in Special Issue
Corrections: Xu, L.; Mondal, D.; Polya, D.A. Positive Association of Cardiovascular Disease (CVD) with Chronic Exposure to Drinking Water Arsenic (As) at Concentrations below the WHO Provisional Guideline Value: A Systematic Review and Meta-Analysis. Int. J. Environ. Res. Public Health 2020, 17, 2536
Previous Article in Journal
Trunk Flexion Monitoring among Warehouse Workers Using a Single Inertial Sensor and the Influence of Different Sampling Durations
Previous Article in Special Issue
A Simplified Questionnaire for the Assessment of Inorganic Arsenic Intake in a Japanese Population
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJERPH
Volume 17
Issue 19
10.3390/ijerph17197119
ijerph-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Groundwater Arsenic Distribution in India by Machine Learning Geospatial Modeling

by
Joel Podgorski
1,*,†,
Ruohan Wu
1,
Biswajit Chakravorty
2 and
David A. Polya
1,*
1
Department of Earth and Environmental Sciences and Williamson Research Centre for Molecular Environmental Science, University of Manchester, Manchester M13 9PL, UK
2
Centre for Flood Management Studies, National Institute of Hydrology, Water and Land Management Institute Complex, Phulwarisharif, Patna, Bihar 801505, India
*
Authors to whom correspondence should be addressed.
†
Now at Department Water Resources and Drinking Water, Eawag, Swiss Federal Institute of Aquatic Science and Technology, 8600 Dübendorf, Switzerland.
Int. J. Environ. Res. Public Health 2020, 17(19), 7119; https://doi.org/10.3390/ijerph17197119
Submission received: 7 September 2020 / Revised: 24 September 2020 / Accepted: 25 September 2020 / Published: 28 September 2020
(This article belongs to the Special Issue Arsenic Exposure in Environment and Human Health)
Browse Figures
Versions Notes

Abstract

:
Groundwater is a critical resource in India for the supply of drinking water and for irrigation. Its usage is limited not only by its quantity but also by its quality. Among the most important contaminants of groundwater in India is arsenic, which naturally accumulates in some aquifers. In this study we create a random forest model with over 145,000 arsenic concentration measurements and over two dozen predictor variables of surface environmental parameters to produce hazard and exposure maps of the areas and populations potentially exposed to high arsenic concentrations (>10 µg/L) in groundwater. Statistical relationships found between the predictor variables and arsenic measurements are broadly consistent with major geochemical processes known to mobilize arsenic in aquifers. In addition to known high arsenic areas, such as along the Ganges and Brahmaputra rivers, we have identified several other areas around the country that have hitherto not been identified as potential arsenic hotspots. Based on recent reported rates of household groundwater use for rural and urban areas, we estimate that between about 18–30 million people in India are currently at risk of high exposure to arsenic through their drinking water supply. The hazard models here can be used to inform prioritization of groundwater quality testing and environmental public health tracking programs.

1. Introduction

Around the world, but particularly so in India, there is an ever-increasing dependence on groundwater for drinking water supplies and irrigation [1,2]. This is related, in part, to population and economic growth as well as to climate change.
Groundwater is generally much less susceptible to biological and other sources of anthropogenic contamination than is surface water. Its longer residence time and exposure to varying geochemical environments in an aquifer, however, can subject groundwater to the accumulation of various chemical elements in sufficiently high concentrations to pose a health risk to those using it for drinking or cooking [3]. Examples of such naturally occurring (geogenic) contaminants include arsenic, fluoride, manganese, and uranium. Of these, arsenic is one of the most serious contaminants, both in terms of toxicity and ubiquity, which is due to its widespread presence in trace amounts in minerals found in all types of rocks and sediments [3,4]. Many of the large-scale occurrences of geogenic arsenic contamination of groundwater are found in Asia and are due to the release of arsenic found in recently deposited sediments that are exposed to geochemical conditions that are either predominantly reducing (e.g., Ganges-Brahmaputra and Mekong deltas [5]) or oxidizing (e.g., Indus plain [6]). The dominant mobilization mechanisms involve microbially mediated reductive dissolution of host Fe(III) oxyhydroxide minerals and/or reduction of arsenic [7] in reducing environments, while in general intra-aquifer concentrations may be strongly modified by pH- and competitive anion-dependent reversible sorption processes [8]. Other common but less widespread sources or mechanisms of arsenic release into aquifers include the oxidation of sulfide minerals and geothermal activity [9,10].
Long-term exposure to arsenic can lead to various skin diseases, cancers, and cardiovascular diseases [3]. The most common intake pathways include drinking arsenic-contaminated groundwater or consuming high inorganic arsenic crops, particularly rice and those grown in high arsenic soils and/or irrigated with arsenic-contaminated water [11]. Although at least some of the arsenic found in food is present in a less toxic organic form, the arsenic present in groundwater predominantly occurs as one of the more toxic inorganic species, that is, arsenate or arsenite [3]. For this reason, the World Health Organization (WHO) recommends keeping arsenic concentrations in drinking water as low as possible. Although it has a guideline concentration of 10 µg/L, this is only provisional due in part to the difficulties of removing arsenic from water [12]. Likewise, India has set the concentration of 10 µg/L as a requirement (“acceptable limit”), whereas 50 µg/L is kept as a permissible limit in the absence of alternate sources [13].
Aside from some of the well-known arsenic-contaminated areas of India, such as along the Ganges and Brahmaputra rivers in parts of Assam, Bihar, Uttar Pradesh, and West Bengal, groundwater arsenic is not comprehensively tested throughout the country. The complete picture of arsenic contamination in India may therefore not be fully understood. There may also exist in the country areas of arsenic groundwater contamination that have not yet been identified. In order to help determine where high concentrations of arsenic in groundwater may exist in India, we have employed machine learning with a comprehensive dataset of arsenic concentrations and various environmental parameters to produce a model of arsenic-contaminated groundwater for the whole of India. This should indicate where in the country high groundwater arsenic concentrations are likely to be found where no arsenic measurements currently exist. Such an approach has been previously been carried out for the states of Gujarat [14] and Uttar Pradesh [15], as well as the entire world [16], but never solely for all of the country of India or with the substantially larger dataset of arsenic concentrations as in this study. All other factors being equal, a modeling study conducted on a smaller area allows the model to focus on, and better characterize, the arsenic occurrences in that area and thereby produce a more accurate model.

2. Materials and Methods

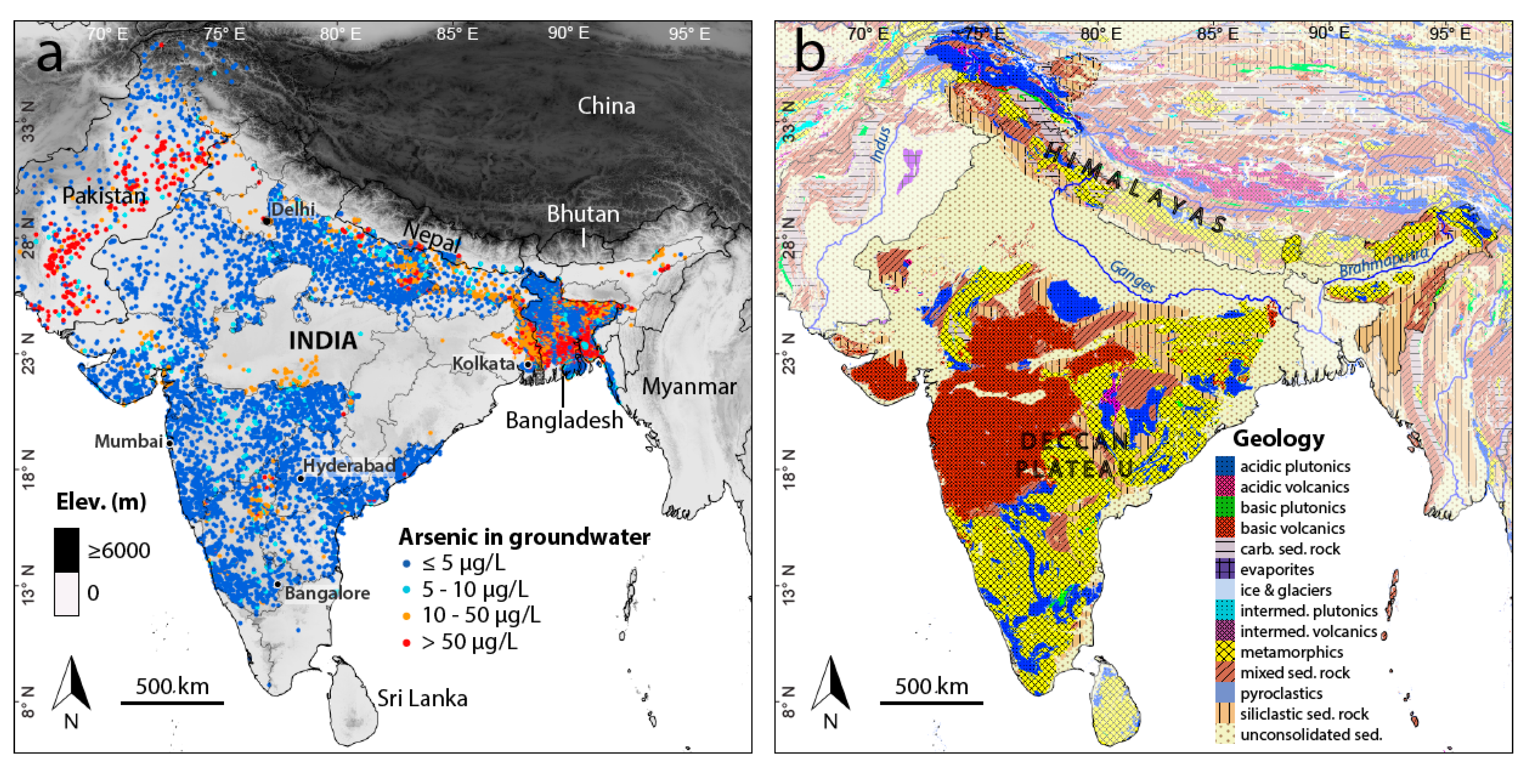
2.1. Arsenic Concentration Measurements

A total of 145,099 geographically distinct arsenic concentration measurements in groundwater were assembled from a multitude of sources including from a systematic compilation of published sources (Table 1). Although the focus of this study is on India, data from adjoining countries, where available, were incorporated to help characterize the occurrence of arsenic in border areas. As such, data acquisition was concentrated on India, which contributed 91% of the data, whereas available datasets from the neighboring countries of Bangladesh (3%), Nepal (5%), and Pakistan (1%) were also included. Reported concentrations were mainly determined by ICP-MS or AA, although some field kit test measurements assured by cross-calibration with laboratory measurements were also included, particularly for areas with otherwise limited data. However, the model sensitivity to the precision of the arsenic measurements in the dataset is lessened by the fact that we convert them to binary format before modeling (see below).
As many data are heavily concentrated in a few areas in West Bengal and to a lesser degree Bihar and the Terai (Nepal), an effort was made to reduce the disproportionately high frequency of data coming from these areas and thereby temper their influence on the model. To this end, the concentration measurements were averaged to generate individual data points corresponding to the 1-km × 1-km resolution of the predictor variables where more than one original data point was located within a 1-km × 1-km pixel. This considerably reduced the size of the dataset to 23,799 data points (Figure 1), with the breakdown by country being: India (74%), Bangladesh (15%), Nepal (8%), and Pakistan (3%). The resulting cumulative distribution of arsenic concentrations is shown in Figure S1, with 42% of the concentrations exceeding 10 µg/L. As explained below, a binary target variable was modeled, for which the arsenic concentrations were first recoded to either 0 or 1 according to them being either less than or equal to 10 µg/L or greater than 10 µg/L.

2.2. Predictor Variables

Although the target of the modeling is the concentration of arsenic located at some depth from the surface, only parameters determined at the surface are available in a spatially continuous sense across all of India. This is due to the generally high cost and/or difficulty of obtaining relevant subsurface data (e.g., geophysical measurements, drill logs) across the entire country.
In total, 26 different spatially continuous parameters were used as predictor variables in modeling (Table 2). These variables were selected based on their known or perceived function as proxies for the accumulation of arsenic in groundwater [16]. Most of the variables are related to climate or the surface geology, which includes metamorphic and sedimentary rocks in the Himalayas in the north, volcanic and metamorphic units in Deccan plateau in the south, and extensive unconsolidated sediments along the Ganges and Brahmaputra rivers in between (Figure 1b). In addition, included are many soil parameters, which are influenced by both climate and geology, as well as land cover, topography, and water table depth. All but two of the variables are available as 1-km x 1-km rasters (30 arc-second resolution). The two exceptions are the categorical variables of land cover and lithology, both of which are provided as polygon files that were then converted to the same 30 arc-second resolution (1 km at the equator). In preparation for modeling, the geographical coordinates of the 23,799 arsenic data points were used to retrieve the corresponding values of these predictor variables and added to a modeling table.

2.3. Prediction Modeling

The arsenic concentration dataset and predictor variables described above were used to create a statistical prediction model of the occurrence of arsenic in groundwater exceeding the WHO and national India guideline concentration of arsenic in drinking water of 10 µg/L. A binary rather than a continuous response variable was chosen due to the anticipated application of the resulting prediction model being to address progressing towards fuller compliance with the 10 µg/L regulatory standard. Furthermore, as we were restricted by necessity to using surface parameters to predict arsenic concentrations at depth, modeling a binary target variable circumvents some of the associated uncertainty and as a consequence should improve the model’s effectiveness.
Although other statistical learning approaches, such as logistic regression and support vector machines, were initially attempted, the random forest method [59] was ultimately adopted due its superior prediction performance in initial tests and was implemented using the R programming language [60]. Random forests are ensembles of decision trees that are grown with elements of introduced randomness. The data used to grow an individual tree are randomly selected by sampling with replacement from the full (training) dataset, which results in about 2/3 of the data rows being utilized, some of which multiple times. Furthermore, the number of predictor variables made available at each branch is restricted and the variables are randomly chosen. Because not all variables are considered simultaneously, any possible effects of multicollinearity among predictors can generally be disregarded in a random forest [61].
The typical number of variables made available at each branch of the trees grown in a random forest is the square root of the number of predictors, which in this case would have been five (taking the square root of 26). This parameter was tuned in order to find the optimal value to use with our dataset by trying values between 1 and 26 (the total number of variables) and comparing the results. This showed that making 10 variables available at each branch produces the most accurate model as measured against the out-of-bag (OOB) data that are randomly sorted out of each tree grown.
For the actual model, the full dataset of 23,799 data points was randomly split into training (80%) and testing (20%) datasets. This was done by stratified sampling so as to maintain the same balance between low and high cases (0 or 1) of the binary target variable, for which 42% of values were greater than 10 µg/L. The training dataset was used to develop the model (encompassing 10,001 trees), which was then cross validated with the testing dataset to determine its accuracy in predicting low (≤10 µg/L) and high (>10 µg/L) arsenic concentrations on new data. The model was then applied to the 26 spatially continuous predictor variables to create a map of the probability of the occurrence of the concentration of arsenic in groundwater exceeding 10 µg/L for all of India.

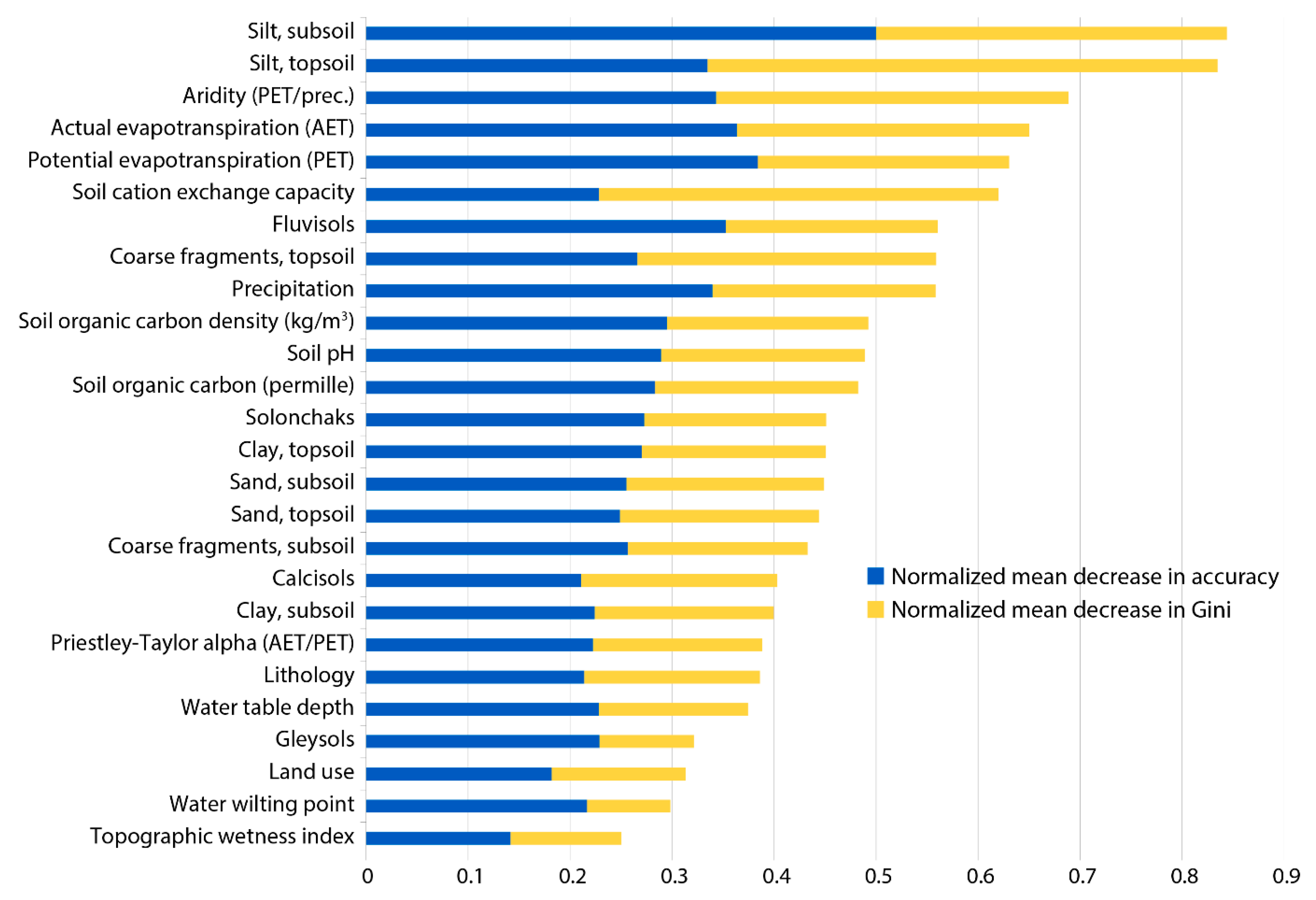
2.4. Importance of Predictor Variables

The effect of the predictor variables on the random forest model was evaluated directly through two statistics: (i) decrease in accuracy and (ii) decrease in Gini node impurity. In calculating both of these, the values of each predictor variable were randomly shuffled in turn and the resulting decrease in accuracy and decrease in Gini node impurity (how well the target variable is split at a branch) were measured on the OOB data of each tree and averaged. A higher (positive) value indicates a greater relative importance of a variable, whereas a negative value (corresponding to greater accuracy or node purity when the values are reassigned) shows that a variable does not benefit a model and should be removed.
As the measures of random forest variable importance described above do not indicate how a predictor variable relates to the target variable, e.g., with a positive or negative trend, Pearson correlations between each (continuous) predictor variable and the proportion of arsenic measurements exceeding 10 µg/L were calculated. This was done by first ordering the values of each predictor and placing them into 16 bins, each containing the same number of values. The proportion of arsenic measurements in each bin greater than 10 µg/L was then calculated. The number of bins was determined using Sturges’ formula (1 + log2 n) [62]. The correlation was calculated between the average value of the predictor in each bin and the proportion of high arsenic concentrations.

2.5. Estimating Potentially Affected Population

The prediction map generated from the random forest model was subsequently used to estimate the population potentially exposed to high concentrations of arsenic in drinking water. The first step of this procedure was to determine the areas at high risk of having arsenic concentrations greater than 10 µg/L. This was done using two approaches that have been described in more detail by Podgorski and Berg [16]. The sensitivity and specificity, that is, the correct classification of high and low values, respectively, were plotted for 100 probabilities between 0 and 1. Where both curves intersect indicates the probability cutoff at which the model classifies low and high values equally well. The second approach that was used follows a similar procedure that instead finds the intersection of the positive predictive value (PPV) and negative predictive value (NPV), which are defined as rate of correct positive and negative predictions, respectively. These analyses for determining how to interpret the model were conducted with all available data (training and testing datasets). Each probability threshold found with these two approaches was subsequently used to identify high hazard areas on the probability map. The two sets of high hazard areas were then used for further calculations to produce a range of values of populations at risk.
The populations living in the high hazard areas determined according to the above procedure were then multiplied by the modeled probabilities. The population figures were taken from a population model for 2020 based on existing patterns of development [63]. The at-risk population was further refined by differentiating between rural and urban areas [55] and multiplying by recent (2016) estimated nationwide usage rates of untreated groundwater in rural (0.637) and urban (0.238) areas, respectively [64].

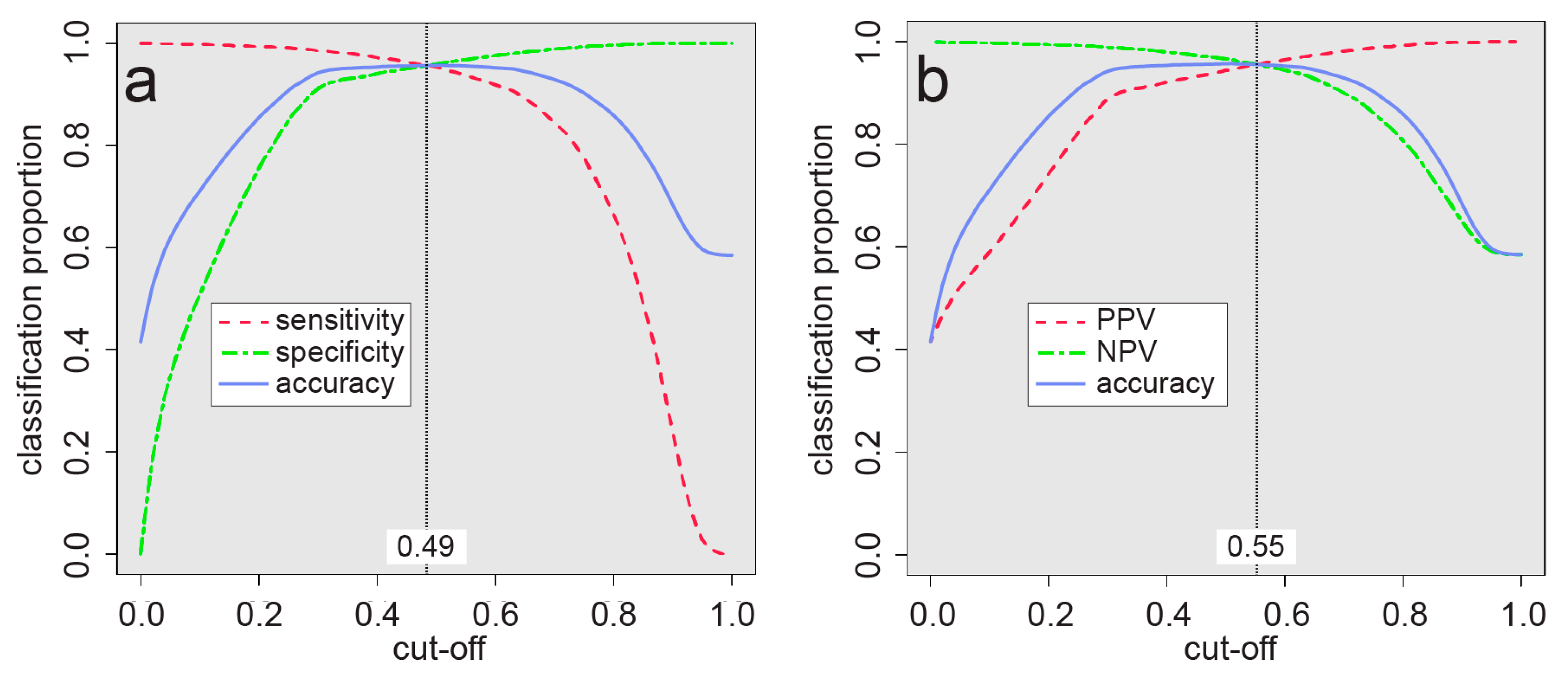
3. Results and Discussion

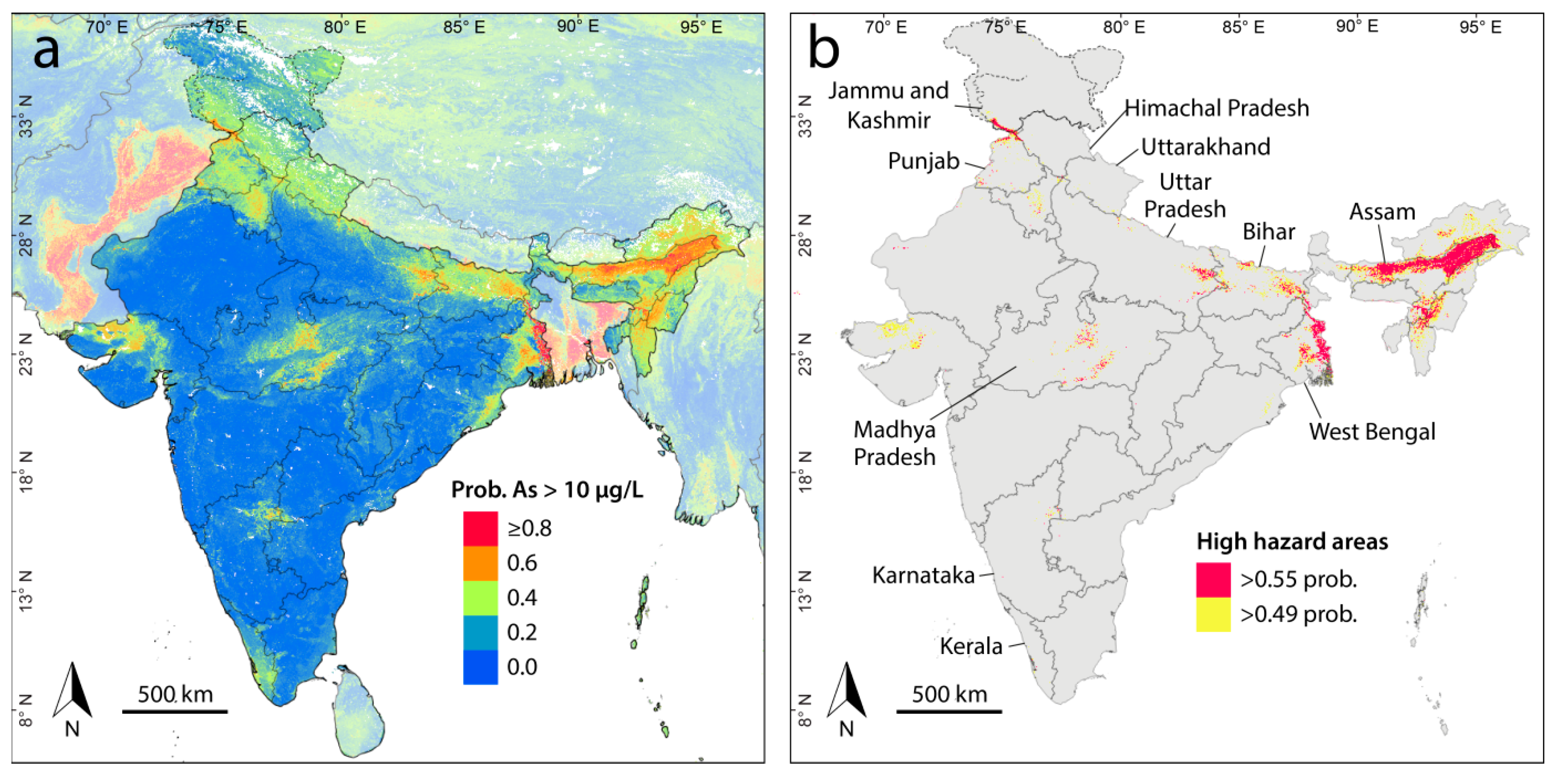
3.1. Arsenic Prediction Model

The cross-validation results of the final random forest model as applied to the test dataset are shown in Table 3. The area under the ROC (receiver operator characteristic) curve (AUC) is 0.86, which in general can range between 0.5 (random model) and 1 (perfect model) and represents how well a binary model can predict both low and high values as assessed over numerous probability cutoff values [65]. The AUC of this model is generally a better result than that of similar regional or country-scale groundwater quality studies (where reported), for example, 0.84 for fluoride in India [66], 0.71–0.83 for arsenic in Gujarat [14], 0.82 for arsenic in the USA [67], 0.80 for arsenic in Pakistan [6], or 0.74 for arsenic in Uttar Pradesh [15]. The overall accuracy of the model as applied to the test dataset of 0.79 is significantly higher than the no information rate of 0.58 (p value < 2.2 × 10−16) and is comparable to the average accuracy with OOB samples of 0.77. The no information rate refers to the accuracy that would be achieved without a model and is simply the proportion of the more frequent class of the dataset, i.e., 58% of the arsenic measurement points are equal to or less than 10 µg/L. Similarly, the Cohen’s kappa statistic [68] (0.5606) is an indicator of accuracy beyond what could be expected by chance and varies from 0 (no agreement) to 1 (perfect agreement).
Despite the spatial averaging of data to 1-km pixels, there still remains a much higher density of data points in a few regions, particularly in West Bengal where nearly 50% of the averaged data points are located. In order to test if such an imbalance considerably biases the model by allocating excessive weight to the conditions found in a particular region, the data from West Bengal were randomly split into 10 subsets that were each modeled separately with the rest of the dataset. The results of the 10 different models were averaged and compared with the single model using the full dataset (containing all West Bengal data). As the model performance was essentially identical, e.g., AUC of 0.86 and balanced accuracy of 0.78, the simpler approach of using a single model was retained and that of splitting the West Bengal data was not further pursued.
Early attempts to separately model areas corresponding to reducing environments, arid-oxidizing environments, and sulfide oxidation arsenic mobilization processes did not result in considerably different predictions or accuracy and were therefore abandoned in favor of a single model for India. It appears that the single model is able to effectively account for different geochemical environments due to utilizing the same parameters of climate, geology, and soil pH that were used to define the different environments. For example, in the ten thousand trees that make up the random forest, splits would have been made on significant differences in these parameters, which is similar in principle to having done so manually.
The arsenic prediction map generated from the final random forest model is displayed in Figure 2a. As most of the data used in the model is from India with the data from neighboring countries having been incorporated merely to help characterize border areas, the analysis that follows will focus only on India. Nonetheless, the arsenic prediction map including the rest of South Asia is presented in Figure S2, which, as seen with model continuity across international borders, also serves as a reminder that political boundaries do not necessarily coincide with those of natural systems.
The prediction model (Figure 2a) captures known arsenic-prone areas in the alluvial sediments along the Ganges and Brahmaputra plains [27] and in Gujarat [14] and Punjab [43]. It also identifies less well-known or previously undocumented areas such as Haryana, Jammu and Kashmir, and central Madhya Pradesh. Elevated arsenic hazard also appears in Himachal Pradesh, Kerala, and Uttarakhand, from where no arsenic concentration data were available to us. Consistent with the findings of Sovann and Polya [69] for Cambodia, this confirms that small alluvial systems, in addition to the larger systems, such as those of the Ganges, Brahmaputra, and Mekong, may also host elevated groundwater arsenic concentrations. This highlights some of the advantages and uses of a prediction model based on machine learning rather than spatial interpolation. That is, predictions can be made in areas removed from where concentration measurements exist by relying on statistical relationships between measurements in other areas and predictor variables that cover the entire model domain. The model can then be used to prioritize areas for testing where there is a dearth of data. The results of new water quality testing can then in turn be fed back into the model to further improve it.

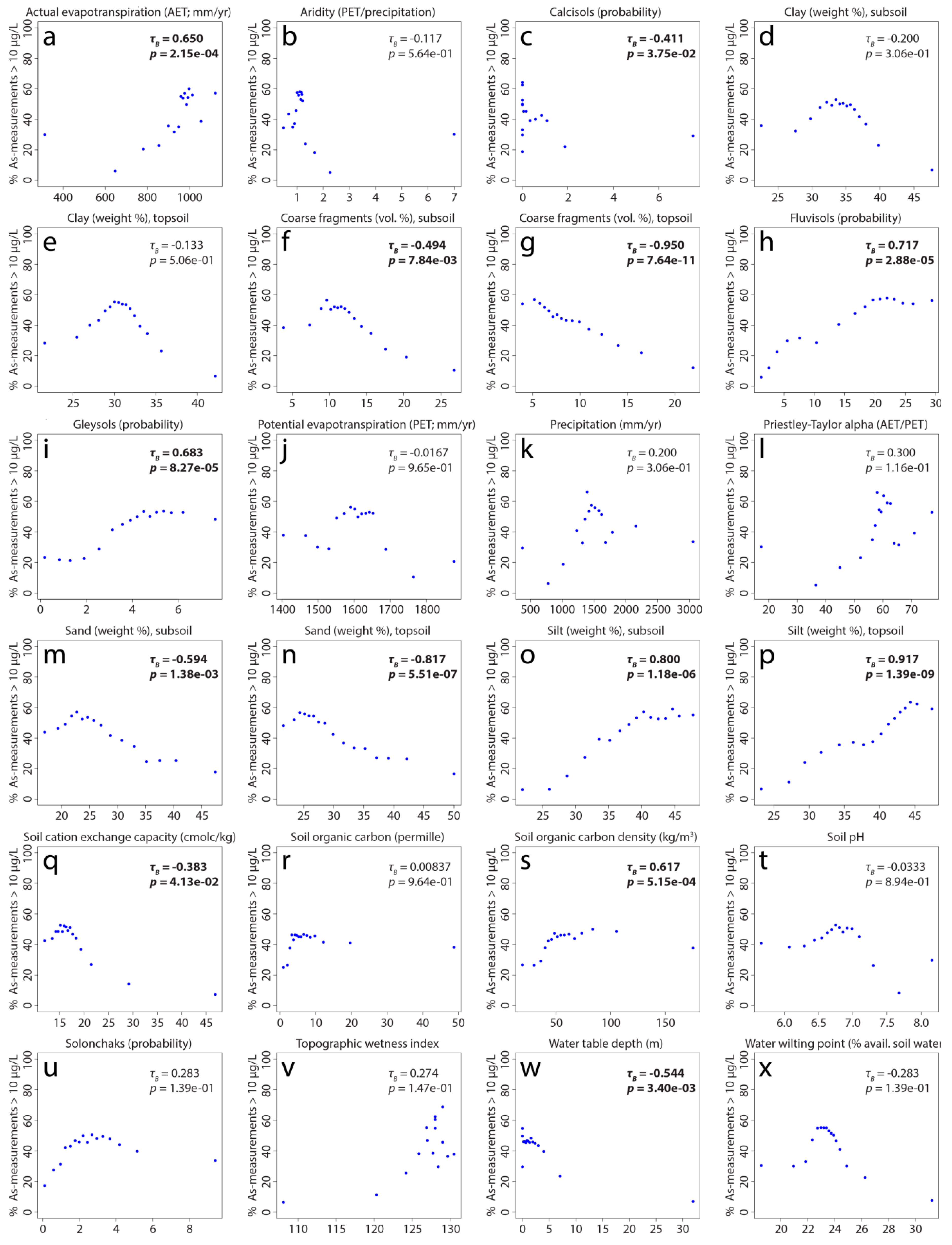
3.2. Influence of Predictor Variables

The importance of the predictor variables in the random forest model was assessed as the mean decrease in accuracy and mean decrease in Gini impurity. Each of these was normalized by the maximum value calculated among the predictor variables, and both are displayed together in Figure 3. This shows both silt variables (subsoil and topsoil) placing markedly above the others in importance, followed by aridity and both actual and potential evapotranspiration. The least important variables relative to the others are topographic wetness index, water wilting point, gleysols, and land use. Nevertheless, none of the predictors has a negative importance value, which suggests that they are all beneficial to the model.
In order to better understand how the predictor variables may relate to high arsenic concentrations (>10 µg/L), the proportion of high arsenic measurements were plotted against the averages of binned predictor values, for which rank-order correlations (Kendall Tau-b) were also calculated (Figure 4). The strongest rank-order correlations were found with topsoil coarse fragments (−0.95), silt in both the topsoil (0.92) and subsoil (0.80), topsoil sand (−0.82), fluvisols (0.72), gleysols (0.68), and actual evapotranspiration (0.65). Well-defined peaks are also observed with subsoil and topsoil clay (Figure 4d,e), subsoil coarse fragments (Figure 4f), subsoil and topsoil sand (Figure 4m,n), soil cation exchange capacity (Figure 4q), soil pH (Figure 4t), and water wilting point (Figure 4x), which highlights why it can be important to use a nonlinear classifier for modeling, such as random forest, to capture such relationships.
The importance of gleysols and their positive correlation with high arsenic concentrations can be linked to chemically reducing conditions, which are conducive to arsenic release [7,9], brought about by the poor drainage associated with this soil type. The negative relationship between soil cation exchange capacity and groundwater arsenic is at first glance counterintuitive given that higher CEC may give rise to higher pHs at which anionic, deprotonated As(III) or As(V) species will be more likely to desorb. Accordingly, this relationship might instead reflect the typically higher clay/silt contents of high CEC soils. The inverse correlation with water table depth is likely related to the occurrence of higher arsenic concentrations in the shallower Holocene layers of alluvial sedimentary systems [70] and that tend to contain higher concentrations of labile reactive organics associated with arsenic mobilization [71,72,73]. Furthermore, the strong dependence of the model on the silt content of soil, including a positive relationship with high arsenic concentrations, points toward the occurrence of high arsenic concentrations beneath floodplains, as do similar relationships with fluvisols.
Many of the observations made above are compatible with each other and are consistent with the reductive dissolution of arsenic in known high arsenic-hazard areas of Figure 2a found within unconsolidated sediments (Figure 1b), particularly along the Ganges and Brahmaputra rivers. Notable exceptions to this are the arsenic areas in central Madhya Pradesh (Figure 2a), which occur primarily within mafic volcanic rocks as well as the high hazard areas located in acidic plutonic rocks (e.g., granite) in Kerala and northeast Karnataka. The last example may be due to the oxidation of arsenic-bearing sulfide minerals, which is likely responsible for high arsenic concentrations in areas of historical gold mining activity in Karnataka [74].

3.3. Populations at Risk

The estimated arsenic-risk areas based on the probability cutoffs of 0.49 and 0.55 (see Figure 5) are shown in Figure 2b, in which most of the risk areas are seen to be concentrated along the Brahmaputra river (Assam) and the lower half of the Ganges river (Uttar Pradesh, Bihar, and West Bengal). Other notable risk areas are found in Jammu and Kashmir, Punjab, Gujarat, Madhya Pradesh, and most of the states neighboring Assam. The proportion of land area and populations that are potentially affected are broken down by state/territory in Table 4. Because only grid cells with a probability exceeding 0.49 or 0.55 were considered, underestimation may occur where there is localized arsenic contamination. In total, we estimate that between about 18 and 30 million people in India may be currently consuming arsenic in groundwater at concentrations exceeding 10 µg/L. This population estimate is substantially lower than that estimated (~41 million) for the five most impacted Indian states by Chakraborti et al. [75] and is consistent with the estimate of 31 million derivable from Ravenscroft et al. [9]. It is difficult to state possible reasons for these differences as the methods used to calculate these other estimates are not clear. Our range of potentially affected population is also toward the lower end of the range of 18–90 million estimated for India as part of a global groundwater arsenic prediction model [16], which highlights how a separate study, such as this one, concentrated on a single area can lead to more precise results.

4. Conclusions

The purpose of the hazard models produced here is to offer an overview of where high concentrations of geogenic arsenic are likely to be found in groundwater across the whole of India, with some insight into the physical processes at work, as well as to assess the size of the populations potentially affected. Particularly since arsenic is often not routinely analyzed in many areas without a known problem, the maps should serve as a guide to identifying where additional testing should be conducted as well as in assessing health impacts. In addition to drinking water supplies, the hazard map is relevant to the utilization and siting of wells for the irrigation of crops.
Although this study is based on over 145,000 groundwater samples, targeted testing is still required to determine if a specific well is highly contaminated with arsenic or not. This is due, at least in part, to the heterogeneous nature of aquifers that can lead to great variability of groundwater arsenic concentrations over short distances. Further, additional groundwater arsenic concentration data would help improve the model, particularly in areas (e.g, in parts of Maydha Pradesh) in which anthropogenic processes may have had a material influence on groundwater arsenic concentrations and thereby the rendered model.
Despite the hazard model presented here being very effective in predicting high groundwater arsenic concentrations, it is unable to account for the depth dependency of arsenic in an aquifer, which, for example, can vary according to sediment age and/or redox conditions as well as 3-D heterogeneous permeability structures [76]. As such, it can be assumed that the predictions become less accurate with greater depth, as was demonstrated in a recent global study [16]. Although ~3/4 of the modeled data points used here have an associated well depth, essentially all of these data were confined to just a few areas in West Bengal and Bihar. Given the size of India and its variations in climate and geology, it was not feasible to generalize depth relationships based on data from just a small part of the country. However, incorporating depth as a predictor variable could be effective in a smaller-scale study of a single region.
Another dimension that could enhance the modeling is that of time. For example, accounting for fluctuations in arsenic concentrations relative to the monsoon season could possibly improve the accuracy of the model, particularly in areas with extensive hyporheic zones undergoing surface water–groundwater exchange and particularly including those proximal to rivers with large differences in post- and pre-monsoonal stages. Any long-term secular trends in arsenic concentration related to aquifer exploitation [77,78,79,80], aquifer depletion, or climate change could also produce useful results. This was not possible in this study due to each of the arsenic measurement points representing spatially distinct locations that also generally lacked information on the timing of sampling.
The population estimates rely on a single country-wide set of groundwater-use rates for rural and urban areas. Knowing this rate at a finer scale (e.g., state, division, and district) could be expected to lead to more accurate results. In order get a better grasp of who is physically impacted by high groundwater arsenic concentrations, exposure studies and environmental public health tracking [81] leveraging the arsenic hazard map produced here would be very helpful.

Supplementary Materials

The following are available online at https://www.mdpi.com/1660-4601/17/19/7119/s1, Figure S1: Cumulative frequency of groundwater arsenic concentrations, Figure S2: Prediction model of arsenic in groundwater for South Asia, Table S1: Importance of predictor variables.

Author Contributions

Conceptualization, J.P. and D.A.P.; methodology, software, validation, formal analysis, J.P. with input from R.W.; data curation, R.W. and J.P.; writing—original draft preparation, J.P.; writing—review and editing J.P., R.W., B.C. and D.A.P.; supervision and project administration, D.A.P.; funding acquisition, D.A.P. & J.P. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Engineering and Physical Sciences Research Council (UK) (IAA Impact Support Fund Award via University of Manchester); the Swiss Agency for Development and Cooperation (project no. 7F-09963.01.01), the Natural Environmental Research Council (UK) (NE/R003386/1) and DST (India) (DST/TM/INDO-UK/2K17/55(C) & 55(G)).

Acknowledgments

We thank NERC (UK) and DST (India) for their joint funding of the Newton Bhabha Indo-UK Water Quality project, FAR-GANGA (www.farganga.org). We thank colleagues at the FAR-GANGA stakeholder partner, the Central Ground Water Board (CGWB, Faridabad, India), for the acquisition and provision of many of the groundwater arsenic data utilized in this study. We acknowledge the further support of and/or discussions with Benjamin Ambühl, Michael Berg, Abhijit Mukherjee, Prashant Rai, Laura A. Richards and Dipankar Saha. The views expressed in this work do not necessarily reflect those of any of the funders, organizations, or individuals that we acknowledge here.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

References

  1. Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
  3. Polya, D.A.; Middleton, D.R. Arsenic in drinking water: Sources & human exposure. In Best Practice Guide on the Control of Arsenic in Drinking Water, 1st ed.; Bhattacharya, P., Polya, D.A., Draganovic, D., Eds.; International Water Association Publishing: London, UK, 2017; Chapter 1; ISBN 9781843393856. [Google Scholar]
  4. Smedley, P.; Kinniburgh, D. A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 2002, 17, 517–568. [Google Scholar] [CrossRef] [Green Version]
  5. Charlet, L.; Polya, D.A. Arsenic in shallow, reducing groundwaters in southern Asia: An environmental health disaster. Elements 2006, 2, 91–96. [Google Scholar] [CrossRef]
  6. Podgorski, J.E.; Eqani, S.A.M.A.S.; Khanam, T.; Ullah, R.; Shen, H.; Berg, M. Extensive arsenic contamination in high-pH unconfined aquifers in the Indus Valley. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Islam, F.S.; Gault, A.G.; Boothman, C.; Polya, D.A.; Charnock, J.M.; Chatterjee, D.; Lloyd, J.R. Role of metal-reducing bacteria in arsenic release from Bengal delta sediments. Nature 2004, 430, 68–71. [Google Scholar] [CrossRef]
  8. Richards, L.A.; Casanueva-Marenco, M.J.; Magnone, D.; Sovann, C.; Van Dongen, B.E.; Polya, D.A. Contrasting sorption behaviours affecting groundwater arsenic concentration in Kandal Province, Cambodia. Geosci. Front. 2019, 10, 1701–1713. [Google Scholar] [CrossRef]
  9. Ravenscroft, P.; Brammer, H.; Richards, K. Arsenic Pollution: A GLOBAL Synthesis; Wiley-Blackwell: Chichester, UK, 2009; p. 588. [Google Scholar]
  10. Polya, D.A.; Lawson, M. Geogenic and anthropogenic arsenic hazard in groundwaters and soils: Distribution, nature, origin, and human exposure routes. In Arsenic—Exposure Sources, Health Risks, and Mechanisms of Toxicity, 1st ed.; States, J.C., Ed.; Wiley: Hoboken, NJ, USA, 2016; Chapter 2; pp. 23–60. ISBN 978-1-118-51114-5. [Google Scholar]
  11. Dittmar, J.; Voegelin, A.; Roberts, L.C.; Hug, S.J.; Saha, G.C.; Ali, M.A.; Badruzzaman, A.B.M.; Kretzschmar, R. Spatial distribution and temporal variability of arsenic in irrigated rice fields in Bangladesh. 2. Paddy soil. Environ. Sci. Technol. 2007, 41, 5967–5972. [Google Scholar] [CrossRef]
  12. WHO. Guidelines for drinking-water quality. WHO Chron. 2011, 38, 104–108. [Google Scholar]
  13. Bureau of Indian Standards (BIS). Indian Standard Drinking Water-Specification (Second Revision) IS: 10500; Bureau of Indian Standards (BIS): New Delhi, India, 2012; p. 16.
  14. Wu, R.; Podgorski, J.; Berg, M.; Polya, D.A. Geostatistical model of the spatial distribution of arsenic in groundwaters in Gujarat State, India. Environ. Geochem. Health 2020. published online. [Google Scholar] [CrossRef]
  15. Bindal, S.; Singh, C.K. Predicting groundwater arsenic contamination: Regions at risk in highest populated state of India. Water Res. 2019, 159, 65–76. [Google Scholar] [CrossRef]
  16. Podgorski, J.; Berg, M. Global threat of arsenic in groundwater. Science 2020, 368, 845–850. [Google Scholar] [CrossRef]
  17. Kumar, M.; Ramanathan, A.; Rahman, M.M.; Naidu, R. Concentrations of inorganic arsenic in groundwater, agricultural soils and subsurface sediments from the middle Gangetic plain of Bihar, India. Sci. Total Environ. 2016, 573, 1103–1114. [Google Scholar] [CrossRef]
  18. Shah, B.A. Status of groundwater arsenic pollution of Mirzapur district in Holocene aquifers from parts of the Middle Ganga Plain, India. Environ. Earth Sci. 2015, 73, 1505–1514. [Google Scholar] [CrossRef]
  19. Ghosh, T.; Kanchan, R. Geoenvironmental appraisal of groundwater quality in Bengal alluvial tract, India: A geochemical and statistical approach. Environ. Earth Sci. 2014, 72, 2475–2488. [Google Scholar] [CrossRef]
  20. Sailo, L.; Mahanta, C. Arsenic mobilization in the Brahmaputra plains of Assam: Groundwater and sedimentary controls. Environ. Monit. Assess. 2014, 186, 6805–6820. [Google Scholar] [CrossRef] [PubMed]
  21. Ghosh, S.; Sar, P. Identification and characterization of metabolic properties of bacterial populations recovered from arsenic contaminated ground water of North East India (Assam). Water Res. 2013, 47, 6992–7005. [Google Scholar] [CrossRef]
  22. Shah, B.A. Role of Quaternary stratigraphy on arsenic-contaminated groundwater from parts of Barak Valley, Assam, North–East India. Environ. Earth Sci. 2012, 66, 2491–2501. [Google Scholar] [CrossRef]
  23. Chandra, S.; Ahmed, S.; Nagaiah, E.; Singh, S.K.; Chandra, P. Geophysical exploration for lithological control of arsenic contamination in groundwater in Middle Ganga Plains, India. Phys. Chem. Earth Parts A/B/C 2011, 36, 1353–1362. [Google Scholar] [CrossRef]
  24. Chauhan, V.S.; Nickson, R.; Chauhan, D.; Iyengar, L.; Sankararamakrishnan, N. Ground water geochemistry of Ballia district, Uttar Pradesh, India and mechanism of arsenic release. Chemosphere 2009, 75, 83–91. [Google Scholar] [CrossRef]
  25. Nath, B.; Stüben, D.; Mallik, S.B.; Chatterjee, D.; Charlet, L. Mobility of arsenic in West Bengal aquifers conducting low and high groundwater arsenic. Part I: Comparative hydrochemical and hydrogeological characteristics. Appl. Geochem. 2008, 23, 977–995. [Google Scholar] [CrossRef]
  26. Shah, B.A. Role of Quaternary stratigraphy on arsenic-contaminated groundwater from parts of Middle Ganga Plain, UP–Bihar, India. Environ. Geol. 2008, 53, 1553–1561. [Google Scholar] [CrossRef]
  27. Nickson, R.; Sengupta, C.; Mitra, P.; Dave, S.; Banerjee, A.; Bhattacharya, A.; Basu, S.; Kakoti, N.; Moorthy, N.; Wasuja, M. Current knowledge on the distribution of arsenic in groundwater in five states of India. J. Environ. Sci. Health Part A 2007, 42, 1707–1718. [Google Scholar] [CrossRef]
  28. McArthur, J.; Ravenscroft, P.; Banerjee, D.; Milsom, J.; Hudson-Edwards, K.A.; Sengupta, S.; Bristow, C.; Sarkar, A.; Tonkin, S.; Purohit, R. How paleosols influence groundwater flow and arsenic pollution: A model from the Bengal Basin and its worldwide implication. Water Resour. Res. 2008, 44, W11411. [Google Scholar] [CrossRef]
  29. Kar, S.; Maity, J.P.; Jean, J.-S.; Liu, C.-C.; Nath, B.; Yang, H.-J.; Bundschuh, J. Arsenic-enriched aquifers: Occurrences and mobilization of arsenic in groundwater of Ganges Delta Plain, Barasat, West Bengal, India. Appl. Geochem. 2010, 25, 1805–1814. [Google Scholar] [CrossRef]
  30. Maity, J.P.; Nath, B.; Chen, C.-Y.; Bhattacharya, P.; Sracek, O.; Bundschuh, J.; Kar, S.; Thunvik, R.; Chatterjee, D.; Ahmed, K.M. Arsenic-enriched groundwaters of India, Bangladesh and Taiwan—Comparison of hydrochemical characteristics and mobility constraints. J. Environ. Sci. Health Part A 2011, 46, 1163–1176. [Google Scholar] [CrossRef]
  31. Paul, D.; Kazy, S.K.; Gupta, A.K.; Pal, T.; Sar, P. Diversity, metabolic properties and arsenic mobilization potential of indigenous bacteria in arsenic contaminated groundwater of West Bengal, India. PLoS ONE 2015, 10, e0118735. [Google Scholar] [CrossRef] [Green Version]
  32. Saha, D.; Sahu, S. A decade of investigations on groundwater arsenic contamination in Middle Ganga Plain, India. Environ. Geochem. Health 2016, 38, 315–337. [Google Scholar] [CrossRef]
  33. Sharma, S.; Kaur, J.; Nagpal, A.K.; Kaur, I. Quantitative assessment of possible human health risk associated with consumption of arsenic contaminated groundwater and wheat grains from Ropar Wetand and its environs. Environ. Monit. Assess. 2016, 188, 506. [Google Scholar] [CrossRef]
  34. Chatterjee, D.; Roy, R.; Basu, B. Riddle of arsenic in groundwater of Bengal Delta Plain—Role of non-inland source and redox traps. Environ. Geol. 2005, 49, 188–206. [Google Scholar] [CrossRef]
  35. Shukla, D.P.; Dubey, C.; Singh, N.P.; Tajbakhsh, M.; Chaudhry, M. Sources and controls of Arsenic contamination in groundwater of Rajnandgaon and Kanker District, Chattisgarh Central India. J. Hydrol. 2010, 395, 49–66. [Google Scholar] [CrossRef]
  36. Shah, B.A. Arsenic-contaminated groundwater in Holocene sediments from parts of middle Ganga plain, Uttar Pradesh, India. Curr. Sci. 2010, 98, 1359–1365. [Google Scholar]
  37. Hazarika, S.; Bhuyan, B. Fluoride, arsenic and iron content of groundwater around six selected tea gardens of Lakhimpur District, Assam, India. Arch. Appl Sci. Res. 2013, 5, 57–61. [Google Scholar]
  38. Mukherjee, A.; Fryar, A.E.; Rowe, H.D. Regional-scale stable isotopic signatures of recharge and deep groundwater in the arsenic affected areas of West Bengal, India. J. Hydrol. 2007, 334, 151–161. [Google Scholar] [CrossRef]
  39. Mukherjee, A.; Fryar, A.E.; Eastridge, E.M.; Nally, R.S.; Chakraborty, M.; Scanlon, B.R. Controls on high and low groundwater arsenic on the opposite banks of the lower reaches of River Ganges, Bengal basin, India. Sci. Total Environ. 2018, 645, 1371–1387. [Google Scholar] [CrossRef]
  40. Olea, R.A.; Raju, N.J.; Egozcue, J.J.; Pawlowsky-Glahn, V.; Singh, S. Advancements in hydrochemistry mapping: Methods and application to groundwater arsenic and iron concentrations in Varanasi, Uttar Pradesh, India. Stoch. Environ. Res. Risk Assess. 2018, 32, 241–259. [Google Scholar] [CrossRef] [Green Version]
  41. Chidambaram, S.; Thilagavathi, R.; Thivya, C.; Karmegam, U.; Prasanna, M.V.; Ramanathan, A.; Tirumalesh, K.; Sasidhar, P. A study on the arsenic concentration in groundwater of a coastal aquifer in south-east India: An integrated approach. Environ. Dev. Sustain. 2017, 19, 1015–1040. [Google Scholar] [CrossRef]
  42. UNEP. Water Quality. In 2005 State of the UNEP GEMS/Water Global Network and Annual Report; UNEP: Nairobi, Kenya, 2005. [Google Scholar]
  43. Kumar, A.; Singh, C.K.; Bostick, B.; Nghiem, A.; Mailloux, B.; van Geen, A. Regulation of groundwater arsenic concentrations in the Ravi, Beas, and Sutlej floodplains of Punjab, India. Geochim. et Cosmochim. Acta 2020, 276, 384–403. [Google Scholar] [CrossRef]
  44. Ambühl, B.; Department Sanitation, Water and Solid Waste for Development, Eawag, Swiss Federal Institute of Aquatic Science and Technology, 8600 Dübendorf, Switzerland. Unpublished Data Shared by Personal Communication, 2019.
  45. Richards, L.A.; Kumar, A.; Shankar, P.; Gaurav, A.; Ghosh, A.; Polya, D.A. Distribution and Geochemical Controls of Arsenic and Uranium in Groundwater-Derived Drinking Water in Bihar, India. Int. J. Environ. Res. Public Health 2020, 17, 2500. [Google Scholar] [CrossRef] [Green Version]
  46. Central Ground Water Board. Groundwater Year Book—2015–2016 Gujarat state and UT of Daman & Diu. Available online: http://cgwb.gov.in/Regions/GW-year-Books/GWYB-2015-16/GWYB%20WCR%202015-16.pdf (accessed on 2 May 2019).
  47. Central Ground Water Board. Ground Water Quality in Shallow Aquifers in India; Supplemented by further location-specific data for Andhra Pradesh, Rajasthan, Telengana, Uttar Pradesh directly from provided by CGWB, 2019–2020; CGWB: Faridabad, India, 2018. Available online: http://cgwb.gov.in/documents/Waterquality/GW_Quality_in_shallow_aquifers.pdf (accessed on 2 May 2019).
  48. Kinniburgh, D.; Smedley, P. Arsenic Contamination of Groundwater in Bangladesh; British Geological Survey: Nottingham, UK, 2001. [Google Scholar]
  49. Shrestha, B.R.; Whitney, J.W.; Shrestha, K.B. The State of Arsenic in Nepal-2003; National Arsenic Steering Committee (Nepal) & Environmental and Public Health Organization (Nepal): Kathmandu, Nepal, 2004; p. 126. ISBN 99933-895-4-4. [Google Scholar]
  50. Nickson, R.; McArthur, J.; Shrestha, B.; Kyaw-Myint, T.; Lowry, D. Arsenic and other drinking water quality issues, Muzaffargarh District, Pakistan. Appl. Geochem. 2005, 20, 55–68. [Google Scholar] [CrossRef]
  51. Trabucco, A.; Zomer, R. Global Soil Water Balance Geospatial Database. CGIAR Consortium for Spatial Information. 2010. Published online CGIAR-CSI GeoPortal. Available online: http://www.cgiar-csi.org (accessed on 15 April 2016).
  52. Trabucco, A.; Zomer, R.J. Global Aridity Index (Global-Aridity) and Global Potential Evapo-Transpiration (Global-PET) Geospatial Database; CGIAR Consortium for Spatial Information. 2009. CGIAR-CSI GeoPortal. Available online: http://www.cgiar-csi.org (accessed on 11 February 2015).
  53. Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
  54. Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [Green Version]
  55. Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sens. Environ. 2010, 114, 168–182. [Google Scholar] [CrossRef]
  56. Hengl, T. Global landform and lithology class at 250 m based on the USGS global ecosystem map (Version 1.0). Lithology, Zenodo, 5 October 2018. [Google Scholar] [CrossRef]
  57. Hengl, T. Global DEM derivatives at 250 m, 1 km and 2 km based on the MERIT DEM (Version 1.0). Topographic Wetness Index, Zenodo, 5 October 2018. [Google Scholar] [CrossRef]
  58. Fan, Y.; Li, H.; Miguez-Macho, G. Global patterns of groundwater table depth. Science 2013, 339, 940–943. [Google Scholar] [CrossRef] [Green Version]
  59. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  60. R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
  61. Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; Volume 1. pp. 278–282. [Google Scholar] [CrossRef]
  62. Sturges, H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926, 21, 65–66. [Google Scholar] [CrossRef]
  63. Gao, J. Global Population Projection Grids Based on Shared Socioeconomic Pathways (SSPs), Downscaled 1-km Grids, 2010–2100; NASA Socioeconomic Data and Applications Center (SEDAC): Palisades, NY, USA, 2019. [Google Scholar]
  64. JMP Global Data on Water Supply, Sanitation and Hygiene (WASH). Available online: https://washdata.org/data/household#!/ (accessed on 29 August 2019).
  65. Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
  66. Podgorski, J.E.; Labhasetwar, P.; Saha, D.; Berg, M. Prediction modeling and mapping of groundwater fluoride contamination throughout India. Environ. Sci. Technol. 2018, 52, 9889–9898. [Google Scholar] [CrossRef] [Green Version]
  67. Ayotte, J.D.; Medalie, L.; Qi, S.L.; Backer, L.C.; Nolan, B.T. Estimating the high-arsenic domestic-well population in the conterminous United States. Environ. Sci. Technol. 2017, 51, 12443–12454. [Google Scholar] [CrossRef]
  68. Cohen, J. A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
  69. Sovann, C.; Polya, D. Improved groundwater geogenic arsenic hazard map for Cambodia. Environ. Chem. 2014, 11, 595–607. [Google Scholar] [CrossRef]
  70. Fendorf, S.; Michael, H.A.; Van Geen, A. Spatial and temporal variations of groundwater arsenic in South and Southeast Asia. Science 2010, 328, 1123–1127. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  71. Postma, D.; Larsen, F.; Hue, N.T.M.; Duc, M.T.; Viet, P.H.; Nhan, P.Q.; Jessen, S. Arsenic in groundwater of the Red River floodplain, Vietnam: Controlling geochemical processes and reactive transport modeling. Geochim. et Cosmochim. Acta 2007, 71, 5054–5071. [Google Scholar] [CrossRef]
  72. Rowland, H.; Boothman, C.; Pancost, R.; Gault, A.; Polya, D.; Lloyd, J. The role of indigenous microorganisms in the biodegradation of naturally occurring petroleum, the reduction of iron, and the mobilization of arsenite from West Bengal aquifer sediments. J. Environ. Qual. 2009, 38, 1598–1607. [Google Scholar] [CrossRef]
  73. Magnone, D.; Richards, L.A.; Polya, D.A.; Bryant, C.; Jones, M.; Van Dongen, B.E. Biomarker-indicated extent of oxidation of plant-derived organic carbon (OC) in relation to geomorphology in an arsenic contaminated Holocene aquifer, Cambodia. Sci. Rep. 2017, 7, 1–12. [Google Scholar] [CrossRef] [Green Version]
  74. Chakraborti, D.; Rahman, M.M.; Murrill, M.; Das, R.; Patil, S.; Sarkar, A.; Dadapeer, H.; Yendigeri, S.; Ahmed, R.; Das, K.K. Environmental arsenic contamination and its health effects in a historic gold mining area of the Mangalur greenstone belt of Northeastern Karnataka, India. J. Hazard. Mater. 2013, 262, 1048–1055. [Google Scholar] [CrossRef] [Green Version]
  75. Chakraborti, D.; Rahman, M.M.; Das, B.; Chatterjee, A.; Das, D.; Nayak, B.; Pal, A.; Chowdhury, U.K.; Ahmed, S.; Biswas, B.K. Groundwater arsenic contamination and its health effects in India. Hydrogeol. J. 2017, 25, 1165–1181. [Google Scholar] [CrossRef]
  76. Sahu, S.; Saha, D. Role of shallow alluvial stratigraphy and Holocene geomorphology on groundwater arsenic contamination in the Middle Ganga Plain, India. Environ. Earth Sci. 2015, 73, 3523–3536. [Google Scholar] [CrossRef]
  77. Harvey, C.F.; Swartz, C.H.; Badruzzaman, A.B.M.; Keon-Blute, N.; Yu, W.; Ashraf Ali, M.; Jay, J.; Beckie, R.; Niedan, V.; Brabander, D.; et al. Arsenic mobility and groundwater extraction in Bangladesh. Science 2002, 298, 1602–1606. [Google Scholar] [CrossRef] [Green Version]
  78. Polya, D.A.; Charlet, L. Rising arsenic risk? Nat. Geosci. 2009, 2, 383–384. [Google Scholar] [CrossRef]
  79. Neumann, R.B.; Ashfaque, K.N.; Badruzzaman, A.B.M.; Ali, M.A.; Shoemaker, J.K.; Harvey, C.F. Anthropogenic influences on groundwater arsenic concentrations in Bangladesh. Nat. Geosci. 2010, 3, 46–52. [Google Scholar] [CrossRef]
  80. Lawson, M.; Polya, D.A.; Boyce, A.J.; Bryant, C.; Mondal, D.; Shantz, A.; Ballentine, C.J. Pond-derivedorganic carbon driving changes in arsenic hazard found in Asian groundwaters. Environ. Sci. Technol. 2013, 47, 7085–7094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  81. Public Health England. Environmental Public Health Tracking in England. Report on Recent Activities December 2018; Public Health England Report GW-352; Public Health England: London, UK, 2019.
Ijerph 17 07119 g001 550
Figure 1. Groundwater arsenic data points and simplified geology of the Indian subcontinent. (a) Spatially averaged arsenic data points used in modeling along with topography in India and neighboring countries. (b) Lithology of the Indian subcontinent.
Figure 1. Groundwater arsenic data points and simplified geology of the Indian subcontinent. (a) Spatially averaged arsenic data points used in modeling along with topography in India and neighboring countries. (b) Lithology of the Indian subcontinent.
Ijerph 17 07119 g001
Ijerph 17 07119 g002 550
Figure 2. Arsenic hazard maps. (a) Probability of arsenic concentration in groundwater exceeding 10 µg/L. (b) High hazard areas in India based on probability cutoffs of 0.49 and 0.55.
Figure 2. Arsenic hazard maps. (a) Probability of arsenic concentration in groundwater exceeding 10 µg/L. (b) High hazard areas in India based on probability cutoffs of 0.49 and 0.55.
Ijerph 17 07119 g002
Ijerph 17 07119 g003 550
Figure 3. Normalized variable importance in terms of mean decrease in accuracy and mean decrease in Gini as calculated on the test dataset. Both decrease in accuracy and decrease in Gini were normalized by their respective greatest values (see Table S1).
Figure 3. Normalized variable importance in terms of mean decrease in accuracy and mean decrease in Gini as calculated on the test dataset. Both decrease in accuracy and decrease in Gini were normalized by their respective greatest values (see Table S1).
Ijerph 17 07119 g003
Ijerph 17 07119 g004 550
Figure 4. Correlations of predictor variables (a–x) with percentages of arsenic data points exceeding 10 µg/L in 16 equally sized bins. Kendall correlations (τB) with a statistically significant p value (95% confidence level) are shown in bold.
Figure 4. Correlations of predictor variables (a–x) with percentages of arsenic data points exceeding 10 µg/L in 16 equally sized bins. Kendall correlations (τB) with a statistically significant p value (95% confidence level) are shown in bold.
Ijerph 17 07119 g004
Ijerph 17 07119 g005 550
Figure 5. Analyses of model performance using full modeling dataset. (a) Sensitivity and specificity were found to be equivalent at a probability cutoff of 0.49 with a corresponding accuracy of 96%. (b) Positive predictive value (PPV) and negative predictive value (NPV) were found to be equivalent at a probability cutoff of 0.55 also with a corresponding accuracy of 96%.
Figure 5. Analyses of model performance using full modeling dataset. (a) Sensitivity and specificity were found to be equivalent at a probability cutoff of 0.49 with a corresponding accuracy of 96%. (b) Positive predictive value (PPV) and negative predictive value (NPV) were found to be equivalent at a probability cutoff of 0.55 also with a corresponding accuracy of 96%.
Ijerph 17 07119 g005
Table
Table 1. Summary of groundwater arsenic concentration data used in the model. Existing arsenic measurements taken from over 30 sources, mainly from India but also from some neighboring South Asian countries. Summaries are given for before and after spatial averaging.
Table 1. Summary of groundwater arsenic concentration data used in the model. Existing arsenic measurements taken from over 30 sources, mainly from India but also from some neighboring South Asian countries. Summaries are given for before and after spatial averaging.
Country
[Data Sources]		Number of Data Points, before Spatial Averaging
(% of Total)		Mean (±Standard Deviation) As Concentration, before Spatial AveragingNumber of Data Points, after Spatial Averaging
(% of Total)		Mean (±Standard Deviation) As Concentration, after Spatial Averaging
India [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]132,028 (91%)53 ± 451 µg/L17,528 (74%)33 ± 162 µg/L
Bangladesh [42,48]4215 (3%)62 ± 139 µg/L3674 (15%)56 ± 120 µg/L
Nepal [49]7575 (5%)15 ± 62 µg/L1846 (8%)16 ± 66 µg/L
Pakistan [6,50]1279 (1%)103 ± 123 µg/L760 (3%)71 ± 98 µg/L
Total145,09752 ± 438 µg/L23,80837 ± 150 µg/L
Table
Table 2. Predictor variables and descriptions. The 26 parameters used as predictor variables in modeling are grouped into the categories ‘Climate’, ‘Soil’ and ‘Other’. Their resolution is one square km at the equator.
Table 2. Predictor variables and descriptions. The 26 parameters used as predictor variables in modeling are grouped into the categories ‘Climate’, ‘Soil’ and ‘Other’. Their resolution is one square km at the equator.
VariableDescription
Climate
Actual evapotranspiration (AET) [51]Average rate of actual evapotranspiration (mm/yr)
AridityPET/Precipitation
Potential evapotranspiration (PET) [52]Average rate of potential evapotranspiration (mm/yr)
Precipitation [53]Average rate of precipitation (mm/yr)
Priestley-Taylor alpha coefficient [51]AET/PET
Soil
Calcisols [54]Probability of the occurrence of calcisols
Clay, subsoil [54]Weight % of clay particles (<0.0002 mm) at 2 m depth
Clay, topsoil [54]Weight % of clay particles (<0.0002 mm) at 0 m depth
Coarse fragments, subsoil [54]Volumetric % of coarse fragments (>2 mm) at 2 m depth
Coarse fragments, topsoil [54]Volumetric % of coarse fragments (>2 mm) at 0 m depth
Fluvisols [54]Probability of the occurrence of fluvisols
Gleysols [54]Probability of the occurrence of gleysols
Sand, subsoil [54]Weight % of sand particles (0.05–2 mm) at 2 m depth
Sand, topsoil [54]Weight % of sand particles (0.05–2 mm) at 0 m depth
Silt, subsoil [54]Weight % of silt particles (0.0002–0.05 mm) at 2 m depth
Silt, topsoil [54]Weight % of silt particles (0.0002–0.05 mm) at 0 m depth
Soil cation exchange capacity [54]Cation exchange capacity (cmolc/kg) at 2 m depth
Soil organic carbon [54]Soil organic carbon (permille) at 2 m depth
Soil organic carbon density [54]Soil organic carbon density (kg/m3) at 2 m depth
Soil pH [54]Soil pH measured in water at 2 m depth
Solonchaks [54]Probability of the occurrence of solonchaks
Water wilting point [54]Vol. % of available soil water until wilting point at 2 m depth
Other
Land cover [55]17 different land cover categories according to the International Geosphere-Biosphere Programme (IGBP)
Lithology [56]15 different categories of lithology
Topographic wetness index [57]Combination of upslope contributing area and slope
Water table depth [58]Mean water table depth (m)
Table
Table 3. Confusion matrix and other statistics resulting from the analysis of the final random forest model with the test dataset at a probability cutoff of 0.5.
Table 3. Confusion matrix and other statistics resulting from the analysis of the final random forest model with the test dataset at a probability cutoff of 0.5.
Reference
Prediction01
02223462
15611514
StatisticValue
Accuracy (Acc)0.7851
No information rate (NIR)0.5849
p value (Acc > NIR)<2.2 × 10−16
Cohen’s kappa0.5606
Sensitivity0.7662
Specificity0.7985
Positive predictive value0.7296
Negative predictive value0.8279
Prevalence0.4151
Balanced accuracy0.7823
Table
Table 4. Area and population potentially exposed to arsenic concentrations greater than 10 µg/L by state/territory. Based on probabilities in Figure 2a exceeding 0.49 and 0.55 along with the rates [64] of household groundwater use in rural and urban areas. See text for limitations.
Table 4. Area and population potentially exposed to arsenic concentrations greater than 10 µg/L by state/territory. Based on probabilities in Figure 2a exceeding 0.49 and 0.55 along with the rates [64] of household groundwater use in rural and urban areas. See text for limitations.
State/TerritoryPercentage of Land Area ExposedPopulation Exposed
Andaman and Nicobar0.4–2.9%300–2700
Andhra Pradesh<0.1%2700–6600
Arunachal Pradesh4.3–21.6%69,800–157,700
Assam42.3–59.7%6,536,000–8,771,100
Bihar3.0–12.0%1,226,800–4,636,500
Chandigarhn/an/a
Chhattisgarh<0.1%700–1100
Dadra and Nagar Haveli and Daman and Diun/an/a
Delhin/an/a
Goan/an/a
Gujarat0.3–4.0%19,300–97,300
Haryana0.4–5.0%39,200–447,200
Himachal Pradesh0.4–0.9%36,800–76,900
Jammu and Kashmir0.7–1.1%337,800–470,800
Jharkhand0.2–0.6%103,600–231,400
Karnataka0.1–0.5%29,400–93,900
Kerala<0.4%10,400–77,300
Madhya Pradesh0.7–2.1%201,200–552,100
Maharashtra<0.1%300–1700
Manipur8.6–22.7%46,500–121,900
Meghalaya0.2–1.5%3300–13,800
Mizoram4.5–18.0%23,500–82,400
Nagaland5.9–21.5%54,300–188,600
Odisha<0.4%1300–194,600
Puducherryn/an/a
Punjab2.3–6.8%299,100–788,500
Rajasthan<0.1%2300–10,800
Sikkimn/an/a
Tamil Nadu<0.1%200–200
Telangana<0.2%4100–12,900
Tripura0.1–1.4%800–10,000
Uttar Pradesh1.0–2.4%1,222,800–2,458,500
Uttarakhand<0.7%900–42,300
West Bengal12.9–20.5%7,432,200–10,144,700
Total2.0–4.2%17,710,000–29,690,000

Share and Cite

MDPI and ACS Style

Podgorski, J.; Wu, R.; Chakravorty, B.; Polya, D.A. Groundwater Arsenic Distribution in India by Machine Learning Geospatial Modeling. Int. J. Environ. Res. Public Health 2020, 17, 7119. https://doi.org/10.3390/ijerph17197119

AMA Style

Podgorski J, Wu R, Chakravorty B, Polya DA. Groundwater Arsenic Distribution in India by Machine Learning Geospatial Modeling. International Journal of Environmental Research and Public Health. 2020; 17(19):7119. https://doi.org/10.3390/ijerph17197119

Chicago/Turabian Style

Podgorski, Joel, Ruohan Wu, Biswajit Chakravorty, and David A. Polya. 2020. "Groundwater Arsenic Distribution in India by Machine Learning Geospatial Modeling" International Journal of Environmental Research and Public Health 17, no. 19: 7119. https://doi.org/10.3390/ijerph17197119

APA Style

Podgorski, J., Wu, R., Chakravorty, B., & Polya, D. A. (2020). Groundwater Arsenic Distribution in India by Machine Learning Geospatial Modeling. International Journal of Environmental Research and Public Health, 17(19), 7119. https://doi.org/10.3390/ijerph17197119

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop