Statistical Parametric Mapping Reveals Subtle Gender Differences in Angular Movements in Table Tennis Topspin Backhand
Abstract
1. Introduction
1.1. Table Tennis Kinematics in Scientific Literature
1.2. Variability—An Interesting Issue in Table Tennis
1.3. Statistical Parametric Mapping
1.4. Research Goals Motivation
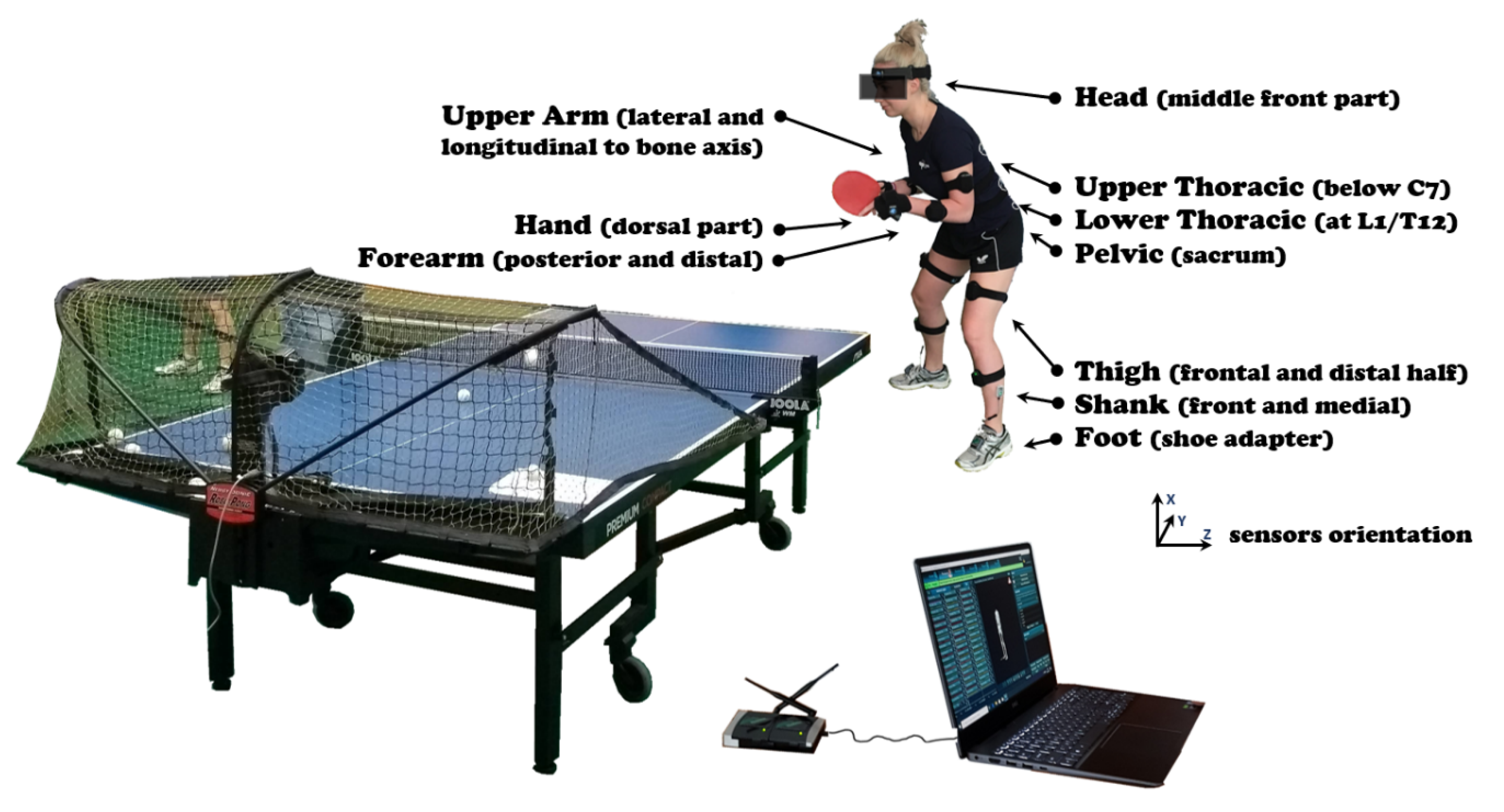
2. Materials and Methods
- rotation type: backspin
- speed (determines both speed and spin, where 0 is the minimum, and 30 is the maximum): 11
- left position (leftmost position to which the ball is delivered): 15
- wing (robot’s head angle indicator): 9.5
- frequency (time interval between balls thrown): 1.4 s
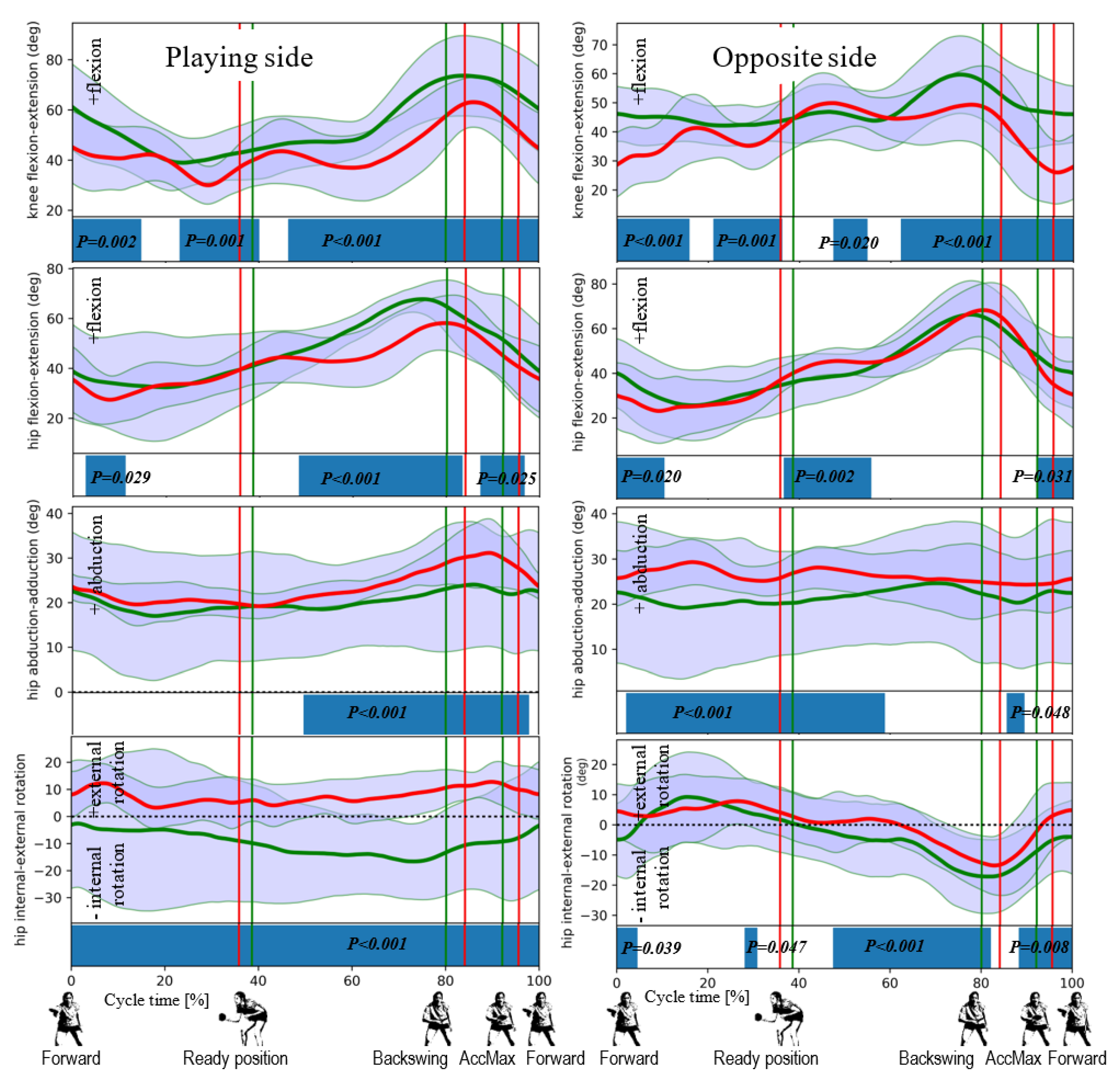
- Knee flexion-extension (KFE): movement of the tibia with respect to the femur coordinate system in the sagittal plane due to the rotation of the proximal–distal axis about the mediolateral axis; a negative sign denotes extension, and positive sign flexion;
- Hip flexion-extension (HFE): movement of the femur with respect to the pelvis coordinate system in the sagittal plane due to the rotation of the proximal–distal axis about the mediolateral axis; a negative sign denotes extension, while positive flexion;
- Hip abduction-adduction (HAA): movement of the femur with respect to the pelvis coordinate system in the frontal plane due to the rotation of the proximal–distal axis out of the sagittal plane; a negative sign denotes adduction, while positive abduction;
- Hip internal-external rotation (HIER): internal or external movement of the femur with respect to the pelvis coordinate system in the transversal plane due to the rotation about the proximal–distal axis; a negative sign denotes internal, while positive external rotation;
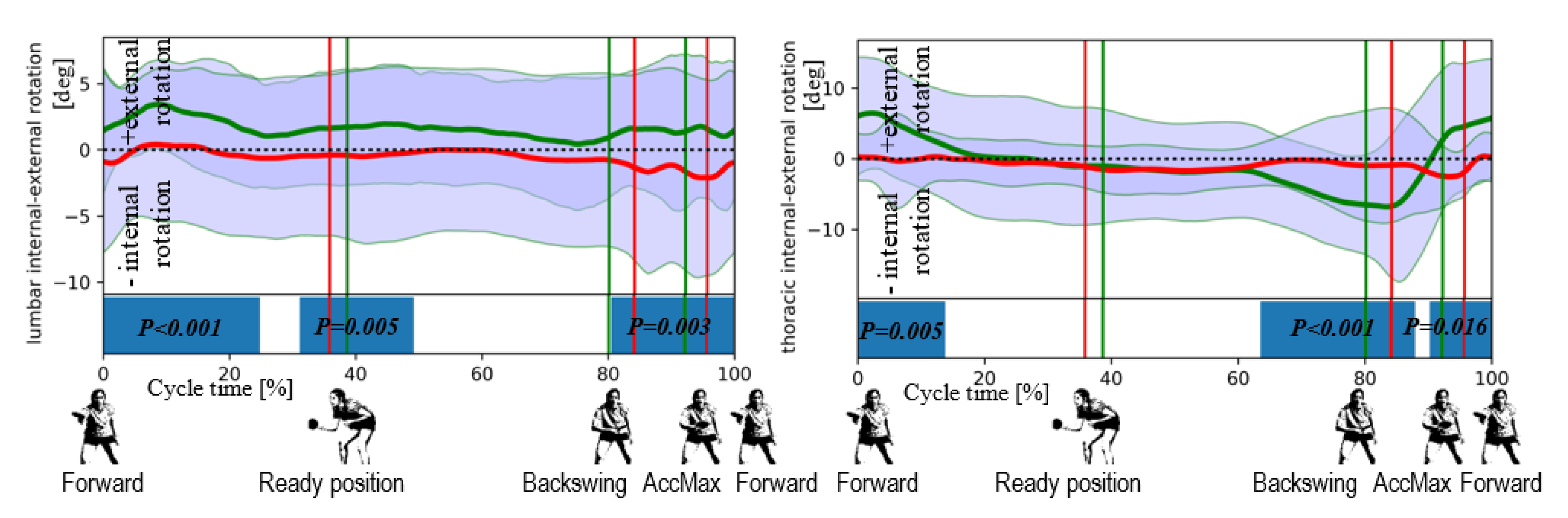
- Lumbar internal-external rotation (LIER): internal or external movement of the loins in the transversal plane due to the rotation about the loin longitudinal axis; a negative sign denotes internal, while positive external rotation;
- Thoracic internal-external rotation (ThIER): internal or external movement of the thorax relative to the global coordination system in the transversal plane due to the rotation about the thorax longitudinal axis; a negative sign denotes internal, while positive external rotation.
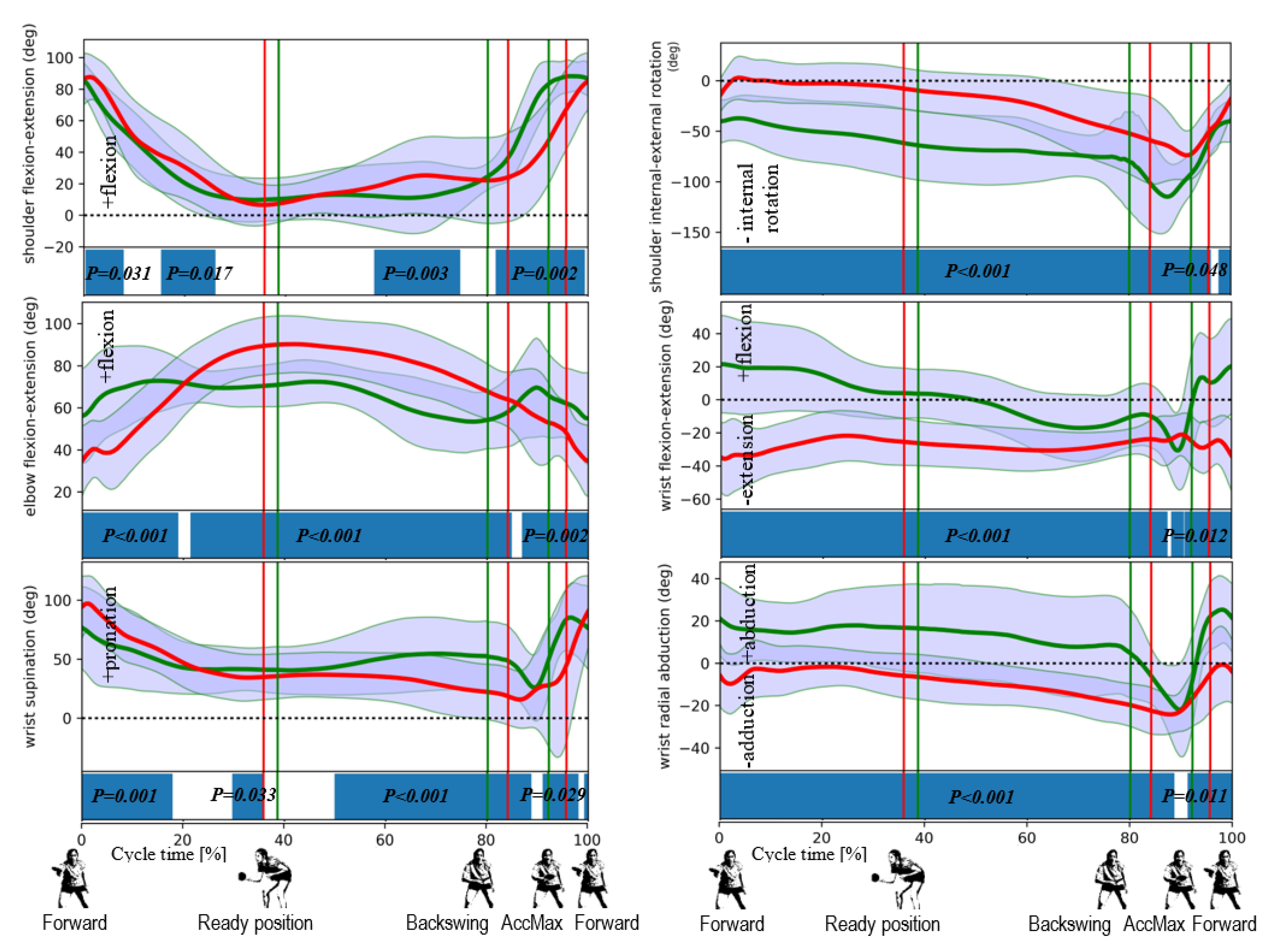
- Shoulder flexion-extension (ShFE): movement of the humerus relative to the thorax in the sagittal plane; a negative sign denotes extension, while positive flexion;
- Shoulder abduction-adduction (ShAA): movement of the humerus relative to the thorax in the frontal plane; a negative sign denotes adduction, while positive abduction;
- Shoulder internal-external rotation (ShIER): movement of the humerus relative to the thorax in the transversal plane; a negative sign denotes internal (medial), while positive external (lateral) rotation;
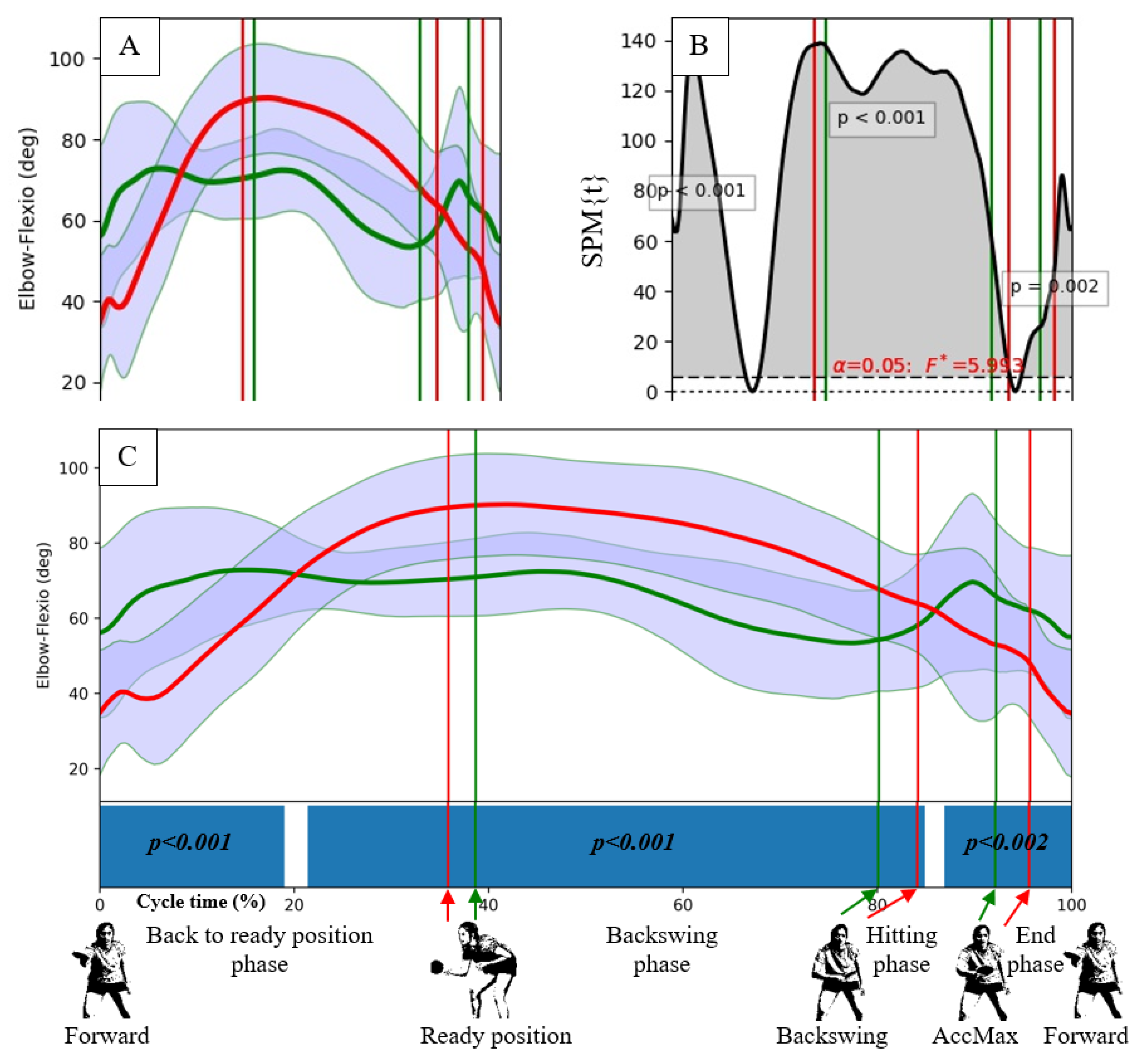
- Elbow flexion-extension (EFE): movement of the forearm relative to the humerus along the transversal axis; a negative sign denotes (hyper)extension, while positive flexion;
- Wrist flexion-extension (WFE): movement of the wrist relative to the radius along the transversal axis and measured between the upper arm and hand sensors; a negative sign denotes extension, while positive flexion;
- Wrist supination-pronation (WSup): movement of the wrist relative to the radius along the axis and measured between the upper arm and hand sensors; pronation is a positive rotation, while supination is a negative rotation;
- Wrist radial abduction-adduction (WRad): movement of the wrist relative to the radius and measured between the upper arm and hand sensors; adduction (or ulnar deviation) is negative, while abduction (or ulnar deviation) is positive.
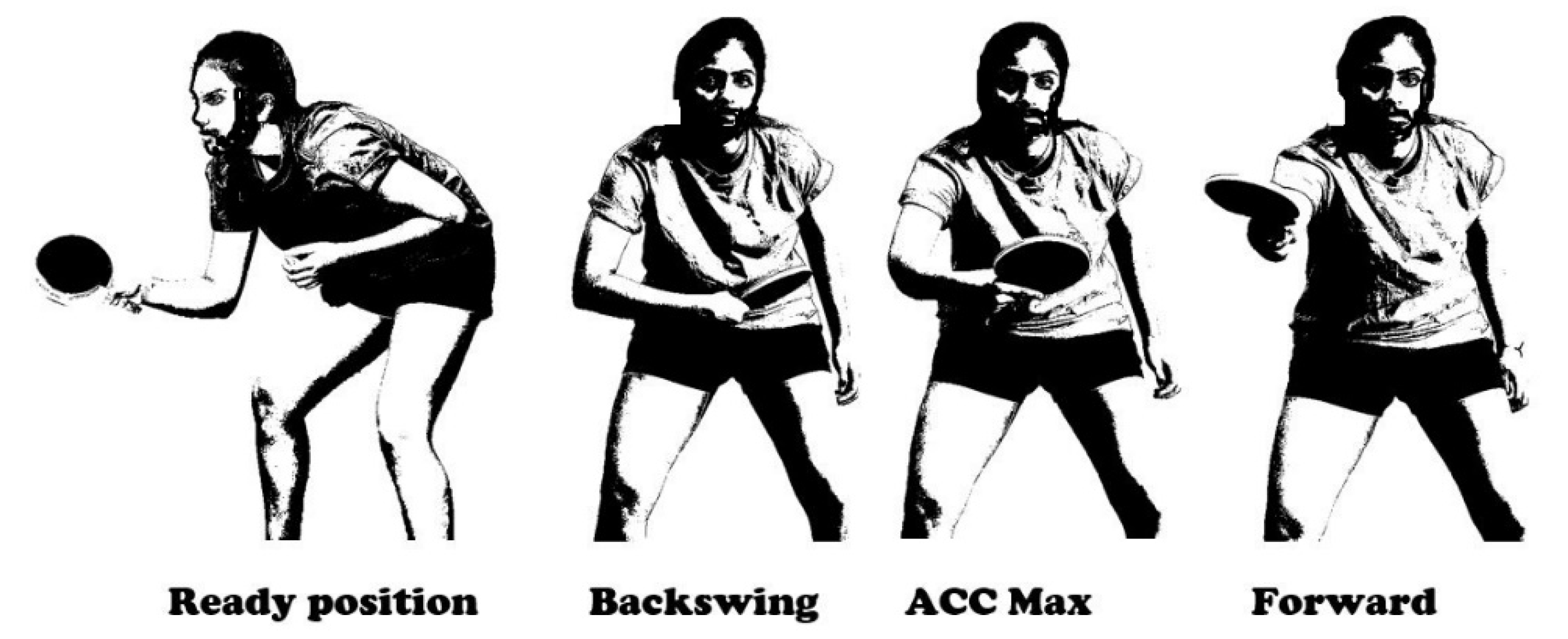
- Ready position: the hand is not moving after the previous stroke, just before the swing;
- Backswing: the moment when the hand changes direction from backward to forward in the sagittal plane after the swing;
- ACCMax: the moment when the hand reaches the maximum acceleration;
- Forward: the moment when the hand changes direction from forward to backward in the sagittal plane after the stroke (the end of the cycle and the beginning of next cycle).
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Malagoli Lanzoni, I.; Katsikadelis, M.; Straub, G.; Djokic, Z. Footwork technique used in elite table tennis matches. Int. J. Racket Sports Sci. 2020, 1, 44–48. [Google Scholar]
- Malagoli Lanzoni, I.; di Michele, R.; Merni, F. A notational analysis of shot characteristics in top level table tennis players. Eur. J. Sport Sci. 2013, 14, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Iino, Y.; Yoshioka, S.; Fukashiro, S. Uncontrolled manifold analysis of joint angle variability during table tennis forehand. Hum. Mov. Sci. 2017, 56, 98–108. [Google Scholar] [CrossRef]
- Malagoli Lanzoni, I.; Bartolomei, S.; di Michele, R.; Fantozzi, S. A kinematic comparison between long-line and cross-court top spin forehand in competitive table tennis players. J. Sports Sci. 2018, 36, 2637–2643. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Fu, L.; Gu, Y.; Mei, Q.; Fu, F.; Fernandez, J. Comparative study of kinematics and muscle activity between elite and amateur table tennis players during topspin loop against backspin movements. J. Hum. Kinet. 2018, 64, 25–33. [Google Scholar] [CrossRef]
- Iino, Y.; Mori, T.; Kojima, T. Contributions of upper limb rotations to racket velocity in table tennis backhands against topspin and backspin. J. Sports Sci. 2008, 26, 287–293. [Google Scholar] [CrossRef]
- Iino, Y.; Kojima, T. Kinematics of table tennis topspin forehands: Effects of performance level and ball spin. J. Sports Sci. 2009, 27, 1311–1321. [Google Scholar] [CrossRef] [PubMed]
- Iino, Y.; Kojima, T. Kinetics of the upper limb during table tennis topspin forehands in advanced and intermediate players. Sports Biomech. 2011, 10, 361–377. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Zhang, Y.; Baker, J.; Gu, Y. Effects of performance level on lower limb kinematics during table tennis forehand loop. Acta Bioeng. Biomech. 2016, 18, 149–155. [Google Scholar] [PubMed]
- Bańkosz, Z.; Winiarski, S. The kinematics of table tennis racquet: Differences between topspin strokes. J. Sports Med. Phys. Fit. 2017, 57, 202–213. [Google Scholar] [CrossRef]
- Bańkosz, Z.; Winiarski, S. Correlations between angular velocities in selected joints and velocity of table tennis racket during topspin forehand and backhand. J. Sports Sci. Med. 2018, 17, 330–338. [Google Scholar] [PubMed]
- Sekiya, H.; Tanaka, Y. Movement modifications related to psychological pressure in a table tennis forehand task. Percept. Mot. Skills 2019, 126, 143–156. [Google Scholar] [CrossRef] [PubMed]
- Summers, J.J.; Anson, J.G. Current status of the motor program: Revisited. Hum. Mov. Sci. 2009, 28, 566–577. [Google Scholar] [CrossRef] [PubMed]
- Stergiou, N.; Decker, L.M. Human movement variability, nonlinear dynamics, and pathology: Is there a connection? Hum. Mov. Sci. 2011, 30, 869–888. [Google Scholar] [CrossRef]
- Scholz, J.P.; Schöner, G. Use of the uncontrolled manifold (UCM) approach to understand motor variability, motor equivalence, and self-motion. Adv. Exp. Med. Biol. 2014, 826, 91–100. [Google Scholar] [CrossRef]
- Bartlett, R.; Wheat, J.; Robins, M. Is movement variability important for sports biomechanists? Sports Biomech. 2007, 6, 224–243. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. Experimental design and statistical parametric mapping. In Human Brain Function, 2nd ed.; Frackowiak, R.S.J., Friston, K.J., Frith, C.D., Dolan, R.J., Price, C.J., Zeki, S., Ashburner, J.T., Penny, W.D., Eds.; Elsevier: Amsterdam, The Netherlands, 2004; pp. 599–632. [Google Scholar]
- Pataky, T.C.; Robinson, M.A.; Vanrenterghem, J. Vector field statistical analysis of kinematic and force trajectories. J. Biomech. 2013, 46, 2394–2401. [Google Scholar] [CrossRef]
- Pataky, T.C. One-dimensional statistical parametric mapping in Python. Comput. Methods Biomech. Biomed. Eng. 2012, 15, 295–301. [Google Scholar] [CrossRef] [PubMed]
- Pataky, T.C.; Goulermas, J.Y. Pedobarographic statistical parametric mapping (pSPM): A pixel-level approach to foot pressure image analysis. J. Biomech. 2008, 41, 2136–2143. [Google Scholar] [CrossRef]
- Robinson, M.A.; Vanrenterghem, J.; Pataky, T.C. Statistical Parametric Mapping (SPM) for alpha-based statistical analyses of multi-muscle EMG time-series. J. Electromyogr. Kinesiol. 2015, 25, 14–19. Available online: http://www.ncbi.nlm.nih.gov/pubmed/25465983 (accessed on 9 September 2020).
- Serrien, B.; Goossens, M.; Baeyens, J. Statistical parametric mapping of biomechanical one-dimensional data with Bayesian inference. Int. Biomech. 2019, 6, 9–18. [Google Scholar] [CrossRef]
- Pataky, T.C. Generalised n-dimensional biomechanical field analysis using statistical parametric mapping. J. Biomech. 2010, 43, 1976–1982. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, R.J.; van Wieringen, P.W.C. Timing an attacking forehand drive in table tennis. J. Exp. Psychol. Hum. 1990, 16, 21–29. [Google Scholar] [CrossRef]
- Sheppard, A.; Li, F.X. Expertise and the control of interception in table tennis. Eur. J. Sport Sci. 2007, 7, 213–222. [Google Scholar] [CrossRef]
- Bańkosz, Z.; Winiarski, S. Using wearable inertial sensors to estimate kinematic parameters and variability in the table tennis topspin forehand stroke. Appl. Bionics Biomech. 2020, 8413948. [Google Scholar] [CrossRef] [PubMed]
- Bańkosz, Z.; Winiarski, S.; Malagoli Lanzoni, I. Gender differences in kinematic parameters of topspin forehand and backhand in table tennis. Int. J. Environ. Res. Public Health 2020, 17, 5742. [Google Scholar] [CrossRef]
- Sharif Bidabadi, S.; Murray, I.; Lee, G.Y.F. Validation of foot pitch angle estimation using inertial measurement unit against marker-based optical 3D motion capture system. Biomed. Eng. Lett. 2018, 8, 283–290. [Google Scholar] [CrossRef]
- Wu, G.; van der Helm, F.C.T.; Veeger, H.E.J.; Makhsous, M.; van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. ISB recommendation on definitions of joint coordinate systems of various joints for the reporting of human joint motion—Part II: Shoulder, elbow, wrist and hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef]
- Wu, G.; Siegler, S.; Allard, P.; Kirtley, C.; Leardini, A.; Rosenbaum, D.; Whittle, M.; D’Lima, D.D.; Cristofolini, L.; Witte, H.; et al. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion—Part I: Ankle, hip, and spine. J. Biomech. 2002, 35, 543–548. [Google Scholar] [CrossRef]
- Kontaxis, A.; Cutti, A.G.; Johnson, G.R.; Veeger, H.E.J. A framework for the definition of standardised protocols for measuring upper-extremity kinematics. Clin. Biomech. 2009, 24, 246–253. [Google Scholar] [CrossRef]
- Serrien, B.; Baeyens, J.P. Systematic review and meta-analysis on proximal-to-distal sequencing in team handball: Prospects for talent detection? J. Hum. Kinet. 2018, 63, 9–21. [Google Scholar] [CrossRef]
- Fuchs, P.X.; Lindinger, S.J.; Schwameder, H. Kinematic analysis of proximal-to-distal and simultaneous motion sequencing of straight punches. Sports Biomech. 2018, 17, 512–530. [Google Scholar] [CrossRef]
- Bańkosz, Z.; Winiarski, S. The evaluation of changes of angles in selected joints during topspin forehand in table tennis. Mot. Control. 2018, 22, 314–337. [Google Scholar] [CrossRef]
- Ferdinands, R.E.D.; Kersting, U.G.; Marshall, R. Kinematic and kinetic energy analysis of segmental sequencing in cricket fast bowling. Sport Technol. 2013, 6, 10–21. [Google Scholar] [CrossRef]
- Liu, H.; Leigh, S.; Yu, B. Sequences of upper and lower extremity motions in javelin throwing. J. Sports Sci. 2010, 28, 1459–1467. [Google Scholar] [CrossRef]
- Bańkosz, Z.; Winiarski, S. Kinematic parameters of topspin forehand in table tennis and their inter- and intra-individual variability. J. Sports Sci. Med. 2020, 19, 138–148. [Google Scholar] [PubMed]
- Carrasco Paez, L.; de la Fuente, F.P.; Martinez, E. Somatotype and body composition of young top-level table tennis players. Int. J. Table Tennis Sci. 2010, 6, 175–177. Available online: https://www.researchgate.net/publication/274456511_Somatotype_and_Body_Composition_of_Young_Top-level_Table_Tennis_Players (accessed on 9 September 2020).
- Zagatto, A.; Milioni, F.; Freitas, I.F.; Arcangelo, S.A.; Padulo, J. Body composition of table tennis players: Comparison between performance level and gender. Sport Sci. Health 2015, 12, 49–54. [Google Scholar] [CrossRef]
- Tamaki, S.; Yoshida, K.; Yamada, K. A shot number based approach to performance analysis in table tennis. J. Hum. Kinet. 2017, 55, 7–18. [Google Scholar] [CrossRef]
- Betzler, N.F.; Monk, S.A.; Wallace, E.S.; Otto, S.R. Variability in clubhead presentation characteristics and ball impact location for golfers’ drives. J. Sports Sci. 2012, 30, 439–448. [Google Scholar] [CrossRef]
- Miller, S.A. Variability in basketball shooting: Practical implications. In International Research in Sports Biomechanics; Hong, Y., Ed.; Routledge: London, UK, 2002; pp. 27–34. [Google Scholar]
- Langdown, B.L.; Bridge, M.W.; Fli, F.X. Impact position variability in golfers of differing skill level. Int. J. Golf. Sci. 2013, 2, 142–151. [Google Scholar] [CrossRef]
| Variable | Ready | Backswing | ACCMax | Forward |
|---|---|---|---|---|
| Female | 35.82 ± 14.83 | 84.10 ± 3.44 | 86.19 ± 1.37 | 95.60 ± 3.19 |
| Male | 38.62 ± 14.30 | 80.07 ± 5.36 | 89.77 ± 2.18 | 92.11 ± 3.36 |
| p of Wilcoxon test | 0.08 | <0.01 ٭ | <0.01 ٭ | <0.01 ٭ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bańkosz, Z.; Winiarski, S. Statistical Parametric Mapping Reveals Subtle Gender Differences in Angular Movements in Table Tennis Topspin Backhand. Int. J. Environ. Res. Public Health 2020, 17, 6996. https://doi.org/10.3390/ijerph17196996
Bańkosz Z, Winiarski S. Statistical Parametric Mapping Reveals Subtle Gender Differences in Angular Movements in Table Tennis Topspin Backhand. International Journal of Environmental Research and Public Health. 2020; 17(19):6996. https://doi.org/10.3390/ijerph17196996
Chicago/Turabian StyleBańkosz, Ziemowit, and Sławomir Winiarski. 2020. "Statistical Parametric Mapping Reveals Subtle Gender Differences in Angular Movements in Table Tennis Topspin Backhand" International Journal of Environmental Research and Public Health 17, no. 19: 6996. https://doi.org/10.3390/ijerph17196996
APA StyleBańkosz, Z., & Winiarski, S. (2020). Statistical Parametric Mapping Reveals Subtle Gender Differences in Angular Movements in Table Tennis Topspin Backhand. International Journal of Environmental Research and Public Health, 17(19), 6996. https://doi.org/10.3390/ijerph17196996






