Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7
Abstract
:1. Introduction
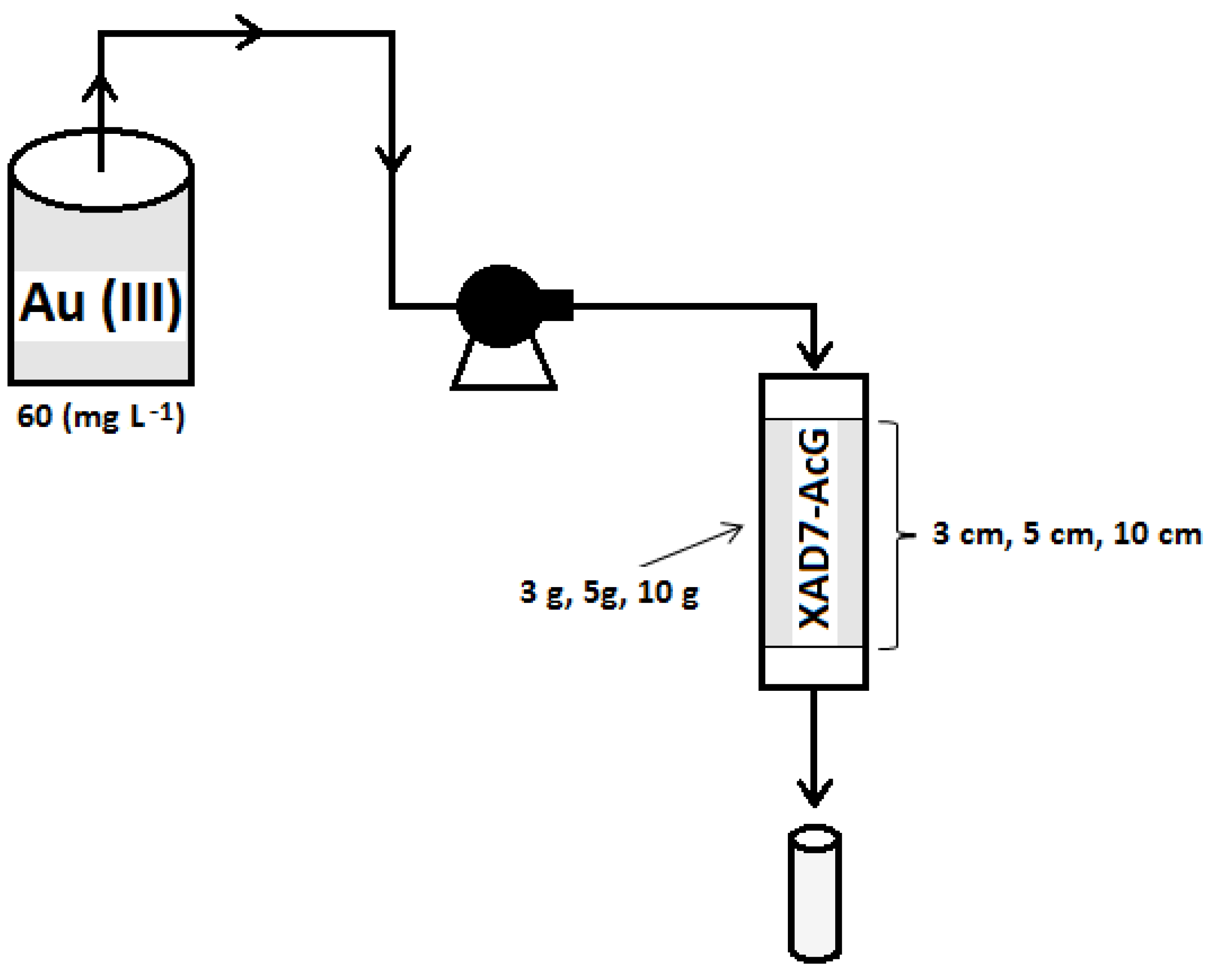
2. Materials and Methods
3. Results and Discussion
3.1. XAD7-AcG Material Caracterization
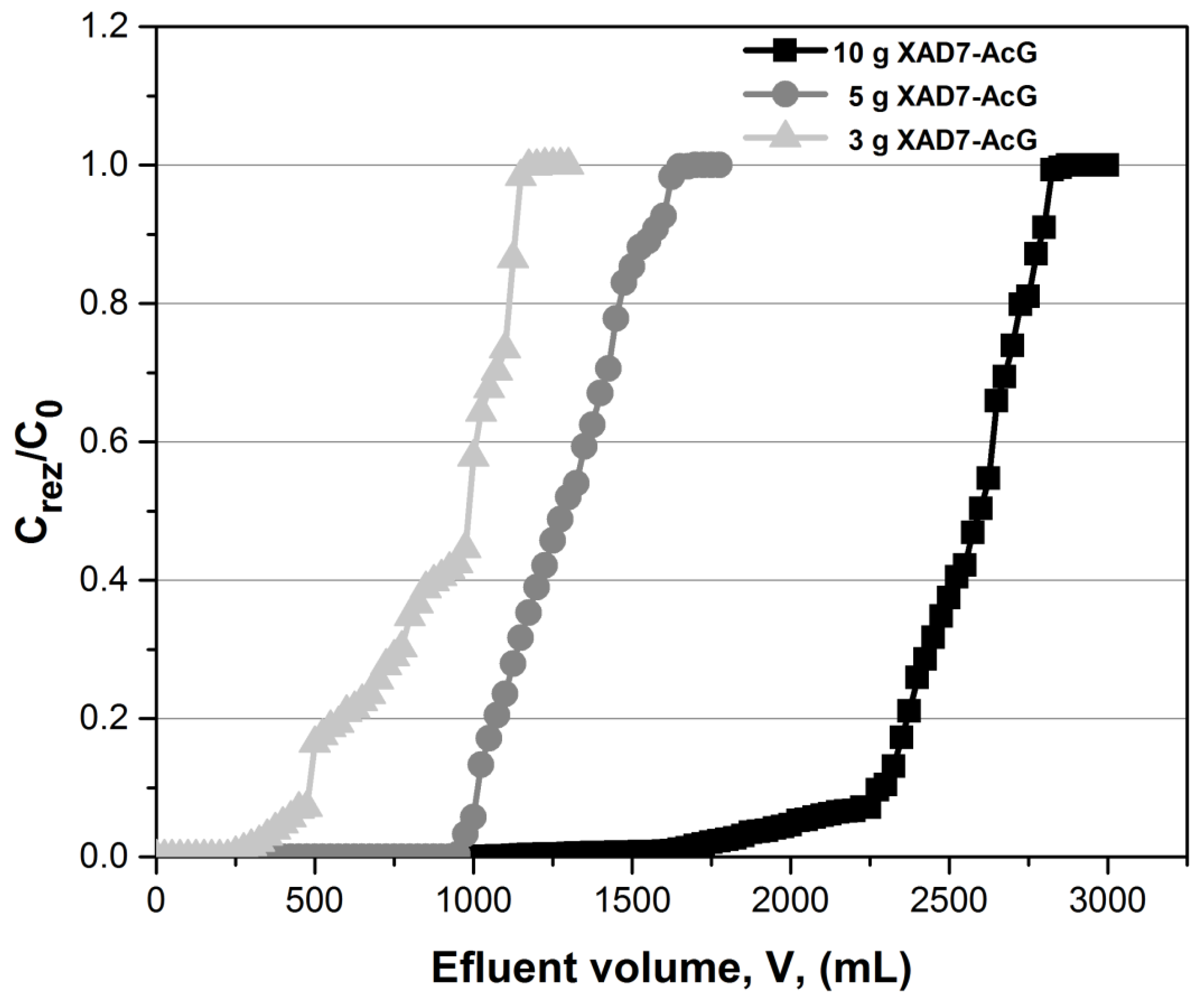
3.2. Fixed-Bed Column Adsorption Studies
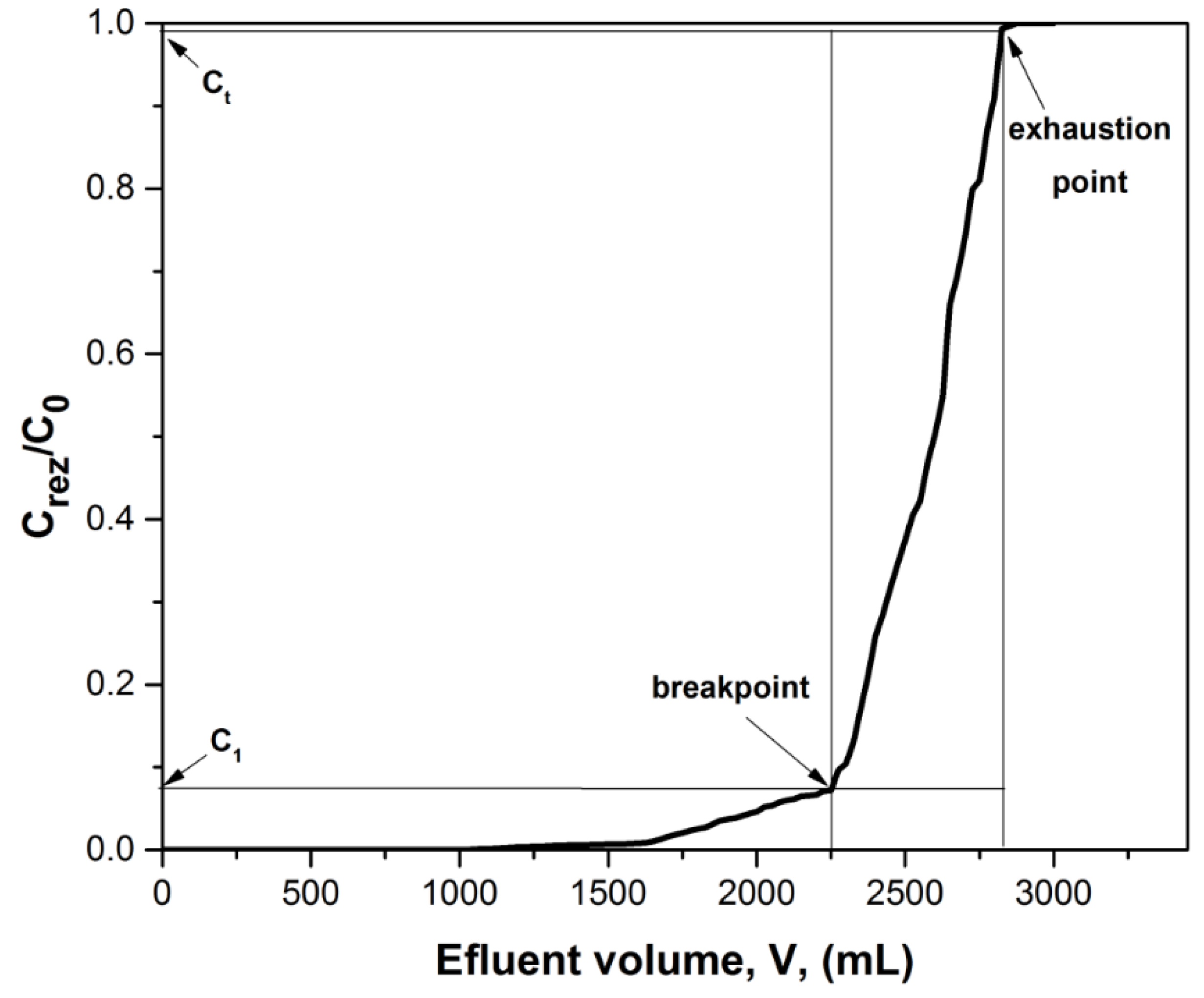
3.2.1. Mass Transfer Zone
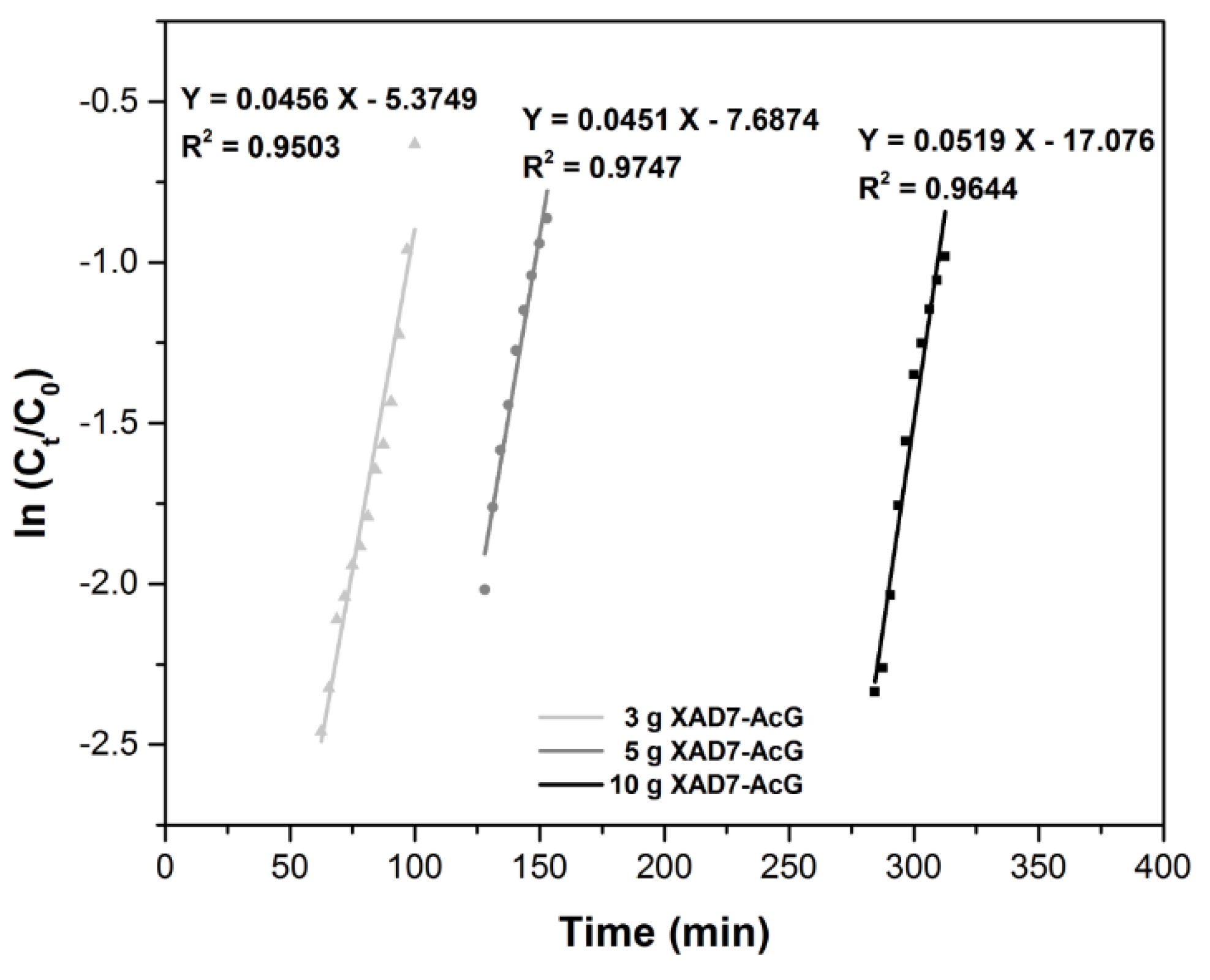
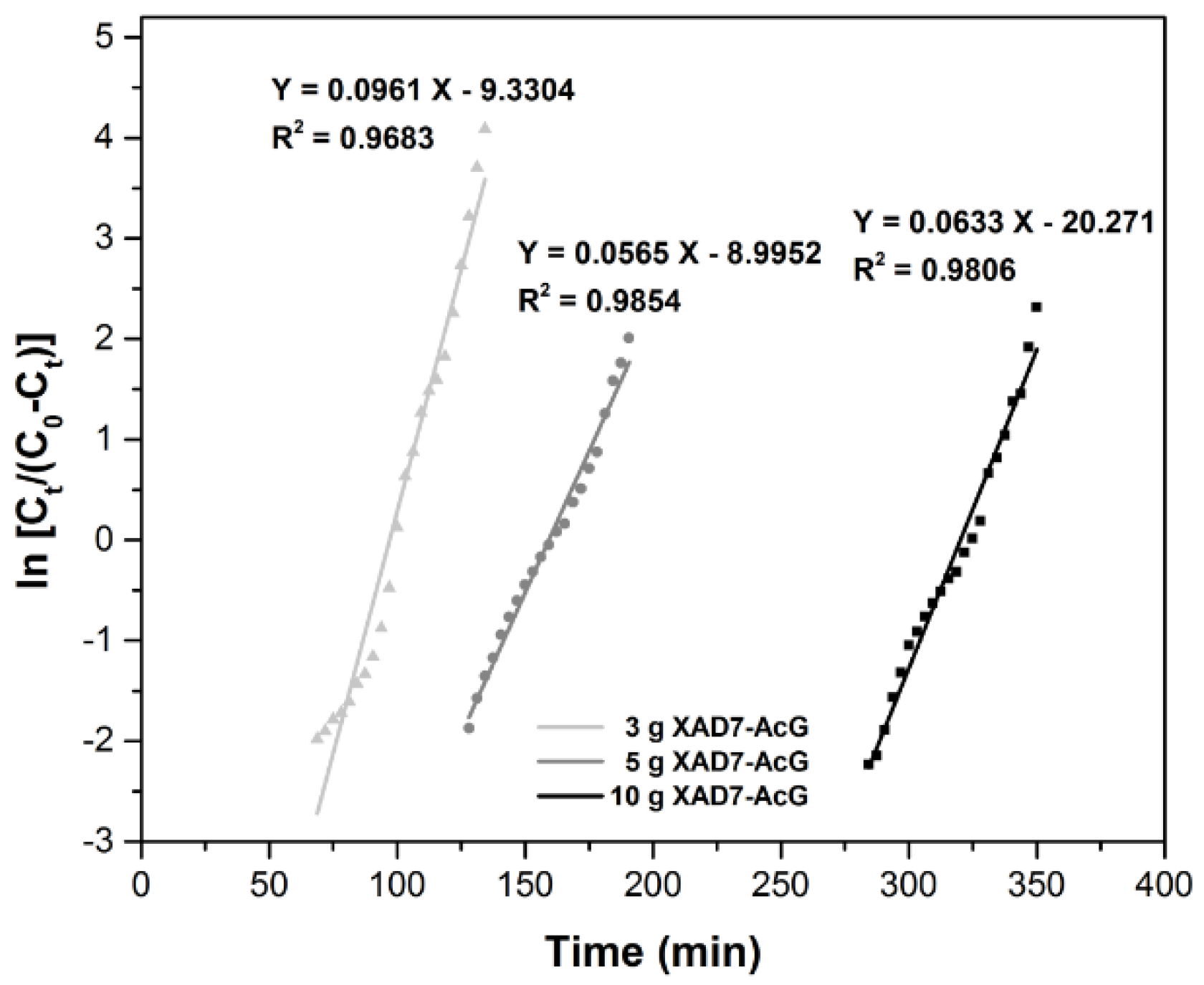
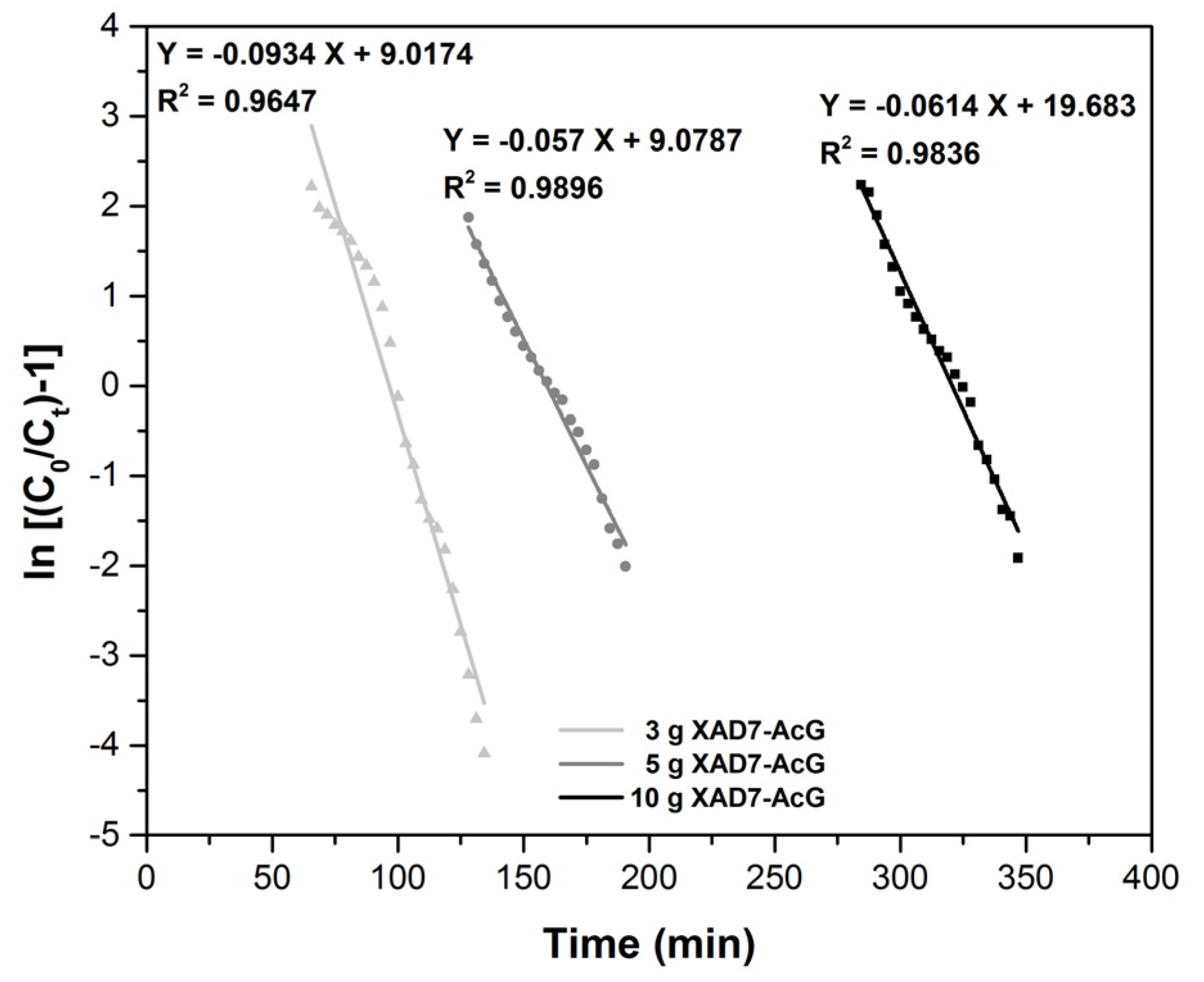
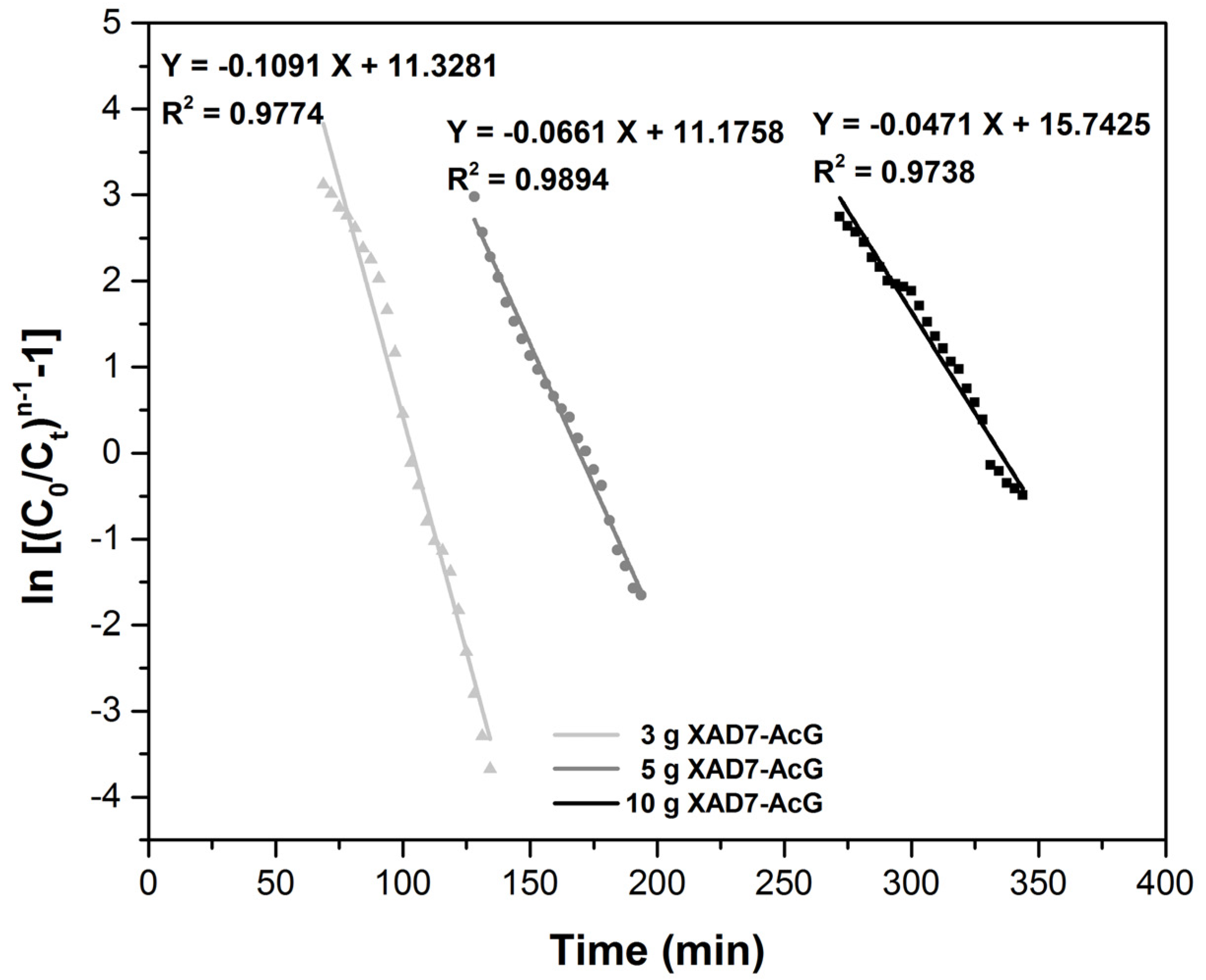
3.2.2. Adsorption Models for Column Study
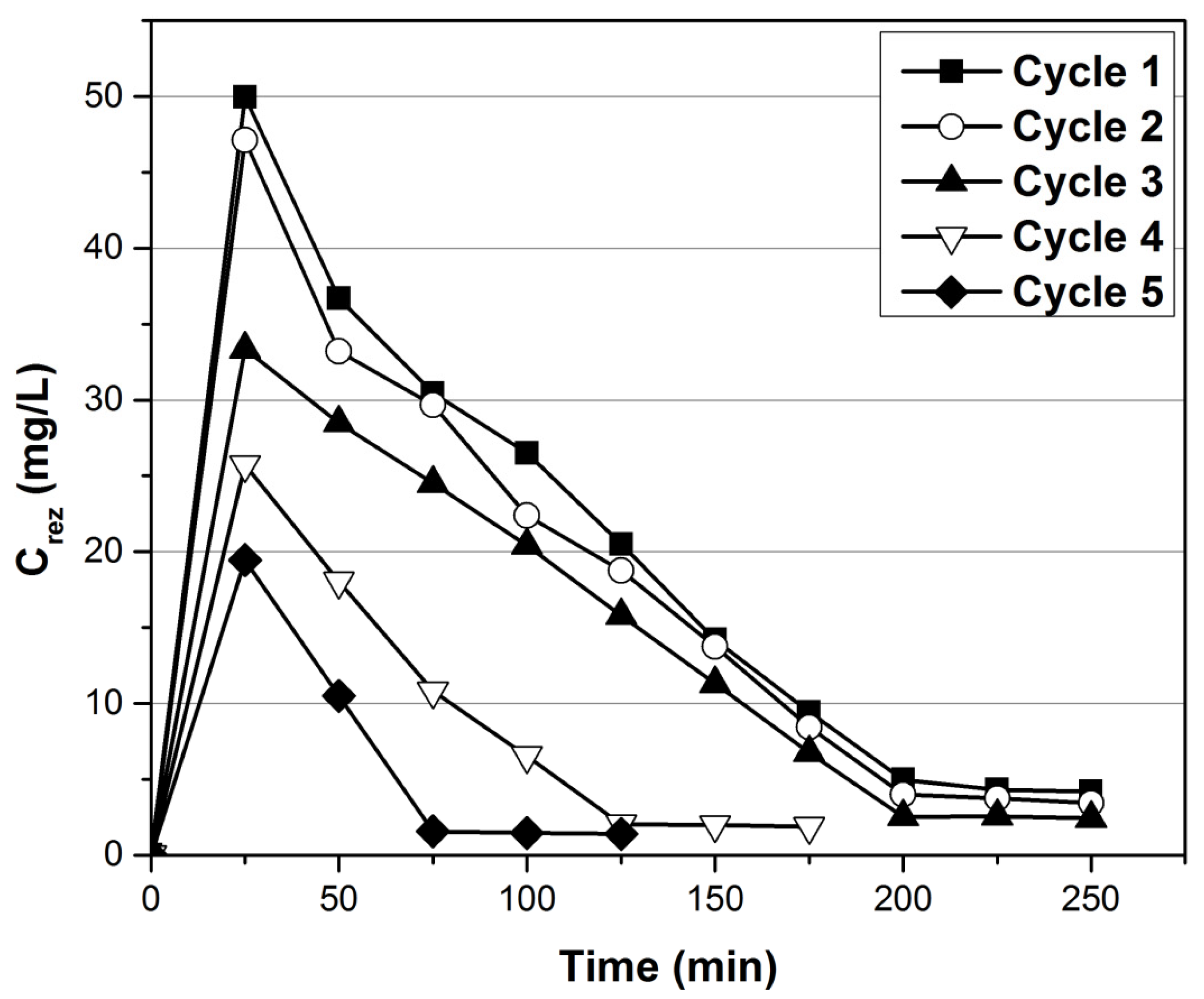
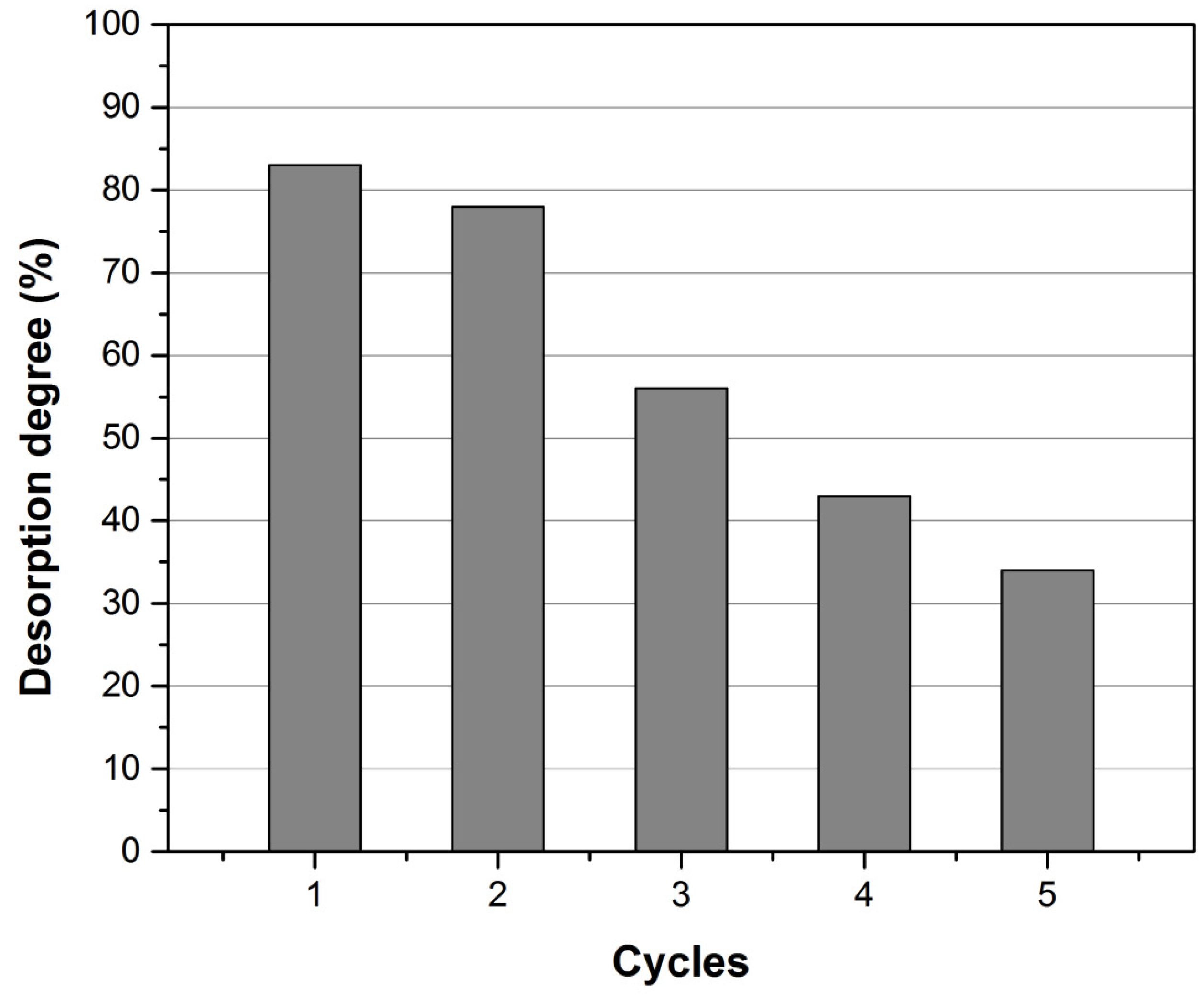
3.3. Desorption Studies
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Patel, H. Fixed-bed column adsorption study: A comprehensive review. Appl. Water. Sci. 2019, 9, 45. [Google Scholar] [CrossRef] [Green Version]
- Dabrowski, A. Adsorption—From theory to practice. Adv. Colloid Interface Sci. 2001, 93, 135–224. [Google Scholar] [CrossRef]
- Selim, K.A.; Youssef, M.A.; Abd El-Rahiem, F.H.; Hassan, M.S. Dye removal using some surface modified silicate minerals. Int. J. Min. Sci. Technol. 2014, 24, 183–189. [Google Scholar] [CrossRef]
- Kafshgari, F.; Keshtkar, A.R.; Mousavian, M.A. Study of Mo (VI) removal from aqueous solution: Application of different mathematical models to continuous biosorption data. Iran. J. Environ. Health Sci. Eng. 2013, 10, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miralles, N.; Valderrama, C.; Casas, I.; Martınez, M.; Florido, A. Cadmium and Lead Removal from Aqueous Solution by Grape Stalk Wastes: Modeling of a Fixed-Bed Column. J. Chem. Eng. Data 2010, 55, 3548–3554. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, A.; Hasegawa, H.; Sugimoto, W.; Maki, T.; Ueda, K. Adsorption of gold(III), platinum(IV) and palladium(II) onto glycine modified crosslinked chitosan resin. Bioresour. Technol. 2008, 99, 3801–3809. [Google Scholar] [CrossRef]
- Spitzer, M.; Rodnei, B. Selective electrochemical recovery of gold and silver from cyanide aqueous effluents using titanium and vitreous carbon cathodes. Hydrometallurgy 2004, 74, 233–242. [Google Scholar] [CrossRef]
- Syed, S. Recovery of gold from secondary sources—A review. Hydrometallurgy 2012, 115–116, 30–51. [Google Scholar] [CrossRef]
- Cui, J.; Zhang, L. Metallurgical recovery of metals from electronic waste: A review. J. Hazard. Mater. 2008, 158, 228–256. [Google Scholar] [CrossRef]
- Fleming, C.A. Hydrometallurgy of precious metals recovery. Hydrometallurgy 1992, 30, 127–162. [Google Scholar] [CrossRef] [Green Version]
- Rhee, K.I.; Lee, J.C.; Lee, C.K.; Joo, K.H.; Yoon, J.K.; Kang, H.R.; Kim, Y.S.; Sohn, H.J. A Recovery of Gold from Electronic Scrap by Mechanical Separation, Acid Leaching and Electrowinning. In Recycling Metals and Engineered Materials; Queneau, P.B., Peterson, R.D., Eds.; TMS Publication: Pittsburgh, PA, USA, 1995; pp. 469–478. [Google Scholar]
- Yap, C.Y.; Mohamed, N. An electro-generative process for the recovery of gold from cyanide solutions. Chemosphere 2007, 67, 1502–1510. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, J.E. Recovering precious metals from electronic scrap. J. Miner. Metall. Mater. Soc. 1992, 44, 43–48. [Google Scholar] [CrossRef]
- Lee, J.C.; Song, H.T.; Yoo, J.M. Present status of the recycling of waste electrical and electronic equipment in Korea. Resour. Conserv. Recycl. 2007, 50, 380–397. [Google Scholar] [CrossRef]
- Mack, C.; Wilhelmi, B.; Duncan, J.R.; Burgess, J.E. Biosorption of precious metals. Biotechnol. Adv. 2007, 25, 264–271. [Google Scholar] [CrossRef] [PubMed]
- Safarzadeh, M.S.; Bafghi, M.S.; Moradkhani, D.; Ilkhchi, M.O. A review on hydrometallurgical extraction and recovery of cadmium from various resources. Miner. Eng. 2007, 20, 211–220. [Google Scholar] [CrossRef]
- Sum, E.Y.L. The Recovery of Metals from Electronic Scrap. J. Miner. Metall. Mater. Soc. 1991, 43, 53–61. [Google Scholar] [CrossRef]
- Jafari, S.; Wilson, B.P.; Hakalahti, M.; Tammelin, T.; Kontturi, E.; Lundstrom, M.; Sillanpaa, M. Recovery of Gold from Chloride Solution by TEMPO-Oxidized Cellulose Nanofiber Adsorbent. Sustainability 2019, 11, 1406. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhou, Y.; Zhou, Y.; Lei, J.; Pu, S. Cyclodextrin modified filter paper for removal of cationic dyes/Cu ions from aqueous solutions. Water Sci. Technol. 2018, 78, 2553–2563. [Google Scholar] [CrossRef]
- Liu, Q.; Zhou, Y.; Lu, J.; Zhou, Y. Novel cyclodextrin-based adsorbents for removing pollutants from wastewater: A critical review. Chemosphere 2020, 241, 125043. [Google Scholar] [CrossRef]
- Syed, S. A green technology for recovery of gold from non-metallic secondary sources. Hydrometallurgy 2006, 82, 48–53. [Google Scholar] [CrossRef]
- Vences-Alvarez, E.; Razo-Flores, E.; Lazaro, I.; Briones-Gallardo, R.; Velasco-Martinez, G.; Rangel-Mendez, R. Gold recovery from very dilute solutions from a mine in closing process: Adsorption-desorption onto carbon materials. J. Mol. Liq. 2017, 240, 549–555. [Google Scholar] [CrossRef]
- Bui, T.H.; Lee, W.; Jeon, S.B.; Kim, K.W.; Lee, Y. Enhanced Gold(III) adsorption using glutaraldehyde-crosslinked chitosan beads: Effect of crosslinking degree on adsorption selectivity, capacity, and mechanism. Sep. Purif. Technol. 2020, 248, 116989. [Google Scholar] [CrossRef]
- Yi, Q.; Fan, R.; Xie, F.; Min, H.; Zhang, Q.; Luo, Z. Selective Recovery of Au(III) and Pd(II) from Waste PCBs Using Ethylenediamine Modified Persimmon Tannin Adsorbent. Procedia Environ. Sci. 2016, 31, 185–194. [Google Scholar] [CrossRef] [Green Version]
- Cortina, J.L.; Warshawsky, A. Developments in Solid-Liquid Extraction by Solvent-Impregnated Resins. In Ion Exchange and Solvent Extraction; Marinsky, J.A., Marcus, Y., Eds.; Marcel Dekker Inc.: New York, NY, USA, 1997; pp. 195–293. [Google Scholar]
- Mihailescu, M.; Negrea, A.; Ciopec, M.; Davidescu, C.M.; Negrea, P.; Duteanu, N.; Rusu, G. Gold (III) adsorption from dilute waste solutions onto Amberlite XAD7 resin modified with L-glutamic acid. Sci. Rep. 2019, 9, 8757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vasanth Kumar, K.; Subanandam, K.; Bhagavanulu, D.V.S. Making GAC sorption economy. Pollut. Res. 2004, 23, 439–444. [Google Scholar]
- Gupta, V.K.; Ali, I. Environmental Water: Advances in Treatment, Remediation and Recycling; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Crittenden, B.; Thomas, W.J. Adsorption Technology and Design; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Chowdhury, Z.Z.; Zain, S.M.; Rashid, A.K.; Rafique, R.F.; Khalid, K. Breakthrough Curve Analysis for Column Dynamics Sorption of Mn(II) Ions from Wastewater by Using Mangostana garcinia Peel-Based Granular-Activated Carbon. J. Chem. 2013, 2013, 959761. [Google Scholar] [CrossRef] [Green Version]
- Hasanzadeh, M.; Ansari, R.; Ostovar, F. Synthesis and application of CeO2/sawdust nanocomposite for removal of As(III) ions from aqueous solutions using a fixed bed column system. Glob. NEST J. 2016, 19, 7–16. [Google Scholar]
- Shafeeyan, M.S.; Daud, W.M.A.W.; Shamiri, A. A review of mathematical modeling of fixed-bed columns for carbon dioxide adsorption. Chem. Eng. Res. Des. 2014, 92, 961–988. [Google Scholar] [CrossRef]
- Yang, Q.; Zhong, Y.; Li, X.; Li, X.; Luo, K.; Wua, X.; Chen, H.; Liu, Y.; Zeng, G. Adsorption-coupled reduction of bromate by Fe(II)–Al(III) layered double hydroxide in fixed-bed column: Experimental and breakthrough curves analysis. J. Ind. Eng. Chem. 2015, 28, 54–59. [Google Scholar] [CrossRef]
- Han, R.; Wang, Y.; Zhao, X.; Wang, Y.; Xie, F.; Cheng, J. Adsorption of methylene blue by phoenix tree leaf powder in a fixed-bed column: Experiments and prediction of breakthrough curves. Desalination 2009, 245, 284–297. [Google Scholar] [CrossRef]
- Bohart, G.S.; Adams, E.Q. Some aspects of the behavior of charcoal with respect to chlorine. J. Am. Chem. Soc. 1920, 42, 523–544. [Google Scholar] [CrossRef] [Green Version]
- Woumfo, E.D.; Siewe, J.M.; Njopwouo, D. A fixed-bed column for phosphate removal from aqueous solutions using an andosol-bagasse mixture. J. Environ. Manag. 2015, 151, 450–460. [Google Scholar] [CrossRef] [PubMed]
- Vilvanathan, S.; Shanthakumar, S. Column adsorption studies on nickel and cobalt removal from aqueous solution using native and biochar form of Tectona grandis. Environ. Prog. Sustain. 2017, 36, 1030–1038. [Google Scholar] [CrossRef]
- Thomas, H.C. Heterogeneous Ion Exchange in a Flowing System. J. Am. Chem. Soc. 1944, 66, 1664–1667. [Google Scholar] [CrossRef]
- Han, R.; Zhang, J.; Zou, W.; Xiao, H.; Shi, J.; Liu, H. Biosorption of copper(II) and lead(II) from aqueous solution by chaff in a fixed-bed column. J. Hazard. Mater. 2006, 133, 262–268. [Google Scholar] [CrossRef] [PubMed]
- Han, R.; Wang, Y.; Zou, W.; Wang, Y.; Shi, J. Comparison of linear and nonlinear analysis in estimating the Thomas model parameters for methylene blue adsorption onto natural zeolite in fixed-bed column. J. Hazard. Mater. 2007, 145, 331–335. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.; Aikat, K.; Halder, G. Ranitidine hydrochloride sorption onto superheated steam activated biochar derived from mung bean husk in fixed bed column. J. Environ. Chem. Eng. 2016, 4, 488–497. [Google Scholar] [CrossRef]
- Dlugosz, O.; Banach, M. Sorption of Ag+ and Cu2+ by Vermiculite in a Fixed-Bed Column: Design, Process Optimization and Dynamics Investigations. Appl. Sci. 2018, 8, 2221. [Google Scholar] [CrossRef] [Green Version]
- Madan, S.S.; De, B.S.; Wasewar, K.L. Adsorption performance of packed bed column for benzylformic acid removal using CaO2 nanoparticles. Chem. Data Collect. 2019, 23, 100267. [Google Scholar] [CrossRef]
- Santos, N.T.; Landers, R.; da Silva, M.G.C.; Vieira, M.G.A. Adsorption of Gold Ions onto Sericin and Alginate Particles Chemically Crosslinked by Proanthocyanidins: A Complete Fixed-Bed Column Study. Ind. Eng. Chem. Res. 2020, 59, 318–328. [Google Scholar] [CrossRef]
- Wasikiewicz, J.M.; Nagasawa, N.; Tamada, M.; Mitomo, H.; Yoshii, F. Adsorption of metal ions by carboxymethylchitin and carboxymethylchitosan hydrogels. Nucl. Instrum. Methods Phys. Res. B 2005, 236, 617–623. [Google Scholar] [CrossRef]
- Tsolele, R.; Mtunzi, F.M.; Klink, M.J.; Pakade, V.E. An alternative low-cost adsorbent for gold recovery from cyanide-leached liquors: Adsorption isotherm and kinetic studies. Adsorp. Sci. Technol. 2018, 37, 3–23. [Google Scholar] [CrossRef] [Green Version]
- Calderon, A.R.M.; Alorro, R.D.; Tadesse, B.; Yoo, K.; Tabelin, C.B. Repurposing of nickeliferous pyrrhotite from mine tailings as magnetic adsorbent for the recovery of gold from chloride solution. Resour. Conserv. Recycl. 2020, 161, 104971. [Google Scholar] [CrossRef]
- Pangeni, B.; Paudyal, H.; Inoue, K.; Kawakita, H.; Ohto, K.; Alam, S. Selective recovery of gold(III) using cotton cellulose treated with concentrated sulfuric acid. Cellulose 2012, 19, 381–391. [Google Scholar] [CrossRef]
- Abdolali, A.; Ngo, H.H.; Guo, W.; Zhou, J.L.; Zhang, J.; Liang, S.; Chang, S.W.; Nguyen, D.D.; Liu, Y. Application of a breakthrough biosorbent for removing heavy metals from synthetic and real wastewaters in a lab-scale continuous fixed-bed column. Bioresour. Technol. 2017, 229, 78–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]

| Column Parameters | ||||
|---|---|---|---|---|
| Bohart-Adams Model | Material Amount (g) | KB-A (L mg−1 min−1) | N0 (mg L−1) | R2 |
| 10 | 8.6 × 10−4 | 1099.6 | 0.9644 | |
| 5 | 7.5 × 10−4 | 1141.9 | 0.9747 | |
| 3 | 7.4 × 10−4 | 1146.2 | 0.9503 | |
| Yoon-Nelson Model | Material Amount (g) | KY-N (min−1) | Τ (min) | R2 |
| 10 | 0.0633 | 320.23 | 0.9806 | |
| 5 | 0.0565 | 159.2 | 0.9854 | |
| 3 | 0.0253 | 97.09 | 0.9683 | |
| Thomas Model | Material Amount (g) | KTh (L mg−1 min−1) | qTh (mg g−1) | R2 |
| 10 | 1.02 × 10−3 | 13.376 | 0.9836 | |
| 5 | 1.05 × 10−3 | 13.379 | 0.9896 | |
| 3 | 1.56 × 10−3 | 13.520 | 0.9647 | |
| Clark Model | Material Amount (g) | r (min−1) | A | R2 |
| 10 | 0.0471 | 68.5 × 10−5 | 0.9738 | |
| 5 | 0.0661 | 70.9 × 10−3 | 0.9894 | |
| 3 | 0.1091 | 82.4 × 10−3 | 0.9774 | |
| Adsorbent | Adsorption Capacity (mg g−1) | Reference |
|---|---|---|
| Sericin andalginate particle-based adsorbent SAPAS | 57.91 | [44] |
| Amberlite XAD7 type functionalized with L-glutamic acid (XAD7-AcG). | 13.5 | This study |
| Carboxymethyl chitin | 11.86 | [45] |
| Macadamia-activated carbon (MAC) | 9.13 | [46] |
| Magnetic nickeliferous pyrrhotite | 6.9 | [47] |
| Cotton cellulose | 1.22 * | [48] |
| Activated carbon F400 | 0.25 ** | [22] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Negrea, A.; Mihailescu, M.; Mosoarca, G.; Ciopec, M.; Duteanu, N.; Negrea, P.; Minzatu, V. Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7. Int. J. Environ. Res. Public Health 2020, 17, 6868. https://doi.org/10.3390/ijerph17186868
Negrea A, Mihailescu M, Mosoarca G, Ciopec M, Duteanu N, Negrea P, Minzatu V. Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7. International Journal of Environmental Research and Public Health. 2020; 17(18):6868. https://doi.org/10.3390/ijerph17186868
Chicago/Turabian StyleNegrea, Adina, Maria Mihailescu, Giannin Mosoarca, Mihaela Ciopec, Narcis Duteanu, Petru Negrea, and Vasile Minzatu. 2020. "Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7" International Journal of Environmental Research and Public Health 17, no. 18: 6868. https://doi.org/10.3390/ijerph17186868
APA StyleNegrea, A., Mihailescu, M., Mosoarca, G., Ciopec, M., Duteanu, N., Negrea, P., & Minzatu, V. (2020). Estimation on Fixed-Bed Column Parameters of Breakthrough Behaviors for Gold Recovery by Adsorption onto Modified/Functionalized Amberlite XAD7. International Journal of Environmental Research and Public Health, 17(18), 6868. https://doi.org/10.3390/ijerph17186868








