Preparing for the Next Wave of COVID-19: Resilience in the Face of a Spreading Pandemic
Abstract
1. Need for Integrated Knowledge
2. Uncertainties in Viral Outbreaks
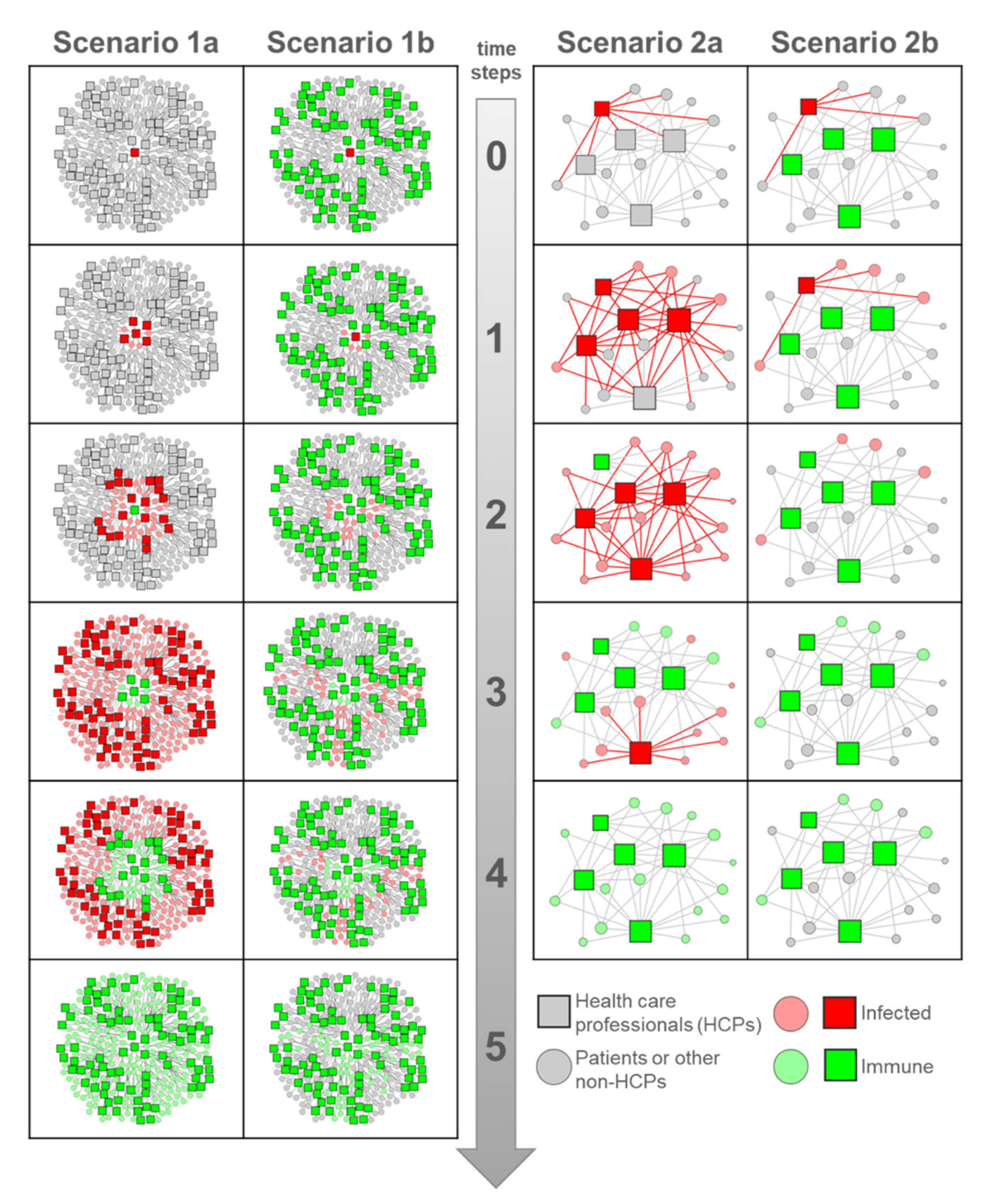
3. Network Scenarios: The Super-Spreaders
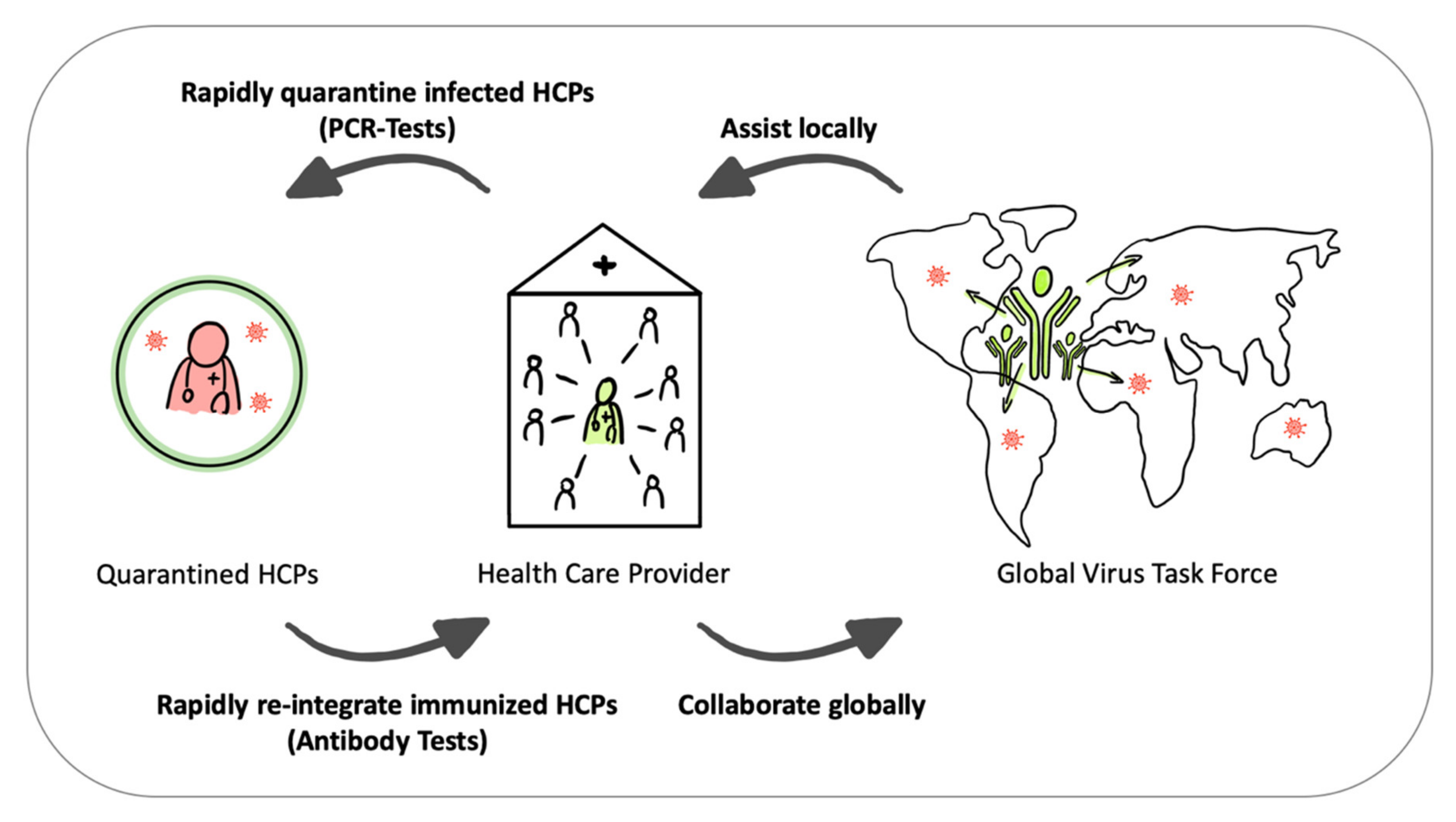
4. From Super-Spreaders to Virus Task Force
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Steiner, G. From probabilistic functionalism to a mental simulation of innovation: By collaboration from vulnerabilities to resilient societal systems. Environ. Syst. Decis. 2018, 38, 92–98. [Google Scholar] [CrossRef]
- Zhang, S.; Diao, M.; Yu, W.; Pei, L.; Lin, Z.; Chen, D. Estimation of the reproductive number of novel coronavirus (COVID-19) and the probable outbreak size on the Diamond Princess cruise ship: A data-driven analysis. Int. J. Infect. Dis. 2020, 93, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Guan, X.; Wu, P.; Wang, X.; Zhou, L.; Tong, Y.; Ren, R.; Leung, K.S.; Lau, E.H.; Wong, J.Y.; et al. Early Transmission Dynamics in Wuhan, China, of Novel Coronavirus-Infected Pneumonia. N. Engl. J. Med. 2020, 382, 1199–1207. [Google Scholar] [CrossRef] [PubMed]
- Guerra, F.M.; Bolotin, S.; Lim, G.; Heffernan, J.; Deeks, S.L.; Li, Y.; Crowcroft, N.S. The basic reproduction number (R0) of measles: A systematic review. Lancet Infect. Dis. 2017, 17, e420–e428. [Google Scholar] [CrossRef]
- Nikbakht, R.; Baneshi, M.R.; Bahrampour, A. Estimation of the Basic Reproduction Number and Vaccination Coverage of Influenza in the United States (2017–18). J. Res. Health Sci. 2018, 18, e00427. [Google Scholar] [PubMed]
- Xia, Z.-Q.; Wang, S.-F.; Li, S.-L.; Huang, L.-Y.; Zhang, W.-Y.; Sun, G.-Q.; Gai, Z.-T.; Jin, Z. Modeling the transmission dynamics of Ebola virus disease in Liberia. Sci. Rep. 2015, 5, 13857. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; McGoogan, J.M. Characteristics of and Important Lessons from the Coronavirus Disease 2019 (COVID-19) Outbreak in China: Summary of a Report of 72314 Cases from the Chinese Center for Disease Control and Prevention. JAMA 2020, 323, 1239–1242. [Google Scholar] [CrossRef]
- Verity, R.; Okell, L.C.; Dorigatti, I.; Winskill, P.; Whittaker, C.; Imai, N.; Cuomo-Dannenburg, G.; Thompson, H.; Walker, P.G.T.; Fu, H.; et al. Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 2020, 20, 669–677. [Google Scholar] [CrossRef]
- Lauer, S.A.; Grantz, K.H.; Bi, Q.; Jones, F.K.; Zheng, Q.; Meredith, H.R.; Azman, A.S.; Reich, N.G.; Lessler, J. The Incubation Period of Coronavirus Disease 2019 (COVID-19) From Publicly Reported Confirmed Cases: Estimation and Application. Ann. Intern. Med. 2020, 172, 577–582. [Google Scholar] [CrossRef] [PubMed]
- Stein, R.A. Super-spreaders in infectious diseases. Int. J. Infect. Dis. 2011, 15, e510–e513. [Google Scholar] [CrossRef] [PubMed]
- Adam, D.; Wu, P.; Wong, J.; Lau, E.; Tsang, T.; Cauchemez, S.; Leung, G.; Cowling, B. Clustering and superspreading potential of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) infections in Hong Kong. Res. Sq. 2020. preprint. [Google Scholar]
- Li, Y.; Yu, I.T.S.; Xu, P.; Lee, J.H.W.; Wong, T.W.; Ooi, P.L.; Sleigh, A.C. Predicting Super Spreading Events during the 2003 Severe Acute Respiratory Syndrome Epidemics in Hong Kong and Singapore. Am. J. Epidemiol. 2004, 160, 719–728. [Google Scholar] [CrossRef] [PubMed]
- James, A.; Pitchford, J.W.; Plank, M.J. An event-based model of superspreading in epidemics. Proc. R. Soc. B Boil. Sci. 2006, 274, 741–747. [Google Scholar] [CrossRef] [PubMed]
- Borgatti, S.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Bucuvalas, J.; Fronzetti Colladon, A.; Gloor, P.A.; Grippa, F.; Horton, J.; Timme, E. Increasing Interactions in Healthcare Team through Architectural Interventions and Interpersonal Communication Analysis. J. Healthc. Inf. Manag. JHIM 2014, 28, 58–65. [Google Scholar]
- The Lancet. COVID-19: Protecting health-care workers. Lancet 2020, 395, 922. [Google Scholar] [CrossRef]
- Li, Y.-K.; Peng, S.; Li, L.-Q.; Wang, Q.; Ping, W.; Zhang, N.; Fu, X. Clinical and Transmission Characteristics of Covid-19—A Retrospective Study of 25 Cases from a Single Thoracic Surgery Department. Curr. Med. Sci. 2020, 40, 295–300. [Google Scholar] [CrossRef] [PubMed]
- Lessells, R.; Moosa, Y.; de Olivaira, T. Report into a Nosocomial Outbreak of Coronavirus Disease 2019 (COVID-19) at Netcare St. Augustine’s Hospital. Durban; Nelson R Mandela School of Medicine, University of Kawzulu-Natal: Durban, South Africa, 2020. [Google Scholar]
- Brandes, U.; Wagner, D. Analysis and visualization of social networks. In Graph Drawing Software; Springer: Berlin/Heidelberg, Germany, 2004; pp. 321–340. [Google Scholar]
- Linkov, I.; Bridges, T.; Creutzig, F.; Decker, J.; Fox-Lent, C.; Kröger, W.; Lambert, J.H.; Levermann, A.; Montreuil, B.; Nathwani, J.; et al. Changing the resilience paradigm. Nat. Clim. Chang. 2014, 4, 407–409. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Steiner, G.; Zenk, L.; Schernhammer, E. Preparing for the Next Wave of COVID-19: Resilience in the Face of a Spreading Pandemic. Int. J. Environ. Res. Public Health 2020, 17, 4098. https://doi.org/10.3390/ijerph17114098
Steiner G, Zenk L, Schernhammer E. Preparing for the Next Wave of COVID-19: Resilience in the Face of a Spreading Pandemic. International Journal of Environmental Research and Public Health. 2020; 17(11):4098. https://doi.org/10.3390/ijerph17114098
Chicago/Turabian StyleSteiner, Gerald, Lukas Zenk, and Eva Schernhammer. 2020. "Preparing for the Next Wave of COVID-19: Resilience in the Face of a Spreading Pandemic" International Journal of Environmental Research and Public Health 17, no. 11: 4098. https://doi.org/10.3390/ijerph17114098
APA StyleSteiner, G., Zenk, L., & Schernhammer, E. (2020). Preparing for the Next Wave of COVID-19: Resilience in the Face of a Spreading Pandemic. International Journal of Environmental Research and Public Health, 17(11), 4098. https://doi.org/10.3390/ijerph17114098





