Spectral Feature Selection Optimization for Water Quality Estimation
Abstract
1. Introduction
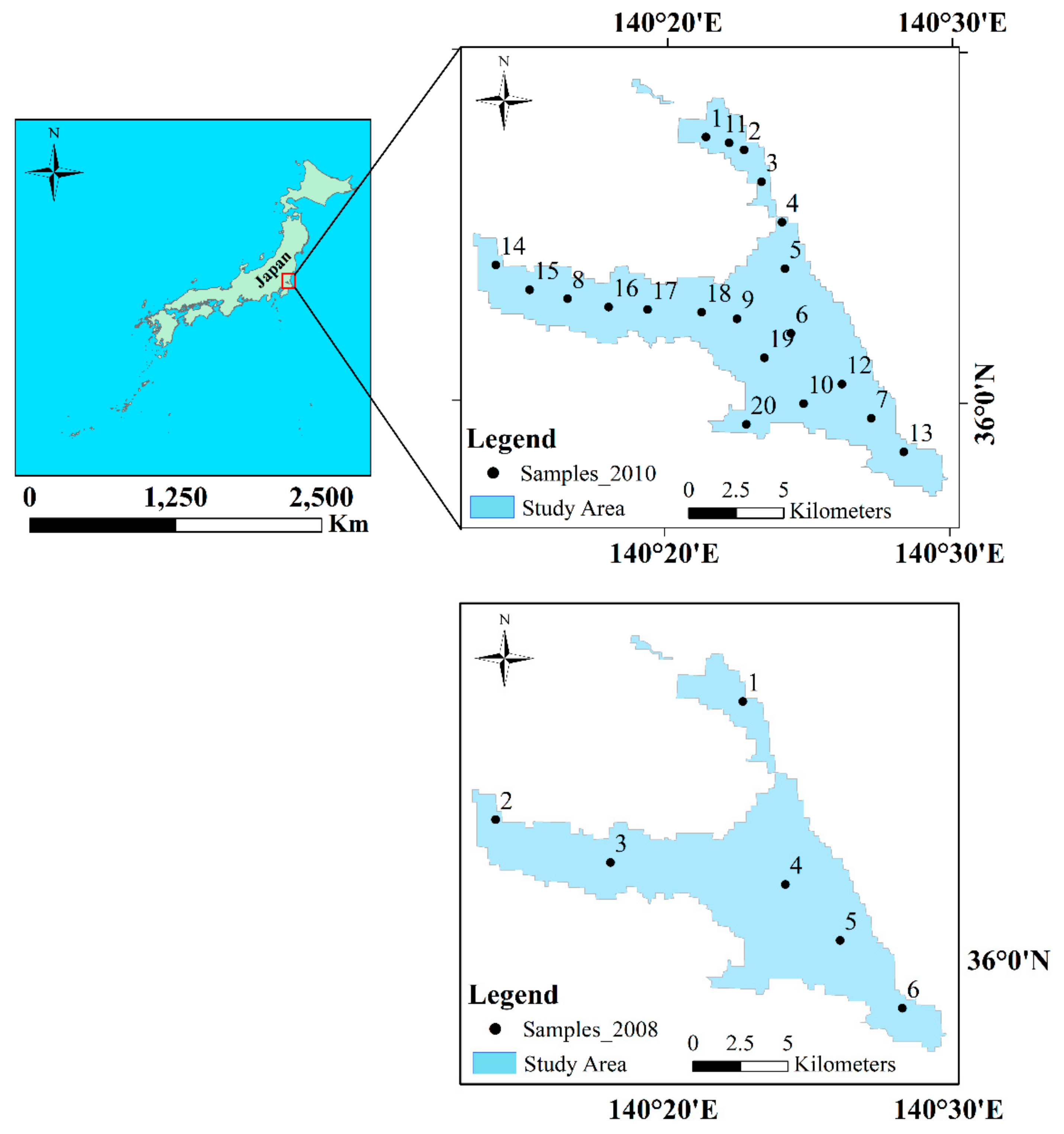
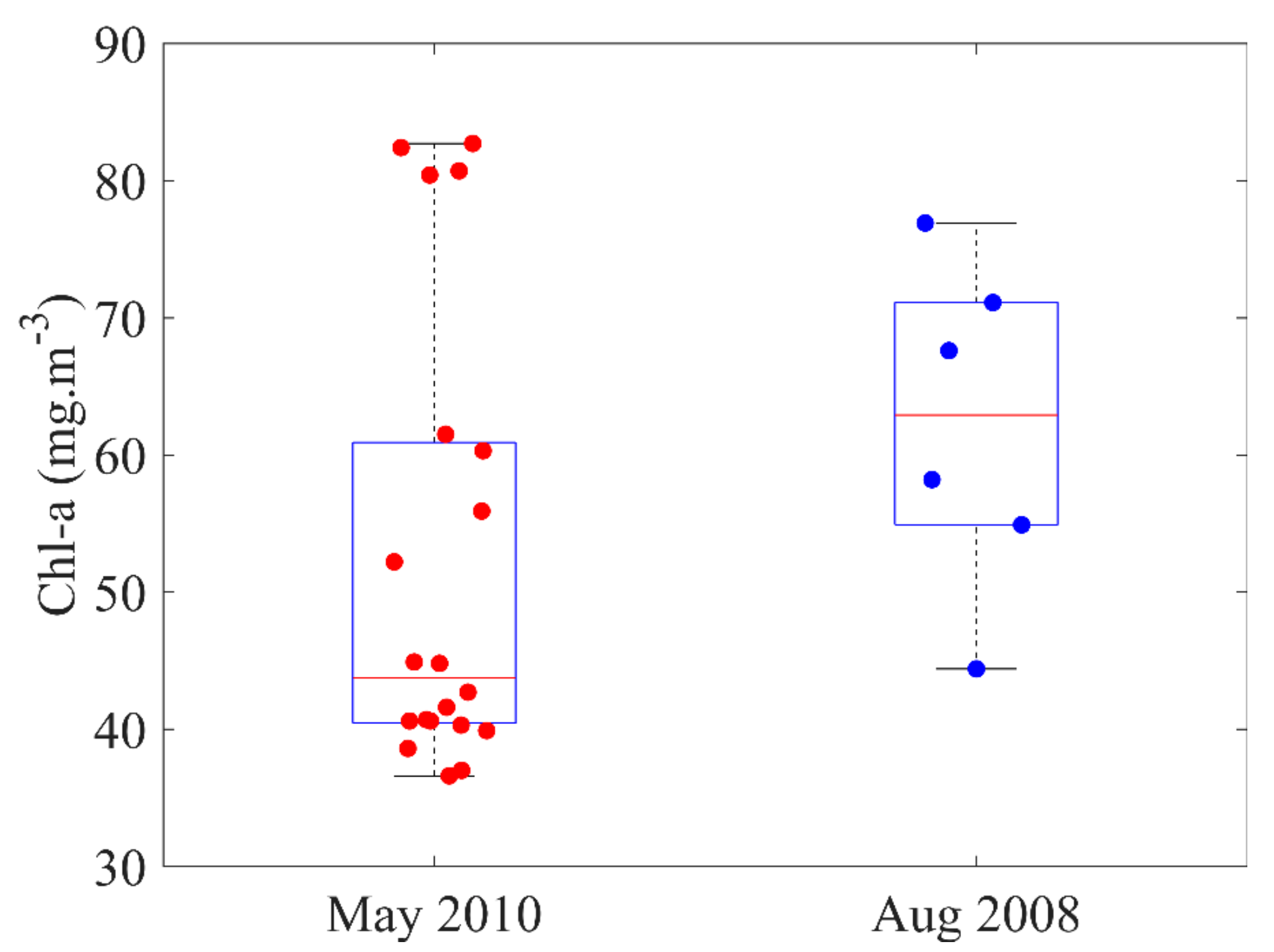
2. Materials and Study Area
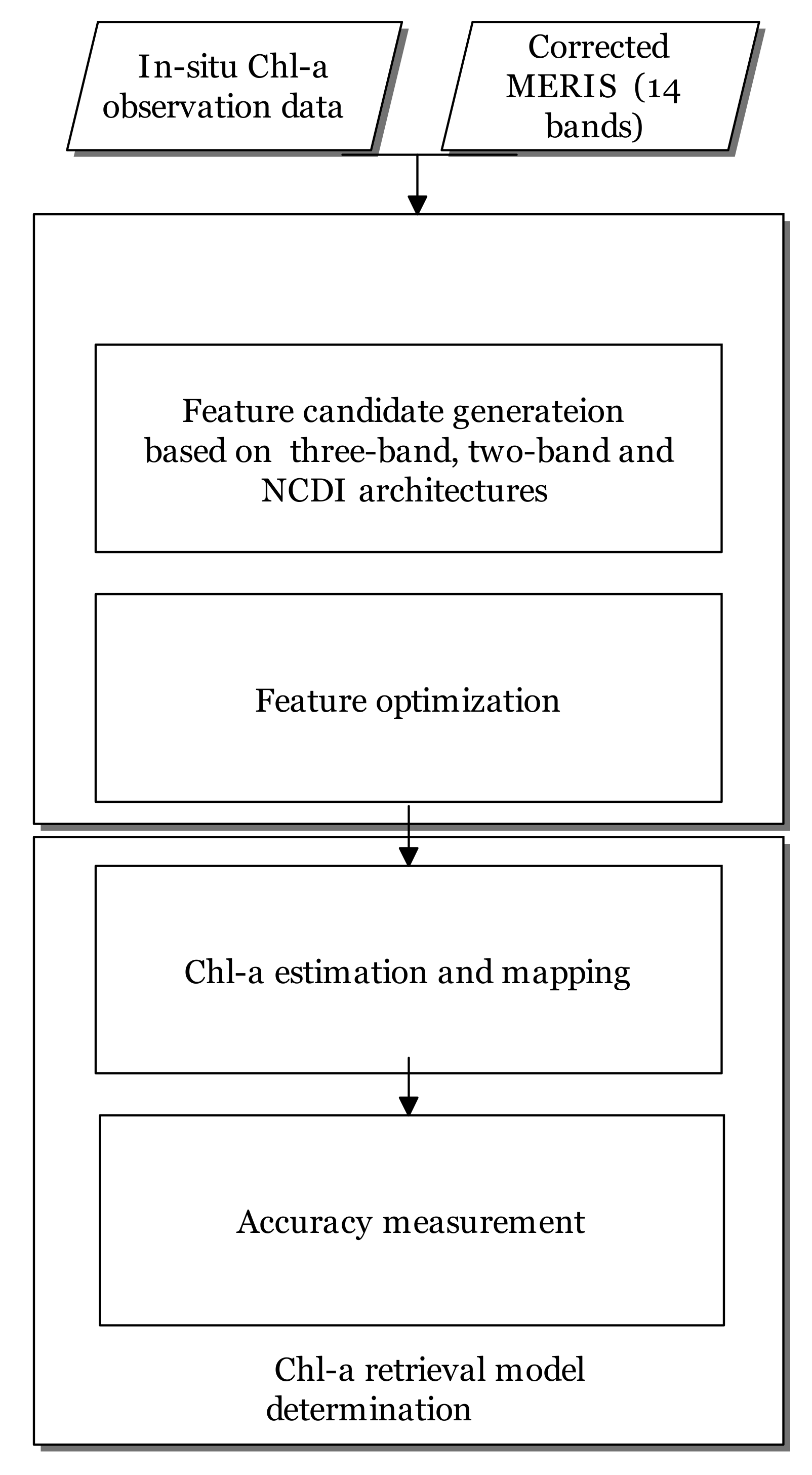
3. Methods
3.1. Feature Candidate Generation
3.2. Feature Optimization
3.3. Chl-A Estimation, Mapping, and Validation
4. Results
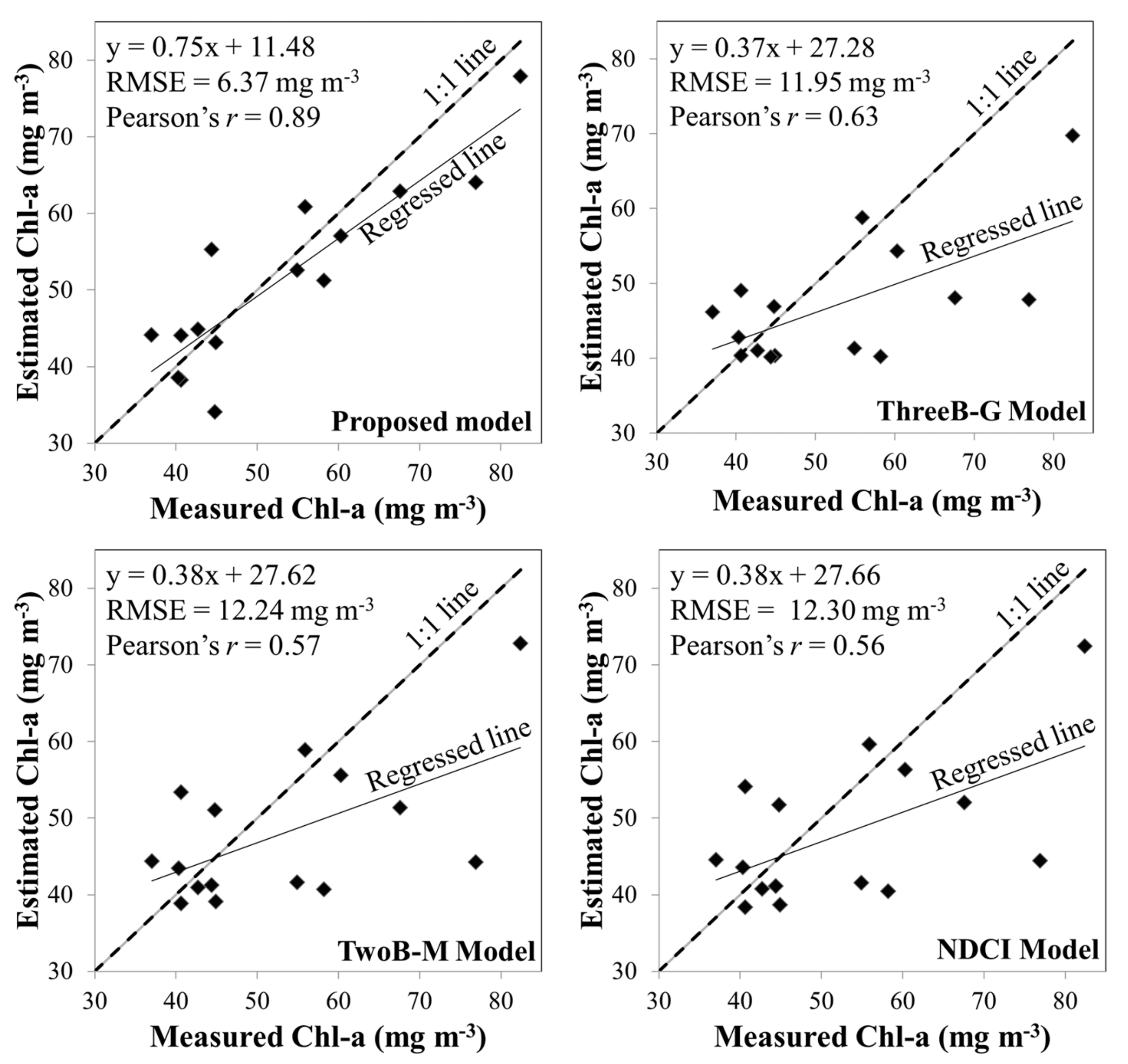
4.1. Results of Feature Optimization
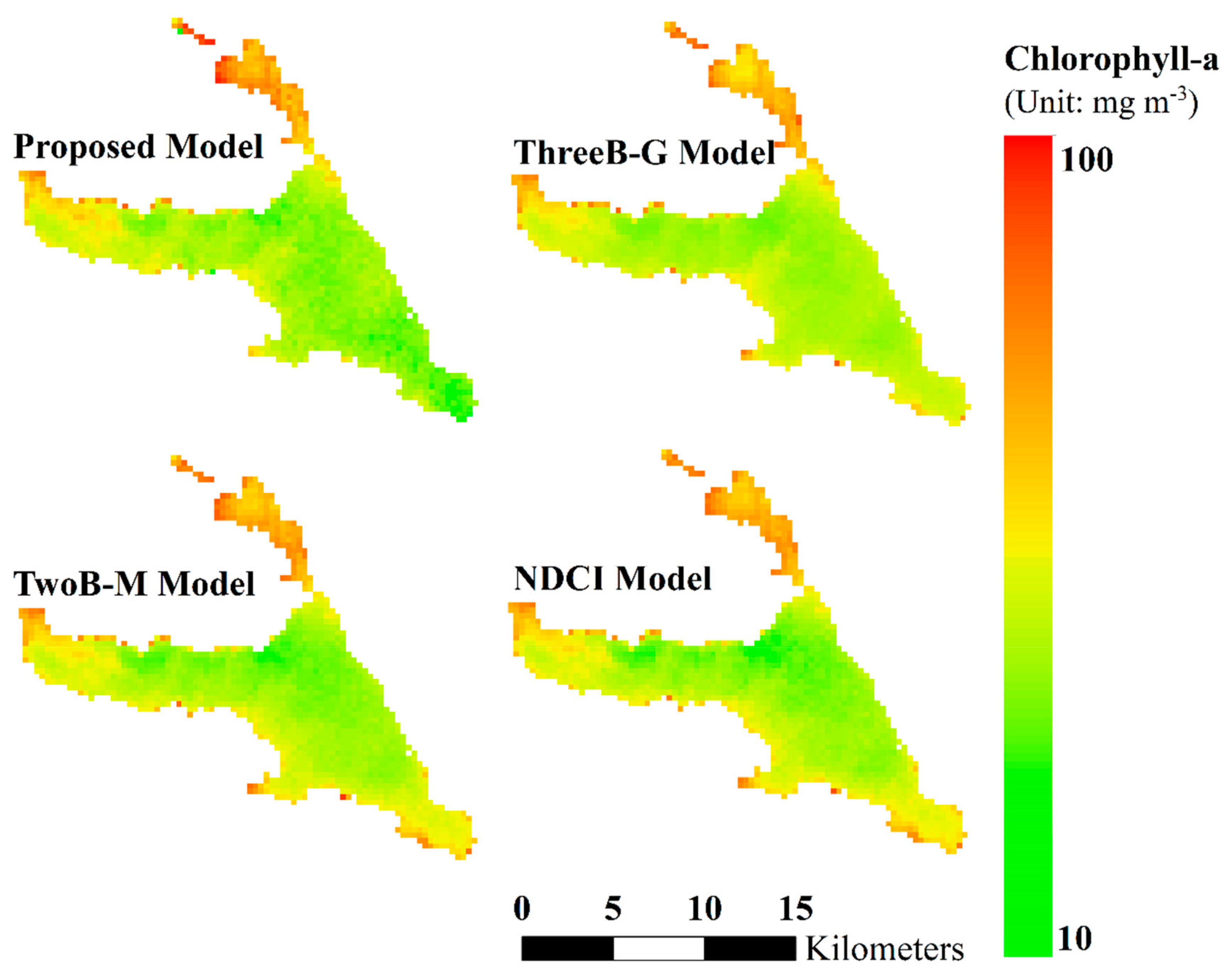
4.2. Mapping with Various Spectral Features
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gholizadeh, M.; Melesse, A.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
- Chu, H.J.; Kong, S.J.; Chang, C.H. Spatio-temporal water quality mapping from satellite images using geographically and temporally weighted regression. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 1–11. [Google Scholar] [CrossRef]
- Reif, M. Remote Sensing for Inland Water Quality Monitoring: A US Army Corps of Engineers Perspective; No. ERDC/EL-TR-11-13; Engineer Research and Development Center Vicksburg MS Environmental Lab: Vicksburg, MS, USA, 2011. [Google Scholar]
- Brando, V.E.; Dekker, A.G. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Glasgow, H.B.; Burkholder, J.M.; Reed, R.E.; Lewitus, A.J.; Kleinman, J.E. Real-time remote monitoring of water quality: A review of current applications, and advancements in sensor, telemetry, and computing technologies. J. Exp. Mar. Biol. Ecol. 2004, 300, 409–448. [Google Scholar] [CrossRef]
- Snyder, J.; Boss, E.; Weatherbee, R.; Thomas, A.C.; Brady, D.; Newell, C. Oyster aquaculture site selection using Landsat 8-Derived Sea surface temperature, turbidity, and chlorophyll a. Front. Mar. Sci. 2017, 4, 190. [Google Scholar] [CrossRef]
- Kuhn, C.; de Matos Valerio, A.; Ward, N.; Loken, L.; Sawakuchi, H.O.; Kampel, M.; Vermote, E. Performance of Landsat-8 and Sentinel-2 surface reflectance products for river remote sensing retrievals of chlorophyll-a and turbidity. Remote Sens. Environ. 2019, 224, 104–118. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Gordon, H.R.; Brown, O.B.; Evans, R.H.; Brown, J.W.; Smith, R.C.; Baker, K.S.; Clark, D.K. A semianalytic radiance model of ocean color. J. Geophys. Res. Atmos. 1988, 93, 10909–10924. [Google Scholar] [CrossRef]
- Parra, L.; Rocher, J.; Escrivá, J.; Lloret, J. Design and development of low cost smart turbidity sensor for water quality monitoring in fish farms. Aquac. Eng. 2018, 81, 10–18. [Google Scholar] [CrossRef]
- Darecki, M.; Stramski, D. Temporal-spatial evaluation of MODIS and SeaWiFS bio-optical algorithms in the Baltic Sea. Remote Sens. Environ. 2004, 89, 326–350. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability on the remote estimation of chlorophyll-a concentration in turbid productive waters: Experimental results. Appl. Opt. 2005, 44, 412–422. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Dall’Olmo, G.; Moses, W.; Rundquist, D.C.; Barrow, T.; Fisher, T.R.; Holz, J. A simple semi-analytical model for remote estimation of chlorophyll-a in turbid waters: Validation. Remote Sens. Environ. 2008, 112, 3582–3593. [Google Scholar] [CrossRef]
- Phu, S.T.P. Research on the Correlation Between Chlorophyll-a and Organic Matter BOD, COD, Phosphorus, and Total Nitrogen in Stagnant Lake Basins. In Sustainable Living with Environmental Risks; Springer: Tokyo, Japan, 2014; pp. 177–191. [Google Scholar]
- Knaeps, E.; Raymaekers, D.; Sterckx, S.; Odermatt, D. An intercomparison of analytical inversion approaches to retrieve water quality for two distinct inland waters. In Proceedings of the ESA Hyperspectral Workshop 2010, ESA/ESRIN, Frascati, Italy, 17–19 March 2019; pp. 17–19. [Google Scholar]
- Gons, H.J. Optical teledetection of chlorophyll a in turbid inland waters. Environ. Sci. Technol. 1999, 33, 1127–1132. [Google Scholar] [CrossRef]
- Gons, H.J. A chlorophyll-retrieval algorithm for satellite imagery (Medium Resolution Imaging Spectrometer) of inland and coastal waters. J. Plankton Res. 2002, 24, 947–951. [Google Scholar] [CrossRef]
- Moses, W.J.; Gitelson, A.A.; Berdnikov, S.; Povazhnyy, V. Satellite estimation of chlorophyll-a concentration using the red and NIR bands of MERIS—The Azov Sea case study. IEEE Geosci. Remote Sens. Lett. 2009, 6, 845–849. [Google Scholar] [CrossRef]
- Le, C.; Li, Y.; Zha, Y.; Sun, D.; Huang, C.; Lu, H. A four-band semi-analytical model for estimating chlorophyll a in highly turbid lakes: The case of Taihu Lake, China. Remote Sens. Environ. 2009, 113, 1175–1182. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Koike, K.; Nhuan, M.T. Improved accuracy of chlorophyll-a concentration estimates from MODIS Imagery using a two-band ratio algorithm and geostatistics: As applied to the monitoring of eutrophication processes over Tien Yen Bay (Northern Vietnam). Remote Sens. 2013, 6, 421–442. [Google Scholar] [CrossRef]
- Pallottini, M.; Goretti, E.; Gaino, E.; Selvaggi, R.; Cappelletti, D.; Cereghino, R. Invertebrate diversity in relation to chemical pollution in an Umbrian stream system (Italy). C. R. Biol. 2015, 338, 511–520. [Google Scholar] [CrossRef]
- Li, X.; Sha, J.; Wang, Z.L. Chlorophyll-A Prediction of Lakes with Different Water Quality Patterns in China Based on Hybrid Neural Networks. Water 2017, 9, 524. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A.; Rundquist, D.C. Towards a unified approach for remote estimation of chlorophyll-a in both terrestrial vegetation and turbid productive waters. Geophys. Res. Lett. 2003, 30, 1938. [Google Scholar] [CrossRef]
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]
- Han, L.; Rundquist, D.C. Comparison of NIR/RED ratio and first derivative of reflectance in estimating algal-chlorophyll concentration: A case study in a turbid reservoir. Remote Sens. Environ. 1997, 62, 253–261. [Google Scholar] [CrossRef]
- Jaelani, L.M.; Matsushita, B.; Yang, W.; Fukushima, T. Evaluation of four MERIS atmospheric correction algorithms in Lake Kasumigaura, Japan. Int. J. Remote Sens. 2013, 34, 8967–8985. [Google Scholar] [CrossRef]
- Gurlin, D.; Gitelson, A.A.; Moses, W.J. Remote estimation of Chl-a concentration in turbid productive waters-Return to a simple two-band NIR-red model? Remote Sens. Environ. 2011, 115, 3479–3490. [Google Scholar] [CrossRef]
- SCOR-UNESCO. Determination of Photosynthetic Pigment in Seawater. In Monographs on Oceanographic Methodology; SCOR-UNESCO: Paris, France, 1966; Volume 1, pp. 11–18. [Google Scholar]
- Zibordi, G.; Mélin, F.; Hooker, S.B.; D’Alimonte, D.; Holben, B. An autonomous above-water system for the validation of ocean color radiance data. IEEE Trans. Geosci. Remote Sens. 2004, 42, 401–415. [Google Scholar] [CrossRef]
- Jeong, K.S.; Kim, D.K.; Shin, H.S.; Yoon, J.D.; Kim, H.W.; Joo, G.J. Impact of summer rainfall on the seasonal water quality variation (chlorophyll a) in the regulated Nakdong River. KSCE J. Civ. Eng. 2011, 15, 983–994. [Google Scholar] [CrossRef]
- Jaelani, L.M.; Matsushita, B.; Yang, W.; Fukushima, T. An improved atmospheric correction algorithm for applying MERIS data to very turbid inland waters. Int. J. Appl. Earth Obs. Geoinf. 2015, 39, 128–141. [Google Scholar] [CrossRef]
- Levrini, G.; Delvart, S. MERIS Product Handbook; European Space Agency (ESA): Paris, France, 2011. [Google Scholar]
- Yang, W.; Wang, K.; Zuo, W. Neighborhood Component Feature Selection for High-Dimensional Data. J. Comput. 2012, 7, 161–168. [Google Scholar] [CrossRef]
- Dall’Olmo, G.; Gitelson, A.A. Effect of bio-optical parameter variability and uncertainties in reflectance measurements on the remote estimation of chlorophyll-a concentration in turbid productive waters: Modeling results. Appl. Opt. 2006, 45, 3577–3592. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Zhou, J.; Gurlin, D.; Moses, W.; Ioannou, I.; Ahmed, S.A. Algorithms for remote estimation of chlorophyll-a in coastal and inland waters using red and near infrared bands. Opt. Express 2010, 18, 24109–24125. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sakuno, Y.; Yajima, H.; Yoshioka, Y.; Sugahara, S.; Abd Elbasit, M.; Adam, E.; Chirima, J. Evaluation of Unified Algorithms for Remote Sensing of Chlorophyll-a and Turbidity in Lake Shinji and Lake Nakaumi of Japan and the Vaal Dam Reservoir of South Africa under Eutrophic and Ultra-Turbid Conditions. Water 2018, 10, 618. [Google Scholar] [CrossRef]
- Salem, S.; Higa, H.; Kim, H.; Kobayashi, H.; Oki, K.; Oki, T. Assessment of chlorophyll-a algorithms considering different trophic statuses and optimal bands. Sensors 2017, 17, 1746. [Google Scholar] [CrossRef] [PubMed]
- Salem, S.; Higa, H.; Kim, H.; Kazuhiro, K.; Kobayashi, H.; Oki, K.; Oki, T. Multi-algorithm indices and look-up table for chlorophyll-a retrieval in highly turbid water bodies using multispectral data. Remote Sens. 2017, 9, 556. [Google Scholar] [CrossRef]
- Salem, S.; Strand, M.; Higa, H.; Kim, H.; Kazuhiro, K.; Oki, K.; Oki, T. Evaluation of MERIS chlorophyll-a retrieval processors in a complex turbid lake Kasumigaura over a 10-year mission. Remote Sens. 2017, 9, 1022. [Google Scholar] [CrossRef]
- Ha, N.T.T.; Thao, N.T.P.; Koike, K.; Nhuan, M.T. Selecting the Best Band Ratio to Estimate Chlorophyll-a Concentration in a Tropical Freshwater Lake Using Sentinel 2A Images from a Case Study of Lake Ba Be (Northern Vietnam). ISPRS Int. J. Geo-Inf. 2017, 6, 290. [Google Scholar] [CrossRef]
- Carder, K.L.; Chen, F.R.; Cannizzaro, J.P.; Campbell, J.W.; Mitchell, B.G. Performance of the MODIS semi-analytical ocean color algorithm for chlorophyll-a. Adv. Space Res. 2004, 33, 1152–1159. [Google Scholar] [CrossRef]
- Gitelson, A. The peak near 700 nm on radiance spectra of algae and water: Relationships of its magnitude and position with chlorophyll concentration. Int. J. Remote Sens. 1992, 13, 3367–3373. [Google Scholar] [CrossRef]
- Yang, W.; Matsushita, B.; Chen, J.; Fukushima, T.; Ma, R. An enhanced three-band index for estimating chlorophyll-a in turbid case-II waters: Case studies of Lake Kasumigaura, Japan, and Lake Dianchi, China. IEEE Geosci. Remote Sens. Lett. 2010, 7, 655–659. [Google Scholar] [CrossRef]
| Selected Spectral Bands | Possible Feature Candidates | Models | Of Candidates | Notation |
|---|---|---|---|---|
| Three-band model (Equation (1)) | 30 | |||
| Two-band model (Equation (2)) | 10 | |||
| , | NDCI (Equation (3)) | 10 |
| Model Name | Model Feature |
|---|---|
| OptiM-1 | |
| OptiM-2 | |
| OptiM-3 | |
| OptiM-4 | |
| OptiM-5 | |
| ThreeB-G [13] | } |
| TwoB-M [18] | } |
| NDCI [25] |
| Models | ||||
|---|---|---|---|---|
| OptiM-1 | 0.77 | 235.32 | – | 0.57 |
| OptiM-2 | 1.93 | 174.26 | – | 0.61 |
| OptiM-3 | −7.74 | 94.03 | 106.40 | 0.61 |
| OptiM-4 | −174.57 | 691.61 | −280.42 | 0.62 |
| OptiM-5 | 48.51 | −183.61 | – | 0.59 |
| ThreeB-G [13] | 24.91 | 115.14 | – | 0.44 |
| TwoB-M [18] | −87.93 | 103.95 | – | 0.55 |
| NDCI [25] | 9.17 | 295.02 | – | 0.55 |
| Models | RMSE | Pearson’s Coefficient | m |
|---|---|---|---|
| No. of testing samples (n = 16) | |||
| OptiM-1 | 11.91 | 0.58 | 0.40 |
| OptiM-2 | 9.14 | 0.77 | 0.57 |
| OptiM-3 | 6.37 | 0.89 | 0.75 |
| OptiM-4 | 13.65 | 0.52 | 0.56 |
| OptiM-5 | 9.56 | 0.71 | 0.54 |
| ThreeB-G [13] | 11.95 | 0.63 | 0.37 |
| TwoB-M [18] | 12.24 | 0.57 | 0.38 |
| NDCI [25] | 12.30 | 0.56 | 0.38 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Nguyen, M.; Lin, C.-H.; Chu, H.-J.; Muhamad Jaelani, L.; Aldila Syariz, M. Spectral Feature Selection Optimization for Water Quality Estimation. Int. J. Environ. Res. Public Health 2020, 17, 272. https://doi.org/10.3390/ijerph17010272
Van Nguyen M, Lin C-H, Chu H-J, Muhamad Jaelani L, Aldila Syariz M. Spectral Feature Selection Optimization for Water Quality Estimation. International Journal of Environmental Research and Public Health. 2020; 17(1):272. https://doi.org/10.3390/ijerph17010272
Chicago/Turabian StyleVan Nguyen, Manh, Chao-Hung Lin, Hone-Jay Chu, Lalu Muhamad Jaelani, and Muhammad Aldila Syariz. 2020. "Spectral Feature Selection Optimization for Water Quality Estimation" International Journal of Environmental Research and Public Health 17, no. 1: 272. https://doi.org/10.3390/ijerph17010272
APA StyleVan Nguyen, M., Lin, C.-H., Chu, H.-J., Muhamad Jaelani, L., & Aldila Syariz, M. (2020). Spectral Feature Selection Optimization for Water Quality Estimation. International Journal of Environmental Research and Public Health, 17(1), 272. https://doi.org/10.3390/ijerph17010272







