In-Water and On-Land Swimmers’ Symmetry and Force Production
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Design and Procedures
2.3. Measures
2.4. Statistical Analysis
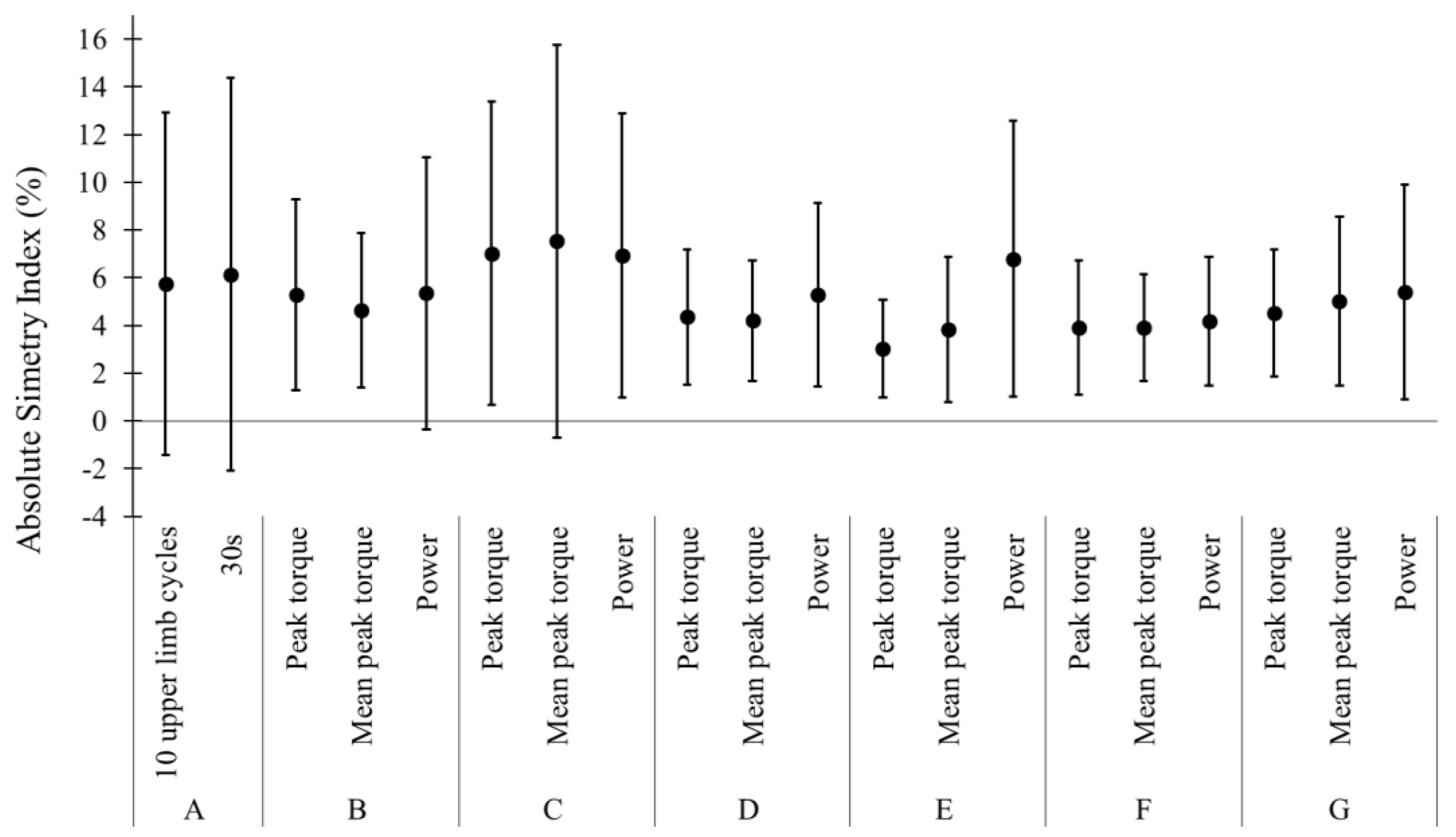
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sharp, R.L.; Troup, J.P. Relationship between power and sprint freestyle. Med. Sci. Sports Exerc. 1982, 14, 53–56. [Google Scholar] [CrossRef] [PubMed]
- Girold, S.; Calmels, P.; Maurin, D.; Milhau, N.; Chatard, J.C. Assisted and resisted sprint training in swimming. J. Strength Cond. Res. 2006, 20, 547. [Google Scholar] [PubMed]
- Ribeiro, J.; Figueiredo, P.; Morais, S.; Alves, F.; Toussaint, H.; Vilas-Boas, J.P.; Fernandes, R.J. Biomechanics, energetics and coordination during extreme swimming intensity: Effect of performance level. J. Sports Sci. 2017, 35, 1614–1621. [Google Scholar] [CrossRef] [PubMed]
- Yeater, R.A.; Martin, R.B.; White, M.K.; Gilson, K.H. Tethered swimming forces in the crawl, breast and back strokes and their relationship to competitive performance. J. Biomech. 1981, 14, 527–537. [Google Scholar] [CrossRef]
- Morouço, P.G.; Marinho, D.A.; Keskinen, K.L.; Badillo, J.J.; Marques, M.C. Tethered swimming can be used to evaluate force contribution for short-distance swimming performance. J. Strength Cond. Res. 2014, 28, 3093–3099. [Google Scholar] [CrossRef]
- Santos, K.B.; Bento, P.C.; Pereira, G.; Rodacki, A.L. The relationship between propulsive force in tethered swimming and 200-m front crawl performance. J. Strength Cond. Res. 2016, 30, 2500–2507. [Google Scholar] [CrossRef]
- Barbosa, T.M.; Bragada, J.A.; Reis, V.M.; Marinho, D.A.; Carvalho, C.; Silva, A.J. Energetics and biomechanics as determining factors of swimming performance: Updating the state of the art. J. Sci. Med. Sport 2010, 13, 262–269. [Google Scholar] [CrossRef]
- Sanders, R.H.; Thow, J.; Fairweather, M. Asymmetries in swimming: Where do they come from. J. Swim. Res. 2011, 18, 1–11. [Google Scholar]
- Annett, M. Handedness and cerebral dominance: The right shift theory. J. Neuropsychiatry Clin. Neurosci. 1998, 10, 459–469. [Google Scholar] [CrossRef]
- Sanders, R.; Thow, J.; Alcock, A.; Fairweather, M.; Riach, I.; Mather, F. How can asymmetries in swimming be identified and measured? Available online: https://swimmingcoach.org/journal/manuscript-sanders-vol19.pdf (accessed on 31 October 2019).
- Toubekis, A.G.; Gourgoulis, V.; Tokmakidis, S.P. Tethered swimming as an evaluation tool of single arm-stroke force. In Biomechanics and Medicine in Swimming XI; Norwegian School of Sport Science: Oslo, Norway, 2010; pp. 296–299. [Google Scholar]
- Batalha, N.; Marmeleira, J.; Garrido, N.; Silva, A.J. Does a water-training macrocycle really create imbalances in swimmers’ shoulder rotator muscles? Eur. J. Sport Sci. 2015, 15, 167–172. [Google Scholar] [CrossRef]
- Rupp, S.; Berninger, K.; Hopf, T. Shoulder problems in high level swimmers-impingement, anterior instability, muscular imbalance? Int. J. Sports Med. 1995, 16, 557–562. [Google Scholar] [CrossRef] [PubMed]
- Secchi, L.L.; Muratt, M.D.; Ciolac, E.G.; Greve, J. Knee muscles isokinetic evaluation in short distance elite swimmers: A comparison between symmetric and asymmetric swimming styles. Isokinet. Exerc. Sci. 2011, 19, 261–264. [Google Scholar] [CrossRef]
- Dos Santos, K.B.; Pereira, G.; Papoti, M.; Bento, P.C.B.; Rodacki, A. Propulsive force asymmetry during tethered swimming. Int. J. Sports Med. 2013, 34, 606–611. [Google Scholar] [CrossRef] [PubMed]
- Morouço, P.G.; Marinho, D.A.; Fernandes, R.J.; Marques, M.C. Quantification of upper limb kinetic asymmetries in front crawl swimming. Hum. Mov. Sci. 2015, 40, 185–192. [Google Scholar] [CrossRef]
- Morouço, P.; Keskinen, K.L.; Vilas-Boas, J.P.; Fernandes, R.J. Relationship between tethered forces and the four swimming techniques performance. J. Appl. Biomech. 2011, 27, 161–169. [Google Scholar] [CrossRef]
- Gastin, P. Energy system interaction and relative contribution during maximal exercise. Sport Med. 2001, 31, 725–741. [Google Scholar] [CrossRef]
- Soares, S.M.; Fernandes, R.J.; Machado, J.L.; Maia, J.A.; Daly, D.J.; Vilas-Boas, J.P. Assessment of Fatigue Thresholds in 50-m All-Out Swimming. Int. J. Sport Physiol. Perform. 2014, 9, 959–965. [Google Scholar] [CrossRef][Green Version]
- Bar-Or, O. The Wingate anaerobic test: An update on methodology, reliability and validity. Sports Med. 1987, 4, 381–394. [Google Scholar] [CrossRef]
- Robinson, R.O.; Herzog, W.; Nigg, B.M. Use of force platform variables to quantify the effects of chiropractic manipulation on gait symmetry. J. Manip. Physiol. Ther. 1987, 10, 172–176. [Google Scholar]
- Blikman, T.; Stevens, M.; Bulstra, S.K.; Van den Akker-Scheek, I.; Reininga, I.H. Reliability and validity of the Dutch version of the International Physical Activity Questionnaire in patients after total hip arthroplasty or total knee arthroplasty. J. Orthop. Sports Phys. Ther. 2013, 43, 650–659. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Routledge Academic: New York, NY, USA, 1988. [Google Scholar]
- Bland, J.M.; Altman, D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986, 327, 307–310. [Google Scholar] [CrossRef]
- Kunitson, V.; Port, K.; Pedak, K. Relationship between isokinetic muscle strength and 100 meters finswimming time. J. Hum. Sport Exerc. 2015, 10. [Google Scholar] [CrossRef]
- Miyashita, M.; Kanehisa, H. Effects of isokinetic, isotonic and swim training on swimming performance. In Biomechanics and Medicine in Swimming IV; Spiegel Online GmbH: Hamburg, Germany, 1983; pp. 329–334. [Google Scholar]
- Reilly, M.F.; Kame, V.D.; Termin, B.; Tedesco, M.E.; Pendergast, D.R. Relationship between freestyle swimming speed and stroke mechanics to isokinetic muscle function. J. Swim. Res. 1990, 6, 16–21. [Google Scholar]
- Dalamitros, A.A.; Manou, V.; Christoulas, K.; Kellis, S. Knee muscles isokinetic evaluation after a six-month regular combined swim and dry-land strength training period in adolescent competitive swimmers. J. Hum. Kinet. 2015, 49, 195–200. [Google Scholar] [CrossRef] [PubMed]
- Morouço, P.; Neiva, H.; González-Badillo, J.J.; Garrido, N.; Marinho, D.A.; Marques, M.C. Associations between dry land strength and power measurements with swimming performance in elite athletes: A pilot study. J. Hum. Kinet. 2011, 29, 105–112. [Google Scholar] [CrossRef]
- Loturco, I.; Barbosa, A.C.; Nocentini, R.K.; Pereira, L.A.; Kobal, R.; Kitamura, K.; Nakamura, F.Y. A correlational analysis of tethered swimming, swim sprint performance and dry-land power assessments. Int. J. Sports Med. 2016, 37, 211–218. [Google Scholar] [CrossRef]
- Evershed, J.; Burkett, B.; Mellifont, R. Musculoskeletal screening to detect asymmetry in swimming. Phys. Ther. Sport 2014, 14, 33–38. [Google Scholar] [CrossRef]
- Figueiredo, P.; Seifert, L.; Vilas-Boas, J.P.; Fernandes, R.J. Individual profiles of spatio-temporal coordination in high intensity swimming. Hum. Mov. Sci. 2012, 31, 1200–1212. [Google Scholar] [CrossRef]
- Gonjo, T.; McCabe, C.; Sousa, A.; Ribeiro, J.; Fernandes, R.J.; Vilas-Boas, J.P.; Sanders, R. Differences in kinematics and energy cost between front crawl and backstroke below the anaerobic threshold. Eur. J. Appl. Physiol. 2018, 118, 1107–1118. [Google Scholar] [CrossRef]
- Seifert, L.; Chollet, D.; Allard, P. Upper limb coordination symmetry and breathing effect in front crawl. Hum. Mov. Sci. 2005, 24, 234–256. [Google Scholar] [CrossRef]

| Isokinetic Variables | Front Crawl and Backstroke Tethered Swimming | |||
|---|---|---|---|---|
| 10 Upper Limb Actions | 30 s | |||
| Preferred | Nonpreferred | Preferred | Nonpreferred | |
| Upper limb simulated action | ||||
| Peak torque 90°/s | 0.83 | 0.92 | 0.82 | 0.90 |
| Mean peak torque 90°/s | 0.80 | 0.94 | 0.79 | 0.91 |
| Mean power 90°/s | 0.80 | 0.96 | 0.79 | 0.93 |
| Peak torque 300°/s | 0.62 | 0.67 | 0.66 | 0.66 |
| Mean torque 300°/s | 0.64 | 0.72 | 0.68 | 0.71 |
| Mean power 300°/s | 0.81 | 0.94 | 0.83 | 0.92 |
| Knee extension | ||||
| Peak torque 90°/s | 0.68 | 0.90 | 0.68 | 0.81 |
| Mean peak torque 90°/s | 0.80 | 0.90 | 0.78 | 0.84 |
| Mean power 90°/s | 0.79 | 0.91 | 0.78 | 0.85 |
| Peak torque 300°/s | 0.73 | 0.92 | 0.71 | 0.86 |
| Mean torque 300°/s | 0.72 | 0.93 | 0.69 | 0.89 |
| Mean power 300°/s | 0.71 | 0.96 | 0.69 | 0.94 |
| Combined | ||||
| Peak torque 90°/s | 0.79 | 0.91 | 0.78 | 0.85 |
| Peak torque 300°/s | 0.69 | 0.84 | 0.72 | 0.84 |
| Mean peak torque 90°/s | 0.79 | 0.94 | 0.78 | 0.89 |
| Mean peak torque 300°/s | 0.65 | 0.87 | 0.69 | 0.87 |
| Mean power 90°/s | 0.83 | 0.92 | 0.83 | 0.87 |
| Mean power 300°/s | 0.76 | 0.83 | 0.72 | 0.85 |
| Variables | Preferred | Nonpreferred | Effect Size | Bias | 95% CI |
|---|---|---|---|---|---|
| Upper limb simulated action | |||||
| Peak torque 90°/s (N × m) | 95.10 ± 36.96 | 93.89 ± 35.14 | −0.14 | 1.5 ± 13.4 | −25–28 |
| Mean peak torque 90°/s ( N × m) | 87.78 ± 33.92 | 86.19 ±31.72 | −0.15 | 1.9 ± 10.8 | −19–23 |
| Mean power 90°/s (W) | 99.72 ± 38.46 | 98.47 ± 36.89 | −0.13 | −2.0 ± 9.8 | −17–21 |
| Peak torque 300°/s (N × m) | 100.92 ± 23.76 | 105.22 ± 22.93 | −0.28 | −1.8 ± 16.9 | −35–31 |
| Mean peak Torque 300°/s ( N × m) | 93.63 ± 23.46 | 95.64 ± 20.50 | −0.03 | −0.6 ± 18.5 | −37–36 |
| Mean power 300°/s (W) | 186.55 ± 90.21 | 192.69 ± 86.71 | −0.11 | −1.6 ± 12.7 | −26–23 |
| Knee extension | |||||
| Peak torque 90°/s (N × m) | 185.60 ± 50.06 | 186.86 ± 50.30 | −0.08 | 0.6 ± 10.7 | −20–22 |
| Mean peak torque 90°/s ( N × m) | 171.25 ± 47.09 | 170.72 ± 44.29 | −0.03 | 1.0 ± 10.5 | −20–22 |
| Mean power 90°/s (W) | 173.51 ± 51.67 | 177.41 ± 47.48 | −0.16 | −0.6 ± 10.6 | −21–20 |
| Peak torque 300°/s (N × m) | 124.36 ± 39.95 | 127.34 ± 38.57 | −0.27 | −0.9 ± 11.8 | −24–22 |
| Mean peak torque 300°/s ( N × m) | 114.33 ± 36.98 | 116.48 ± 35.02 | −0.18 | −0.7 ± 12.7 | −26–24 |
| Mean power 300°/s (W) | 306.94 ± 110.05 | 307.93 ± 91.57 | −0.02 | −0.1 ± 15.0 | −29–29 |
| Combined | |||||
| Peak torque at 90°/s (N × m) | 280.70 ± 85.52 | 280.75 ± 83.84 | −0.02 | 0.9 ± 11.3 | −21–23 |
| Peak torque 300°/s (N × m) | 225.28 ± 61.35 | 232.56 ± 58.45 | −0.30 | −1.3 ± 13.7 | −28–26 |
| Mean peak torque 90°/s ( N × m) | 259.03 ± 79.99 | 256.91 ± 75.01 | −0.03 | −0.6 ± 14.7 | −29–28 |
| Mean peak torque 300°/s ( N × m) | 207.97 ± 57.93 | 212.12 ± 53.12 | −0.16 | 1.3 ± 10.4 | −19–22 |
| Mean power 90°/s (W) | 273.23 ± 87.72 | 275.88 ± 82.97 | −0.10 | 0.2 ± 9.7 | −19–19 |
| Mean power 300°/s (W) | 493.79 ± 197.05 | 500.62 ± 175.73 | −0.05 | −0.8 ± 13.0 | −26–25 |
| Tethered swimming | |||||
| 10 upper limb actions (N) | 183.20 ± 49.41 | 186.68 ± 56.17 | −0.10 | - | - |
| 30 s (N) | 177.71 ± 49.55 | 183.44 ± 56.31 | −0.19 | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, D.D.; Soares, S.; Zacca, R.; Marinho, D.A.; Silva, A.J.; Pyne, D.B.; Vilas-Boas, J.P.; Fernandes, R.J. In-Water and On-Land Swimmers’ Symmetry and Force Production. Int. J. Environ. Res. Public Health 2019, 16, 5018. https://doi.org/10.3390/ijerph16245018
Carvalho DD, Soares S, Zacca R, Marinho DA, Silva AJ, Pyne DB, Vilas-Boas JP, Fernandes RJ. In-Water and On-Land Swimmers’ Symmetry and Force Production. International Journal of Environmental Research and Public Health. 2019; 16(24):5018. https://doi.org/10.3390/ijerph16245018
Chicago/Turabian StyleCarvalho, Diogo D., Susana Soares, Rodrigo Zacca, Daniel A. Marinho, António J. Silva, David B. Pyne, J. Paulo Vilas-Boas, and Ricardo J. Fernandes. 2019. "In-Water and On-Land Swimmers’ Symmetry and Force Production" International Journal of Environmental Research and Public Health 16, no. 24: 5018. https://doi.org/10.3390/ijerph16245018
APA StyleCarvalho, D. D., Soares, S., Zacca, R., Marinho, D. A., Silva, A. J., Pyne, D. B., Vilas-Boas, J. P., & Fernandes, R. J. (2019). In-Water and On-Land Swimmers’ Symmetry and Force Production. International Journal of Environmental Research and Public Health, 16(24), 5018. https://doi.org/10.3390/ijerph16245018










