1. Introduction
Cancer has always been a serious threat to human health. To reduce the incidence of cancer, one important means is to use medicines, such as vaccines, to prevent cancer. However, medicines are special commodities, and their logistics links are quite different from general logistics. Any improper operation in the process of cold chain logistics of medicines may have a significant impact on the quality of medicines and endanger the safety of drug use. This makes the selection of a safe and effective drug cold chain logistics supplier for major pharmaceutical enterprises key to ensuring the safety of refrigerated medicines.
Drug cold chain logistics is a supply chain system that stores and transports medicines from production point to use point at the recommended temperature to ensure the quality of medicines [
1]. Different from a general food cold chain logistics system, drug cold chain logistics has many characteristics, such as multi-batch, small batches, timeliness, high operating costs, high coordination of all links in the cold chain, unpredictability, strict qualification examination of business enterprises, high requirements for drug quality standards, and difficult monitoring. Hence, it has requirements, including high standards, high investment, high precision, strict supervision, and high-quality personnel. In recent years, with the innovation of medical technology and new drug research and development technology, the number of cold-chain medicines requiring cryopreservation has increased. However, due to the particularity of the operating environment and equipment requirements, drug cold chain logistics is facing greater risks than other logistics activities. Hence, from the perspective of risk avoidance, through the evaluation of the key risk factors existing in the drug cold-chain logistics suppliers, selecting the drug cold-chain logistics supplier with the lowest comprehensive risk and then realizing the effective control of the risk of drug cold-chain logistics is of great significance to ensure the quality and safety of medicines in enterprises. However, few studies in the literature [
1,
2] have researched the evaluation and selection of drug cold chain logistics suppliers.
Language is a suitable way to express human cognition and experts can conduct evaluation based on a given linguistic term set (LTS). However, for the evaluation of some complex problems, experts usually hesitate between several linguistic terms because of some vague or uncertain factors. The hesitant fuzzy linguistic term set (HFLTS) [
3], as a generalized form of fuzzy linguistic approach, is an effective tool for expressing several linguistic terms at the same time. However, when expressing the evaluation information of most experts with several linguistic terms, the experts may have different preferences for different linguistic terms, which leads to the limitation of the HFLTS in expressing experts’ cognition. In this regard, the probabilistic linguistic term set (PLTS) [
4] was developed, which allocates corresponding probabilities to each linguistic term and thus can express complex linguistic information flexibly. Since the evaluation of cold-chain logistics suppliers is qualitative and complex, it is appropriate to use the PLTS as an evaluation tool to express experts’ opinions.
As the selection of drug cold chain logistics suppliers usually involves the evaluation of multiple alternatives under multiple criteria, it is a typical multiple criteria decision-making (MCDM) problem that requires the use of an appropriate MCDM model to solve the problem [
5]. At present, different MCDM models have been used to solve the problems of selecting the optimal renewable energy [
6], selecting a chief accounting officer [
7], evaluating the service quality [
8], selecting the best green capacity investment project [
9], and evaluating the market segment [
10]. Furthermore, various MCDM methods have been extended to solve the decision-making problems in different fields under the probabilistic linguistic environment. For example, Wu and Liao [
11] combined the QFD (quality function deployment) and PL-ORESTE (organísation, rangement et Synthèse de données relarionnelles, in French) method and then evaluated the innovative product design based on customer requirements; Wu et al. [
12] proposed the PL-MULTIMOORA (multiplicative multiobjective optimization by ratio analysis) method and then applied it to select shared karaoke television brands; Liao et al. [
13] developed a procedure of the PL-ELECTRE (ELimination Et Choix Traduisant la REalite, in French) III method to evaluate the nurse–patient relationship; Wu and Liao [
14] introduced a comprehensive multiple criteria group decision-making method, which integrated the probabilistic linguistic information with the GLDS (gained and lost dominance score) method to select an optimal green enterprise; Yu et al. [
15] developed the PL-PROMETHEE (preference ranking organization method for enrichment evaluation) method for the evaluation of meteorological disaster risk; and Liu and Teng [
16] put forward an extended PL-TODIM (an acronym in Portuguese of interactive and multicriteria decision making) method for the selection of products.
In the process of solving MCDM problems, the determination of criteria weights and the ranking of alternatives are two important aspects. The SWARA (stepwise weight assessment ratio analysis) method [
17] is an effective method to determine the weights of criteria. Compared with the commonly used AHP (analytic hierarchy process) method, this method does not need a large number of pairwise comparisons and has high consistency. Compared with the BWM (best worst method) [
18], this method does not need to solve complex linear objective functions, has less computational complexity, and is easy to understand. To ensure the reliability of the MCDM results, in this study, we introduce an adjustment coefficient to derive the criteria weights. In addition, the CoCoSo (combined compromise solution) method [
19] has high stability and reliability regarding the ranking of alternatives. The deletion or addition of alternatives has less impact on the final ranking results obtained by this method than TOPSIS (technique for order preference by similarity to ideal solution), VIKOR (visekriterijumska optimizacija i kompromisno resenje), and other MCDM models. However, the final aggregation operator in this method has shortcomings. In this respect, the DNMA (double normalization-based multiple aggregation) method [
20] can effectively overcome the shortcomings of the original CoCoSo method. Hence, in this study, we propose an improved CoCoSo method based on the DNMA method.
To sum up, because the SWARA and CoCoSo methods have their own advantages in determining the weights of criteria and the ranking of alternatives, we extended the SWARA method and improved the CoCoSo method to a probabilistic linguistic environment to form an integrated MCDM model to solve the selection problem of drug cold chain logistics suppliers. This study aimed to:
Analyze the defects of the final aggregation operator in the original CoCoSo method and propose a new integration function to improve the CoCoSo method;
Introduce an adjustment coefficient to the SWARA method to make the criteria weights reasonable;
Develop an integrated MCDM model based on the combination of the SWARA and CoCoSo methods under the probabilistic linguistic environment; and
Apply the developed integrated MCDM model to select the optimal drug cold chain logistic suppliers for pharmaceutical manufacturing enterprises in China, and then highlight the advantage of the PL-CoCoSo method by comparative analysis.
This study is organized as follows:
Section 2 briefly reviews the literature on drug chain logistics supplier selection, the concepts of PLTSs, and the idea of the SWARA and CoCoSo methods.
Section 3 proposes an improvement of the CoCoSo method with a new integration function.
Section 4 presents an integrated MCDM model based on the combination of the PL-SWARA and PL-CoCoSo methods. A case study concerning the risk evaluation and selection of drug cold chain logistic suppliers and the relative comparative analysis is given in
Section 5. Final conclusions are drawn in
Section 6.
3. The Improved CoCoSo Method
In this section, two defects of the original CoCoSo method regarding its final integration function are described. To overcome these defects, an improved CoCoSo method with a new integration function is proposed based on the DNMA method to aggregate the three subordinate utility values and subordinate ranks with respect to each alternative determined by the CoCoSo method.
3.1. Defects of the Final Integration Function in the Original CoCoSo Method
On the one hand, from the three aggregation strategies shown as Equations (A7)–(A9) in the original CoCoSo method, we can find that the value ranges of the three subordinate compromise performance values are , , . It is obvious that the effect of the values of on the final results is much greater than that of the values of and . That is to say, the dimensions of , , and are different. However, the final integration function of the original CoCoSo method, shown as Equation (A10), does not normalize the three values or assign different weights to the aggregation values, which leads to the values of having a decisive impact on the final results in most cases, and thus it easy for the final results to have low reliability.
Example 1. Suppose that the performance values of three alternatives obtained by the three aggregation strategies are as follows: From this matrix, we can get the rankings of the alternatives under three aggregation strategies as: , , . According to the compromise performance values of the alternatives computed by Equation (A10), i.e., , , and , we can deduce the final ranking result as . However, such a ranking result is clearly inconsistent with the reality since the final ranking result is completely dominated by and the results in terms of and that are contrary to that of are neglected. It shows that the optimal solution is not based on the compromise idea.
On the other hand, the final integration function of the original CoCoSo method only considers the performance values of alternatives generated by three aggregation strategies but ignores the rank of each alternative under different aggregation strategies, which may cause irrational results.
Example 2. Suppose that the subordinate compromise performance values of three alternatives obtained by the three aggregation strategies are as follows: From this matrix, we can get the rankings of the alternatives under three aggregation strategies as: , , . The compromise performance values of the alternatives are calculated as , , and , which implies the final ranking result as . This result is different from the ranking results obtained by the three strategies. Moreover, without considering the subordinate rankings, the values of have a greater impact than those of and on the final ranking result, which leads to the result being unstable and unreasonable.
3.2. A New Integration Function for the CoCoSo Method
The double normalization-based multiple aggregation (DNMA) method, as a novel MCDM method, was proposed by Liao and Wu [
20]. The final integration function of the DNMA method comprehensively considers the subordinate utility values and the ranks of alternatives, and thus the final ranking result has high reliability. Inspired by this method, we introduce a new function to integrate the three subordinate performance values under three aggregation strategies as follows:
where
refers to the normalized values of
corresponding to alternative
by vector normalization, and
refers to the rank of alternative
with respect to values of
.
refers to the number of aggregation strategies and
.
Remark 1. Since this function unifies the dimensions of three aggregation strategies in the calculation process, it is no longer necessary to normalize the three aggregation strategy values before using the function.
Example 3. For Example 1, we can calculate the compromise performance values of the three alternatives by Equation (2). Then, we have,, and, and thus the final ranking resultcan be obtained. This ranking result reduces the decisive influence of the value of on the final result in this example, and the ranking results based on the values of and are fully considered. In this sense, the ranking result deduced by Equation (2) is more in line with the idea of compromise.
Example 4. For Example 2, the compromise performance values of the three alternatives, i.e., , , and , can be calculated by Equation (2), and thus the final ranking result is . The ranking results of alternative under the three aggregation strategies are 2, 3, and 1, respectively, and those of alternative under the three aggregation strategies are 3, 1, and 3, respectively. In the case of reducing the impact of the value of on the final ranking result, alternative should rank higher than alternative . Hence, the new integration function that considers the compromise performance values and ranks of alternatives is more reasonable than that of the original CoCoSo method.
4. An Integrated MCDM Model Based on the PL-SWARA and PL-CoCoSo Methods
In this section, we extend the SWARA method to the probabilistic linguistic context and employ the PL-SWARA method to derive criteria weights. Then, we extend the CoCoSo method to the probabilistic linguistic context and apply the PL-CoCoSo method to rank alternatives. Afterwards, the procedure of the integrated MCDM model is presented.
4.1. Determine the Weights of Criteria Based on the PL-SWARA Method
First, after a series of evaluation criteria being established, an expert or multiple experts () will be invited to rank the criteria based on their importance. In this regard, if more than one expert is invited, the ranking results they provide need to be consistent to reduce the deviation of the result.
The importance ranking of the criteria can be determined as
, where
is the most important criterion in these criteria and
is the least important one. Next, the probabilistic linguistic evaluation about the importance of criterion
relative to criterion
is provided by an expert or multiple experts according the linguistic term set
:
. Converting the expert’s probabilistic linguistic evaluation information into PLEs, the expectation values of these PLEs are calculated and normalized by vector normalization to obtain the relative importance of criterion
,
. In the case of multiple experts, it is necessary to aggregate the values given by different experts by the weighted average aggregation operator shown as Equation (3) and normalized the value by vector normalization to obtain
:
where
represents the expectation values of the PLEs under criterion
corresponding to expert
, and
represent the weights of experts with
.
To reduce the impact of the uncertainty of criterion weights on the final results, we can introduce an adjustment coefficient of the weight of each criterion according to the expectation value of the PLE for the criterion, and the larger the sum of the difference values between these PLEs is, the smaller the weight of the criterion should be. Hence, by calculating the difference between the expectation values, the adjustment coefficient can be deduced below:
when
,
. Because the comparative evaluation between criteria starts from the second criterion, the difference value with respect to criterion
equals 0.
Afterwards, the subordinate weights of criteria can be derived by the following equation:
Finally, we can derive the final weight of each criterion by:
4.2. Rank the Alternatives by the PL-CoCoSo Method
The expert or multiple experts are required to evaluate a series of alternatives,
, over a set of criteria,
, based on a linguistic term set provided in advance. If only one expert gives linguistic evaluation information, he/she needs to assign probabilities to each linguistic term to form a probabilistic linguistic decision matrix. If more than one expert gives linguistic evaluation information, the probabilistic linguistic decision matrix can be obtained by aggregating the number of each linguistic term in each expert’s linguistic decision matrix. Then, a probabilistic linguistic decision matrix is obtained as:
where
represents the PLE of alternative
under criterion
.
Next, based on the expectation function given as Equation (1), the expectation value of each PLE in the probabilistic linguistic decision matrix is calculated. Then, we normalize the expectation value under each criterion according to the type of criterion.
For benefit criteria, we have:
For cost criteria, we have:
Based on the weights of criteria derived by the PL-SWARA method, we respectively compute the arithmetically weighted sum,
, and the geometrically weighted sum,
, for each alternative by the following equations:
Afterwards, through three aggregation strategies, we can combine
and
and obtain three subordinate compromise performance values for each alternative. The first aggregation strategy stands on the mean of
and
, as shown in Equation (11). The second aggregation strategy stands on the sum of the comparison of
and
with the worst one, as shown in Equation (12). The third aggregation strategy stands on the balanced compromise of
and
, as shown in Equation (13), and the parameter
is a balance parameter determined by experts according to their preferences. If the experts pay more attention to the comprehensive performances of alternatives, they can assign a larger value to
; if the experts pay more attention to the outstanding performances of alternatives, they can give
a smaller value:
Eventually, we utilize the final integration function shown as Equation (2) to attain the final compromise values of alternatives, and determine the optimal alternative in descending order of the final compromise values.
4.3. Procedure of the Integrated MCDM Method with the Combination of the PL-SWARA and PL-CoCoSo Methods
Based on the analyses in
Section 3.1 and
Section 3.2, we can develop an integrated MCDM method which includes the following six steps:
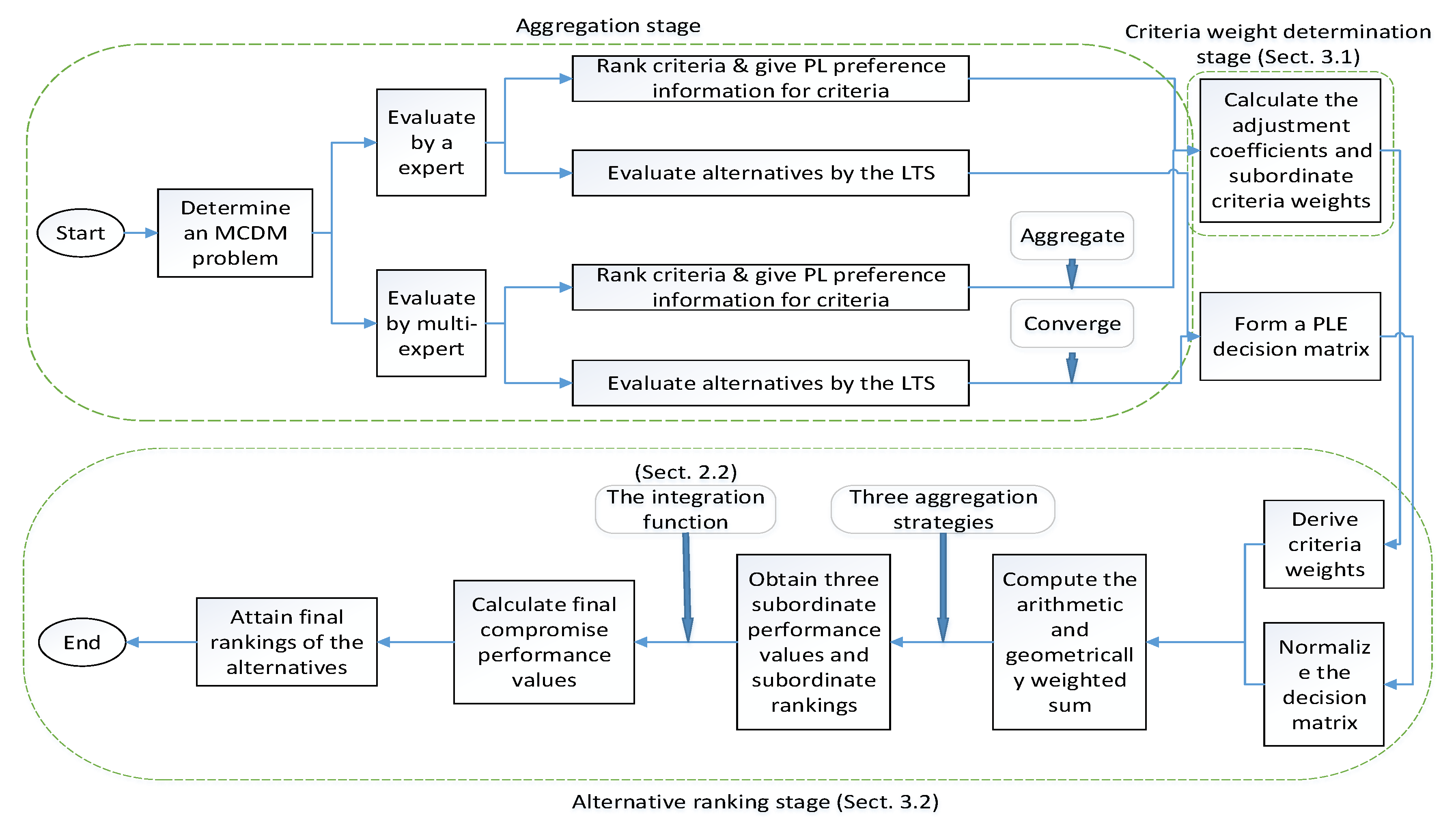
Step 1. Determine an MCDM problem that involves multiple alternatives and criteria. An expert or expert group is invited to rank the criteria via pairwise comparisons to obtain the probabilistic linguistic preference information on the importance of criteria. For the expert group, it is necessary to aggregate the information of each expert by Equation (3).
Step 2. Calculate the adjustment coefficients by Equation (4) and deduce the subordinate criteria weights by Equation (5).
Step 3. Derive the final weights of criteria by Equation (6).
Step 4. Ask the expert or expert group to evaluate the alternatives over the criteria according to the given linguistic term set. For the expert group, it is necessary to aggregate the linguistic evaluation information of each expert to form a probabilistic linguistic decision matrix.
Step 5. Normalize the decision matrix by Equations (7) and (8). Then, combine those normalization values and the criteria weights derived in Step 3 to compute the arithmetically and geometrically weighted sum by Equations (9) and (10). Next, three aggregation strategies shown as Equations (11)–(13) are used to obtain the subordinate performance values and subordinate rankings of the alternatives.
Step 6. Compute the final compromise performance value of each alternative by the integration function given as Equation (2) to attain the final ranking of the alternatives and determine the optimal alternative.
The flowchart of this integrated MCDM model is shown in
Figure 1.
6. Conclusions
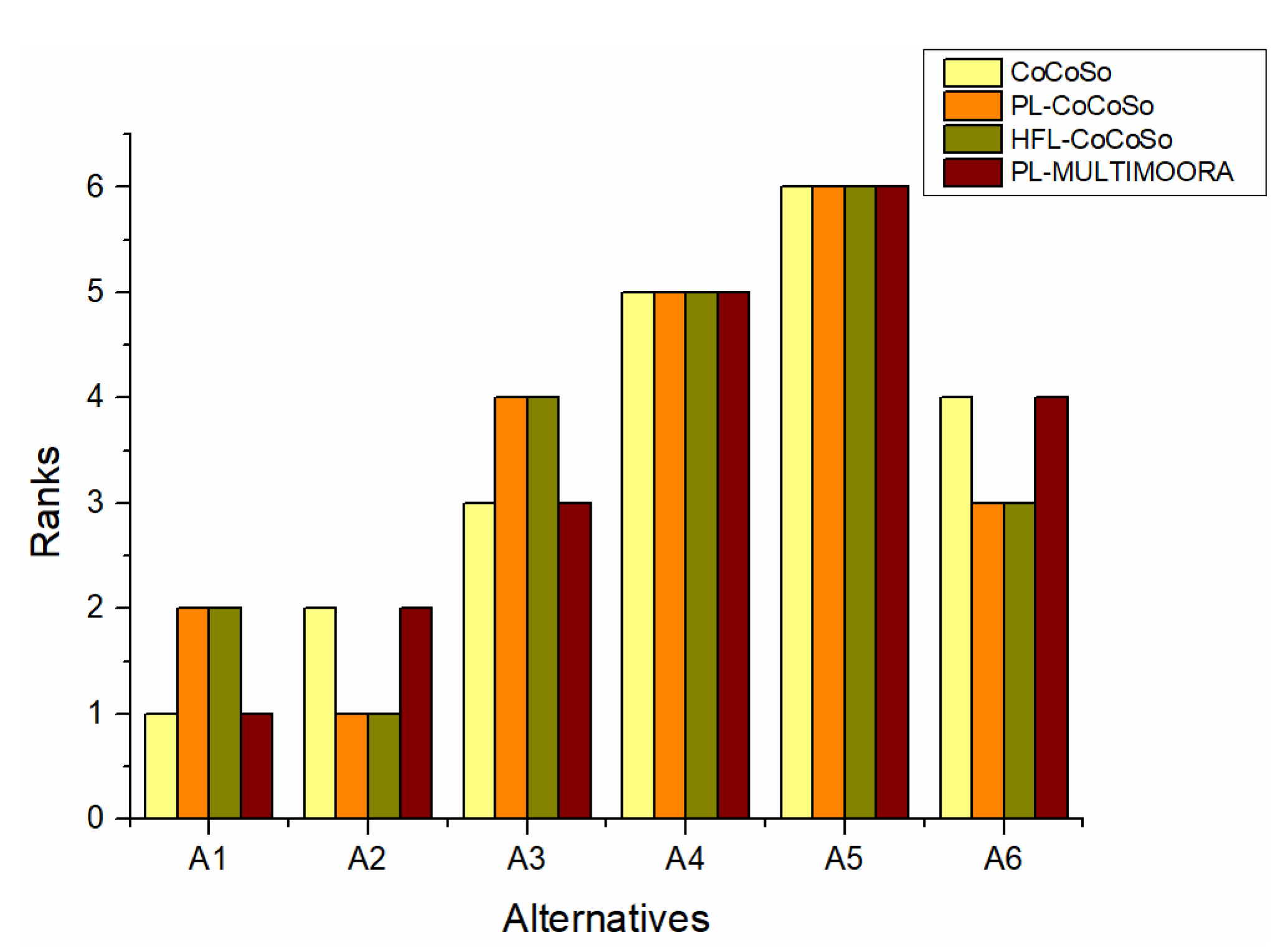
Cancer has seriously endangered human health and has a high mortality rate. Because medicines are the main means to prevent and treat cancer, it is vital to ensure the quality of medicines during transportation and storage, which makes it of great significance for most drug manufacturers to evaluate and select a drug cold chain logistics supplier from the perspective of risk aversion. To solve this problem, an integrated MCDM model was proposed in this paper. In this MCDM model, we extended the SWARA method and improved the CoCoSo method to a probabilistic linguistic environment. Then, the proposed integrated MCDM model was used to solve the decision-making problem of selecting drug cold chain logistics suppliers. By the case study, we highlighted the simplicity of the PL-SWARA method in deriving the weights of risk evaluation criteria with respect to cold chain logistics suppliers, and the reliability of the PL-CoCoSo method in determining the ranking of cold chain logistics suppliers.
In this paper, the comparison between the proposed method and other MCDM methods was still inadequate. For future research, we will consider applying the proposed method to solve decision-making problems in other fields to enhance the applicability of this method, and compare this method with other methods to further analyze the advantages and disadvantages of this method. In addition, we will explore other MCDM models to solve the decision-making problem in the field of drug cold chain logistics.