In this section, we illustrate the process of using the GADP and Gaussian CGADP methods by applying them to an empirical study including a set of data obtained by a questionnaire on sleep quality from 186 patients who were all Chinese woman. Some questions involved in this questionnaire are listed in
Table 3. As we discussed in the previous section, both methods divide attributes into two categories (confident attributes and non-confident attributes), generate perturbed data to mask the confident attributes, then release the perturbed data and the data of non-confident attributes. For this empirical study, the answers to the first five sleep-related questions are confidential and are denoted as
, while the other two are non-confidential and are denoted as
To be consistent with the above, in the rest of this section we let
denote the perturbed data and
denote the released data. Furthermore, we compare the efficacy of the two methods.
To protect the privacy of all respondents, hospitals or the data owners may apply the SDC methods to mask the confident attributes of the original survey data and release the masked and non-confident data to researchers for analysis. In the following subsection, we apply GADP and Gaussian CGADP methods to the dataset.
3.1. Applying the GADP Method
Firstly, we need to determine the parameters of the GADP method based on
Table 5 and
Table 6:
Under the GADP method introduced in
Section 2.1, we generate the perturbed data
according to Equations (2) and (3), as follows:
where
Based on Equations (3) and (10), we have
Combining Equation (3) with Equations (11) and (12), we can get
We use the above information to perform GADP to obtain the perturbed data
, and these data are released together with the non-confidential data
. Perturbed data using the GADP can be found in
Table 7. By analyzing the released data
, we get the statistical information of
, which are shown in
Table 8 and
Table 9.
Comparing the means and standard deviations in
Table 8 with the corresponding values in
Table 5, we find that there is only a small deviation in the means and standard deviations between the perturbed and original data. This is because the perturbed data are generated according to Equation (2), which helps to keep the means and standard deviations close to those of original data. However, when comparing the Pearson’s correlation matrix in
Table 5 and the Spearman’s Rank correlation matrix in
Table 6 with the corresponding matrix in
Table 8 and
Table 9, respectively, we find that many values of them become different from those of the original data. We divide these changes between the correlation matrix calculated from the original survey data and the perturbed data into two categories: (i) in which the sign of the correlation coefficient between the two attributes has changed; (ii) in which the signs of the correlation coefficients are the same, but their absolute difference is greater than a threshold. As discussed in
Section 2, we expect the perturbed data would carry the same statistical information as in the original database when applying data perturbation. In this study, we set a small threshold of 0.05 to allow some variation in correlation values due to randomness in simulating samples. These two changes show that the correlation between the attributes in the original survey data are changed after using the SDC method. The first one means that if two attributes in the original survey data are positively correlated, they become negatively correlated by analyzing the perturbed data. Referring to
Table 5 and
Table 6, we find that there are two changes belonging to (i), which are marked with ^ in
Table 8 and
Table 9.
The second one means that even if the sign of the correlation coefficient between the two attributes remains unchanged, the absolute value of the correlation coefficient changes greatly. That is, the strength of the correlation between the attributes has changed. Comparing
Table 6 and
Table 9, we find that there are 17 changes belonging to (ii), which are marked with # if the absolute difference of the correlation is >0.05. All these biases can mislead researchers, since only the perturbed data are available to them. We see that the GADP method helps to produce perturbed data with close means and standard deviations to those of the original data, but the values in the correlation matrices differ substantially from those of the original data. The main reason for these biases is that the normal assumption of the GADP method is not satisfied in this case. The GADP method assumes normal marginals for all of the variables, which clearly is not true for this dataset with a large number of zeros observed in the survey data.
3.2. Applying the Gaussian CGADP m = Method
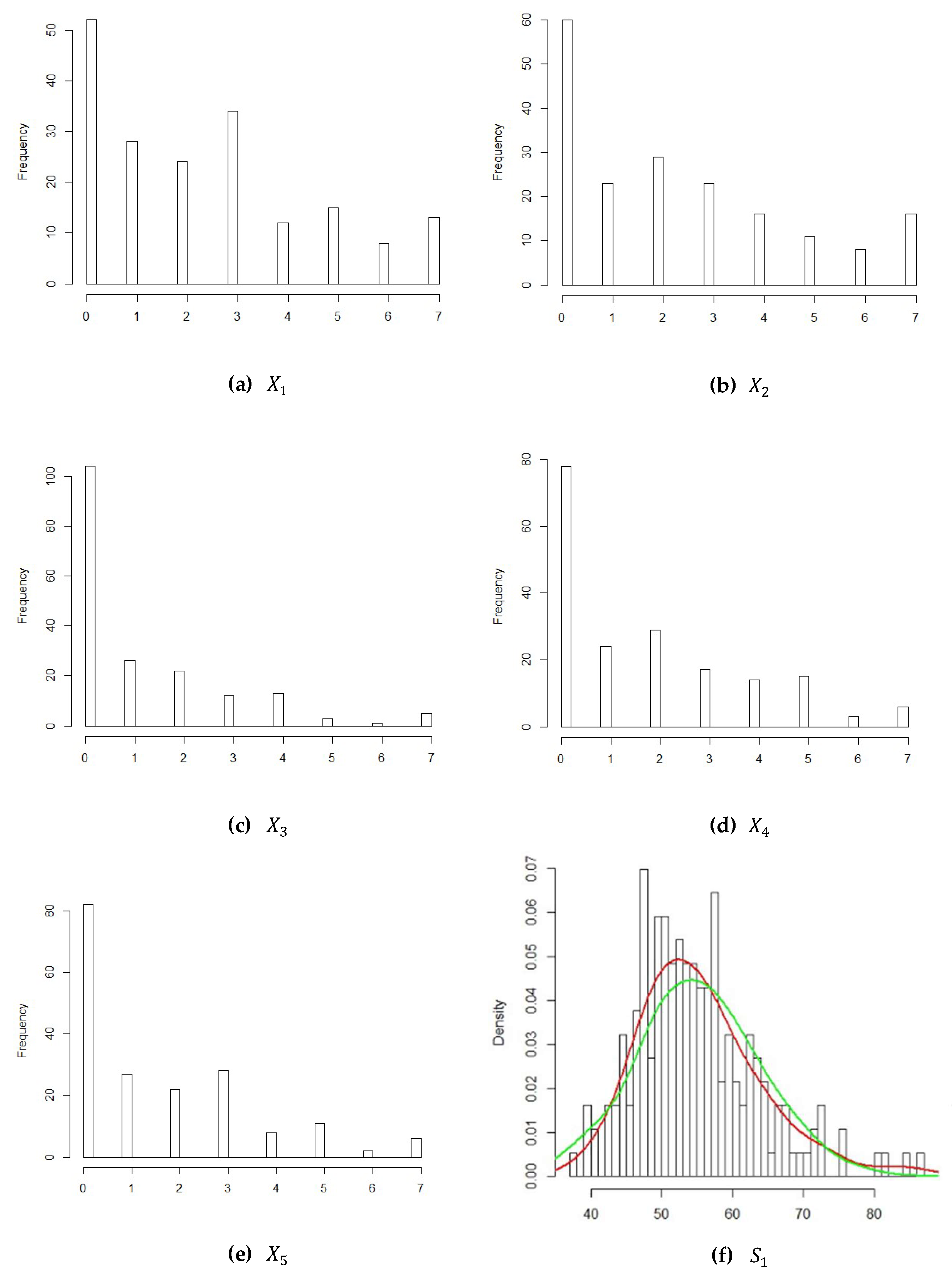
We should first determine the marginal distributions of attributes when we use the Gaussian CGADP method. For this empirical example, to fit the distribution of each attribute, we examine the frequency histograms using the statistical software R, and the results are shown in
Figure 3.
We found that only
likely follow normal distributions. We use the Maximum-likelihood Fitting Method of Univariate Distributions, which can be implemented with R to fit the corresponding distribution for each attribute. After fitting, we use the one-sample Kolmogorov–Smirnov (K-S) test to verify the goodness of fit. The parameters, the values of K-S test and the
p-values of K-S test, are also shown in
Table 10.
From
Table 10, we can see that all
p-values of the Kolmogorov–Smirnov test were larger than 0.05, meaning that each of the marginal distributions should not be rejected. All parameters of each marginal distribution were estimated. In
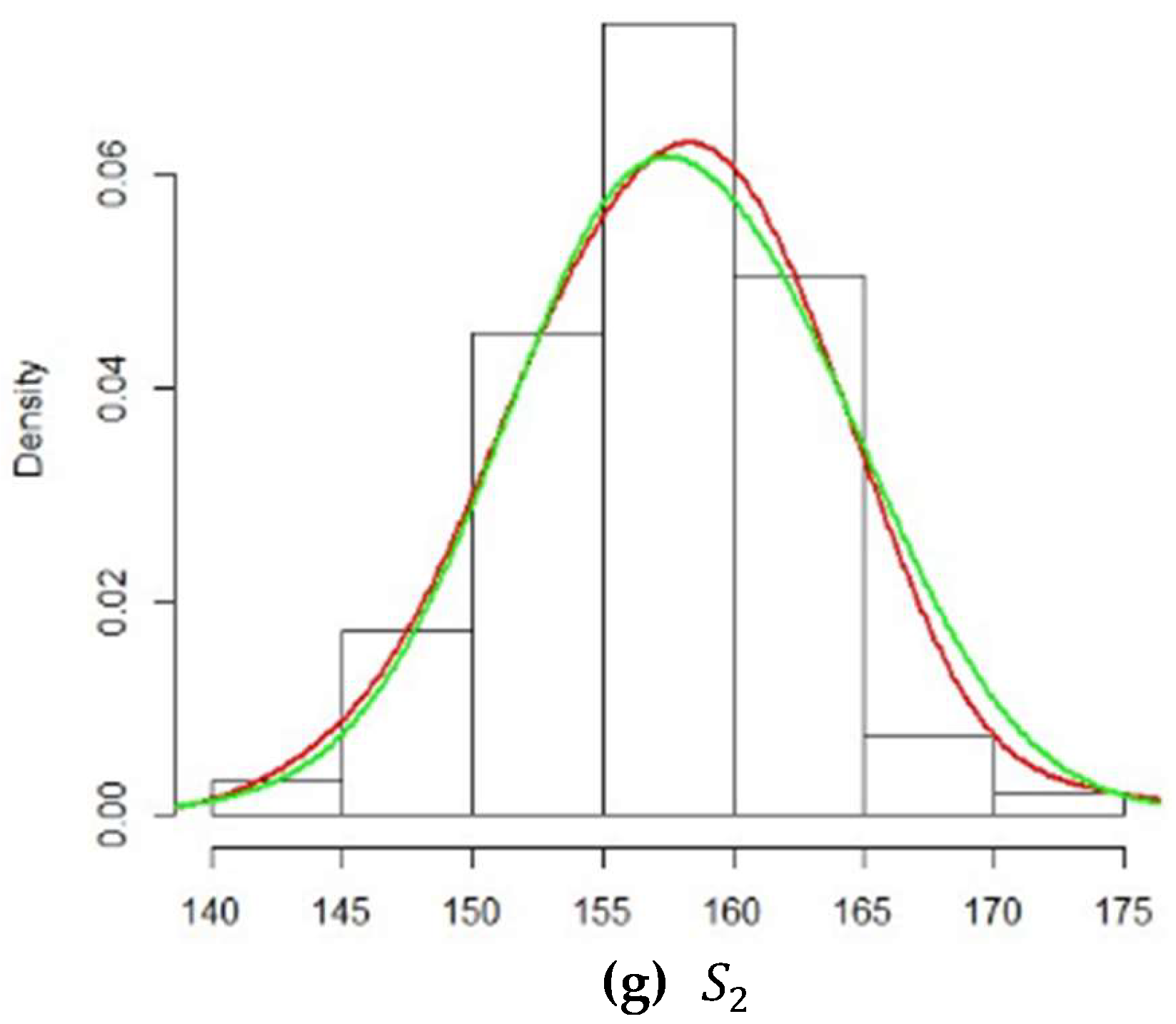
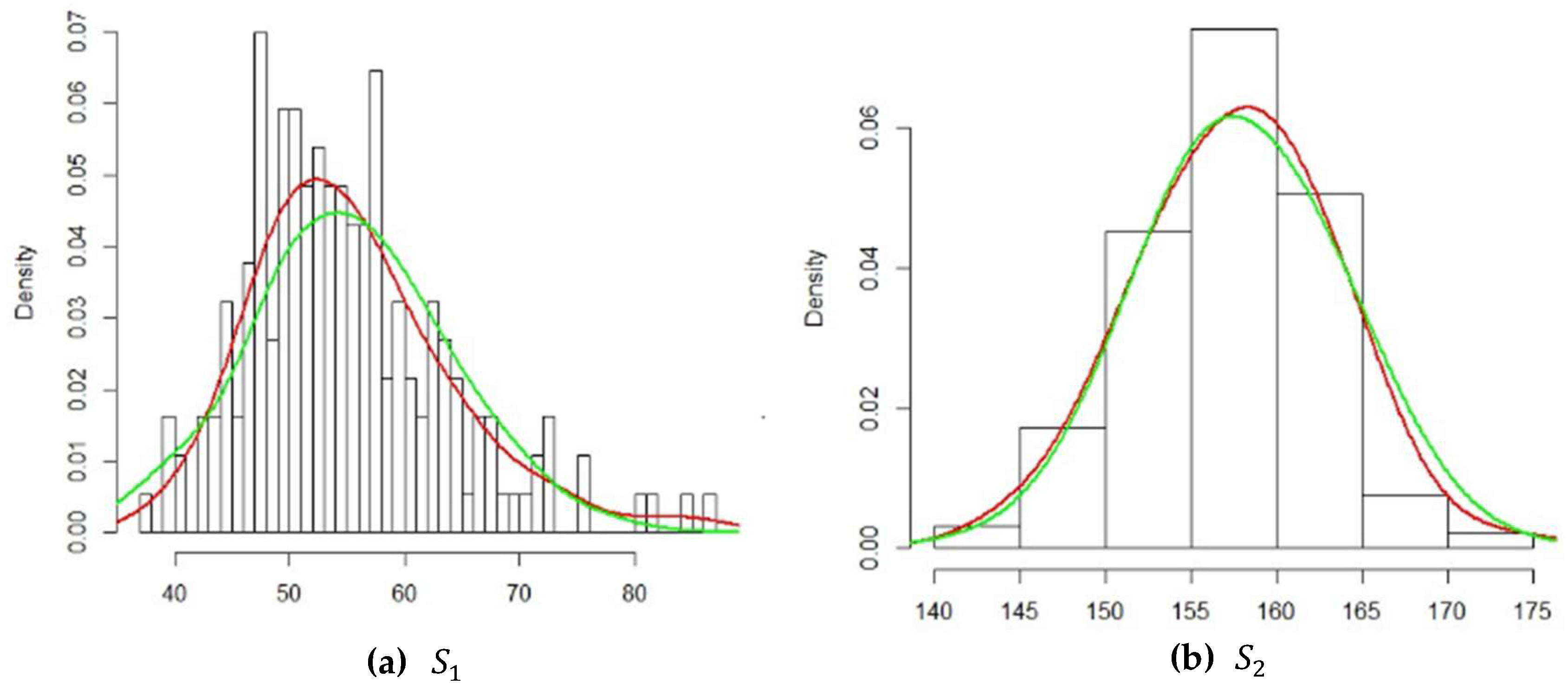
Figure 4, we compare the density curve of each attribute with the density of the corresponding fitted distribution. The red curves in (a) and (b) stand for the density of
, respectively. The green curves in (a) and (b) stand for the density of the normal distribution.
So far, we have determined the marginal distribution of , as follows:
As for attributes
, it is more reasonable to assume discrete distributions. In other words, their marginal distributions cannot be normal. Now we model the confidential survey data as a discrete distribution and keep the non-confidential data as normal distribution. CGADP is based on Sklar’s Theorem, which states that the copula for the joint distribution is unique if all the marginal distributions for each variable are continuous. The mix of discrete and continuous marginals would not guarantee the uniqueness of the copula, but still we could apply CGADP by assuming that a Gaussian copula is the copula for the joint distribution in this empirical study. We first find reasonable discrete distributions to serve as the marginals for the survey data. The results of the Chi-square goodness of fit test for the survey data is shown in
Table 11.
As shown in the graphics of the density plots in
Figure 3, most of the values recorded in the survey data were 0, and the frequency was clearly higher than for other values. Hence, instead of simply fitting a negative binomial distribution, we fit a zero inflated negative binomial distribution (ZINB) or zero adjusted negative binomial (ZANB) as the marginals for the confidential data. The
p-values were all higher than 0.05, indicating that the proposed distributions provide a good fit for the survey data.
We first transform the data according to Equation (6).
According to the Definition 2, we obtain a joint distribution by combining all the marginal distributions, the Pearson’s correlation and the Gaussian copula function. The data are derived in such way have two properties: (i) the marginal distribution of each attribute is the same as the proposed marginal distributions above; (ii) the Spearman’s Rank correlation matrix of is consistent with that of the original survey data . The data meets the assumptions of the GADP method, so we apply the GADP method to to derive . Then, we calculate the mean vector and the covariance matrix of .
According to assumptions of the GADP method, we have . Furthermore, we have
Based on Equation (8), we can generate
from the following distribution:
Furthermore, we obtain the perturbed data
based on Equation (9); specifically,
Finally, we combine the perturbed data
and the data of the non-confident attributes
and release
to researchers. Perturbed data using CGADP can be found in
Table 12. Analyzing the released data
, we can derive the statistical information, which is shown in
Table 13 and
Table 14. Values are marked with ^ if the sign changed after perturbation, or with # if the value greatly deviated from the original data by 0.05.
Comparing means and standard deviations in
Table 13 with the corresponding values in
Table 5, we can easily find that the mean of the perturbed data using CGADP is slightly higher than that of the original data. The standard deviations are close to the original data, although they are not as close as those in GADP.
As for the correlation matrix in
Table 13 and
Table 14, we can compare values of them with
Table 5 and
Table 6, respectively, to find only one entry in the Pearson’s correlation matrix belonging to (i), which is marked with ^. In addition, there are 13 changes belonging to (ii), which are marked with #. This means the absolute value of these 13 correlation coefficients has been noticeably changed. We can see that there is an improvement in the closeness of the correlation matrices when using CGADP. This is because the assumed marginals are now discrete, which fits the data better than the normal marginals in GADP. The only noticeable downside of using Gaussian CGADP is that the means of the perturbed data using CGADP slightly deviate from the means of the original data. This could be due to using a mix of discrete and continuous marginals when applying CGADP.