Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation?
Abstract
:1. Introduction
- (1)
- A bi-level regional water resource allocation model with multi-followers is established, which can better represent the actual watershed distribution model.
- (2)
- This paper considers not only the cooperation among sub-regions, but also the impact of information asymmetry on regional water resources allocation.
- (3)
- The results of this study will help basin authority and sub-regional managers to improve their water diversion plans.
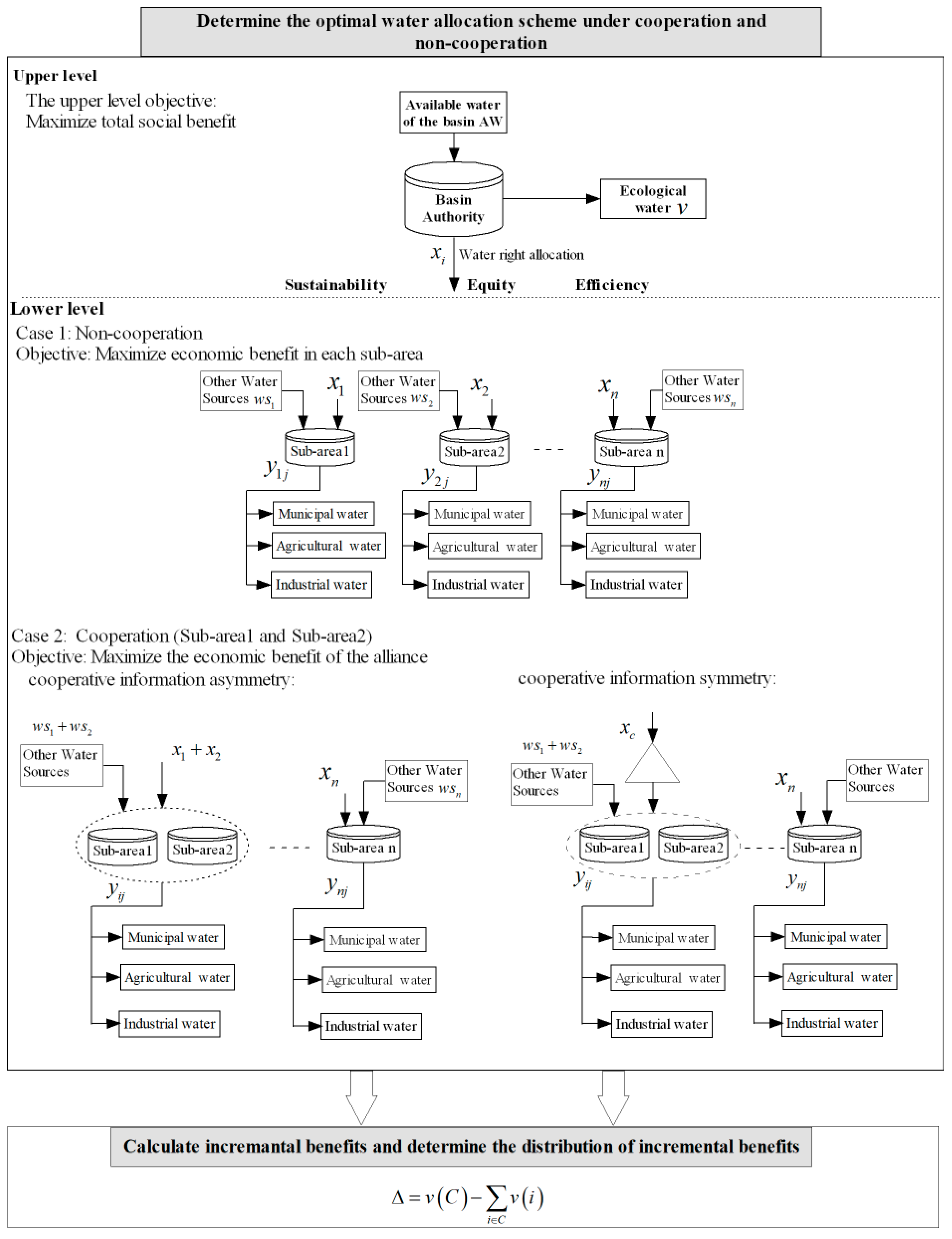
2. Problem Statement
3. Modeling
3.1. Level of Decision-Making for Basin Authority
3.2. Level of Decision-Making for the Manager of a Sub-Area
3.3. Water Allocation Model under Cooperation and Non-Cooperation
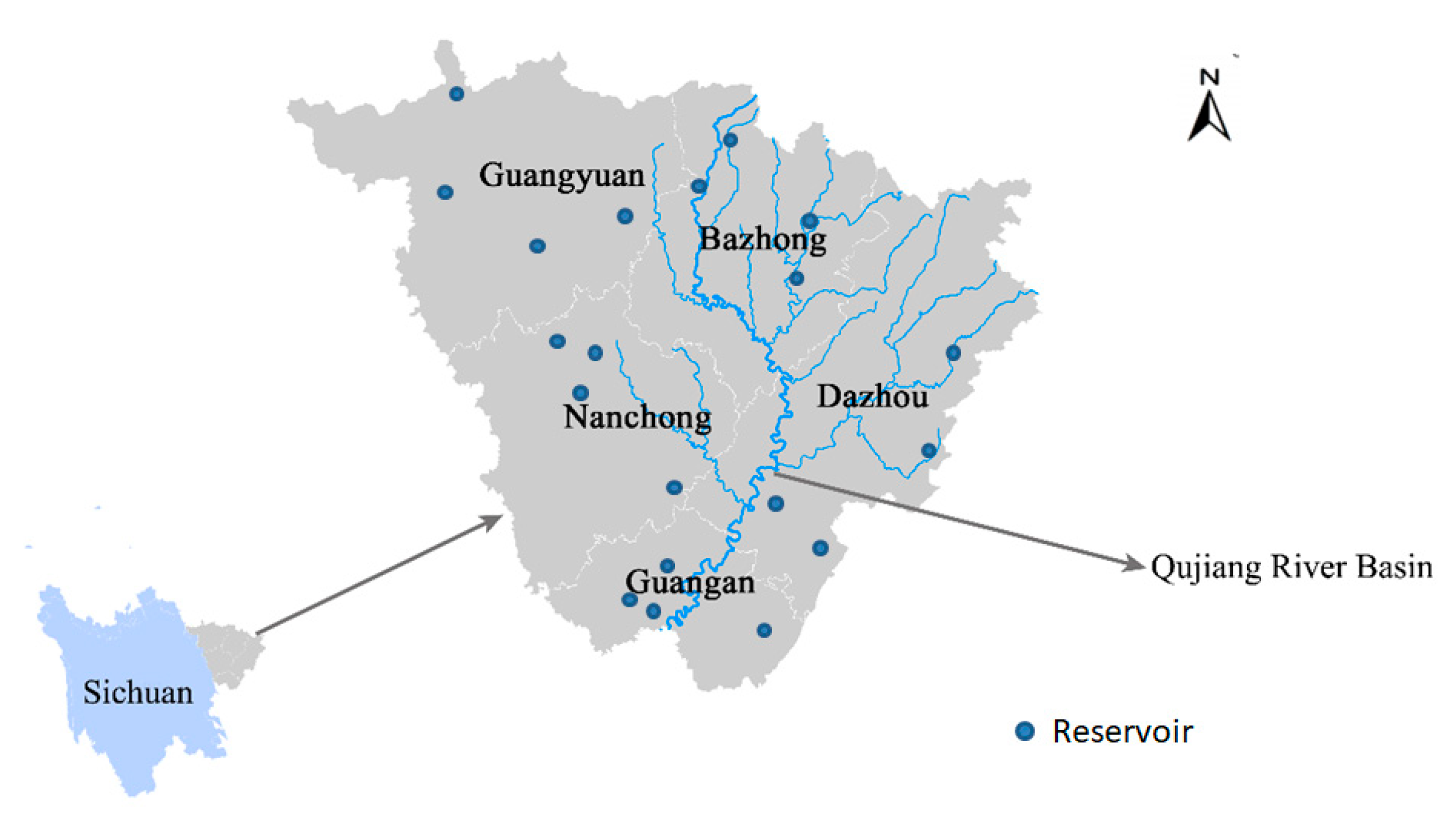
4. Case Study: Qujiang River Basin
4.1. Case Description
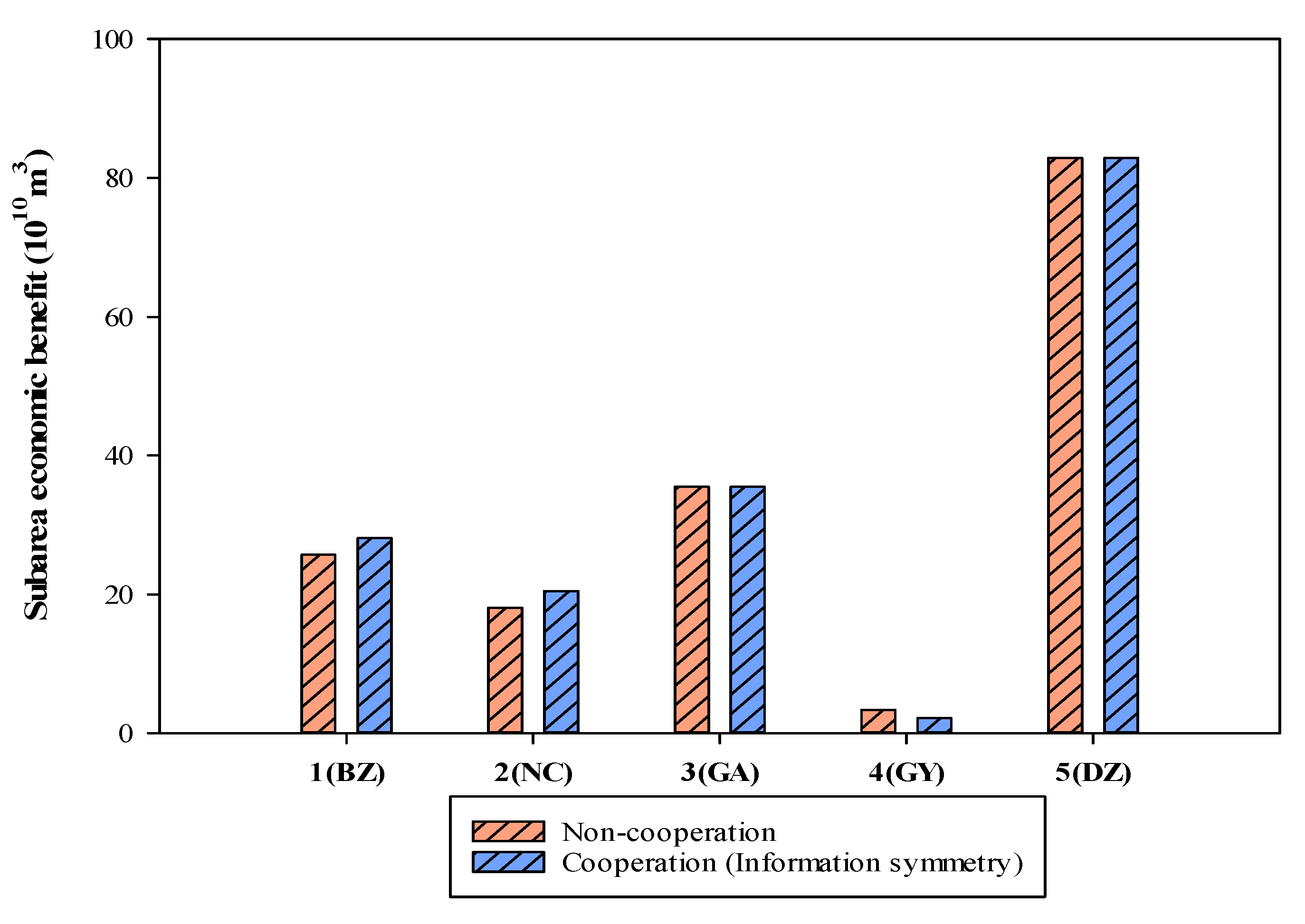
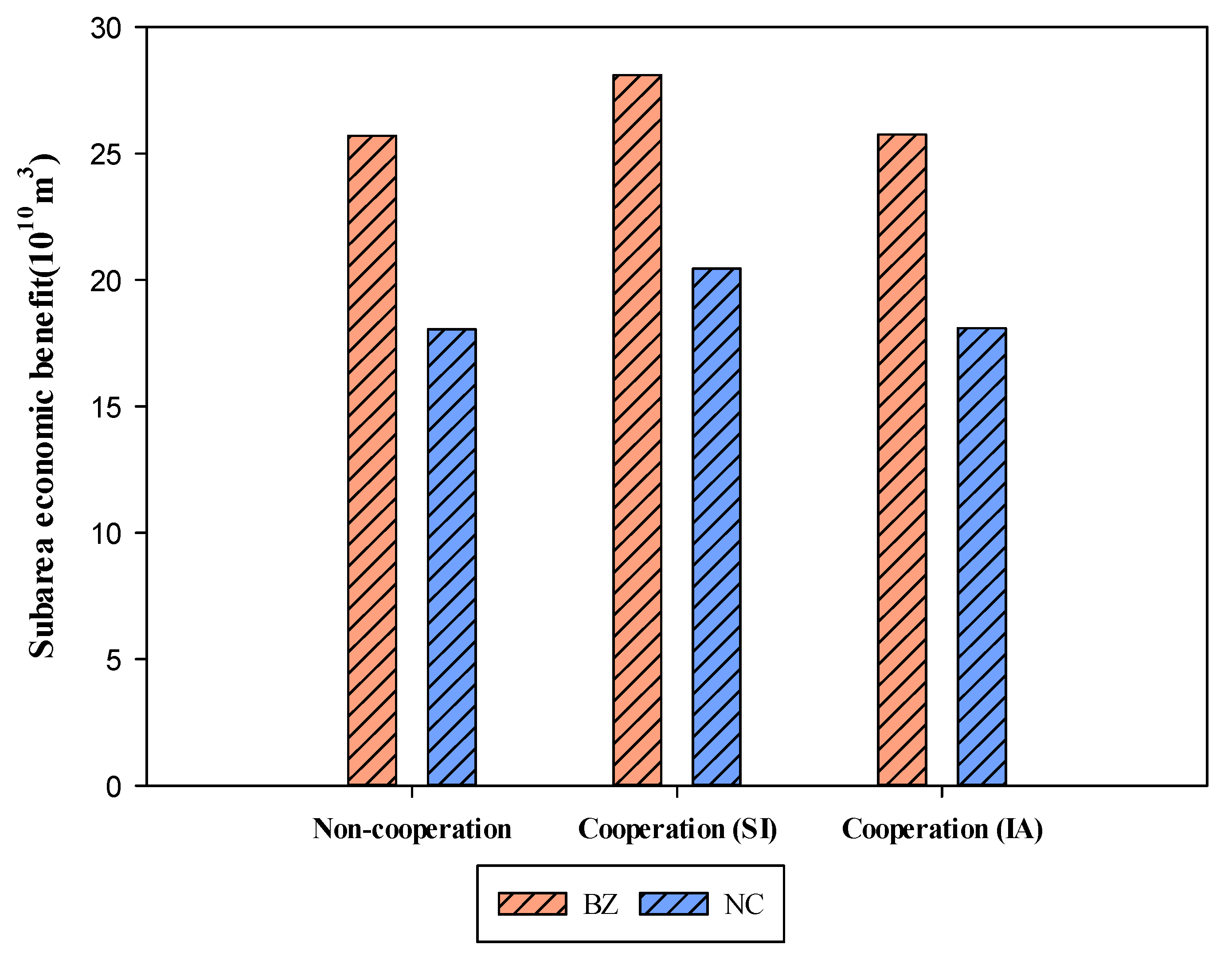
4.2. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Nomenclatures
- 1.
- Subscripts:
- = index of sub-area in the river basin, where,
- = index of water user in the sub-area, where
- 2.
- Decision Variables:
- = public ecological water rights to maintain the ecological environment of the river basin (107m3/Annual);
- = initial water rights of sub-area , determined by the upper level decision maker (107m3/Annual);
- = water withdrawal of user in sub-area , determined by the lower level decision maker (107m3/Annual);
- 3.
- Objective function:
- Max F = Objective function of Basin Authority (Maximize total social benefit, 1010 Yuan);
- Max = Objective function of sub-area (Maximize economic benefit in each sub-area, 1010 Yuan);
- 4.
- Parameters:
- = available water in the river basin (107m3/Annual);
- = minimal ecological water requirement of the river basin (107m3/Annual);
- = the ecology efficiency parameter for the river basin in unit of water supply (Yuan/m3);
- = the unit water cost for user (Yuan/m3);
- = maximum storage capacity of sub-area (107m3/Annual);
- = water transfer loss ratio from basin authority to sub-area ;
- = other water sources such as the rainfall and the groundwater in sub-area (107m3/Annual);
- = benefit parameter for water user in sub-area per unit of water allocated (Yuan/m3);
- = minimal water requirement for user in sub-area (107m3/Annual);
- = normal water requirement for user in sub-area (107m3/Annual);
- = Total economic benefit value of water user in sub-area (1010 Yuan/Annual).
References
- Bakker, K. Water security: Research challenges and opportunities. Science 2012, 337, 914–915. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.M.; Huang, G.H.; Wang, S.; Fan, Y.R. Water resources management under uncertainty: Factorial multi-stage stochastic program with chance constraints. Stoch. Environ. Res. Risk Assess. 2016, 30, 945–957. [Google Scholar] [CrossRef]
- Eliasson, J. The rising pressure of global water shortages. Nature 2015, 517, 6. [Google Scholar] [CrossRef]
- Slaibi, A.; Silverbrand, I.J. Efficiency and equity in the distribution of renewable resources: Water allocation in the jordan river watershed. SSRN Electron. J. 2009, 100, 563–568. [Google Scholar] [CrossRef]
- Roa Garcia, M.C. Equity, Efficiency and Sustainability in Water Allocation in the Andes: Trade-offs in a Full World. Water Altern. Interdiscip. J. Water Politics Dev. 2014, 7, 298–319. [Google Scholar]
- Xu, J.; Tu, Y.; Zeng, Z. Bilevel Optimization of Regional Water Resources Allocation Problem under Fuzzy Random Environment. J. Water Resour. Plan. Manag. 2013, 139, 246–264. [Google Scholar] [CrossRef]
- Liu, D.; Chen, X.; Lou, Z. A model for the optimal allocation of water resources in a saltwater intrusion area: A case study in pearl river delta in china. Water Resour. Manag. 2010, 24, 63–81. [Google Scholar] [CrossRef]
- Hu, Z.; Wei, C.; Yao, L.; Li, L.; Li, C. A multi-objective optimization model with conditional value-at-risk constraints for water allocation equality. J. Hydrol. 2016, 542, 330–342. [Google Scholar] [CrossRef]
- Li, M.; Guo, P. A multi-objective optimal allocation model for irrigation water resources under multiple uncertainties. Appl. Math. Model. 2014, 38, 4897–4911. [Google Scholar] [CrossRef]
- Kaldor, N. Marktform und Gleichgewicht by H. von Stackelberg. Economica 1936, 3, 227–230. [Google Scholar] [CrossRef]
- Wen, U.P.; Hsu, S.T. Linear bi-level programming problems—A review. J. Oper. Res. Soc. 1991, 42, 125–133. [Google Scholar]
- Xu, J.; Hou, S.; Yao, L.; Li, C. Integrated waste load allocation for river water pollution control under uncertainty: A case study of Tuojiang River, China. Environ. Sci. Pollut. Res. 2017, 24, 17741–17759. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.N.; Wei, C.T.; Yao, L.M.; Zeng, Z.Q. Integrating Equality and Stability to Resolve Water Allocation Issues with a Multiobjective Bilevel Programming Model. J. Water Resour. Plan. Manag. 2016, 142, 04016013. [Google Scholar] [CrossRef]
- Madani, K. Game theory and water resources. J. Hydrol. 2010, 381, 225–238. [Google Scholar] [CrossRef]
- Wang, L.; Fang, L.; Hipel, K.W. Basin-wide cooperative water resources allocation. Eur. J. Oper. Res. 2008, 190, 798–817. [Google Scholar] [CrossRef]
- Sadegh, M.; Kerachian, R. Water resources allocation using solution concepts of fuzzy cooperative games: Fuzzy least core and fuzzy weak least core. Water Resour. Manag. 2011, 25, 2543–2573. [Google Scholar] [CrossRef]
- He, Y.; Yang, J.; Chen, X. Allocating river water in a cooperative way: A case study of the Dongjiang River Basin, South China. Stoch. Environ. Res. Risk Assess. 2018, 32, 3083–3097. [Google Scholar] [CrossRef]
- Madani, K.; Hooshyar, M. A game theory–reinforcement learning (gt–rl) method to develop optimal operation policies for multi-operator reservoir systems. J. Hydrol. 2014, 519, 732–742. [Google Scholar] [CrossRef]
- Jianjian, S.; Chuntian, C.; Xiufei, Z.; Binbin, Z. Coordinated operations of multiple-reservoir cascaded hydropower plants with cooperation benefit allocation. Energy 2018, 153, 509–518. [Google Scholar]
- Xu, B.; Ma, Y.; Zhong, P.A.; Yu, Z.; Zhang, J.; Zhu, F. Bargaining model of synergistic revenue allocation for the joint operations of a multi-stakeholder cascade reservoir system. Water Resour. Manag. 2018, 32, 4625–4642. [Google Scholar] [CrossRef]
- Guo, X.; Hu, T.; Zhang, T.; Lv, Y. Bilevel model for multi-reservoir operating policy in inter-basin water transfer-supply project. J. Hydrol. 2012, 424, 252–263. [Google Scholar] [CrossRef]
- Degefu, D.M.; He, W.; Yuan, L.; Zhao, J.H. Water allocation in transboundary river basins under water scarcity: A cooperative bargaining approach. Water Resour. Manag. 2016, 30, 4451–4466. [Google Scholar] [CrossRef]
- Lu, Y.B.; Wan, Z.P.; Hu, T.S.; Chen, Z. Bilevel programming model for optimal allocation of water resources. Theory Pract. Syst. Eng. 2009, 29, 115–120. [Google Scholar]
- Tu, Y.; Zhou, X.; Gang, J.; Liechty, M.; Xu, J.; Lev, B. Administrative and market-based allocation mechanism for regional water resources planning. Resour. Conserv. Recy. 2015, 95, 156–173. [Google Scholar] [CrossRef]
| Relevant Literature | Bi-Level | Cooperation | Information Asymmetry |
|---|---|---|---|
| Xu et al., 2013 [6] | X | - | - |
| Xu and co-workers, 2017 [12] | X | - | - |
| Hu and co-workers, 2016 [13] | X | - | - |
| Madani, 2010 [14] | - | X | - |
| Wang et al., 2008 [15] | - | X | - |
| Sadegh et al., 2011 [16] | - | X | - |
| He et al., 2018 [17] | - | X | - |
| This paper | X | X | X |
| Sub-Area | ||||||
|---|---|---|---|---|---|---|
| Industry | Agriculture | Domestic | ||||
| 1 (BZ) | 0.45 | 428 | 1000 | 60.61 | 42.55 | 43.86 |
| 2 (NC) | 0.38 | 239 | 800 | 54.35 | 34.48 | 32.26 |
| 3 (GA) | 0.30 | 340 | 800 | 67.57 | 47.62 | 47.17 |
| 4 (GY) | 0.50 | 29 | 600 | 74.07 | 31.25 | 37.88 |
| 5 (DZ) | 0.32 | 635 | 1200 | 86.96 | 43.11 | 45.45 |
| Sub-Area | Industry | Agriculture | Domestic | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 (BZ) | 87 | 488 | 1.2 | 319 | 765 | 0.2 | 114 | 155 | 1.0 |
| 2 (NC) | 56 | 72 | 1.2 | 363 | 420 | 0.2 | 57 | 78 | 1.0 |
| 3 (GA) | 164 | 251 | 1.2 | 332 | 443 | 0.2 | 67 | 96 | 1.0 |
| 4 (GY) | 10 | 28 | 1.2 | 34 | 42 | 0.2 | 7 | 8 | 1.0 |
| 5 (DZ) | 324 | 683 | 1.2 | 342 | 611 | 0.2 | 217 | 281 | 1.0 |
| Sub-Area | Allocation Amount (107 m3/Annual) | Economic Benefit (1010 Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1(BZ) | 232.72 | 123.00 | 319.00 | 114.00 | 25.703 | 7.307 | 13.510 | 4.886 | 167.938 |
| 2(NC) | 408.06 | 72.00 | 363.00 | 57.00 | 18.052 | 3.827 | 12.444 | 1.782 | |
| 3(GA) | 442.86 | 251.00 | 332.00 | 67.00 | 35.496 | 16.659 | 15.743 | 3.093 | |
| 4(GY) | 80.00 | 28.00 | 34.00 | 7.00 | 3.354 | 2.040 | 1.056 | 0.258 | |
| 5(DZ) | 822.06 | 683.00 | 342.00 | 217.00 | 82.895 | 58.574 | 14.675 | 9.646 | |
| Sub-Area | Allocation Amount (107 m3/Annual) | Economic Benefit (1010 Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1(BZ) | 676.78 | 218.21 | 319.00 | 114.00 | 48.562 | 12.964 | 13.510 | 4.886 | 171.637 |
| 2(NC) | 56.00 | 363.00 | 57.00 | 2.976 | 12.444 | 1.782 | |||
| 3(GA) | 442.86 | 251.00 | 332.00 | 67.00 | 35.496 | 16.659 | 15.743 | 3.093 | |
| 4(GY) | 44.00 | 11.76 | 34.00 | 7.00 | 2.171 | 0.857 | 1.056 | 0.258 | |
| 5(DZ) | 822.06 | 683.00 | 342.00 | 217.00 | 82.895 | 58.574 | 14.675 | 9.646 | |
| Sub-Area | Allocation Amount (107 m3/Annual) | Economic Benefit (1010 Yuan) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1(BZ) | 640.78 | 138.99 | 319.00 | 114.00 | 43.855 | 8.257 | 13.510 | 4.886 | 168.038 |
| 2(NC) | 56.00 | 363.00 | 57.00 | 2.976 | 12.444 | 1.782 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, L.; Chen, X.; Zhao, L.; Xiao, A. Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation? Int. J. Environ. Res. Public Health 2019, 16, 4292. https://doi.org/10.3390/ijerph16214292
Pan L, Chen X, Zhao L, Xiao A. Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation? International Journal of Environmental Research and Public Health. 2019; 16(21):4292. https://doi.org/10.3390/ijerph16214292
Chicago/Turabian StylePan, Li, Xudong Chen, Lu Zhao, and Anran Xiao. 2019. "Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation?" International Journal of Environmental Research and Public Health 16, no. 21: 4292. https://doi.org/10.3390/ijerph16214292
APA StylePan, L., Chen, X., Zhao, L., & Xiao, A. (2019). Does Information Asymmetry Impact Sub-Regions’ Cooperation of Regional Water Resource Allocation? International Journal of Environmental Research and Public Health, 16(21), 4292. https://doi.org/10.3390/ijerph16214292





