Assessment of River Water Quality Based on an Improved Fuzzy Matter-Element Model
Abstract
:1. Introduction
2. Methodology
2.1. Study Area
2.2. Improved Fuzzy Matter-Element (IFME) Model
2.2.1. Determination of Membership Degree in the Fuzzy Matter Element Model by SPA
2.2.2. Determination of Weights by VCM
- Normalize the indicator value matrix.The normalized matrix is obtained by Equation (4-1) as follows:where efficiency indicators refer to indicators that correlate positively with normalization results, and cost indicators refer to indicators that correlate negatively with normalization results.
- Calculate the average value of each indicator :
- Calculate the mean squared deviation of each indicator :
- Calculate the variable coefficient of each indicator :
- Determine the weight of each indicator by normalization:
2.3. River Water Quality Assessment by the IFME Method
2.3.1. Selection of Water Quality Indicators
2.3.2. Calculation of the Membership Degree of Each Indicator
2.3.3. Generation of the Compound Fuzzy Matter-Element
2.3.4. Calculation of Fuzzy Closeness Degree
2.3.5. Calculation of the Grade Characteristic Value (H) and Grade of the River Water Quality
3. Results and Discussion
3.1. Water Quality Assessment Results of Caoqiao River
3.2. Compared with Other Different Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Singh, K.P.; Malik, A.; Sinha, S. Water quality assessment and apportionment of pollution sources of Gomti rver (India) using multivariate statistical techniques—A case study. Anal. Chim. Acta 2005, 538, 355–374. [Google Scholar] [CrossRef]
- Muangthong, S.; Shrestha, S. Assessment of surface water quality using multivariate statistical techniques: Case study of the Nampong River and Songkhram River, Thailand. Environ. Monit. Assess. 2015, 187, 548. [Google Scholar] [CrossRef]
- Perrin, J.L.; Raïs, N.; Chahinian, N.; Moulin, P.; Ijjaali, M. Water quality assessment of highly polluted rivers in a semi-arid mediterranean zne Oued Fez and Sebou River (Morocco). J. Hydrol. 2014, 510, 26–34. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, X.; Engel, B. Water environment carrying capacity in Bosten Lake basin. J. Clean. Prod. 2018, 199, 574–583. [Google Scholar] [CrossRef]
- Pan, G.; Xu, Y.; Yu, Z.; Song, S.; Zhang, Y. Analysis of river health variation under the background of urbanization based on entropy weight and matter-element model: A case study in Huzhou City in the Yangtze River Delta, China. Environ. Res. 2015, 139, 31–35. [Google Scholar] [CrossRef]
- Fulazzaky, M.A. Water Quality Evaluation System to Assess the Brantas River Water. Water Resour. Manag. 2009, 23, 3019–3033. [Google Scholar] [CrossRef]
- Wang, Y.; Ran, W. Comprehensive Eutrophication Assessment Based on Fuzzy Matter Element Model and Monte Carlo-Triangular Fuzzy Numbers Approach. Int. J. Environ. Res. Public Health 2019, 16, 1769. [Google Scholar] [CrossRef]
- Mohamed, I.; Othman, F.; Ibrahim, A.I.; Alaa-Eldin, M.E.; Yunus, R.M. Assessment of water quality parameters using multivariate analysis for Klang River basin, Malaysia. Environ. Monit. Assess. 2015, 187, 4182. [Google Scholar] [CrossRef]
- Ouyang, Y. Evaluation of river water quality monitoring stations by principal component analysis. Water Res. 2005, 39, 2621–2635. [Google Scholar] [CrossRef]
- Olkowska, E.; Kudłak, B.; Tsakovski, S.; Ruman, M.; Simeonov, V.; Polkowska, Z. Assessment of the water quality of Klodnica River catchment using self-organizing maps. Sci. Total Environ. 2014, 476, 477–484. [Google Scholar] [CrossRef]
- Noori, R.; Sabahi, M.; Karbassi, A.; Baghvand, A.; Zadeh, H.T.; Karbassi, A. Multivariate statistical analysis of surface water quality based on correlations and variations in the data set. Desalination 2010, 260, 129–136. [Google Scholar] [CrossRef]
- Bouza-Deaño, R.; Rodriguez, M.T.; Fernández-Espinosa, A. Trend study and assessment of surface water quality in the Ebro River (Spain). J. Hydrol. 2008, 361, 227–239. [Google Scholar] [CrossRef]
- Huang, J.; Xie, R.; Yin, H.; Zhou, Q. Assessment of water quality and source apportionment in a typical urban river in China using multivariate statistical methods. Water Supply 2018, 18, 1841–1851. [Google Scholar] [CrossRef]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009, 220, 888–895. [Google Scholar] [CrossRef]
- Kim, S.E.; Seo, I.W. Artificial Neural Network ensemble modeling with conjunctive data clustering for water quality prediction in rivers. J. Hydro Environ. Res. 2015, 9, 325–339. [Google Scholar] [CrossRef]
- Ocampo-Duque, W.; Ferré-Huguet, N.; Domingo, J.L.; Schuhmacher, M. Assessing water quality in rivers with fuzzy inference systems: A case study. Environ. Int. 2006, 32, 733–742. [Google Scholar] [CrossRef]
- Ocampo-Duque, W.; Osorio, C.; Piamba, C.; Schuhmacher, M.; Domingo, J.L. Water quality analysis in rivers with non-parametric probability distributions and fuzzy inference systems: Application to the Cauca River, Colombia. Environ. Int. 2013, 52, 17–28. [Google Scholar] [CrossRef]
- Feio, M.; Aguiar, F.; Almeida, S.; Ferreira, M.; Feio, M.; Aguiar, F.; Ferreira, T. AQUAFLORA: A predictive model based on diatoms and macrophytes for streams water quality assessment. Ecol. Indic. 2012, 18, 586–598. [Google Scholar] [CrossRef]
- Cai, W. Matter Element Model and Application; Science and Technology Literature Press: Beijing, China, 1994. (In Chinese) [Google Scholar]
- Su, M.; Yang, Z.; Chen, B. Set pair analysis for urban ecosystem health assessment. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 1773–1780. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment of the People’s Republic of China. GB3838-2002 Environmental Quality Standards for Surface Water; Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2002.
- Huang, J.; Yin, H.; Chapra, S.C.; Zhou, Q. Modelling Dissolved Oxygen Depression in an Urban River in China. Water 2017, 9, 520. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, W.; You, B.; Bian, B. Research of Environmental Sciences; Chinese Research Academy of Environmental Sciences: Beijing, China, 2009; pp. 1150–1155. (In Chinese) [Google Scholar]
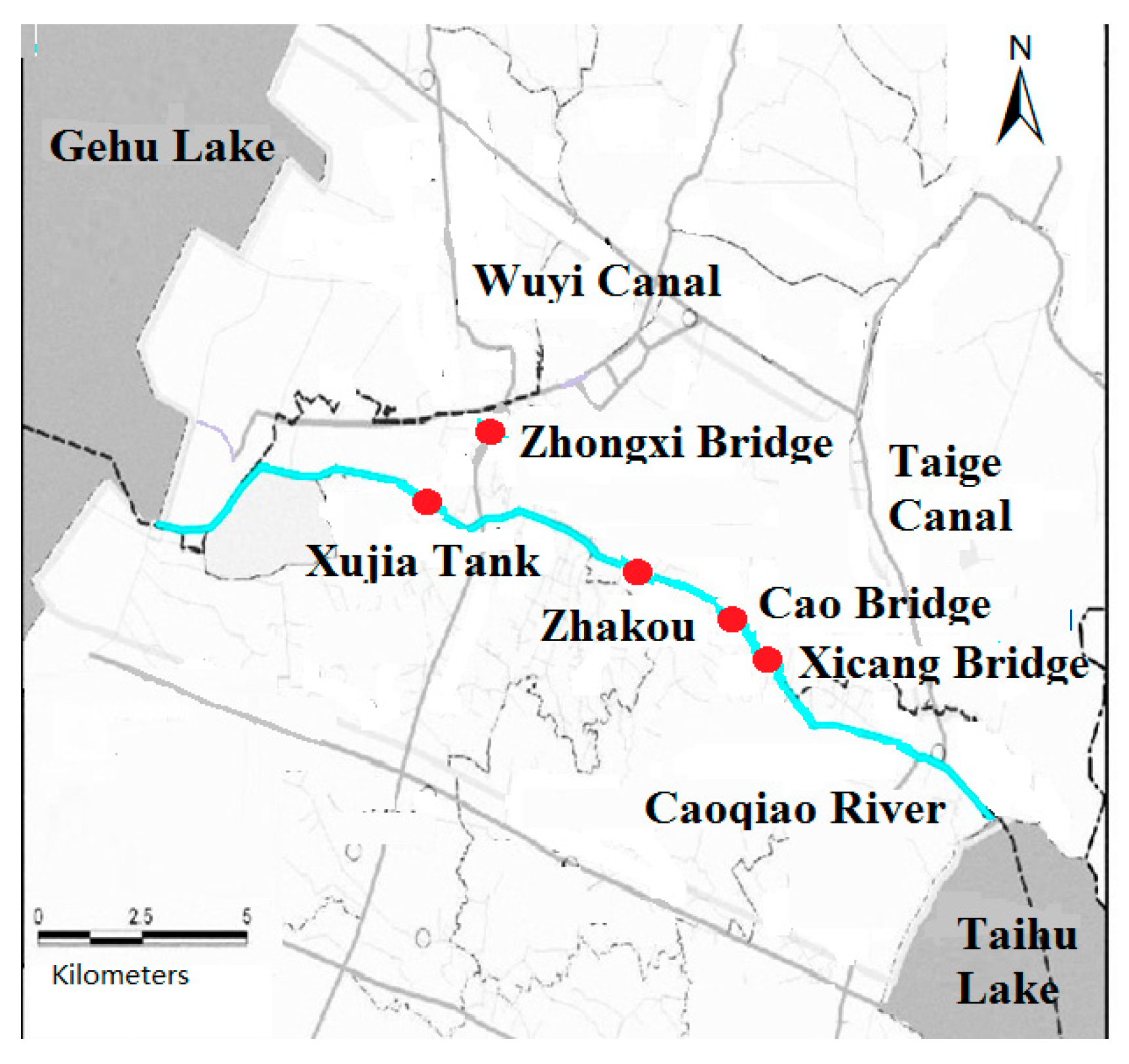
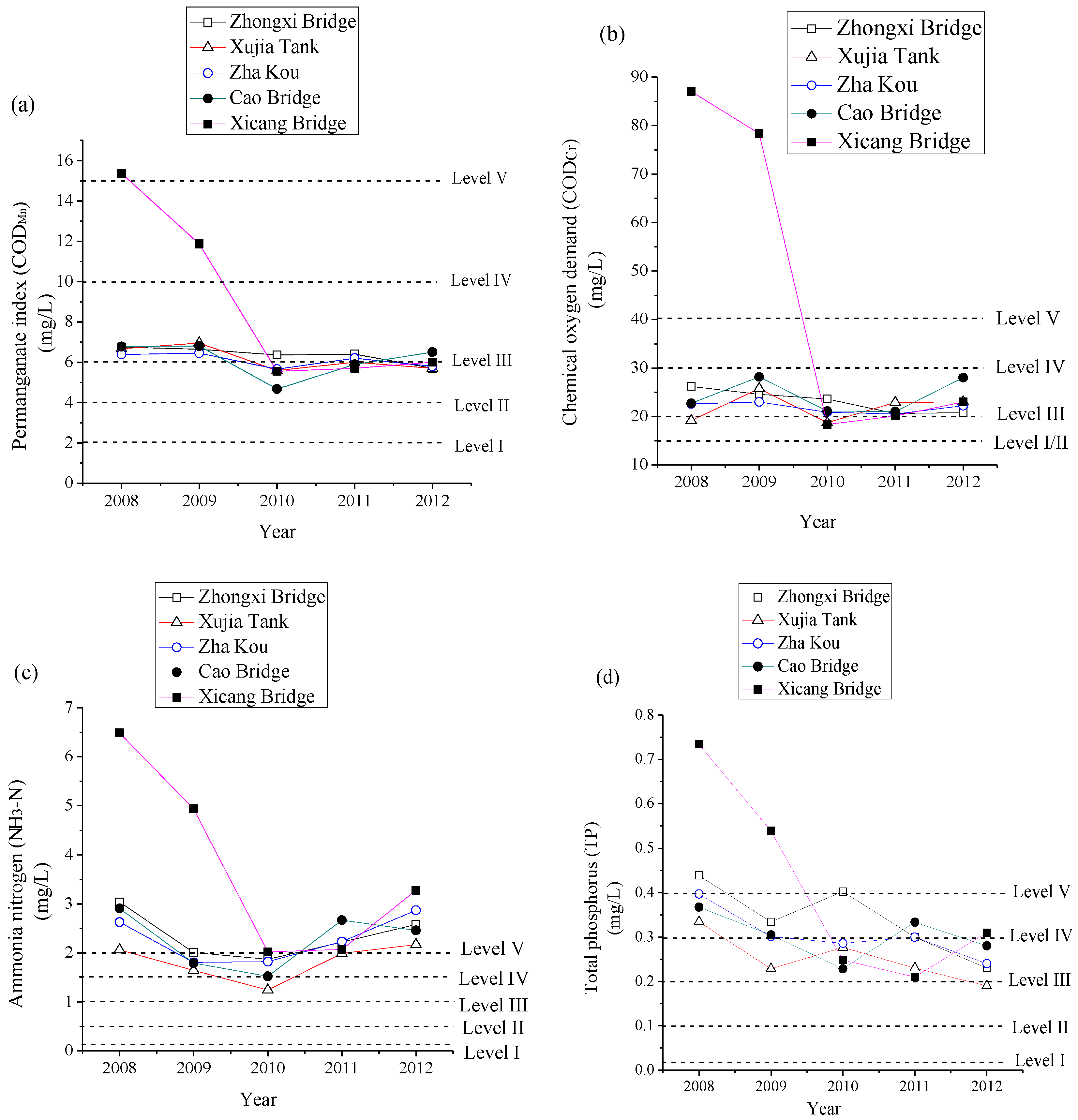
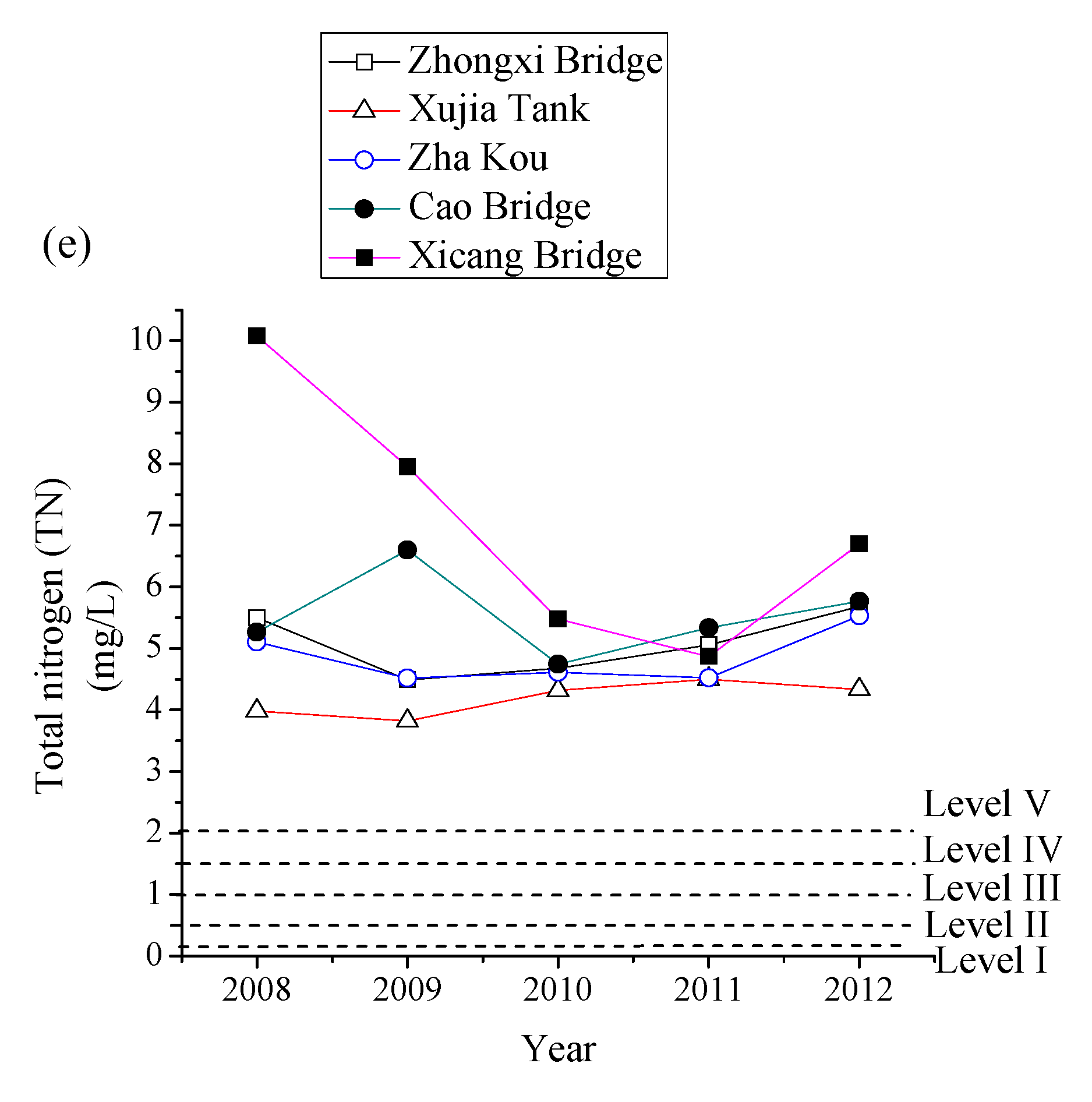
| Indicators | I | II | III | IV | V | Weights |
|---|---|---|---|---|---|---|
| CODMn | 2 | 4 | 6 | 10 | 15 | 0.15 |
| CODCr | 15 | 15 | 20 | 30 | 40 | 0.22 |
| NH3-N | 0.15 | 0.5 | 1 | 1.5 | 2 | 0.16 |
| TP | 0.02 | 0.1 | 0.2 | 0.3 | 0.4 | 0.25 |
| TN | 0.2 | 0.5 | 1 | 1.5 | 2 | 0.22 |
| Station | I | II | III | IV | V | Below Level V | Hm | Level |
|---|---|---|---|---|---|---|---|---|
| Zhongxi Bridge | 0.00 | 0.00 | 0.14 | 0.21 | 0.12 | 0.53 | 5.04 | V |
| Xujia tank | 0.00 | 0.04 | 0.26 | 0.35 | 0.14 | 0.22 | 4.23 | IV |
| Zhakou | 0.00 | 0.01 | 0.19 | 0.33 | 0.20 | 0.27 | 4.51 | V |
| Cao Bridge | 0.00 | 0.05 | 0.27 | 0.34 | 0.13 | 0.22 | 4.20 | IV |
| Xicang Bridge | 0.00 | 0.05 | 0.25 | 0.26 | 0.06 | 0.37 | 4.45 | IV |
| Station | 2008 | 2009 | 2010 | 2011 | 2012 | Avarage | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Hm | Level | Hm | Level | Hm | Level | Hm | Level | Hm | Level | Hm | |
| Zhongxi Bridge | 5.24 | V | 4.90 | V | 5.04 | V | 4.71 | V | 4.50 | V | 4.88 |
| Xujia Tank | 4.76 | V | 4.48 | IV | 4.23 | IV | 4.49 | IV | 4.45 | IV | 4.48 |
| Zhakou | 5.01 | V | 4.63 | V | 4.51 | V | 4.71 | V | 4.57 | V | 4.69 |
| Cao Bridge | 4.95 | V | 4.77 | V | 4.20 | IV | 4.79 | V | 4.83 | V | 4.71 |
| Xicang Bridge | 6.00 | VI | 5.83 | VI | 4.45 | IV | 4.44 | IV | 4.94 | V | 5.13 |
| Methods | Zhongxi Bridge | Zhakou | Xujia Tank | Xicang Bridge | Cao Bridge |
|---|---|---|---|---|---|
| Fuzzy matter-element model | V | VI | VI | VI | VI |
| Comprehensive index method | V | VI | VI | VI | VI |
| Fuzzy comprehensive method | V | III | III | III | III |
| Bayesian method | V | III | III | III | III |
| Improved fuzzy matter-element model | V | VI | VI | VI | VI |
| Station | I | II | III | IV | V | Level |
|---|---|---|---|---|---|---|
| Zhongxi Bridge | 0.00 | 0.00 | 0.28 | 0.14 | 0.59 | V |
| Xujia Tank | 0.00 | 0.09 | 0.42 | 0.27 | 0.22 | III |
| Zhakou | 0.00 | 0.03 | 0.36 | 0.29 | 0.32 | III |
| Cao Bridge | 0.00 | 0.00 | 0.47 | 0.25 | 0.23 | III |
| Xicang Bridge | 0.00 | 0.11 | 0.48 | 0.20 | 0.22 | III |
| Station | I | II | III | IV | V | Level |
|---|---|---|---|---|---|---|
| Zhongxi Bridge | 0.09 | 0.10 | 0.25 | 0.15 | 0.41 | V |
| Xujia tank | 0.11 | 0.14 | 0.36 | 0.27 | 0.12 | III |
| Zhakou | 0.08 | 0.11 | 0.35 | 0.29 | 0.17 | III |
| Cao Bridge | 0.10 | 0.17 | 0.36 | 0.27 | 0.10 | III |
| Xicang Bridge | 0.12 | 0.15 | 0.33 | 0.16 | 0.24 | III |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Ran, W.; Wu, L.; Wu, Y. Assessment of River Water Quality Based on an Improved Fuzzy Matter-Element Model. Int. J. Environ. Res. Public Health 2019, 16, 2793. https://doi.org/10.3390/ijerph16152793
Wang Y, Ran W, Wu L, Wu Y. Assessment of River Water Quality Based on an Improved Fuzzy Matter-Element Model. International Journal of Environmental Research and Public Health. 2019; 16(15):2793. https://doi.org/10.3390/ijerph16152793
Chicago/Turabian StyleWang, Yumin, Weijian Ran, Lei Wu, and Yifeng Wu. 2019. "Assessment of River Water Quality Based on an Improved Fuzzy Matter-Element Model" International Journal of Environmental Research and Public Health 16, no. 15: 2793. https://doi.org/10.3390/ijerph16152793
APA StyleWang, Y., Ran, W., Wu, L., & Wu, Y. (2019). Assessment of River Water Quality Based on an Improved Fuzzy Matter-Element Model. International Journal of Environmental Research and Public Health, 16(15), 2793. https://doi.org/10.3390/ijerph16152793






