The Stability and Complexity Analysis of a Low-Carbon Supply Chain Considering Fairness Concern Behavior and Sales Service
Abstract
1. Introduction
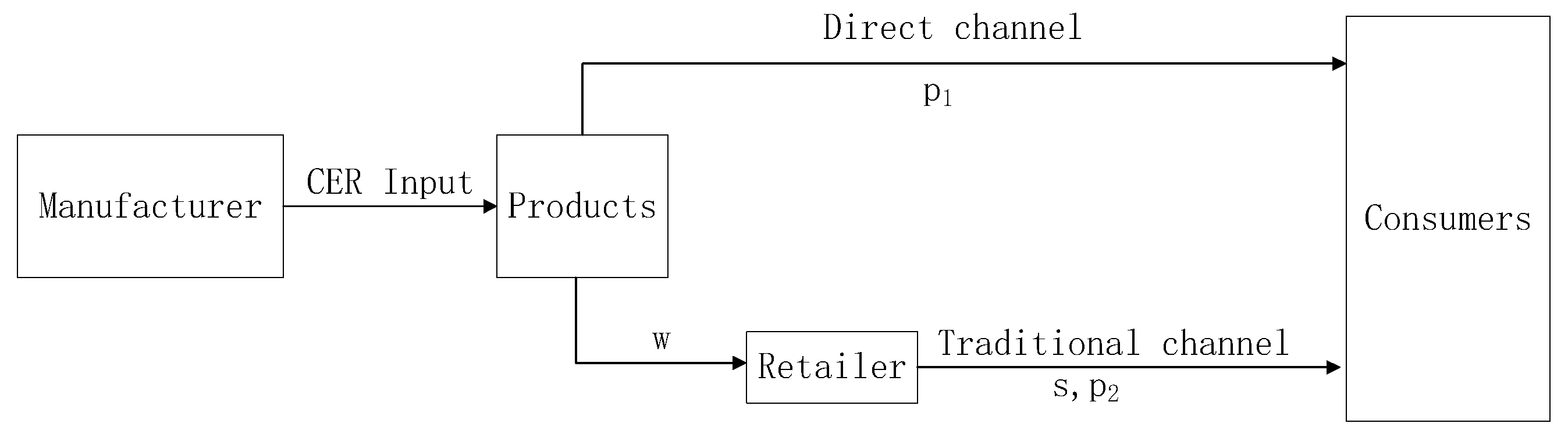
2. Model Description
2.1. Basic Model Description
2.2. Symbol Description
| Retail price of products in the direct channel and traditional channel | |
| The level of carbon emission reduction of the manufacturer | |
| The basic market scale of products | |
| Wholesale price of products | |
| Production cost of products | |
| The service input of the traditional channel provided by the retailer | |
| The price elasticity coefficient of price | |
| The cross-price elasticity coefficient of price | |
| Demand for products | |
| The cost of carbon emission reduction of products | |
| The service cost of the retailer | |
| The customer’s loyalty to the direct channel | |
| The customer’s loyalty to the demand caused by carbon emission reduction | |
| The sensitivity of the demand for carbon emission reduction | |
| Cost coefficient of carbon emission reduction of products | |
| Cost coefficient of service | |
| The profits of the manufacturer and retailer | |
| The utilities of the manufacturer and retailer |
2.3. Profit Functions
3. Equilibrium Points and Local Stability of Dynamic System (6)
3.1. Equilibrium Points
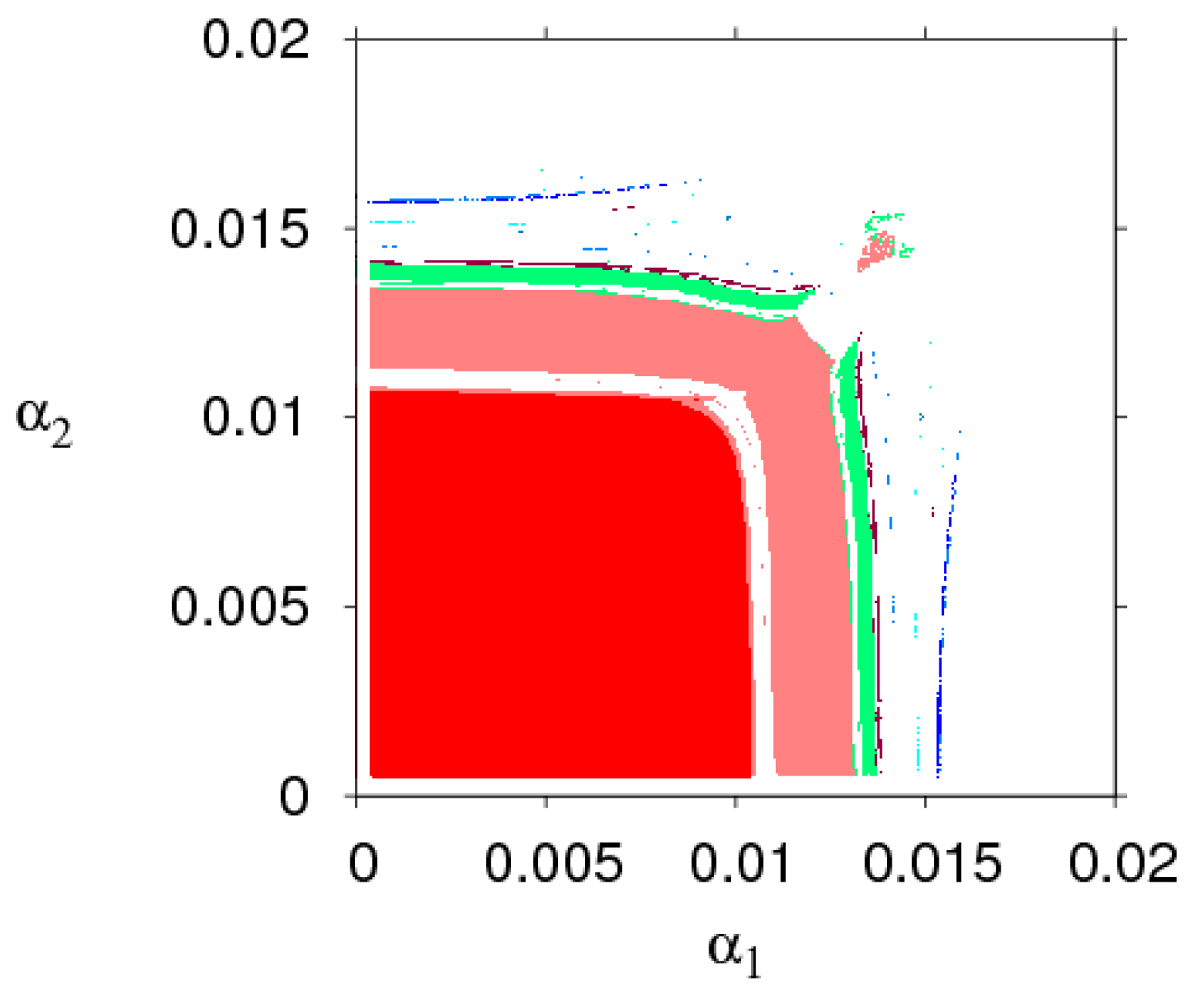
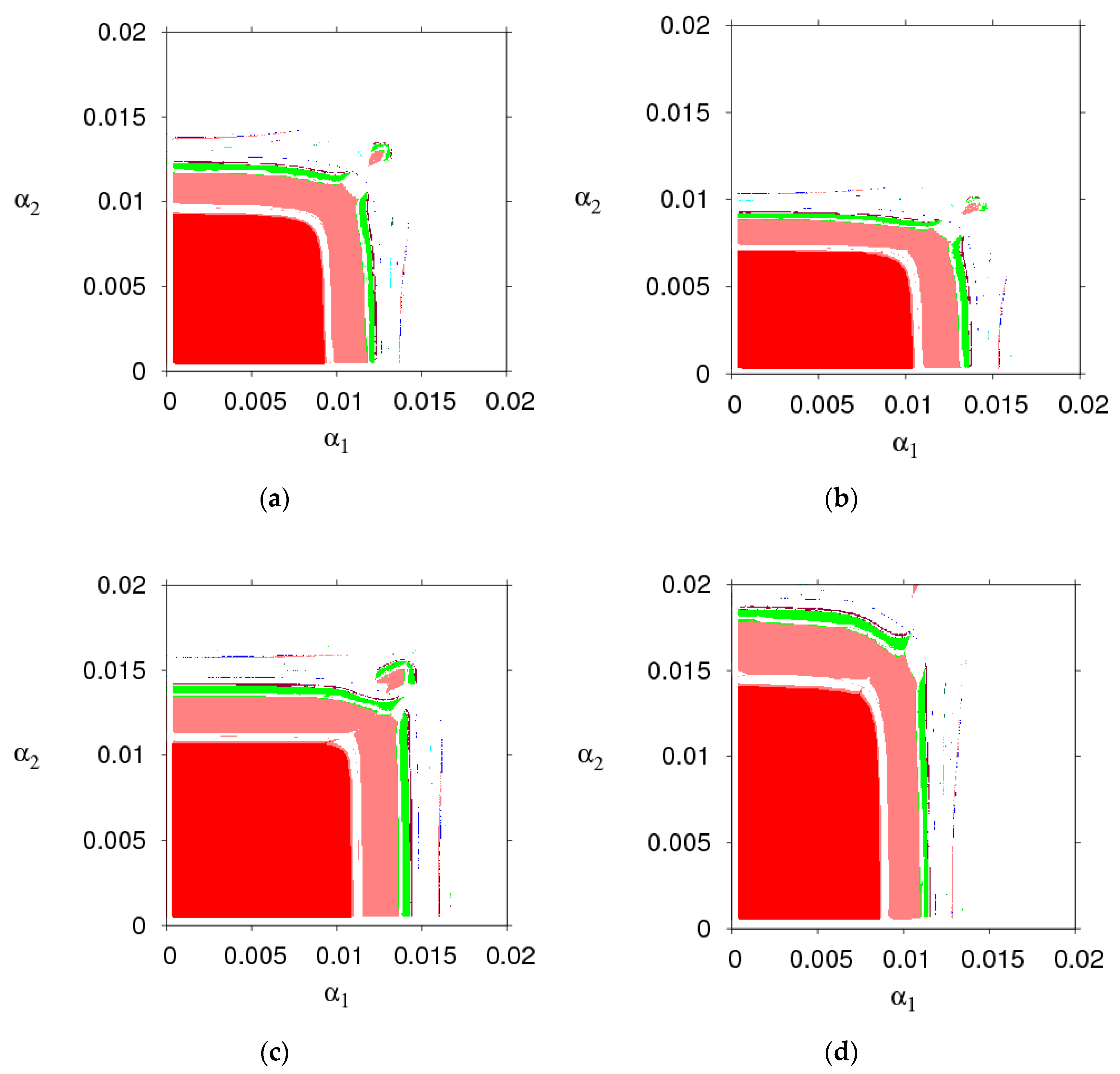
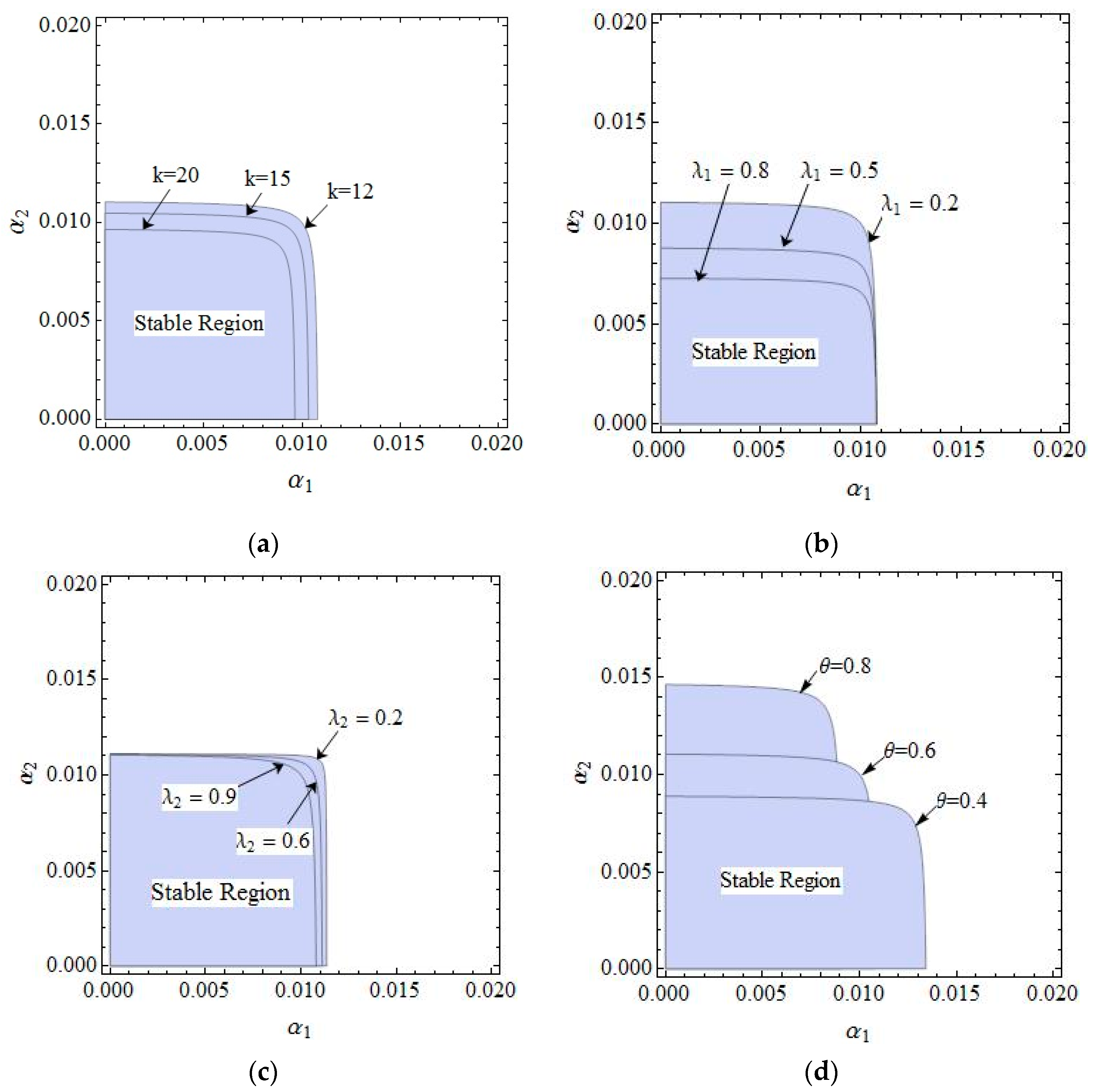
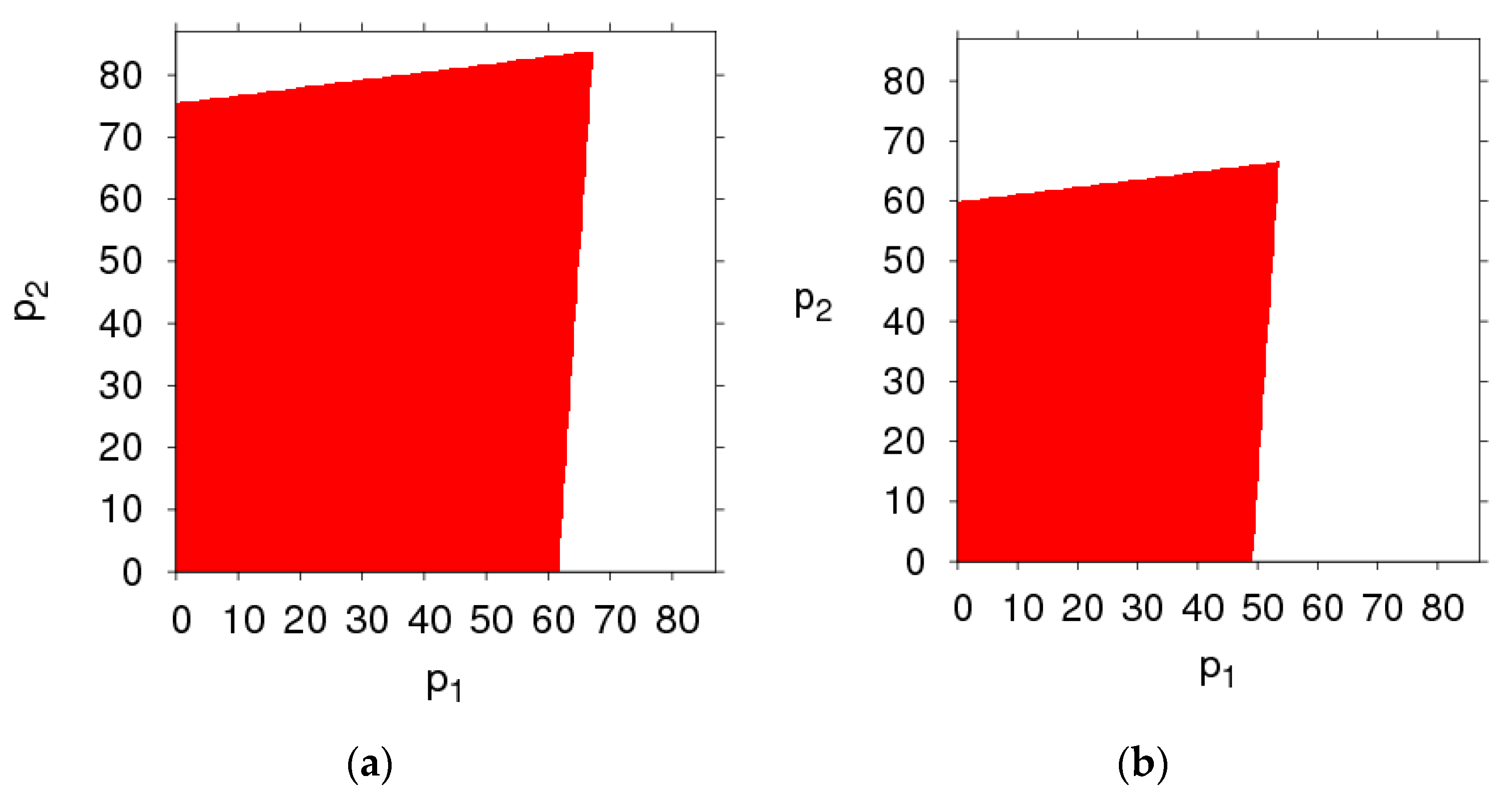
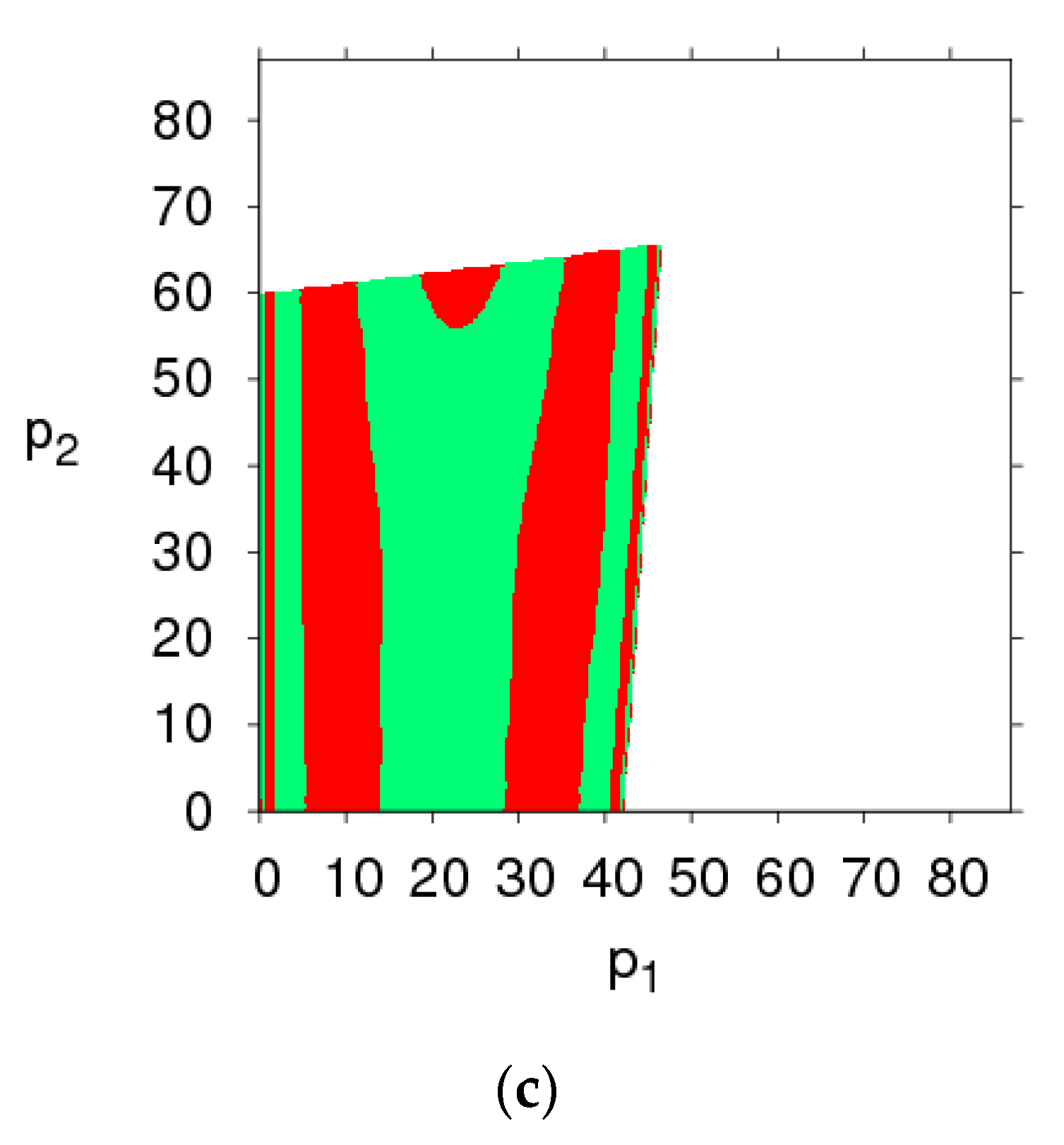
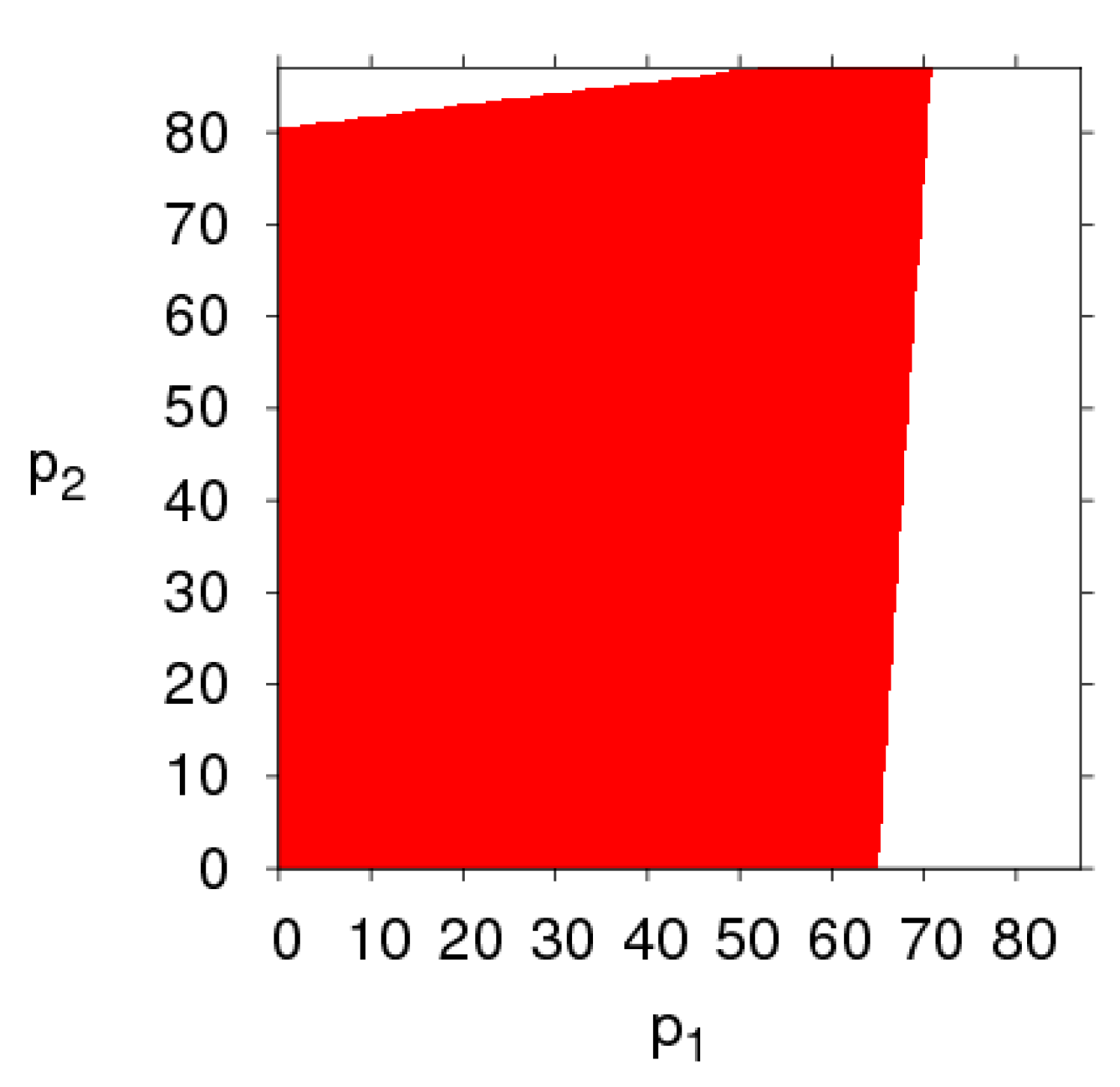
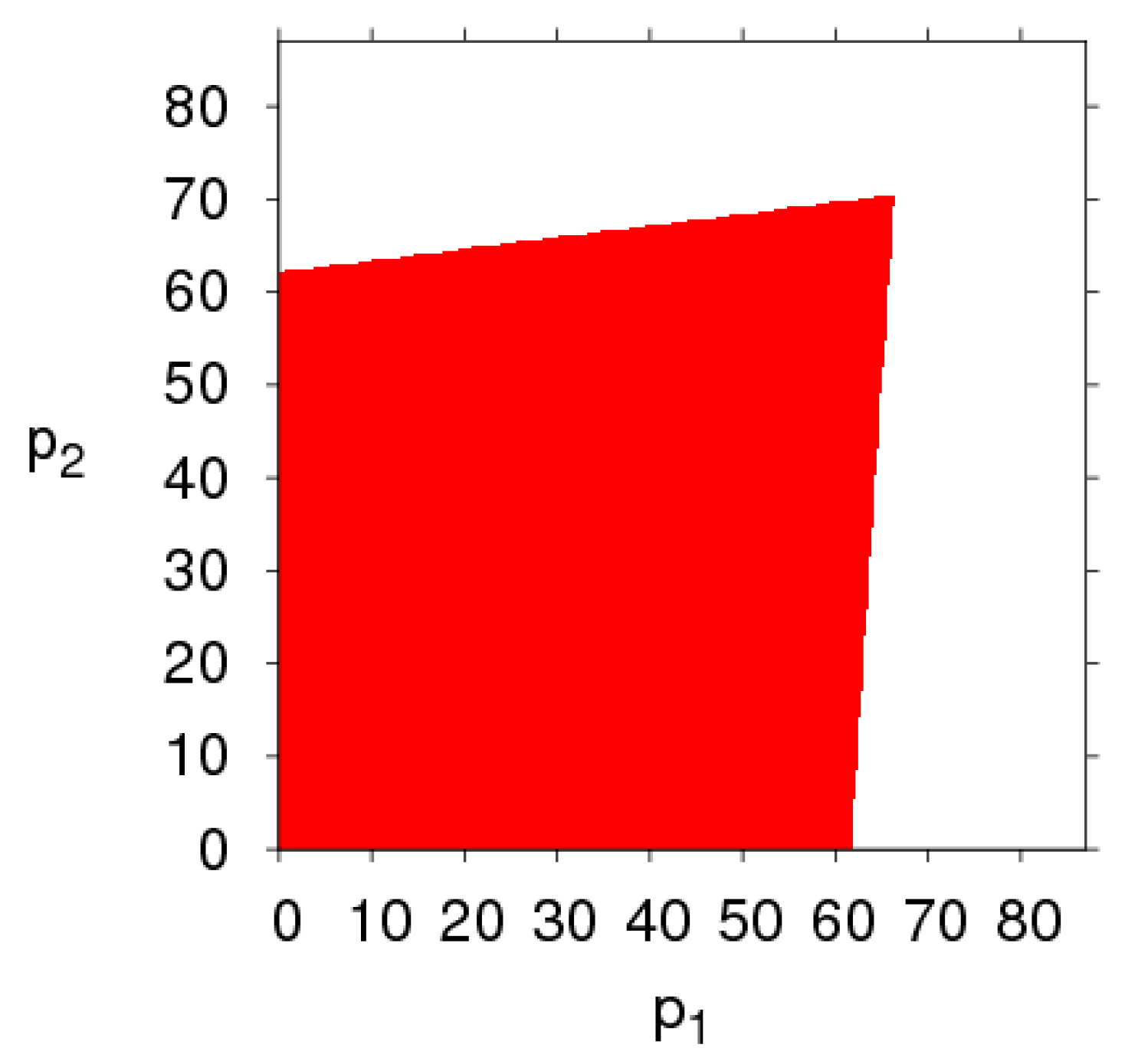
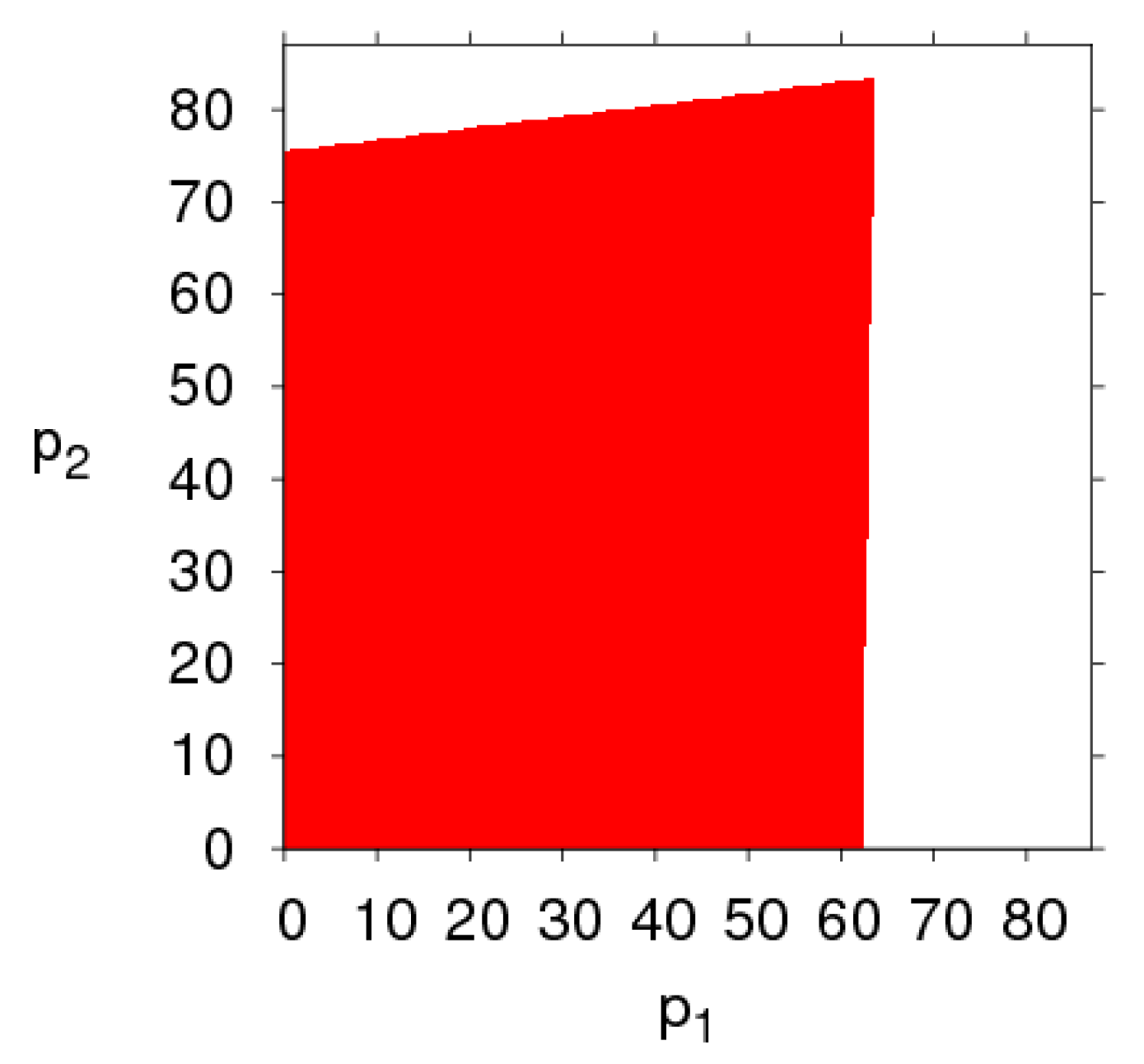
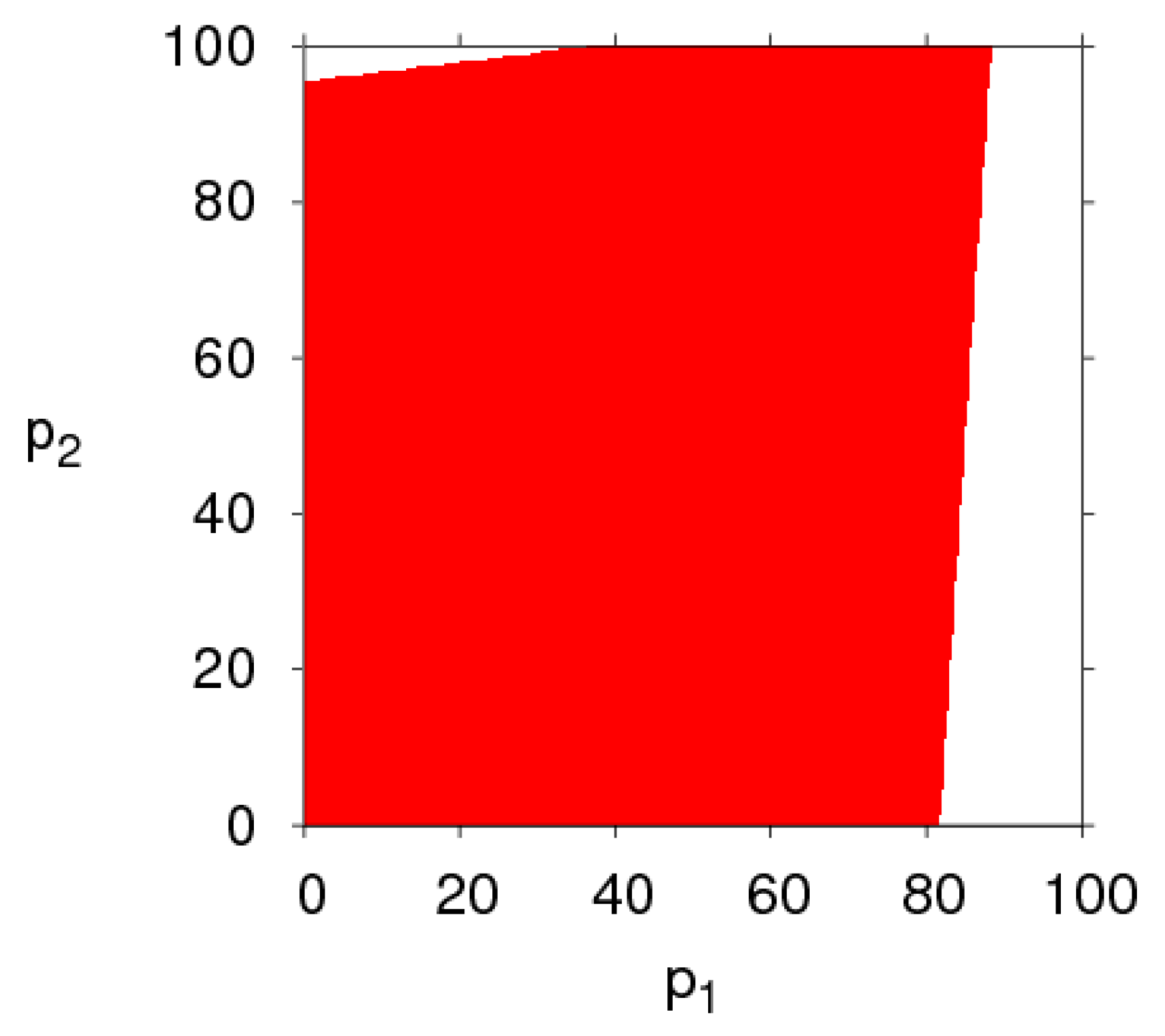
3.2. The Stable Region of the Dynamic System (6) for Parameters Changing
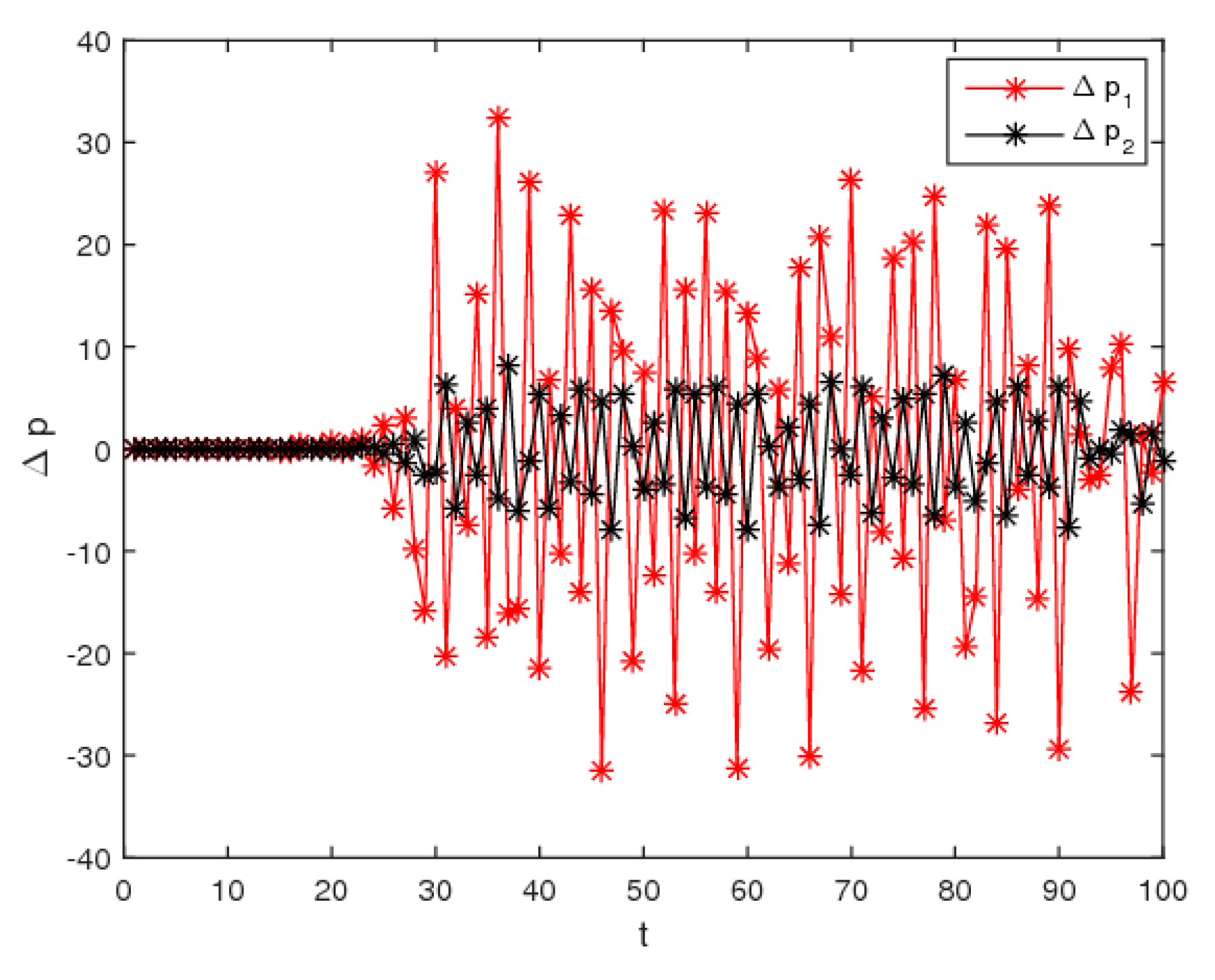
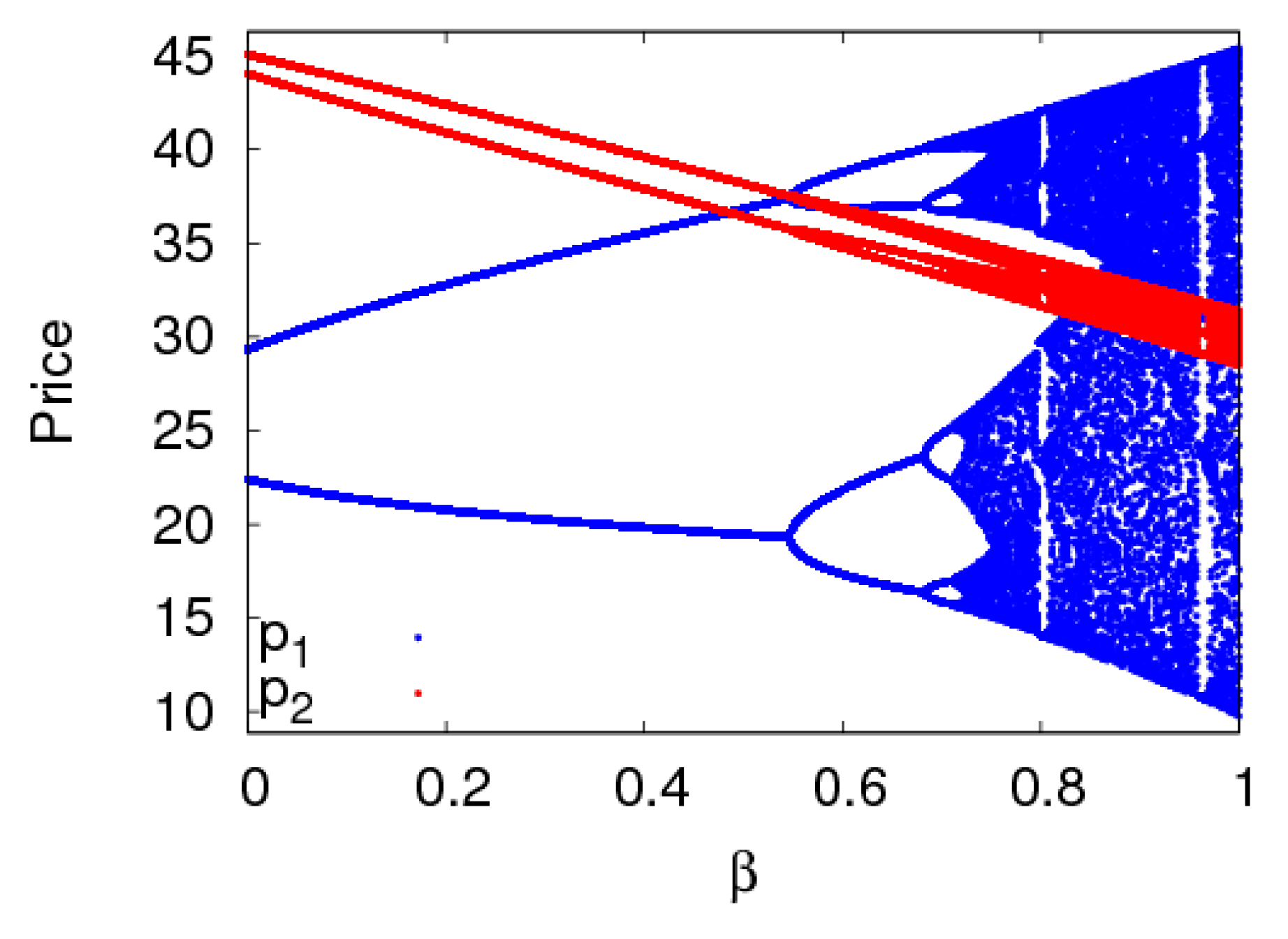
4. The Numerical Simulation of the Dynamic System (6)
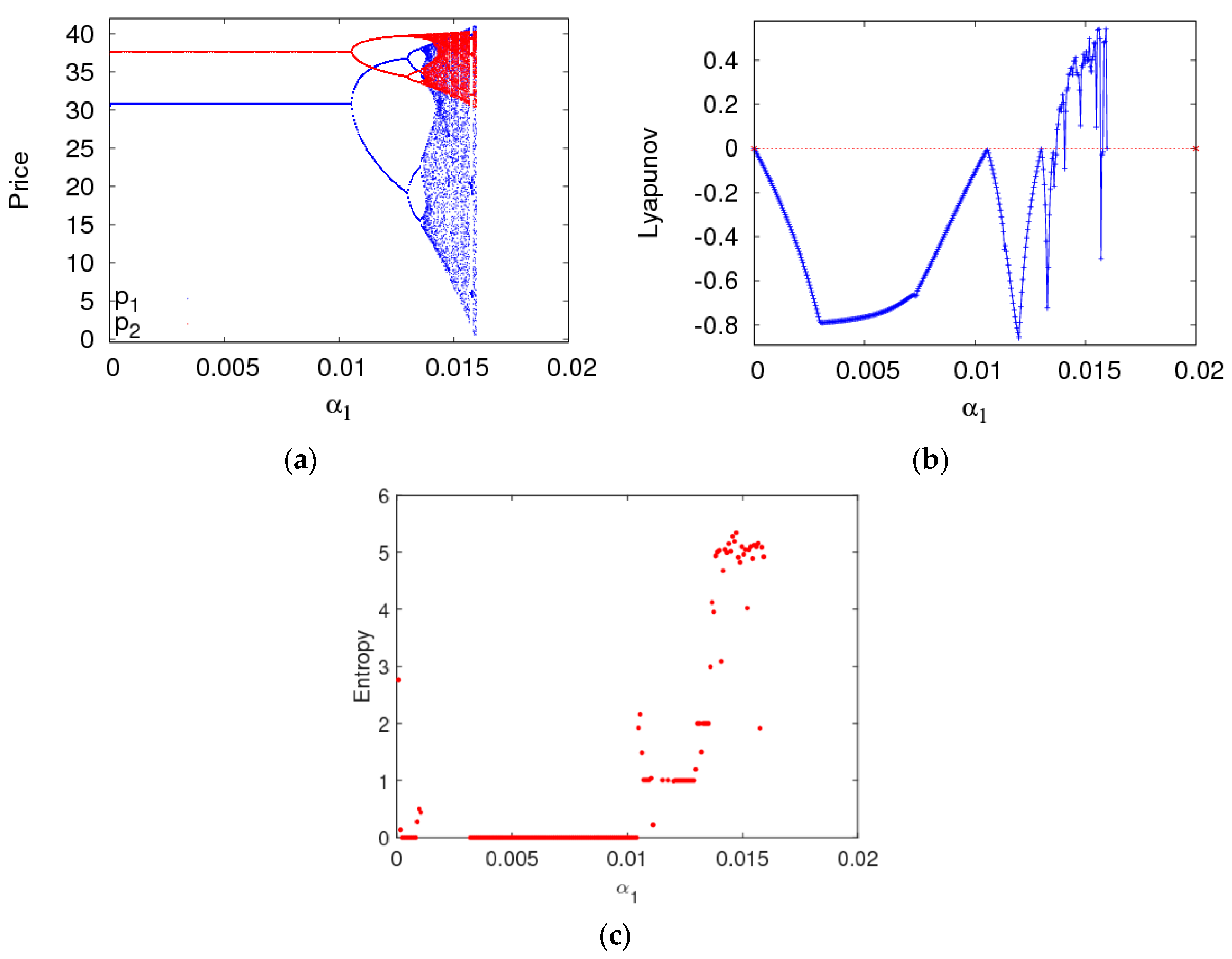
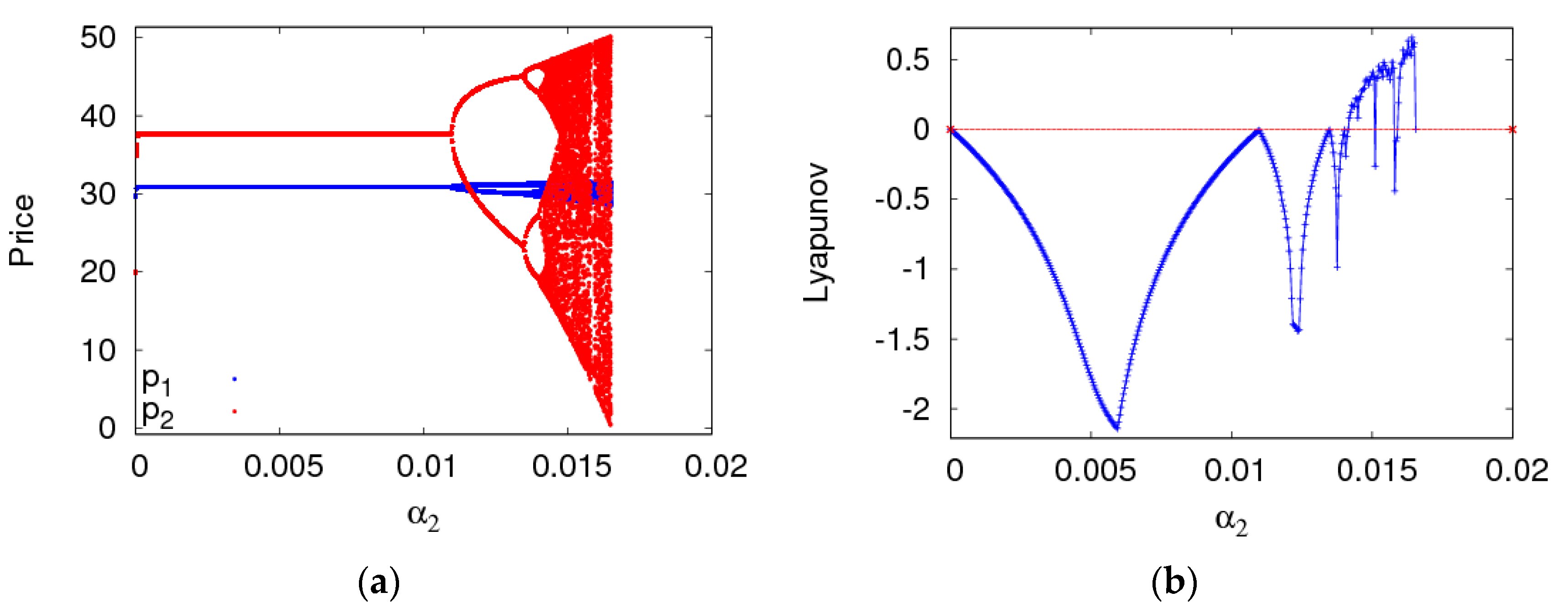
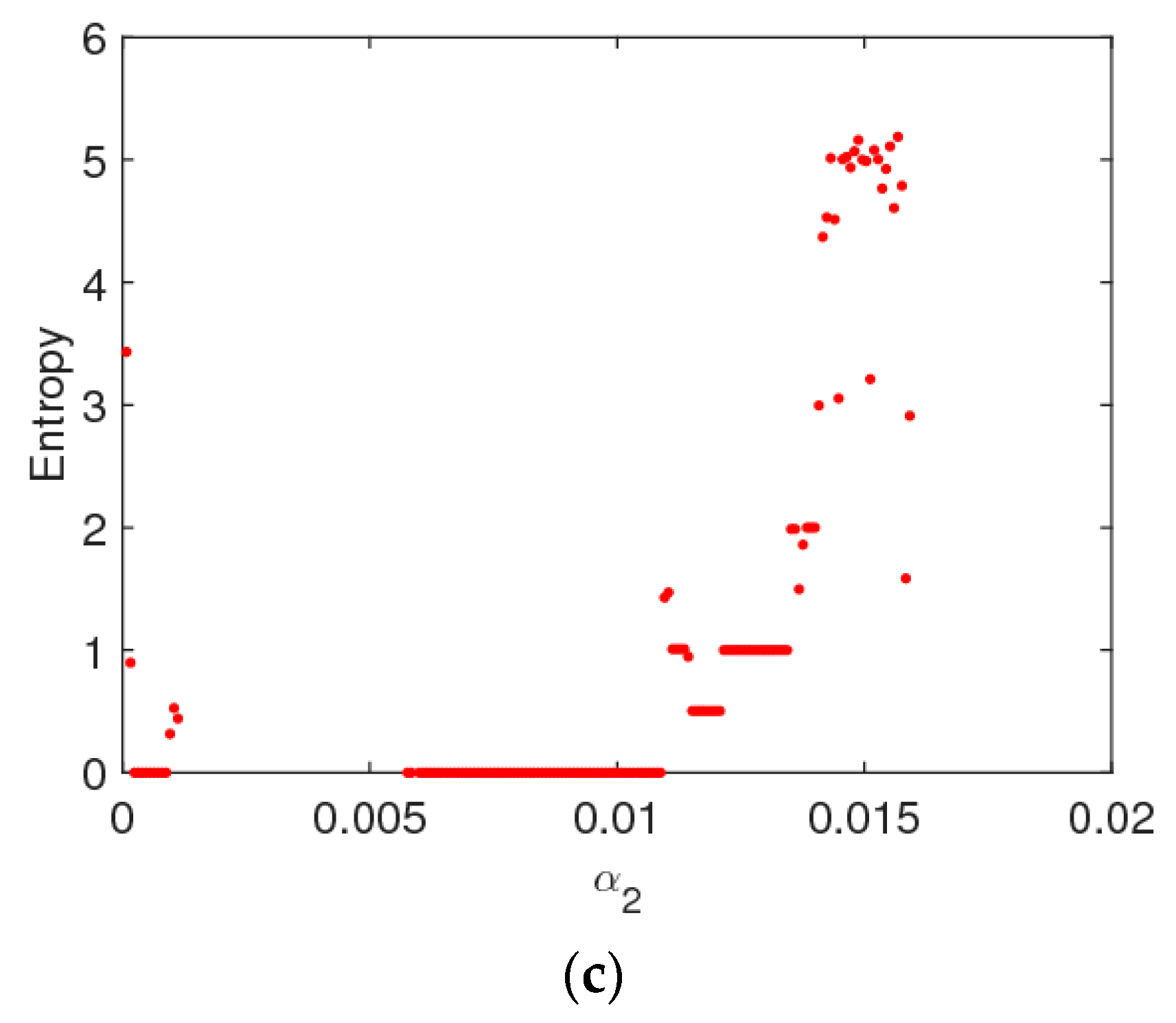
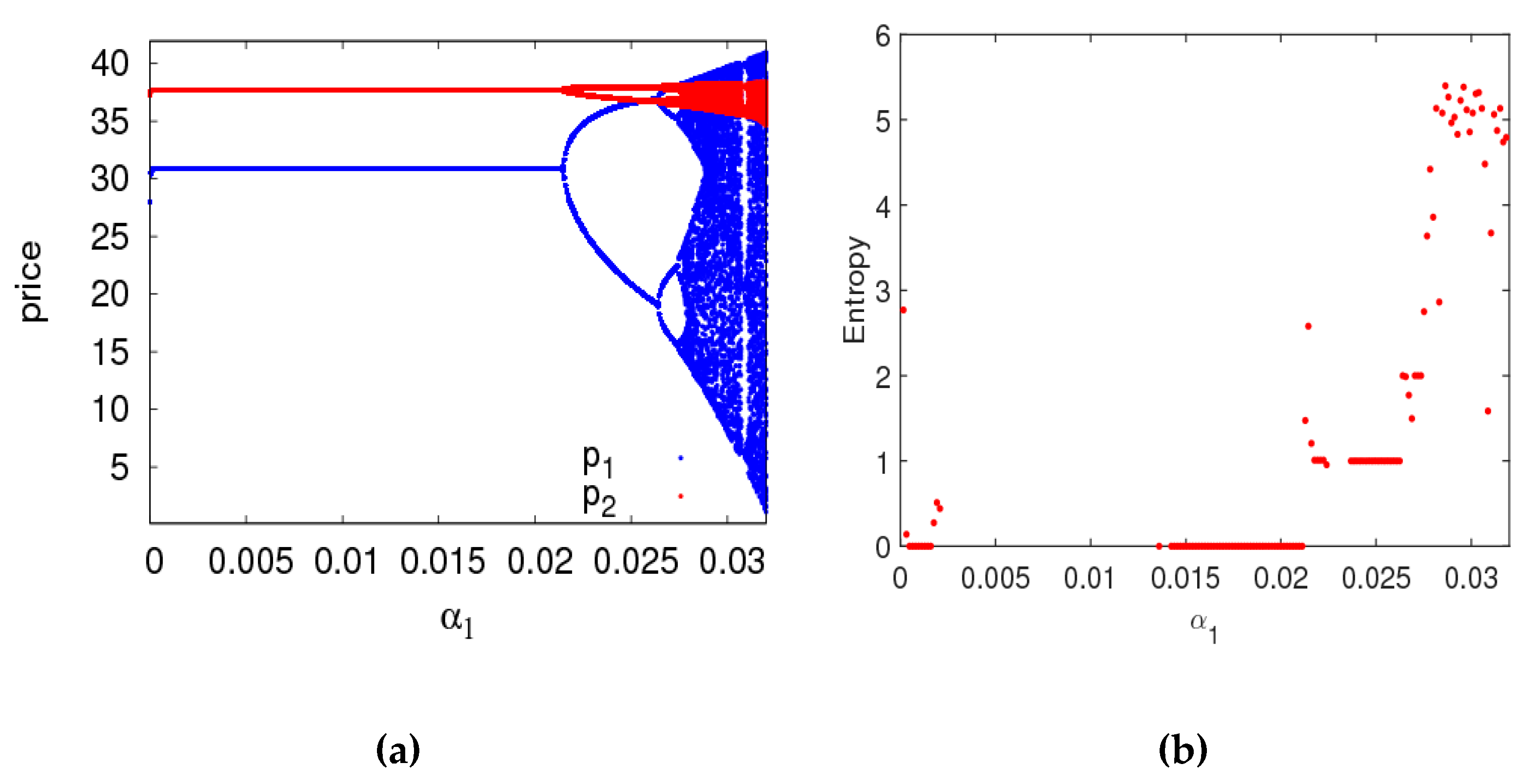
4.1. The Complexity Entropy Analysis of the Dynamic System (6) with the Price Adjustment Speed
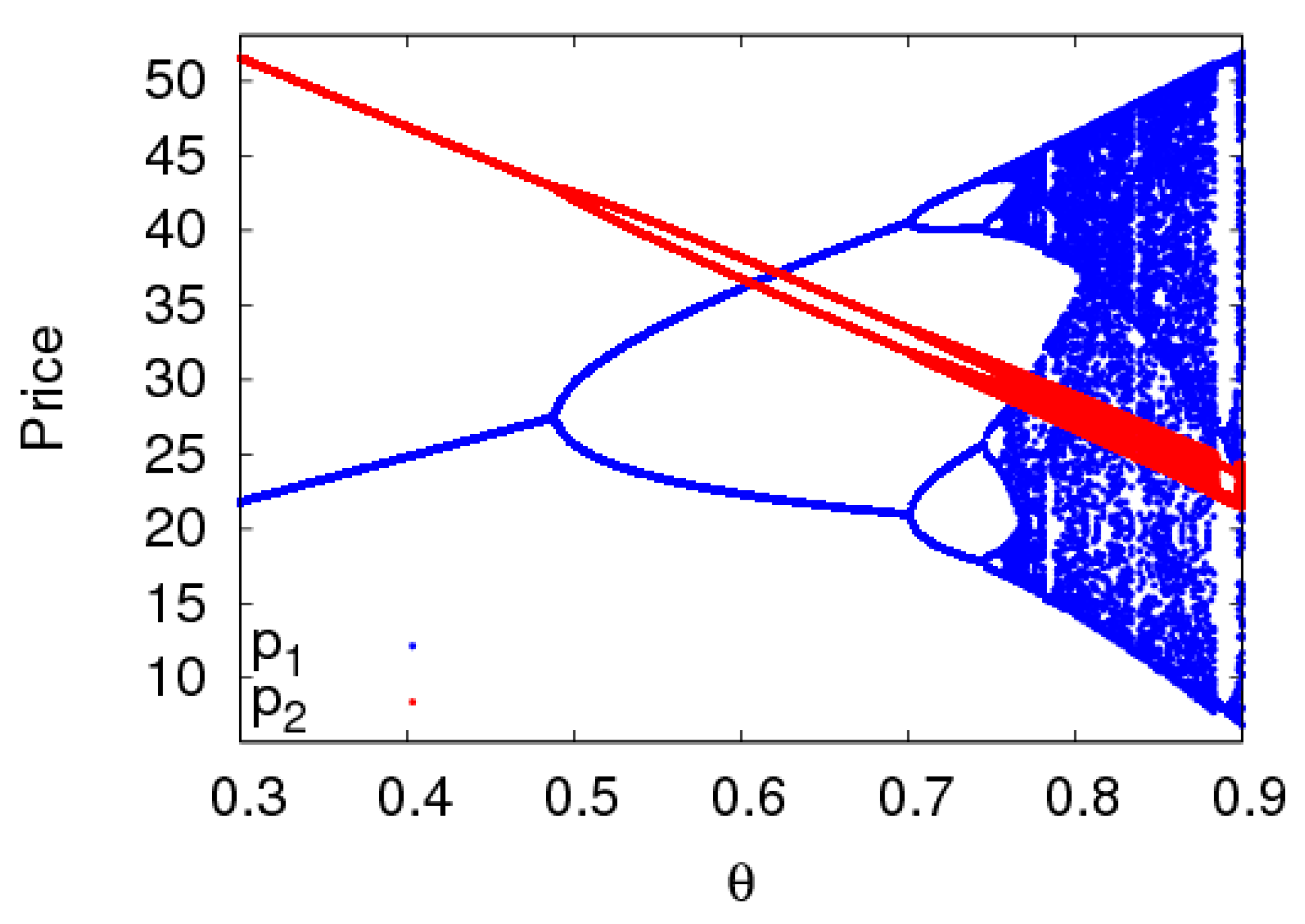
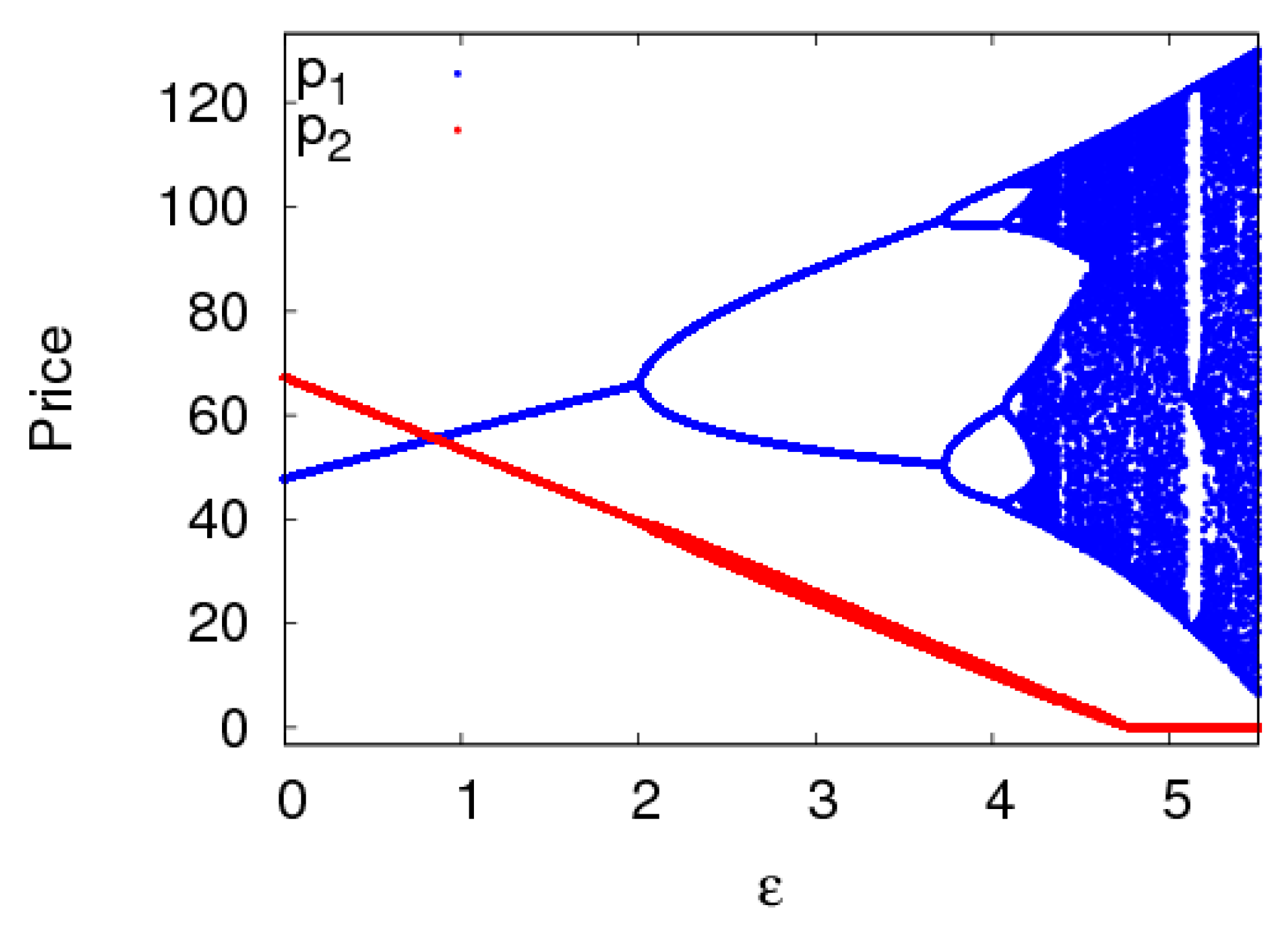
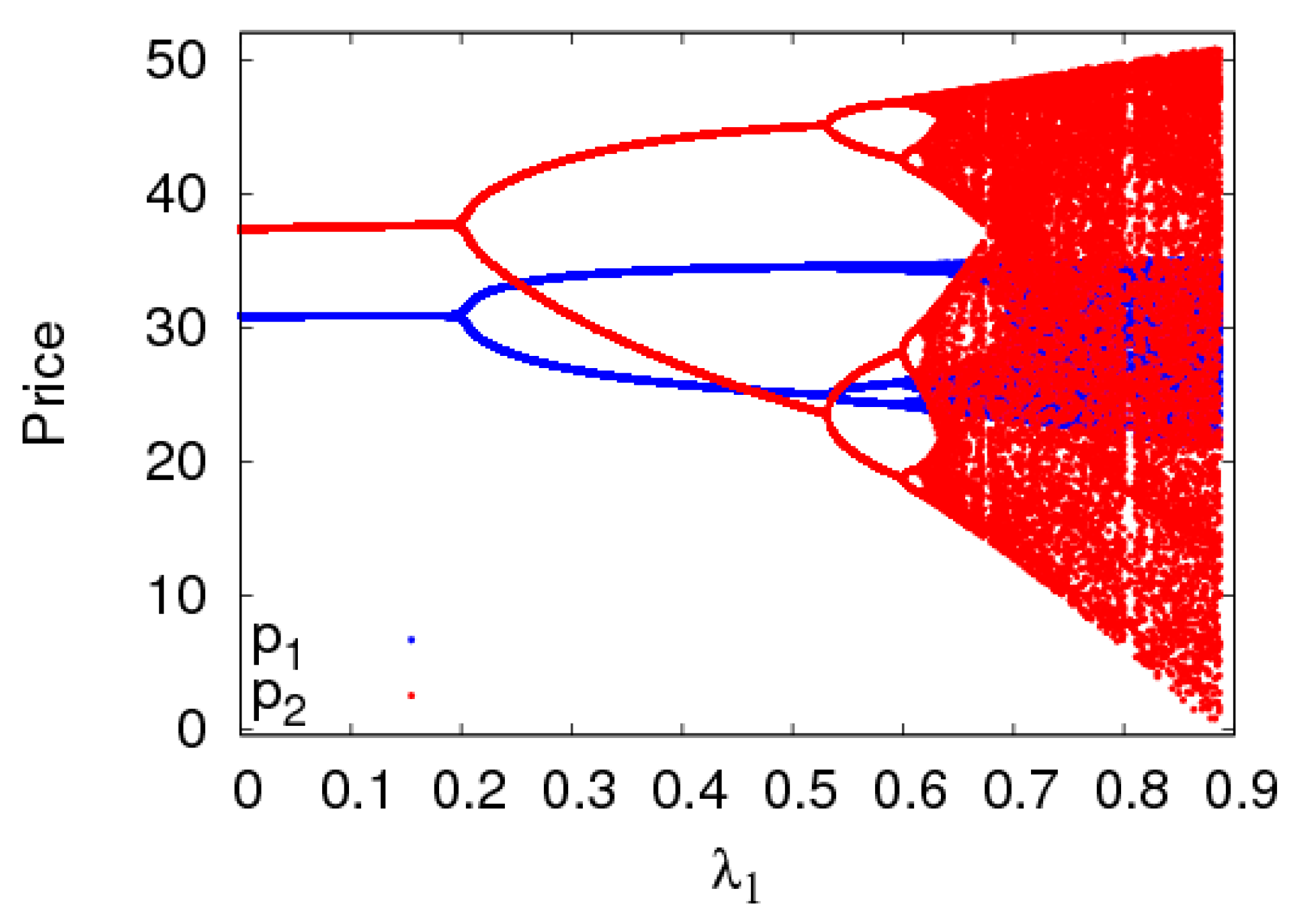
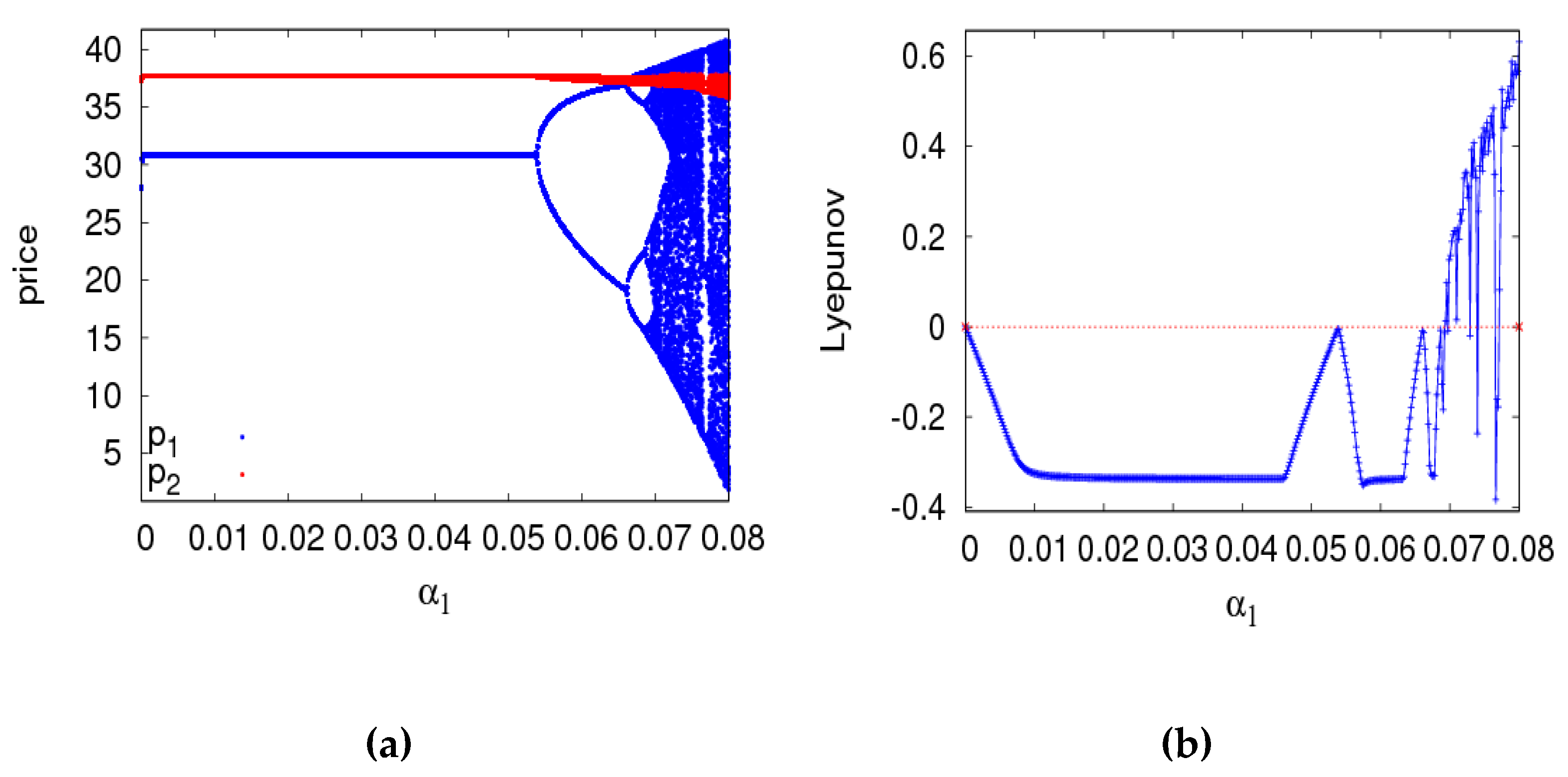
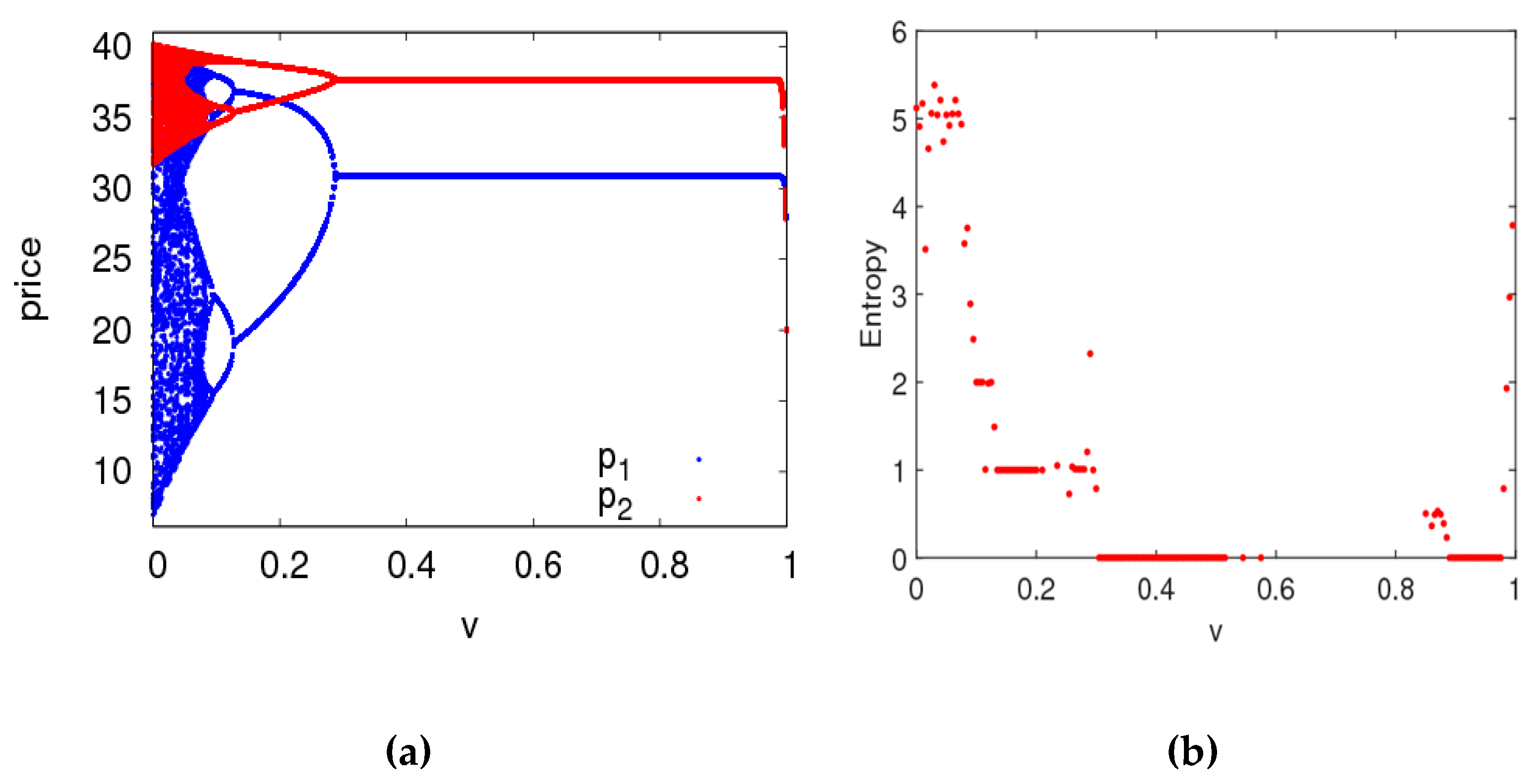
4.2. The Dynamic Characteristics of the Dynamic System (6) with Parameters Changing
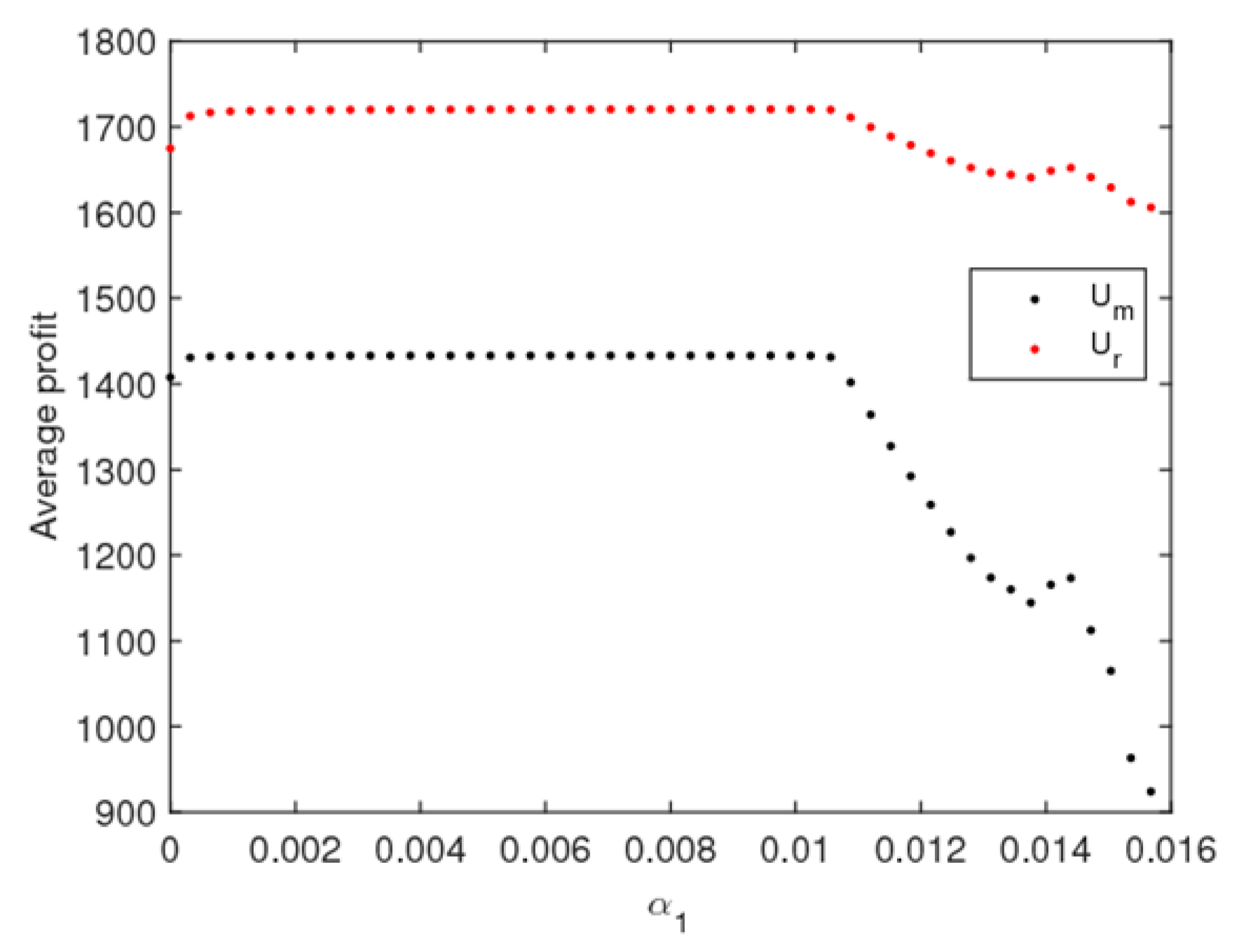
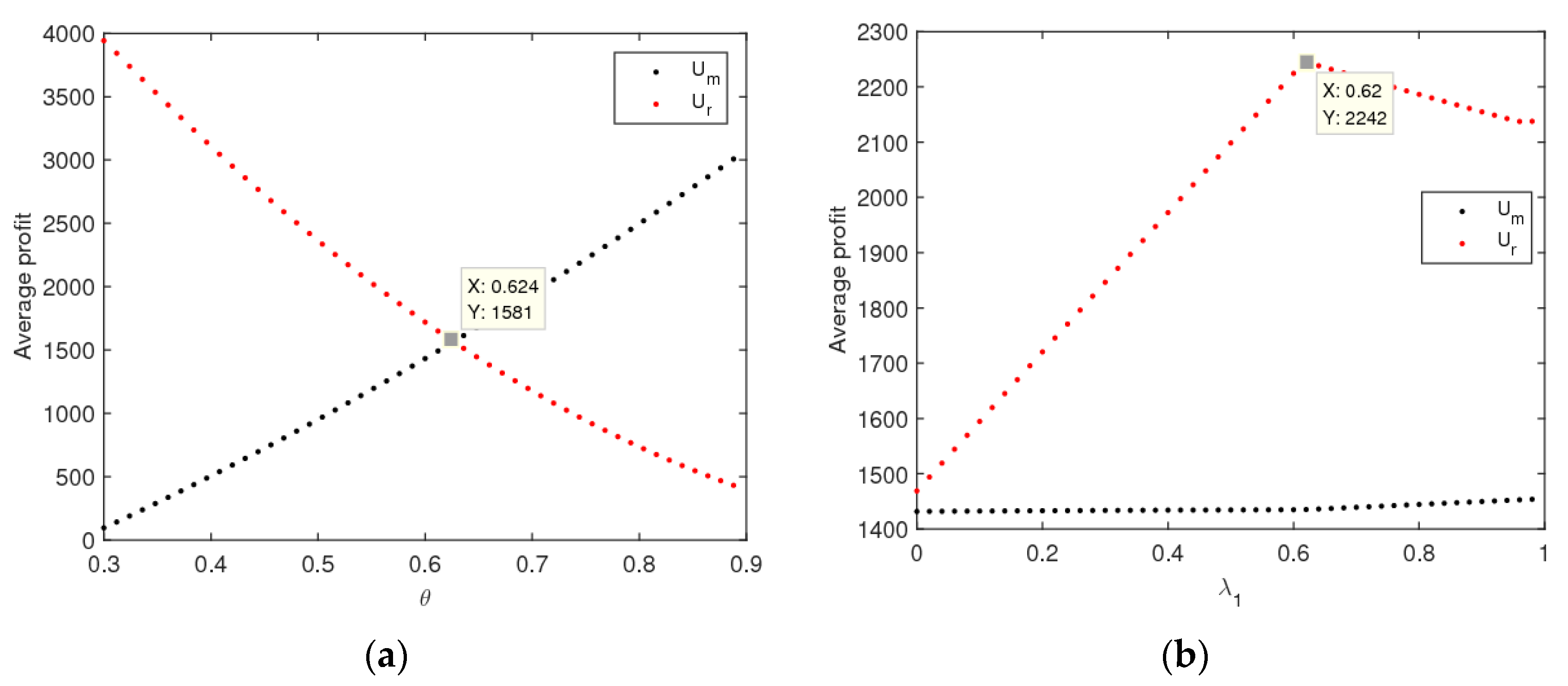
4.3. The Effect of Price Adjustment Speed on the Utilities of the Dynamic System (6)
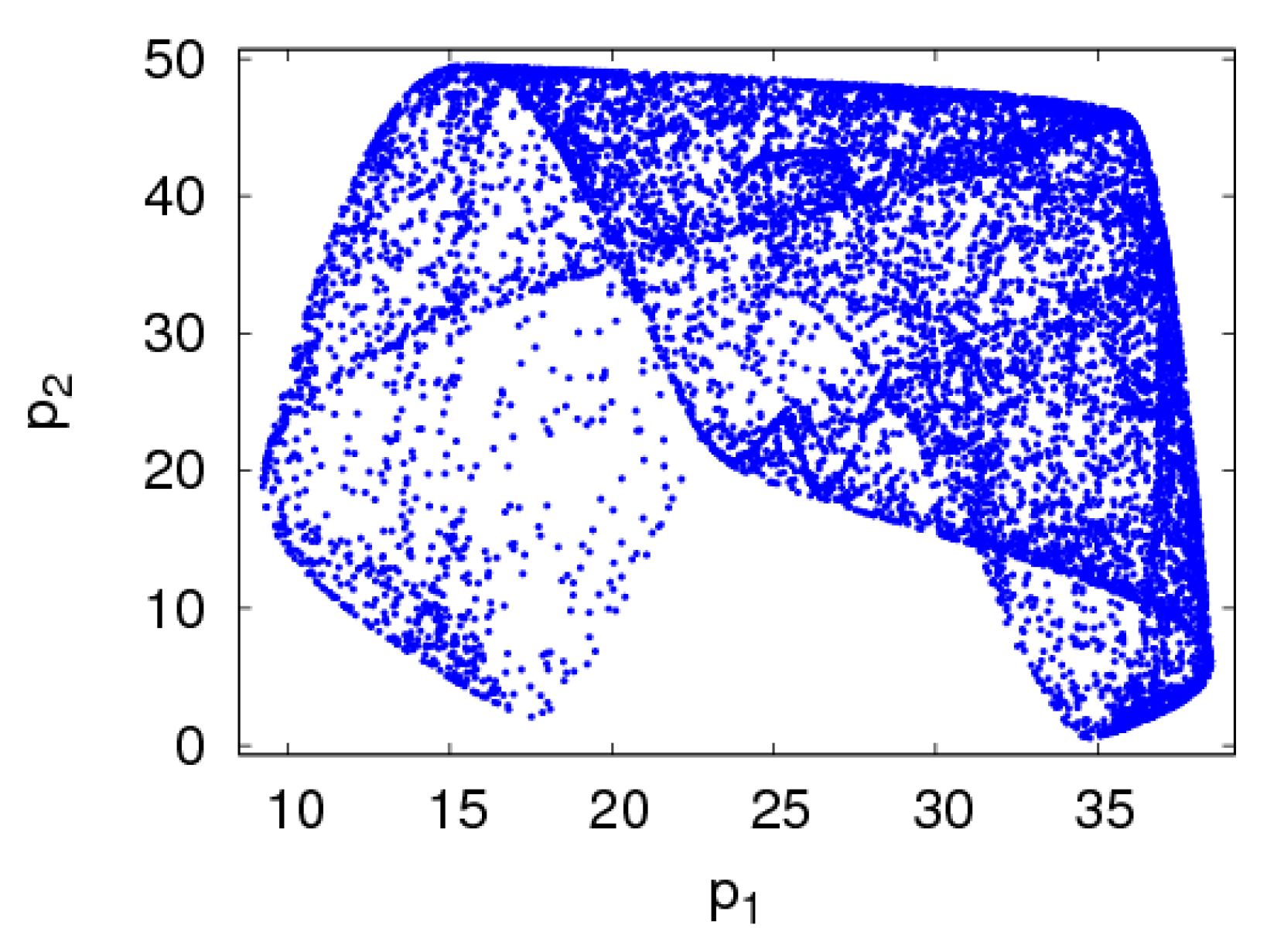
5. Global Stability of the Dynamic System (6)
6. Chaos Control
7. Conclusions
- (1)
- The fairness concern of the manufacturer has little effect on the stability region of the system, while that of the retailer reduces the stability region of the system. The CER of the manufacturer can shrink the system’s stability region, increasing customers’ preference for the direct channel can reduce the price adjustment stable range of the direct channel and expand that of the traditional channel. The manufacturer and retailer should pay attention to the size of CER and fairness concern level in order to keep the system in a stable state.
- (2)
- The system will enter a chaotic state through flip bifurcation with the increase of the price adjustment speed. In a chaotic state, the average utilities of the manufacturer and retailer all decline, while that of the retailer declines even more. In a stable state, the manufacturer should improve the customers’ preference for the direct channel and the retailer should choose the appropriate fairness concern level to achieve the maximum utility. Selecting appropriate control parameters, the system can return to a stable state from chaos using the state feedback control method.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cicconi, P.; Landi, D.; Germani, M.; Russo, A.C. A support approach for the conceptual design of energy efficient cooker hoods. Appl. Energy 2017, 206, 222–239. [Google Scholar] [CrossRef]
- Brandenburg, M. Low carbon supply chain configuration for a new product-a goal programming approach. Int. J. Prod. Res. 2015, 53, 1–23. [Google Scholar] [CrossRef]
- Hariga, M.; As’Ad, R.; Shamayleh, A. Integrated economic and environmental models for a multi stage cold supply chain under carbon tax regulation. J. Clean. Prod. 2017, 166, 1357–1371. [Google Scholar] [CrossRef]
- Li, H.; Wang, C.; Shang, M.; Ou, W. Pricing, Carbon Emission Reduction, Low-Carbon Promotion and Returning Decision in a Closed-Loop Supply Chain under Vertical and Horizontal Cooperation. Int. J. Environ. Res. Public Health 2017, 14, 1332. [Google Scholar] [CrossRef] [PubMed]
- Xia, L.; Guo, T.; Qin, J.; Yue, X.H.; Zhu, N. Carbon emission reduction and pricing policies of a supply chain considering reciprocal preferences in cap-and-trade system. Ann. Oper. Res. 2018, 268, 149–175. [Google Scholar] [CrossRef]
- Zhang, L.; Xue, B.; Liu, X. Carbon Emission Reduction with Regard to Retailer’s Fairness Concern and Subsidies. Sustainability 2018, 10, 1209. [Google Scholar] [CrossRef]
- Cicconi, P.; Landi, D.; Germani, M. An Ecodesign approach for the lightweight engineering of cast iron parts. Int. J. Adv. Manuf. Technol. 2018, 99, 2365–2388. [Google Scholar] [CrossRef]
- Ji, S.; Dan, Z.; Peng, X. Joint Decisions on Emission Reduction and Inventory Replenishment with Overconfidence and Low-Carbon Preference. Sustainability 2018, 10, 1119. [Google Scholar]
- Du, S.; Hu, L.; Wang, L. Low-carbon supply policies and supply chain performance with carbon concerned demand. Ann. Oper. Res. 2017, 255, 569–590. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Lei, Y. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Bao, M.J.; Chen, X.H.; Xu, X.H. Co-op advertising and emission reduction cost sharing contracts and coordination in low-carbon supply chain based on fairness concerns. J. Clean. Prod. 2016, 133, 402–413. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Ye, X. Differential game model of joint emission reduction strategies and contract design in a dual-channel supply chain. J. Clean. Prod. 2018, 190, 592–607. [Google Scholar] [CrossRef]
- Rahmani, D.; Mahoodian, V. Strategic and operational supply chain network design to reduce carbon emission considering reliability and robustness. J. Clean. Prod. 2017, 149, 607–620. [Google Scholar] [CrossRef]
- Qin, J.J.; Ren, L.G.; Xia, L.J. Carbon Emission Reduction and Pricing Strategies of Supply Chain under Various Demand Forecasting Scenarios. Asia Pac. J. Oper. Rese. 2017, 34, 1740005. [Google Scholar] [CrossRef]
- Li, X.; Shi, D.; Li, Y.J.; Zhen, X.P. Impact of Carbon Regulations on the Supply Chain with Carbon Reduction Effort. IEEE Trans. Syst Man Cybern. Syst. 2019, 49, 1218–1227. [Google Scholar] [CrossRef]
- Zhang, L.H.; Song, X.B.; Zhang, G.W.; Lin, G.L. Adoption and coordination of carbon reduction technology in supply chain based on carbon tax. Comput. Integr. Manuf. Syst. 2017, 23, 883–891. [Google Scholar]
- Tsay, A.A.; Agrawal, N. Channel Dynamics Under Price and Service Competition. Manuf. Serv. Op. Manag. 2000, 2, 372–391. [Google Scholar] [CrossRef]
- Xie, J.P.; Zhang, W.S.; Liang, L.; Xia, Y.; Yin, J.; Yang, G. The revenue and cost sharing contract of pricing and servicing policies in a dual-channel closed-loop supply chain. J. Clean. Prod. 2018, 191, 361–368. [Google Scholar] [CrossRef]
- Zhou, Z.P.; Liu, X.B.; Pei, J.; Pardolos, P.M.; Cheng, H. Competition of pricing and service investment between iot-based and traditional manufacturers. J. Ind. Manag. Optim. 2018, 14, 1203–1218. [Google Scholar] [CrossRef]
- Ma, J.H.; Li, T.; Ren, W.B. Research on the Complexity of Dual-Channel Supply Chain Model in Competitive Retailing Service Market. Int. J. Bifurc. Chaos 2017, 27. [Google Scholar] [CrossRef]
- Jafar, S.S.; Hashem, A.; Ramin, S.; Sahebi, H. Retailer Stackelberg game in a supply chain with pricing and service decisions and simple price discount contract. PLoS ONE. 2018, 13, e0195109. [Google Scholar]
- Zhou, Y.W.; Guo, J.S.; Zhou, W.H. Pricing/service strategies for a dual-channel supply chain with free riding and service-cost sharing. Int. J. Prod. Econ. 2018, 196, 198–210. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, C. Dynamic pricing strategy and coordination in a dual-channel supply chain considering service value. Appl. Math. Model. 2018, 54, 722–742. [Google Scholar] [CrossRef]
- Dan, B.; Zhang, S.G.; Zhou, M. Strategies for warranty service in a dual-channel supply chain with value-added service competition. Int. J. Prod. Res. 2017, 56, 5677–5699. [Google Scholar] [CrossRef]
- Huang, Y.M.; Li, Q.X.; Zhang, Y.M. The Complexity Analysis for Price Game Model of Risk-Averse Supply Chain Considering Fairness Concern. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Li, Q.X.; Zhang, Y.H.; Huang, Y. The Complexity Analysis in Dual-Channel Supply Chain Based on Fairness Concern and Different Business Objectives. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Li, Q.Q.; Xiao, T.J.; Qiu, Y.Z. Price and carbon emission reduction decisions and revenue-sharing contract considering fairness concerns. J. Clean. Prod. 2018, 190, 303–314. [Google Scholar] [CrossRef]
- Ma, P.; Li, K.W.; Wang, Z.J. Pricing decisions in closed-loop supply chains with marketing effort and fairness concerns. Int. J. Prod. Res. 2017, 55, 6710–6731. [Google Scholar] [CrossRef]
- Chen, J.X.; Zhou, Y.W.; Zhong, Y. A pricing/ordering model for a dyadic supply chain with buyback guarantee financing and fairness concerns. Int. J. Prod. Res. 2017, 55, 5287–5304. [Google Scholar] [CrossRef]
- Li, Q.H.; Li, B. Dual-Channel Supply Chain Equilibrium Problems Regarding Retail Services and Fairness Concerns. Appl. Math. Model. 2016, 40, 7349–7367. [Google Scholar] [CrossRef]
- Niu, B.Z.; Cui, Q.Q.; Zhang, J. Impact of channel power and fairness concern on supplier’s market entry decision. J. Oper. Res. Soc. 2017, 68, 1570–1581. [Google Scholar] [CrossRef]
- Liu, Z.; Zheng, X.X.; Gong, B.G. Joint Decision-Making and the Coordination of a Sustainable Supply Chain in the Context of Carbon Tax Regulation and Fairness Concerns. Int. J. Environ. Res. Public Health 2017, 14, 1464. [Google Scholar] [CrossRef] [PubMed]
- Du, B.S.; Liu, Q.; Li, G.P. Coordinating Leader-Follower Supply Chain with Sustainable Green Technology Innovation on Their Fairness Concerns. Int. J. Environ. Res. Public Health 2017, 14, 1357. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Hou, P.W.; Li, Q.H. Cooperative advertising in a dual-channel supply chain with a fairness concern of the manufacturer. IMA J. Manag. Math. 2017, 28, 259–277. [Google Scholar] [CrossRef]
- Liang, G.B.; Qin, Y.H. The game model of fuzzy fairness concern for supplier and retailer. J. Interdiscip. Math. 2017, 20, 1537–1542. [Google Scholar] [CrossRef]
- Puu, T. The chaotic duopolists revisited. J. Econ. Behav. Org. 2004, 33, 385–394. [Google Scholar] [CrossRef]
- Lou, W.D.; Ma, J.H. Complexity of sales effort and carbon emission reduction effort in a two-parallel household appliance supply chain model. Appl. Math. Model. 2018, 64, 398–425. [Google Scholar] [CrossRef]
- Wu, F.; Ma, J.H. The equilibrium, complexity analysis and control in epiphytic supply chain with product horizontal diversification. Nonlinear Dyn. 2018, 93, 2145–2158. [Google Scholar] [CrossRef]
- Huang, Y.M.; Li, Q.X. The Entropy Complexity of an Asymmetric Dual-Channel Supply Chain with Probabilistic Selling. Entropy 2018, 20, 543. [Google Scholar] [CrossRef]
- Ma, J.H.; Wang, H.W. Complexity analysis of dynamic noncooperative game models for closed-loop supply chain with product recovery. Appl. Math. Model. 2014, 38, 5562–5572. [Google Scholar] [CrossRef]
- Li, Q.X.; Ma, J.H. Research on price Stackelberg game model with probabilistic selling based on complex system theory. Commun. Nonlinear Sci. Numer. Simul. 2016, 30, 387–400. [Google Scholar] [CrossRef]
- Huang, Y.M.; Liu, L.; Qi, E.S. The dynamic decision in risk-averse complementary product manufacturers with corporate social responsibility. Kybernetes 2016, 45, 244–265. [Google Scholar] [CrossRef]
- Matouk, A.E.; Elsadany, A.A.; Xin, B. Neimark–Sacker bifurcation analysis and complex nonlinear dynamics in a heterogeneous quadropoly game with an isoelastic demand function. Nonlinear Dyn. 2017, 89, 2533–2552. [Google Scholar] [CrossRef]
- Du, S.; Du, C.; Liang, L. Supply chain coordination considering fairness concerns. J. Manag. Sci. 2010, 13, 41–48. [Google Scholar]
- Cui, T.H.; Raju, J.S.; Zhang, Z.J. Fairness and Channel Coordination. Manag. Sci. 2007, 53, 1303–1314. [Google Scholar]
- Du, J.G.; Huang, T.W.; Sheng, Z.H. Analysis of decision-making in economic chaos control. Nonlinear Anal. Real World Appl. 2009, 10, 2493–2501. [Google Scholar] [CrossRef]
- Holyst, J.A.; Urbanowicz, K. Chaos control in economical model by time-delayed feedback method. Phys. A Stat. Mech. Appl. 2000, 287, 587–598. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Chen, X.; Huang, Y. The Stability and Complexity Analysis of a Low-Carbon Supply Chain Considering Fairness Concern Behavior and Sales Service. Int. J. Environ. Res. Public Health 2019, 16, 2711. https://doi.org/10.3390/ijerph16152711
Li Q, Chen X, Huang Y. The Stability and Complexity Analysis of a Low-Carbon Supply Chain Considering Fairness Concern Behavior and Sales Service. International Journal of Environmental Research and Public Health. 2019; 16(15):2711. https://doi.org/10.3390/ijerph16152711
Chicago/Turabian StyleLi, Qiuxiang, Xingli Chen, and Yimin Huang. 2019. "The Stability and Complexity Analysis of a Low-Carbon Supply Chain Considering Fairness Concern Behavior and Sales Service" International Journal of Environmental Research and Public Health 16, no. 15: 2711. https://doi.org/10.3390/ijerph16152711
APA StyleLi, Q., Chen, X., & Huang, Y. (2019). The Stability and Complexity Analysis of a Low-Carbon Supply Chain Considering Fairness Concern Behavior and Sales Service. International Journal of Environmental Research and Public Health, 16(15), 2711. https://doi.org/10.3390/ijerph16152711



