Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis
Abstract
:1. Introduction
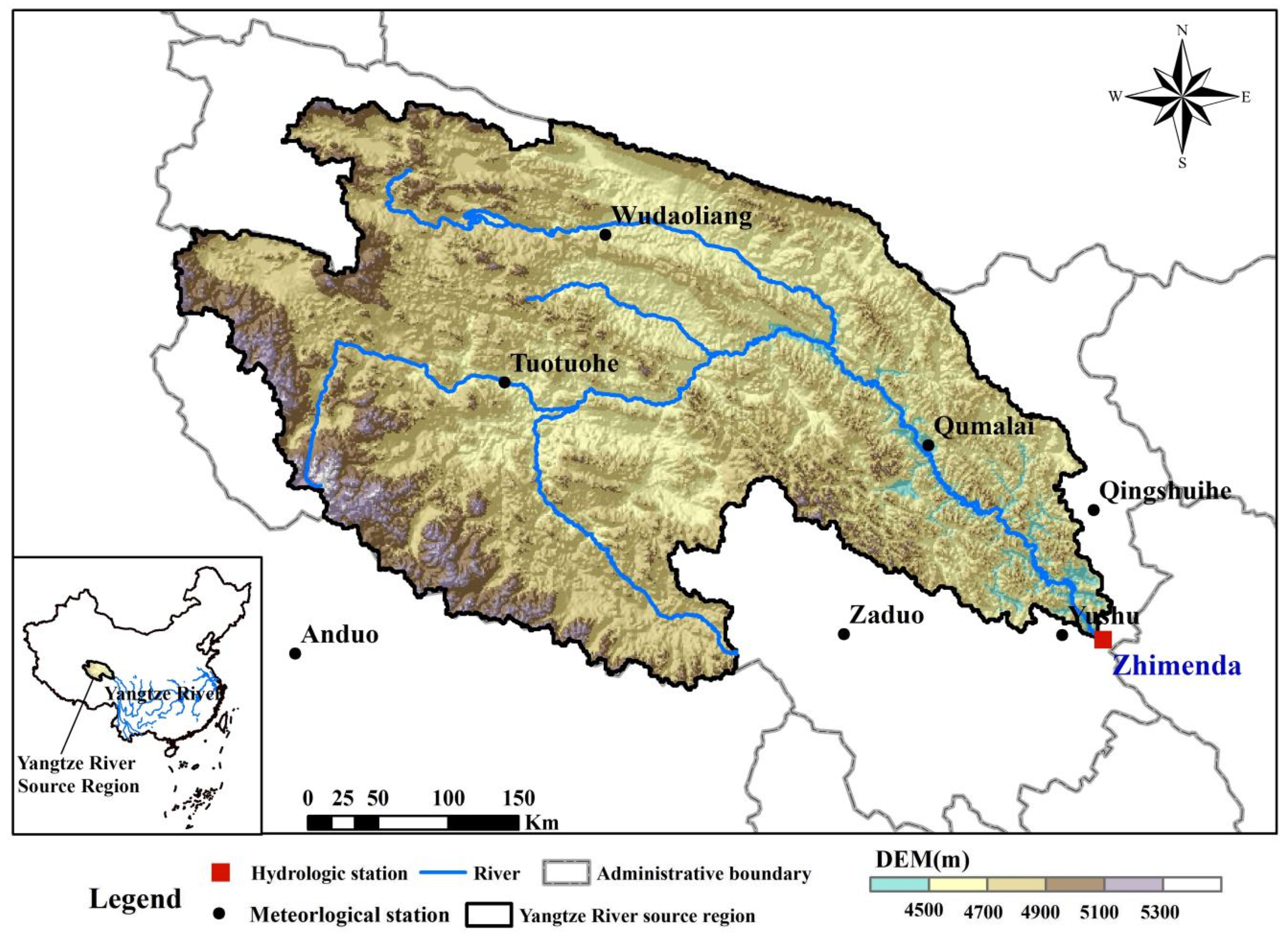
2. Study Area and Data
2.1. Study Area
2.2. Data
3. Methodologies
3.1. Trend Test and Change Point Detection
3.1.1. Non-Parametric Mann-Kendall Trend Analysis
3.1.2. Change Point Analysis Methods
3.2. Runoff Change Attribution Identification
3.2.1. Water Balance Model Based on Choudhury-Yang Equation
3.2.2. Elasticity Coefficient
3.2.3. Quantification of Contributions of Climatic Variables and Underlying Surface Changes to Runoff Change
4. Results
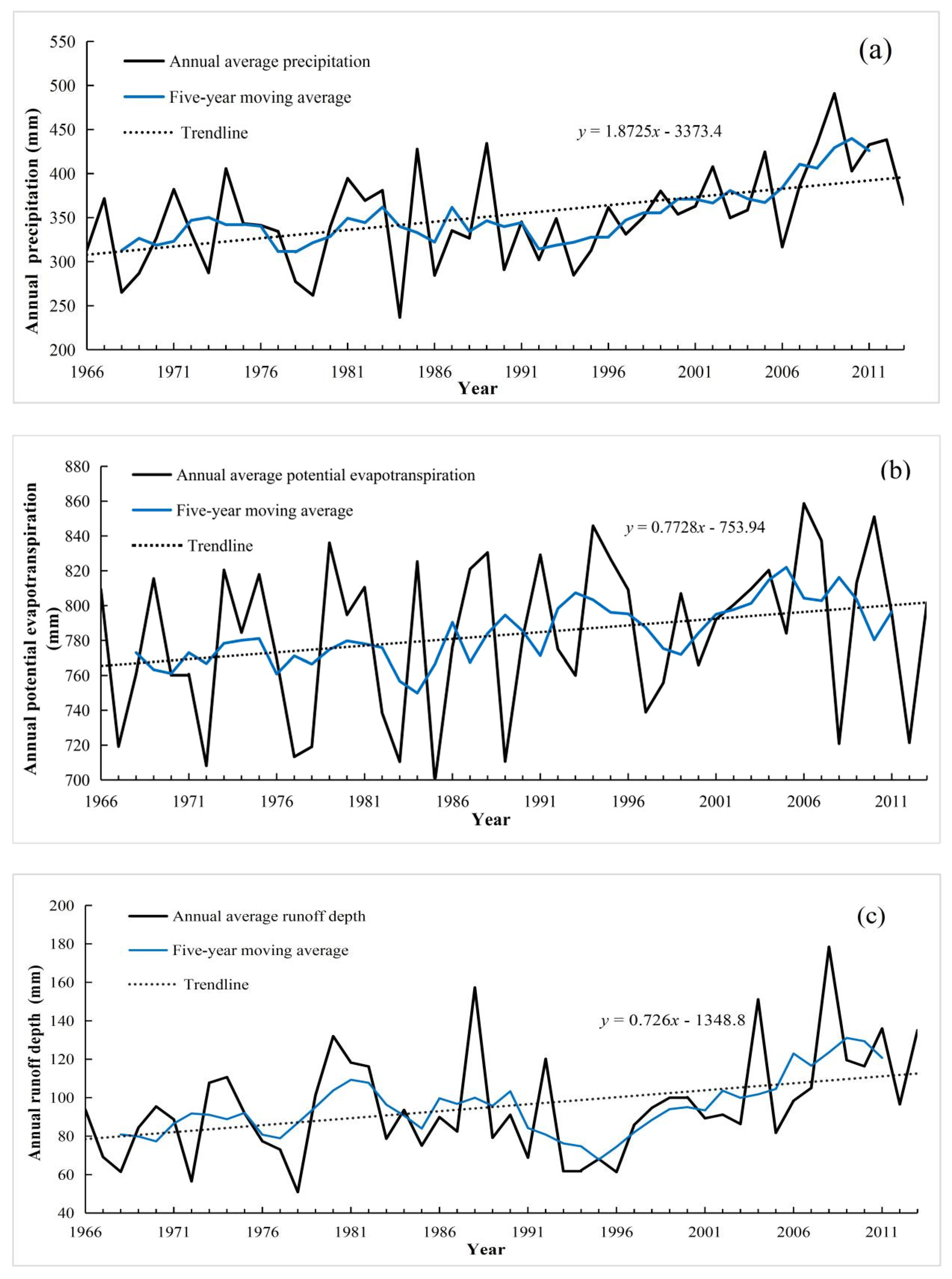
4.1. Trend Analysis of Hydrometeorological Variables
4.2. Attribution of Runoff Variation
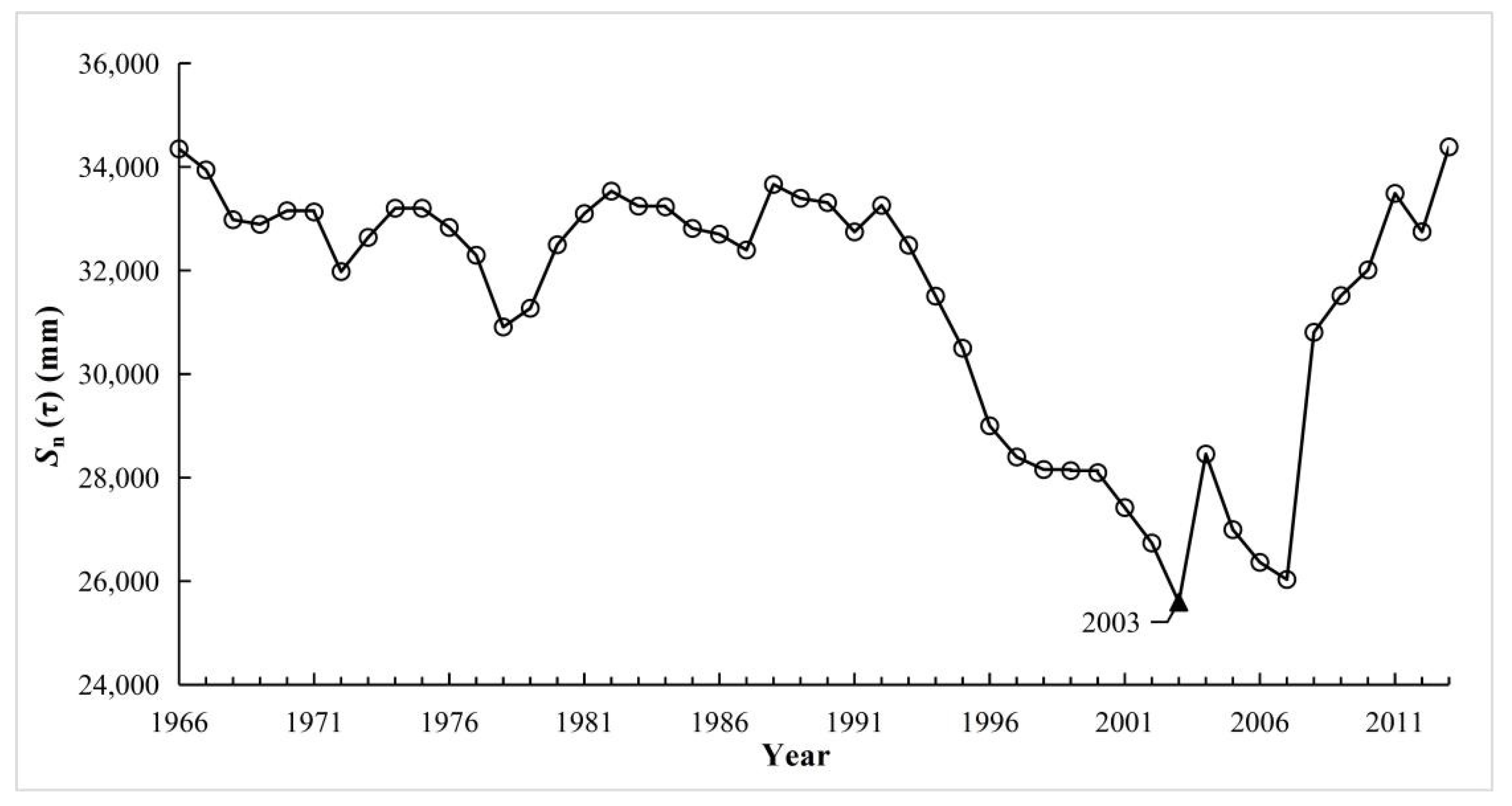
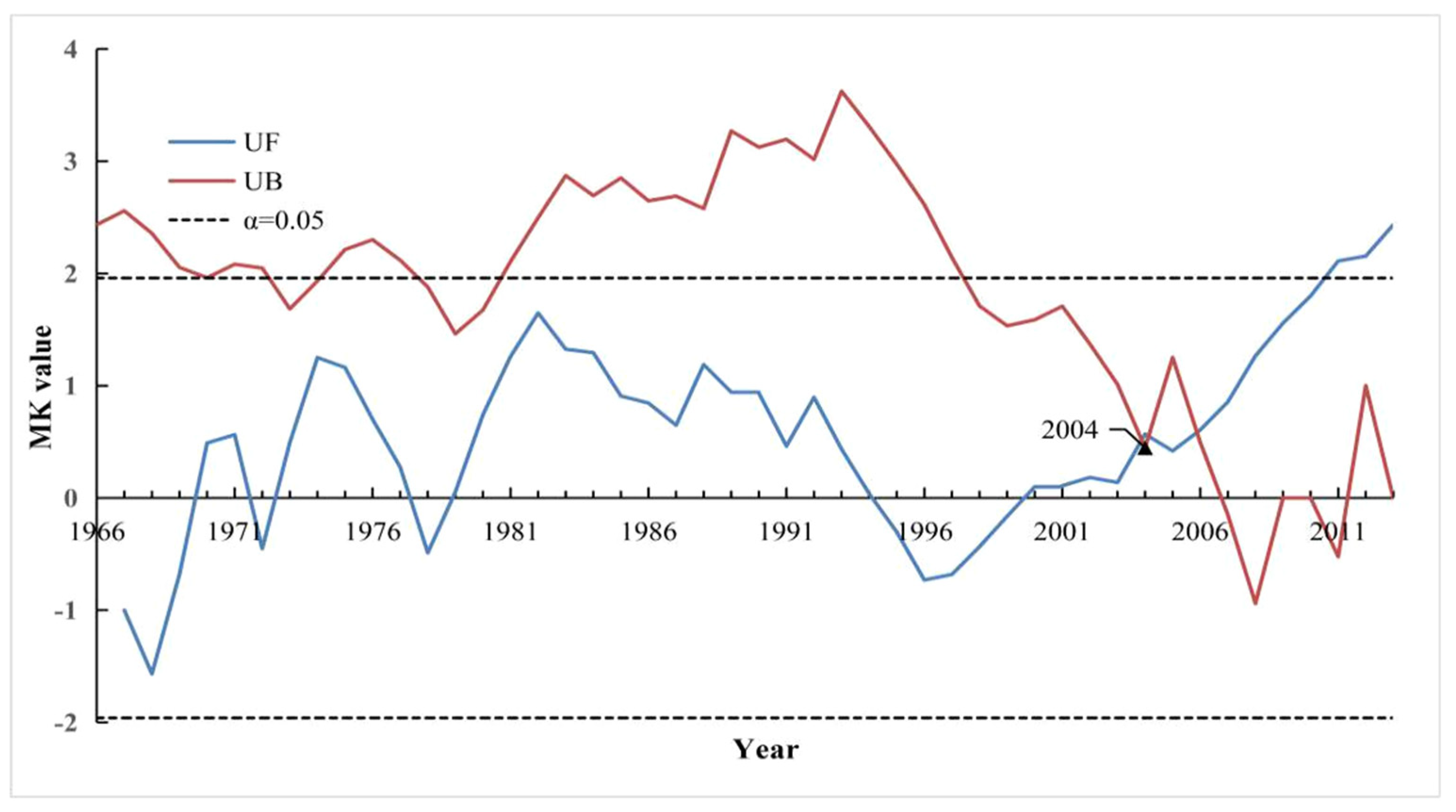
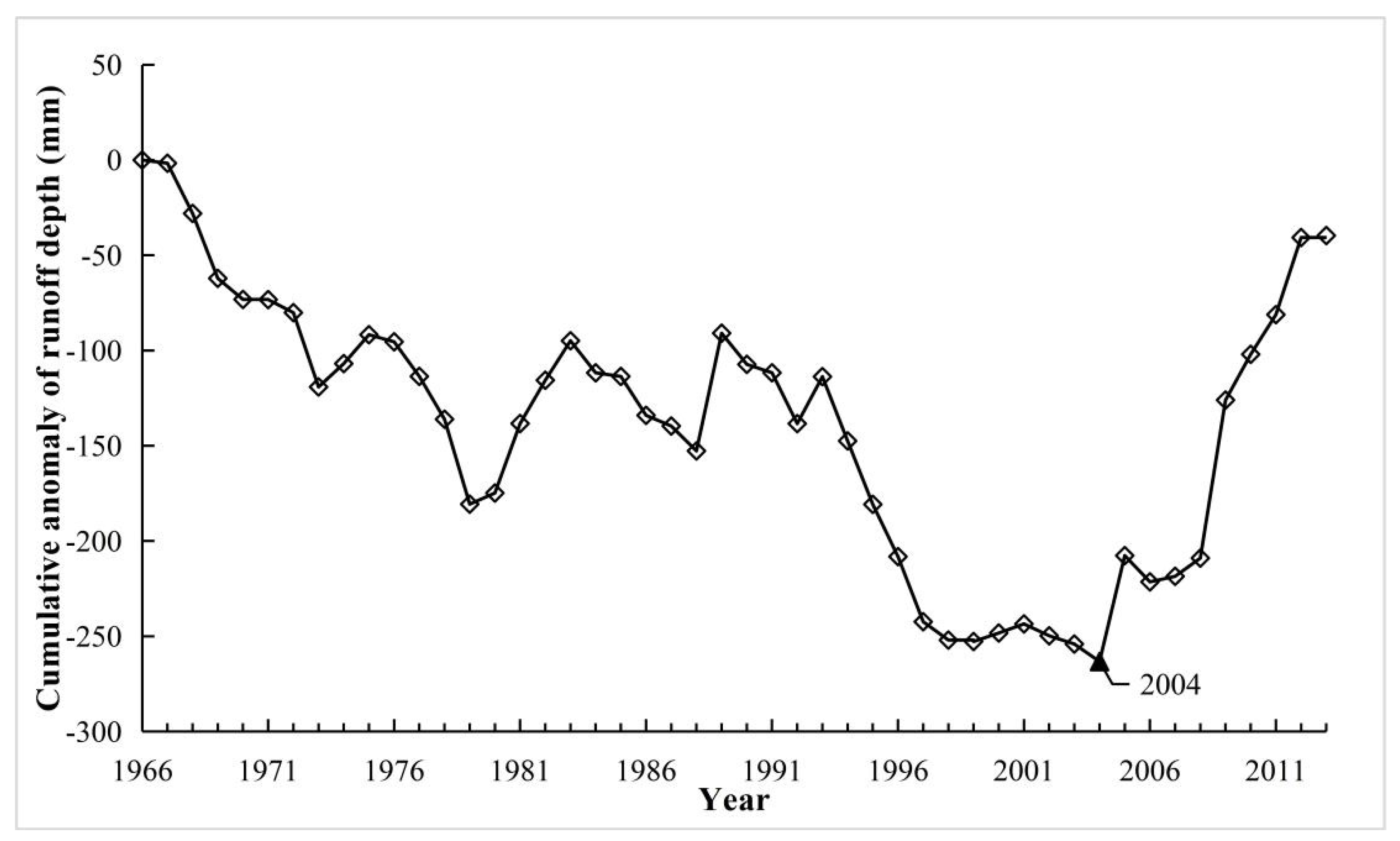
4.2.1. Change Point Analysis of Runoff
4.2.2. Sensitivity Analysis of Runoff to Climatic Variables and Underlying Surface Changes
4.2.3. Attribution Identification of Runoff Change
5. Discussion
5.1. Factors Affecting the Accuracy of the Assessment Results
5.2. Impacts of Glaciers and Frozen Soil on the Runoff Change
5.3. Several Issues to be Further Studied
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yuan, Z.; Yan, D.H.; Yang, Z.Y.; Yin, J.; Zhang, C.; Yuan, Y. Projection of surface water resources in the context of climate change in typical regions of China. Hydrolog. Sci. J. 2016, 62, 283–293. [Google Scholar] [CrossRef]
- Li, J.Z.; Li, X.B. Impacts of Precipitation Changes and Human Activities on Annual Runoff of Chao River Basin during Past 45 years. Sci. Geogr. Sinica. 2008, 28, 809–813. [Google Scholar]
- Li, Q.J. Investigation of Runoff Evolution at the Headwaters of Yangtze River and Its Driving Forces. J. Yangtze River Sci. Res. Inst. 2018, 35, 1–5. [Google Scholar]
- Arnell, N.W.; Reynard, N.S. The effects of climate change due to global warming on river flows in Great Britain. J. Hydrol. 1996, 183, 397–424. [Google Scholar] [CrossRef]
- Młyński, D.; Cebulska, M.; Wałęga, A. Trends, Variability, and Seasonality of Maximum Annual Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef]
- Młyński, D.; Wałęga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating Maximum Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef]
- Zhang, L.P.; Yu, S.Y.; Duan, Y.B.; Shan, L.J.; Chen, X.C.; Xu, Z.X. Quantitative Assessment of the Effects of Climate Change and Human Activities on Runoff in the Yongding River Basin. Adv. Clim. Change Res. 2013, 9, 391–397. [Google Scholar]
- Li, B.; Su, H.B.; Chen, F.; Li, H.B.; Zhang, R.H.; Tian, J.; Chen, S.H.; Yang, Y.M.; Rong, Y.A. Separation of the impact of climate change and human activity on streamflow in the upper and middle reaches of the Taoer River, Northeastern China. Theor. Appl. Climatol. 2014, 118, 271–283. [Google Scholar] [CrossRef]
- Liu, B.; Chen, L.Q.; Zhou, S.; Zhang, T.Y. Attribution Analysis of Runoff Change in Chongqing Section of Upper Yangtze River. Res. Environ. Yangtze Basin 2018, 27, 1333–1341. [Google Scholar]
- Yuan, Z.; Yan, D.H.; Yang, Z.Y.; Xu, J.J.; Huo, J.J.; Zhou, Y.L.; Zhang, C. Attribution assessment and projection of natural runoff change in the Yellow River Basin of China. Mitig. Adapt. Strateg. Glob. Chang. 2016, 23, 27–49. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.Y.; Yang, Y.Z. SWAT Model of Runoff Study under Different Land Use Land Cover Scenarios in Source Region of the Yangtze River. Res. Soil Water Conserv. 2012, 19, 119–124. [Google Scholar]
- Zhang, S.R.; Lu, X.X. Hydrological responses to precipitation variation and diverse human activities in a mountainous tributary of the lower Xijiang, China. Catena 2009, 77, 130–142. [Google Scholar] [CrossRef]
- Twine, T.E.; Kucharik, C.J.; Foley, J.A. Effects of land cover change on the energy and water balance of the Mississippi River basin. J. Hydrometeorol. 2004, 5, 640–655. [Google Scholar] [CrossRef]
- Coe, M.T.; Foley, J.A. Human and natural impacts on the water resources of the Lake Chad basin. J. Geophys. Res. 2001, 106, 3349–3356. [Google Scholar] [CrossRef]
- Zeng, S.D.; Xia, J.; Du, H. Separating the effects of climate change and human activities on runoff over different time scales in the Zhang River basin. Stoch. Environ. Res. Risk Assess. 2014, 28, 401–413. [Google Scholar] [CrossRef]
- Li, L.J.; Li, B.; Liang, L.Q.; Li, J.Y.; Liu, Y.M. Effect of climate change and land use on stream flow in the upper and middle reaches of the Taoer River, Northeastern China. Forestry Stud. China 2010, 12, 107–115. [Google Scholar] [CrossRef]
- Wang, W.G.; Shao, Q.X.; Yang, T.; Peng, S.Z.; Xing, W.Q.; Sun, F.C.; Luo, Y.F. Quantitative assessment of the impact of climate variability and human activities on runoff changes: A case study in four catchments of the Haihe River basin, China. Hydrol. Process. 2013, 28, 1158–1174. [Google Scholar] [CrossRef]
- Lorup, J.K.; Refsgaard, J.C.; Mazvimavi, D. Assessing the effect of land use change on catchment runoff by combined use of statistical tests and hydrological modelling: Case studies from Zimbabwe. J. Hydrol. 1998, 3, 147–163. [Google Scholar] [CrossRef]
- Zuo, D.P.; Xu, Z.X.; Wu, W.; Zhao, J.; Zhao, F.F. Identification of Streamflow Response to Climate Change and Human Activities in the Wei River Basin, China. Water Resour. Res. 2014, 28, 833–851. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M.; Limbrunner, J.F. Climate elasticity of streamflow in the United States. Water Resour. Res. 2001, 37, 1771–1781. [Google Scholar] [CrossRef]
- Liang, W.; Bai, D.; Jin, Z.; You, Y.C.; Li, J.X.; Yang, Y.T. A Study on the Streamflow Change and its Relationship with Climate Change and Ecological Restoration Measures in a Sediment Concentrated Region in the Loess Plateau, China. Water Resour. Manage. 2015, 29, 4045–4060. [Google Scholar] [CrossRef]
- Su, Z.H.; Chen, W.Z. Runoff in Source Region of the Yangtze River in Recent 60 Years: Variation Characteristics and Trend Analysis. Chin. Agric. Bull. 2016, 32, 166–171. [Google Scholar]
- Xie, C.W.; Ding, Y.J.; Liu, S.Y. Changes of weather and hydrological environment for the last 50 years in the source regions of Yangtze and Yellow Rivers. Ecol Environ. 2004, 13, 520–523. [Google Scholar]
- Chen, J. Water Cycle Mechanism in the Source Region of Yangtze River. J. Yangtze River Sci. Res. Inst. 2013, 30, 1–5. [Google Scholar]
- Wu, X.J.; Lu, A.X.; Wang, L.H.; Zhang, H.W. Spatial and Temporal Distribution and Trend of Snow Albedo Changes in the Source Region of the Yangtze River in Last Decade Based on MODIS. Sci. Geogr. Sinica. 2013, 33, 371–377. [Google Scholar]
- Ding, Y.J.; Yang, J.P.; Liu, S.Y.; Chen, R.S.; Wang, G.X.; Shen, Y.P.; Wang, J.; Xie, C.W.; Zhang, S.Q. Exploration of Eco-environment Range in the Sour Regions of the Yangtze and Yellow Rivers. Acta Geogr. Sin. 2003, 58, 519–526. [Google Scholar]
- Li, Y.; Li, Q.J.; Liu, X.S.; Duan, S.Q.; Cai, Y.Q. Analysis of Runoff Variation in Source Region of Yangtze River. Hydrology 2017, 37, 92–95. [Google Scholar]
- Zhang, D.; Liang, K.; Nie, R.; Gu, R.Y. Estimation of evapotranspiration and sensitivity to climate and the underlying surface based on the Budyko Framework. Resour. Sci. 2016, 38, 1140–1148. [Google Scholar]
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1084. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- David, F.N.; Kendall, M.G. Rank Correlation Methods. Biometrika 1950, 37, 190. [Google Scholar] [CrossRef]
- Wang, Y.F.; Chen, Y.; Chen, X.W. Runoff trend detection in the Minjiang River Basin with TFPW-MK method. Sci. Soil Water Conserv. 2013, 11, 96–102. [Google Scholar]
- Liu, M.; Wang, Y.Y. Exploring in Durbin-Watson autocorrelation test. J. Quant. Tech. Econ. 2014, 31, 153–160. [Google Scholar]
- Jiang, C.; Li, D.Q.; Gao, Y.N.; Liu, W.F.; Zhang, L.B. Impact of climate variability and anthropogenic activity on streamflow in the Three Rivers Headwater Region, Tibetan Plateau, China. Theor. Appl. Climatol. 2017, 129, 667–681. [Google Scholar] [CrossRef]
- Zhan, C.S.; Zeng, S.D.; Jiang, S.S.; Wang, H.X.; Ye, W. An Integrated Approach for Partitioning the Effect of Climate Change and Human Activities on Surface Runoff. Water Resour. Manag. 2014, 28, 3843–3858. [Google Scholar] [CrossRef]
- Wong, H.; Hu, B.Q.; Ip, W.C.; Xia, J. Change-point analysis of hydrological time series using grey relational method. J. Hydrol. 2006, 324, 323–338. [Google Scholar] [CrossRef]
- Jiang, S.H.; Ren, L.L.; Yong, B.; Yang, X.L.; Liu, X.F. The effects of climate variability and human activities on runoff from the Laohahe River Basin in Northern China. Water Resour. Protect. 2010, 26, 1–4. [Google Scholar]
- Huang, S.Z.; Huang, Q.; Chen, Y.T. Quantitative Estimation on Contributions of Climate Changes and Human Activities to Decreasing Runoff in Weihe River Basin, China. Chin. Geogr. Sci. 2015, 25, 569–581. [Google Scholar] [CrossRef]
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Technology, 2nd ed.; China Meteorological Press: Beijing, China, 2007. [Google Scholar]
- Wang, G.S.; Xia, J.; Chen, J. Quantification of effects of climate variations and human activities on runoff by a monthly water balance model: A case study of the Chaobai River basin in northern China. Water Resour. Res. 2009, 45, 206–216. [Google Scholar] [CrossRef]
- Budyko, M.I. Climate and Life; Academic Press: San Diego, CA, USA, 1974. [Google Scholar]
- Schreiber, P. Über die Beziehungen zwischen dem Niederschlagund der Wasserführung der Flüsse in Mitteleuropa. Meteorol. Z. 1904, 21, 441–452. [Google Scholar]
- Ol’Dekop, E.M. On evaporation from the surface of river basins. T. Meteorol. Obs. 1911, 4, 200. [Google Scholar]
- Pike, J.G. The estimation of annual run-off from meteorological data in a tropical climate. J. Hydrol. 1964, 2, 116–123. [Google Scholar] [CrossRef]
- Budyko, M.I. The Heat Balance of the Earth’s Surface. Soviet. Geogr. 1961, 2, 3–13. [Google Scholar] [CrossRef]
- Fu, B. On the calculation of the evaporation from land surface. Sci. Atmos. Sinica. 1981, 5, 23–31. [Google Scholar]
- Choudhury, B.J. Evaluation of an equation for annual evaporation using field observations and results from a biophysical model. J. Hydrol. 1999, 216, 99–110. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D.; Lei, Z.; Sun, F. New analytical derivation of the mean annual water–energy balance equation. Water Resour. Res. 2008, 44, 1–9. [Google Scholar] [CrossRef]
- Xu, X.Y.; Yang, D.W.; Yang, H.B.; Lei, H.M. Attribution analysis based on the Budyko hypothesis for detecting the dominant cause of runoff decline in Haihe basin. J. Hydrol. 2014, 510, 530–540. [Google Scholar] [CrossRef]
- Waggoner, P.E. Climate change and US water resources. Wiley 1990, 89, 129–130. [Google Scholar]
- Zhang, M.L.; Wen, Z.; Dong, J.H.; Wang, D.K.; Hou, Y.D.; Wang, B.; Guo, Z.Y.; Wei, H.T. Response mechanism of climate warming on the thermal-moisture dynamics of active layer in permafrost region considering the effect of rainfall. Rock Soil Mech. 2019, 40, 1–9. [Google Scholar]
- Wang, G.X.; Li, Y.S.; Wang, Y.B.; Shen, Y.P. Impacts of Alpine Ecosystem and Climate Changes on Surface Runoff in the Headwaters of the Yangtze River. J. Glaciol. Geocryol. 2007, 29, 159–168. [Google Scholar]
- Xia, J.; Ma, X.Y.; Zou, L.; Wang, Y.L.; Jing, C.X. Quantitative analysis of the effects of climate change and human activities on runoff in the Upper Hanjiang River basin. South North Water Transfers Water Sci. Technol. 2017, 15, 1–6. [Google Scholar]
- Immerzeel, W.W.; Van Beek, L.P.H.; Bierkens, M.F.P. Climate Change Will Affect the Asian Water Towers. Science 2010, 328, 1382–1385. [Google Scholar] [CrossRef] [PubMed]
| Formula | Parameter | Reference |
|---|---|---|
| none | Schreiber (1904) [42] | |
| none | Ol’dekop (1911) [43] | |
| none | Pike (1964) [44] | |
| none | Budyko (1958) [45] | |
| ω | Fu (1981) [46] | |
| α | Choudhury (1999) [47], Yang et al. (2008) [48] |
| Variables | Durbin-Watson (DW) Test | Average Annual Value (mm) | Change Ratio (mm/10 a) | Mann-Kendall (MK) Trend Test | |
|---|---|---|---|---|---|
| Test Statistics | Significance Level | ||||
| P | - | 351.92 | 18.725 | 2.90 | 0.01 |
| E0 | - | 783.60 | 7.228 | 1.65 | 0.10 |
| R | - | 95.53 | 7.26 | 2.43 | 0.05 |
| Period | E0 (mm) | R (mm) | P (mm) | n | E0/P | Elasticity Coefficient | Area Proportion (%) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| εE0 | εp | εn | Grassland | Bare Land | ||||||
| Base period (1966–2003) | 779.18 | 88.60 | 337.95 | 1.10 | 2.31 | −0.80 | 1.80 | −1.53 | 84.66 | 13.56 |
| Impacted period (2004–2013) | 800.40 | 121.85 | 405.023 | 1.09 | 1.97 | −0.75 | 1.75 | −1.34 | 84.98 | 13.20 |
| Change (δ) | 21.22 | 33.25 | 67.073 | −0.01 | −0.34 | 0.05 | −0.05 | 0.19 | 0.32 | −0.36 |
| Relative change (%) | 2.72 | 37.53 | 19.85 | −0.91 | −14.72 | −6.25 | −2.80 | −12.42 | 0.37 | −2.62 |
| Base Period | Impacted Period | dRP | dRE0 | dRn | dR | dR′ | Δ | RE (%) | Contribution Ratio | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ηP | ηE0 | ηn | ηo | |||||||||
| 1966–2003 | 2004–2013 | 33.14 | −2.02 | 1.29 | 33.25 | 32.41 | −0.84 | −2.5 | 99.7 | −6.08 | 3.88 | 2.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Chen, J.; Xu, J.; Lin, Y.; Yuan, Z.; Zhou, M. Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis. Int. J. Environ. Res. Public Health 2019, 16, 2506. https://doi.org/10.3390/ijerph16142506
Liu J, Chen J, Xu J, Lin Y, Yuan Z, Zhou M. Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis. International Journal of Environmental Research and Public Health. 2019; 16(14):2506. https://doi.org/10.3390/ijerph16142506
Chicago/Turabian StyleLiu, Junlong, Jin Chen, Jijun Xu, Yuru Lin, Zhe Yuan, and Mingyuan Zhou. 2019. "Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis" International Journal of Environmental Research and Public Health 16, no. 14: 2506. https://doi.org/10.3390/ijerph16142506
APA StyleLiu, J., Chen, J., Xu, J., Lin, Y., Yuan, Z., & Zhou, M. (2019). Attribution of Runoff Variation in the Headwaters of the Yangtze River Based on the Budyko Hypothesis. International Journal of Environmental Research and Public Health, 16(14), 2506. https://doi.org/10.3390/ijerph16142506





