Toward an Improved Air Pollution Warning System in Quebec
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Statistical Methodology
- Choose maximum lags for air pollution indicators;
- Compute an excess mortality (EM) series from the mortality data;
- Determine extreme EM episodes as targets of the APHWS;
- Choose the best indicators–thresholds combination.
2.2.1. Choose Maximum Lags for Air Pollution Indicators
2.2.2. Compute an Excess Mortality Series
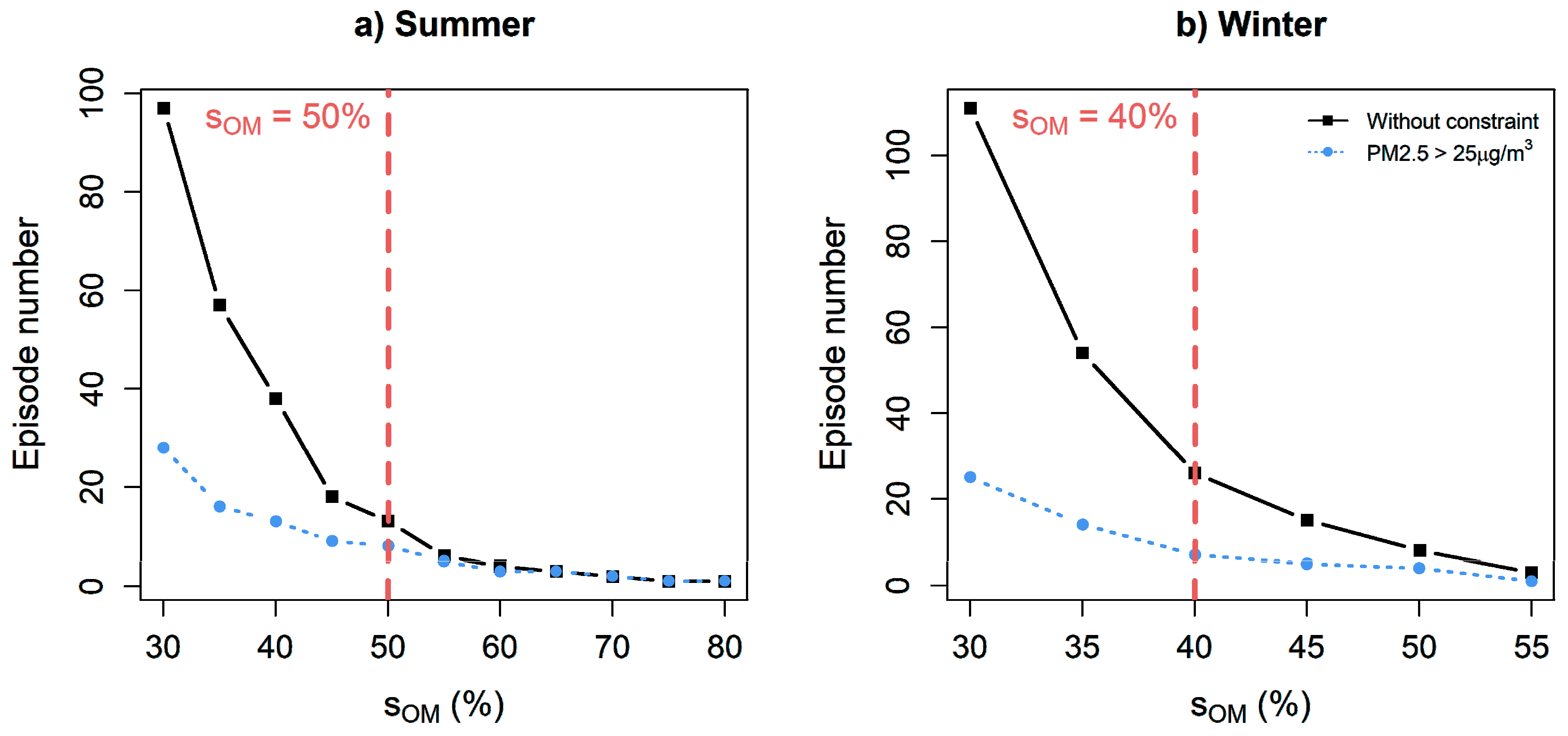
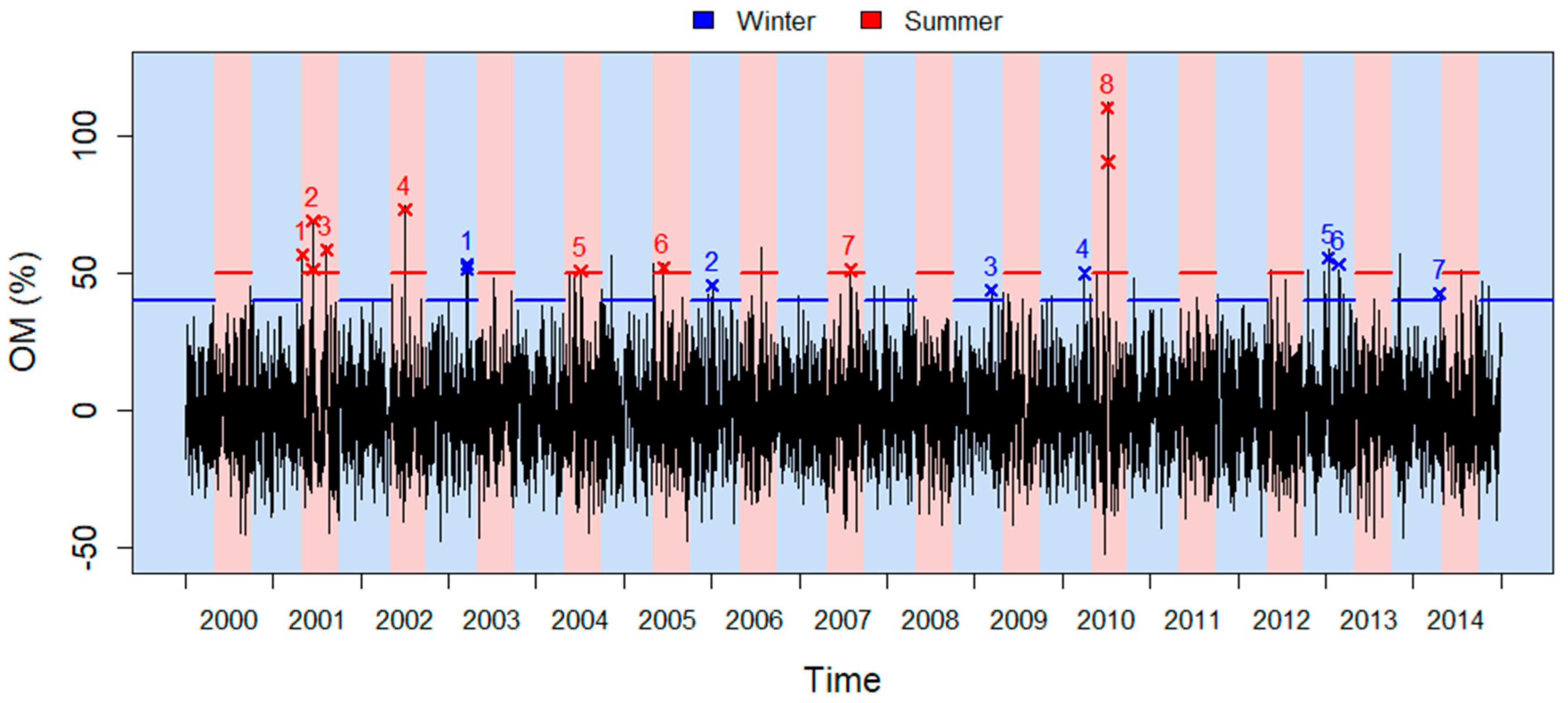
2.2.3. Determine Significant Excess Mortality Episodes
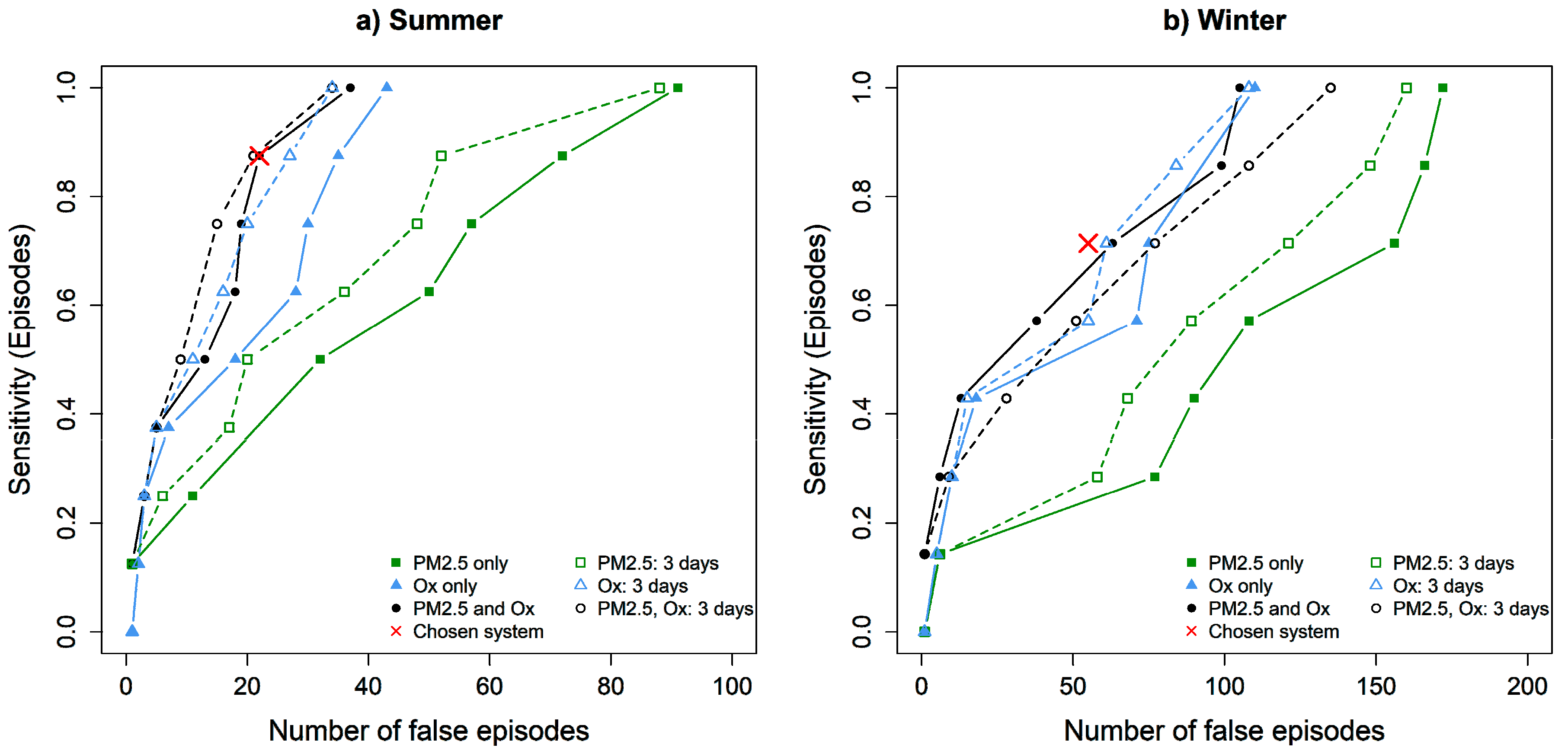
2.2.4. Choose the Best Combination of Indicators–Thresholds
3. Results
3.1. Results for Montreal’s APHWS
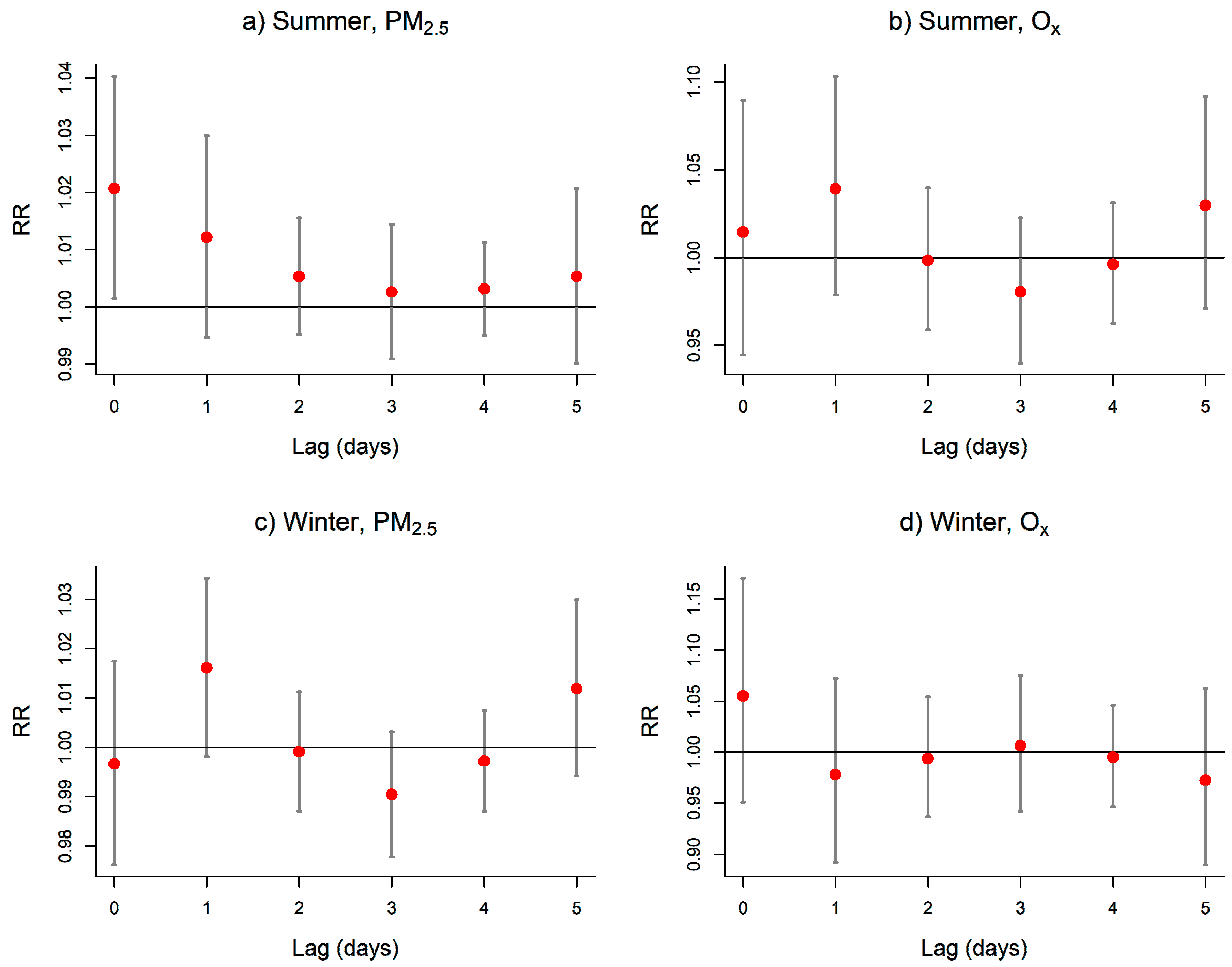
3.1.1. Choice of Lags
3.1.2. Excess Mortality Episodes
3.1.3. Final Indicators and Thresholds
3.2. Sensitivity Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Review of Evidence on Health Aspects of Air Pollution—REVIHAAP Project; World Health Organization: Geneva, Switzerland, 2013. [Google Scholar]
- Dominici, F.; Peng, R.D.; Bell, M.L.; Pham, L.; McDermott, A.; Zeger, S.L.; Samet, J.M. Fine Particulate Air Pollution and Hospital Admission for Cardiovascular and Respiratory Diseases. JAMA 2006, 295, 1127–1134. [Google Scholar] [CrossRef] [PubMed]
- Requia, W.J.; Adams, M.D.; Arain, A.; Papatheodorou, S.; Koutrakis, P.; Mahmoud, M. Global Association of Air Pollution and Cardiorespiratory Diseases: A Systematic Review, Meta-Analysis, and Investigation of Modifier Variables. Am. J. Public Health 2018, 108, S123–S130. [Google Scholar] [CrossRef] [PubMed]
- Achilleos, S.; Kioumourtzoglou, M.-A.; Wu, C.-D.; Schwartz, J.D.; Koutrakis, P.; Papatheodorou, S.I. Acute effects of fine particulate matter constituents on mortality: A systematic review and meta-regression analysis. Environ. Int. 2017, 109, 89–100. [Google Scholar] [CrossRef] [PubMed]
- Vodonos, A.; Awad, Y.A.; Schwartz, J. The concentration-response between long-term PM2.5 exposure and mortality: A meta-regression approach. Environ. Res. 2018, 166, 677–689. [Google Scholar] [CrossRef] [PubMed]
- Medina-Ramón, M.; Schwartz, J. Who is More Vulnerable to Die from Ozone Air Pollution? Epidemiology 2008, 19, 672–679. [Google Scholar] [CrossRef] [PubMed]
- Mills, I.C.; Atkinson, R.W.; Kang, S.; Walton, H.; Anderson, H.R. Quantitative systematic review of the associations between short-term exposure to nitrogen dioxide and mortality and hospital admissions. BMJ Open 2015, 5, e006946. [Google Scholar] [CrossRef] [PubMed]
- Brook, R.D.; Rajagopalan, S.; Pope, C.A.; Brook, J.R.; Bhatnagar, A.; Diez-Roux, A.V.; Holguin, F.; Hong, Y.; Luepker, R.V.; Mittleman, M.A.; et al. Particulate Matter Air Pollution and Cardiovascular Disease: An Update to the Scientific Statement From the American Heart Association. Circulation 2010, 121, 2331–2378. [Google Scholar] [CrossRef] [PubMed]
- Cascio, W.E. Wildland fire smoke and human health. Sci. Total Environ. 2018, 624, 586–595. [Google Scholar] [CrossRef]
- Reid, C.E.; Brauer, M.; Johnston, F.H.; Jerrett, M.; Balmes, J.R.; Elliott, C.T. Critical Review of Health Impacts of Wildfire Smoke Exposure. Environ. Health Perspect. 2016, 124, 1334–1343. [Google Scholar] [CrossRef]
- Castner, J.; Guo, L.; Yin, Y. Ambient air pollution and emergency department visits for asthma in Erie County, New York 2007–2012. Int. Arch. Occup. Environ. Health 2018, 91, 205–214. [Google Scholar] [CrossRef]
- Tétreault, L.-F.; Doucet, M.; Gamache, P.; Fournier, M.; Brand, A.; Kosatsky, T.; Smargiassi, A.; Tétreault, L.-F.; Doucet, M.; Gamache, P.; et al. Severe and Moderate Asthma Exacerbations in Asthmatic Children and Exposure to Ambient Air Pollutants. Int. J. Environ. Res. Public Health 2016, 13, 771. [Google Scholar] [CrossRef] [PubMed]
- Kelly, F.J.; Fuller, G.W.; Walton, H.A.; Fussell, J.C. Monitoring air pollution: Use of early warning systems for public health. Respirology 2012, 17, 7–19. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Zhu, Z. Research and application of a novel hybrid air quality early-warning system: A case study in China. Sci. Total Environ. 2018, 626, 1421–1438. [Google Scholar] [CrossRef]
- Jiang, P.; Li, C.; Li, R.; Yang, H. An innovative hybrid air pollution early-warning system based on pollutants forecasting and Extenics evaluation. Knowl.-Based Syst. 2019, 164, 174–192. [Google Scholar] [CrossRef]
- Environment and Climate Change Canada. Canadian Environmental Sustainability Indicators: Air Quality; Environment and Climate Change Canada: Gatineau, PQ, Canada, 2018.
- Stieb, D.M.; Burnett, R.T.; Smith-Doiron, M.; Brion, O.; Shin, H.H.; Economou, V. A New Multipollutant, No-Threshold Air Quality Health Index Based on Short-Term Associations Observed in Daily Time-Series Analyses. J. Air Waste Manag. Assoc. 2008, 58, 435–450. [Google Scholar] [CrossRef] [PubMed]
- Ministère du Développement Durable, Environnement et Lutte contre les Changements Climatiques Indice de la qualité de l’air. Available online: http://www.iqa.mddefp.gouv.qc.ca/contenu/calcul.htm (accessed on 12 October 2018).
- Xu, Y.; Yang, W.; Wang, J. Air quality early-warning system for cities in China. Atmos. Environ. 2017, 148, 239–257. [Google Scholar] [CrossRef]
- World Health Organization. WHO Air Quality Guidelines for Particulate Matter, Ozone, Nitrogen Dioxide and Sulfur Dioxide: Global Update 2005; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Atkinson, R.W.; Kang, S.; Anderson, H.R.; Mills, I.C.; Walton, H.A. Epidemiological time series studies of PM2.5 and daily mortality and hospital admissions: A systematic review and meta-analysis. Thorax 2014, 69, 660–665. [Google Scholar] [CrossRef]
- Rodriguez-Villamizar, L.A.; Magico, A.; Osornio-Vargas, A.; Rowe, B.H. The effects of outdoor air pollution on the respiratory health of Canadian children: A systematic review of epidemiological studies. Can. Respir. J. 2015, 22, 282–292. [Google Scholar] [CrossRef]
- Wang, C.; Tu, Y.; Yu, Z.; Lu, R. PM2.5 and Cardiovascular Diseases in the Elderly: An Overview. Int. J. Environ. Res. Public Health 2015, 12, 8187–8197. [Google Scholar] [CrossRef]
- Analitis, A.; de’ Donato, F.; Scortichini, M.; Lanki, T.; Basagana, X.; Ballester, F.; Astrom, C.; Paldy, A.; Pascal, M.; Gasparrini, A.; et al. Synergistic Effects of Ambient Temperature and Air Pollution on Health in Europe: Results from the PHASE Project. Int. J. Environ. Res. Public Health 2018, 15, 1856. [Google Scholar] [CrossRef]
- Cairncross, E.K.; John, J.; Zunckel, M. A novel air pollution index based on the relative risk of daily mortality associated with short-term exposure to common air pollutants. Atmos. Environ. 2007, 41, 8442–8454. [Google Scholar] [CrossRef]
- Islam, M.S.; Chaussalet, T.J.; Koizumi, N. Towards a threshold climate for emergency lower respiratory hospital admissions. Environ. Res. 2017, 153, 41–47. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chebana, F.; Martel, B.; Gosselin, P.; Giroux, J.-X.; Ouarda, T.B. A general and flexible methodology to define thresholds for heat health watch and warning systems, applied to the province of Québec (Canada). Int. J. Biometeorol. 2013, 57, 631–644. [Google Scholar] [CrossRef] [PubMed]
- Hajat, S.; Sheridan, S.C.; Allen, M.J.; Pascal, M.; Laaidi, K.; Yagouti, A.; Bickis, U.; Tobias, A.; Bourque, D.; Armstrong, B.G.; et al. Heat–Health Warning Systems: A Comparison of the Predictive Capacity of Different Approaches to Identifying Dangerously Hot Days. Am. J. Public Health 2010, 100, 1137–1144. [Google Scholar] [CrossRef] [PubMed]
- Benmarhnia, T.; Bailey, Z.; Kaiser, D.; Auger, N.; King, N.; Kaufman, J.S. A Difference-in-Differences Approach to Assess the Effect of a Heat Action Plan on Heat-Related Mortality, and Differences in Effectiveness According to Sex, Age, and Socioeconomic Status (Montreal, Quebec). Environ. Health Perspect. 2016, 124, 1694–1699. [Google Scholar] [CrossRef] [PubMed]
- Zimek, A.; Schubert, E.; Kriegel, H.-P. A survey on unsupervised outlier detection in high-dimensional numerical data. Stat. Anal. Data Min. ASA Data Sci. J. 2012, 5, 363–387. [Google Scholar] [CrossRef]
- Bratsch, S.G. Standard Electrode Potentials and Temperature Coefficients in Water at 298.15 K. J. Phys. Chem. Ref. Data 1989, 18, 1–21. [Google Scholar] [CrossRef]
- Lavigne, E.; Burnett, R.T.; Weichenthal, S. Association of short-term exposure to fine particulate air pollution and mortality: Effect modification by oxidant gases. Sci. Rep. 2018, 8, 16097. [Google Scholar] [CrossRef]
- Williams, M.L.; Atkinson, R.W.; Anderson, H.R.; Kelly, F.J. Associations between daily mortality in London and combined oxidant capacity, ozone and nitrogen dioxide. Air Qual. Atmos. Health 2014, 7, 407–414. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage; FAO: Rome, Italy, 1998. [Google Scholar]
- Statistics Canada Comparability of ICD-10 and ICD-9 for Mortality Statistics in Canada; Statistics Canada: Ottawa, ON, Canada, 2005.
- Pascal, M.; Laaidi, K.; Ledrans, M.; Baffert, E.; Caserio-Schönemann, C.; Le Tertre, A.; Manach, J.; Medina, S.; Rudant, J.; Empereur-Bissonnet, P. France’s heat health watch warning system. Int. J. Biometeorol. 2006, 50, 144–153. [Google Scholar] [CrossRef]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Distributed lag non-linear models. Stat. Med. 2010, 29, 2224–2234. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Scheipl, F.; Armstrong, B.; Kenward, M.G. A penalized framework for distributed lag non-linear models. Biom 2017, 73, 938–948. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Guo, Y.; Hashizume, M.; Kinney, P.L.; Petkova, E.P.; Lavigne, E.; Zanobetti, A.; Schwartz, J.D.; Tobias, A.; Leone, M.; et al. Temporal Variation in Heat–Mortality Associations: A Multicountry Study. Environ. Health Perspect. 2015, 123, 1200–1207. [Google Scholar] [CrossRef] [PubMed]
- Buteau, S.; Goldberg, M.S.; Burnett, R.T.; Gasparrini, A.; Valois, M.-F.; Brophy, J.M.; Crouse, D.L.; Hatzopoulou, M. Associations between ambient air pollution and daily mortality in a cohort of congestive heart failure: Case-crossover and nested case-control analyses using a distributed lag nonlinear model. Environ. Int. 2018, 113, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Chiu, Y.; Chebana, F.; Abdous, B.; Bélanger, D.; Gosselin, P. Mortality and morbidity peaks modeling: An extreme value theory approach. Stat. Methods Med. Res. 2016, 0962280216662494. [Google Scholar] [CrossRef] [PubMed]
- Bustinza, R.; Lebel, G.; Gosselin, P.; Belanger, D.; Chebana, F. Health impacts of the July 2010 heat wave in Quebec, Canada. BMC Public Health 2013, 13, 56. [Google Scholar] [CrossRef]
- Jhun, I.; Fann, N.; Zanobetti, A.; Hubbell, B. Effect modification of ozone-related mortality risks by temperature in 97 US cities. Environ. Int. 2014, 73, 128–134. [Google Scholar] [CrossRef] [PubMed]
- Giroux, J.-X.; Chebana, F.; Gosselin, P.; Bustinza, R. Indicateurs et valeurs-seuils météorologiques pour les systèmes de veille-avertissement canicule pour le Québec: Mise à jour de l’étude de 2010 et développement d’un logiciel de calcul pour les systèmes d’alerte; Institut National de la Santé Publique du Québec: Quebec City, PQ, Canada, 2017; p. 62. [Google Scholar]
- Sapkota, A.; Symons, J.M.; Kleissl, J.; Wang, L.; Parlange, M.B.; Ondov, J.; Breysse, P.N.; Diette, G.B.; Eggleston, P.A.; Buckley, T.J. Impact of the 2002 Canadian forest fires on particulate matter air quality in Baltimore city. Environ. Sci. Technol. 2005, 39, 24–32. [Google Scholar] [CrossRef]
- Réseau de surveillance de la qualité de l’air. Environmental Assessment Report 2017: Air Quality in Montreal; Service de l’Environnement: Montreal, QC, Canada, 2017. [Google Scholar]
- Koop, G.; Tole, L. An investigation of thresholds in air pollution-mortality effects. Environ. Model. Softw. 2006, 21, 1662–1673. [Google Scholar] [CrossRef]
- Gasparrini, A.; Guo, Y.; Hashizume, M.; Lavigne, E.; Zanobetti, A.; Schwartz, J.; Tobias, A.; Tong, S.; Rocklöv, J.; Forsberg, B.; et al. Mortality risk attributable to high and low ambient temperature: A multicountry observational study. Lancet 2015, 386, 369–375. [Google Scholar] [CrossRef]
- Smith, R.; McDougal, K. Costs of Pollution in Canada: Measuring the Impacts on Families, Businesses and Governments; International Institute for Sustainable Development: Winnipeg, MB, Canada, 2017; p. 145. [Google Scholar]
- Toutant, S.; Gosselin, P.; Bélanger, D.; Bustinza, R.; Rivest, S. An Open Source Web Application for the Surveillance and Prevention of the Impacts on Public Health of Extreme Meteorological Events: The SUPREME System. Int. J. Health Geogr. 2011, 10, 39. [Google Scholar] [CrossRef] [PubMed]
- Voorhees, S.S.; Sakai, R.; Araki, S.; Sato, H.; Otsu, A. Cost-Benefit Analysis Methods for Assessing Air Pollution Control Programs in Urban Environments—A Review. Environ. Health Prev. Med. 2001, 6, 63–73. [Google Scholar] [CrossRef] [PubMed]
| Variable | Montreal | Quebec City | ||
|---|---|---|---|---|
| Summer | Winter | Summer | Winter | |
| Mortality count | 33.6 | 39.5 | 3.1 | 3.9 |
| Max PM2.5 (μg/m3) | 18.4 | 19.9 | 17.3 | 19.7 |
| Max Ox (ppb) | 28.1 | 22.0 | 24.9 | 23.9 |
| Temperature (°C) | 17.9 | −1.0 | 14.4 | −4.3 |
| Relative humidity (%) | 67.0 | 69.0 | 65.1 | 66.6 |
| Minimum | 1st Quartile | Median | Mean | 3rd Quartile | Maximum | Standard Deviation | |
|---|---|---|---|---|---|---|---|
| Summer | −52.4 | −13.4 | −0.7 | 0.1 | 11.6 | 110.4 | 18.3 |
| Winter | −47.5 | −11.2 | −0.6 | 0.0 | 10.4 | 58.8 | 16.1 |
| City | Season | PM2.5 (μg/m3) | Ox (ppb) | Sensitivity (%) | FA per Year | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Days | Episodes | Days | Episodes | ||||||||
| Montreal | Summer | 0.9 | 0.1 | 31 | 0.5 | 0.5 | 43 | 22.4 | 87.5 | 3.1 | 1.5 |
| Winter | 0.5 | 0.5 | 25 | 0.8 | 0.2 | 26 | 15.4 | 71.4 | 8.0 | 3.7 | |
| Quebec City | Summer | 0.5 | 0.5 | 32 | 0.8 | 0.2 | 23 | 20.4 | 85.7 | 4.7 | 2.6 |
| Winter | 0.5 | 0.5 | 33 | 0.7 | 0.3 | 21 | 9.5 | 50 | 15.5 | 7.4 | |
| Geographic Scale | PM2.5 | O3 | NO2 | Ox | Reference | |||
|---|---|---|---|---|---|---|---|---|
| Indicator | Threshold (μg/m3) | Indicator | Threshold (ppb) | Indicator | Threshold (ppb) | Threshold (ppb) | ||
| World | 24-h mean | 25 | 8-h mean | 50 | 1-h mean | 106 | 69 * | [19] |
| Canada | 24-h mean | 27 | 8-h mean | 62 | 1-h mean | 60 | 61 * | [16] |
| Province of Quebec | 1-h mean | 30 | 1-h mean | 80 | 1-h mean | 213 | 125 * | [18] |
| Montreal | 3-h mean | 35 | - | - | - | - | - | [46] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Masselot, P.; Chebana, F.; Lavigne, É.; Campagna, C.; Gosselin, P.; Ouarda, T.B.M.J. Toward an Improved Air Pollution Warning System in Quebec. Int. J. Environ. Res. Public Health 2019, 16, 2095. https://doi.org/10.3390/ijerph16122095
Masselot P, Chebana F, Lavigne É, Campagna C, Gosselin P, Ouarda TBMJ. Toward an Improved Air Pollution Warning System in Quebec. International Journal of Environmental Research and Public Health. 2019; 16(12):2095. https://doi.org/10.3390/ijerph16122095
Chicago/Turabian StyleMasselot, Pierre, Fateh Chebana, Éric Lavigne, Céline Campagna, Pierre Gosselin, and Taha B.M.J. Ouarda. 2019. "Toward an Improved Air Pollution Warning System in Quebec" International Journal of Environmental Research and Public Health 16, no. 12: 2095. https://doi.org/10.3390/ijerph16122095
APA StyleMasselot, P., Chebana, F., Lavigne, É., Campagna, C., Gosselin, P., & Ouarda, T. B. M. J. (2019). Toward an Improved Air Pollution Warning System in Quebec. International Journal of Environmental Research and Public Health, 16(12), 2095. https://doi.org/10.3390/ijerph16122095







