Geographic Imputation of Missing Activity Space Data from Ecological Momentary Assessment (EMA) GPS Positions
Abstract
1. Introduction
2. Materials and Methods
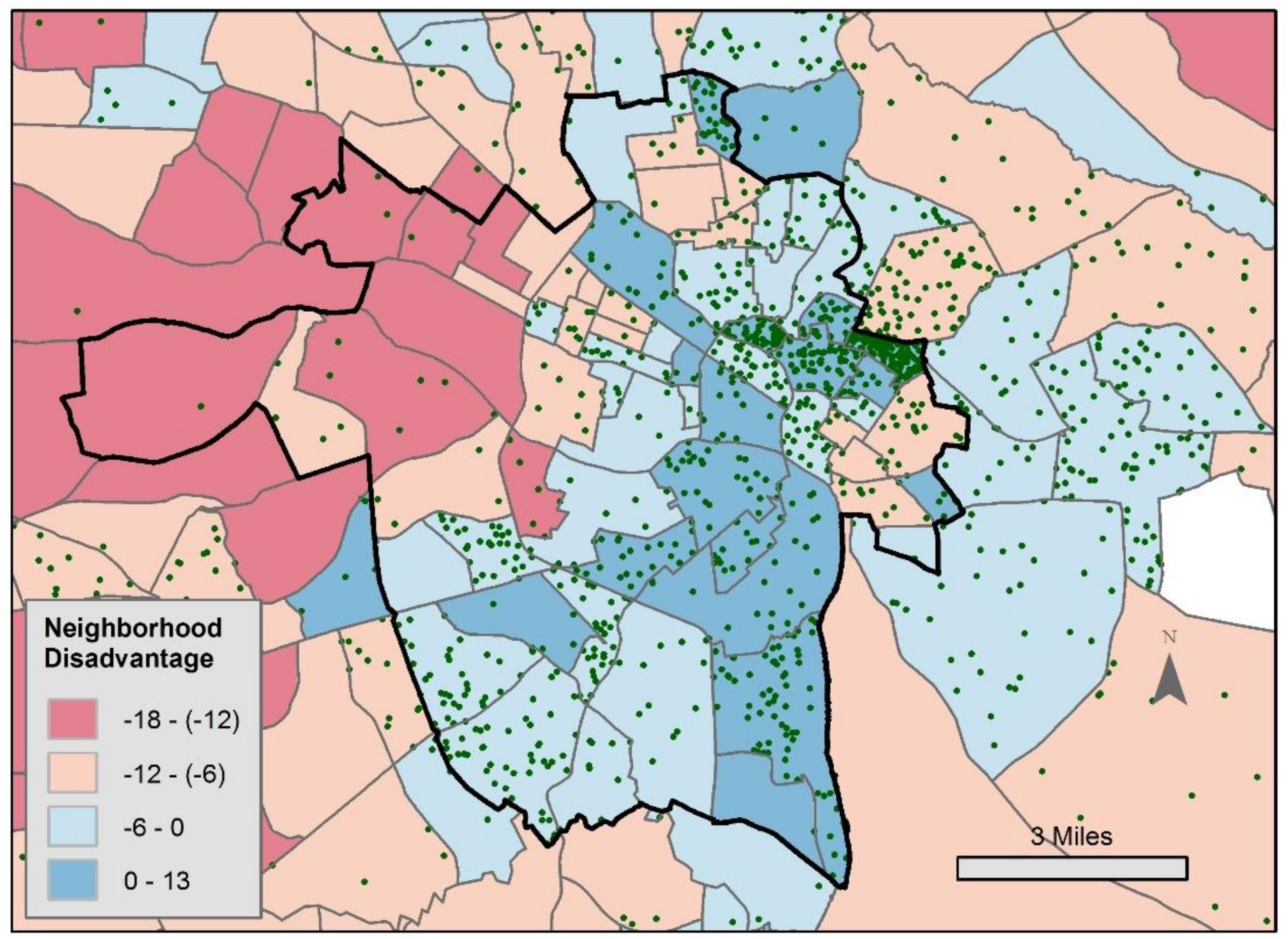
2.1. Study Setting
2.2. Measures
2.3. Analytic Plan
3. Results
3.1. Descriptive Statistics
3.2. Correlation of Observed and Imputed Neighborhood Disadvantage for Different Imputation Methods
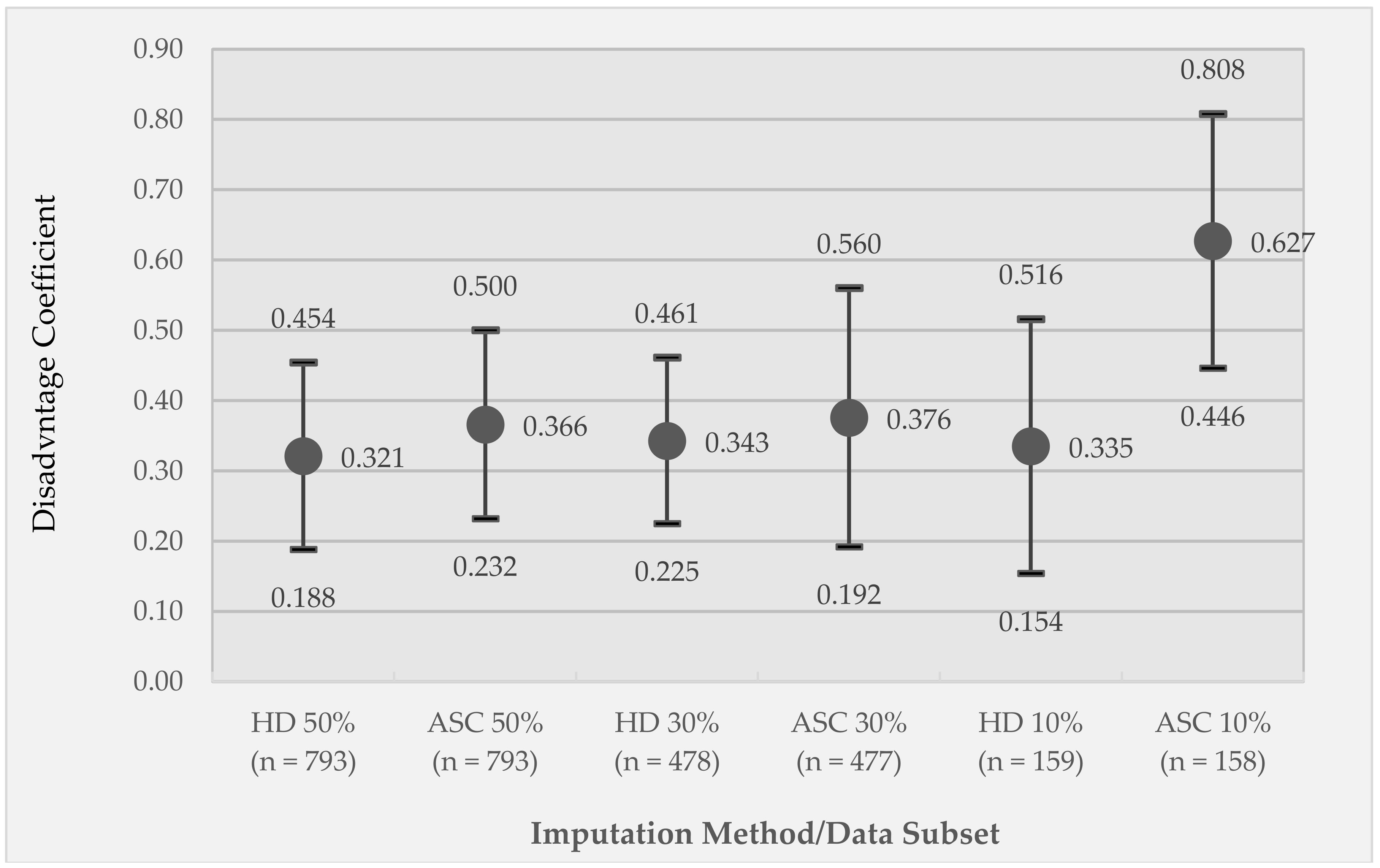
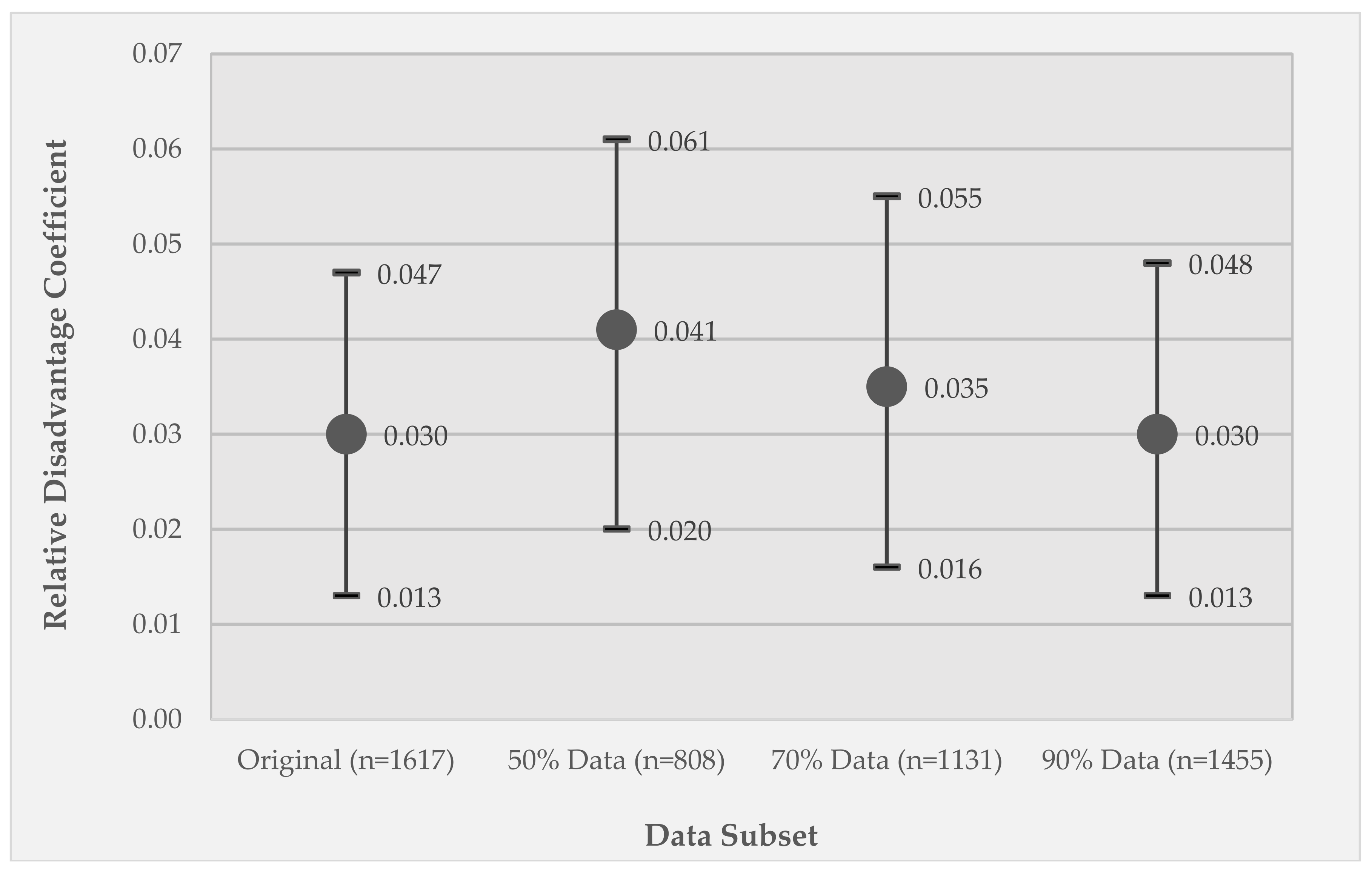
3.3. Comparison of Model 1 GEE Relative Disadvantage Coefficients between the Original Data Set and the Listwise Deletion and Imputed Data Sets
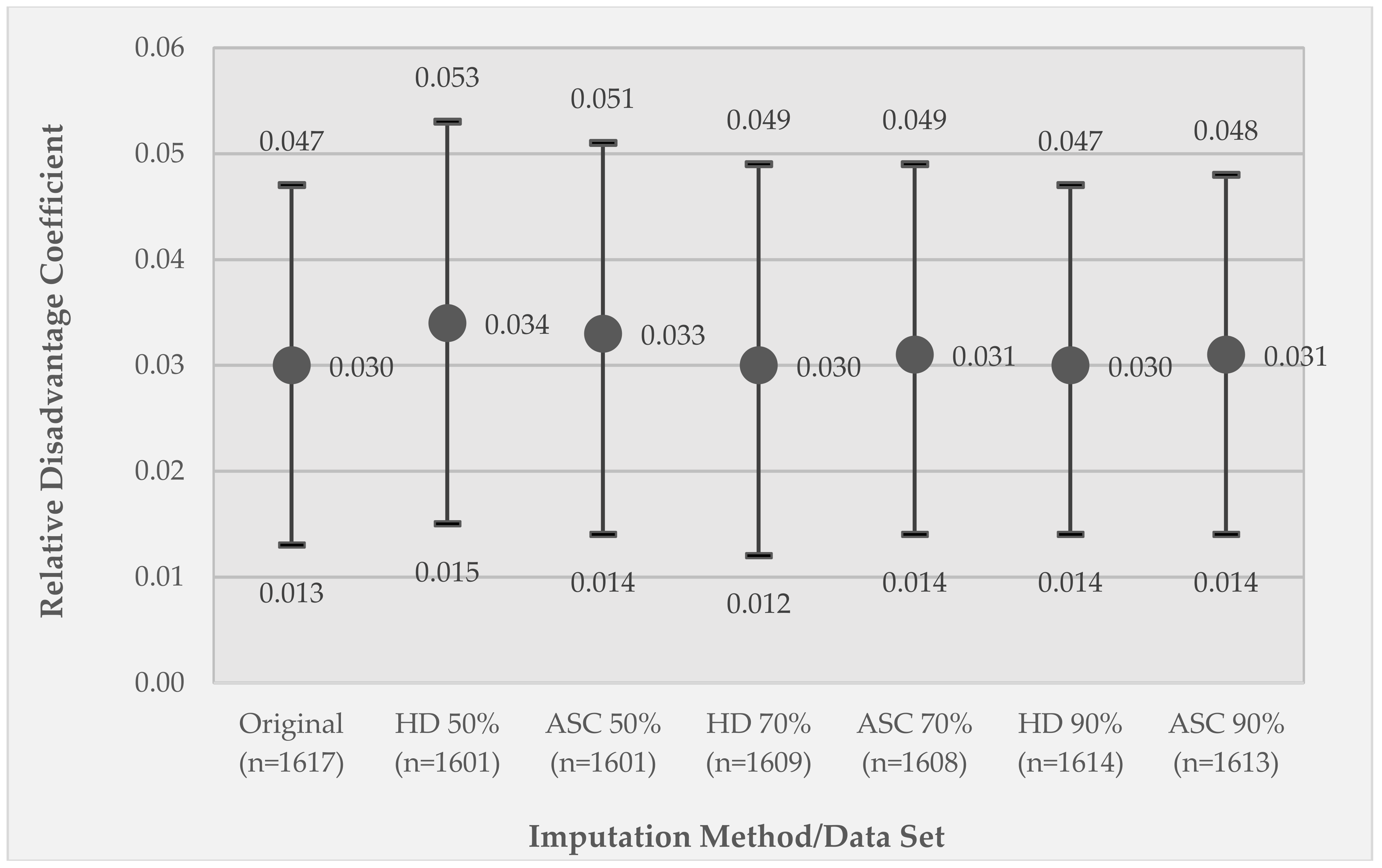
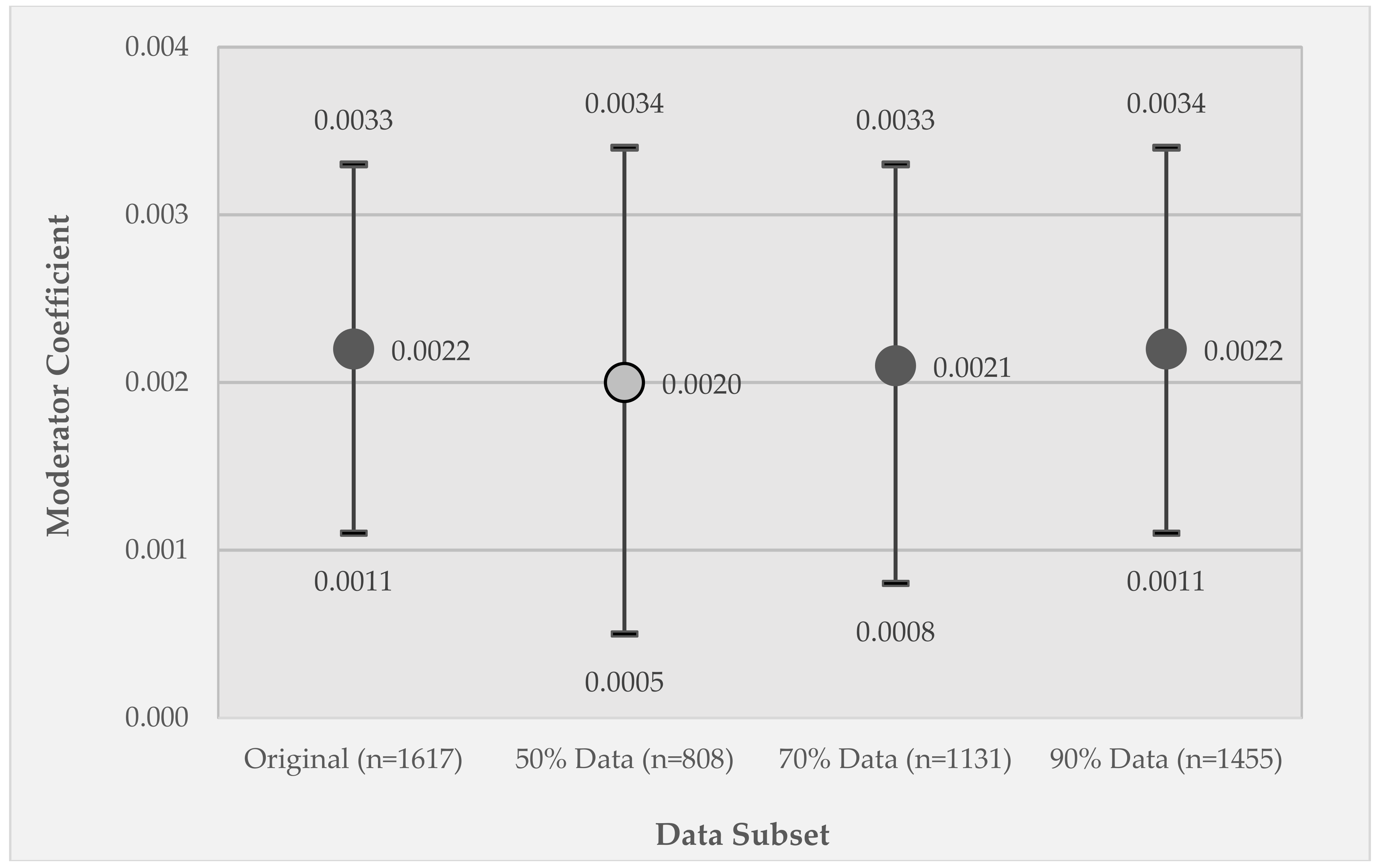
3.4. Comparison of Model 2 GEE Moderator Coefficients between the Original Data Set and the Listwise Deletion and Imputed Data Sets
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Richardson, D.B.; Volkow, N.D.; Kwan, M.-P.; Kaplan, R.M.; Goodchild, M.F.; Croyle, R.T. Spatial turn in health research. Science 2013, 339, 1390–1392. [Google Scholar] [CrossRef] [PubMed]
- Wild, C.P. The exposome: From concept to utility. Int. J. Epidemiol. 2012, 41, 24–32. [Google Scholar] [CrossRef] [PubMed]
- Diez Roux, A.; Mair, C. Neighborhoods and health. Ann. N. Y. Acad. Sci. 2010, 1186, 125–145. [Google Scholar] [CrossRef]
- Browning, C.R.; Soller, B. Moving beyond neighborhood: Activity spaces and ecological networks as contexts for youth development. Cityscape 2014, 16, 165–196. [Google Scholar] [PubMed]
- Kwan, M.-P. The limits of the neighborhood effect: Contextual uncertainties in geographic, environmental, health, and social science research. Ann. Am. Assoc. Geogr. 2018. [Google Scholar] [CrossRef]
- Mennis, J.; Yoo, E.-H.E. Geographic information science and the analysis of place and health. Trans. GIS 2018, 22, 842–854. [Google Scholar] [CrossRef]
- Golledge, R.G.; Stimson, R.J. Spatial Behavior: A Geographic Perspective; Guilford Press: New York, NY, USA, 1997. [Google Scholar]
- Mennis, J.; Mason, M.; Ambrus, A. Urban greenspace is associated with reduced psychological stress among adolescents: A geographic ecological momentary assessment (GEMA) analysis of activity space. Landsc. Urban Plan. 2018, 174, 1–9. [Google Scholar] [CrossRef]
- Mennis, J.; Mason, M.J. People, places, and adolescent substance use: Integrating activity space and social network data for analyzing health behavior. Ann. Assoc. Am. Geogr. 2011, 101, 272–291. [Google Scholar] [CrossRef]
- Zenk, S.N.; Schulz, A.J.; Matthews, S.A.; Odoms-Young, A.; Wilbur, J.; Wegrzyn, L.; Gibbs, K.; Braunschweig, C.; Stokes, C. Activity space environment and dietary and physical activity behaviors: A pilot study. Health Place 2011, 17, 1150–1161. [Google Scholar] [CrossRef]
- Yoo, E.; Rudra, C.; Glasgow, M.; Mu, L. Geospatial estimation of individual exposure to air pollutants: Moving from static monitoring to activity-based dynamic exposure assessment. Ann. Assoc. Am. Geogr. 2015, 105, 915–926. [Google Scholar] [CrossRef]
- Helbich, M.; van Emmichoven, M.J.Z.; Dijst, M.J.; Kwan, M.-P.; Pierik, F.H.; de Vries, S.I. Natural and built environmental exposures on children’s active school travel: A Dutch global positioning system-based cross-sectional study. Health Place 2016, 39, 101–109. [Google Scholar] [CrossRef] [PubMed]
- Stahler, G.J.; Mennis, J.; Baron, D. Geospatial technology and the exposome: New perspectives on addiction. Am. J. Public Health 2013, 103, 1354–1356. [Google Scholar] [CrossRef] [PubMed]
- Kwan, M.-K. GIS methods in time-geographic research: Geocomputation and geovisualization of human activity patterns. Geogr. Ann. Ser. B Hum. Geogr. 2005, 86, 267–280. [Google Scholar] [CrossRef]
- Shiffman, S.; Stone, A.A.; Hufford, M.R. Ecological momentary assessment. Ann. Rev. Clin. Psychol. 2008, 4, 1–32. [Google Scholar] [CrossRef]
- Kirchner, T.R.; Shiffman, S. Spatio-temporal determinants of mental health and well-being: Advances in geographically-explicit ecological momentary assessment (GEMA). Soc. Psychiatry Psychiatr. Epidemiol. 2016, 51, 1211–1223. [Google Scholar] [CrossRef] [PubMed]
- Mennis, J.M.; Mason, M.; Light, J.; Rusby, J.; Westling, E.; Way, T.; Zharakis, N.; Flay, B. Does substance use moderate the association of neighborhood disadvantage with perceived stress and safety in the activity spaces of urban youth. Drug Alcohol Depend. 2016, 165, 288–292. [Google Scholar] [CrossRef] [PubMed]
- Epstein, D.H.; Tyburski, M.; Craig, I.M.; Phillips, K.A.; Jobes, M.L.; Vahabzadeh, M.; Mezghanni, M.; Lin, J.-L.; Furr-Holden, C.D.M.; Preston, K.L. Real-time tracking of neighborhood surroundings and mood in urban drug misusers: Application of a new method to study behavior in its geographical context. Drug Alcohol Depend. 2014, 134, 22–29. [Google Scholar] [CrossRef]
- Freisthler, B.; Lipperman-Kreda, S.; Bersamin, M.; Gruenewald, P.J. Tracking the when, where, and with whom of alcohol use: Integrating ecological momentary assessment and geospatial data to examine risk for alcohol-related problems. Alcohol Res. Curr. Rev. 2014, 36, 29–38. [Google Scholar]
- Mcquoid, J.; Thrul, J.; Ling, P. A geographically explicit ecological momentary assessment (GEMA) mixed method for understanding substance use. Soc. Sci. Med. 2018, 202, 89–98. [Google Scholar] [CrossRef]
- Mennis, J.; Mason, M.J.; Ambrus, A.; Way, T.; Henry, K. The spatial accuracy of geographic ecological momentary assessment (GEMA): Error and bias due to subject and environmental characteristics. Drug Alcohol Depend. 2017, 178, 188–193. [Google Scholar] [CrossRef]
- Zandbergen, P.A.; Barbeau, S.J. Positional accuracy of assisted GPS data from high sensitivity GPS-enabled mobile phones. J. Navig. 2011, 64, 381–399. [Google Scholar] [CrossRef]
- Watkins, K.L.; Regan, S.D.; Nguyen, N.; Businelle, M.S.; Kendzor, D.E.; Lam, C.; Balis, D.; Cuevas, A.G.; Cao, Y.; Reitzel, L.R. Advancing cessation research by integrating EMA and geospatial methodologies: Associations between tobacco retail outlets and real-time smoking urges during a quit attempt. Nicot. Tob. Res. 2014, 16, S93–S101. [Google Scholar] [CrossRef] [PubMed]
- Birhrmann, K.; Ersboll, A.K. Estimating range of influence in case of missing spatial data: A simulation study on binary data. Int. J. Health Geogr. 2015, 14, 1. [Google Scholar] [CrossRef] [PubMed]
- Reich, B.J.; Chang, H.H.; Strickland, M.J. Spatial health effects analysis with uncertain residential locations. Stat. Methods Med. Res. 2014, 23, 156–168. [Google Scholar] [CrossRef] [PubMed]
- Oliver, M.N.; Matthews, K.A.; Siadaty, M.; Hauck, F.R.; Pickle, L.W. Geographic bias related to geocoding in epidemiologic studies. Int. J. Health Geogr. 2005, 4, 29. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Manjourides, J.; Cohen, T.; Hu, Y.; Jiang, Q. Spatial measurement errors in the field of spatial epidemiology. Int. J. Health Geogr. 2016, 15, 21. [Google Scholar] [CrossRef] [PubMed]
- Pigott, T.D. A review of methods for missing data. Educ. Res. Eval. 2001, 7, 353–383. [Google Scholar] [CrossRef]
- Peugh, J.L.; Enders, C.K. Missing data in educational research: A review of reporting practices and suggestions for improvement. Rev. Educ. Res. 2004, 74, 525–556. [Google Scholar] [CrossRef]
- Graham, J.W. Missing data analysis: Making it work in the real world. Ann. Rev. Psychol. 2009, 60, 549–576. [Google Scholar] [CrossRef]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data, 2nd ed.; Wiley: London, UK, 2002. [Google Scholar]
- Carpenter, J.; Kenward, M. Multiple Imputation and its Application; Wiley: London, UK, 2013. [Google Scholar]
- Rezvan, P.H.; Lee, K.J.; Simpson, J.A. The rise of multiple imputation: A review of the reporting and implementation of the method in medical research. BMC Med. Res. Methodol. 2015, 15, 30. [Google Scholar] [CrossRef]
- Henry, K.A.; Boscoe, F.P. Estimating the accuracy of geographical imputation. Int. J. Health Geogr. 2008, 7, 3. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.W. A Geocoding Best Practices Guide; The North American Association of Central Cancer Registries: Springfield, IL, USA, 2008. [Google Scholar]
- Boscoe, F.P. The science and art of geocoding: Tips for improving match rates and handling unmatched cases in analysis. In Geocoding Health Data; Rushton, G., Armstrong, M.P., Gittler, J., Greene, B.R., Pavlik, C.E., West, M.M., Zimmerman, D.L., Eds.; CRC Press: New York, NY, USA, 2008; pp. 95–110. [Google Scholar]
- Zimmerman, D.L. Statistical methods for incompletely and incorrectly geocoded cancer data. In Geocoding Health Data; Rushton, G., Armstrong, M.P., Gittler, J., Greene, B.R., Pavlik, C.E., West, M.M., Zimmerman, D.L., Eds.; CRC Press: New York, NY, USA, 2008; pp. 165–180. [Google Scholar]
- Walter, S.R.; Rose, N. Random property allocation: A novel geographic imputation procedure based on a complete geocoded address file. Spat. Spatio-Temporal Epidemiol. 2013, 6, 7–16. [Google Scholar] [CrossRef]
- Bocci, C.; Rocco, E. Estimates for geographical domains through geoadditive models in presence of incomplete geographical information. Stat. Methods Appl. 2014, 23, 283–305. [Google Scholar] [CrossRef]
- Hibbert, J.D.; Liese, A.D.; Lawson, A.; Porter, D.E.; Puett, R.C.; Standiford, D.; Liu, L.; Dabelea, D. Evaluating geographic imputation approaches for zip code level data: An application to a study of pediatric diabetes. Int. J. Health Geogr. 2009, 8, 54. [Google Scholar] [CrossRef] [PubMed]
- Curriero, F.C.; Kulldorff, M.; Boscoe, F.P.; Klassen, A.C. Using imputation to provide location information for nongeocoded addresses. PLoS ONE 2010, 5, e8998. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, T.-C.; Matthews, S.A. Inferring censored geo-information with non-representative data. In Machine Learning and Data Mining in Pattern Recognition; Perner, P., Ed.; Springer: Basel, Switzerland, 2016; Volume 9729, pp. 229–235. ISBN 978-3-319-41919-0. [Google Scholar]
- Meseck, K.; Jankowska, M.M.; Schipperijn, J.; Natarajan, L.; Godbole, S.; Carson, J.; Temoto, M.; Crist, K.; Kerr, J. Is missing geographic positioning system data in accelerometry studies a problem, and is imputation the solution? Geospat. Health 2016, 11, 403. [Google Scholar] [CrossRef] [PubMed]
- Mason, M.J.; Mennis, J.; Light, J.; Rusby, J.; Westling, E.; Crewe, S.; Way, T.; Flay, B.; Zaharakis, N.M. Parents, peers, and places: Young urban adolescents’ microsystems and substance use involvement. J. Child Fam. Stud. 2016, 25, 1441–1450. [Google Scholar] [CrossRef] [PubMed]
- Mason, M.; Light, J.; Mennis, J.; Rusby, J.; Westling, E.; Way, T.; Zaharakis, N.; Flay, B. Neighborhood disorder, peer network health, and substance use among young urban adolescents. Drug Alcohol Depend. 2017, 178, 208–214. [Google Scholar] [CrossRef] [PubMed]
- Moberg, D.P.; Hahn, L. The adolescent drug involvement scale. J. Adolesc. Chem. Depend. 1991, 2, 75–88. [Google Scholar] [CrossRef]
- Ross, C.E.; Mirowsky, J. Neighborhood disadvantage, neighborhood disorder and health. J. Health Sociol. Behav. 2001, 42, 258–276. [Google Scholar] [CrossRef]
- Rubin, D.B. Inference and missing data. Biometrika 1976, 63, 581–592. [Google Scholar] [CrossRef]
- Andridge, R.R.; Little, R.J.A. A review of hot deck imputation for survey non-response. Int. Stat. Rev. 2010, 78, 40–64. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, A.E.; Bazzi, A.R.; Fish, S. Ethical considerations and potential threats to validity for three methods commonly used to collect geographic information in studies among people who use drugs. Addict. Behav. 2016, 61, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Rudolph, A.E.; Young, A.M.; Havens, J.R. Privacy, confidentiality, and safety considerations for conducting geographic momentary assessment studies among persons who use drugs and men who have sex with men. J. Urban Health 2018. [Google Scholar] [CrossRef] [PubMed]
- Mennis, J. Dasymetric spatiotemporal interpolation. Prof. Geogr. 2016, 68, 92–102. [Google Scholar] [CrossRef]

| Independent Variable | Model 1 | Model 2 |
|---|---|---|
| Intercept | 1.872 *** (1.648–2.096) | 1.753 *** (1.534–1.973) |
| Age 14 (Ref = Age 13) | 0.094 (−0.197–0.384) | 0.090 (−0.196–0.376) |
| Male (Ref = Female) | −0.168 (−0.449–0.113) | −0.184 (−0.460–0.091) |
| White (Ref = Af. American) | −0.569 *** (−0.959–(−0.188)) | −0.422 * (−0.789–(−0.056)) |
| Other Race (Ref = Af. American) | 0.169 (−0.286–0.624) | 0.316 (−0.146–0.778) |
| Substance Use | 0.027 *** (0.017–0.037) | 0.001 (−0.020–0.017) |
| Relative Disadvantage | 0.030 *** (0.013–0.047) | 0.031 *** (0.021–0.041) |
| Sub. Use X Rel. Disadvantage | 0.002 *** (0.001–0.003) |
| Variable | Valid N (# Subjects) | Minimum | Maximum | Mean (SD) |
|---|---|---|---|---|
| Original Disadvantage | 1617 (137) | −18.54 | 13.47 | −1.68 (7.30) |
| HD 50% Disadvantage | 1601 (127) | −18.54 | 13.47 | −2.77 (7.10) |
| ASC 50% Disadvantage | 1601 (127) | −18.54 | 13.47 | −1.97 (6.93) |
| HD 70% Disadvantage | 1609 (132) | −18.54 | 13.47 | −1.60 (7.33) |
| ASC 70% Disadvantage | 1608 (132) | −18.54 | 13.47 | −1.85 (6.96) |
| HD 90% Disadvantage | 1614 (135) | −18.54 | 13.47 | −1.89 (7.36) |
| ASC 90% Disadvantage | 1613 (135) | −18.54 | 13.47 | −1.62 (7.21) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mennis, J.; Mason, M.; Coffman, D.L.; Henry, K. Geographic Imputation of Missing Activity Space Data from Ecological Momentary Assessment (EMA) GPS Positions. Int. J. Environ. Res. Public Health 2018, 15, 2740. https://doi.org/10.3390/ijerph15122740
Mennis J, Mason M, Coffman DL, Henry K. Geographic Imputation of Missing Activity Space Data from Ecological Momentary Assessment (EMA) GPS Positions. International Journal of Environmental Research and Public Health. 2018; 15(12):2740. https://doi.org/10.3390/ijerph15122740
Chicago/Turabian StyleMennis, Jeremy, Michael Mason, Donna L. Coffman, and Kevin Henry. 2018. "Geographic Imputation of Missing Activity Space Data from Ecological Momentary Assessment (EMA) GPS Positions" International Journal of Environmental Research and Public Health 15, no. 12: 2740. https://doi.org/10.3390/ijerph15122740
APA StyleMennis, J., Mason, M., Coffman, D. L., & Henry, K. (2018). Geographic Imputation of Missing Activity Space Data from Ecological Momentary Assessment (EMA) GPS Positions. International Journal of Environmental Research and Public Health, 15(12), 2740. https://doi.org/10.3390/ijerph15122740




