Hotspot Identification for Shanghai Expressways Using the Quantitative Risk Assessment Method
Abstract
:1. Introduction
- (1)
- A new HSID method is developed based on the QRA technique. The occurrence of crashes is treated as the risk, and the probability and consequences of this risk are respectively modeled. While the crash occurrence probability for all passing vehicles is expressed by the expected crash frequency at each segment, the consequences refer to the total social losses (i.e., direct losses and indirect losses) of crashes. Thus, the high-risk sites are identified, where not only many crashes occur, but also the traffic operation is heavily influenced by crashes.
- (2)
- A classical Empirical Bayes (EB) method is used to calculate the expected crash frequency for each site. Since observed frequency and prediction of the frequency of crashes are both considered in EB, the Bayesian negative binomial model is introduced as the crash prediction model (CPM).
- (3)
- Total social losses are used as the consequences of crashes. That is to say, the direct occupant injuries and property losses and the additional delay losses caused by a crash are both considered. The two parts of losses are quantitatively monetized. While the direct losses are estimated based on the crash type, additional delay losses are calculated using the queue theory.
2. Literature Review
3. Study Area and Data Collection
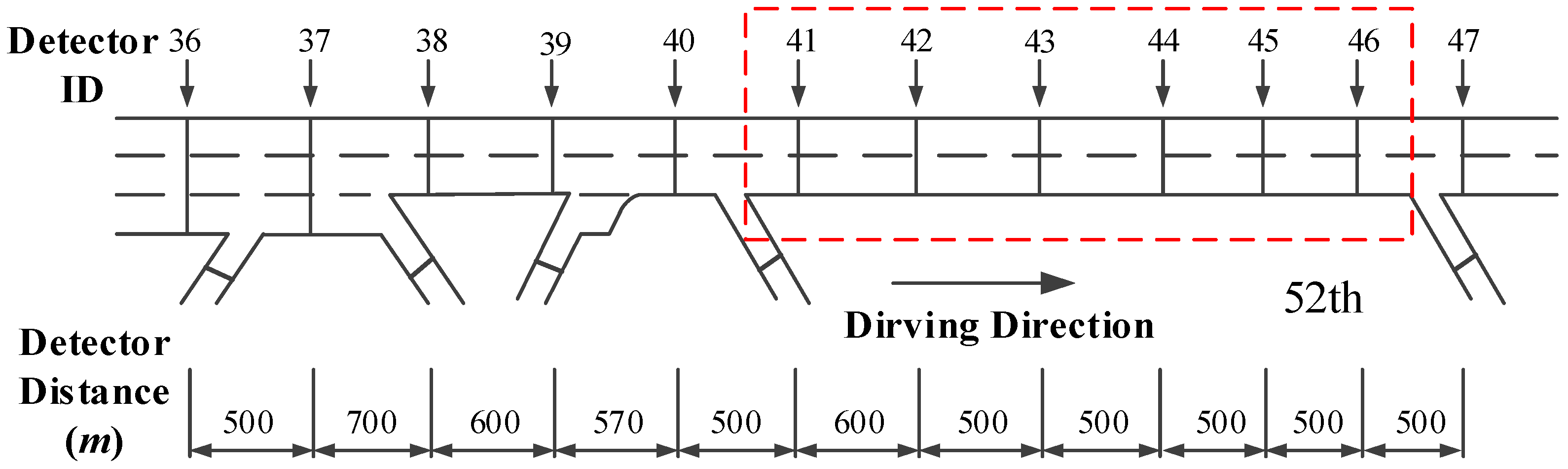
3.1. Study Area
3.2. Traffic Flow Data
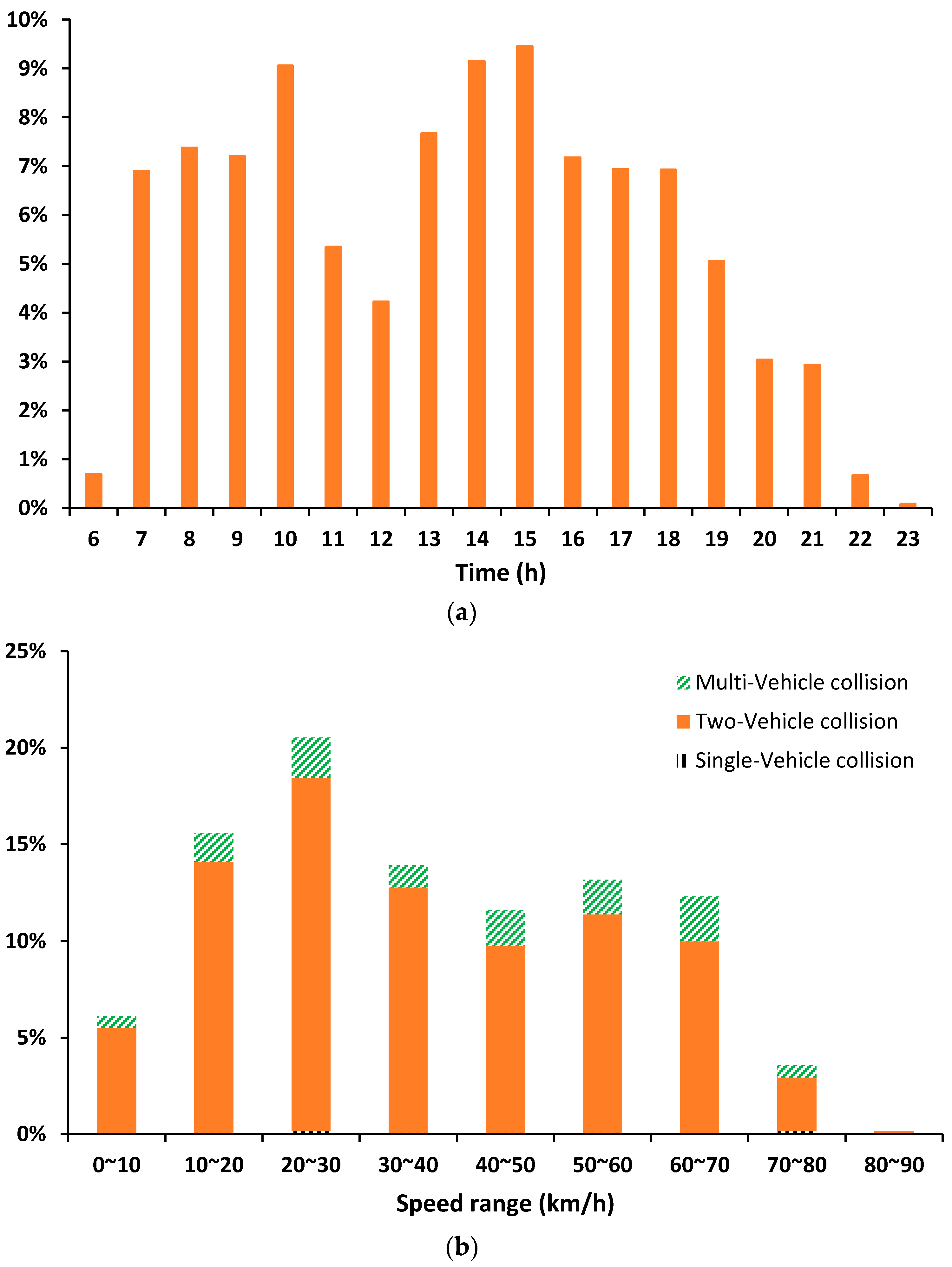
3.3. Crash Data
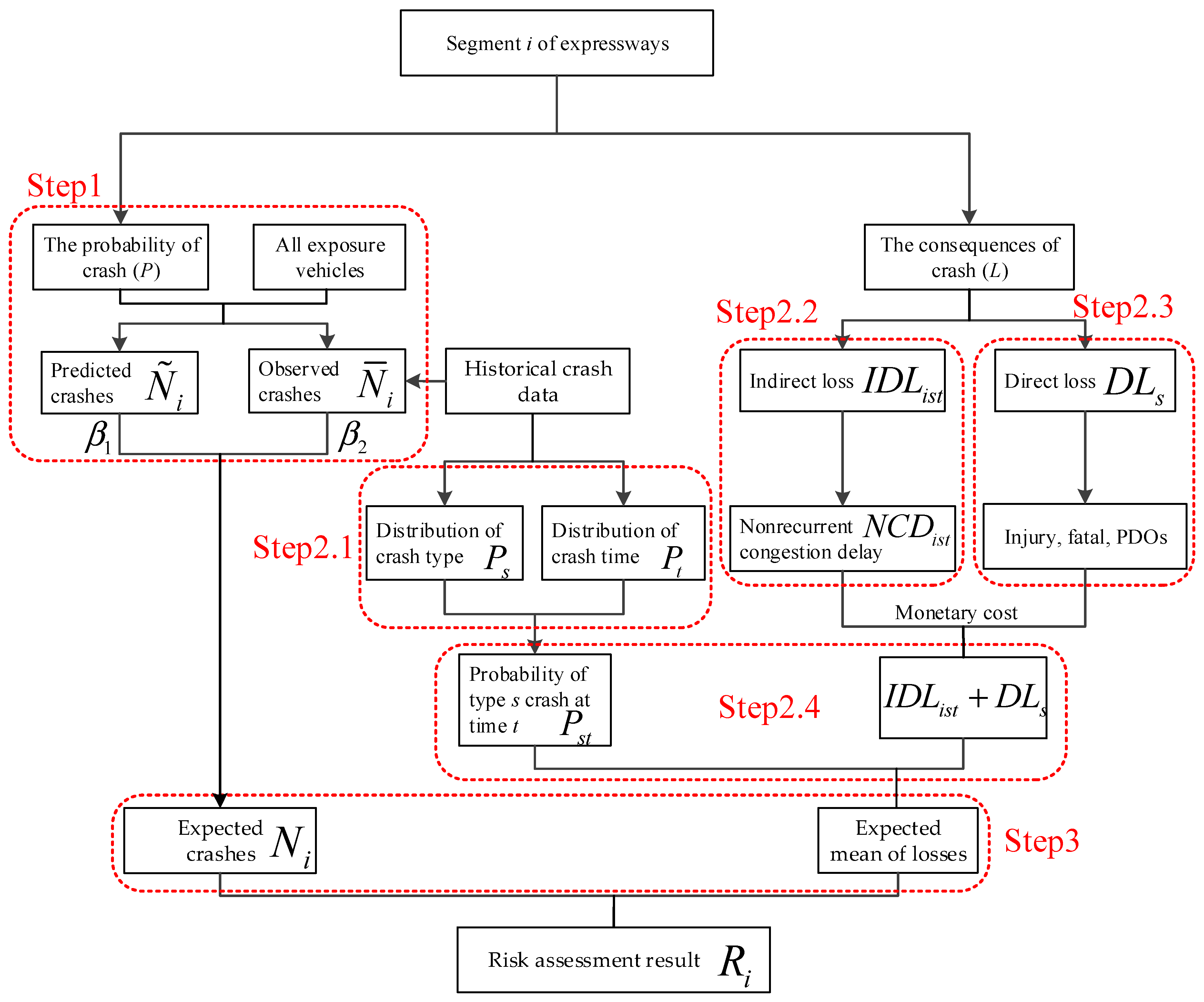
4. Methodology
Crash Risk Assessment Model
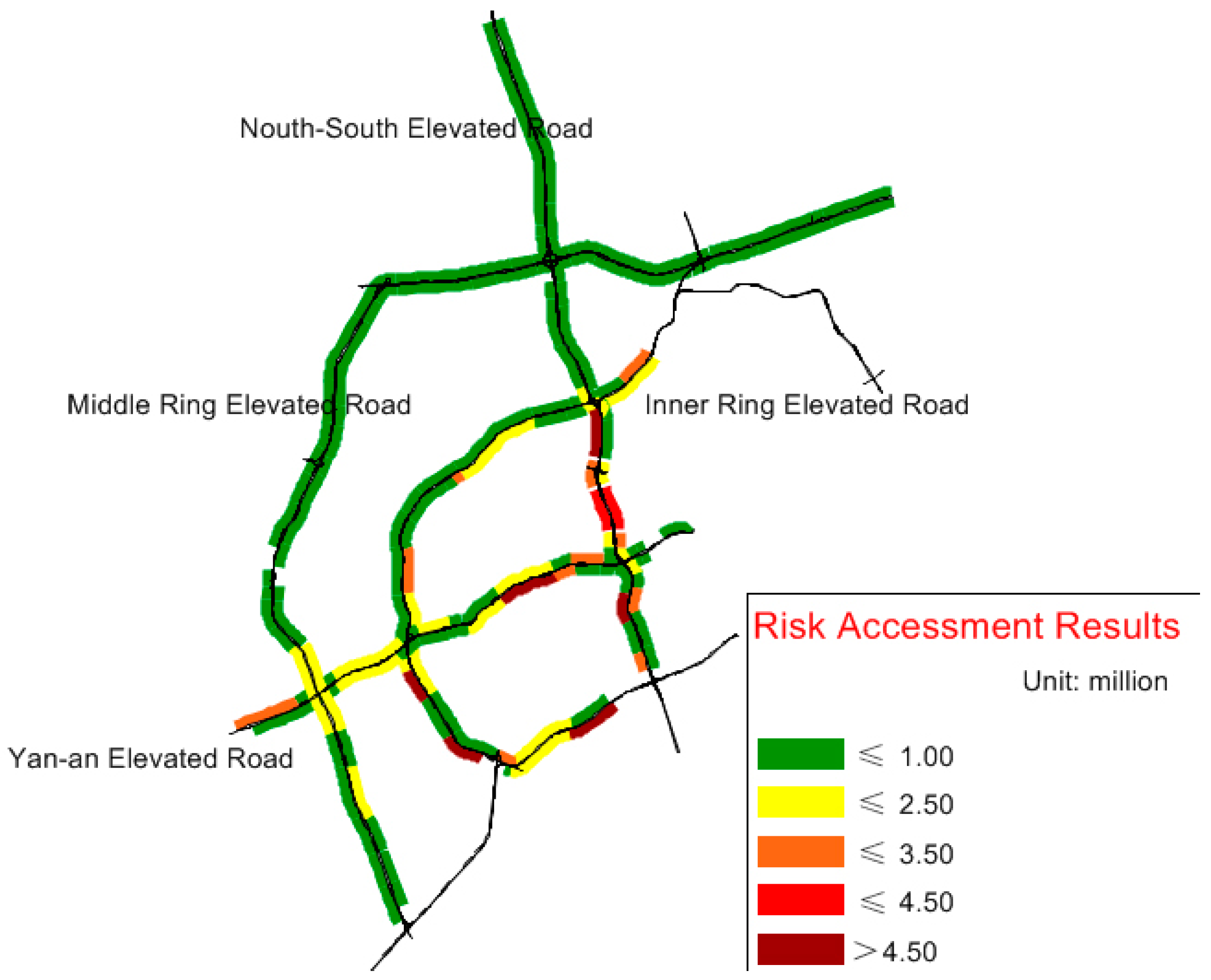
5. Case Study
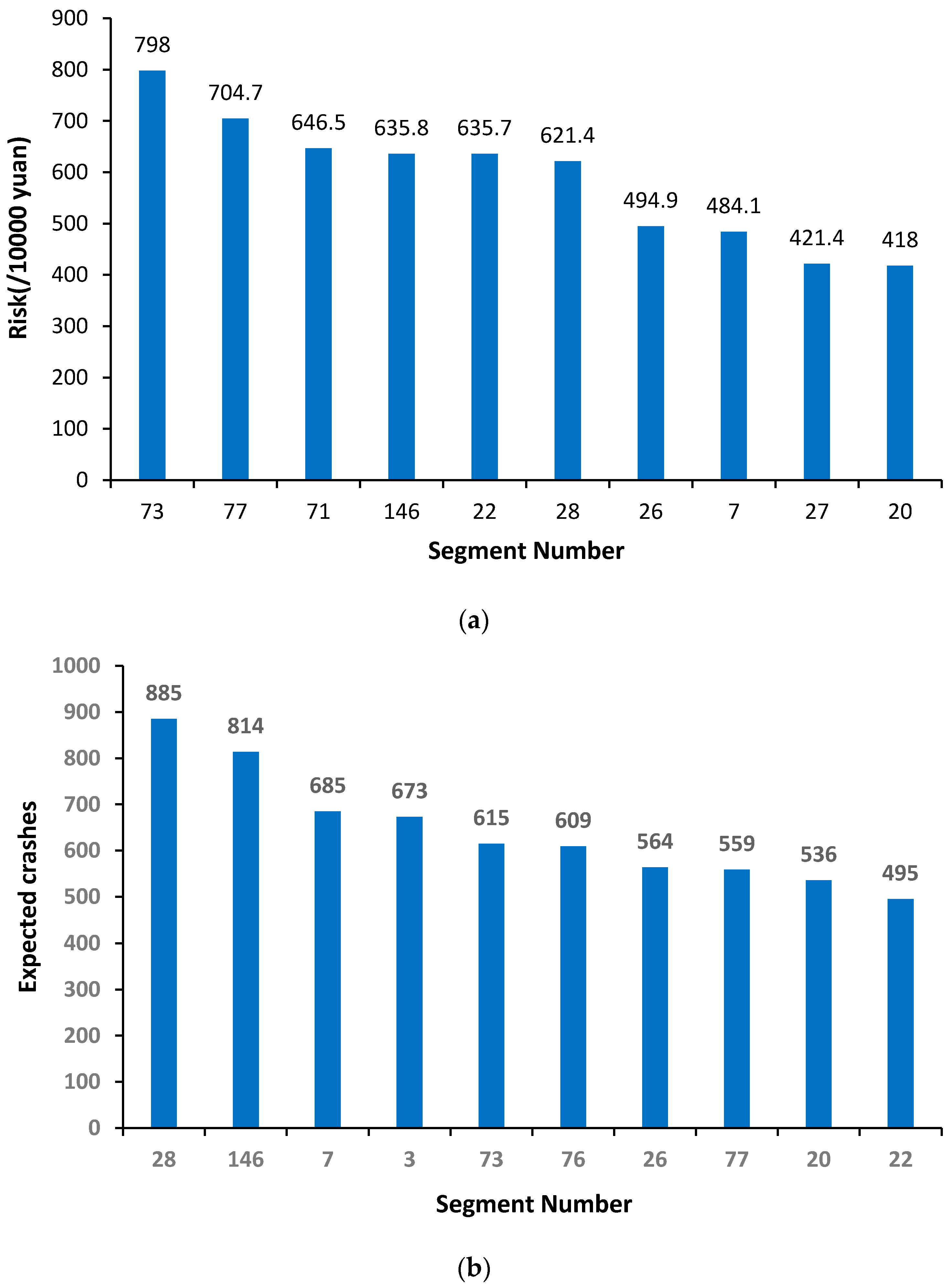
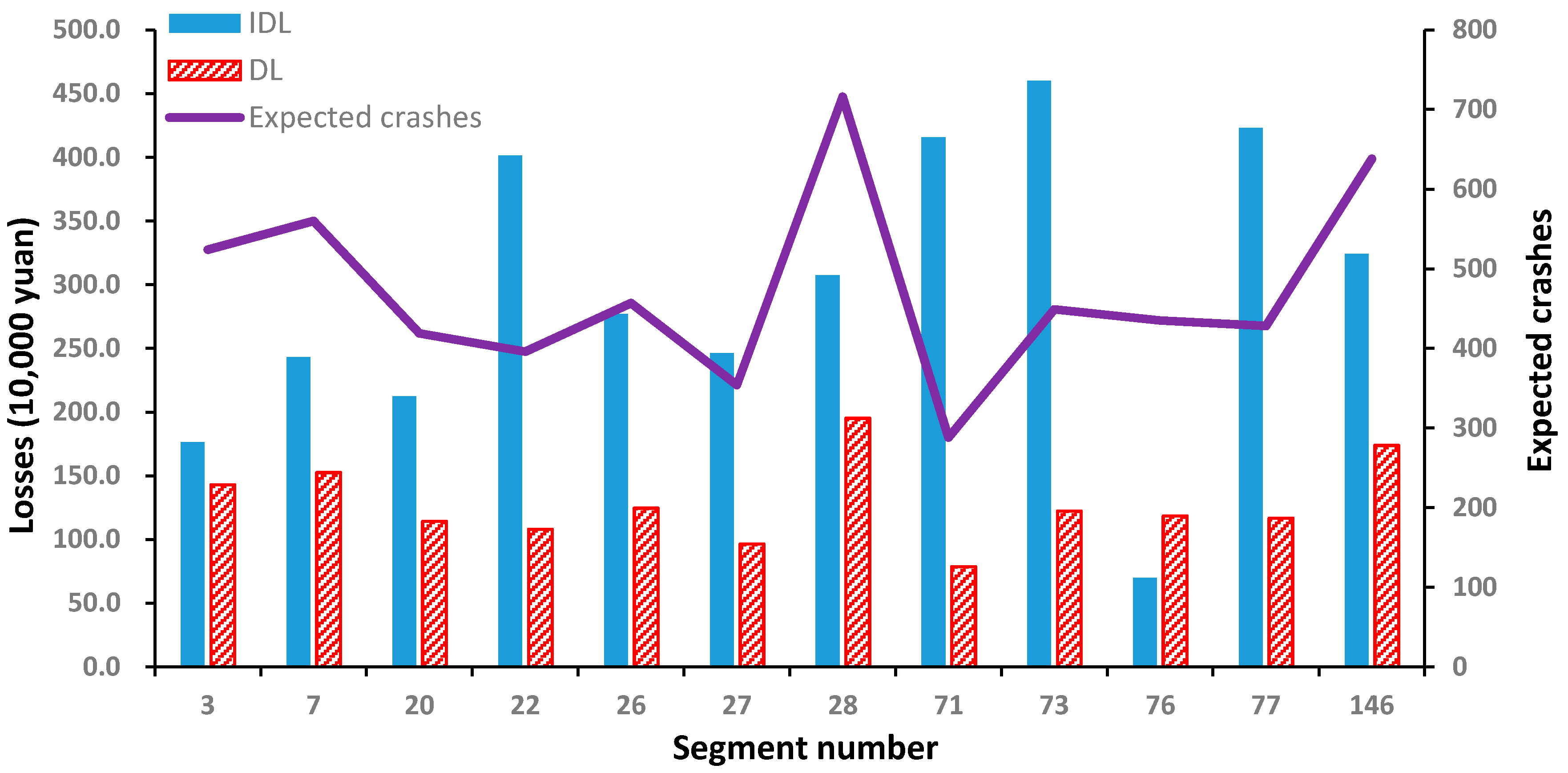
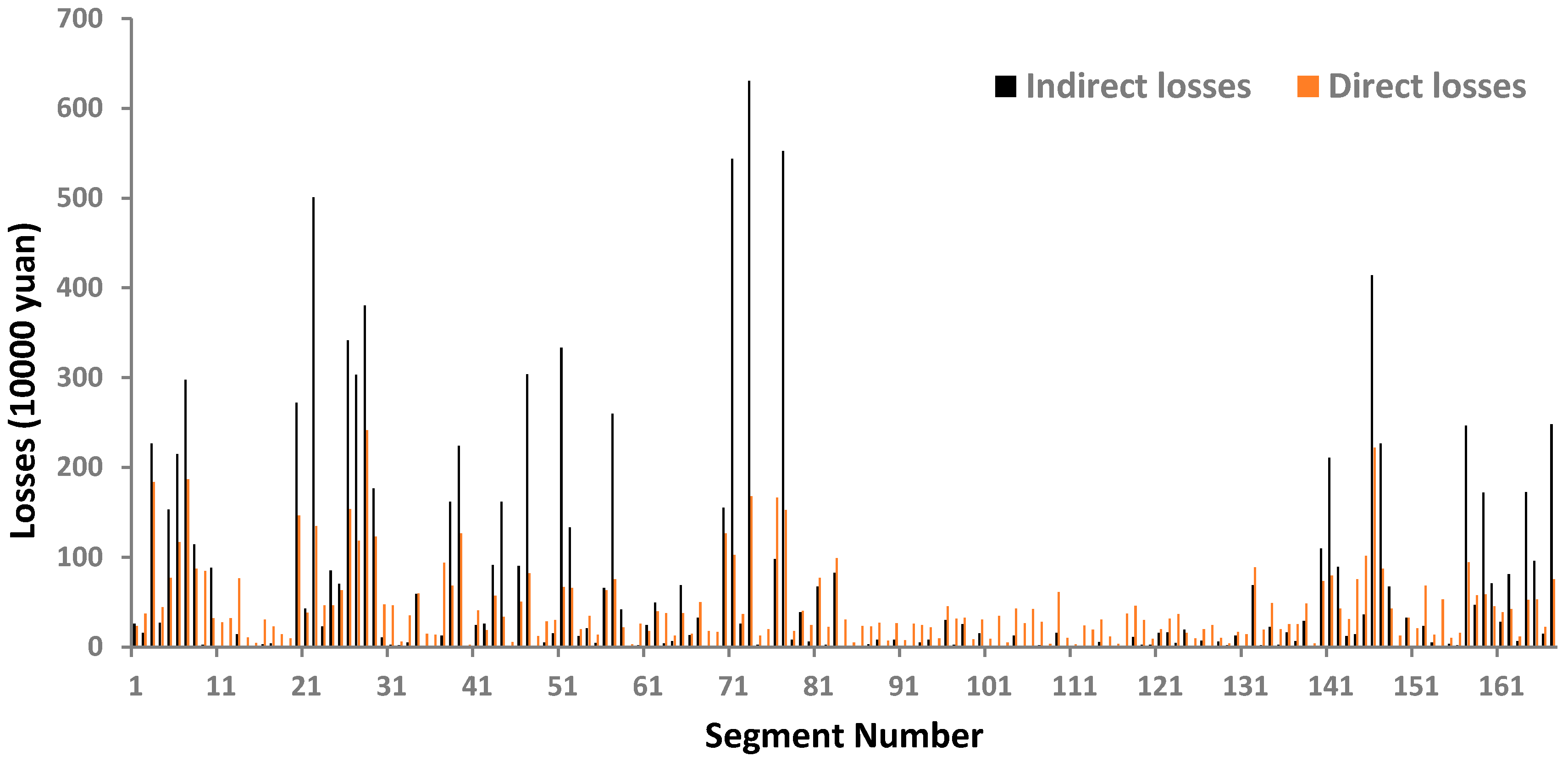
6. Results and Analysis
7. Conclusions
- (1)
- The use of the QRA method enables the identification of a set of high-risk sites that reveal the potential total crash costs to society. The case study results show that the rankings of hotspots are different between the conventional EB method and the new QRA method.
- (2)
- In the QRA framework for the probability of crashes, in order to take full account of the uncertainty existing between roadway characteristics and crashes, EB combined with the Bayesian negative binomial model is used to calculate the expected number of crashes. It is shown that the classical EB is applicable and provides a robust result for the probability of crashes.
- (3)
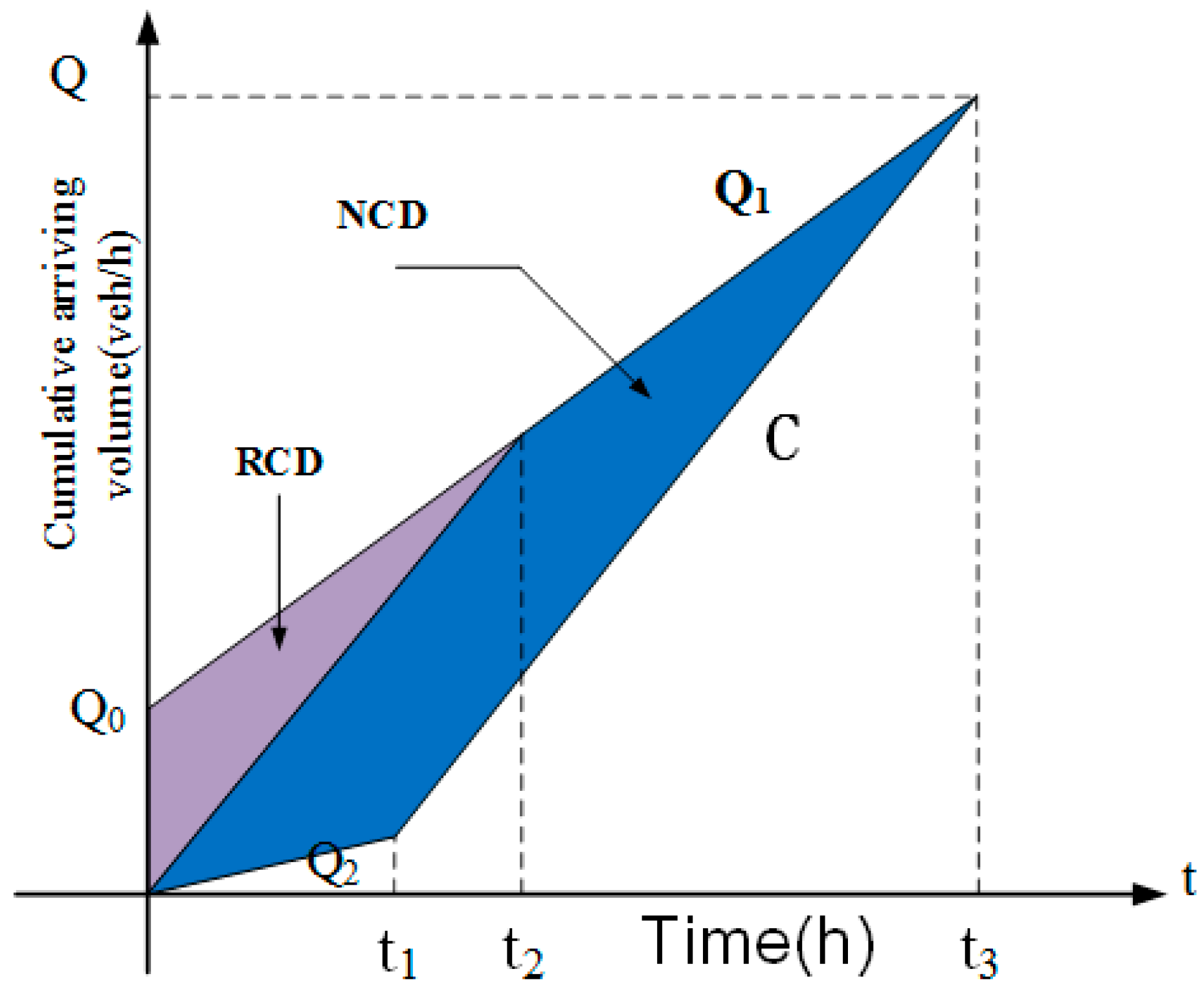
- In the QRA framework, for the consequences of crashes, the equivalent monetary index is applied to unify the direct and indirect losses. Indirect losses of crashes are quantitatively estimated by using the queue theory. The traffic situation when crashes happen and the crash type are sampled using Monte Carlo sampling.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sun, J.; Li, T.; Li, F.; Chen, F. Analysis of safety factors for urban expressways considering the effect of congestion in Shanghai, China. Accid. Anal. Prev. 2016, 95, 503–511. [Google Scholar] [CrossRef] [PubMed]
- Systematics, C. Traffic Congestion and Reliability Trends and Advanced Strategies for Congestion Mitigation; FHWA Report; US Department of Transportation, Federal Highway Administration: McLean, VA, USA, 2005.
- Skabardonis, A.; Varaiya, P.; Petty, K. Measuring recurrent and nonrecurrent traffic congestion. Transp. Res. Rec. 2003, 1856, 118–124. [Google Scholar] [CrossRef]
- Council, F.; Zaloshnja, E.; Miller, T.; Persaud, B.N. Crash Cost Estimates by Maximum Police-Reported Injury Severity within Selected Crash Geometries; Federal Highway Administration: McLean, VA, USA, 2005.
- The Ministry of Public Security Road Traffic Accident Data Collection Table 2006. Available online: http://ishare.iask.sina.com.cn/f/13441736.html (accessed on 13 November 2016).
- Deacon, J.A.; Zegeer, C.V.; Deen, R.C. Identification of Hazardous Rural Highway Locations; Reseach Report No. 410; Transportation Research Board: Washington, DC, USA, 1975. [Google Scholar]
- Persaud, B.N. Statistical Methods in Highway Safety Analysis, NCHRP Synthesis 295; Transportation Research Board: Washington, DC, USA, 2001. [Google Scholar]
- Huang, H.; Chin, H.; Haque, M. Empirical evaluation of alternative approaches in identifying crash hot spots: Naive ranking, empirical bayes, and full bayes methods. Transp. Res. Rec. 2009, 2013, 32–41. [Google Scholar] [CrossRef]
- Laughland, J.C.; Haefner, L.E.; Hall, J.W.; Clough, D.R. Methods for Evaluating Highway Safety Improvements; No. HS-018 724; Transportation Research Board: Washington, DC, USA, 1975. [Google Scholar]
- Persaud, B.; Lyon, C.; Nguyen, T. Empirical bayes procedure for ranking sites for safety investigation by potential for safety improvement. Transp. Res. Rec. 1999, 1665, 7–12. [Google Scholar] [CrossRef]
- Hauer, E.; Harwood, D.; Council, F.; Griffith, M. Estimating safety by the empirical bayes method: A tutorial. Transp. Res. Rec. 2002, 1784, 126–131. [Google Scholar] [CrossRef]
- Elvik, R. State-of-the-Art Approaches to Road Accident Black Spot Management and Safety Analysis of Road Networks; Transport Konomisk Institute: Oslo, Norway, 2007. [Google Scholar]
- Cheng, W.; Washington, S.P. Experimental evaluation of hotspot identification methods. Accid. Anal. Prev. 2005, 37, 870–881. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, L.; Thorpe, N. Mobile safety cameras: Estimating casualty reductions and the demand for secondary healthcare. J. Appl. Stat. 2013, 40, 2385–2406. [Google Scholar] [CrossRef]
- Heydari, S.; Miranda-Moreno, L.; Amador, L. Does prior specification matter in hotspot identification and before-after studies in road safety. Transp. Res. Rec. 2013, 2392, 31–39. [Google Scholar] [CrossRef]
- Miranda-Moreno, L.F.; Fu, L. Traffic safety study: Empirical bayes or full bayes? In Proceedings of the Transportation Research Board 86th Annual Meeting, Washington, DC, USA, 21–25 January 2007.
- Montella, A. A comparative analysis of hotspot identification methods. Accid. Anal. Prev. 2010, 42, 571–581. [Google Scholar] [CrossRef] [PubMed]
- Sacchi, E.; Sayed, T.; El-Basyouny, K. Multivariate full bayesian hot spot identification and ranking: New technique. Transp. Res. Rec. 2015, 2515, 1–9. [Google Scholar] [CrossRef]
- Washington, S.; Haque, M.; Oh, J.; Lee, D. In identifying black spots using property damage only equivalency (PDOE) factors. In Proceedings of the 16th International Conference Road Safety on Four Continents (RS4C 2013), Beijing, China, 15–17 May 2013.
- Tarko, A.; Kanodia, M. Hazard elimination program-manual on improving safety of Indiana road intersections and sections. Joint Transp. Res. Program 2004, 1–2, 112. [Google Scholar]
- Wang, C.; Quddus, M.A.; Ison, S.G. Predicting accident frequency at their severity levels and its application in site ranking using a two-stage mixed multivariate model. Accid. Anal. Prev. 2011, 43, 1979–1990. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Kockelman, K.M.; Damien, P. A multivariate poisson-lognormal regression model for prediction of crash counts by severity, using Bayesian methods. Accid. Anal. Prev. 2008, 40, 964–975. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Qu, X.; Yong, K.T.; Wong, Y.H. Qra model-based risk impact analysis of traffic flow in urban road tunnels. Risk Anal. 2011, 31, 1872–1882. [Google Scholar] [CrossRef] [PubMed]
- Tu, H.; Li, H.; Van Lint, H.; van Zuylen, H. Modeling travel time reliability of freeways using risk assessment techniques. Transp. Res. A-Policy 2012, 46, 1528–1540. [Google Scholar] [CrossRef]
- Tamasi, G.; Demichela, M. Risk assessment techniques for civil aviation security. Reliab. Eng. Syst. Saf. 2011, 96, 892–899. [Google Scholar] [CrossRef]
- Stroeve, S.H.; Blom, H.A.; Bakker, G.B. Systemic accident risk assessment in air traffic by monte carlo simulation. Saf. Sci. 2009, 47, 238–249. [Google Scholar] [CrossRef]
- American Association of State Highway Transportation Officials (AASHTO). Highway Safety Manual; AASHTO: Washington, DC, USA, 2010; Volume 2. [Google Scholar]
- Chung, Y.; Recker, W.W. A methodological approach for estimating temporal and spatial extent of delays caused by freeway accidents. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1454–1461. [Google Scholar] [CrossRef]
- Chin, S.; Franzese, O.; Greene, D.; Hwang, H.; Gibson, R. Temporary Losses of Highway Capacity and Impacts on Performance; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2002. [Google Scholar]
- Morales, J.M. Analytical procedures for estimating freeway traffic congestion. ITE J. 1987, 57, 45–49. [Google Scholar]
- Goolsby, M.E. Influence of incidents on freeway quality of service. Highway Res. Rec. 1971, 349, 41–46. [Google Scholar]
- Shanghai Public Security Bureau. Shanghai Road Traffic Accident Statistics Yearbook; SPSB Report; Shanghai Public Security Bureau: Shanghai, China, 2014.
- Shanghai Municipal Government. Shanghai Economic Operation Report; DRC Report; Development Research Center, Shanghai Municipal Government: Shanghai, China, 2014.
- Yu, H.; Liu, P.; Chen, J.; Wang, H. Comparative analysis of the spatial analysis methods for hotspot identification. Accid. Anal. Prev. 2014, 66, 80–88. [Google Scholar] [CrossRef] [PubMed]
- Loo, B.P.Y.; Yao, S.; Wu, J. Spatial point analysis of road crashes in Shanghai: A GIS-based network kernel density method. In Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–6.

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Li, T.; Sun, J.; Chen, F. Hotspot Identification for Shanghai Expressways Using the Quantitative Risk Assessment Method. Int. J. Environ. Res. Public Health 2017, 14, 20. https://doi.org/10.3390/ijerph14010020
Chen C, Li T, Sun J, Chen F. Hotspot Identification for Shanghai Expressways Using the Quantitative Risk Assessment Method. International Journal of Environmental Research and Public Health. 2017; 14(1):20. https://doi.org/10.3390/ijerph14010020
Chicago/Turabian StyleChen, Can, Tienan Li, Jian Sun, and Feng Chen. 2017. "Hotspot Identification for Shanghai Expressways Using the Quantitative Risk Assessment Method" International Journal of Environmental Research and Public Health 14, no. 1: 20. https://doi.org/10.3390/ijerph14010020
APA StyleChen, C., Li, T., Sun, J., & Chen, F. (2017). Hotspot Identification for Shanghai Expressways Using the Quantitative Risk Assessment Method. International Journal of Environmental Research and Public Health, 14(1), 20. https://doi.org/10.3390/ijerph14010020





