Empirical Analysis and Modeling of Stop-Line Crossing Time and Speed at Signalized Intersections
Abstract
:1. Introduction
2. Past Research
3. Data Preparation
3.1. Site Descriptions
3.2. Data Collection and Reduction
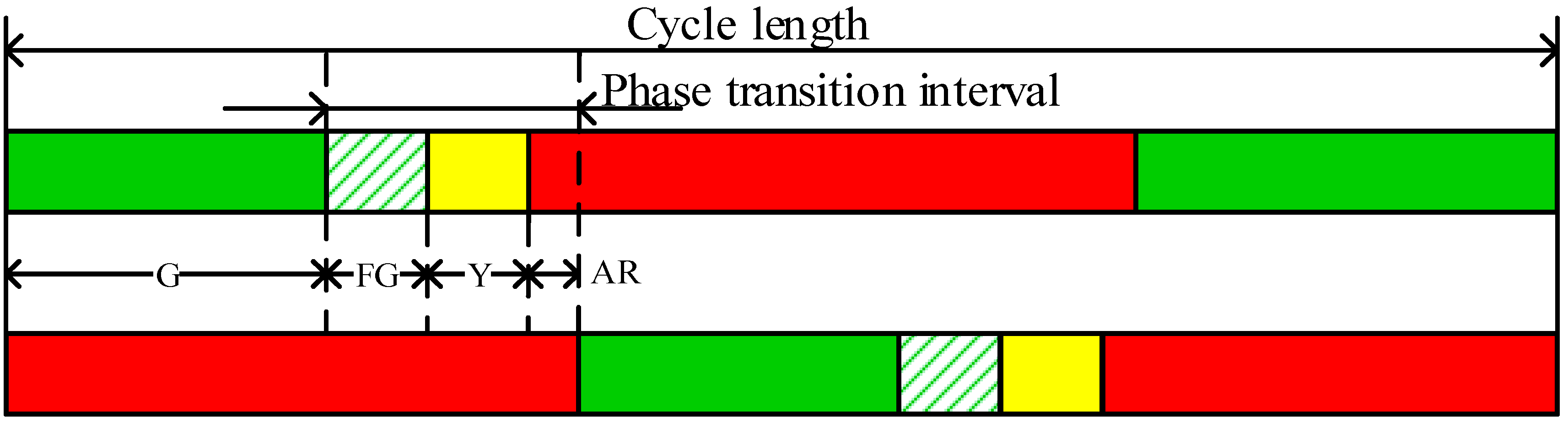
4. Statistical Characteristics of Stop-Line Crossing Behavior
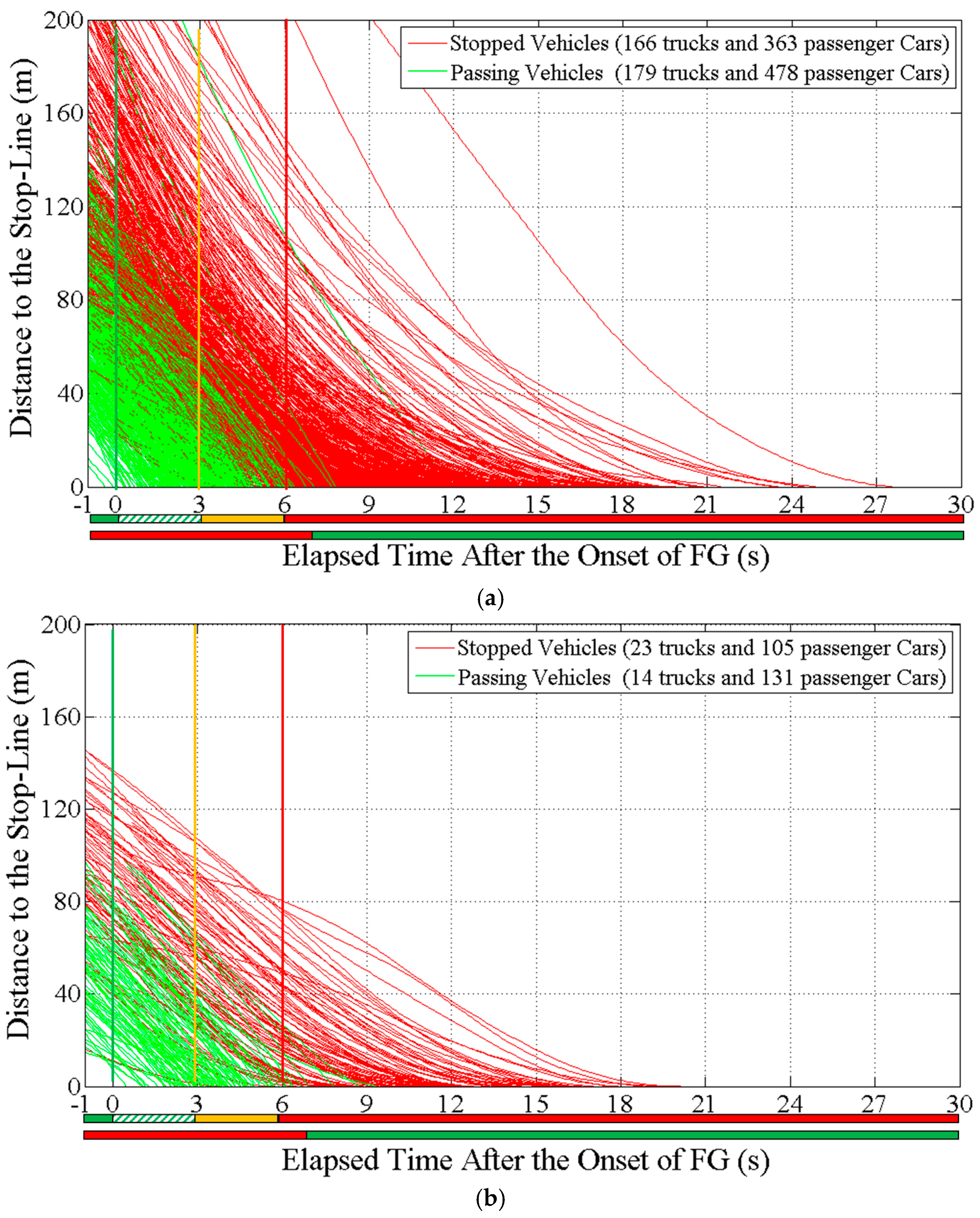
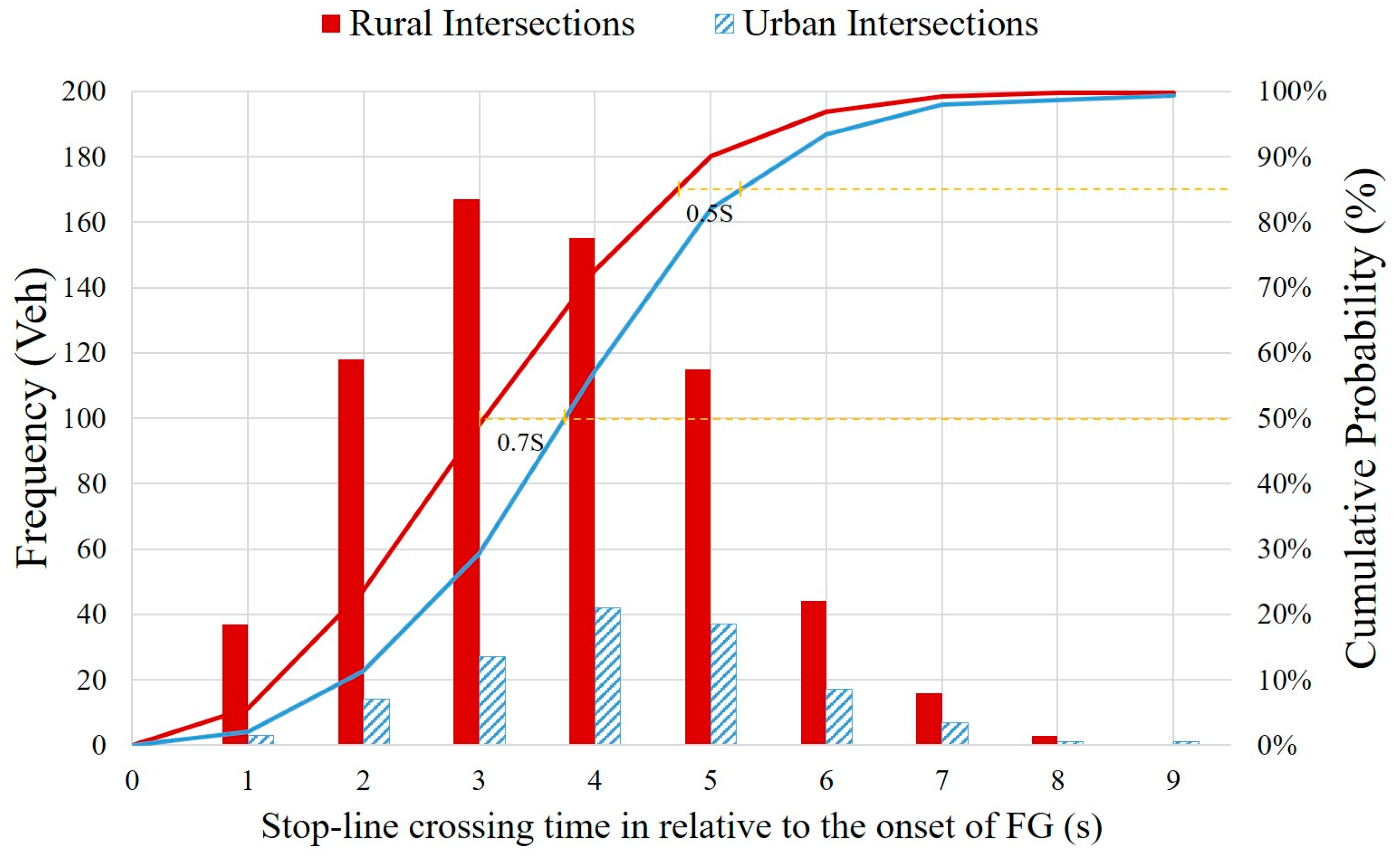
4.1. Statistical Characteristics of Stop-Line Crossing Time
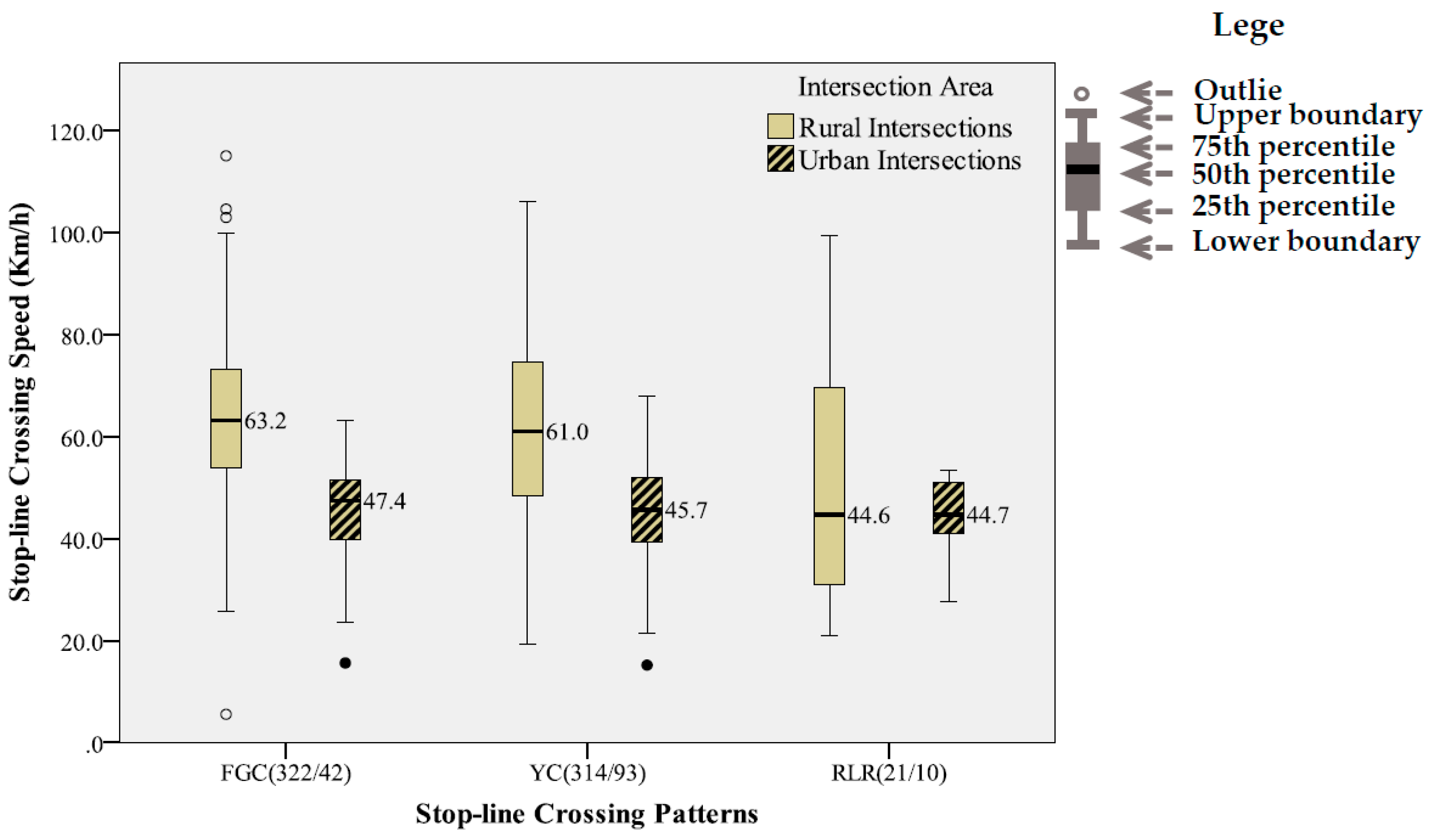
4.2. Statistical Characteristics of Stop-Line Crossing Speed
5. Prediction of Stop-Line Crossing Time and Speed
5.1. Prediction of Stop-Line Crossing Time
- VT = Vehicle Type, binary variable, 1 = Truck and 0 = Passenger Car;
- AT = Area Type, binary variable, 1 = Urban Area and 0 = Rural Area;
- IT = Intersection Type, binary variable, 1 = Large Intersection and 0 = Small Intersection;
- VFG = Speed at the onset of FG (km/h), continuous variable;
- DFG = Distance to the stop-line at the onset of FG (m), continuous variable.
5.2. Prediction of Stop-Line Crossing Speed
6. Conclusions
- Compared with the rural intersections, the urban intersections had a higher ratio of stop-line crossings during the Y interval and an approximately 0.7 s longer stop-line crossing time which is defined as the elapsed time after the onset of FG.
- Not only approaching speed and distance to the stop-line at the onset of FG, but also area type, imposed a significant influence on the ratios of the FGC and YC patterns to the STOP pattern. Area type also positively contributed to the ratio of the YC pattern to the STOP pattern; in addition, the ratio of RLR to STOP was higher at the large intersections with a long cycle length.
- The larger the approaching speed and the distance to the stop-line were, the higher the stop-line crossing speed was. Stop-line crossing speed was also significantly higher for the rural intersections, the passenger cars, and the FGC pattern.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, K.; Xu, Y.; Wang, P.; Wang, F. Impacts of flashing green on dilemma zone behavior at high-speed intersections: Empirical study in China. J. Transp. Eng. 2015, 141, 04015005. [Google Scholar] [CrossRef]
- Ma, W.; Liu, Y.; Yang, X. Investigating the impacts of green signal countdown devices: Empirical approach and case study in China. J. Transp. Eng. 2010, 136, 1049–1055. [Google Scholar] [CrossRef]
- Federal Highway Administration (FHWA). Manual on Uniform Traffic Control Devices (MUTCD); Department of Transportation: Washington, DC, USA, 2009.
- Japan Society of Traffic Engineers. Manual on Traffic Signal Control, Revised ed.; Maruzen Publishing Co., Ltd.: Tokyo, Japan, 2006. [Google Scholar]
- Forschungsgesellschaft für Straßen- und Verkehrswesen (FGSV). (Guidelines for Traffic Signals) Richtlinien für Lichtsignalanlagen; RiLSA: Köln, Germany, 1992. (In German) [Google Scholar]
- Leaflet, T.A. General Principles of Traffic Control by Light Signals; Department for Transport: London, UK, 2006.
- Austroads. Guide to Traffic Engineering Practice Series: Traffic Signals; Austroads: Sydney, Australia, 2003. [Google Scholar]
- Devalla, J.; Biswas, S.; Ghosh, I. The effect of countdown timer on the approach speed at signalised intersections. Procedia Comput. Sci. 2015, 52, 920–925. [Google Scholar] [CrossRef]
- Transportation Research Board. Highway Capacity Manual 2010 (HCM 2010); National Research Council: Washington, DC, USA, 2010. [Google Scholar]
- Tang, K.; Kuwahara, M.; Tanaka, S. Design of intergreen times based on safety reliability. Transp. Res. Rec. 2011, 2259, 213–222. [Google Scholar] [CrossRef]
- Zimmerman, K.; Bonneson, J. Investigation of time into red for red light-related crashes. Transp. Res. Rec. 2005, 1922, 21–28. [Google Scholar] [CrossRef]
- Transportation Research Board. Highway Safety Manual 2010 (HSM 2010); National Research Council: Washington, DC, USA, 2010. [Google Scholar]
- Sunkari, S.; Messer, C.; Charara, H. Performance of advance warning for end of green system for high-speed signalized intersections. Transp. Res. Rec. 2005, 1925, 176–184. [Google Scholar] [CrossRef]
- Appiah, J.; Naik, B.; Wojtal, R.; Rilett, L. Safety Effectiveness of Actuated Advance Warning Systems. Transp. Res. Rec. 2011, 2250, 19–24. [Google Scholar] [CrossRef]
- Yan, X.; Liu, Y.; Xu, Y. Effect of audio in-vehicle red light-running warning message on driving behavior based on a driving simulator experiment. Traffic Inj. Prev. 2014, 16, 48–54. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, L.; Zhou, K.; Zhang, W. Dynamic all-red extension at a signalized intersection: A framework of probabilistic modeling and performance evaluation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 166–179. [Google Scholar] [CrossRef]
- Prashker, J.N.; Mahalel, D. The relationship between an option space and drivers’ indecision at signalized intersection approaches. Transp. Res. B Methodol. 1989, 23, 401–413. [Google Scholar] [CrossRef]
- Tang, K.; Zhu, S.; Xu, Y.; Wang, F. Modeling drivers’ dynamic decision-making behavior during the phase transition period: An analytical approach based on hidden markov model theory. IEEE Trans. Intell. Transp. Syst. 2016, 17, 206–214. [Google Scholar] [CrossRef]
- Mahalel, D.; Zaidel, D.M. Safety evaluation of a flashing-green light in a traffic signal. Traffic Eng. Control 1985, 26, 79–81. [Google Scholar]
- Newton, C.; Mussa, R.N.; Sadalla, E.K.; Burns, E.K.; Matthias, J. Evaluation of an alternative traffic light change anticipation system. Accid. Anal. Prev. 1997, 29, 201–209. [Google Scholar] [CrossRef]
- Köll, H.; Bader, M.; Axhausen, K.W. Driver behaviour during flashing green before amber: A comparative study. Accid. Anal. Prev. 2004, 36, 273–280. [Google Scholar] [CrossRef]
- Prashker, J.N.; Mahalel, D. The flashing green light paradox. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 279–288. [Google Scholar]
- Tang, K.; Xu, Y.; Wang, F.; Oguchi, T. Exploring stop-go decision zones at rural high-speed intersections with flashing green signal and insufficient yellow time in China. Accid. Anal. Prev. 2016, 95, 470–478. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Li, Z.; Yi, P.; Duemmel, K. Quantifying dynamic factors contributing to dilemma zone at high-speed signalized intersections. Transp. Res. Rec. 2011, 2259, 202–212. [Google Scholar] [CrossRef]
- Gates, T.J.; Noyce, D.A. Dilemma zone driver behavior as a function of vehicle type, time of day, and platooning. Transp. Res. Rec. 2010, 2149, 84–93. [Google Scholar] [CrossRef]
- Papaioannou, P. Driver behaviour, dilemma zone and safety effects at urban signalised intersections in Greece. Accid. Anal. Prev. 2007, 39, 147–158. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Abbas, M. stochastic dilemma hazard model at high-speed signalized intersections. J. Transp. Eng. 2010, 136, 448–456. [Google Scholar] [CrossRef]
- Elmitiny, N.; Yan, X.; Radwan, E.; Russo, C.; Nashar, D. Classification analysis of driver’s stop/go decision and red-light running violation. Accid. Anal. Prev. 2010, 42, 101–111. [Google Scholar] [CrossRef] [PubMed]
- Rakha, H.; El-Shawarby, I.; Setti, J.R. Characterizing driver behavior on signalized intersection approaches at the onset of a yellow-phase trigger. IEEE Trans. Intell. Transp. Syst. 2008, 8, 630–640. [Google Scholar] [CrossRef]
- Hurwitz, D.S.; Knodler, M.A.; Nyquist, B. Evaluation of driver behavior in type II dilemma zones at high-speed signalized intersections. J. Traffic Transp. Eng. 2011, 137, 277–286. [Google Scholar] [CrossRef]
- Moore, D.D.A. Fuzzy logic for improved dilemma zone identification: A simulator study. Transp. Res. Rec. 2012, 2384, 25–34. [Google Scholar] [CrossRef]
| Intersections | Cao’an Road & Jiasongbei Road | Cao’an Road & Xiangjiang Road | Cao’an Road & Caofeng Road | Siping Road & Dalian Road | Rende Road & Jipu Road |
|---|---|---|---|---|---|
| Area Type | Rural Area | Urban Area | |||
| Speed Limit | 80 km/h | 50 km/h | |||
| Approaches | EB | EB | WB/EB | EB | NB |
| Lane Configuration | L-T-T-T-R | L-T-T-T-R | L-T-T-T-TR | L-L-T-TR | L-TR |
| Intersection Size | 72 m | 72 m | 48 m | 64 m | 40 m |
| Cycle Length | 161 s | 160 s | 104 s | 200 s | 86 s |
| Number of Phases | 4 | 4 | 3 | 4 | 2 |
| Green Time | 38 s | 45 s | 45 s | 77 s | 45 s |
| Flashing Green Time | 3 s | 3 s | 3 s | 3 s | 3 s |
| Yellow Time | 3 s | 3 s | 3 s | 3 s | 3 s |
| All-Red Time | 1 s | 1 s | 1 s | 2 s | 1 s |
| Observation Time Periods | 12 AM Peak Hours and 6 PM Off-Peak Hours | 4 AM Peak Hours and 4 PM Off-Peak Hours | 8 AM Peak Hours | 8 PM Peak Hours | 2 AM Peak Hours and 8 PM Off-Peak Hours |
| First-to-Go Vehicles (Passenger Cars/Trucks) | 201 (156/45) | 153 (119/34) | 165 (115/50) | 177 (127/50) | 112 (103/9) |
| Last-to-Stop Vehicle (Passenger Cars/Trucks) | 156 (111/45) | 101 (77/24) | 272 (175/97) | 75 (68/7) | 53 (37/16) |
| FGC (Passenger Cars/Trucks) | 111 (85/26) | 62 (49/13) | 58 (35/23) | 91 (63/28) | 40 (38/2) |
| YC (Passenger Cars/Trucks) | 83 (65/18) | 82 (64/18) | 104 (78/26) | 84 (63/21) | 63 (58/5) |
| RLR (Passenger Cars/Trucks) | 7 (6/1) | 9 (6/3) | 3 (2/1) | 2 (1/1) | 9 (7/2) |
| Intersection Area Types | Variables | Statistical Parameters | Stop-Line Crossing Patterns | |||
|---|---|---|---|---|---|---|
| FGC | YC | RLR | STOP | |||
| Rural Intersections (Speed Limit: 80 km/h) | DFG, m | Mean | 35.0 | 72.0 | 92.1 | 104.8 |
| Standard Deviation | 15.3 | 20.4 | 22.6 | 37.2 | ||
| Min | 3.2 | 6.3 | 49.8 | 23.1 | ||
| Max | 98.1 | 125.6 | 132.9 | 217.7 | ||
| # (%) | 322 (27.2%) | 314 (26.5%) | 21 (1.8%) | 529 (44.6%) | ||
| VFG, km/h | Mean | 63.4 | 61.8 | 50.4 | 59.3 | |
| Standard Deviation | 15.1 | 17.6 | 23.9 | 18.9 | ||
| Min | 5.6 | 19.4 | 20.9 | 16.7 | ||
| Max | 115.0 | 106.2 | 99.3 | 118.9 | ||
| # (%) | 322 (27.2%) | 314 (26.5%) | 21 (1.8%) | 529 (44.6%) | ||
| Urban Intersections (Speed Limit: 50 km/h) | DFG, m | Mean | 28.8 | 52.6 | 80.2 | 95.8 |
| Standard Deviation | 14.0 | 15.0 | 16.2 | 26.9 | ||
| Min | 7.5 | 20.9 | 53.2 | 39.8 | ||
| Max | 82.8 | 93.6 | 97.6 | 163.2 | ||
| # (%) | 42 (15.4%) | 93 (34.1%) | 10 (3.7%) | 128 (46.9%) | ||
| VFG, km/h | Mean | 45.9 | 45.5 | 44.4 | 39.2 | |
| Standard Deviation | 10.3 | 10.4 | 7.6 | 8.7 | ||
| Min | 15.6 | 15.5 | 27.7 | 16.4 | ||
| Max | 63.1 | 68.0 | 53.3 | 64.5 | ||
| # (%) | 42 (15.4%) | 93 (34.1%) | 10 (3.7%) | 128 (46.9%) | ||
| Variables | FGC | YC | RLR | |||
|---|---|---|---|---|---|---|
| B | Sig. | B | Sig. | B | Sig. | |
| Constant | 2.454 *** | 0.001 | 1.156 *** | 0.003 | −3.226 *** | 0.001 |
| Vehicle Type, | −0.181 | 0.638 | −0.088 | 0.656 | 0.271 | 0.524 |
| Area Type, | −0.196 | 0.654 | 0.528 ** | 0.020 | 0.563 | 0.200 |
| Intersection Type, | 0.300 | 0.364 | 0.097 | 0.568 | 1.267 * | 0.008 |
| Speed at the Onset of FG (km/h), VFG | 0.256 *** | <0.001 | 0.080 *** | <0.001 | 0.002 | 0.865 |
| Distance to the Stop-Line at the Onset of FG (m), DFG | −0.316 *** | <0.001 | −0.078 *** | <0.001 | −0.011 | 0.135 |
| Summary Statistics | Number of observations: 1459 veh; Log-likelihood at constant: 3335.696; Log-likelihood at convergence: 1497.164; McFadden R2: 0.551; Hit Ratio: 87.6%. | |||||
| Variables | B | Standard Error | t | Sig. |
|---|---|---|---|---|
| Constant | 41.749 *** | 2.102 | 19.863 | 0.000 |
| Vehicle Type, | −4.407 *** | 0.845 | −5.215 | 0.000 |
| Area Type, | −12.247 *** | 1.02 | −12.009 | 0.000 |
| Distance to the Stop-Line at the Onset of FG (m), DFG | 0.212 *** | 0.024 | 8.798 | 0.000 |
| Speed at the Onset of FG (km/h), VFG | 0.336 *** | 0.028 | 12.152 | 0.000 |
| Stop-Line Crossing Patterns, | −5.925 *** | 1.044 | −5.673 | 0.000 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, K.; Wang, F.; Yao, J.; Sun, J. Empirical Analysis and Modeling of Stop-Line Crossing Time and Speed at Signalized Intersections. Int. J. Environ. Res. Public Health 2017, 14, 9. https://doi.org/10.3390/ijerph14010009
Tang K, Wang F, Yao J, Sun J. Empirical Analysis and Modeling of Stop-Line Crossing Time and Speed at Signalized Intersections. International Journal of Environmental Research and Public Health. 2017; 14(1):9. https://doi.org/10.3390/ijerph14010009
Chicago/Turabian StyleTang, Keshuang, Fen Wang, Jiarong Yao, and Jian Sun. 2017. "Empirical Analysis and Modeling of Stop-Line Crossing Time and Speed at Signalized Intersections" International Journal of Environmental Research and Public Health 14, no. 1: 9. https://doi.org/10.3390/ijerph14010009
APA StyleTang, K., Wang, F., Yao, J., & Sun, J. (2017). Empirical Analysis and Modeling of Stop-Line Crossing Time and Speed at Signalized Intersections. International Journal of Environmental Research and Public Health, 14(1), 9. https://doi.org/10.3390/ijerph14010009






