Neighborhood Landscape Spatial Patterns and Land Surface Temperature: An Empirical Study on Single-Family Residential Areas in Austin, Texas
Abstract
:1. Introduction
2. Methods
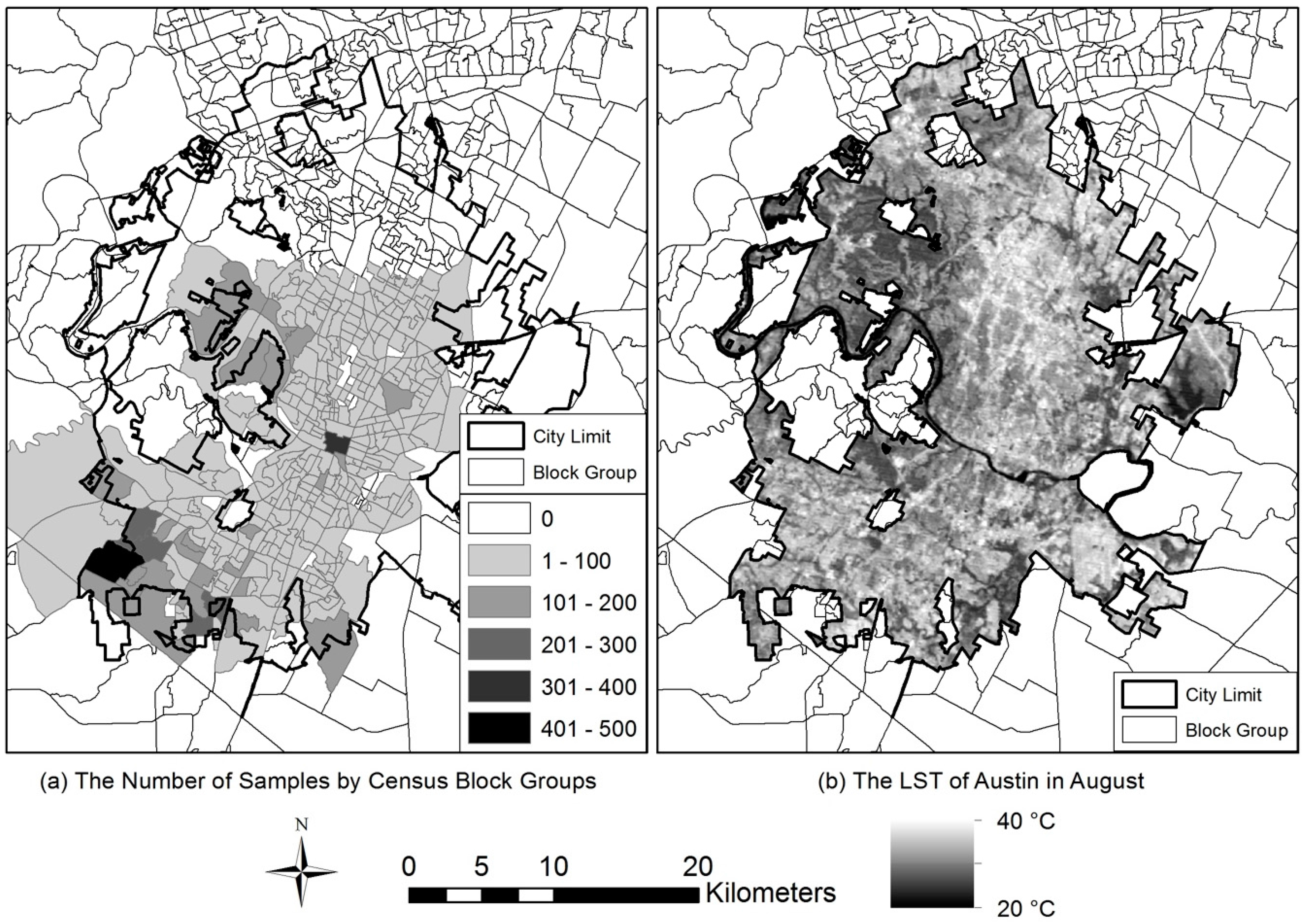
2.1. Study Location and Samples
2.2. Measuring Landscape Spatial Patterns
2.3. Calculating LST
2.4. Data Analysis
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| COHESION | patch cohesion index |
| DN | digital number |
| DOQQ | Digital Orthophoto Quarter Quadrangles |
| GIS | Geographic Information Systems |
| LST | land surface temperatures |
| MNN | mean nearest neighbor distance |
| MPS | mean patch size |
| MSI | mean shape index |
| NDVI | Normalized Difference Vegetation Index |
| NP | number of patches |
| OLS | ordinary least square |
| PLAND | percentage of tree cover |
| TNRIS | Texas Natural Resource Information System |
| TOA | top-of-atmosphere |
| UHI | urban heat island |
| VIF | Variance Inflation Factor |
References
- Kuo, F.E.; Sullivan, W.C. Environment and crime in the inner city: Does vegetation reduce crime? Environ. Behav. 2001, 33, 343–367. [Google Scholar] [CrossRef]
- Hartig, T.; Johansson, G.; Kylin, C. Residence in the social ecology of stress and restoration. J. Soc. Issues 2003, 59, 611–636. [Google Scholar] [CrossRef]
- Kaplan, S. The restorative benefits of nature: Toward an integrative framework. J. Environ. Psychol. 1995, 15, 169–182. [Google Scholar] [CrossRef]
- Ulrich, R.S.; Simons, R.F.; Losito, B.D.; Fiorito, E.; Miles, M.A.; Zelson, M. Stress recovery during exposure to natural and urban environments. J. Environ. Psychol. 1991, 11, 201–230. [Google Scholar] [CrossRef]
- Tyrväinen, L.; Miettinen, A. Property prices and urban forest amenities. J. Environ. Econ. Manag. 2000, 39, 205–223. [Google Scholar] [CrossRef]
- Kim, J.-H.; Lee, C.; Sohn, W. Urban natural environments, obesity, and health-related quality of life among hispanic children living in inner-city neighborhoods. Int. J. Environ. Res. Public Health 2016, 13. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.-H.; Lee, C.; Olvara, N.E.; Ellis, C.D. The role of landscape spatial patterns on obesity in hispanic children residing in inner-city neighborhoods. J. Phys. Act. Health 2014, 11, 1449–1457. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhou, W.; Ouyang, Z. Relationship between land surface temperature and spatial pattern of greenspace: What are the effects of spatial resolution? Landsc. Urban Plan. 2013, 114, 1–8. [Google Scholar] [CrossRef]
- Zhou, W.; Huang, G.; Cadenasso, M.L. Does spatial configuration matter? Understanding the effects of land cover pattern on land surface temperature in urban landscapes. Landsc. Urban Plan. 2011, 102, 54–63. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Emmanuel, R.; Krüger, E. Urban heat island and its impact on climate change resilience in a shrinking city: The case of glasgow, UK. Build. Environ. 2012, 53, 137–149. [Google Scholar] [CrossRef]
- Lai, L.-W.; Cheng, W.-L. Air quality influenced by urban heat island coupled with synoptic weather patterns. Sci. Total Environ. 2009, 407, 2724–2733. [Google Scholar] [CrossRef] [PubMed]
- Peng, S.; Piao, S.; Ciais, P.; Friedlingstein, P.; Ottle, C.; Bréon, F.-M.; Nan, H.; Zhou, L.; Myneni, R.B. Surface urban heat island across 419 global big cities. Environ. Sci. Technol. 2012, 46, 696–703. [Google Scholar] [CrossRef] [PubMed]
- Streutker, D.R. A remote sensing study of the urban heat island of Houston, Texas. Int. J. Remote Sens. 2002, 23, 2595–2608. [Google Scholar] [CrossRef]
- Rooney, C.; McMichael, A.J.; Kovats, R.S.; Coleman, M.P. Excess mortality in england and wales, and in greater London, during the 1995 heatwave. J. Epidemiol. Community Health 1998, 52, 482–486. [Google Scholar] [CrossRef] [PubMed]
- Urban, A.; Davídkovová, H.; Kyselý, J. Heat- and cold-stress effects on cardiovascular mortality and morbidity among urban and rural populations in the Czech Republic. Int. J. Biometeorol. 2013, 58, 1057–1068. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, J.; Samet, J.; Patz, J. Heat stress and public health: A critical review. Annu. Rev. Public Health 2008, 29, 41–55. [Google Scholar]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C.J. Including the urban heat island in spatial heat health risk assessment strategies: A case study for Birmingham, UK. Int. J. Health Geogr. 2011, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Lo, C.P.; Quattrochi, D. Land-use and land-cover change, urban heat island phenomenon, and health implications. Photogramm. Eng. Remote Sens. 2003, 69, 1053–1063. [Google Scholar] [CrossRef]
- Schuman, S.H. Patterns of urban heat-wave deaths and implications for prevention: Data from New York and St. Louis during July, 1966. Environ. Res. 1972, 5, 59–75. [Google Scholar] [CrossRef]
- Basu, R.; Samet, J.M. Relation between elevated ambient temperature and mortality: A review of the epidemiologic evidence. Epidemiol. Rev. 2002, 24, 190–202. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.; Zheng, Y.; Tang, X.; Guo, C.; Li, L.; Song, G.; Zhen, X.; Yuan, D.; Kalkstein, A.J.; Li, F.; et al. The urban heat island and its impact on heat waves and human health in Shanghai. Int. J. Biometeorol. 2009, 54, 75–84. [Google Scholar] [CrossRef] [PubMed]
- Kleerekoper, L.; van Esch, M.; Salcedo, T.B. How to make a city climate-proof, addressing the urban heat island effect. Resour. Conserv. Recycl. 2012, 64, 30–38. [Google Scholar] [CrossRef]
- Humpel, N.; Owen, N.; Leslie, E. Environmental factors associated with adults’ participation in physical activity: A review. Am. J. Prev. Med. 2002, 22, 188–199. [Google Scholar] [CrossRef]
- Saelens, B.E.; Handy, L.S. Built environment correlates of walking: A review. Med. Sci. Sports Exerc. 2008, 40, S550–S566. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Moudon, A.V. Physical activity and environment research in the health field: Implications for urban and transportation planning practice and research. J. Plan. Lit. 2004, 19, 147–181. [Google Scholar] [CrossRef]
- Oke, T.R. Review of Urban Climatology, 1973–1976; Secretariat of the World Meteorological Organization: Geneva, Switzerland, 1979. [Google Scholar]
- Guo, G.; Wu, Z.; Xiao, R.; Chen, Y.; Liu, X.; Zhang, X. Impacts of urban biophysical composition on land surface temperature in urban heat island clusters. Landsc. Urban Plan. 2015, 135, 1–10. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Urban heat island analysis using the Landsat TM data and ASTER data: A case study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef]
- Oguz, H. Lst calculator: A program for retrieving land surface temperature from Landsat TM/ETM+ imagery. Environ. Eng. Manag. J. 2013, 12, 549–555. [Google Scholar]
- Schwarz, N.; Schlink, U.; Franck, U.; Großmann, K. Relationship of land surface and air temperatures and its implications for quantifying urban heat island indicators—An application for the city of Leipzig (Germany). Ecol. Indic. 2012, 18, 693–704. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Arnfield, J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Kong, F.; Yin, H.; James, P.; Hutyra, L.R.; He, H.S. Effects of spatial pattern of greenspace on urban cooling in a large metropolitan area of eastern China. Landsc. Urban Plan. 2014, 128, 35–47. [Google Scholar] [CrossRef]
- Buyantuyev, A.; Wu, J. Urban heat islands and landscape heterogeneity: Linking spatiotemporal variations in surface temperatures to land-cover and socioeconomic patterns. Landsc. Ecol. 2010, 25, 17–33. [Google Scholar] [CrossRef]
- Oliveira, S.; Andrade, H.; Vaz, T. The cooling effect of green spaces as a contribution to the mitigation of urban heat: A case study in Lisbon. Build. Environ. 2011, 46, 2186–2194. [Google Scholar] [CrossRef]
- Zoulia, I.; Santamouris, M.; Dimoudi, A. Monitoring the effect of urban green areas on the heat island in Athens. Environ. Monit. Assess. 2009, 156, 275–292. [Google Scholar] [CrossRef] [PubMed]
- Unger, J. Intra-urban relationship between surface geometry and urban heat island: Review and new approach. Clim. Res. 2004, 27, 253–264. [Google Scholar] [CrossRef]
- Declet-Barreto, J.; Brazel, A.J.; Martin, C.A.; Chow, W.T.L.; Harlan, S.L. Creating the park cool island in an inner-city neighborhood: Heat mitigation strategy for Phoenix, AZ. Urban Ecosyst. 2013, 16, 617–635. [Google Scholar] [CrossRef]
- Tan, M.; Li, X. Integrated assessment of the cool island intensity of green spaces in the mega city of Beijing. Int. J. Remote Sens. 2013, 34, 3028–3043. [Google Scholar] [CrossRef]
- Upmanis, H.; Eliasson, I.; Lindqvist, S. The influence of green areas on nocturnal temperatures in a high latitude city (Göteborg, Sweden). Int. J. Climatol. 1998, 18, 681–700. [Google Scholar] [CrossRef]
- Chang, C.-R.; Li, M.-H.; Chang, S.-D. A preliminary study on the local cool-island intensity of Taipei city parks. Landsc. Urban Plan. 2007, 80, 386–395. [Google Scholar] [CrossRef]
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Hamdi, R.; Schayes, G. Sensitivity study of the urban heat island intensity to urban characteristics. Int. J. Climatol. 2008, 28, 973–982. [Google Scholar] [CrossRef]
- Memon, R.A.; Leung, D.Y.C.; Liu, C.-H. An investigation of urban heat island intensity (UHII) as an indicator of urban heating. Atmos. Res. 2009, 94, 491–500. [Google Scholar] [CrossRef]
- Saaroni, H.; Ben-Dor, E.; Bitan, A.; Potchter, O. Spatial distribution and microscale characteristics of the urban heat island in Tel-Aviv, Israel. Landsc. Urban Plan. 2000, 48, 1–18. [Google Scholar] [CrossRef]
- Wilson, J.S.; Clay, M.; Martin, E.; Stuckey, D.; Vedder-Risch, K. Evaluating environmental influences of zoning in urban ecosystems with remote sensing. Remote Sens. Environ. 2003, 86, 303–321. [Google Scholar] [CrossRef]
- Raynolds, M.K.; Comiso, J.C.; Walker, D.A.; Verbyla, D. Relationship between satellite-derived land surface temperatures, arctic vegetation types, and NDVI. Remote Sens. Environ. 2008, 112, 1884–1894. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P.; Michishita, R.; Sasagawa, T. Assessment of multi-resolution and multi-sensor data for urban surface temperature retrieval. Remote Sens. Environ. 2006, 104, 211–225. [Google Scholar] [CrossRef]
- Mackey, C.W.; Lee, X.; Smith, R.B. Remotely sensing the cooling effects of city scale efforts to reduce urban heat island. Build. Environ. 2012, 49, 348–358. [Google Scholar] [CrossRef]
- Julien, Y.; Sobrino, J.A.; Verhoef, W. Changes in land surface temperatures and NDVI values over Europe between 1982 and 1999. Remote Sens. Environ. 2006, 103, 43–55. [Google Scholar] [CrossRef]
- Forman, R.T.; Godron, M. Landscape Ecology; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Pickett, S.T.; Cadenasso, M.L. Landscape ecology: Spatial heterogeneity in ecological systems. Science 1995, 269, 331–334. [Google Scholar] [CrossRef] [PubMed]
- McGarigal, K.; Marks, B.J. Spatial Pattern Analysis Program for Quantifying Landscape Structure; General Technical Report PNW-GTR-351; US Department of Agriculture, Forest Service, Pacific Northwest Research Station: Corvallis, OR, USA, 1995.
- Cao, X.; Onishi, A.; Chen, J.; Imura, H. Quantifying the cool island intensity of urban parks using ASTER and IKONOS data. Landsc. Urban Plan. 2010, 96, 224–231. [Google Scholar] [CrossRef]
- Asgarian, A.; Amiri, B.J.; Sakieh, Y. Assessing the effect of green cover spatial patterns on urban land surface temperature using landscape metrics approach. Urban Ecosyst. 2015, 18, 209–222. [Google Scholar] [CrossRef]
- Maimaitiyiming, M.; Ghulam, A.; Tiyip, T.; Pla, F.; Latorre-Carmona, P.; Halik, Ü.; Sawut, M.; Caetano, M. Effects of green space spatial pattern on land surface temperature: Implications for sustainable urban planning and climate change adaptation. ISPRS J. Photogramm. Remote Sens. 2014, 89, 59–66. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.; Ouyang, Z.; Xu, W.; Zheng, H. Spatial pattern of greenspace affects land surface temperature: Evidence from the heavily urbanized Beijing metropolitan area, China. Landsc. Ecol. 2012, 27, 887–898. [Google Scholar] [CrossRef]
- Yokohari, M.; Brown, R.D.; Kato, Y.; Moriyama, H. Effects of paddy fields on summertime air and surface temperatures in urban fringe areas of Tokyo, Japan. Landsc. Urban Plan. 1997, 38, 1–11. [Google Scholar] [CrossRef]
- Zhang, X.; Zhong, T.; Feng, X.; Wang, K. Estimation of the relationship between vegetation patches and urban land surface temperature with remote sensing. Int. J. Remote Sens. 2009, 30, 2105–2118. [Google Scholar] [CrossRef]
- Xie, M.; Wang, Y.; Chang, Q.; Fu, M.; Ye, M. Assessment of landscape patterns affecting land surface temperature in different biophysical gradients in Shenzhen, China. Urban Ecosyst. 2013, 16, 871–886. [Google Scholar] [CrossRef]
- Du, S.; Xiong, Z.; Wang, Y.-C.; Guo, L. Quantifying the multilevel effects of landscape composition and configuration on land surface temperature. Remote Sens. Environ. 2016, 178, 84–92. [Google Scholar] [CrossRef]
- Connors, J.P.; Galletti, C.S.; Chow, W.T. Landscape configuration and urban heat island effects: Assessing the relationship between landscape characteristics and land surface temperature in Phoenix, Arizona. Landsc. Ecol. 2013, 28, 271–283. [Google Scholar] [CrossRef]
- Li, X.; Li, W.; Middel, A.; Harlan, S.L.; Brazel, A.J.; Turner Ii, B.L. Remote sensing of the surface urban heat island and land architecture in Phoenix, Arizona: Combined effects of land composition and configuration and cadastral–demographic–economic factors. Remote Sens. Environ. 2016, 174, 233–243. [Google Scholar] [CrossRef]
- Liu, H.; Weng, Q. Seasonal variations in the relationship between landscape pattern and land surface temperature in Indianapolis, USA. Environ. Monit. Assess. 2008, 144, 199–219. [Google Scholar] [CrossRef] [PubMed]
- Rhee, J.; Park, S.; Lu, Z. Relationship between land cover patterns and surface temperature in urban areas. GISci. Remote Sens. 2014, 51, 521–536. [Google Scholar] [CrossRef]
- Yue, W.; Liu, Y.; Fan, P.; Ye, X.; Wu, C. Assessing spatial pattern of urban thermal environment in Shanghai, China. Stoch. Environ. Res. Risk Assess. 2012, 26, 899–911. [Google Scholar] [CrossRef]
- American Community Survey (ACS) American Community Survey 5-Year Estimates. Available online: http://www.Census.Gov/Data/Developers/Data-Sets/Acs-Survey-5-Year-Data.html (accessed on 2 November 2015).
- U.S. Climate Data. Climate Austin—Texas. Available online: http://www.usclimatedata.com/climate/austin/texas/united-states/ustx2742 (accessed on 2 November 2015).
- Ward, N. Austin Climate Data; The University of Texas at Austin: Austin, TX, USA, 2009. [Google Scholar]
- Ewing, R. Beyond density, mode choice, and single-purpose trips. Transp. Q. 1995, 49, 15–24. [Google Scholar]
- Lee, C.; Moudon, A.V.; Courbois, J.-Y.P. Built environment and behavior: Spatial sampling using parcel data. Ann. Epidemiol. 2006, 16, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Timperio, A.; Crawford, D.; Telford, A.; Salmon, J. Perceptions about the local neighborhood and walking and cycling among children. Prev. Med. 2004, 38, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Hersperger, A.M. Spatial adjacencies and interactions: Neighborhood mosaics for landscape ecological planning. Landsc. Urban Plan. 2006, 77, 227–239. [Google Scholar] [CrossRef]
- Turner, M.G.; Gardner, R.H.; O’neill, R.V. Landscape Ecology in Theory and Practice; Springer: Berlin, Germany, 2001; Volume 401. [Google Scholar]
- Gustafson, E.J. Quantifying landscape spatial pattern: What is the state of the art? Ecosystems 1998, 1, 143–156. [Google Scholar] [CrossRef]
- Haines-Young, R.; Chopping, M. Quantifying landscape structure: A review of landscape indices and their application to forested landscapes. Prog. Phys. Geogr. 1996, 20, 418–445. [Google Scholar] [CrossRef]
- Turner, M.G. Landscape ecology: What is the state of the science? Annu. Rev. Ecol. Evol. Syst. 2005, 36, 319–344. [Google Scholar] [CrossRef]
- Dramstad, W.; Olson, J.D.; Forman, R.T. Landscape Ecology Principles in Landscape Architecture and Land-Use Planning; Island Press: Washington, DC, USA, 1996. [Google Scholar]
- Forman, R.T. Some general principles of landscape and regional ecology. Landsc. Ecol. 1995, 10, 133–142. [Google Scholar] [CrossRef]
- Forman, R.T. Land Mosaics: The Ecology of Landscapes and Regions (1995); Springer: Berlin, Germany, 2014. [Google Scholar]
- Shafer, C. Beyond park boundaries. In Landscape Planning and Ecological Networks; Cook, E.A., van Lier, H.N., Eds.; Elsevier: New York, NY, USA, 1994; pp. 201–224. [Google Scholar]
- Gong, P.; Mahler, S.; Biging, G.; Newburn, D. Vineyard identification in an oak woodland landscape with airborne digital camera imagery. Int. J. Remote Sens. 2003, 24, 1303–1315. [Google Scholar] [CrossRef]
- Mas, J.-F.; Gao, Y.; Pacheco, J.A. N. Sensitivity of landscape pattern metrics to classification approaches. For. Ecol. Manag. 2010, 259, 1215–1224. [Google Scholar] [CrossRef]
- Beyer, H.L. Geospatial Modelling Environment (Version 0.7. 2.1). Available online: http://www.spatialecology.com/gme/ (accessed on 10 October 2015).
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from landsat tm data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from Landsat TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Morris, C.; Simmonds, I.; Plummer, N. Quantification of the influences of wind and cloud on the nocturnal urban heat island of a large city. J. Appl. Meteorol. 2001, 40, 169–182. [Google Scholar] [CrossRef]
- Chander, G.; Markham, B. Revised landsat-5 tm radiometric calibration procedures and postcalibration dynamic ranges. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2674–2677. [Google Scholar] [CrossRef]
- Markham, B.; Barker, J. Thematic Mapper bandpass solar exoatmospheric irradiances. Int. J. Remote Sens. 1987, 8, 517–523. [Google Scholar] [CrossRef]
- Thorne, K.; Markharn, B.; Barker, P.S.; Biggar, S. Radiometric calibration of landsat. Photogramm. Eng. Remote Sens. 1997, 63, 853–858. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: New York, NY, USA, 2013; Volume 4. [Google Scholar]
- Getis, A. Reflections on spatial autocorrelation. Reg. Sci. Urban Econ. 2007, 37, 491–496. [Google Scholar] [CrossRef]
- Anselin, L.; Syabri, I.; Kho, Y. Geoda: An introduction to spatial data analysis. Geogr. Anal. 2006, 38, 5–22. [Google Scholar] [CrossRef]
- Iojă, C.I.; Grădinaru, S.R.; Onose, D.A.; Vânău, G.O.; Tudor, A.C. The potential of school green areas to improve urban green connectivity and multifunctionality. Urban For. Urban Green. 2014, 13, 704–713. [Google Scholar] [CrossRef]
- Braaker, S.; Ghazoul, J.; Obrist, M.K.; Moretti, M. Habitat connectivity shapes urban arthropod communities: The key role of green roofs. Ecology 2014, 95, 1010–1021. [Google Scholar] [CrossRef] [PubMed]
- Kong, F.; Yin, H.; Nakagoshi, N.; Zong, Y. Urban green space network development for biodiversity conservation: Identification based on graph theory and gravity modeling. Landsc. Urban Plan. 2010, 95, 16–27. [Google Scholar] [CrossRef]

| Criteria | Variables (Acronym) | Formula a | Units (Range) |
|---|---|---|---|
| Size | Percentage of tree cover (PLAND) | % | |
| Fragmentation | Number of patches (NP) | Count | |
| Mean patch size (MPS) | Square-meter (MPS ≥ 0, without limit) | ||
| Shape | Mean shape index (MSI) | None (MSI ≥ 1, without limit) | |
| Isolation | Mean nearest neighbor distance (MNN) | Meter | |
| Connectivity | Patch cohesion index (COHESION) | % |
| Classified Class | Reference Pixels (%) | ||||
|---|---|---|---|---|---|
| Tree | Grass | Impervious Areas | Total | User’s Accuracy | |
| Tree | 15,693 (91.26%) | 3 (0.02%) | 1 (0.01%) | 15,697 (29.95%) | 99.97% |
| Grass | 366 (2.13%) | 16,438 (94.80%) | 10 (0.06%) | 16,814 (32.08%) | 97.76% |
| Impervious areas | 1136 (6.61%) | 899 (5.18%) | 17,867 (99.94%) | 19,902 (37.97%) | 89.77% |
| Total | 17,195 (100.00%) | 17,340 (100.00%) | 17,878 (100.00%) | 52,413 (100.00%) | - |
| Producer’s accuracy | 91.26% | 94.80% | 99.94% | - | - |
| Variables | Mean | SD | Min. | Max. |
|---|---|---|---|---|
| Land Surface Temperature (LST, °C) | 32.60 | 1.90 | 23.60 | 41.40 |
| Landscape spatial characteristics (acronym, unit) | ||||
| Percent of tree cover (PLAND, %) | 37.98 | 11.29 | 3.74 | 77.53 |
| # of tree patches (NP) | 4037.80 | 1504.03 | 972 | 9028 |
| Mean patch size (MPS, m2) | 239.27 | 168.77 | 41.00 | 1331.00 |
| Mean shape index (MSI) | 1.24 | 0.03 | 1.15 | 1.35 |
| Mean nearest neighborhood distance (MNN, m) | 2.60 | 0.43 | 1.96 | 6.00 |
| Patch cohesion index (COHESION, %) | 99.11 | 1.08 | 87.51 | 99.98 |
| Variables | Coefficients | |
|---|---|---|
| Model 1: OLS 1 | Model 2: Spatial Lag | |
| Size | ||
| Percent of tree cover (PLAND) | −0.0037 *** | −0.0027 *** |
| Fragmentation | ||
| Number of patches (NP) | 0.0001 *** | 0.0001 *** |
| Mean patch size (MPS) | −0.0021 *** | −0.0014 *** |
| Shape | ||
| Mean shape index (MSI) | 5.2600 *** | 3.3966 *** |
| Isolation | ||
| Mean nearest neighbor distance (MNN) | 0.7334 *** | 0.4715 *** |
| Connectivity | ||
| Patch cohesion index (COHESION) | −0.0916 *** | −0.0590 *** |
| Constant | 306.8238 *** | 198.0167 *** |
| W LST 2 | 0.3546 *** | |
| R-squared (Pseudo R-squared for the Spatial Lag Model) | 0.5350 | 0.8201 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.-H.; Gu, D.; Sohn, W.; Kil, S.-H.; Kim, H.; Lee, D.-K. Neighborhood Landscape Spatial Patterns and Land Surface Temperature: An Empirical Study on Single-Family Residential Areas in Austin, Texas. Int. J. Environ. Res. Public Health 2016, 13, 880. https://doi.org/10.3390/ijerph13090880
Kim J-H, Gu D, Sohn W, Kil S-H, Kim H, Lee D-K. Neighborhood Landscape Spatial Patterns and Land Surface Temperature: An Empirical Study on Single-Family Residential Areas in Austin, Texas. International Journal of Environmental Research and Public Health. 2016; 13(9):880. https://doi.org/10.3390/ijerph13090880
Chicago/Turabian StyleKim, Jun-Hyun, Donghwan Gu, Wonmin Sohn, Sung-Ho Kil, Hwanyong Kim, and Dong-Kun Lee. 2016. "Neighborhood Landscape Spatial Patterns and Land Surface Temperature: An Empirical Study on Single-Family Residential Areas in Austin, Texas" International Journal of Environmental Research and Public Health 13, no. 9: 880. https://doi.org/10.3390/ijerph13090880
APA StyleKim, J.-H., Gu, D., Sohn, W., Kil, S.-H., Kim, H., & Lee, D.-K. (2016). Neighborhood Landscape Spatial Patterns and Land Surface Temperature: An Empirical Study on Single-Family Residential Areas in Austin, Texas. International Journal of Environmental Research and Public Health, 13(9), 880. https://doi.org/10.3390/ijerph13090880





