Assessment of the Casualty Risk of Multiple Meteorological Hazards in China
Abstract
:1. Introduction
2. Data and Methods
2.1. Data and Preprocessing
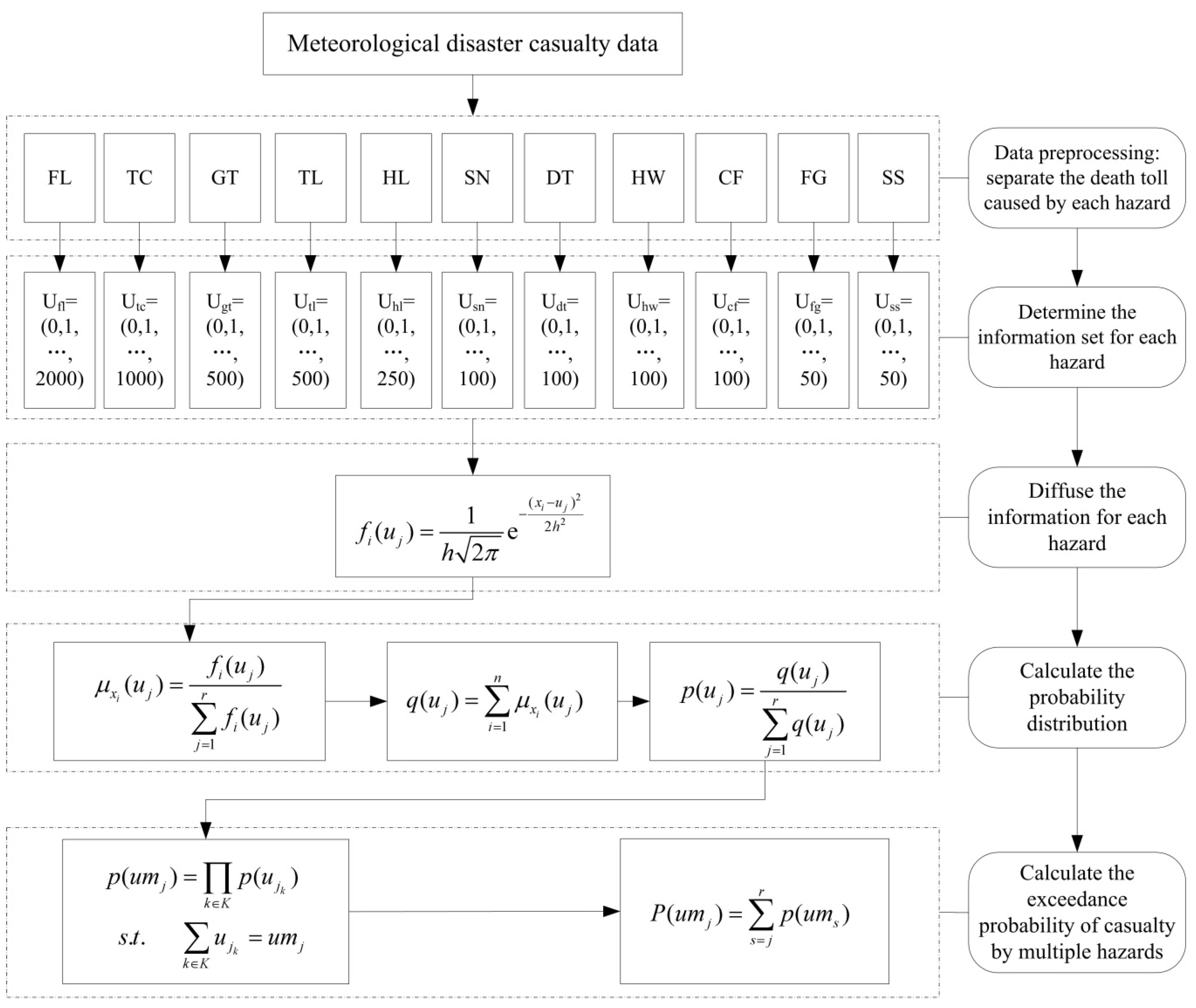
2.2. Methods
Step 1: define the fuzzy set U
Step 2: diffuse information about the number of deaths
Step 3: calculate the probability distribution of deaths caused by each hazard
Step 4: calculate the probability distribution of deaths caused by multiple hazards
Step 5: calculate probability of exceedance of deaths caused by multiple hazards
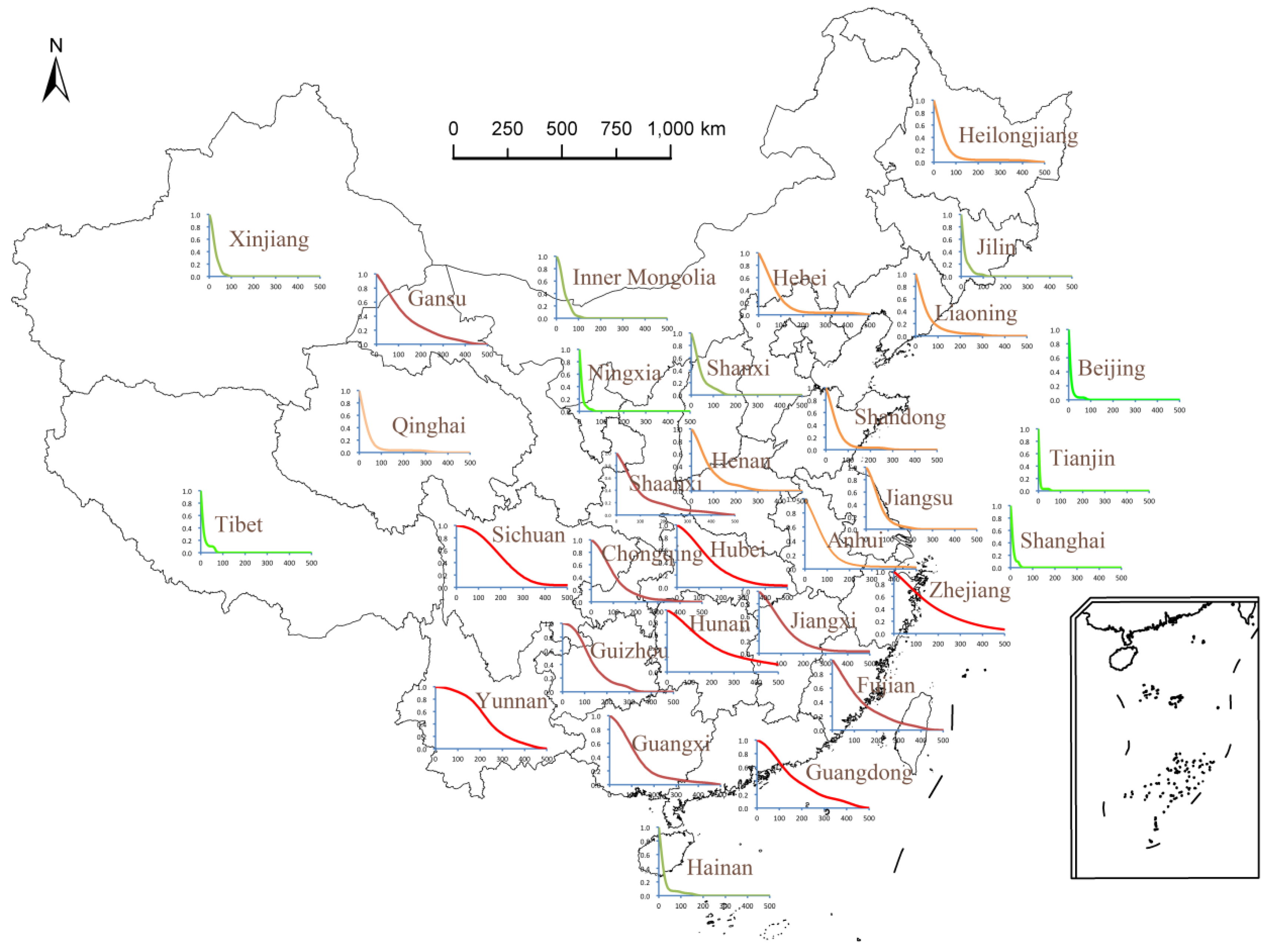
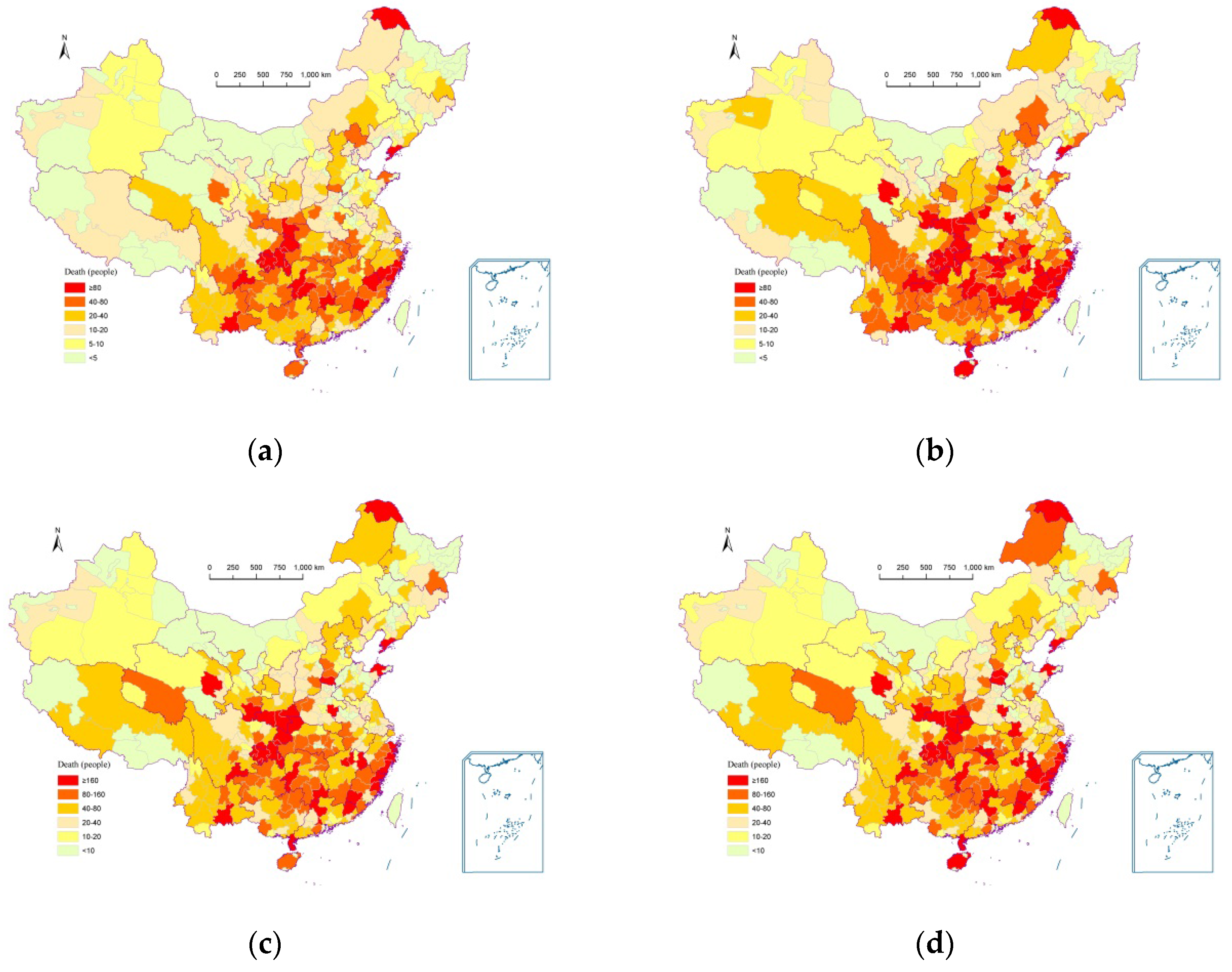
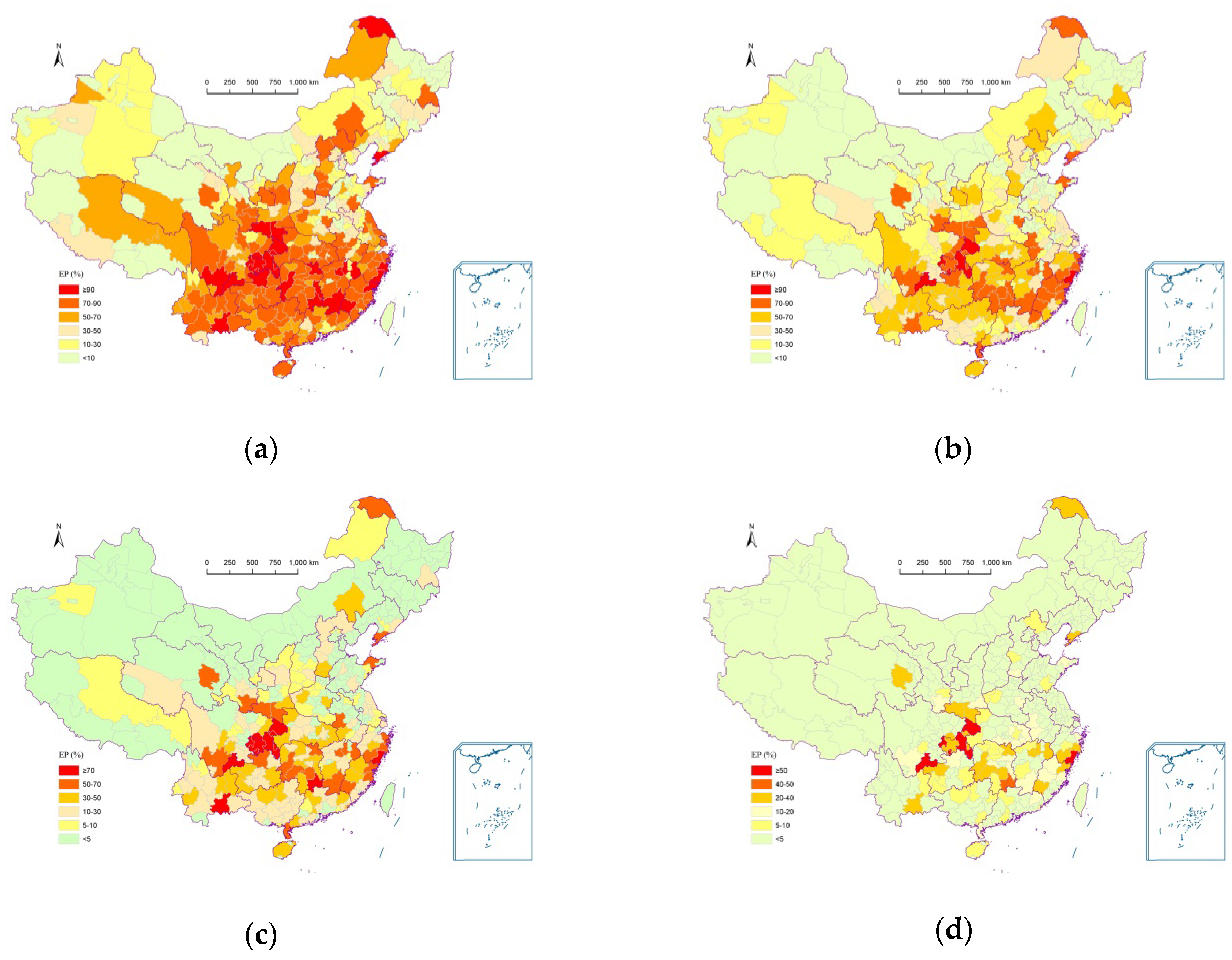
3. Application and Results
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Intergovernmental Panel on Climate Change. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2012. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001. [Google Scholar]
- United Nations. Sendai Framework for Disaster Risk Reduction: 2015–2030; UNISDR: Geneva, Switzerland, 2015. [Google Scholar]
- Zong, Y.; Chen, X. The 1998 Flood on the Yangtze, China. Nat. Hazards 2000, 22, 165–184. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Wei, Y.; Ye, M. Beijing storm of 21 July 2012: Observations and reflections. Nat. Hazards 2013, 67, 969–974. [Google Scholar] [CrossRef]
- Shi, P.; Fang, W.; Dong, W.; Li, N.; Xu, W.; Chen, S. Experience, Lessons and Recommendations of China’s Response to Sleet & Snow Disaster in South China. In Integrated Risk Governance: Science Plan and Case Studies of Large-Scale Disasters; Shi, P., Jaeger, C., Ye, Q., Eds.; Springer Verlag: Berlin, Germany, 2012; pp. 89–118. [Google Scholar]
- Wikipedia. Typhoon Fitow. Available online: http://en.wikipedia.org/wiki/Typhoon_Fitow (accessed on 15 October 2015).
- South Carolina Emergency Management Division Office of the Adjutant General (SCEMDOAG). State of South Carolina Hazards Assessment 2005; University of South Carolina, South Carolina Emergency Management Division Office of the Adjutant General, Hazards Research Lab, Department of Geography, South Carolina, 2006; Available online: http://webra.cas.sc.edu/hvri/docs/SCEMD_Report_2005.pdf (accessed on 17 December 2015).
- Schmidt-Thomé, P. The Spatial Effects and Management of Natural and Technological Hazards in Europe. Available online: http://www.preventionweb.net/english/professional/publications/v.php?id=3621 (accessed on 17 December 2015).
- Thierry, P.; Stieltjes, L.; Kouokam, E.; Nguéya, P.; Salley, P.M. Multi-hazard risk mapping and assessment on an active volcano: The GRINP project at Mount Cameroon. Nat. Hazards 2008, 45, 429–456. [Google Scholar] [CrossRef]
- Shi, P.; Kasperson, R. World Atlas of Natural Disaster Risk; Springer-Verlag: Berlin, Germany; Heidelberg, Germany; Beijing Normal University Press: Beijing, China, 2015; pp. 287–306. [Google Scholar]
- Bell, R.; Glade, T. Multi-Hazard Analysis in Natural Risk Assessments. In Proceedings of the 4th International Conference on Computer Simulation in Risk Analysis and Hazard Mitigation, Rhodes, Greece, 26–29 September 2004; Brebbia, C.A., Ed.; WIT Press: Southampton, UK, 2004. [Google Scholar]
- Arnold, M.; Chen, R.S.; Deichmann, U.; Dilley, M.; Lerner-Lam, A.L. Natural Disaster Hotspots Case Studies; World Bank Publications: Washington, DC, USA, 2006. [Google Scholar]
- Mosquera-Machado, S.; Dilley, M. A comparison of selected global disaster risk assessment results. Nat. Hazards 2009, 48, 439–456. [Google Scholar] [CrossRef]
- Ming, X.; Xu, W.; Li, Y.; Du, J.; Liu, B.; Shi, P. Quantitative multi-hazard risk assessment with vulnerability surface and hazard joint return period. Stoch. Environ. Res. Risk Assess. 2015, 29, 35–44. [Google Scholar] [CrossRef]
- Liu, B.; Siu, Y.L.; Mitchell, G.; Xu, W. Exceedance probability of multiple natural hazards: Risk assessment in China’s Yangtze River Delta. Nat. Hazards 2013, 69, 2039–2055. [Google Scholar] [CrossRef]
- Xu, W.; Tian, Y.; Zhang, Y.; Zheng, J.; Fang, W.; Lv, H.; Yang, X.; Wang, R.; Zhao, T.; Shi, P. Integrated Risk Governance: Natural Hazards and Risk Assessment in the Yangtze River Delta Region; Science Press: Beijing, China, 2014; pp. 104–124. (In Chinese) [Google Scholar]
- Shi, P.; Wang, J.; Fang, X.; Ye, Y.; Gu, Z.; Ge, Y.; Zhuo, L.; Xu, W. Integrated Risk Governance: Risk Assessment and Mapping for Multiple Natural Hazards in the Yangtze River Delta Region; Science Press: Beijing, China, 2014; pp. 202–273. (In Chinese) [Google Scholar]
- Gill, J.C.; Malamud, B.D. Reviewing and visualizing the interactions of natural hazards. Rev. Geophys. 2014, 52, 680–722. [Google Scholar] [CrossRef]
- Huang, C. Principle of information diffusion. Fuzzy Sets Syst. 1997, 91, 69–90. [Google Scholar]
- Shi, P. Atlas of Natural Disaster Risk in China; Science Press: Beijing, China, 2011; pp. 140–153. (In Chinese) [Google Scholar]
- Fang, W.; Wang, J.; Shi, P. Integrated Risk Governance: Database, Risk Mapping and Network Platform; Science Press: Beijing, China, 2011; pp. 134–153. (In Chinese) [Google Scholar]
- Christenson, E.; Elliott, M.; Banerjee, O.; Hamrick, L.; Bartram, J. Climate-Related Hazards: A Method for Global Assessment of Urban and Rural Population Exposure to Cyclones, Droughts, and Floods. Int. J. Environ. Res. Public Health 2014, 11, 2169–2192. [Google Scholar] [CrossRef] [PubMed]
| Natural Hazard | No. (%) of Deaths |
|---|---|
| Heavy rain and floods (including waterlogging and storm-induced geological hazards) | 60,932 (66.79) |
| Typhoon (including typhoon-induced storm surge) | 10,847 (11.89) |
| Gale and tornado | 6585 (7.22) |
| Thunder and lightning | 6344 (6.95) |
| Hail | 2891 (3.17) |
| Snow | 844 (0.93) |
| Drought | 684 (0.75) |
| Heat wave | 620 (0.68) |
| Fog | 484 (0.53) |
| Cold spell and freezing | 352 (0.39) |
| Sand/dust storm | 131 (0.14) |
| Other hazards | 514 (0.56) |
| Province (Municipality, Autonomous Region) | Exceedance Probability at Different Numbers of Deaths | Average Annual Death Toll | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 5 | 10 | 20 | 50 | 100 | 200 | 500 | 1000 | 1500 | ||
| Gansu | 0.993 | 0.983 | 0.965 | 0.930 | 0.820 | 0.635 | 0.323 | 0.042 | 0.034 | 0.026 | 103 |
| Zhejiang | 0.994 | 0.985 | 0.970 | 0.938 | 0.837 | 0.664 | 0.384 | 0.067 | 0.021 | 0 | 155 |
| Hunan | 0.996 | 0.990 | 0.980 | 0.957 | 0.874 | 0.709 | 0.427 | 0.120 | 0 | 0 | 227 |
| Sichuan | 0.999 | 0.998 | 0.996 | 0.991 | 0.963 | 0.866 | 0.506 | 0.035 | 0 | 0 | 220 |
| Jiangxi | 0.994 | 0.984 | 0.966 | 0.927 | 0.786 | 0.518 | 0.169 | 0.030 | 0 | 0 | 130 |
| Hubei | 0.996 | 0.990 | 0.979 | 0.954 | 0.858 | 0.653 | 0.290 | 0.028 | 0 | 0 | 163 |
| Anhui | 0.989 | 0.973 | 0.944 | 0.882 | 0.671 | 0.344 | 0.075 | 0.023 | 0 | 0 | 98 |
| Yunnan | 1.000 | 0.999 | 0.998 | 0.996 | 0.979 | 0.919 | 0.633 | 0 | 0 | 0 | 238 |
| Guangdong | 0.998 | 0.994 | 0.986 | 0.968 | 0.883 | 0.674 | 0.357 | 0 | 0 | 0 | 179 |
| Fujian | 0.992 | 0.980 | 0.958 | 0.912 | 0.760 | 0.524 | 0.250 | 0 | 0 | 0 | 139 |
| Guizhou | 0.999 | 0.998 | 0.995 | 0.987 | 0.924 | 0.654 | 0.189 | 0 | 0 | 0 | 140 |
| Shaanxi | 0.990 | 0.973 | 0.944 | 0.881 | 0.660 | 0.353 | 0.172 | 0 | 0 | 0 | 111 |
| Guangxi | 0.996 | 0.990 | 0.978 | 0.949 | 0.828 | 0.548 | 0.159 | 0 | 0 | 0 | 132 |
| Chongqing | 0.996 | 0.988 | 0.975 | 0.940 | 0.784 | 0.456 | 0.127 | 0 | 0 | 0 | 112 |
| Henan | 0.991 | 0.976 | 0.948 | 0.880 | 0.622 | 0.300 | 0.095 | 0 | 0 | 0 | 86 |
| Hebei | 0.987 | 0.967 | 0.933 | 0.857 | 0.609 | 0.270 | 0.046 | 0 | 0 | 0 | 83 |
| Liaoning | 0.975 | 0.937 | 0.872 | 0.737 | 0.395 | 0.155 | 0.045 | 0 | 0 | 0 | 59 |
| Heilongjiang | 0.972 | 0.930 | 0.859 | 0.718 | 0.361 | 0.098 | 0.036 | 0 | 0 | 0 | 57 |
| Qinghai | 0.966 | 0.913 | 0.824 | 0.647 | 0.247 | 0.055 | 0.034 | 0 | 0 | 0 | 43 |
| Shandong | 0.980 | 0.948 | 0.891 | 0.764 | 0.393 | 0.099 | 0.033 | 0 | 0 | 0 | 53 |
| Jiangsu | 0.991 | 0.975 | 0.944 | 0.865 | 0.556 | 0.170 | 0.024 | 0 | 0 | 0 | 65 |
| Shanxi | 0.980 | 0.947 | 0.882 | 0.727 | 0.304 | 0.117 | 0 | 0 | 0 | 0 | 46 |
| Hainan | 0.943 | 0.854 | 0.698 | 0.413 | 0.082 | 0.051 | 0 | 0 | 0 | 0 | 26 |
| Inner Mongolia | 0.991 | 0.972 | 0.925 | 0.767 | 0.294 | 0.032 | 0 | 0 | 0 | 0 | 40 |
| Jilin | 0.920 | 0.794 | 0.589 | 0.313 | 0.099 | 0.025 | 0 | 0 | 0 | 0 | 21 |
| Xinjiang | 0.983 | 0.948 | 0.861 | 0.611 | 0.140 | 0.001 | 0 | 0 | 0 | 0 | 29 |
| Tibet | 0.901 | 0.736 | 0.479 | 0.210 | 0.103 | 0 | 0 | 0 | 0 | 0 | 16 |
| Ningxia | 0.903 | 0.741 | 0.481 | 0.161 | 0.035 | 0 | 0 | 0 | 0 | 0 | 14 |
| Beijing | 0.868 | 0.666 | 0.383 | 0.123 | 0.034 | 0 | 0 | 0 | 0 | 0 | 12 |
| Tianjin | 0.760 | 0.429 | 0.119 | 0.034 | 0.025 | 0 | 0 | 0 | 0 | 0 | 7 |
| Shanghai | 0.908 | 0.736 | 0.444 | 0.157 | 0.010 | 0 | 0 | 0 | 0 | 0 | 13 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Zhuo, L.; Zheng, J.; Ge, Y.; Gu, Z.; Tian, Y. Assessment of the Casualty Risk of Multiple Meteorological Hazards in China. Int. J. Environ. Res. Public Health 2016, 13, 222. https://doi.org/10.3390/ijerph13020222
Xu W, Zhuo L, Zheng J, Ge Y, Gu Z, Tian Y. Assessment of the Casualty Risk of Multiple Meteorological Hazards in China. International Journal of Environmental Research and Public Health. 2016; 13(2):222. https://doi.org/10.3390/ijerph13020222
Chicago/Turabian StyleXu, Wei, Li Zhuo, Jing Zheng, Yi Ge, Zhihui Gu, and Yugang Tian. 2016. "Assessment of the Casualty Risk of Multiple Meteorological Hazards in China" International Journal of Environmental Research and Public Health 13, no. 2: 222. https://doi.org/10.3390/ijerph13020222
APA StyleXu, W., Zhuo, L., Zheng, J., Ge, Y., Gu, Z., & Tian, Y. (2016). Assessment of the Casualty Risk of Multiple Meteorological Hazards in China. International Journal of Environmental Research and Public Health, 13(2), 222. https://doi.org/10.3390/ijerph13020222







