Modeling Driver Behavior near Intersections in Hidden Markov Model
Abstract
:1. Introduction
2. Methodology
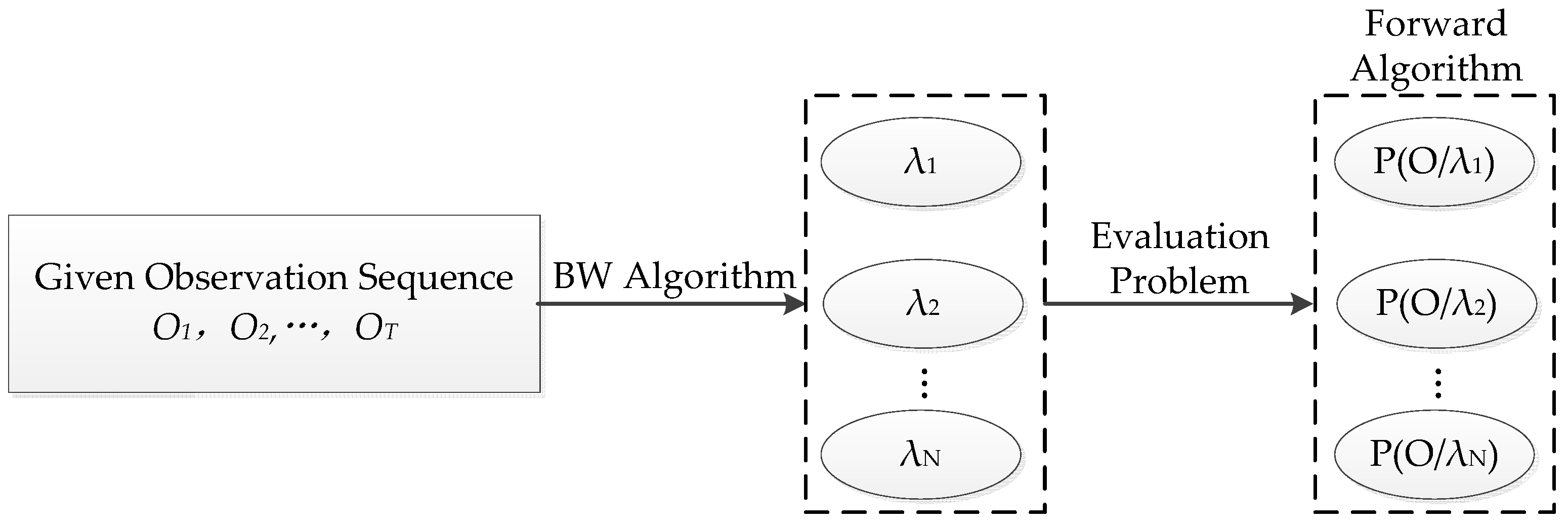
2.1. Hidden Markov Model
- N is the number of possible hidden states in the model. Each individual state can be denoted as , i.e., 1 ≤ I ≤ N. And the state symbol at time t is defined as qt.
- M is the number of observable symbols per state , i.e., 1 ≤ k ≤ M. And the observation symbol at time t is denoted as Ot.
- The state transition probability distribution is denoted as:where aij representing the transition probability from state Si to state Sj, have the following two constraints:andThe constraint indicates that the state Si can reach any other state Sj in one step.
- The observation probability distribution can be indicated as:where bj(k) represents the probability of the state value j at time t with the observation symbol vk.
- The initial state probability distribution , whereπi are the probabilities of Si being the initial state in a state sequence.
2.2. Hidden Markov Driving Model
3. Data Description
3.1. Data Collection
3.2. Vehicle State Sequence
3.3. Model Development
4. Results and Discussion
4.1. Estimation of Driver Behavior
4.1.1. Parameter Calibration Results
4.1.2. Stability of Driver Behavior
4.1.3. Risk of Driver Behavior
4.2. Predicting Driver Behavior
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- National Highway Traffic Safety Administration. Traffic Safety Facts 2010; National Highway Traffic Safety Administration: Washington, DC, USA, 2012.
- Schorr, J.P.; Hamdar, S.H. Safety propensity index for signalized and unsignalized intersections: Exploration and assessment. Accid. Anal. Prev. 2014, 71, 93–105. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Wang, X.; Abdelaty, M.A. Modeling signalized intersection safety with corridor-level spatial correlations. Accid. Anal. Prev. 2010, 42, 84–92. [Google Scholar] [CrossRef] [PubMed]
- Chin, H.C.; Quddus, M.A. Applying the random effect negative binomial model to examine traffic accident occurrence at signalized intersections. Accid. Anal. Prev. 2003, 35, 253–259. [Google Scholar] [CrossRef]
- Wang, X.; Abdel-Aty, M.; Brady, P. Crash estimation at signalized intersections: Significant factors and temporal effect. Transp. Res. Rec. 2006, 10–20. [Google Scholar] [CrossRef]
- Porter, B.E.; England, K.J. Predicting red-light running behavior—A traffic safety study in three urban settings. J. Saf. Res. 2000, 31, 1–8. [Google Scholar] [CrossRef]
- Poch, M.; Mannering, F. Negative binomial analysis of intersection-accident frequencies. J. Transp. Eng. 1996, 122, 105–113. [Google Scholar] [CrossRef]
- Abdelaty, M.A.; Radwan, A.E. Modeling traffic accident occurrence and involvement. Accid. Anal. Prev. 2000, 32, 633–642. [Google Scholar] [CrossRef]
- Jovanis, P.P.; Chang, H.L. Modeling the Relationship of Accidents to Miles Traveled. In Transportation Research Record; No. 1068; Transportation Research Board: Washington, DC, USA, 1986; pp. 42–51. [Google Scholar]
- Jones, B.; Janssen, L.; Mannering, F. Analysis of the frequency and duration of freeway accidents in Seattle. Accid. Anal. Prev. 1991, 23, 239–255. [Google Scholar] [CrossRef]
- Joshua, S.C.; Garber, N.J. Estimating truck accident rate and involvements using Linear and Poisson Regression models. Transp. Plan. Technol. 1990, 15, 41–58. [Google Scholar] [CrossRef]
- Xie, K.; Wang, X.; Huang, H.; Chen, X. Corridor-level signalized intersection safety analysis in Shanghai, China using Bayesian hierarchical models. Accid. Anal. Prev. 2013, 50, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Miaou, S.P. The relationship between truck accidents and geometric design of road sections: Poisson versus negative binomial regressions. Accid. Anal. Prev. 1994, 26, 471–482. [Google Scholar] [CrossRef]
- Miaou, S.P.; Lum, H. Modeling vehicle accidents and highway geometric design relationships. Accid. Anal. Prev. 1993, 25, 689–709. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F.; Barfield, W. Effect of roadway geometrics and environmental factors on rural freeway accident frequencies. Accid. Anal. Prev. 1995, 27, 371–389. [Google Scholar] [CrossRef]
- Abdel-Aty, M.; Wang, X. Crash estimation at signalized intersections along corridors: Analyzing spatial effect and identifying significant factors. Transp. Res. Rec. 2006, 1953, 98–111. [Google Scholar] [CrossRef]
- Lord, D.; Persaud, B. Accident prediction models with and without trend: Application of the generalized estimating equations procedure. Biochem. Int. 2000, 1717, 102–108. [Google Scholar] [CrossRef]
- Ahmed, M.; Huang, H.; Abdel-Aty, M.; Guevara, B. Exploring a Bayesian hierarchical approach for developing safety performance functions for a mountainous freeway. Accid. Anal. Prev. 2011, 43, 1581–1589. [Google Scholar] [CrossRef] [PubMed]
- Anastasopoulos, P.C.; Mannering, F.L. A note on modeling vehicle accident frequencies with random-parameters count models. Accid. Anal. Prev. 2009, 41, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Dinu, R.R.; Veeraragavan, A. Random parameter models for accident prediction on two-lane undivided highways in India. J. Saf. Res. 2011, 42, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Abdelaty, M. Multilevel data and bayesian analysis in traffic safety. Accid. Anal. Prev. 2010, 42, 1556–1565. [Google Scholar] [CrossRef] [PubMed]
- Sabey, B.E.; Taylor, H. The Known Risks We Run: The Highway. In Societal Risk Assessment; Session I; Springer: New York, NY, USA, 1980; pp. 43–70. [Google Scholar]
- Chen, H.; Cao, L.; Logan, D.B. Analysis of risk factors affecting the severity of intersection crashes by logistic regression. Traffic Inj. Prev. 2012, 13, 300–307. [Google Scholar] [CrossRef] [PubMed]
- Cooper, P.J. Differences in accident characteristics among elderly drivers and between elderly and middle-aged drivers. Accid. Anal. Prev. 1990, 22, 499–508. [Google Scholar] [CrossRef]
- Holubowycz, O.T.; Kloeden, C.N.; Mclean, A.J. Age, sex, and blood alcohol concentration of killed and injured drivers, riders, and passengers. Accid. Anal. Prev. 1994, 26, 483–492. [Google Scholar] [CrossRef]
- Kim, K.; Brunner, I.M.; Yamashita, E. Modeling fault among accident—Involved pedestrians and motorists in Hawaii. Accid. Anal. Prev. 2008, 40, 2043–2049. [Google Scholar] [CrossRef] [PubMed]
- Shinar, D.; Schechtman, E.; Compton, R. Self-reports of safe driving behaviors in relationship to sex, age, education and income in the US adult driving population. Accid. Anal. Prev. 2001, 33, 111–116. [Google Scholar] [CrossRef]
- Zhang, G.; Yau, K.K.W.; Chen, G. Risk factors associated with traffic violations and accident severity in China. Accid. Anal. Prev. 2013, 59, 18–25. [Google Scholar] [CrossRef] [PubMed]
- Mogens, F. Speed and income. J. Transp. Econ. Policy 2005, 39, 225–240. [Google Scholar]
- Factor, R.; Mahalel, D.; Yair, G. Inter-group differences in road-traffic crash involvement. Accid. Anal. Prev. 2008, 40, 2000–2007. [Google Scholar] [CrossRef] [PubMed]
- Aoude, G.S.; Desaraju, V.R.; Stephens, L.H.; How, J.P. Driver behavior classification at intersections and validation on large naturalistic data set. IEEE Trans. Intell. Transp. Syst. 2012, 13, 724–736. [Google Scholar] [CrossRef]
- Bougler, B.; Cody, D.; Nowakowski, C. California Intersection Decision Support: A Driver-Centered Approach to Left-Turn Collision Avoidance System Design. Available online: http://www.path.berkeley.edu/sites/default/files/publications/PRR-2008-01.pdf (accessed on 31 August 2016).
- Zou, X.; Levinson, D. Modeling pipeline driving behaviors: A Hidden Markov Model approach. Transp. Res. Rec. 2006, 1980, 16–23. [Google Scholar] [CrossRef]
- Gadepally, V.; Krishnamurthy, A.; Ozguner, U. A framework for estimating driver decisions near intersections. IEEE Trans. Intell. Transp. Syst. 2014, 15, 637–646. [Google Scholar] [CrossRef]
- Oliver, N.; Pentland, A.P. Graphical Models for Driver Behavior Recognition in a Smartcar. In Proceedings of the IEEE Intelligent Vehicles Symposium 2000 (Cat. No.00TH8511), Dearborn, MI, USA, 5 October 2000; pp. 7–12.
- Mitrovic, D. Reliable method for driving events recognition. IEEE Trans. Intell. Transp. Syst. 2005, 6, 198–205. [Google Scholar] [CrossRef]
- Crawford, A. Driver judgment and error during the amber period at traffic light. Ergonomics 1962, 5, 513–532. [Google Scholar] [CrossRef]
- Gazis, D.; Herman, R.; Maradudin, A. The problem of the amber signal light in traffic flow. Oper. Res. 1960, 8, 112–132. [Google Scholar] [CrossRef]
- Baum, L.E.; Petrie, T. Statistical inference for probabilistic functions of finite state Markov chains. Ann. Math. Stat. 1966, 37, 1554–1563. [Google Scholar] [CrossRef]
- Rabiner, L.R. A Tutorial on Hidden Markov Models and Selected Applications in Speech Recognition. Available online: http://www.ece.ucsb.edu/Faculty/Rabiner/ece259/Reprints/tutorial%20on%20hmm%20and%20applications.pdf (accessed on 31 August 2016).
- Cheshomi, S.; Rahati-Q, S.; Akbarzadeh-T, M.R. Hybrid of chaos optimization and Baum-Welch algorithms for HMM training in continuous speech recognition. In Proceedings of the 2010 International Conference on Intelligent Control and Information Processing, Dalian, China, 13–15 August 2010; pp. 83–87.
- Meng, X.; Lee, K.K.; Xu, Y. Human driving behavior recognition based on Hidden Markov Models. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 274–279.
- Zegeer, C.V. Effectiveness of Green-Extension Systems at High-Speed Intersections. Available online: http://uknowledge.uky.edu/cgi/viewcontent.cgi?article=2066&context=ktc_researchreports (accessed on 31 August 2016).
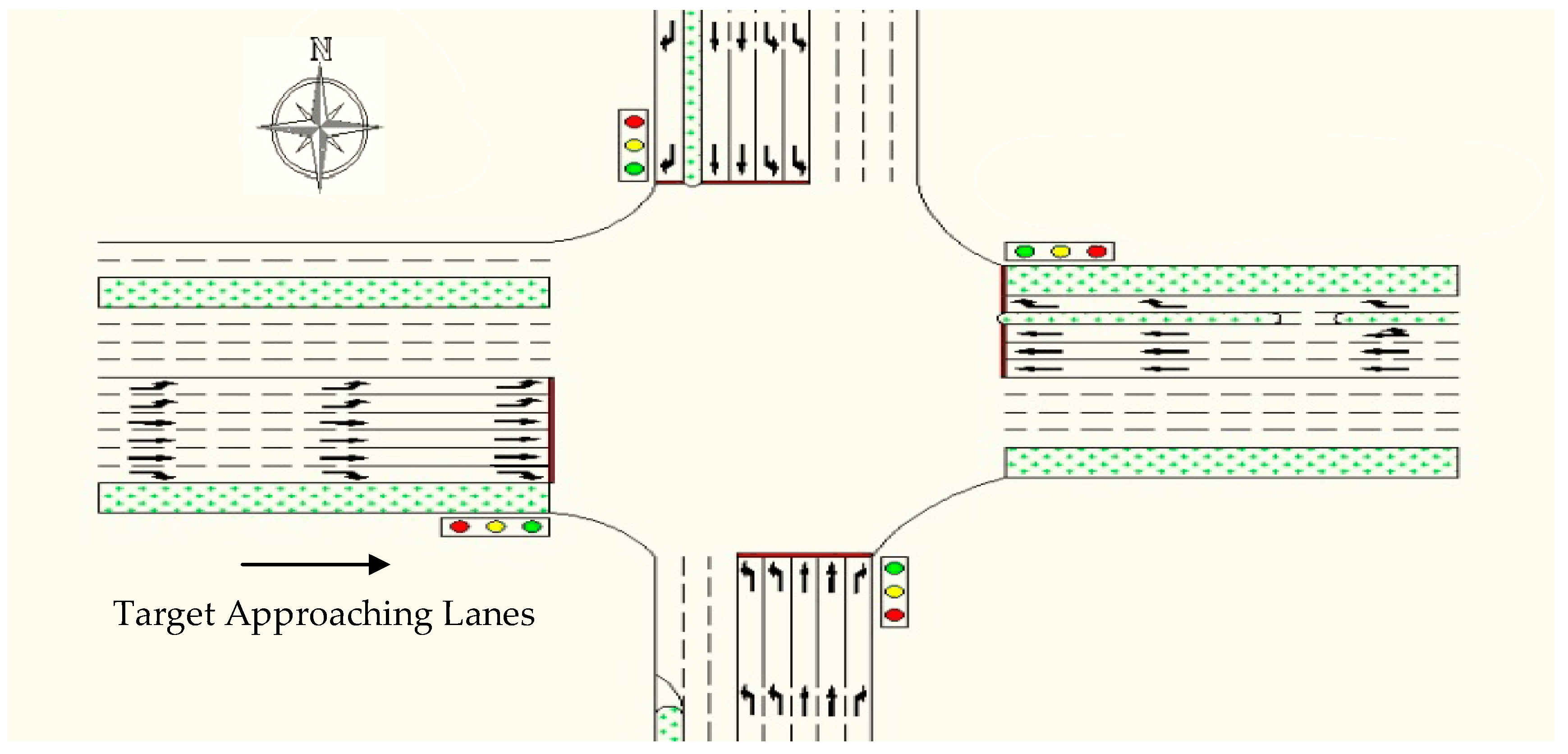

| Lanes | Traffic Volume (vph) | Speed Limit (km/h) | Cycle Length (s) | Green Time (s) |
|---|---|---|---|---|
| straight direction | 1900 | 60 | 190 | 35 |
| Speed | Headway | Queue Length | Signal Light | ||||
|---|---|---|---|---|---|---|---|
| Before (m/s) | After | Before (s) | After | Before | After | Before | After |
| ≤8 | 1 | Head Car | 1 | Head Car | 1 | Green | 1 |
| (8,16) | 2 | (0,6) | 2 | No preceding car stopped | 2 | Red | 2 |
| ≥16 | 3 | ≥6 | 3 | Others | 3 | Yellow | 3 |
| Sequence Number | Speed | Headway | Queue Length | Signal Light |
|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 | 2 |
| 3 | 1 | 1 | 1 | 3 |
| 4 | 1 | 1 | 2 | 1 |
| 5 | 1 | 1 | 2 | 2 |
| 6 | 1 | 1 | 2 | 3 |
| 7 | 1 | 1 | 3 | 1 |
| 8 | 1 | 1 | 3 | 2 |
| 9 | 1 | 1 | 3 | 3 |
| Classification | Included Variables |
|---|---|
| Hidden State Variables | Acceleration |
| Deceleration | |
| Maintain Speed | |
| Stop | |
| Observed Variables | Speed |
| Headway | |
| Queue Length | |
| Signal Light |
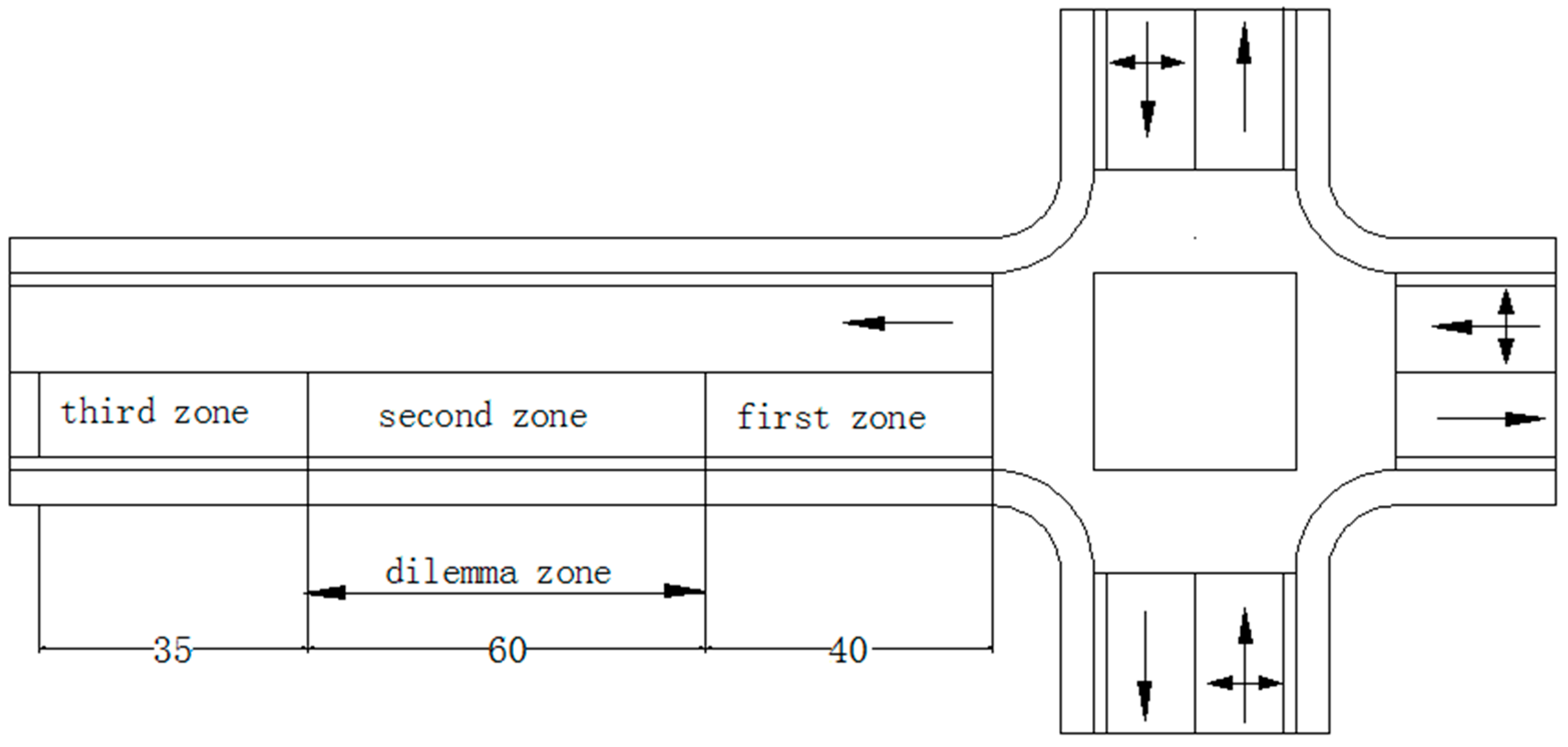
| Road Range | 1st Zone | 2nd Zone (Dilemma Zone) | 3rd Zone |
|---|---|---|---|
| 2-norm of Matrix B | 0.595 | 0.448 | 0.518 |
| Road Range | 1st Zone | 2nd Zone (Dilemma Zone) | 3rd Zone |
|---|---|---|---|
| Risk Index α | −5.437 | −3.343 | −8.881 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; He, Q.; Zhou, H.; Guan, Y.; Dai, W. Modeling Driver Behavior near Intersections in Hidden Markov Model. Int. J. Environ. Res. Public Health 2016, 13, 1265. https://doi.org/10.3390/ijerph13121265
Li J, He Q, Zhou H, Guan Y, Dai W. Modeling Driver Behavior near Intersections in Hidden Markov Model. International Journal of Environmental Research and Public Health. 2016; 13(12):1265. https://doi.org/10.3390/ijerph13121265
Chicago/Turabian StyleLi, Juan, Qinglian He, Hang Zhou, Yunlin Guan, and Wei Dai. 2016. "Modeling Driver Behavior near Intersections in Hidden Markov Model" International Journal of Environmental Research and Public Health 13, no. 12: 1265. https://doi.org/10.3390/ijerph13121265
APA StyleLi, J., He, Q., Zhou, H., Guan, Y., & Dai, W. (2016). Modeling Driver Behavior near Intersections in Hidden Markov Model. International Journal of Environmental Research and Public Health, 13(12), 1265. https://doi.org/10.3390/ijerph13121265





