A Spatial Hierarchical Analysis of the Temporal Influences of the El Niño-Southern Oscillation and Weather on Dengue in Kalutara District, Sri Lanka
Abstract
:1. Introduction
2. Materials and Methods
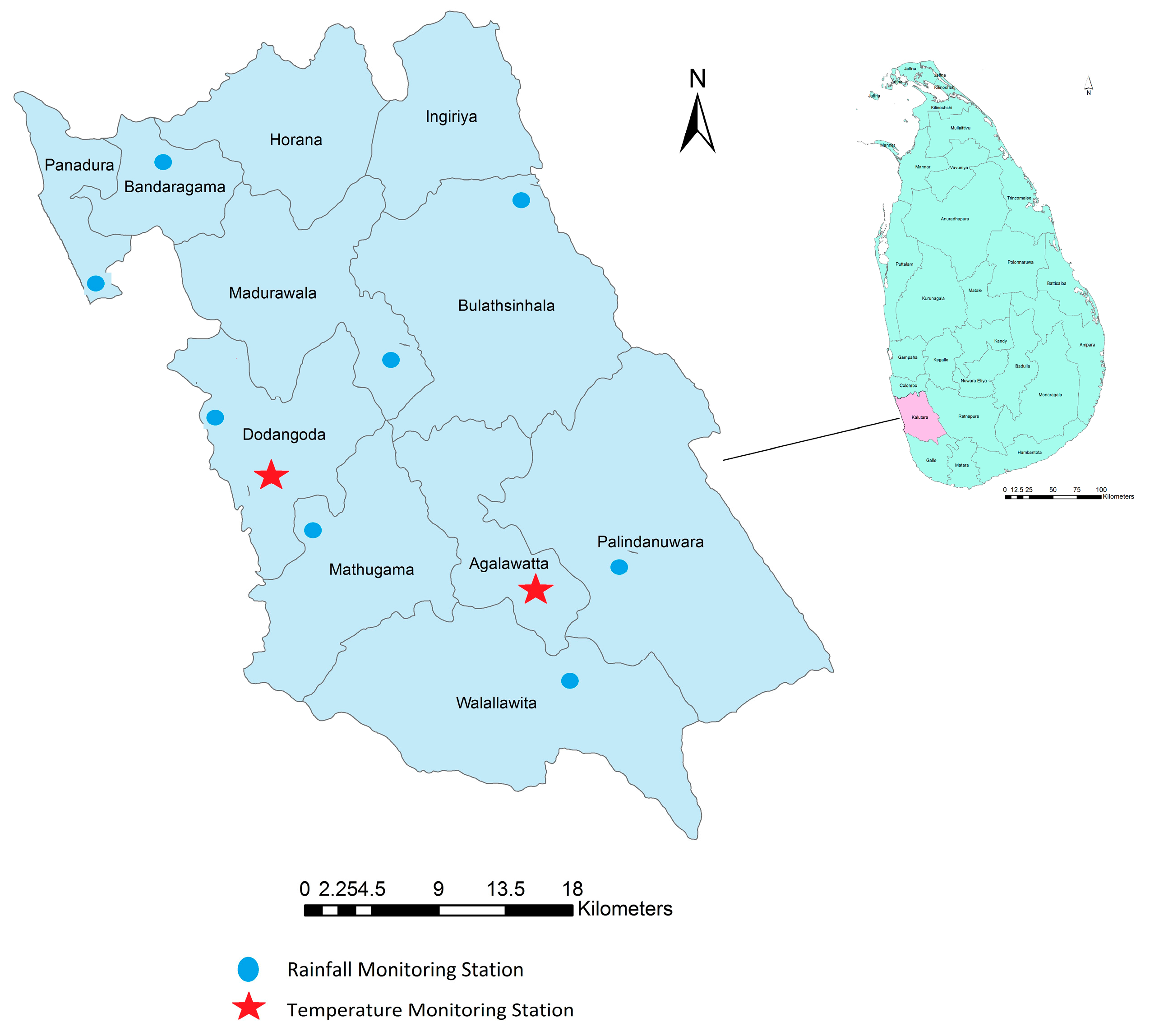
2.1. Study Area
2.2. Data Collection
2.3. Statistical Analysis
2.3.1. First Stage Division Specific Analysis
2.3.2. Second Stage Meta-Analysis
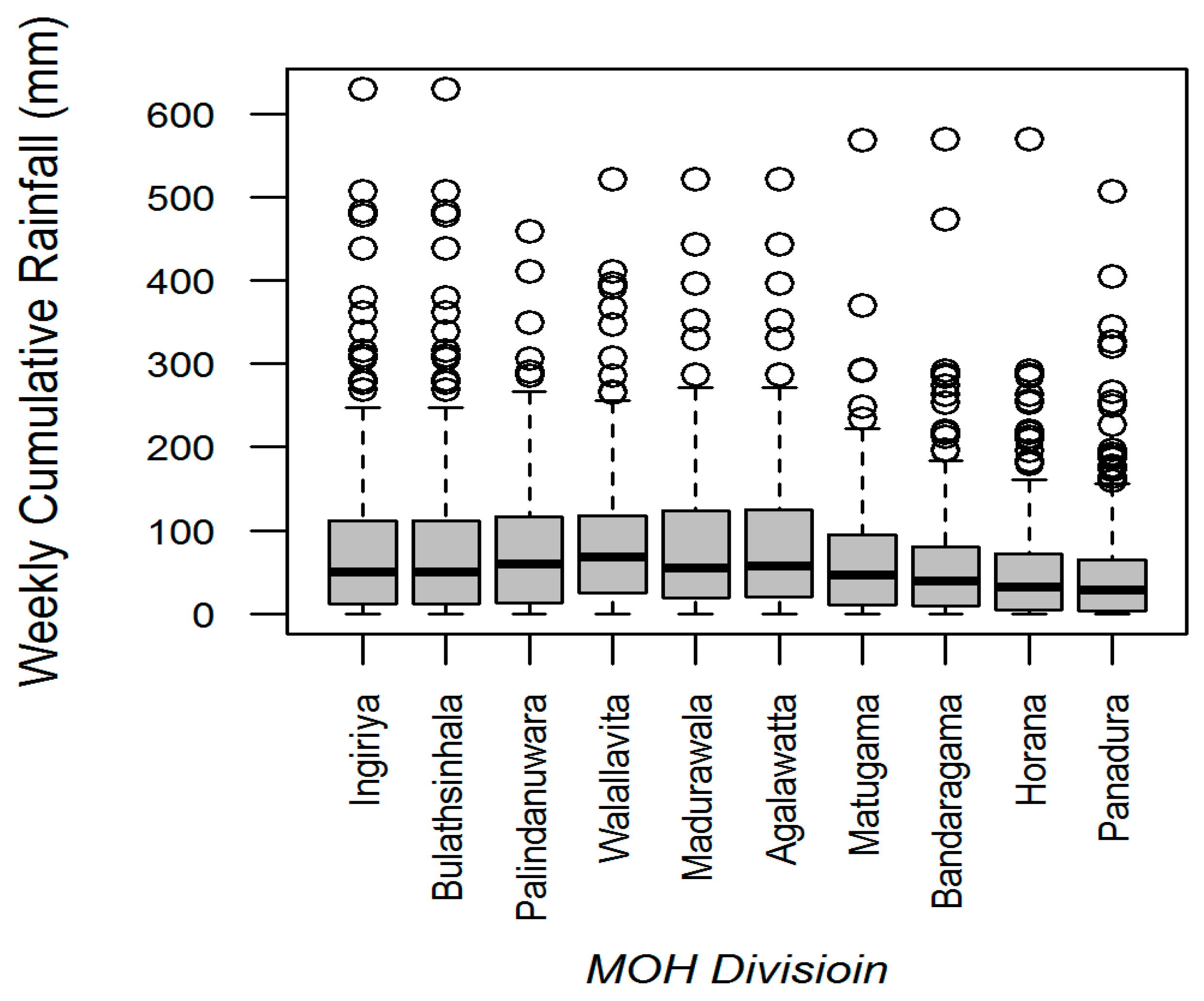
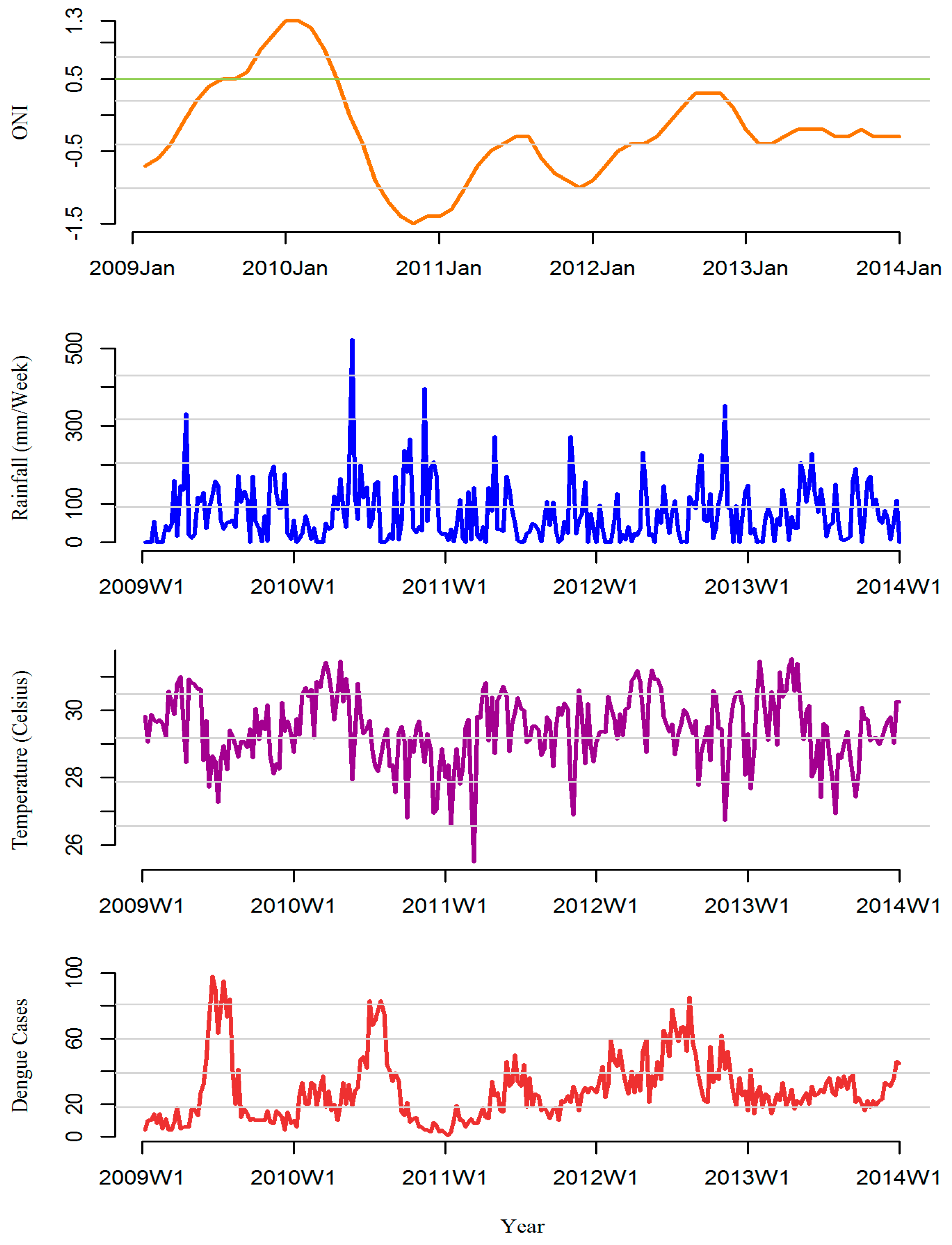
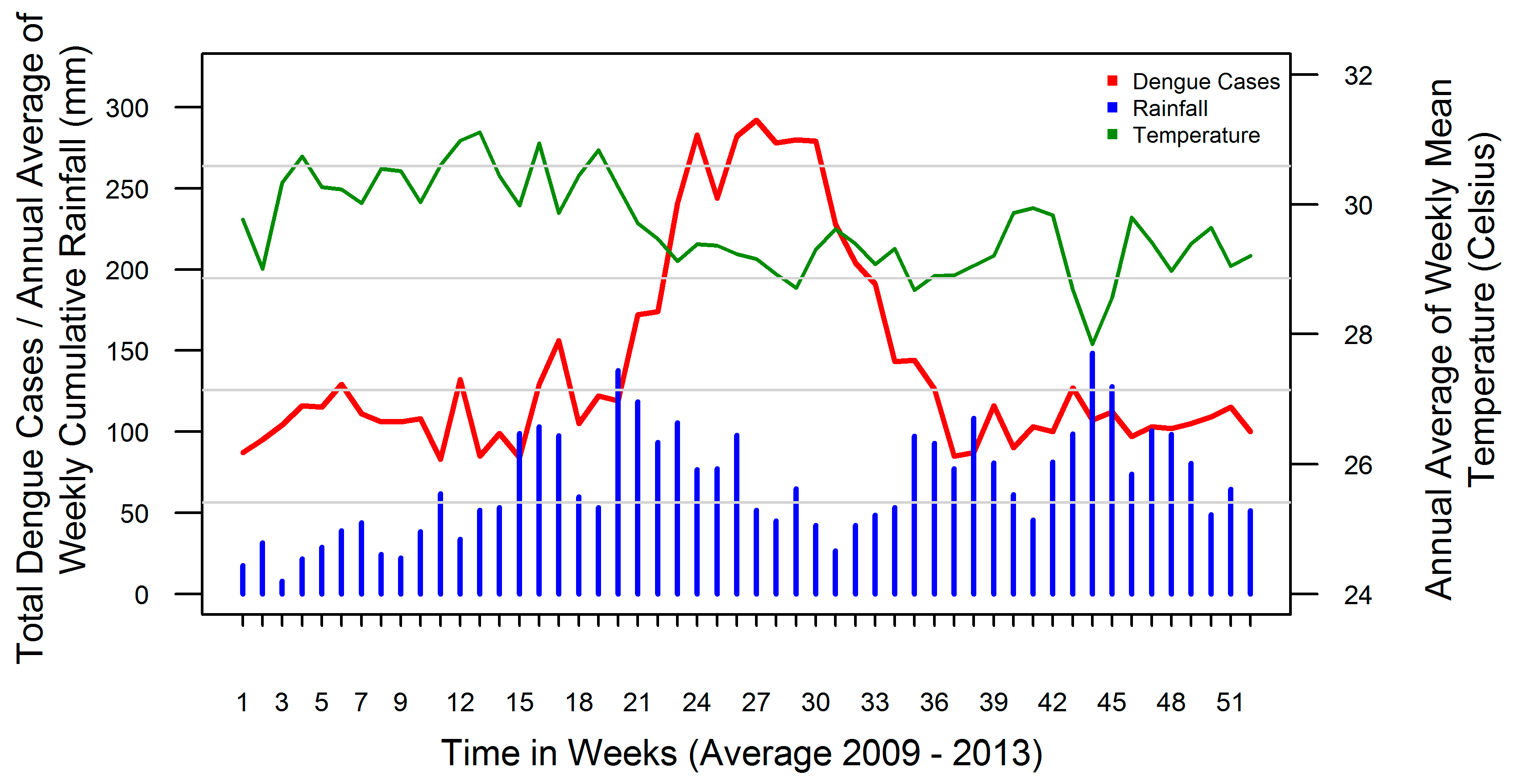
3. Results
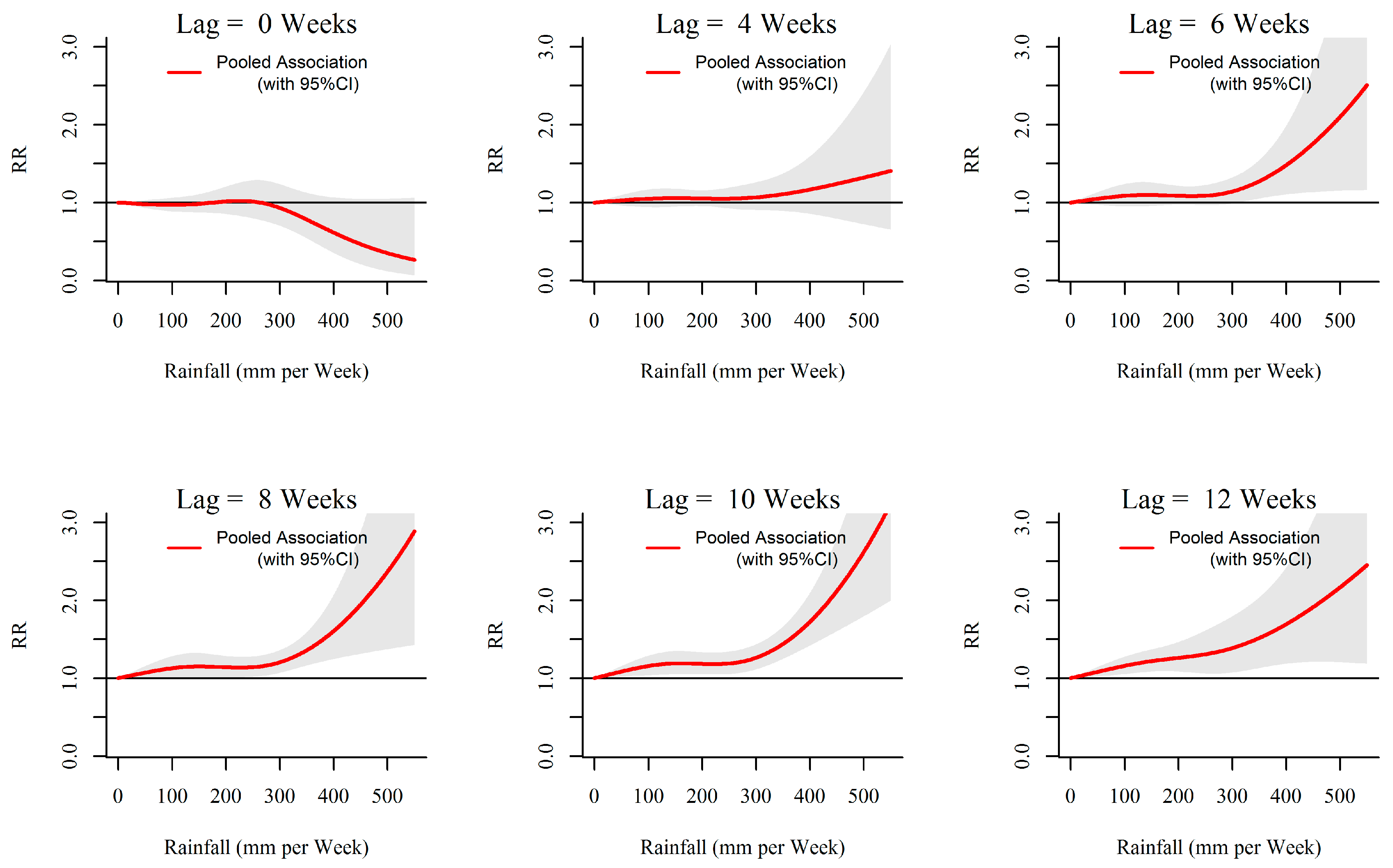
3.1. Rainfall-Dengue Association
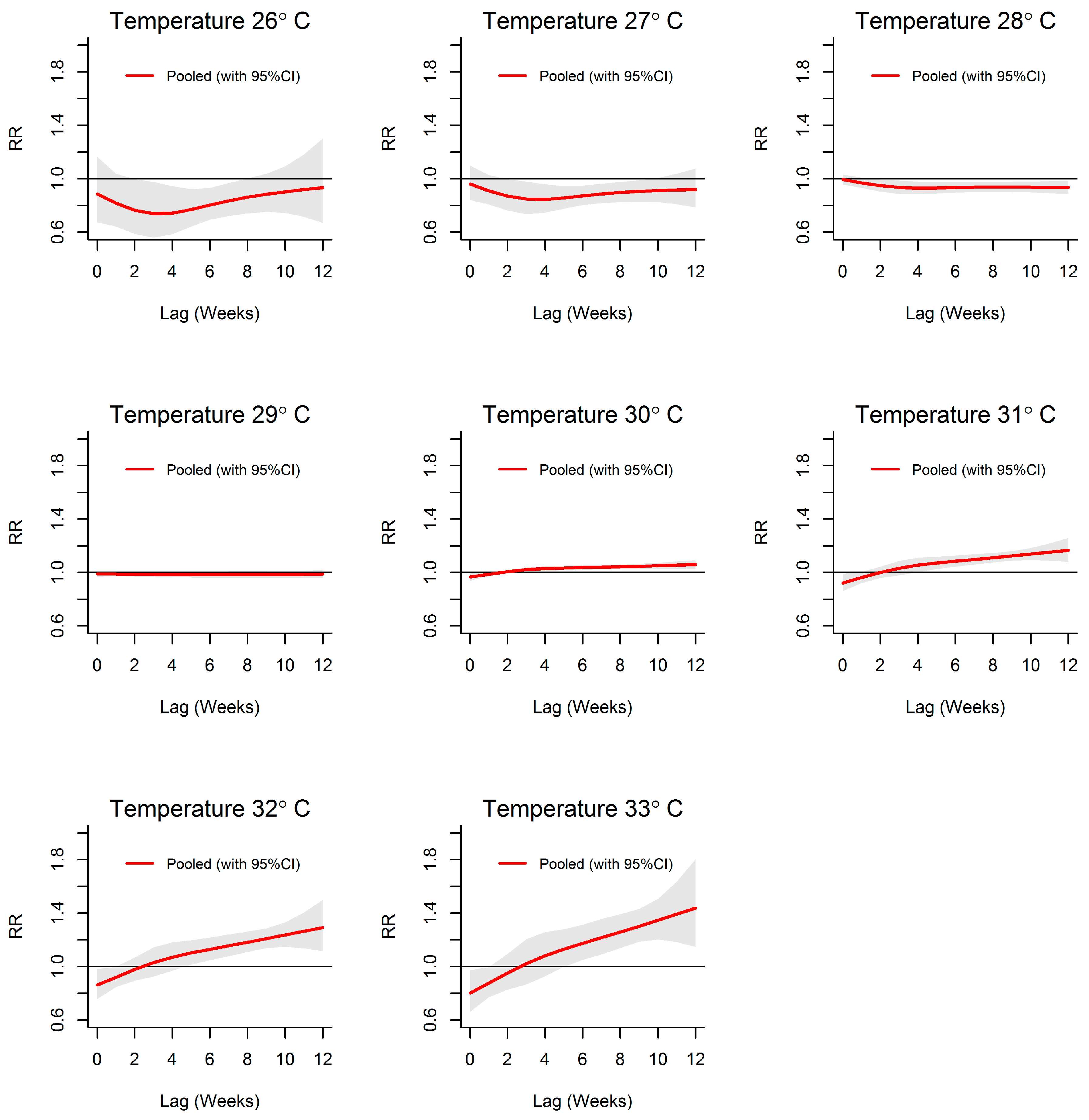
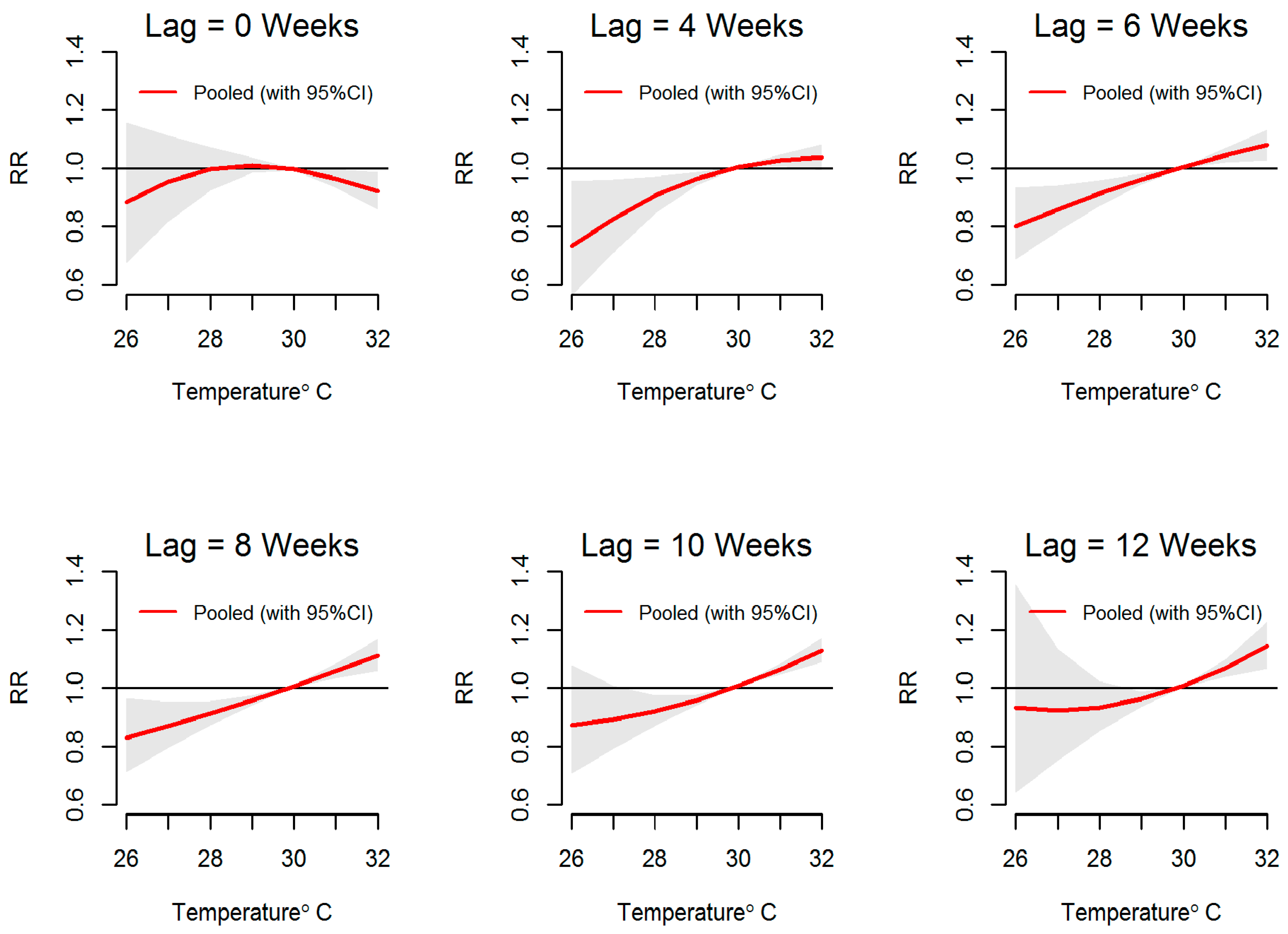
3.2. Temperature-Dengue Association
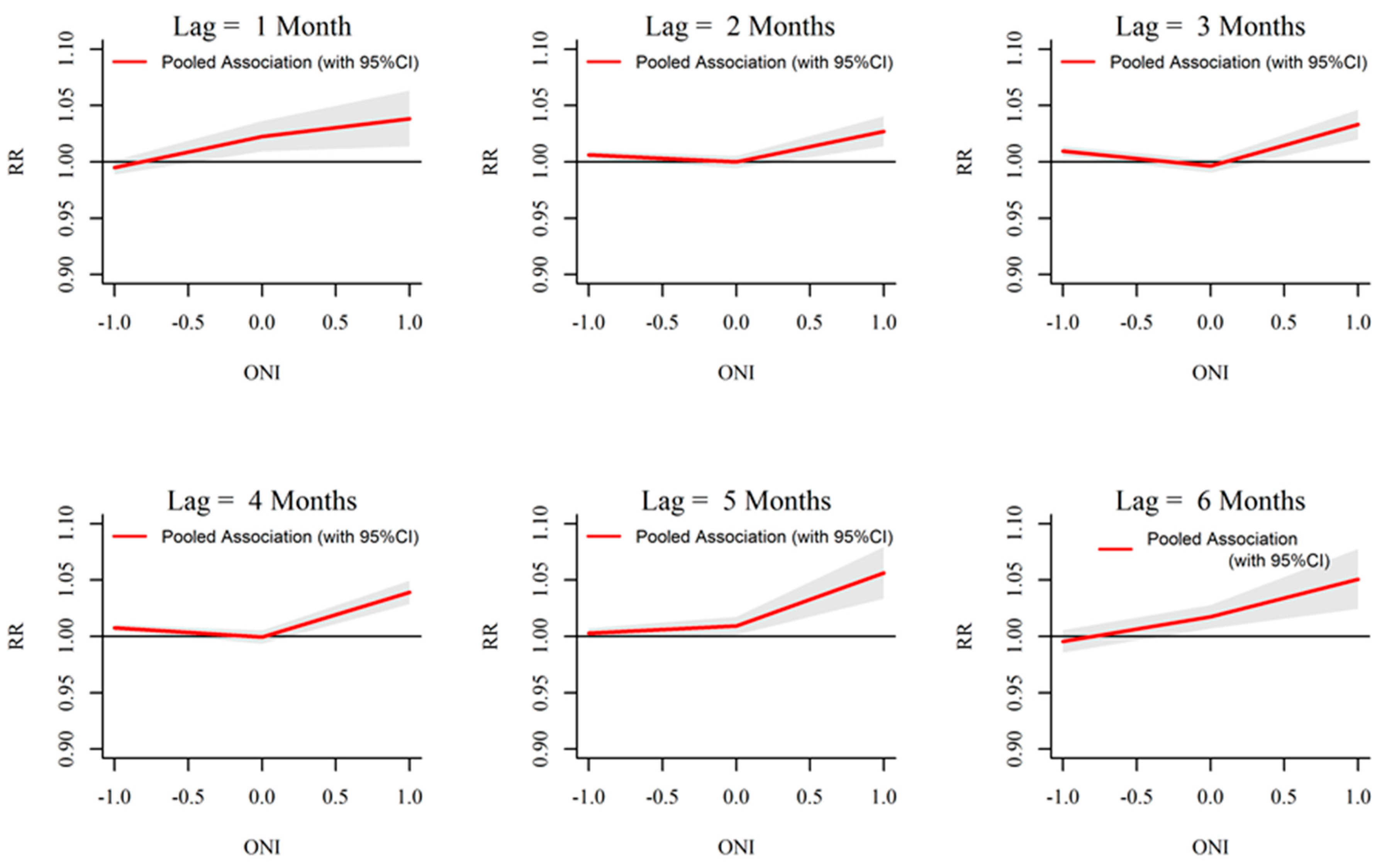
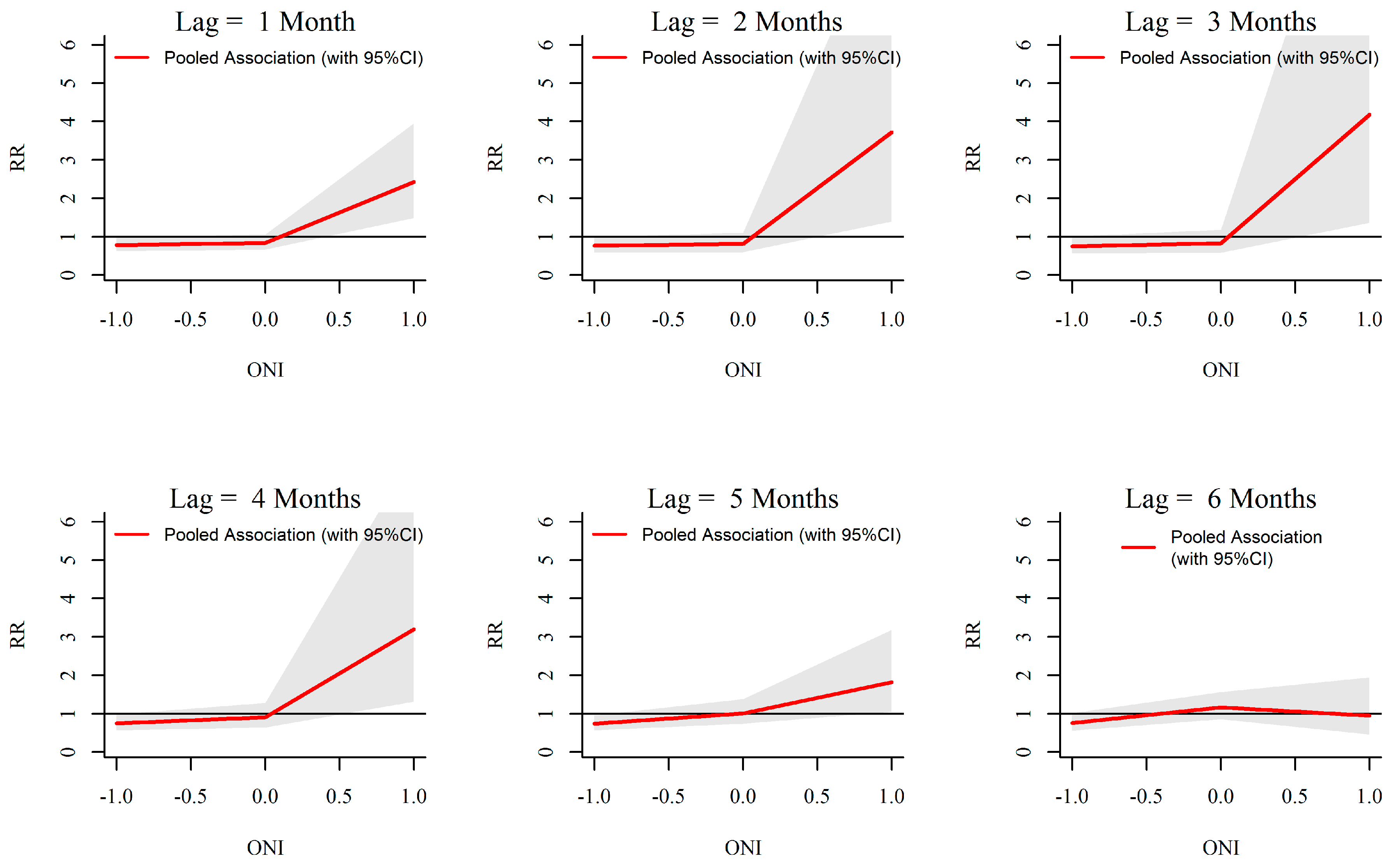
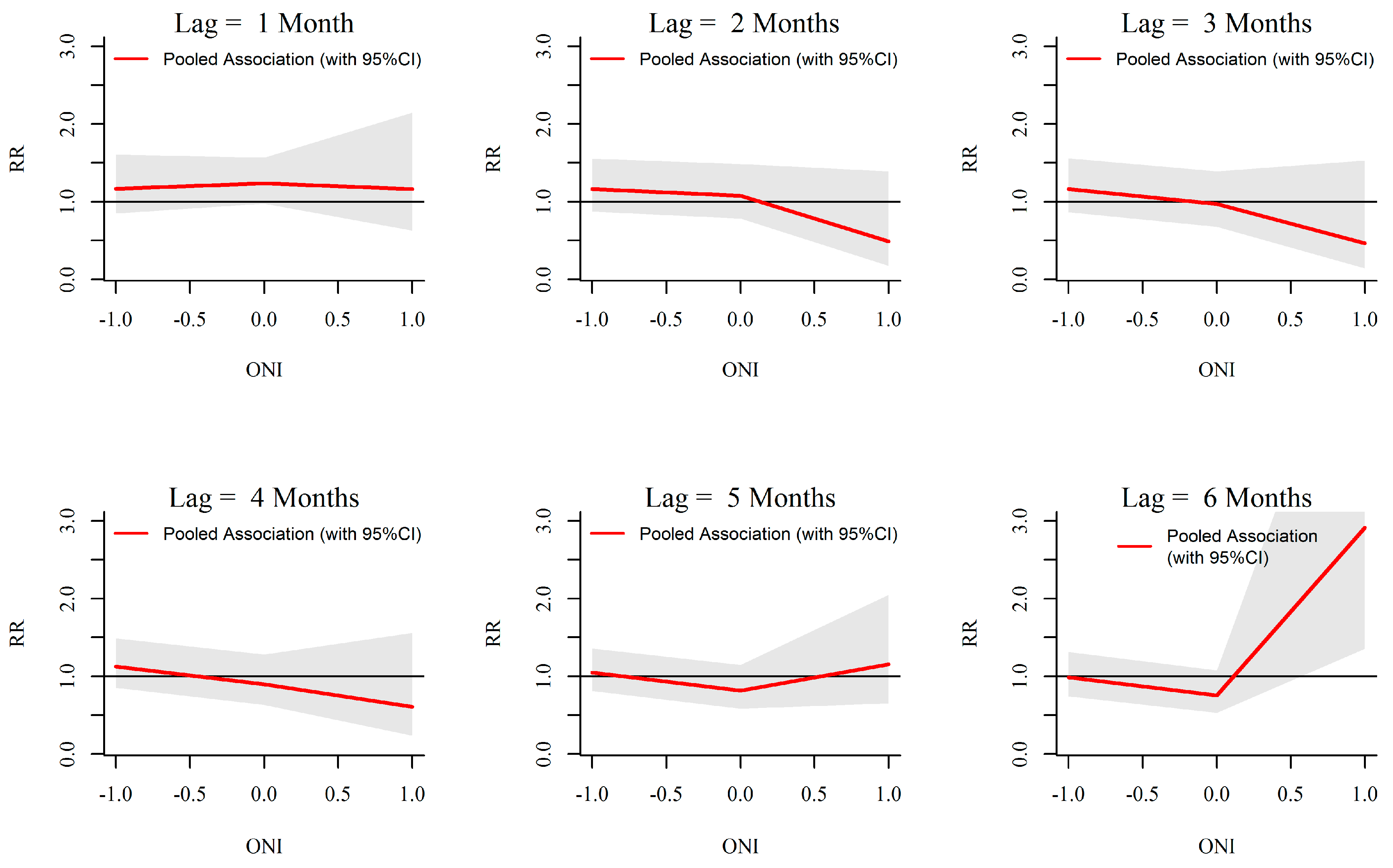
3.3. ONI-Dengue Association
3.4. Assessment of Heterogeneity in Associations among MOH Divisions
4. Discussion
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- WHO. Dengue and Severe Dengue: Fact Sheet. Available online: http://www.who.int/mediacentre/factsheets/fs117/en/ (accessed on 11 November 2014).
- Bhatt, S.; Gething, P.W.; Brady, O.J.; Messina, J.P.; Farlow, A.W.; Moyes, C.L.; Drake, J.M.; Brownstein, J.S.; Hoen, A.G.; Sankoh, O.; et al. The global distribution and burden of dengue. Nature 2013, 496, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Gubler, D.J.; Rosen, L. Quantitative aspects of replication of dengue viruses in Aedes albopictus (Diptera: Culicidae) after oral and parenteral infection. J. Med. Entomol. 1977, 13, 469–472. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Dengue virus-mosquito interactions. Annu. Rev. Entomol. 2008, 53, 273–291. [Google Scholar] [CrossRef] [PubMed]
- Department of Meteorology—Sri Lanka. 2014. Available online: www.meteo.gov.lk (accessed on 10 October 2016).
- Hapuarachchi, H.A.S.U.; Jayawardena, I.M.S.P. Modulation of Seasonal Rainfall in Sri Lanka by ENSO Extremes. Sri Lanka J. Meteorol. 2015, 1, 3–11. [Google Scholar]
- Zubair, L.; Siriwardhana, M.; Chandimala, J.; Yahiya, Z. Predictability of Sri Lankan rainfall based on ENSO. Int. J. Climatol. 2008, 28, 91–101. [Google Scholar] [CrossRef]
- WHO. Dengue Guidelines for Diagnosis, Treatment, Prevention and Control; World Health Organization: Geneva, Switzerland, 2009; pp. 1–14. [Google Scholar]
- Gratz, N.G. Critical review of the vector status of Aedes albopictus. Med. Vet. Entomol. 2004, 18, 215–227. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.A.; Haile, D.G.; Daniels, E.; Mount, G.A. Dynamic life table model for Aedes aegypti (diptera: Culicidae): Simulation results and validation. J. Med. Entomol. 1993, 30, 1018–1028. [Google Scholar] [CrossRef] [PubMed]
- Chan, M.; Johansson, M.A. The incubation periods of Dengue viruses. PLoS ONE 2012, 7, e50972. [Google Scholar] [CrossRef] [PubMed]
- Liu-Helmersson, J.; Stenlund, H.; Wilder-Smith, A.; Rocklöv, J. Vectorial Capacity of Aedes aegypti: Effects of Temperature and Implications for Global Dengue Epidemic Potential. PLoS ONE 2014, 9, e89783. [Google Scholar] [CrossRef] [PubMed]
- Halstead, S.B. Dengue. Lancet 2007, 370, 1644–1652. [Google Scholar] [CrossRef]
- Messer, W.B.; Vitarana, U.T.; Sivananthan, K.; Elvtigala, J.; Preethimala, L.D.; Ramesh, R.; Withana, N.; Gubler, D.J.; De Silva, A.M. Epidemiology of dengue in Sri Lanka before and after the emergence of epidemic dengue hemorrhagic fever. Am. J. Trop. Med. Hyg. 2002, 66, 765–773. [Google Scholar] [PubMed]
- Vitarana, T.; Jayakuru, W.S.; Withine, N. Historical account of dengue haemorrhagic fever in Sri Lanka. Dengue Bull. 1997, 21, 117–118. [Google Scholar]
- Tissera, H.A.; Ooi, E.E.; Gubler, D.J.; Tan, Y.; Logendra, B.; Wahala, W.M.; de Silva, A.M.; Abeysinghe, M.R.; Palihawadana, P.; Gunasena, S.; et al. New dengue virus type 1 genotype in Colombo, Sri Lanka. Emerg. Infect. Dis. 2011, 17, 2053–2055. [Google Scholar] [CrossRef] [PubMed]
- Tissera, H.; Amarasinghe, A.; Gunasena, S.; DeSilva, A.D.; Yee, L.W.; Sessions, O.; Muthukuda, C.; Palihawadana, P.; Lohr, W.; Byass, P.; et al. Laboratory-Enhanced Dengue Sentinel Surveillance in Colombo District, Sri Lanka: 2012–2014. PLoS Negl. Trop. Dis. 2016, 10, e0004477. [Google Scholar] [CrossRef] [PubMed]
- Kanakaratne, N.; Wahala, W.M.P.B.; Messer, W.B.; Tissera, H.A.; Shahani, A.; Abeysinghe, N.; de Silva, A.M.; Gunasekera, M. Severe dengue epidemics in Sri Lanka, 2003–2006. Emerg. Infect. Dis. 2009, 15, 192–199. [Google Scholar] [CrossRef] [PubMed]
- Tam, C.C.; Tissera, H.; de Silva, A.M.; de Silva, A.D.; Margolis, H.S.; Amarasinge, A. Estimates of dengue force of infection in children in Colombo, Sri Lanka. PLoS Negl. Trop. Dis. 2013, 7, e2259. [Google Scholar] [CrossRef] [PubMed]
- Epidemiology Unit Ministry of Health Sri Lanka. Dengue Sentinal Site Surveillance. Available online: http://www.epid.gov.lk/web/index.php?lang=en (accessed on 22 January 2015).
- Hii, Y.L.; Rocklöv, J.; Ng, N.; Tang, C.S.; Pang, F.Y.; Sauerborn, R. Climate variability and increase in intensity and magnitude of dengue incidence in Singapore. Glob. Health Action 2009, 2. [Google Scholar] [CrossRef] [PubMed]
- Cheong, Y.L.; Burkart, K.; Leitão, P.J.; Lakes, T. Assessing weather effects on dengue disease in Malaysia. Int. J. Environ. Res. Public Health 2013, 10, 6319–6334. [Google Scholar] [CrossRef] [PubMed]
- Naish, S.; Dale, P.; Mackenzie, J.S.; McBride, J.; Mengersen, K.; Tong, S. Climate change and dengue: A critical and systematic review of quantitative modelling approaches. BMC Infect. Dis. 2014, 14, 167. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.A.; Cummings, D.A.; Glass, G.E. Multiyear climate variability and dengue—El Niño southern oscillation, weather, and dengue incidence in Puerto Rico, Mexico, and Thailand: A longitudinal data analysis. PLoS Med. 2009, 6, e1000168. [Google Scholar] [CrossRef] [PubMed]
- Sarfraz, M.S.; Tripathi, N.K.; Tipdecho, T.; Thongbu, T.; Kerdthong, P.; Souris, M. Analyzing the spatio-temporal relationship between dengue vector larval density and land-use using factor analysis and spatial ring mapping. BMC Public Health 2012, 12, 853. [Google Scholar] [CrossRef] [PubMed]
- Kuno, G. Review of the factors modulating dengue transmission. Epidemiol. Rev. 1995, 17, 321–335. [Google Scholar] [PubMed]
- Delatte, H.; Gimonneau, G.; Triboire, A.; Fontenille, D. Influence of temperature on immature development, survival, longevity, fecundity, and gonotrophic cycles of Aedes albopictus, vector of chikungunya and dengue in the Indian Ocean. J. Med. Entomol. 2009, 46, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Spiegel, J.; Hattersley, S.B.; Hayden, M.H.; Kittayapong, P.; Nalim, S.; Wang, D.N.C.; Zielinski-Gutiérrez, E.; Gubler, D. Barriers and Bridges to Prevention and Control of Dengue: The Need for a Social–Ecological Approach. EcoHealth 2005, 2, 273–290. [Google Scholar] [CrossRef]
- Struchiner, C.J.; Rocklöv, J.; Wilder-Smith, A.; Massad, E. Increasing Dengue Incidence in Singapore over the Past 40 Years: Population Growth, Climate and Mobility. PLoS ONE 2015, 10, e0136286. [Google Scholar] [CrossRef] [PubMed]
- Edenhofer, O.; Pichs-Madruga, R.; Sokona, Y.; Farahani, E.; Kadner, S.; Seyboth, K.; Adler, A.; Baum, I.; Brunner, S.; Eickemeier, P.; et al. Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. In IPCC Climate Change 2014; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Goto, K.; Kumarendran, B.; Mettananda, S.; Gunasekara, D.; Fujii, Y.; Kaneko, S. Analysis of effects of meteorological factors on dengue incidence in Sri Lanka using time series data. PLoS ONE 2013, 8, e63717. [Google Scholar] [CrossRef] [PubMed]
- Imai, C.; Hashizume, M. A systematic review of methodology: Time series regression analysis for environmental factors and infectious diseases. Trop. Med. Health 2015, 43, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.L.; Dushoff, J.; McKenzie, F.E. The risk of a mosquito-borne infection in a heterogeneous environment. PLoS Biol. 2004, 2, e368. [Google Scholar] [CrossRef] [PubMed]
- Department of Census and Statistics Sri Lanka. Census of Population and Housing 2012—Final Report. In Population by Ethnicity and District According to Divisional Secretary’s Division, 2012; Department of Census and Statistics Sri Lanka, Ed.; Department of Census and Statistics Sri Lanka: Colombo, Sri Lanka, 2012. [Google Scholar]
- The World Bank. World Bank Sri Lanka Country Statistics; The World Bank: Washington, DC, USA, 2014. [Google Scholar]
- Epidemiology Unit Ministry of Health Sri Lanka. Disease Surveillance and Trends. Available online: http://www.epid.gov.lk/web/index.php?lang=en (accessed on 2 December 2014).
- Epidemiology Unit Ministru of Health Sri Lanka. Surveillance Case Definitions for Notifiable Disease in Sri Lanka, 2nd ed.Epidemiology Unit Ministru of Health Sri Lanka: Colombo, Sri Lanka, 2011; Volume 1.
- Tissera, H.; Weeraman, J.; Amarasinghe, A.; Wijewickrama, A.; Palihawadana, P.; Fernando, L. Expediency of dengue illness classification: The Sri Lankan perspective. WHO South-East Asia J. Public Health 2014, 3, 5–7. [Google Scholar]
- Grechka, D.A.; Berezin, S.B.; Emmott, S.L.V.; Smith, M.J.; Purves, D.W. Universal, easy access to geotemporal information: FetchClimate. Ecography 2016, 39, 904–911. [Google Scholar] [CrossRef]
- NASA. Level 3 Land Surface Temperature and Emissivity Daily and 8-Day Global, 1 km; NASA EOSDIS Land Processes DAAC, USGS Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2006.
- NOAA. Cold and Warm Episodes by Season NOAA/National Weather Service; National Oceanic and Atmospheric Administration’s National Weather Service NOAA Center for Weather and Climate Prediction: College Park, MD, USA, 2016.
- Gasparrini, A.; Armstrong, B. Time series analysis on the health effects of temperature: Advancements and limitations. Environ. Res. 2010, 110, 633–638. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Armstrong, B. Reducing and meta-analysing estimates from distributed lag non-linear models. BMC Med. Res. Methodol. 2013, 13, 1. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Distributed lag non-linear models. Stat. Med. 2010, 29, 2224–2234. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Multivariate meta-analysis for non-linear and other multi-parameter associations. Stat. Med. 2012, 31, 3821–3839. [Google Scholar] [CrossRef] [PubMed]
- Gasparrini, A. Modeling exposure-lag-response associations with distributed lag non-linear models. Stat. Med. 2014, 33, 881–899. [Google Scholar] [CrossRef] [PubMed]
- Zeger, S.L.; Irizarry, R.; Peng, R.D. On time series analysis of public health and biomedical data. Annu. Rev. Public Health 2006, 27, 57–79. [Google Scholar] [CrossRef] [PubMed]
- Lowe, R.; Bailey, T.C.; Stephenson, D.B.; Jupp, T.E.; Graham, R.J.; Barcellos, C.; Carvalho, M.S. The development of an early warning system for climate-sensitive disease risk with a focus on dengue epidemics in Southeast Brazil. Stat. Med. 2013, 32, 864–883. [Google Scholar] [CrossRef] [PubMed]
- Hii, Y.L.; Rocklöv, J.; Wall, S.; Ng, L.C.; Tang, C.S.; Ng, N. Optimal Lead Time for Dengue Forecast. PLoS Negl. Trop. Dis. 2012, 6, e1848. [Google Scholar] [CrossRef] [PubMed]
- Bhaskaran, K.; Gasparrini, A.; Hajat, S.; Smeeth, L.; Armstrong, B. Time series regression studies in environmental epidemiology. Int. J. Epidemiol. 2013, 42, 1187–1195. [Google Scholar] [CrossRef] [PubMed]
- Huedo-Medina, T.B.; Sánchez-Meca, J.; Marín-Martínez, F.; Botella, J. Assessing heterogeneity in meta-analysis: Q statistic or I2 index? Psychol. Methods 2006, 11, 193–206. [Google Scholar] [CrossRef] [PubMed]
- Eng, R.D.; Dominici, F.; Louis, T.A. Model choice in time series studies of air pollution and mortality. J. R. Stat. Soc.: Ser. A (Stat. Soc.) 2006, 169, 179–203. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R.F.f.S. Computing: Vienna, Austria, 2014. [Google Scholar]
- Yang, H.M.; Macoris, M.L.; Galvani, K.C.; Andrighetti, M.T.; Wanderley, D.M. Assessing the effects of temperature on the population of Aedes aegypti, the vector of dengue. Epidemiol. Infect. 2009, 137, 1188–1202. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.A.; Brenner, R.J.; Hayes, J.; Daniels, E. Transmission thresholds for dengue in terms of Aedes aegypti pupae per person with discussion of their utility in source reduction efforts. Am. J. Trop. Med. Hyg. 2000, 62, 11–18. [Google Scholar] [PubMed]
- Watts, D.M.; Burke, D.S.; Harrison, B.A.; Whitmire, R.E.; Nisalak, A. Effect of temperature on the vector efficiency of Aedes aegypti for dengue 2 virus. Am. J. Trop. Med. Hyg. 1987, 36, 143–152. [Google Scholar] [PubMed]
- Chen, M.-J.; Lin, C.-Y.; Wu, Y.-T.; Wu, P.-C.; Lung, S.-C.; Su, H.-J. Effects of extreme precipitation to the distribution of infectious diseases in Taiwan, 1994–2008. PLoS ONE 2012, 7, e34651. [Google Scholar] [CrossRef] [PubMed]
- Descloux, E.; Mangeas, M.; Menkes, C.E.; Lengaigne, M.; Leroy, A.; Tehei, T.; Guillaumot, L.; Teurlai, M.; Gourinat, A.; Benzler, J.; et al. Climate-based models for understanding and forecasting dengue epidemics. PLoS Negl. Trop. Dis. 2012, 6, e1470. [Google Scholar] [CrossRef] [PubMed]
- Stewart Ibarra, A.M.; Ryan, S.J.; Beltrán, E.; Mejía, R.; Silva, M.; Muñoz, Á. Dengue vector dynamics (Aedes aegypti) influenced by climate and social factors in Ecuador: Implications for targeted control. PLoS ONE 2013, 8, e78263. [Google Scholar] [CrossRef] [PubMed]
- Bowman, L.R.; Tejeda, G.S.; Coelho, G.E.; Sulaiman, L.H.; Gill, B.S.; McCall, P.J.; Olliaro, P.L.; Ranzinger, S.R.; Quang, L.C.; Ramm, R.S.; et al. Alarm variables for Dengue outbreaks: A multi-centre study in Asia and Latin America. PLoS ONE 2016, 11, e0157971. [Google Scholar] [CrossRef] [PubMed]
- Hii, Y.L.; Zhu, H.; Ng, N.; Ng, L.C.; Rocklöv, J. Forecast of Dengue incidence using temperature and rainfall. PLoS Negl. Trop. Dis. 2012, 6, e1908. [Google Scholar] [CrossRef] [PubMed]
- García, C.; García, L.; Espinosa-Carreón, L.; Ley, C. Abundance and distribution of Aedes aegypti (Diptera: Culicidae), and dengue dispersion in Guasave Sinaloa, Mexico. Rev. Biol. Trop. 2011, 59, 1609–1619. [Google Scholar] [PubMed]
- Chien, L.C.; Yu, H.L. Impact of meteorological factors on the spatiotemporal patterns of dengue fever incidence. Environ. Int. 2014, 73, 46–56. [Google Scholar] [CrossRef] [PubMed]
- Ehelepola, N.D.; Ariyaratne, K. The interrelationship between dengue incidence and diurnal ranges of temperature and humidity in a Sri Lankan city and its potential applications. Glob. Health Action 2015, 8, 29359. [Google Scholar] [CrossRef] [PubMed]
- Tipayamongkholgul, M.; Fang, C.; Klinchan, S.; Liu, C.; King, C. Effects of the El Niño-southern oscillation on dengue epidemics in Thailand, 1996–2005. BMC Public Health 2009, 9, 422. [Google Scholar] [CrossRef] [PubMed]
- Wesolowski, A.; Qureshi, T.; Boni, M.F.; Sundsøy, P.R.; Johansson, M.A.; Rasheed, S.B.; Engø-Monsen, K.; Buckee, C.O. Impact of human mobility on the emergence of dengue epidemics in Pakistan. Proc. Natl. Acad. Sci. USA 2015, 112, 11887–11892. [Google Scholar] [CrossRef] [PubMed]
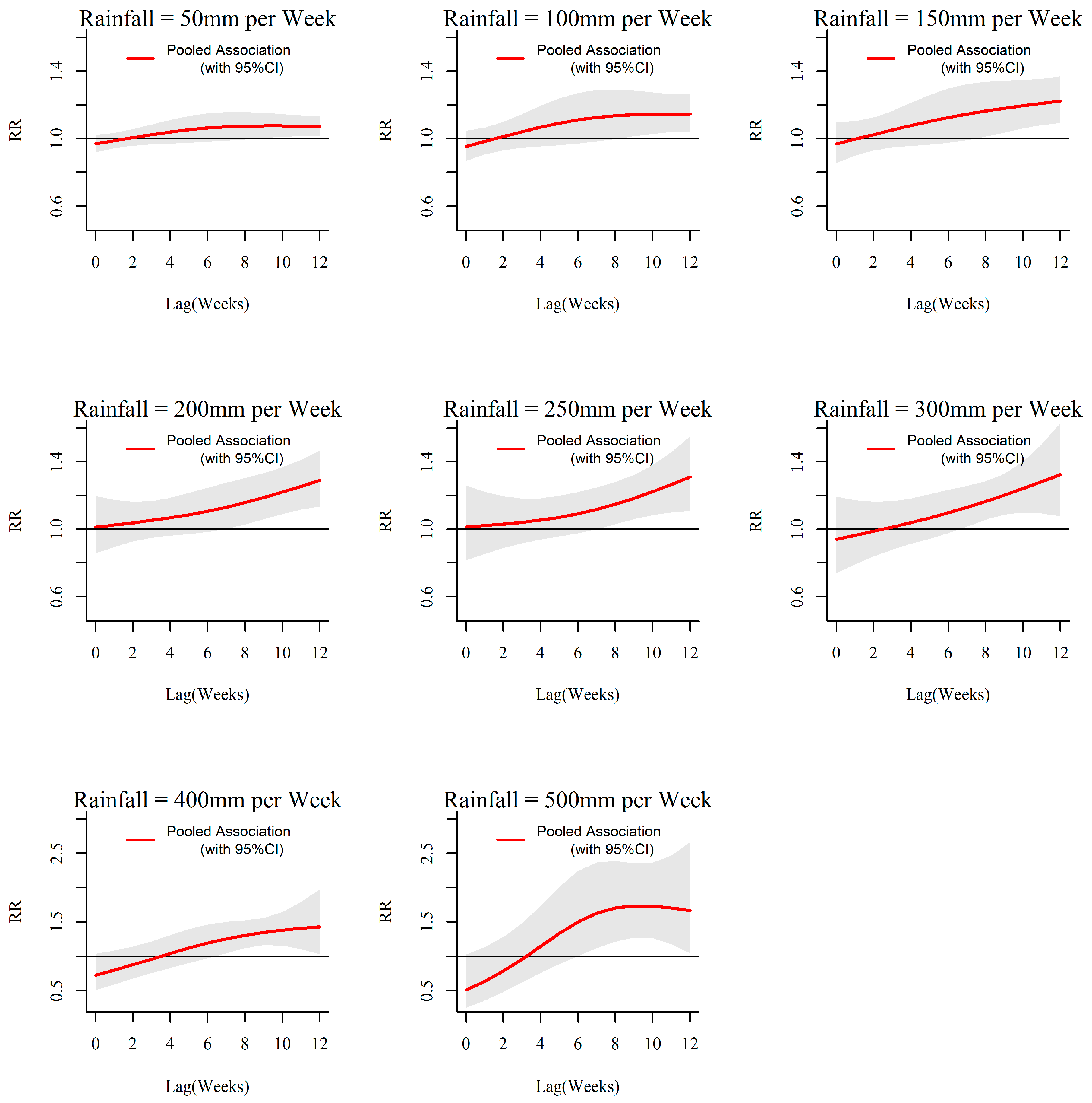
| MOH Division | Land Area (km2) | Population Density (Per km2) | Average Annual Dengue Cases (2009 to 2013) | Average Annual Incidences (Per 100,000 Population) | Weekly Cumulative Precipitation (Range; mm) | Weekly Mean of Evening Temperature (Range; °C) |
|---|---|---|---|---|---|---|
| Panadura | 72 | 3352.4 | 590 | 235.3 | 50.0 (0–508) | 29.43 (25.50–31.55) |
| Matugama | 268 | 507.2 | 179 | 131.7 | 63.2 (0–569) | 29.43 (25.50–31.55) |
| Walallavita | 210 | 279.5 | 126 | 206.3 | 59.6 (0–521) | 29.86 (25.72–33.63) |
| Horana | 110 | 1077.9 | 124 | 108.4 | 53.2 (0–570) | 29.86 (25.72–33.63) |
| Bandaragama | 55 | 2090.5 | 109 | 95.7 | 53.2 (0–570) | 29.43 (25.50–31.55) |
| Ingiriya | 93 | 639.2 | 99 | 168.7 | 77.3 (0–630) | 29.86 (25.72–33.63) |
| Madurawala | 135 | 665.4 | 82 | 92.7 | 52.7 (0–521) | 29.43 (25.50–31.55) |
| Palindanuwara | 270 | 208.0 | 74 | 129.7 | 69.7 (0–460) | 29.86 (25.72–33.63) |
| Bulathsinhala | 210 | 333.8 | 52 | 76.1 | 77.3 (0–630) | 29.86 (25.72–33.63) |
| Agalawatta | 88 | 414.8 | 49 | 121.3 | 52.7 (0–521) | 29.86 (25.72–33.63) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liyanage, P.; Tissera, H.; Sewe, M.; Quam, M.; Amarasinghe, A.; Palihawadana, P.; Wilder-Smith, A.; Louis, V.R.; Tozan, Y.; Rocklöv, J. A Spatial Hierarchical Analysis of the Temporal Influences of the El Niño-Southern Oscillation and Weather on Dengue in Kalutara District, Sri Lanka. Int. J. Environ. Res. Public Health 2016, 13, 1087. https://doi.org/10.3390/ijerph13111087
Liyanage P, Tissera H, Sewe M, Quam M, Amarasinghe A, Palihawadana P, Wilder-Smith A, Louis VR, Tozan Y, Rocklöv J. A Spatial Hierarchical Analysis of the Temporal Influences of the El Niño-Southern Oscillation and Weather on Dengue in Kalutara District, Sri Lanka. International Journal of Environmental Research and Public Health. 2016; 13(11):1087. https://doi.org/10.3390/ijerph13111087
Chicago/Turabian StyleLiyanage, Prasad, Hasitha Tissera, Maquins Sewe, Mikkel Quam, Ananda Amarasinghe, Paba Palihawadana, Annelies Wilder-Smith, Valérie R. Louis, Yesim Tozan, and Joacim Rocklöv. 2016. "A Spatial Hierarchical Analysis of the Temporal Influences of the El Niño-Southern Oscillation and Weather on Dengue in Kalutara District, Sri Lanka" International Journal of Environmental Research and Public Health 13, no. 11: 1087. https://doi.org/10.3390/ijerph13111087
APA StyleLiyanage, P., Tissera, H., Sewe, M., Quam, M., Amarasinghe, A., Palihawadana, P., Wilder-Smith, A., Louis, V. R., Tozan, Y., & Rocklöv, J. (2016). A Spatial Hierarchical Analysis of the Temporal Influences of the El Niño-Southern Oscillation and Weather on Dengue in Kalutara District, Sri Lanka. International Journal of Environmental Research and Public Health, 13(11), 1087. https://doi.org/10.3390/ijerph13111087







