A Method for Formulizing Disaster Evacuation Demand Curves Based on SI Model
Abstract
:1. Introduction
1.1. About the Disaster Evacuation Demand Curve
1.2. Social Influence on Individual Evacuation Decision
1.3. Disaster Evacuation Demand Curve Modeling
1.4. Motivation and Objective of This Study
2. Model Development for Evacuation Demand Curves Estimation Based on SI Model
2.1. Model Framework
2.2. Formulization for Effect of Factors on Disaster Evacuation Demand Curves
2.2.1. Individual Characteristic
2.2.2. Social Influence
Evacuation State Inside the Community
Evacuation State Outside the Community
2.2.3. Geographical Location
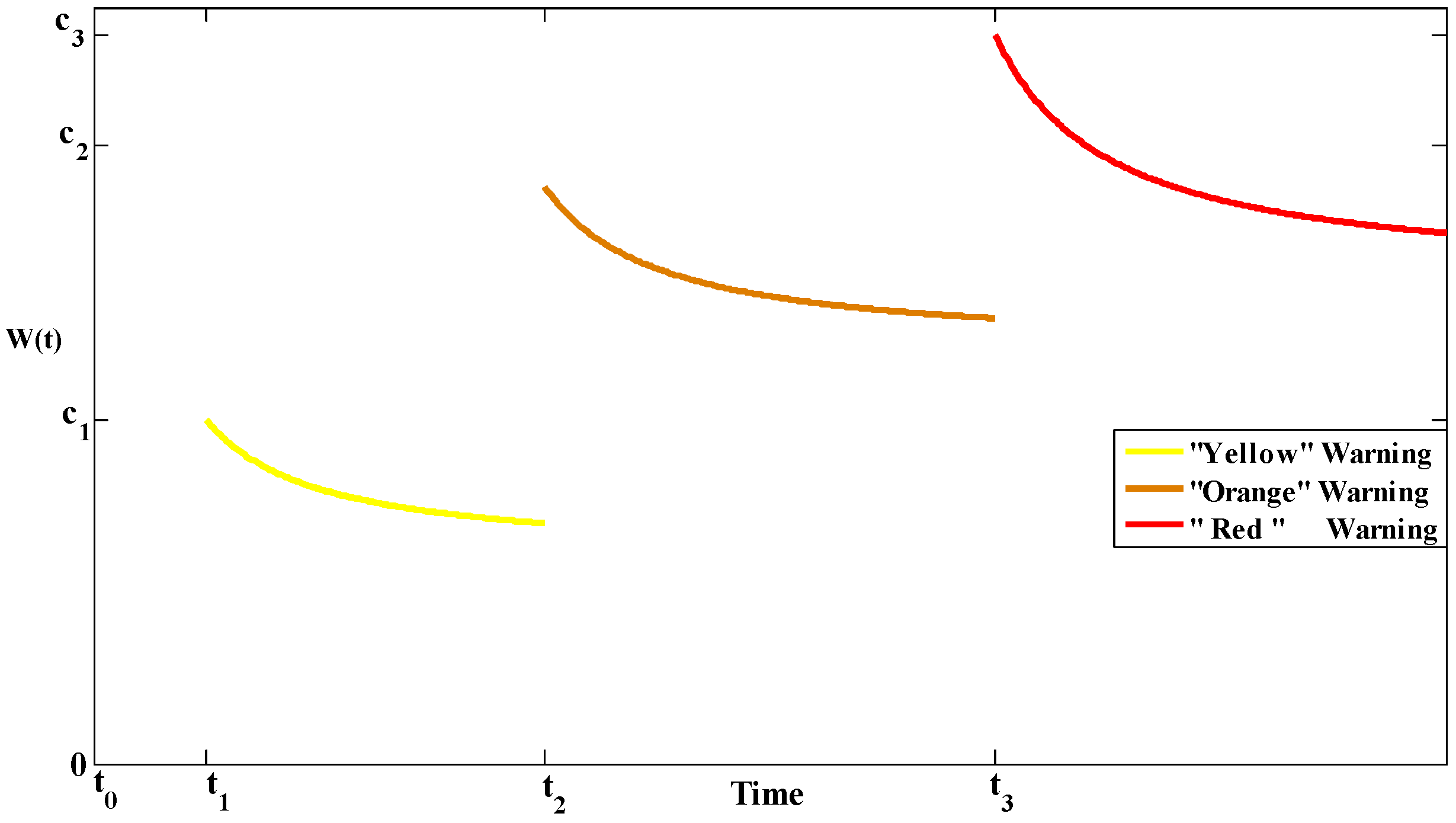
2.2.4. Warning Degree
2.3. The Complete Model for Formulizing a Disaster Evacuation Demand Curve
3. Method for Parameter Sensitivity Analyses
4. Case Study-Tianjin Explosions
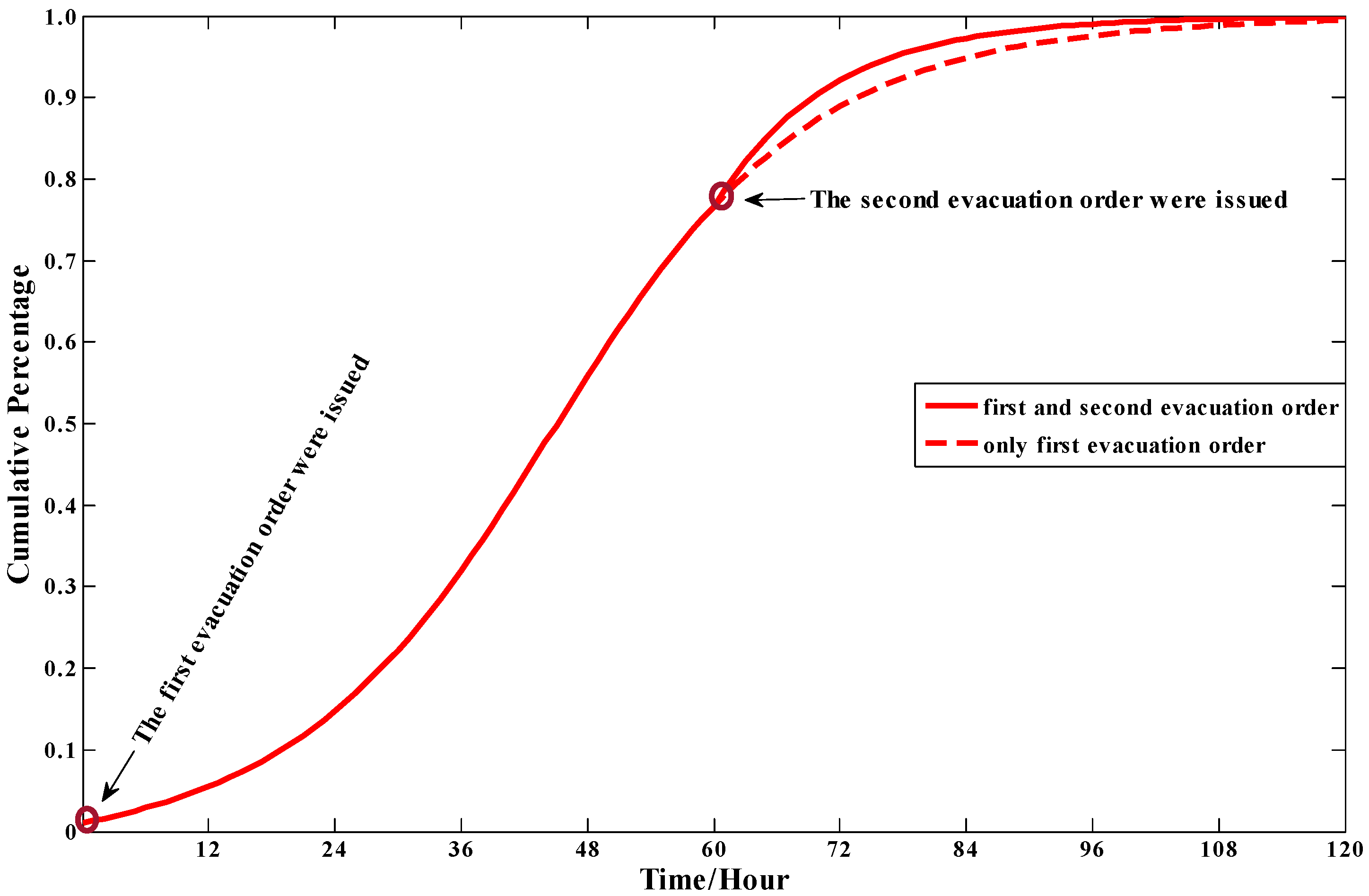
4.1. Tianjin Explosions Description
4.2. Preliminary
4.3. Model Results
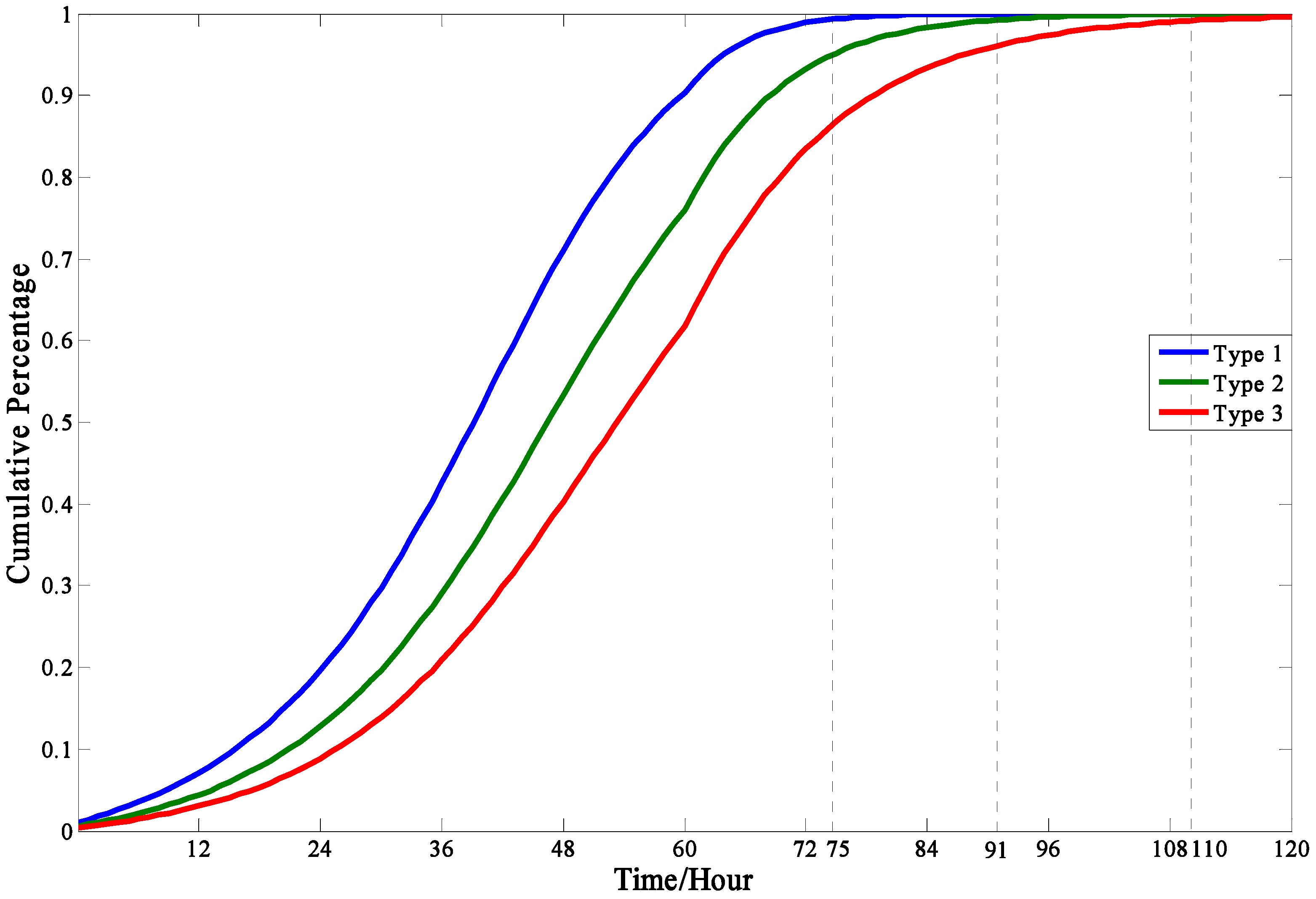
4.3.1. Total Evacuation Demand Curve
4.3.2. Effect of Individual Characteristics
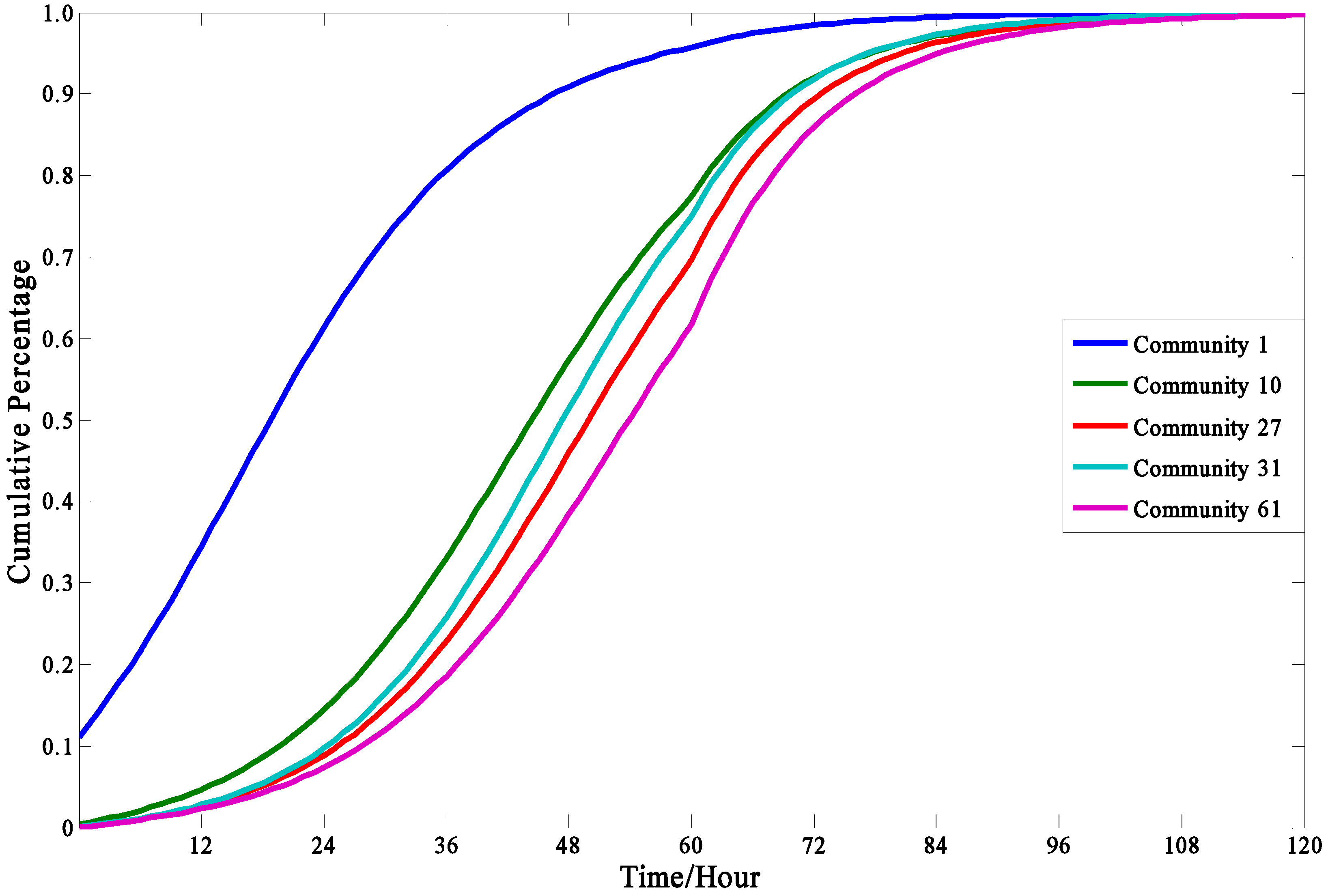
4.3.3. Social Influence and the Effect of Geographic Location
4.3.4. The Effect of Warning Degree
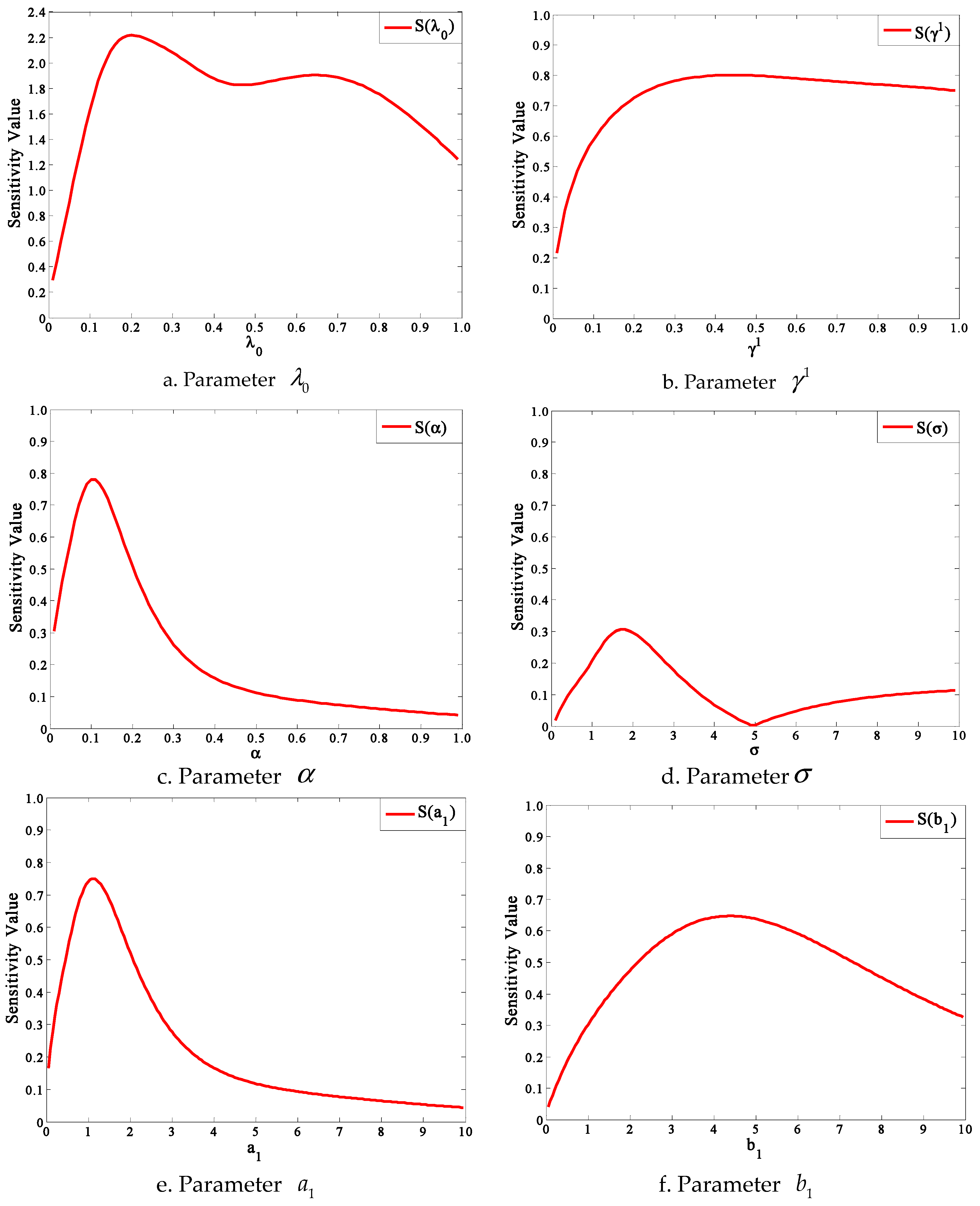
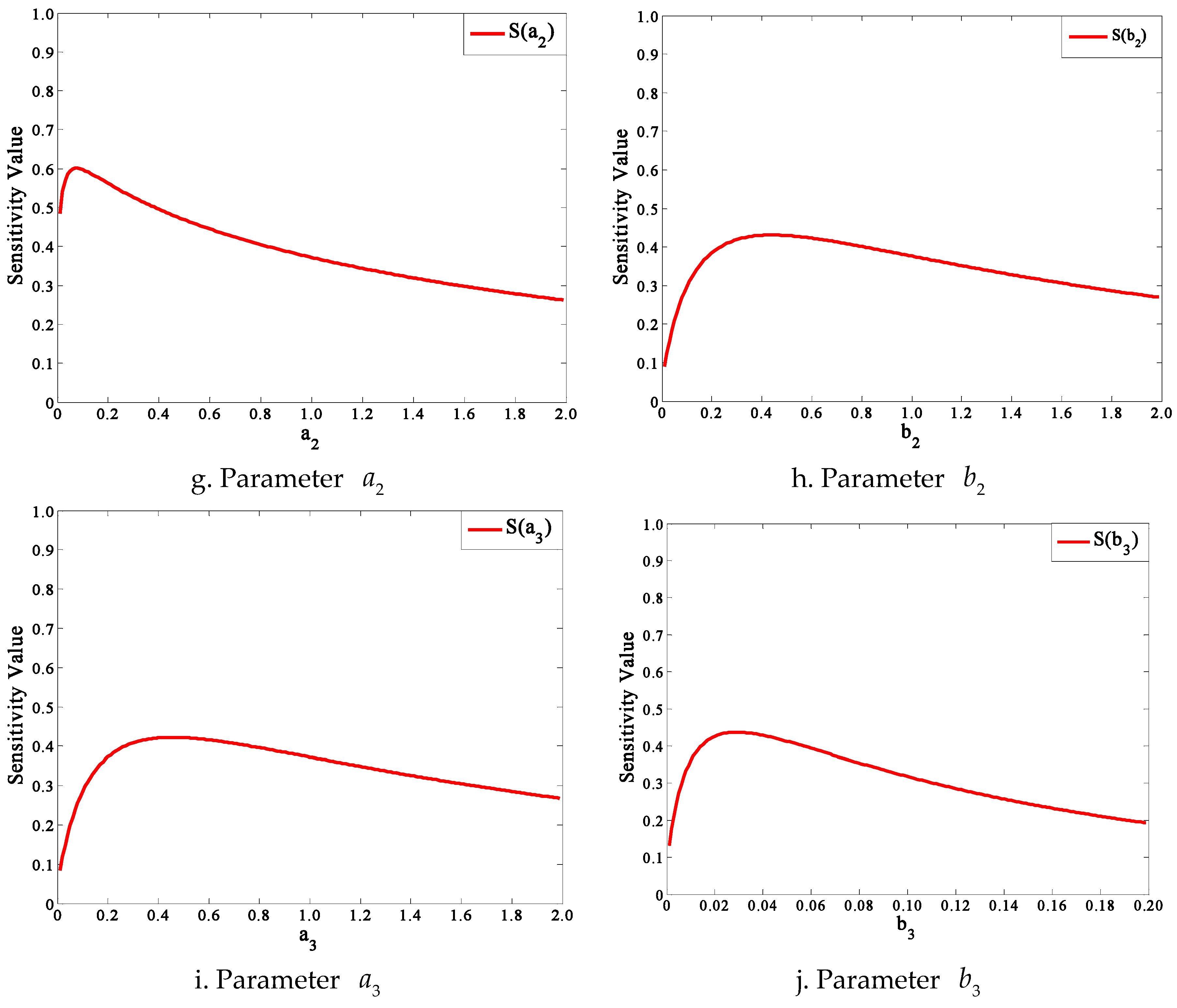
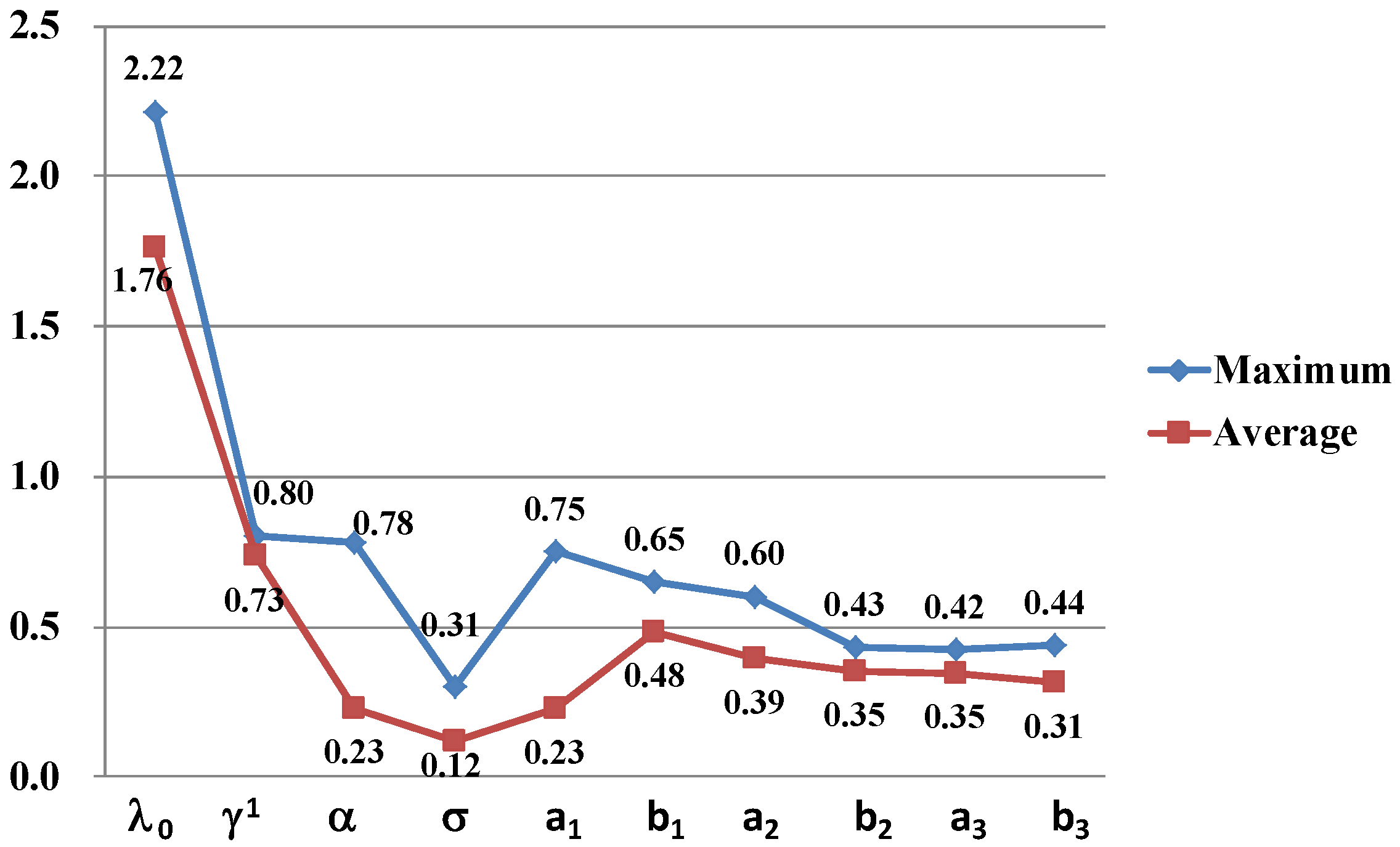
4.4. Sensitivity Analyses
5. Discussion
- The evacuation demand curve in this model is like an S-curve, in which the evacuation demand increasing rate starts increasing slowly, then rapidly, slowly again, and gradually closes to zero. This model result agrees with those obtained in mathematical statistics based on empirical data.
- The individual characteristics can dramatically influence people’s evacuation decision making and the cumulative evacuation demands of the “Impressionable” people are always greater than that of “Neutral” and “Standpat” people.
- The cumulative evacuation demands of people in isolated communities would be less than the communities with many adjacent communities, which can be explained in that the isolated communities lack social influence and people in these areas cannot easily get information on the real-time evacuation state of the society.
- A higher warning degree issued can enhance people′s perceived risk levels so as to significantly increase evacuation demand. Since the influence of warning degrees raised is imposed on the whole people in the risk areas, the authorities can accelerate or slow the evacuation process by changing the warning degree.
- In the sensitivity analyses of parameters, the model is more sensitive to the contact frequency among people over unit time than other parameters. To improve the prediction precision of evacuation demand curves, great attention should be paid to the contact frequency among people.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dixit, V.; Wilmot, C.; Wolshon, B. Modelling Risk Attitudes in Evacuation Departure Choice. Transp. Res. Rec. 2012, 2312, 159–163. [Google Scholar] [CrossRef]
- Madireddy, M.; Kumara, S.; Medeiros, D.J.; Shankar, V.N. Leveraging social networks for efficient hurricane evacuation. Transp. Res. 2014, 77, 199–212. [Google Scholar] [CrossRef]
- CNN.com. CNN Live at Daybreak: Escaping a Hurricane. 2001. Available online: http://edition.cnn.com/TRANSCRIPTS/ (accessed on 21 October 2015).
- National Research Council (U.S.); Transportation Research Board; Committee on the Role of Public Transportation in Emergency Evacuation. The Role of Transit in Emergency Evacuation Special Report; Transportation Research Board: Washington, DC, USA, 2008. [Google Scholar]
- Baker, E.J. Predicting Response to Hurricane Warnings: A Reanalysis of Data from Four Studies. Mass Emerg. 1979, 4, 9–24. [Google Scholar]
- Ozbay, K.; Yazici, A. Analysis of Network-wide Impacts of Behavioral Response Curves for Evacuation Conditions. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 15 September 2006.
- Li, J.; Ozbay, K.; Bartin, B.; Iyer, S.; Carnegie, J. Empirical Evacuation Response Curve during Hurricane Irene in Cape May County, New Jersey. Transp. Res. Rec. 2013. [Google Scholar] [CrossRef]
- Banerjee, A.V. A Simple Model of Herd Behavior. Q. J. Econ. 1992, 107, 797–817. [Google Scholar] [CrossRef]
- Hasan, S.; Ukkusuri, S.V. A threshold model of social contagion process for evacuation decision making. Transp. Res. 2011, 45, 1590–1605. [Google Scholar] [CrossRef]
- Murray-Tuite, P.; Wolshon, B. Evacuation transportation modeling: An overview of research, development, and practice. Transp. Res. Part C. 2013, 27, 25–45. [Google Scholar] [CrossRef]
- Hurricane Andrew: Ethnicity, Gender, and the Sociology of Disasters; Gladwin, H. (Ed.) International Hurricane Center: Miami, FL, USA, 1997; pp. 52–72.
- Bateman, J.M.; Edwards, B. Gender and evacuation: A closer look at why women are more likely to evacuate for hurricanes. Nat. Hazards Rev. 2002, 3, 107–117. [Google Scholar] [CrossRef]
- Elliott, J.R.; Pais, J. Race, class, and Hurricane Katrina: Social differences in human responses to disaster. Soc. Sci. Res. 2006, 35, 295–321. [Google Scholar] [CrossRef]
- Baker, E.J. Hurricane evacuation behavior. Int. J. Mass Emerg. Disasters 1991, 9, 287–310. [Google Scholar]
- Dixit, V.; Pande, A.; Radwan, E.; Abdel-Aty, M. Understanding the Impact of a Recent Hurricane on Mobilization Time during a Subsequent Hurricane. Transp. Res. Rec. 2008, 2041, 49–57. [Google Scholar] [CrossRef]
- Arlikatti, S.; Lindell, M.K.; Prater, C.S.; Zhang, Y. Risk area accuracy and hurricane evacuation expectations of coastal residents. Environ. Behav. 2006, 38, 226–247. [Google Scholar] [CrossRef]
- Dixit, V.; Montz, T.; Wolshon, B. Validation Techniques for Region-Level Microscopic Mass Evacuation Traffic Simulations. Transp. Res. Rec. 2011. [Google Scholar] [CrossRef]
- Bourque, L.B.; Reeder, L.G.; Cherlin, A.; Raven, B.H.; Walton, D.M. The Unpredictable Disaster in a Metropolis: Public Response to the Los Angeles Earthquake of February; UCLA Survey Research Center: Washington, DC, USA, 1971. [Google Scholar]
- Cutter, S.; Barnes, K. Evacuation behavior and Three Mile Island. Disasters 1982, 6, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Vaughan, E. The significance of socioeconomic and ethnic diversity for the risk communication process. Risk Anal. 1995, 15, 169–180. [Google Scholar] [CrossRef]
- Lindell, M.K.; Perry, R.W. Communicating Environmental Risk in Multiethnic Communities; Sage Publications Inc.: Thousand Oaks, CA, USA, 2004. [Google Scholar]
- Lindell, M.K.; Perry, R.W. The protective action decision model: Theoretical modifications and additional evidence. Risk Anal. 2012, 32, 616–632. [Google Scholar] [CrossRef] [PubMed]
- Horney, J.A.; MacDonald, P.D.M.; Berk, P.; Willigen, V.; Kaufman, J.S. Factors Associated with Hurricane Evacuation in North Carolina. In Recent Hurricane Research—Climate, Dynamics, and Societal Impacts; InTech: Rijeka, Croatia, 2011. [Google Scholar]
- Lindell, M.; Prater, C.; Perry, R.; Wu, J.Y. Emblem: An empirically based large-scale evacuation time estimate model. Transp. Res. 2008, 42, 140–154. [Google Scholar]
- Hui, C.; Goldberg, M.; Magdon-ismail, M.; Wallace, W.A.; Systems, E.; Networks, D. Agent-based simulation of the diffusion of warnings. In Proceedings of the 2010 Spring Simulation Multiconference (SpringSim), Orlando, FL, USA, 11–15 April 2010.
- Bikhchandani, S.; Hirshleifer, D.; Welch, I.A. Theory of Fads, Fashion, Custom, and Cultural Change as Informational Cascades. J. Polit. Econ. 1992, 100, 992–1026. [Google Scholar] [CrossRef]
- Hirshleifer, D.; Teoh, S.H. Herd behavior and cascading in capital markets: A review and synthesis (PDF). Eur. Financ. Manag. 2003, 9, 25–66. [Google Scholar] [CrossRef]
- Perry, R.W. Citizen Evacuation in Response to Nuclear and Non-Nuclear Threats. Available online: http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA105812 (accessed on 10 October 2015).
- Quarantelli, E. Social Support Systems: Some Behavioral Patterns in the Context of Mass Evacuation Activities. Available online: http://udspace.udel.edu/handle/19716/1120 (accessed on 16 September 2016).
- Riad, J.K.; Norris, F.H.; Ruback, R.B. Predicting evacuation in two major disasters: Risk perception, social influence, and access to resources. J. Appl. Soc. Psychol. 1999, 29, 918–934. [Google Scholar] [CrossRef]
- Lindell, M.K.; Perry, R.W. Warning mechanisms in emergency response systems. Int. J. Mass Emerg. Disasters 1987, 5, 137–153. [Google Scholar]
- Zeigler, D.J.; Brunn, S.D.; Johnson, J.H., Jr. Evacuation from a nuclear technological disaster. Geogr. Rev. 1981, 71, 1–16. [Google Scholar] [CrossRef]
- Yazici, M.A.; Ozbay, K. Evacuation modelling in the United States: Does the demand model choice matter? Trans. Rev. 2008, 28, 757–779. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Daley, D.J.; Kendall, D.G. Stochastic rumors. IMA J. Appl. Math. 1965, 1, 42–55. [Google Scholar] [CrossRef]
- Maki, D.P.; Thompson, M. Mathematical Models and Applications, with Emphasis on Social, Life, and Management Sciences; Prentice-Hall: Englewood Cliffs, NJ, USA, 1973. [Google Scholar]
- Urbanik, T. Texas Hurricane Evacuation Study. Texas Transportation Institute: College Station, TX, USA, 1978; Available online: https://repositories.tdl.org/tamug-ir/handle/1969.3/26395 (accessed on 8 April 2016).
- Lewis, D.C. Transportation Planning for Hurricane Evacuations. ITE J. 1985, 55, 31–35. [Google Scholar]
- Radwan, A.; Hobeika, A.; Sivasailam, D. A Computer Simulation Model for Rural Network Evacuation under Natural Disasters. ITE J. 1985, 55, 25–30. [Google Scholar]
- Baker, E.J. Hurricane Evacuation in the United States; Pielke, R.A., Jr., Pielke, R.A., Sr., Eds.; Routledge Press: London, UK, 2000; Volume 1, pp. 306–319. [Google Scholar]
- Sorensen, J. Hazard warning systems: Review of 20 years of progress. Nat. Hazards Rev. 2000, 1, 119–125. [Google Scholar] [CrossRef]
- Fu, H. Development of Dynamic Travel Demand Models for Hurricane Evacuation. Ph.D. Thesis, Louisiana State University, Baton Rouge, LA, USA, 2004. [Google Scholar]
- Fu, H.; Wilmot, C. Dynamic Travel Demand Model for Hurricane Evacuation; Transportation Research Board of the National Academies: Washington, DC, USA, 2004. [Google Scholar]
- Fu, H.; Wilmot, C.; Zhang, H.; Baker, E. Modeling the Hurricane Evacuation Response Curve. Transp. Res. Rec. 2007. [Google Scholar] [CrossRef]
- Perry, R.W.; Lindell, M.K. The effects of ethnicity on evacuation decision-making. Int. J. Mass Emerg. Disasters 1991, 9, 47–68. [Google Scholar]
- Newman, M.E. The structure and function of complex networks. SIAM Rev. 2003, 45, 167–256. [Google Scholar] [CrossRef]
- Nagarajan, M.; Shaw, D.; Albores, P. Informal dissemination scenario and the effectiveness of evacuation warning dissemination of households—A simulation study. Procedia Eng. 2010, 3, 139–152. [Google Scholar] [CrossRef]
- National Steering Committee on Public Warning and information—NSCPWI: Third Interim Report. 2003. Available online: https://www.gov.uk/government/groups/national-steering-committee-on-warning-informing-the-public (accessed on 8 April 2016).
- Sina News. Tianjin Explosions Live Reports. Beijing. Available online: http://news.sina.com.cn/c/2015-08-13/064632198536.shtm (accessed on 16 August 2015).
- Jiang, Q.Y.; Xie, J.X.; Ye, J. Mathematical Models; Higher Education Press: Beijing, China, 2011; pp. 136–180. [Google Scholar]
- Perry, R.W. Evacuation decision-making in natural disasters. Mass Emerg. 1979, 4, 25–38. [Google Scholar]
- Wilmot, C.G.; Mei, B. Comparison of alternative trip generation models for Hurricane evacuation. Nat. Hazards Rev. 2004, 5, 170–178. [Google Scholar] [CrossRef]
- Pel, A.J.; Bliemer, M.C.J.; Hoogendoorn, S.P. A review on travel behavior modelling in dynamic traffic simulation models for evacuations. Transportation 2012, 39, 97–123. [Google Scholar] [CrossRef]



| Parameter | ||||||
| Value | 0.25 | 0.5 0.3 0.2 | 0.01 1 | 1 0.1 | 0.01 0.01 | 0.01 0.001 0.2 0.01 |
| Community | Distance to the Explosion Source (km) | Surrounding Community |
|---|---|---|
| 1 | 0.67 | 2, 4 |
| 10 | 2.06 | 8, 9, 16 |
| 27 | 4.12 | 41 |
| 31 | 4.21 | 23, 30, 38, 48, 50 |
| 61 | 6.10 | 60 |
| Parameter | Basic Reference Value | Value Range | Maximum Sensitivity | Average Sensitivity |
|---|---|---|---|---|
| 0.25 | (0–1) | 2.2165 | 1.7619 | |
| 0.5 | (0–1) | 0.8012 | 0.7344 | |
| 0.1 | (0–10) | 0.7795 | 0.2301 | |
| 1 | (0–10) | 0.3051 | 0.1168 | |
| 0.1 | (0–10) | 0.7493 | 0.2281 | |
| 0.1 | (0–10) | 0.6477 | 0.4832 | |
| 0.1 | (0–2) | 0.6005 | 0.3940 | |
| 0.02 | (0–2) | 0.4308 | 0.3522 | |
| 0.1 | (0–2) | 0.4224 | 0.3470 | |
| 0.002 | (0–0.2) | 0.4371 | 0.3131 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Y.; Yan, X. A Method for Formulizing Disaster Evacuation Demand Curves Based on SI Model. Int. J. Environ. Res. Public Health 2016, 13, 986. https://doi.org/10.3390/ijerph13100986
Song Y, Yan X. A Method for Formulizing Disaster Evacuation Demand Curves Based on SI Model. International Journal of Environmental Research and Public Health. 2016; 13(10):986. https://doi.org/10.3390/ijerph13100986
Chicago/Turabian StyleSong, Yulei, and Xuedong Yan. 2016. "A Method for Formulizing Disaster Evacuation Demand Curves Based on SI Model" International Journal of Environmental Research and Public Health 13, no. 10: 986. https://doi.org/10.3390/ijerph13100986
APA StyleSong, Y., & Yan, X. (2016). A Method for Formulizing Disaster Evacuation Demand Curves Based on SI Model. International Journal of Environmental Research and Public Health, 13(10), 986. https://doi.org/10.3390/ijerph13100986






